DOA Estimation and Self-Calibration under Unknown Mutual Coupling
Abstract
:1. Introduction
- (1)
- Time-frequency analysis is utilized to solve the problem of direction-dependent mutual coupling in proposed approach.
- (2)
- Compared with the existing algorithms, the proposed method is improved in estimation accuracy and robustness against mutual coupling.
- (3)
- The proposed method can achieve DOA estimation under multipath or underdetermined conditions.
2. Models and Methods
2.1. Array Signal Model
2.2. Method of DOA and MC Coefficients Estimation
2.2.1. Steering Vector Estimation Based on TFDs
- Step 1:
- Remove the noise: In order to reduce the computation burden and improve the estimation accuracy, it is necessary to set an appropriate threshold to remove the TF points with low energy which may be generated by noise. For each time slice , apply Equation (12) for all frequency points in this slice, and then the TF points with large energy remain:where is a small positive real number and represents the operator of 2-norm.
- Step 2:
- Extract the TF points of self-term: After removing the noise points, the retaining TF points mainly include self-term TF points and cross-term TF points. At the self-term TF points, the STFDs matrix is approximately diagonal, and the values of the principal diagonal elements are much larger than those of the other elements, so the STFDs matrix at self-term TF points yields:where is a positive real number close to but less than 1.
- Step 3:
- Extract the TF points of single-source self-term: For signals which overlap in time-frequency domain, the self-term TF points may be composed of multiple signals. Therefore, it is necessary to extract the single-source self-term TF points from the self-term TF points, which can be accomplished by Equation (14):where is a small positive real threshold and is the largest eigenvalue of .With the three steps above, the single-source self-term TF points are obtained. Then the steering vectors of each signal as well as the noise subspace could be estimated by the eigen-decomposition of their STFDs matrix. However, the above derivation is completed without considering the noise. In the presence of noise, the steering vectors estimated by only a few TF points are biased. Therefore, it is necessary to obtain more accurate information by clustering the multiple single-source self-term TF points of the same signal. A time-frequency clustering method is provided in Step 4.
- Step 4:
- Cluster the TF points of the same signal: The steering vector of each signal can be estimated as the principal eigenvector of STFDs matrix at each TF point. Regarding the steering vector which contains the DOA information as a feature, all self-term TF points can be classified into Q(Q≥K) categories by the classification algorithm. That is to say, if the following conditions are satisfied, TF points of belong to the same category:where d(x,y) is the Euclidean distance between x and y, and is a small positive threshold.
2.2.2. DOA and MC Coefficients Estimation
2.3. Algorithmic Analysis
- 1)
- For the selection of the TFD kernel function, it is known that different TFD kernel functions correspond to different TFD transforms, which can be divided into linear time-frequency transforms and quadratic time-frequency transforms. The Wigner-Ville distribution (WVD) is one of the quadratic TFDs that has better performance in TF focusing and resolution. These two elements are significant in the extraction and clustering of TF points. However, due to the interaction between different signals, cross-terms are generated, which cause false time-frequency information and degrade the estimation accuracy. Therefore, the smoothed pseudo-Wigner-Ville distribution (SPWVD) is utilized to suppress the cross-terms between signals by windowing method in this paper. Similarly, the short-time Fourier transform (STFT) can also provide the accurate time-frequency distribution to solve the problem and we should choose the kernel function flexibly for the different conditions.
- 2)
- This algorithm aims at the estimation of direction-dependent MC, but it is also applicable in the presence of a single MC. The single MC coefficients can be obtained by averaging the estimated MC coefficients of different directions.
- 3)
- The algorithm is based on the condition that the TFDs of the signals do not completely overlap, otherwise the blind separation will not be effective. This condition is easy to be obtained in practice. Even the coherent signals (co-frequency interference or multipath signals with different arrival time due to different propagation paths) has different TFDs. Therefore, the proposed algorithm is also effective for coherent signals with different arrival times.
- 4)
- This algorithm is able to estimate DOA and MC coefficients under undetermined conditions. That means, the algorithm is still effective when the number of array elements is less than the number of signals. This is because the steering vectors of each signal can be estimated using TFDs, which is similar to estimating the DOA and MC coefficients of each signal separately.
- 5)
- For the selection of empirical parameters, we find that is the threshold for noise points removing which depends on the ratio between the power of noise and signals. The lager the ratio is, the larger should be. However, the power of noise distributes in the whole TF domain uniformly while the power of signals mainly distributes on a few TF points. Therefore, the noise to signal ratio is small in general. Usually we set in this paper. is the threshold for the self-term TF points extraction which approaches to 1 and in this paper. is a small positive threshold for the single-source TF points extraction and is fixed at in this paper. is set to cluster the TF points into categories and we set .
3. Numerical Simulation
3.1. Calibration Results of Proposed Algorithm
3.2. RMSE Comparison versus Input Signal-Noise-Ratio (SNR)
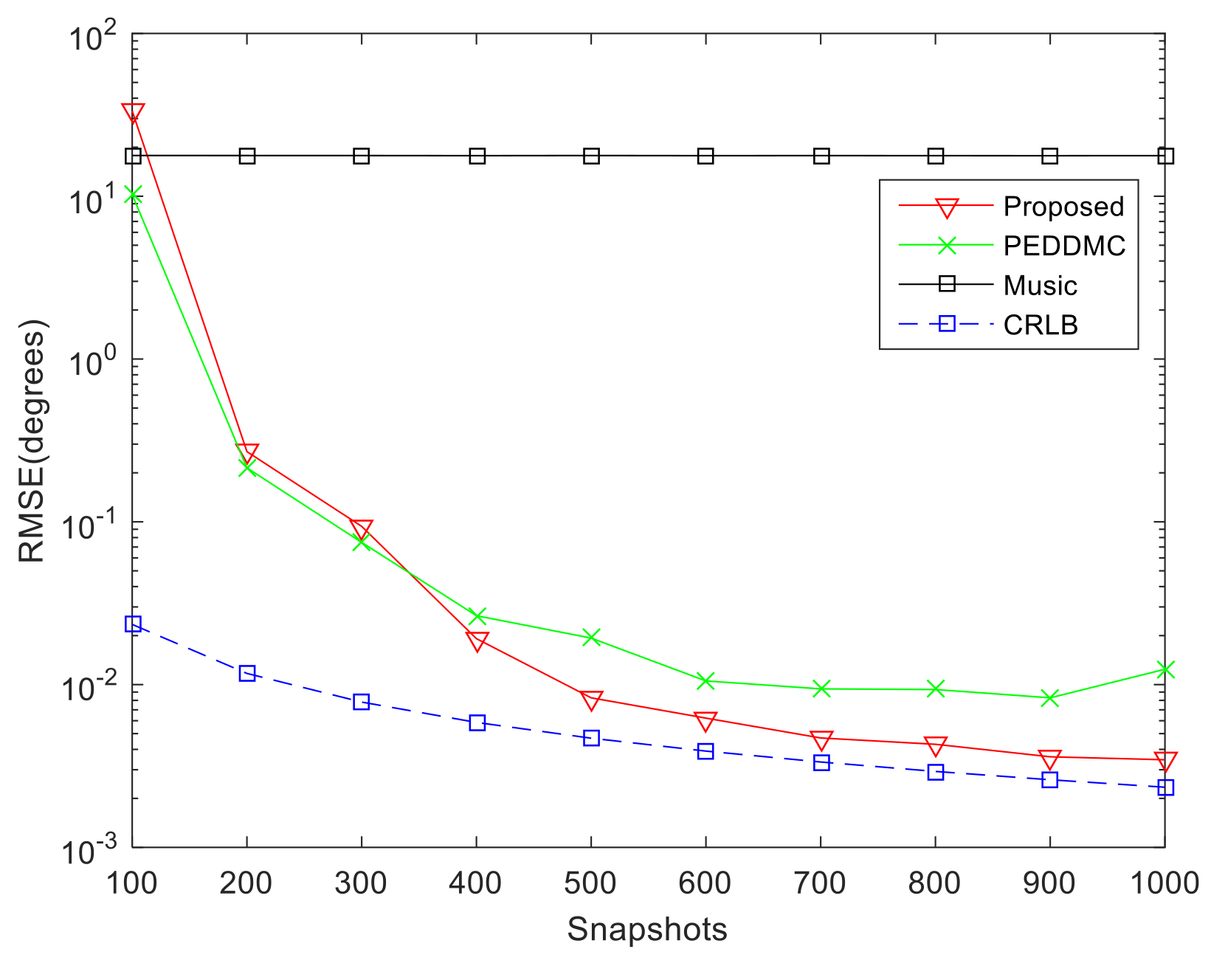
3.3. RMSE Comparison versus Input Snapshots
4. Conclusions
5. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zheng, G.; Feng, C.; Tang, J. ESPRIT-Like Two-Dimensional DOA Estimation for Monostatic MIMO Radar with Electromagnetic Vector Received Sensors under the Condition of Gain and Phase Uncertainties and Mutual Coupling. Sensors 2017, 17, 2457. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, R.; Zhao, Y. A Bias Compensation Method for Distributed Moving Source Localization Using TDOA and FDOA with Sensor Location Errors. Sensors 2018, 18, 3747. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Zhang, Y.; Lin, J.; Guo, R.; Chen, Z. Wideband Direction of Arrival Estimation in the Presence of Unknown Mutual Coupling. Sensors 2017, 17, 230. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yang, L.; Yang, S. Robust Joint Calibration of Mutual Coupling and Channel Gain/Phase Inconsistency for Uniform Circular Array. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1191–1195. [Google Scholar] [CrossRef]
- Hou, Y.; Wen, B.; Tian, Y.; Yang, J. A uniform linear array self-calibration method for UHF river flow detection radar. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1899–1902. [Google Scholar] [CrossRef]
- Friedlander, B.; Weiss, A.J. Direction finding in the presence of mutual coupling. IEEE Trans. Antennas Propag. 1991, 39, 273–284. [Google Scholar] [CrossRef]
- Xie, J.L.; He, Z.S.; Li, H.Y. A fast DOA estimation algorithm for uniform circular arrays in the presence of unknown mutual coupling. Prog. Electromagn. Res. C 2011, 21, 257–271. [Google Scholar] [CrossRef]
- Wang, M.; Ma, X.C.; Yan, S.F.; Hao, C. An auto-calibration algorithm for uniform circular array with unknown mutual coupling. IEEE Antennas Wirel. Propag. Lett. 2015, 5, 315–318. [Google Scholar]
- Dai, J.S.; Bao, X.; Hu, N.; Chang, C.; Xu, W. A recursive RARE algorithm for DOA estimation with unknown mutual coupling. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1593–1596. [Google Scholar]
- Wang, H. An Efficient Algorithm for Direction Finding against Unknown Mutual Coupling. Sensors 2014, 14, 20064–20077. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wang, W.; Gu, Y.; Lei, S. Underdetermined DOA Estimation of Quasi-Stationary Signals Using a Partly-Calibrated Array. Sensors 2017, 17, 702. [Google Scholar] [CrossRef] [PubMed]
- Kraus, J.D.; Marhefka, R.J. Antennas for All Applications; McGraw: New York, NY, USA, 2002. [Google Scholar]
- Wang, B.H.; Hui, H.T.; Leong, M.S. Decoupled 2D Direction of Arrival Estimation Using Compact Uniform Circular Arrays in the Presence of Elevation-Dependent Mutual Coupling. IEEE Trans. Antennas Propag. 2010, 58, 747–755. [Google Scholar] [CrossRef]
- Hui, H.T. Improved compensation for the mutual coupling effect in a dipole array for direction finding. IEEE Trans. Antennas Propag. 2003, 51, 2498–2503. [Google Scholar] [CrossRef]
- Elbir, A. Direction Finding in the Presence of Direction-Dependent Mutual Coupling. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1541–1544. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Zhao, Y.; Zhu, J. Wideband array self-calibration and DOA estimation under large position errors. Digit. Signal Process. 2018, 78, 250–258. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Jing, F. Underdetermined Blind Source Separation of Synchronous Orthogonal Frequency Hopping Signals Based on Single Source Points Detection. Sensors 2017, 17, 2074. [Google Scholar] [CrossRef] [PubMed]



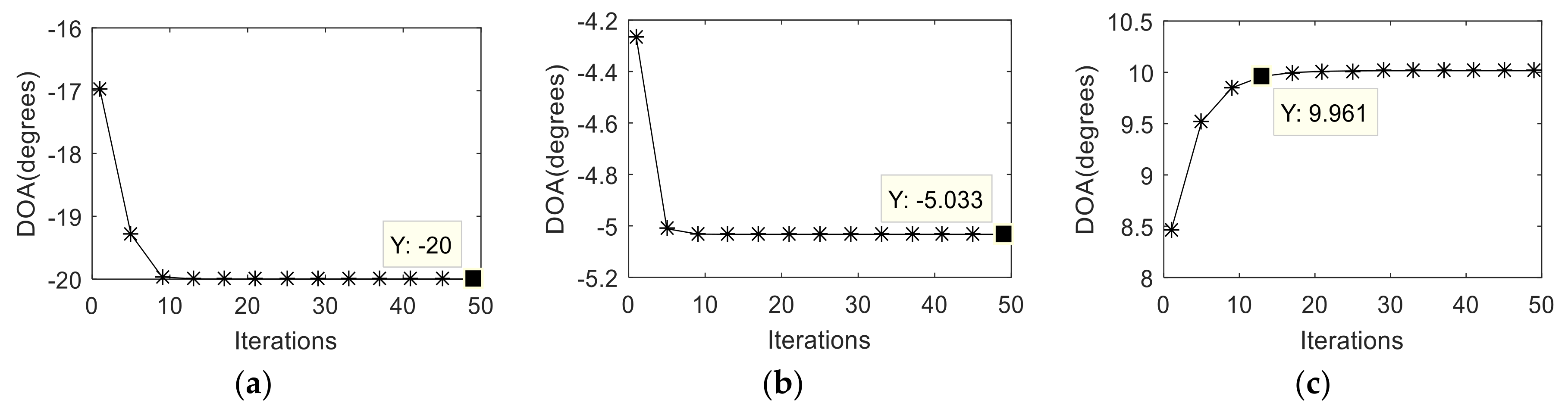
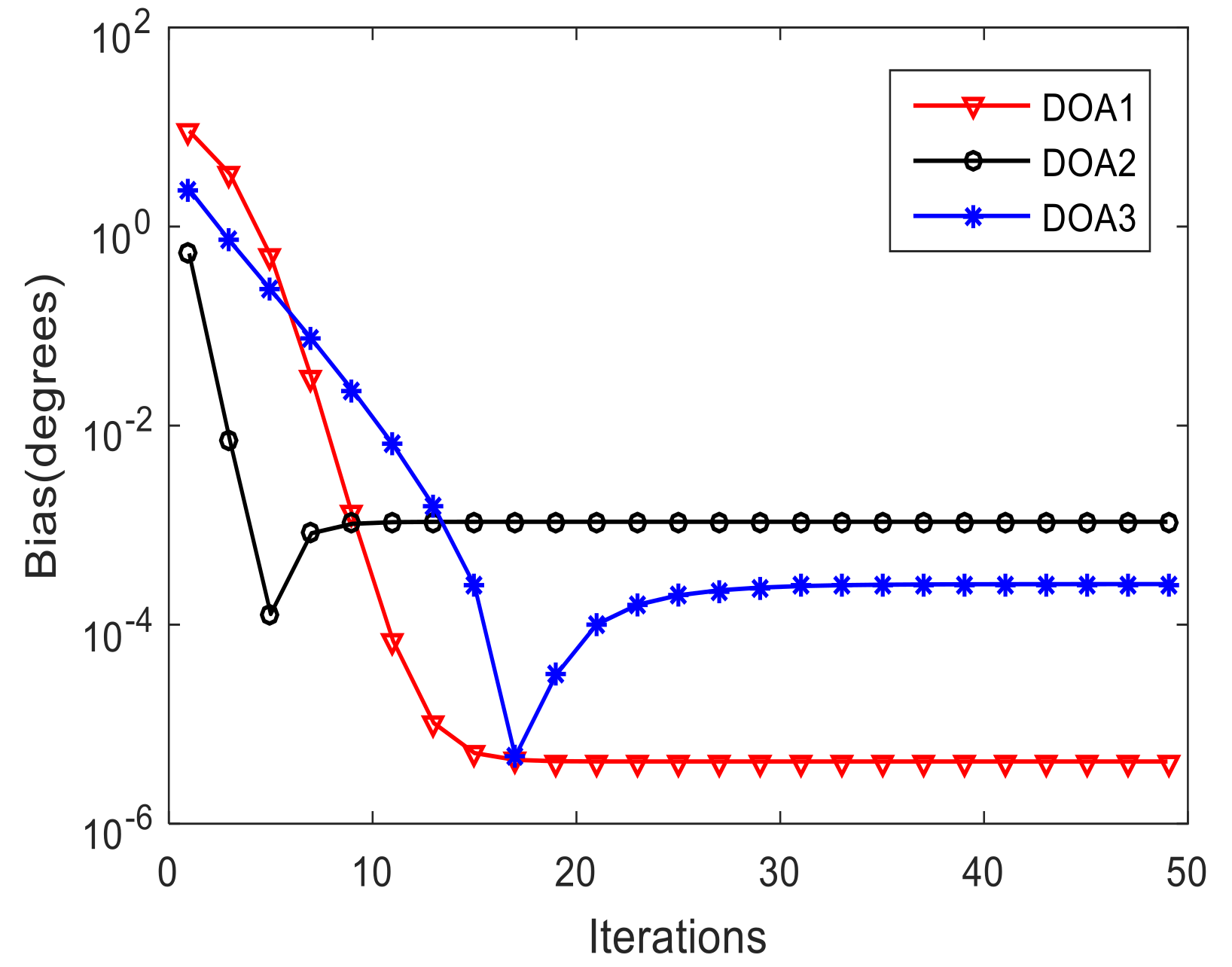
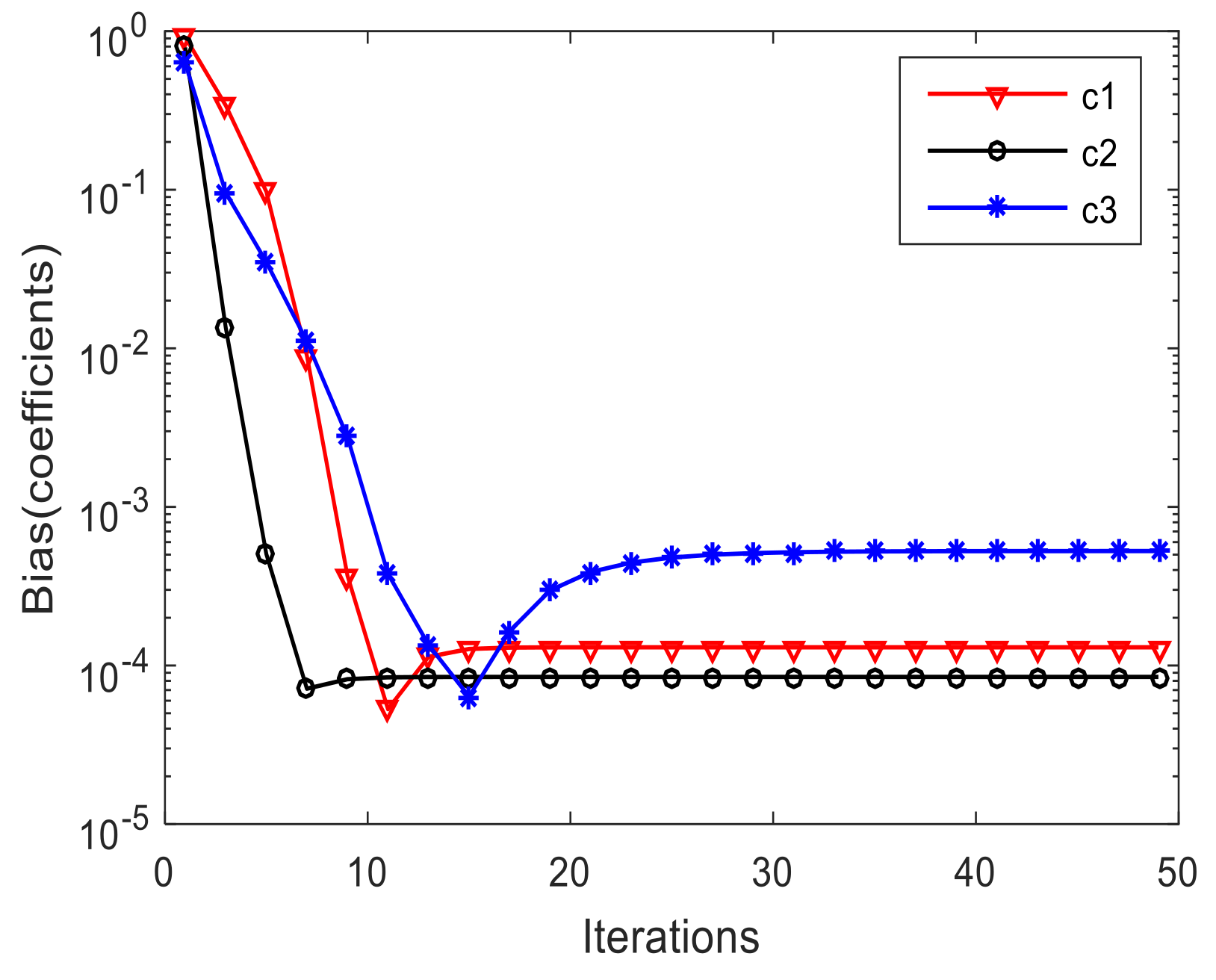

| Step 1. Collect N snapshots and calculate the STFDs of received signal with (9). |
| Step 2. Extract the single source TF points based on (12)–(14). |
| Step 3. Cluster the single source TF points into Q(Q≥K) categories using (15). |
| Step 4. Estimate and of each signal with the K largest classes. |
| Step 5. Construct the transformation matrix with . |
| Step 6. Estimate the MC coefficients based on Equations (22) and (23). |
| Step 7. Construct the MC matrix using the new MC coefficients and estimate the DOAs using (24). |
| Step 8. Repeat Step 5 to Step 7 until the estimation errors is less than the threshold or the iterations have been repeated for certain times. |
| Parameters | LFM Signal 1 | LFM Signal 2 | LFM Signal 3 |
|---|---|---|---|
| Frequency | 500 MHz–515 MHz | 515 MHz–500 MHz | 525 MHz–510 MHz |
| DOA | |||
| Snapshots | 512 | 512 | 512 |
| SNR | |||
| MC coefficients |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, D.; Tang, M.; Chen, S.; Liu, Z.; Zhao, Y. DOA Estimation and Self-Calibration under Unknown Mutual Coupling. Sensors 2019, 19, 978. https://doi.org/10.3390/s19040978
Qi D, Tang M, Chen S, Liu Z, Zhao Y. DOA Estimation and Self-Calibration under Unknown Mutual Coupling. Sensors. 2019; 19(4):978. https://doi.org/10.3390/s19040978
Chicago/Turabian StyleQi, Dong, Min Tang, Shiwen Chen, Zhixin Liu, and Yongjun Zhao. 2019. "DOA Estimation and Self-Calibration under Unknown Mutual Coupling" Sensors 19, no. 4: 978. https://doi.org/10.3390/s19040978
APA StyleQi, D., Tang, M., Chen, S., Liu, Z., & Zhao, Y. (2019). DOA Estimation and Self-Calibration under Unknown Mutual Coupling. Sensors, 19(4), 978. https://doi.org/10.3390/s19040978





