Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview
Abstract
1. Introduction
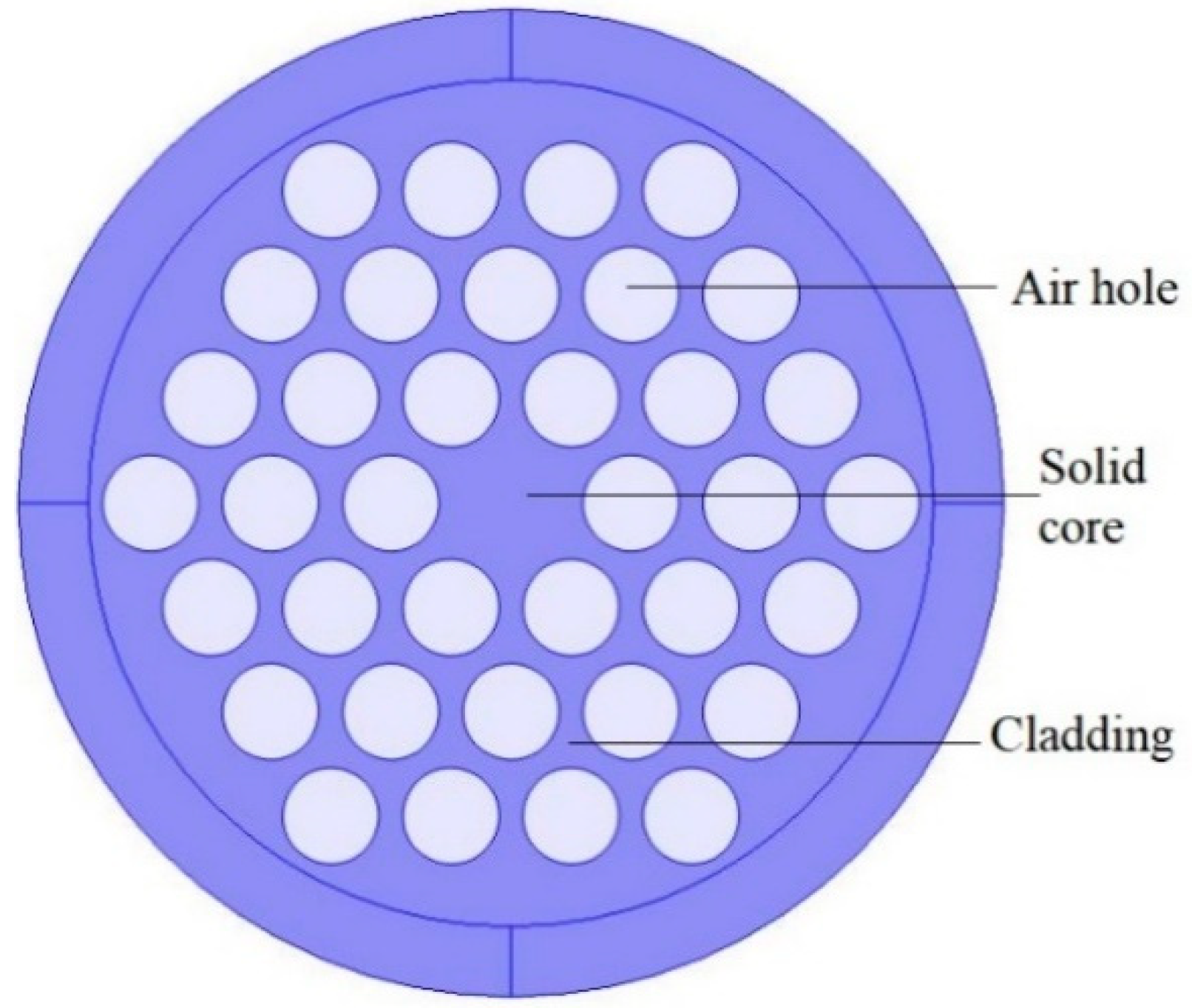
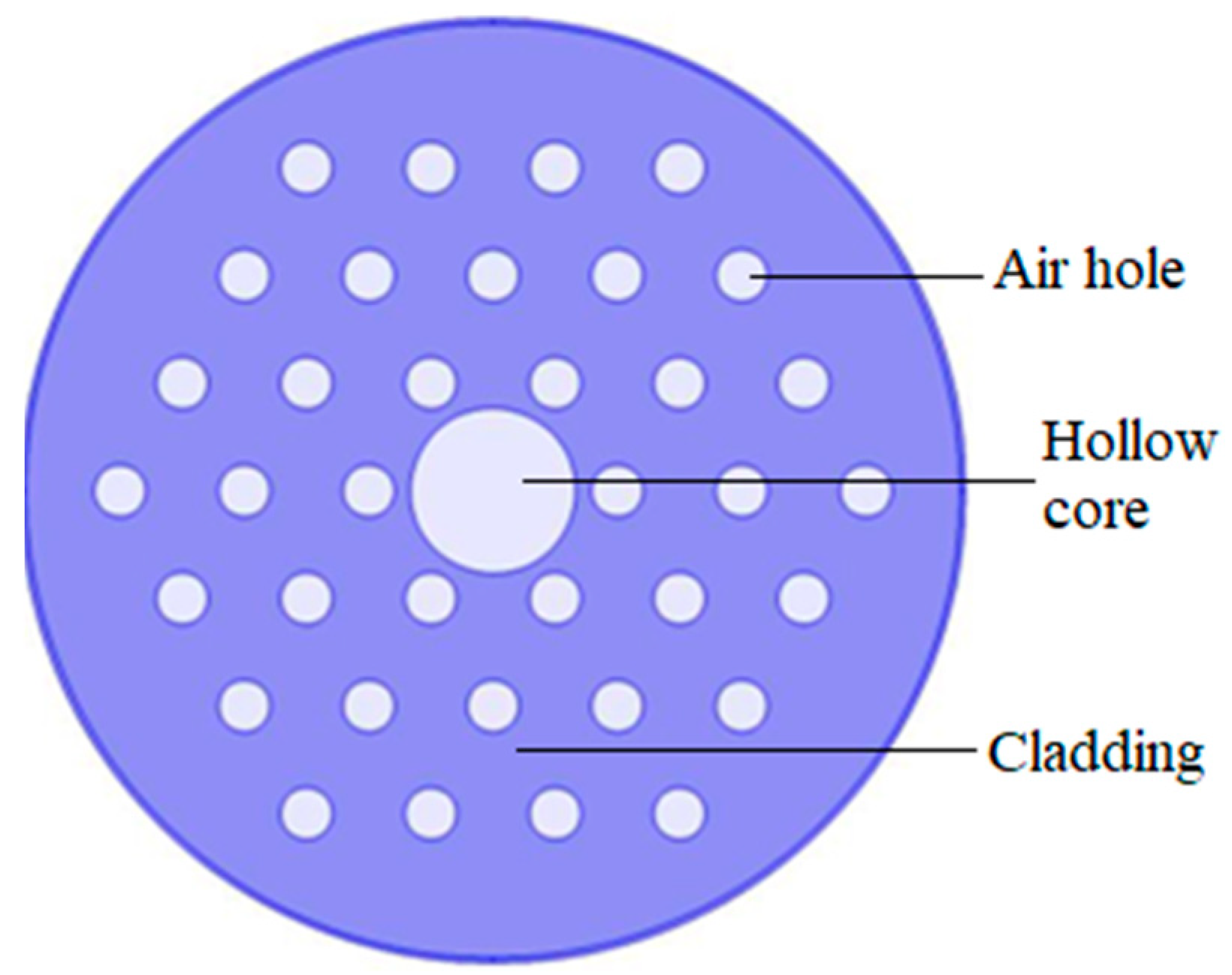
2. Theoretical Framework of PCF
3. Overview of PCF Physical Sensors
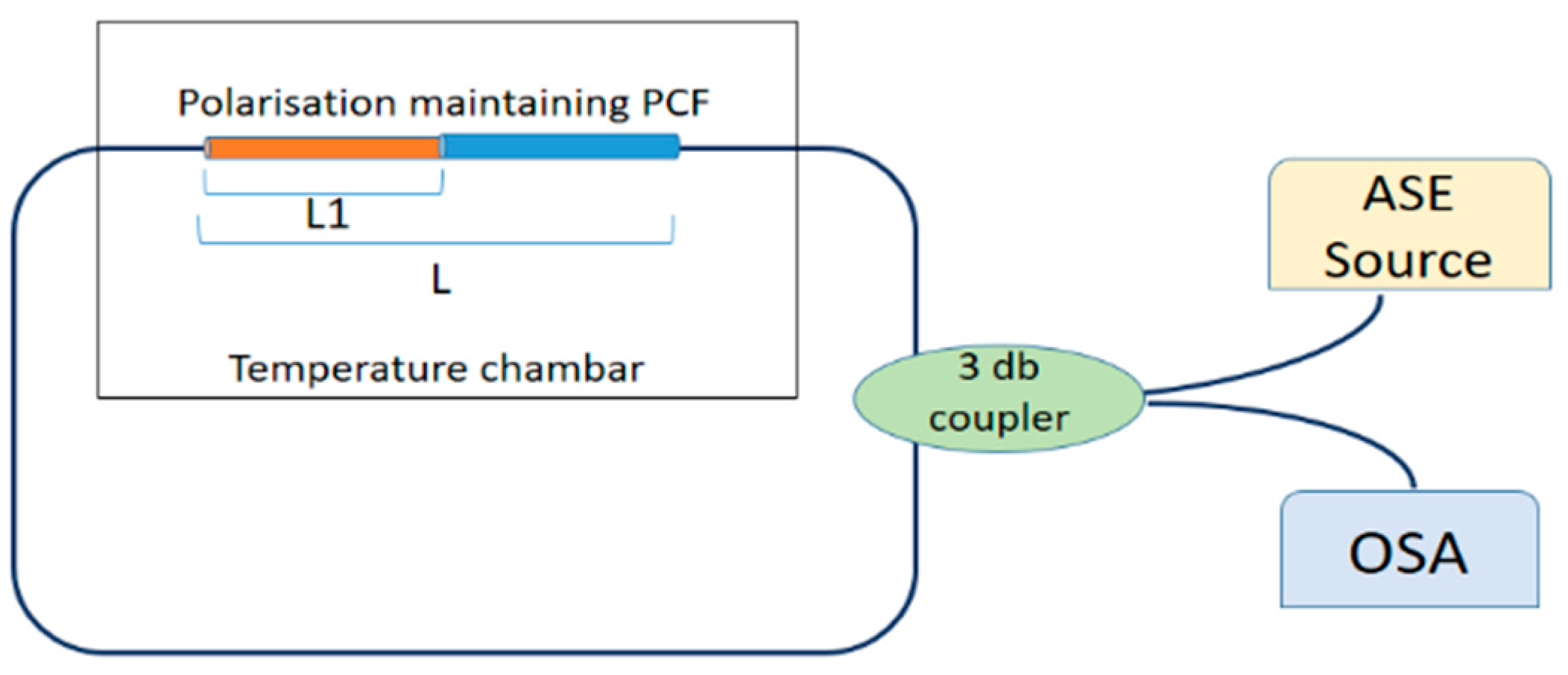
3.1. Temperature Sensors
3.2. Pressure Sensors
3.3. Strain Sensor
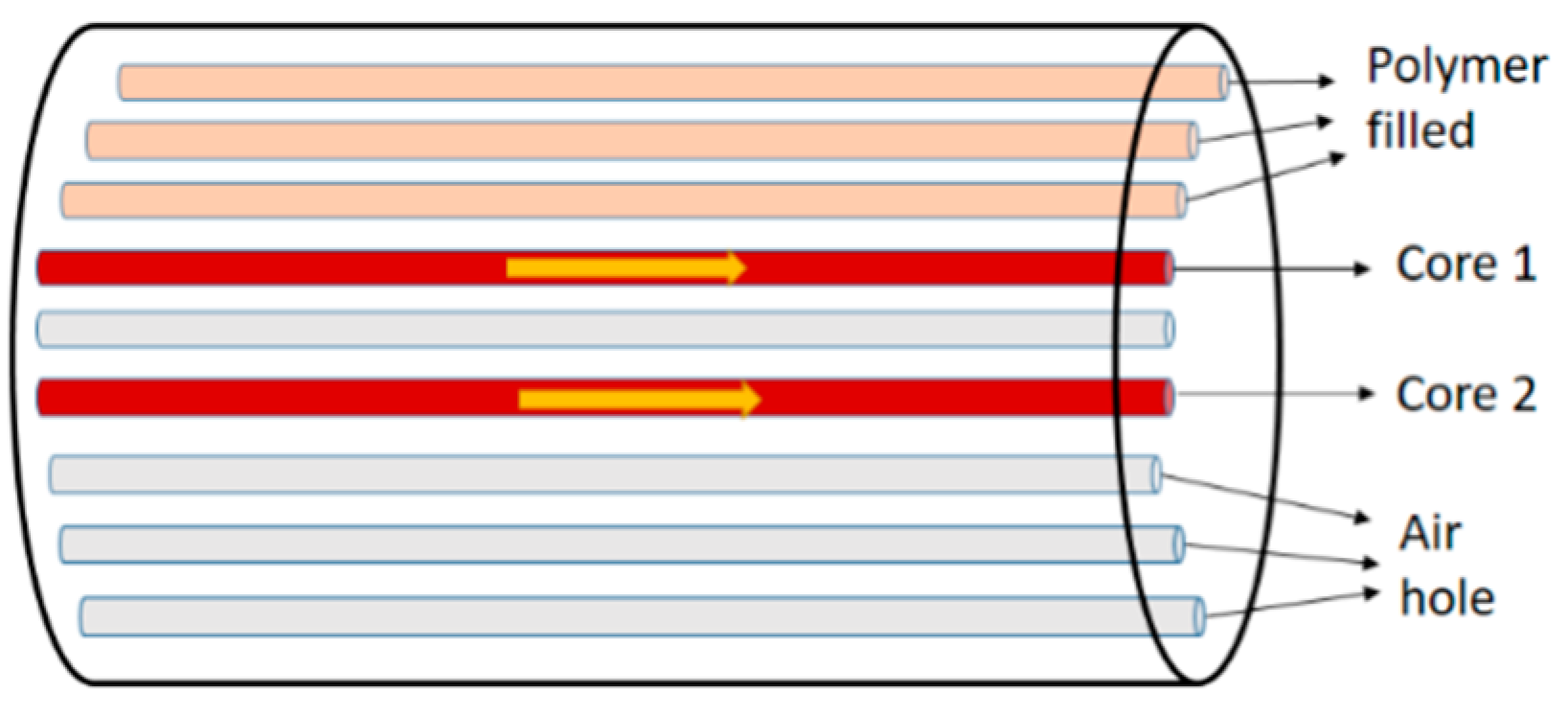
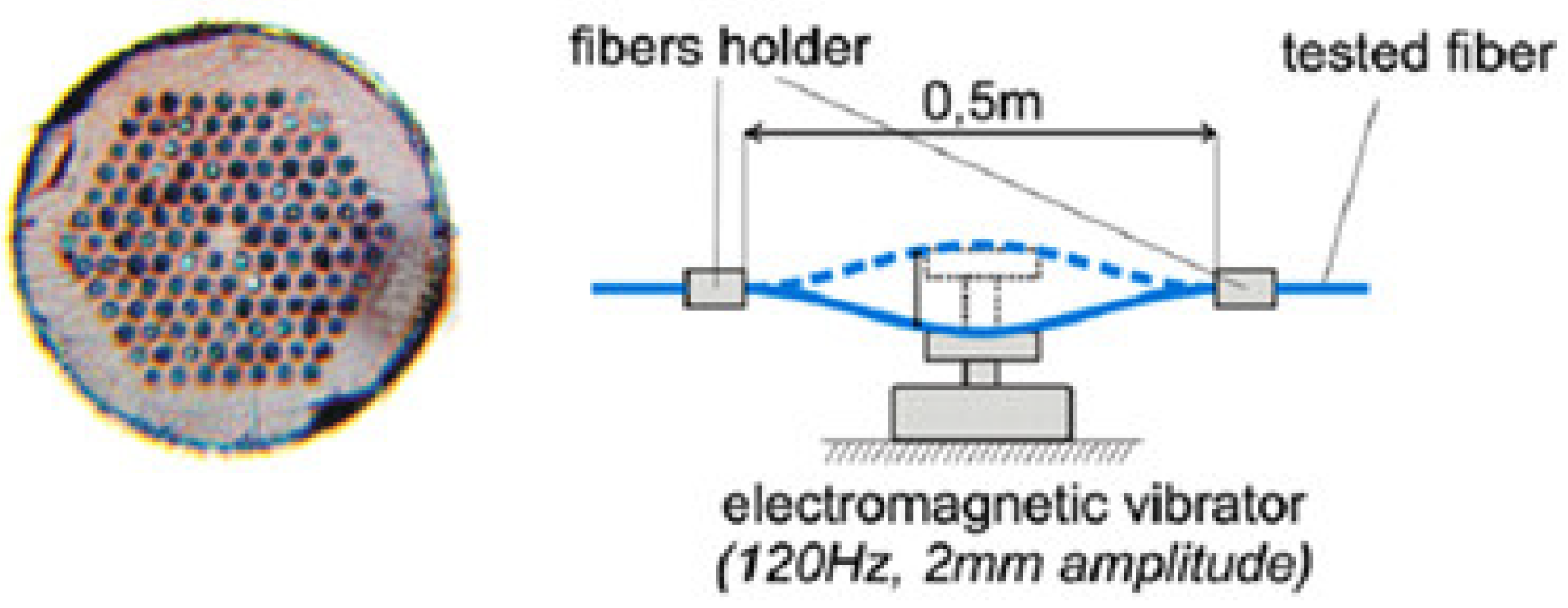
3.4. Twist or Torsion Sensor
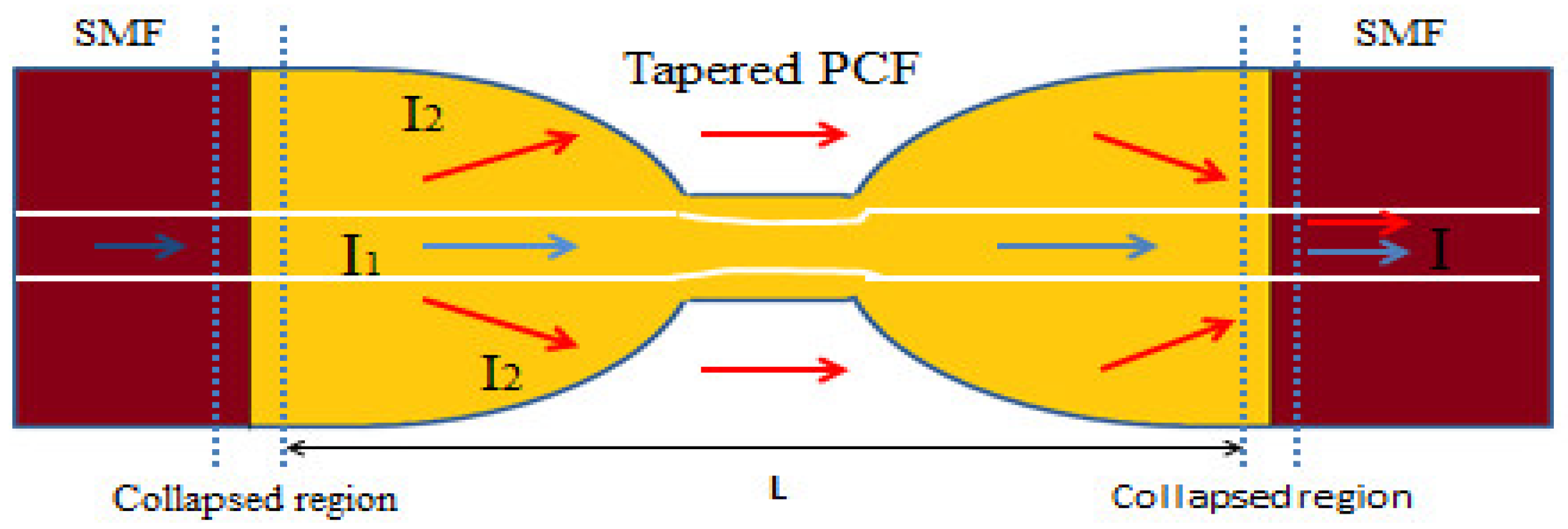
3.5. Curvature or Bend Sensors
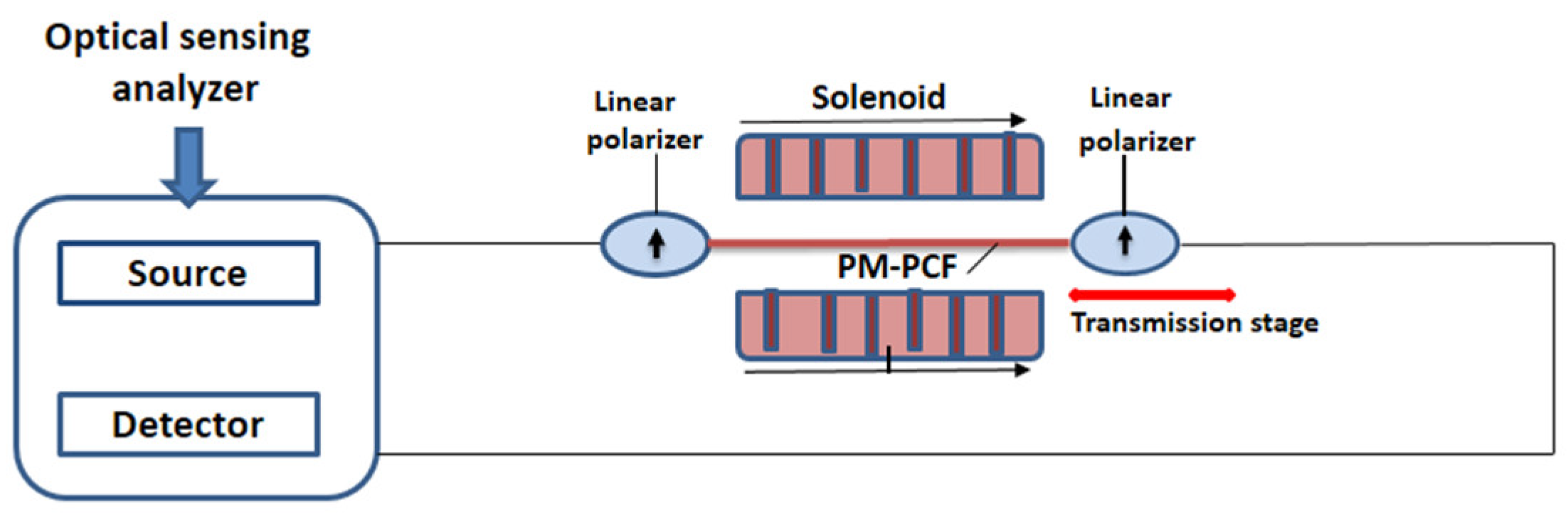
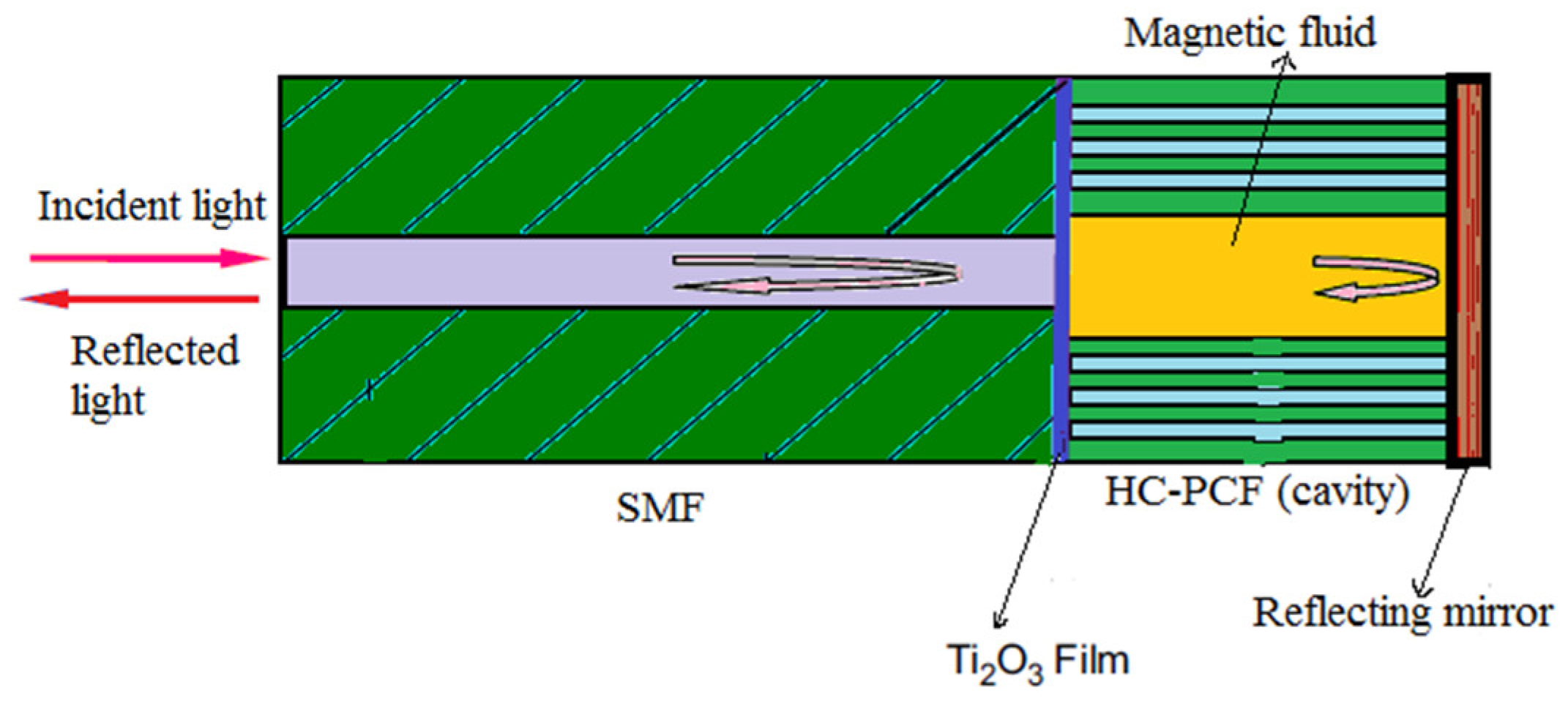
3.6. Electromagnetic Sensors
3.7. Refractive Index Sensors
4. Limitations and Technological Advancement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PCF | Photonic crystal fiber |
| SC-PCF | Solid core photonic crystal fiber |
| HC-PCF | Hollow core photonic crystal fiber |
| NA | Numerical Aperture |
| TIR | Total internal reflection |
| SMF | Single-mode fiber |
| MMF | Multi-mode fiber |
| MOF | Microstructure optical fiber |
| FBG | Fiber brag grating |
| FP Cavity | Fabry–Pérot cavity |
| LPG | Long period grating |
| LMA | Large mode area |
| MZI | Mach–Zehnder interferometer |
| SPR | Surface plasmon resonance |
| LC | Liquid crystal |
| PBG | Photonic band gap fiber |
| DC-PCF | Dual core photonic crystal fiber |
| D-PCF | D shaped photonic crystal fiber |
| LC-PCF | Liquid crystal photonic crystal fiber |
References
- Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. Pure silica single-mode fiber with hexagonal. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C. Photonic crystal fibers. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C.; Wadsworth, W.J.; Arriaga, J.; Mangan, B.J.; Birks, T.A.; Russell, P.S.J. Highly birefringent photonic crystal fibers. Opt. Lett. 2000, 25, 1325–1327. [Google Scholar]
- Mathew, J.; Semenova, Y.; Rajan, G.; Farrell, G. Humidity sensor based on photonic crystal fibre interferometer. Electron. Lett. 2010, 46, 1341. [Google Scholar] [CrossRef]
- Sanghera, J.; Aggarwal, I. Active and passive chalcogenide glass optical fibers for IR applications: A review. J. Non. Cryst. Solids 1999, 256–257, 6–16. [Google Scholar] [CrossRef]
- Russell, P. Photonic Crystal Fibres. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Russell, P.S.J. Photonic-crystal fibers. J. Light. Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Kuhlmey, B.; McPhedran, R.; de Sterke, C.; Robinson, P.; Renversez, G.; Maystre, D. Microstructured optical fibers: Where’s the edge? Opt. Express 2002, 10, 1285. [Google Scholar] [CrossRef]
- Kurokawa, K.; Tajima, K.; Tsujikawa, K.N. Reducing the losses in photonic crystal fibers. In Proceedings of the European Conference on Optical Communication, Glasgow, Scotland, 25–29 September 2005; pp. 25–29. [Google Scholar]
- Roberts, P.J.; Couny, F.; Sabert, H.; Mangan, B.J.; Williams, D.; Farr, L.; Mason, M.; Tomlinson, A.; Birks, T.A.; Knight, J.C.; Russell, P.S.J. Ultimate low loss of hollow-core photonic crystal fibers. Opt. Express 2005, 13, 236–244. [Google Scholar] [CrossRef]
- Mortensen, N.A.; Folkenberg, J.R.; Nielsen, M.D.; Hansen, K.P. Modal cutoff and the V parameter in photonic crystal fibers. Opt. Lett. 2003, 28, 1879–1881. [Google Scholar] [CrossRef]
- Birks, T.A.; Knight, J.C.; Russell, P.S.J. Endlessly single-mode photonic crystal fiber. Opt. Lett. 1997, 22, 961–963. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.P.; Jensen, J.R.; Jacobsen, C.; Simonsen, H.R.; Broeng, J.; Skovgaard, P.M.W.; Petersson, A. Highly Nonlinear Photonic Crystal Fiber with Zero Dispersion at 1.55 µm. In Proceedings of the Optical Fiber Communication Conference and Exhibit, Anaheim, CA, USA, 17–22 March 2002. [Google Scholar]
- Hansen, K.P. Dispersion flattened hybrid-core nonlinear photonic crystal fiber. Opt. Express 2003, 11, 1503–1509. [Google Scholar] [CrossRef] [PubMed]
- Reeves, W.H.; Knight, J.C.; Russell, P.S.J.; Roberts, P.J. Demonstration of ultra-flattened dispersion in photonic crystal fibers. Opt. Express 2002, 10, 609–613. [Google Scholar] [CrossRef] [PubMed]
- Ferrando, A.; Silvestre, E.; Miret, J.J. Nearly zero ultra flattened dispersion in photonic crystal fibers. Opt. Lett. 2000, 25, 790–792. [Google Scholar] [CrossRef] [PubMed]
- Kristiansen, R.E.; Hansen, K.P.; Broeng, J.; Skovgaard, P.M.W.; Nielsen, M.D.; Petersson, A.; Hansen, T.P.; Mangan, B.; Jakobsen, C. Microstructured fibers and their applications. In Proceedings of the Reuni on Espanola de Optoelectr onica OPTOEL, Elche, Spain; 2005; pp. 13–15. [Google Scholar]
- Knight, J.C.; Birks, T.A.; Cregan, R.F.; Russell, P.S.J. Large mode area photonic crystal fiber. Electron. Lett. 1998, 34. [Google Scholar] [CrossRef]
- Ju, J.; Jin, W.; Demokan, S. Properties of a highly birefringent photonic crystal fiber. IEEE Photonics Technol. Lett. 2003, 15, 1375–1377. [Google Scholar] [CrossRef]
- Dadabayev, R.; Shabairou, N.; Zalevsky, Z.; Malka, D. A visible light RBG wavelength demultiplexer based on silicon-nitride multicore PCF. Opt. Laser Technol. 2019, 111, 411–416. [Google Scholar] [CrossRef]
- Malka, D.; Cohen, E.; Zalevsky, Z. Design of 4 × 1 power beam combiner based on multi core photonic crystal fiber. Appl. Sci. 2017, 7, 695. [Google Scholar] [CrossRef]
- Holzwarth, R.; Udem, T.; Hänsch, T.W.; Knight, J.C.; Wadsworth, W.J.; Russell, P.S.J. Optical frequency synthesizer for precision spectroscopy. Phys. Rev. Lett. 2000, 85, 2264–2267. [Google Scholar] [CrossRef]
- Wadsworth, W.J.; Blanch, A.O.; Knight, J.C.; Birks, T.A.; Man, T.-P.M.; Russell, P.S.J. Supercontinuum generation in photonic crystal fibers and optical fiber tapers: A novel light source. J. Opt. Soc. Am. B 2002, 19, 2148–2155. [Google Scholar] [CrossRef]
- Chow, K.K.; Shu, C.; Chinlon, L.; Bjarklev, A. Polarization-insensitive widely tunable wavelength converter based on four-wave mixing in a dispersion-flattened nonlinear photonic Crystal fiber. IEEE Photonics Technol. Lett. 2005, 17, 624–626. [Google Scholar] [CrossRef]
- Pinto, A.M.R.; Frazão, O.; Santos, J.L.; Lopez-Amo, M. Multiwavelength Raman fiber lasers using Hi-Bi photonic crystal fiber loop mirrors combined with random cavities. J. Light. Technol. 2011, 29, 1482–1488. [Google Scholar] [CrossRef]
- Sintov, Y.; Malka, D.; Zalevsky, Z. Prospects for diode-pumped alkali-atom-based hollow-core photonic-crystal fiber lasers. Opt. Lett. 2014, 39, 4655–4658. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.B.; Pedersen, L.H.; Hoiby, P.E.; Nielsen, L.B.; Hansen, T.P.; Folkenberg, J.R.; Riishede, J.; Noordegraaf, D.; Nielsen, K.; Carlsen, A.; et al. Photonic crystal fiber based evanescent-wave sensor for detection of biomolecules in aqueous solutions. Opt. Lett. 2004, 29, 1974–1976. [Google Scholar] [CrossRef] [PubMed]
- Aref, S.H.; Amezcua-Correa, R.; Carvalho, J.P.; Frazão, O.; Caldas, P.; Santos, J.L.; Araújo, F.M.; Latifi, H.; Farahi, F.; Ferreira, L.A.; et al. Modal interferometer based on hollow-core photonic crystal fiber for strain and temperature measurement. Opt. Express 2009, 17, 18669. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, D.N.; Liao, C.R.; Hu, T.; Guo, J.; Wei, H. Temperature-insensitive refractive index sensing by use of micro Fabry-Pérot cavity based on simplified hollow-core photonic crystal fiber. Opt. Lett. 2013, 38, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Crisp, J.; Elliott, B. Introduction to Fiber Optics, 3rd ed.; An Imprint of Elsevier Linacre House: Oxford, UK; Burlington: Jordan Hill, MA, USA, 2005. [Google Scholar]
- Liu, Q.; Li, S.; Chen, H.; Li, J.; Fan, Z. High-sensitivity plasmonic temperature sensor based on photonic crystal fiber coated with nanoscale gold film. Appl. Phys. Express 2015, 8, 046701. [Google Scholar] [CrossRef]
- Feng, W.-Q.; Liu, Z.-Y.; Tam, H.-Y.; Yin, J.-H. The pore water pressure sensor based on Sagnac interferometer with polarization-maintaining photonic crystal fiber for the geotechnical engineering. Measurement 2016, 90, 208–214. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Singh, V.K. Highly Sensitive Surface Plasmon Resonance Based D-Shaped Photonic Crystal Fiber Refractive Index Sensor. Plasmonics 2017, 12, 1367–1372. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Bhardwaj, V.; Singh, V.K. Magnetic field sensor based on selectively magnetic fluid infiltrated dual-core photonic crystal fiber. Opt. Eng. 2016, 55, 026111. [Google Scholar] [CrossRef]
- Wu, Y.; Town, G.E.; Bang, O. Refractive Index Sensing in an All-Solid Twin-Core Photonic Bandgap Fiber. IEEE Sens. J. 2010, 10, 1192. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Singh, V.K. Refractive index sensor based on selectively liquid infiltrated dual core photonic crystal fibers. Photonics Nanostruct. Fundam. Appl. 2015, 15, 46–52. [Google Scholar] [CrossRef]
- Pinto, A.M.R.; Lopez-Amo, M. Photonic Crystal Fibers for Sensing Applications. J. Sens. 2012, 2012, 598178. [Google Scholar] [CrossRef]
- Emiliyanov, G.; Høiby, P.E.; Pedersen, L.H.; Bang, O. Selective serial multi-antibody biosensing with TOPAS microstructured polymer optical fibers. Sensors (Switzerland) 2013, 13, 3242–3251. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Shum, P.; Bay, H.-W.; Yan, M.; Yu, X.; Hu, J.; Hao, J.; Lu, C. Strain-insensitive and high-temperature long-period gratings inscribed in photonic crystal fiber. Opt. Lett. 2005, 30, 367–369. [Google Scholar] [CrossRef] [PubMed]
- Wolinski, T.R.; Szaniawska, K.; Ertman, S.; Lesiak, P.; Domanski, A.W.; Dabrowski, R.; Nowinowski-Kruszelnicki, E.; Wojcik, J. Influence of temperature and electrical fields on propagation properties of photonic liquid-crystal fibres. Meas. Sci. Technol. 2006, 17, 985–991. [Google Scholar] [CrossRef]
- Larrión, B.; Hernáez, M.; Arregui, F.J.; Goicoechea, J.; Bravo, J.; Matías, I.R. Photonic Crystal Fiber Temperature Sensor Based on Quantum Dot Nanocoatings. J. Sens. 2009, 2009. [Google Scholar] [CrossRef]
- Cui, Y.; Shum, P.P.; Hu, D.J.J.; Wang, G.; Humbert, G.; Dinh, X.Q. Temperature sensor by using selectively filled photonic crystal fiber sagnac interferometer. IEEE Photonics J. 2012, 4, 1801–1808. [Google Scholar] [CrossRef]
- Park, B.; Provine, J.; Jung, I.W.; Howe, R.T.; Solgaard, O. Photonic crystal fiber tip sensor for high-temperature measurement. IEEE Sens. J. 2011, 11, 2643–2648. [Google Scholar] [CrossRef]
- Naeem, K.; Kim, B.H.; Kim, B.; Chung, Y. High-sensitivity temperature sensor based on a selectively-polymer-filled two-core photonic crystal fiber in-line interferometer. IEEE Sens. J. 2015, 15, 3998–4003. [Google Scholar] [CrossRef]
- Dong, B.; Shen, Z.; Yu, C.; Wang, Y. Modal Excitations in Fully and Partially Ethanol-Filled Photonic Bandgap Fibers and Their Applications as Fiber Sensors. J. Light. Technol. 2016, 34, 3853–3858. [Google Scholar] [CrossRef]
- Yuan, W.; Khan, L.; Webb, D.J.; Kalli, K.; Rasmussen, H.K.; Stefani, A.; Bang, O. Humidity insensitive TOPAS polymer fiber Bragg grating sensor. Opt. Express 2011, 19, 19731. [Google Scholar] [CrossRef] [PubMed]
- Mileńko, K.; Hu, D.J.J.; Shum, P.P.; Zhang, T.; Lim, J.L.; Wang, Y.; Woliński, T.R.; Wei, H.; Tong, W. Photonic crystal fiber tip interferometer for refractive index sensing. Opt. Lett. 2012, 37, 1373. [Google Scholar] [CrossRef] [PubMed]
- Dhara, P.; Singh, V.K. Effect of MMF stub on the sensitivity of a photonic crystal fiber interferometer sensor at 1550 nm. Opt. Fiber Technol. 2015, 21, 154–159. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Inline microcavity-based PCF interferometer for refractive index and temperature sensing. IEEE Photonics Technol. Lett. 2015, 27, 1325–1328. [Google Scholar] [CrossRef]
- Hameed, M.F.O.; Azab, M.Y.; Heikal, A.M.; El-Hefnawy, S.M.; Obayya, S.S.A. Highly sensitive plasmonic photonic crystal temperature sensor filled with liquid crystal. IEEE Photonics Technol. Lett. 2015, 28, 59–62. [Google Scholar] [CrossRef]
- Dash, J.N.; Dass, S.; Jha, R. Sensors and Actuators A: Physical Photonic crystal fiber microcavity based bend and temperature sensor using micro fiber. Sens. Actuators A Phys. 2016, 244, 24–29. [Google Scholar] [CrossRef]
- Ayyanar, N.; Jayakantha, R.V.; Vigneswaran, D.; Lakshmi, B.; Sumathi, M.; Porsezian, K. Highly efficient compact temperature sensor using liquid in fi ltrated asymmetric dual elliptical core photonic crystal fiber. Opt. Mater. (Amst) 2017, 64, 574–582. [Google Scholar] [CrossRef]
- Naeem, K.; Kwon, I.-B.; Chung, Y. Multibeam Interferometer Using a Photonic Crystal Fiber with Two Asymmetric Cores for Torsion, Strain and Temperature Sensing. Sensors 2017, 17, 132. [Google Scholar] [CrossRef]
- Du, C.; Wang, Q.; Zhao, Y.; Li, J. Highly sensitive temperature sensor based on an isopropanol-filled photonic crystal fiber long period grating. Opt. Fiber Technol. 2017, 34, 12–15. [Google Scholar] [CrossRef]
- Ma, J.; Yu, H.H.; Jiang, X.; Jiang, D.S. High-performance temperature sensing using a selectively filled solid-core photonic crystal fiber with a central air-bore. Opt. Express 2017, 25, 9406–9415. [Google Scholar] [CrossRef] [PubMed]
- Bock, W.J.; Jia, C.; Eftimov, T.; Urbanczyk, W. A photonic crystal fiber sensor for pressure measurements. In Proceedings of the Conference Record–IEEE Instrumentation and Measurement Technology Conference; 2005; Volume 2, pp. 1119–1123. [Google Scholar]
- Martynkien, T.; Szpulak, M.; Statkiewicz, G.; Golojuch, G.; Olszewski, J.; Urbanczyk, W.; Wojcik, J.; Mergo, P.; Makara, M.; Nasilowski, T.; et al. Measurements of sensitivity to hydrostatic pressure and temperature in highly birefringent photonic crystal fibers. Opt. Quantum Electron. 2007, 39, 481–489. [Google Scholar] [CrossRef]
- Fu, H.Y.; Tam, H.Y.; Shao, L.-Y.; Dong, X.; Wai, P.K.A.; Lu, C.; Khijwania, S.K. Pressure sensor realized with polarization-maintaining photonic crystal fiber-based Sagnac interferometer. Appl. Opt. 2008, 47, 2835. [Google Scholar] [CrossRef] [PubMed]
- Martynkien, T.; Statkiewicz-Barabach, G.; Olszewski, J.; Wojcik, J.; Mergo, P.; Geernaert, T.; Sonnenfeld, C.; Anuszkiewicz, A.; Szczurowski, M.K.; Tarnowski, K.; et al. Highly birefringent microstructured fibers with enhanced sensitivity to hydrostatic pressure. Opt. Express 2010, 18, 15113–15121. [Google Scholar] [CrossRef] [PubMed]
- Aref, S.H.; Zibaii, M.I.; Kheiri, M.; Porbeyram, H.; Latifi, H.; Araújo, F.M.; Ferreira, L.A.; Santos, J.L.; Kobelke, J.; Schuster, K.; et al. Pressure and temperature characterization of two interferometric configurations based on suspended-core fibers. Opt. Commun. 2012, 285, 269–273. [Google Scholar] [CrossRef]
- Bock, W.J.; Chen, J.; Mikulic, P.; Eftimov, T.; Korwin-Pawlowski, M. Pressure sensing using periodically tapered long-period gratings written in photonic crystal fibres. Meas. Sci. Technol. 2007, 18, 3098–3102. [Google Scholar] [CrossRef]
- Fávero, F.C.; Quintero, S.M.M.; Silva, V.V.; Martelli, C.; Braga, A.M.B.; Carvalho, I.C.S.; Llerena, R.W.A. Photonic Crystal Fiber Pressure Sensor. In Proceedings of the 20th International Conference on Optical Fibre Sensors, Edinburgh, UK, October 2009; Volume 7503, p. 750364. [Google Scholar]
- Fu, H.Y.; Wu, C.; Tse, M.L.V.; Zhang, L.; Cheng, K.-C.D.; Tam, H.Y.; Guan, B.-O.; Lu, C. High pressure sensor based on photonic crystal fiber for downhole application. Appl. Opt. 2010, 49, 2639. [Google Scholar] [CrossRef]
- Wu, C.; Li, J.; Feng, X.; Guan, B.O.; Tam, H.Y. Side-hole photonic crystal fiber with ultrahigh polarimetric pressure sensitivity. J. Light. Technol. 2011, 29, 943–948. [Google Scholar] [CrossRef]
- Sulejmani, S.; Sonnenfeld, C.; Geernaert, T.; Mergo, P.; Makara, M.; Poturaj, K.; Skorupski, K.; Martynkien, T.; Satkiewicz-Barabach, G.; Olszewski, J.; et al. Control over the pressure sensitivity of Bragg grating-based sensors in highly birefringent microstructured optical fibers. IEEE Photonics Technol. Lett. 2012, 24, 527–529. [Google Scholar] [CrossRef]
- Dobb, H.; Kalli, K.; Webb, D.J. Temperature-insensitive long period grating sensors in photonic crystal fibre. Electron. Lett. 2004, 40, 657–658. [Google Scholar] [CrossRef]
- Frazão, O.; Baptista, J.M.; Santos, J.L. Temperature-Independent Strain Sensor Based on a Hi-Bi Photonic Crystal Fiber Loop Mirror. IEEE Sens. J. 2007, 7, 1453–1455. [Google Scholar] [CrossRef]
- Shi, Q.S.; Lv, F.L.; Wang, Z.W.; Jin, L.J.; Hu, J.J.; Liu, Z.L.; Kai, G.K.; Dong, X. Environmentally stable Fabry-Perot-type strain sensor based on hollow-core photonic bandgap fiber. IEEE Photonics Technol. Lett. 2008, 20, 2008–2010. [Google Scholar] [CrossRef]
- Han, Y.G. Temperature-insensitive strain measurement using a birefringent interferometer based on a polarization-maintaining photonic crystal fiber. Appl. Phys. B Lasers Opt. 2009, 95, 383–387. [Google Scholar] [CrossRef]
- Ferreira, M.S.; Bierlich, J.; Kobelke, J.; Schuster, K.; Santos, J.L.; Frazão, O. Towards the control of highly sensitive Fabry-Pérot strain sensor based on hollow-core ring photonic crystal fiber. Opt. Express 2012, 20, 21946. [Google Scholar] [CrossRef] [PubMed]
- Karim Qureshi, K.; Liu, Z.; Tam, H.Y.; Fahad Zia, M. A strain sensor based on in-line fiber Mach-Zehnder interferometer in twin-core photonic crystal fiber. Opt. Commun. 2013, 309, 68–70. [Google Scholar] [CrossRef]
- Hou, M.; Wang, Y.; Liu, S.; Li, Z.; Lu, P. Multi-components Interferometer Based on Partially-filled Dual-core Photonic Crystal Fiber for Temperature and Strain Sensing. IEEE Sens. J. 2016, 16, 6192–6196. [Google Scholar] [CrossRef]
- Wang, Y.-P.; Xiao, L.; Wang, D.N.; Jin, W. Highly sensitive long-period fiber-grating strain sensor with low temperature sensitivity. Opt. Lett. 2006, 31, 3414–3416. [Google Scholar] [CrossRef]
- Choi, H.Y.; Kim, M.J.; Lee, B.H. All-fiber Mach-Zehnder type interferometers formed in photonic crystal fiber. Opt. Express 2007, 15, 5711–5720. [Google Scholar] [CrossRef]
- Chen, C.; Laronche, A.; Bouwmans, G.; Bigot, L.; Quiquempois, Y. Sensitivity of photonic crystal fiber modes to temperature, strain and external refractive index. Opt. Express 2008, 16, 9645–9653. [Google Scholar] [CrossRef]
- Shin, W.; Lee, Y.L.; Yu, B.A.; Noh, Y.C.; Ahn, T.J. Highly sensitive strain and bending sensor based on in-line fiber Mach-Zehnder interferometer in solid core large mode area photonic crystal fiber. Opt. Commun. 2010, 283, 2097–2101. [Google Scholar] [CrossRef]
- Hu, L.M.; Chan, C.C.; Dong, X.Y.; Wang, Y.P.; Zu, P.; Wong, W.C.; Qian, W.W.; Li, T. Photonic Crystal Fiber Strain Sensor Based on Modified Mach–Zehnder Interferometer. IEEE Photonics J. 2012, 4, 114–118. [Google Scholar] [CrossRef]
- Bai, X.; Fan, D.; Wang, S.; Pu, S.; Zeng, X. Strain Sensor Based on Fiber Ring Cavity Laser with Photonic Crystal Fiber In-Line Mach-Zehnder Interferometer. IEEE Photonics J. 2014, 6. [Google Scholar] [CrossRef]
- Yu, X.; Shum, P.; Fu, S.; Deng, L. Torsion-sensitivity of mechanical long-period grating in photonic crystal fiber. J. Optoelectron. Adv. Mater. 2006, 8, 1247–1249. [Google Scholar]
- Frazao, O.; Jesus, C.; Baptista, J.M.; Santos, J.L.; Roy, P. Fiber-optic interferometric torsion sensor based on a two-LP-mode operation in birefringent fiber. IEEE Photonics Technol. Lett. 2009, 21, 1277–1279. [Google Scholar] [CrossRef]
- Frazão, O.; Silva, R.M.; Kobelke, J.; Schuster, K. Temperature- and strain-independent torsion sensor using a fiber loop mirror based on suspended twin-core fiber. Opt. Lett. 2010, 35, 2777–2779. [Google Scholar] [CrossRef]
- Kim, H.M.; Kim, T.H.; Kim, B.; Chung, Y. Temperature-insensitive torsion sensor with enhanced sensitivity by use of a highly birefringent photonic crystal fiber. IEEE Photonics Technol. Lett. 2010, 22, 1539–1541. [Google Scholar] [CrossRef]
- Chen, W.; Lou, S.; Wang, L.; Zou, H.; Lu, W.; Jian, S. Highly Sensitive Torsion Sensor Based on Sagnac Interferometer Using Side-leakage Photonic Crystal Fiber. IEEE Photonics Technol. Lett. 2011, 23, 1639–1641. [Google Scholar] [CrossRef]
- Zu, P.; Chan, C.C.; Jin, Y.; Gong, T.; Zhang, Y.; Chen, L.H.; Dong, X. A temperature-insensitive twist sensor by using low-birefringence photonic-crystal-fiber-based Sagnac Interferometer. IEEE Photonics Technol. Lett. 2011, 23, 920–922. [Google Scholar] [CrossRef]
- Sierra-Hernandez, J.M.; Castillo-Guzman, A.; Selvas-Aguilar, R.; Vargas-Rodriguez, E.; Gallegos-Arellano, E.; Guzman-Chavez, D.A.; Estudillo-Ayala, J.M.; Jauregui-Vazquez, D.; Rojas-Laguna, A. Torsion sensing setup based on a three beam path Mach-Zehnder interferometer. Microw. Opt. Technol. Lett. 2015, 57, 1857–1860. [Google Scholar] [CrossRef]
- MacPherson, W.N.; Gander, M.J.; McBride, R.; Jones, J.D.C.; Blanchard, P.M.; Burnett, J.G.; Greenaway, A.H.; Mangan, B.; Birks, T.A.; Knight, J.C.; et al. Remotely addressed optical fibre curvature sensor using multicore photonic crystal fibre. Opt. Commun. 2001, 193, 97–104. [Google Scholar] [CrossRef]
- Han, Y.-G.; Song, S.; Kim, G.H.; Lee, K.; Lee, S.B.; Lee, J.H.; Jeong, C.H.; Oh, C.H.; Kang, H.J. Bending sensitivity of long-period fiber gratings inscribed in holey fibers depending on an axial rotation angle. Opt. Lett. 2007, 15, 12866–12871. [Google Scholar] [CrossRef]
- Frazão, O.; Baptista, J.M.; Santos, J.L.; Roy, P. Curvature sensor using a highly birefringent photonic crystal fiber with two asymmetric hole regions in a Sagnac interferometer. Appl. Opt. 2008, 47, 2520–2523. [Google Scholar] [CrossRef] [PubMed]
- Gong, H.P.; Chan, C.C.; Zu, P.; Chen, L.H.; Dong, X.Y. Curvature measurement by using low-birefringence photonic crystal fiber based Sagnac loop. Opt. Commun. 2010, 283, 3142–3144. [Google Scholar] [CrossRef]
- Hwang, K.J.; Kim, G.H.; Lim, S.D.; Lee, K.; Park, J.W.; Lee, S.B. A novel birefringent photonic crystal fiber and its application to curvature measurement. Jpn. J. Appl. Phys. 2011, 50, 4–8. [Google Scholar] [CrossRef]
- Martins, H.; Marques, M.B.; Jorge, P.; Cordeiro, C.M.B.; Frazão, O. Intensity curvature sensor based on photonic crystal fiber with three coupled cores. Opt. Commun. 2012, 285, 5128–5131. [Google Scholar] [CrossRef]
- Ni, K.; Li, T.; Hu, L.; Qian, W.; Zhang, Q.; Jin, S. Temperature-independent curvature sensor based on tapered photonic crystal fiber interferometer. Opt. Commun. 2012, 285, 5148–5150. [Google Scholar] [CrossRef]
- Fiber, C.; Interferometer, S. Curvature Sensor Based on Hollow-Core Photonic. IEEE Sens. J. 2014, 14, 777–780. [Google Scholar]
- Zheng, S.; Shan, B.; Ghandehari, M.; Ou, J. Sensitivity characterization of cladding modes in long-period gratings photonic crystal fiber for structural health monitoring. Meas. J. Int. Meas. Confed. 2015, 72, 43–51. [Google Scholar] [CrossRef]
- Dass, S.; Dash, J.N.; Jha, R. Intensity modulated SMF cascaded tapers with a hollow core PCF based microcavity for curvature sensing. J. Opt. (UK) 2016, 18. [Google Scholar] [CrossRef]
- Mathews, S.; Farrell, G.; Semenova, Y. Liquid crystal infiltrated photonic crystal fibers for electric field intensity measurements. Appl. Opt. 2011, 50, 2628. [Google Scholar] [CrossRef]
- Thakur, H.V.; Nalawade, S.M.; Gupta, S.; Kitture, R.; Kale, S.N. Photonic crystal fiber injected with Fe3O4 nanofluid for magnetic field detection. Appl. Phys. Lett. 2011, 99, 161101. [Google Scholar] [CrossRef]
- Zhao, Y.; Lv, R.Q.; Ying, Y.; Wang, Q. Hollow-core photonic crystal fiber FabryPerot sensor for magnetic field measurement based on magnetic fluid. Opt. Laser Technol. 2012, 44, 899–902. [Google Scholar] [CrossRef]
- Barczak, K. Application of Photonic Crystal Fiber in Optical Fiber Current Sensors. Opt. Acoust. Methods Sci. Technol. 2012, 122, 793–795. [Google Scholar] [CrossRef]
- Candiani, A.; Argyros, A.; Leon-Saval, S.G.; Lwin, R.; Selleri, S.; Pissadakis, S. A loss-based, magnetic field sensor implemented in a ferrofluid infiltrated microstructured polymer optical fiber. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, H.; Song, B.; Liu, B.; Lin, Y.; Liu, H.; Miao, Y.; Liu, Y. Magnetic field sensor based on a photonic crystal fiber taper coated with ferrofluoride. IEEE Photonics Technol. Lett. 2015, 27, 26–29. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Tan, C.; Zhu, C.; Gao, Y.; Ma, H.; Ren, Z. Simultaneous measurement of temperature and magnetic field based on cascaded photonic crystal fibers with surface plasmon resonance. Opt. Int. J. Light Electron. Opt. 2017, 134, 257–263. [Google Scholar] [CrossRef]
- Yin, J.; Ruan, S.; Liu, T.; Jiang, J.; Wang, S.; Wei, H.; Yan, P. All-fiber-optic vector magnetometer based on nano-magnetic fluids filled double-clad photonic crystal fiber. Sens. Actuators B Chem. 2017, 238, 518–524. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.G.; Wang, X. Sensing characteristics of a MF-filled photonic crystal fiber Sagnac interferometer for magnetic field detecting. Sens. Actuators B Chem. 2017, 242, 949–955. [Google Scholar] [CrossRef]
- De, M.; Singh, V.K. Magnetic fluid infiltrated dual core photonic crystal fiber based highly sensitive magnetic field sensor. Opt. Laser Technol. 2018, 106. [Google Scholar] [CrossRef]
- Minkovich, V.; Villatoro, J.; Monzón-Hernández, D.; Calixto, S.; Sotsky, A.; Sotskaya, L. Holey fiber tapers with resonance transmission for high-resolution refractive index sensing. Opt. Express 2005, 13, 7609–7614. [Google Scholar] [CrossRef]
- Phan Huy, M.C.; Laffont, G.; Dewynter, V.; Ferdinand, P.; Roy, P.; Auguste, J.-L.; Pagnoux, D.; Blanc, W.; Dussardier, B. Three-hole microstructured optical fiber for efficient fiber Bragg grating refractometer. Opt. Lett. 2007, 32, 2390–2392. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Chan, C.C. Photonic bandgap fiber for refractive index measurement. Sens. Actuators B Chem. 2007, 128, 46–50. [Google Scholar] [CrossRef]
- Jha, R.; Villatoro, J.; Badenes, G.; Pruneri, V. Refractometry based on a photonic crystal fiber interferometer. Opt. Lett. 2009, 34, 617. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.K.C.; Kuhlmey, B.T.; Eggleton, B.J. Ultrasensitive photonic crystal fiber refractive index sensor. Opt. Lett. 2009, 34, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Dash, J.N.; Jha, R. Graphene-Based Birefringent Photonic Crystal Fiber. IEEE Photonics Technol. Lett. 2014, 26, 1092–1095. [Google Scholar] [CrossRef]
- Rifat, A.A.; Haider, F.; Ahmed, R.; Mahdiraji, G.A.; Adikan, F.R.M.; Miroshnichenko, A.E. Highly sensitive selectively coated photonic crystal fiber-based plasmonic sensor. Opt. Lett. 2018, 43, 891–894. [Google Scholar] [CrossRef] [PubMed]
- Jha, R.; Villatoro, J.; Badenes, G. Ultrastable in reflection photonic crystal fiber modal interferometer for accurate refractive index sensing. Appl. Phys. Lett. 2008, 93, 2006–2009. [Google Scholar] [CrossRef]
- Kim, H.J.; Kown, O.J.; Lee, S.B.; Han, Y.G. Measurement of temperature and refractive index based on surface long-period gratings deposited onto a D-shaped photonic crystal fiber. Appl. Phys. B Lasers Opt. 2011, 102, 81–85. [Google Scholar] [CrossRef]
- Mudhana, G.; Park, K.S.; Ryu, S.Y.; Lee, B.H. Fiber-Optic Probe Based on a Bifunctional Lensed Photonic Crystal Fiber for Refractive Index Measurements of Liquids. IEEE Sens. J. 2011, 11, 1178–1183. [Google Scholar] [CrossRef]
- Lee, K.J.; Liu, X.; Vuillemin, N.; Lwin, R.; Leon-Saval, S.G.; Argyros, A.; Kuhlmey, B.T. Refractive index sensor based on a polymer fiber directional coupler for low index sensing. Opt. Express 2014, 22, 17497. [Google Scholar] [CrossRef]
- Rifat, A.A.; Mahdiraji, G.A.; Sua, Y.M.; Ahmed, R.; Shee, Y.G.; Adikan, F.R.M. Highly sensitive multi-core flat fiber surface plasmon resonance refractive index sensor. Opt. Express 2016, 24, 2485. [Google Scholar] [CrossRef]
- An, G.; Li, S.; Yan, X.; Zhang, X.; Yuan, Z.; Wang, H.; Zhang, Y.; Hao, X.; Shao, Y.; Han, Z. Extra-broad Photonic Crystal Fiber Refractive Index Sensor Based on Surface Plasmon Resonance. Plasmonics 2017, 12, 465–471. [Google Scholar] [CrossRef]
- Santos, D.F.; Guerreiro, A.; Baptista, J.M. SPR optimization using metamaterials in a D-type PCF refractive index sensor. Opt. Fiber Technol. 2017, 33, 83–88. [Google Scholar] [CrossRef]
- Liu, C.; Yang, L.; Liu, Q.; Wang, F.; Sun, Z.; Sun, T. Analysis of a Surface Plasmon Resonance Probe Based on Photonic Crystal Fibers for Low Refractive Index Detection. Plasmonics 2017. [Google Scholar] [CrossRef]
- Hasan, R.; Member, S.; Akter, S.; Rifat, A.A.; Rana, S.; Ahmed, K.; Ahmed, R.; Subbaraman, H.; Abbott, D. Spiral Photonic Crystal Fiber-Based Dual-Polarized. IEEE Sens. J. 2018, 18, 133–140. [Google Scholar] [CrossRef]
- Tsigaridas, G.; Karvouniaris, V.; Chalkiadakis, G.; Persephonis, P. Novel design of refractive index sensors and biosensors based on a dual-core micro-structured optical fiber. arXiv, 2014; arXiv:1411.4123123. [Google Scholar]
- Zhang, P.; Zhang, J.; Yang, P.; Dai, S.; Wang, X.; Zhang, W. Fabrication of chalcogenide glass photonic crystal fibers with mechanical drilling. Opt. Fiber Technol. 2015, 26, 176–179. [Google Scholar] [CrossRef]
- Ebendorff-Heidepriem, H.; Schuppich, J.; Dowler, A.; Lima-Marques, L.; Monro, T.M. 3D-printed extrusion dies: A versatile approach to optical material processing. Opt. Mater. Express 2014, 4, 1494. [Google Scholar] [CrossRef]
- Bise, R.T.; Trevor, D. Solgel-derived micro-structured fibers: Fabrication and characterization. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 6–11 March 2005. [Google Scholar]
- Ghazanfari, A.; Li, W.; Leu, M.C.; Hilmas, G.E. A novel freeform extrusion fabrication process for producing solid ceramic components with uniform layered radiation drying. Addit. Manuf. 2017, 15, 102–112. [Google Scholar] [CrossRef]
- Cox, F.M.; Argyros, A.; Large, M.C.J.; Kalluri, S. Surface enhanced Raman scattering in a hollow core microstructured optical fiber. Opt. Express 2007, 15, 13675–13681. [Google Scholar] [CrossRef] [PubMed]
- Rindorf, L.; Jensen, J.B.; Dufva, M.; Pedersen, L.H.; Høiby, P.E.; Bang, O. Photonic crystal fiber long-period gratings for biochemical sensing. Opt. Express 2006, 14, 8224–8231. [Google Scholar] [CrossRef] [PubMed]
- Gauvreau, B.; Hassani, A.; Fassi Fehri, M.; Kabashin, A.; Skorobogatiy, M. Photonic bandgap fiber-based Surface Plasmon Resonance sensors. Opt. Express 2007, 15, 11413–11426. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Chen, Y.; Li, X.; Yin, Z.; Wang, L.; Geng, Y.; Hong, X. Characteristics of D-shaped photonic crystal fiber surface plasmon resonance sensors with different side-polished lengths. Appl. Opt. 2017, 56, 1550–1555. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Y.; Yariv, A. Fabrication of functional microstructured optical fibers through a selective-filling technique. Appl. Phys. Lett. 2004, 85, 5182–5184. [Google Scholar] [CrossRef]
- Xiao, L.; Jin, W.; Demokan, M.; Ho, H.; Hoo, Y.; Zhao, C. Fabrication of selective injection microstructured optical fibers with a conventional fusion splicer. Opt. Express 2005, 13, 9014–9022. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liao, C.R.; Wang, D.N. Femtosecond laser-assisted selective infiltration of microstructured optical fibers. Opt. Express 2010, 18, 18035. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Yuan, W.; Hansen, O.; Bang, O. Selective filling of photonic crystal fibers using focused ion beam milled microchannels. Opt. Express 2011, 19, 17585. [Google Scholar] [CrossRef] [PubMed]
- Brolo, G. Nanoplasmonic structures in optical fibers. In Nanoplasmonic Sensors; Springer: Berlin, Germany, 2012; pp. 289–315. [Google Scholar]
- Zhang, Z.; Zhang, F.; Min, Z.; Ye, P. Gas sensing properties of index-guided PCF with air-core. Opt. Laser Technol. 2008, 40, 167–174. [Google Scholar] [CrossRef]
- Atakaramians, S.; Shahraam, A.V.; Ebendorff-Heidepriem, H.; Nagel, M.; Fischer, B.M.; Abbott, D.; Monro, T.M. THz porous fibers: Design, fabrication and experimental characterization. Opt. Express 2009, 17, 14053. [Google Scholar] [CrossRef] [PubMed]




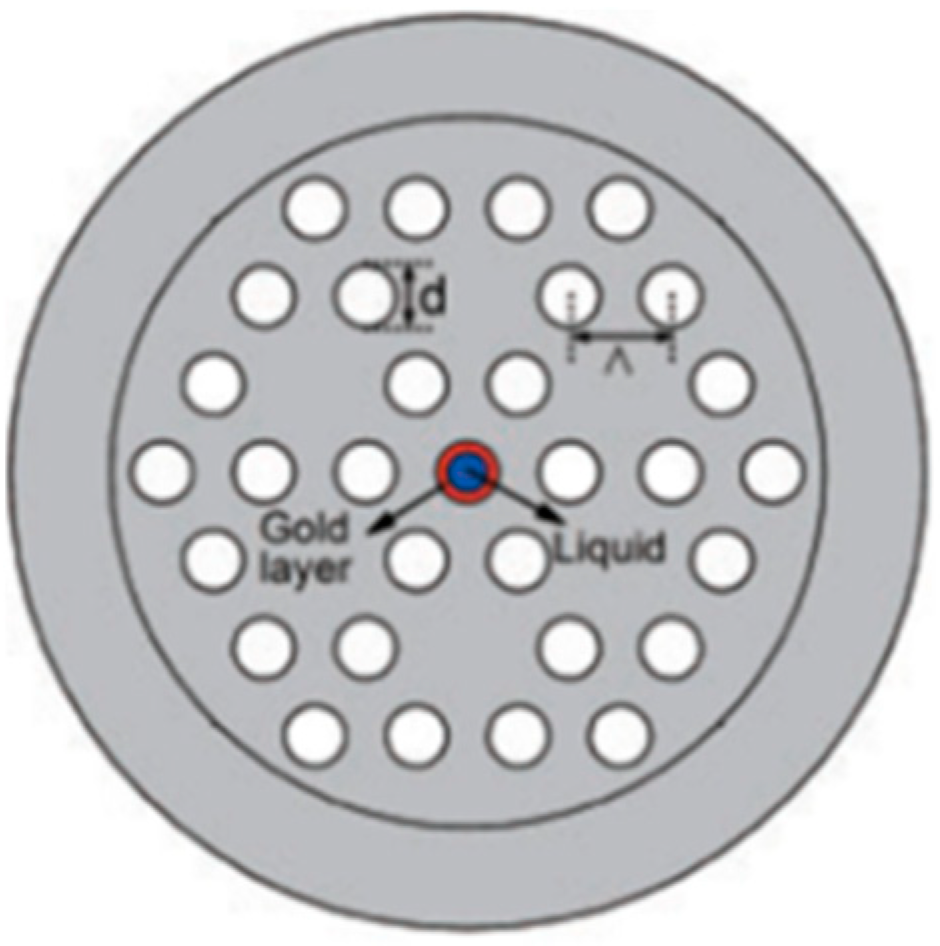
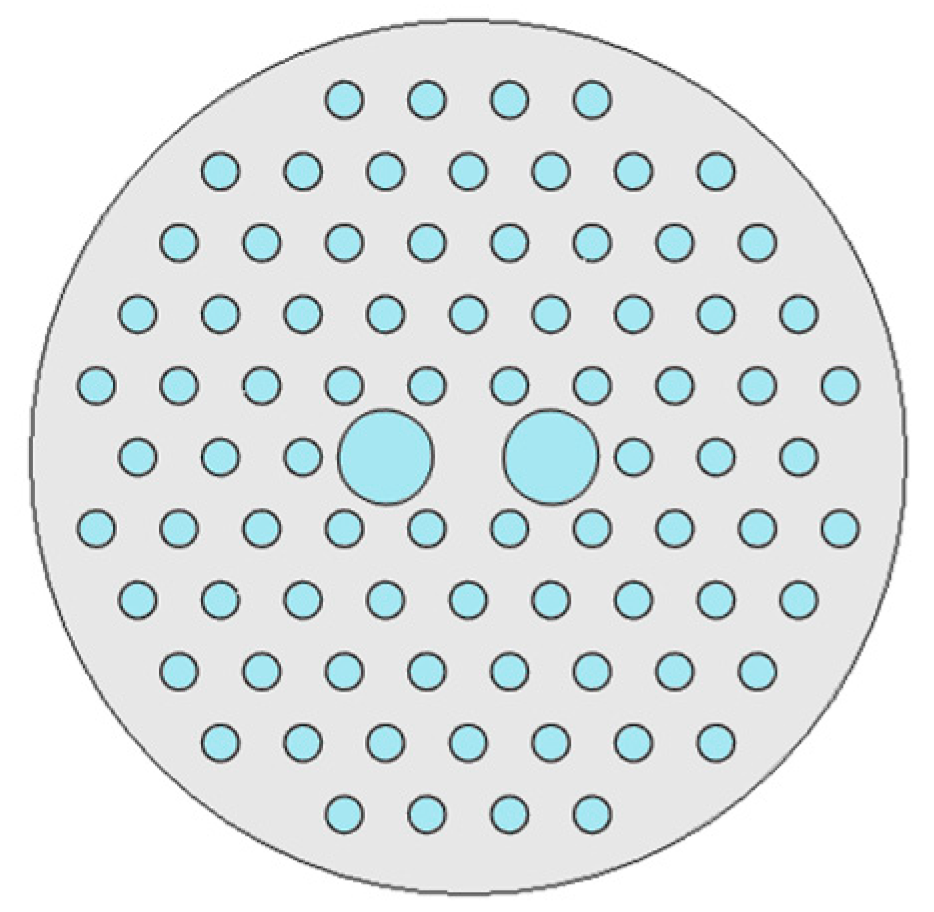

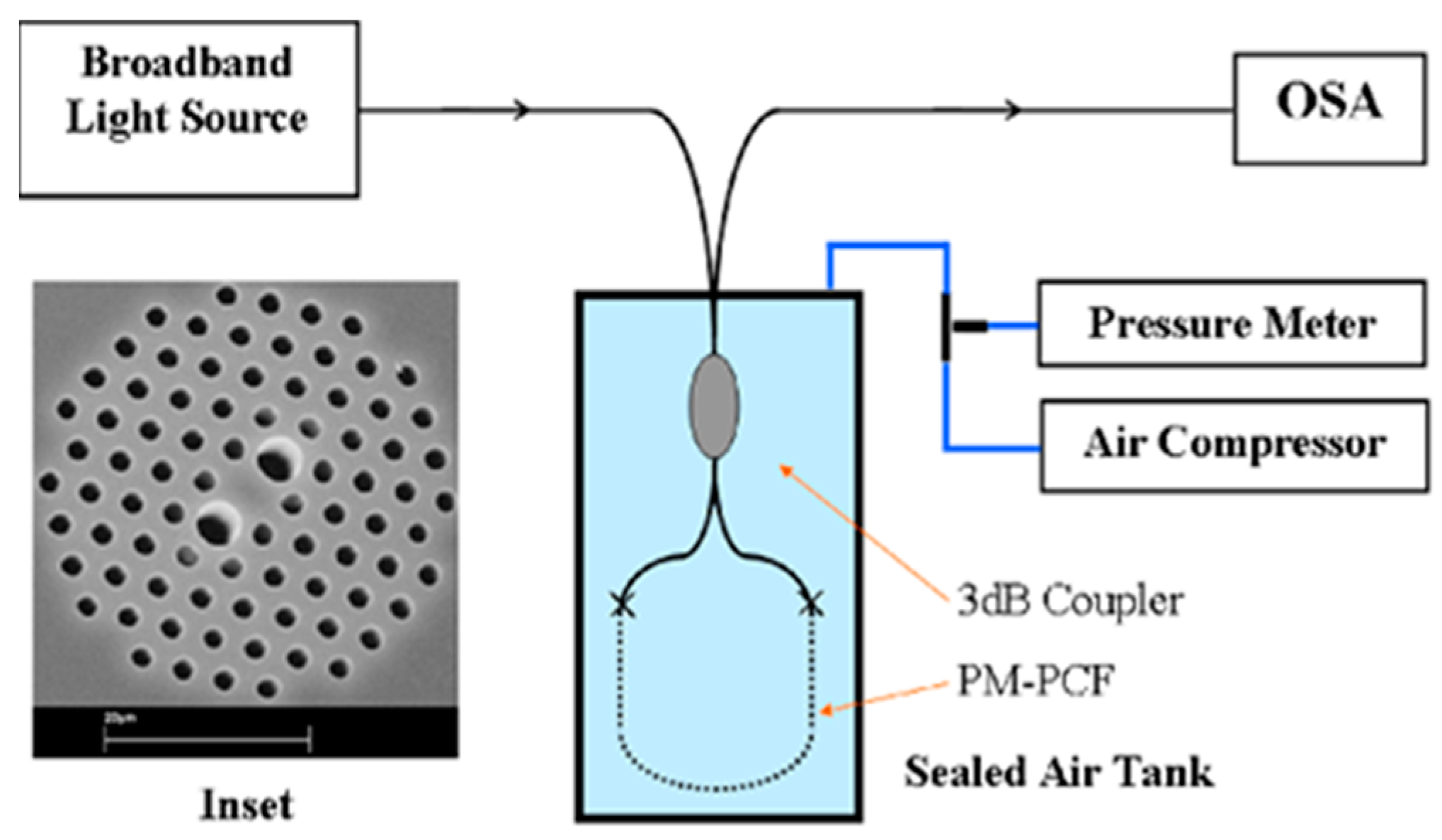
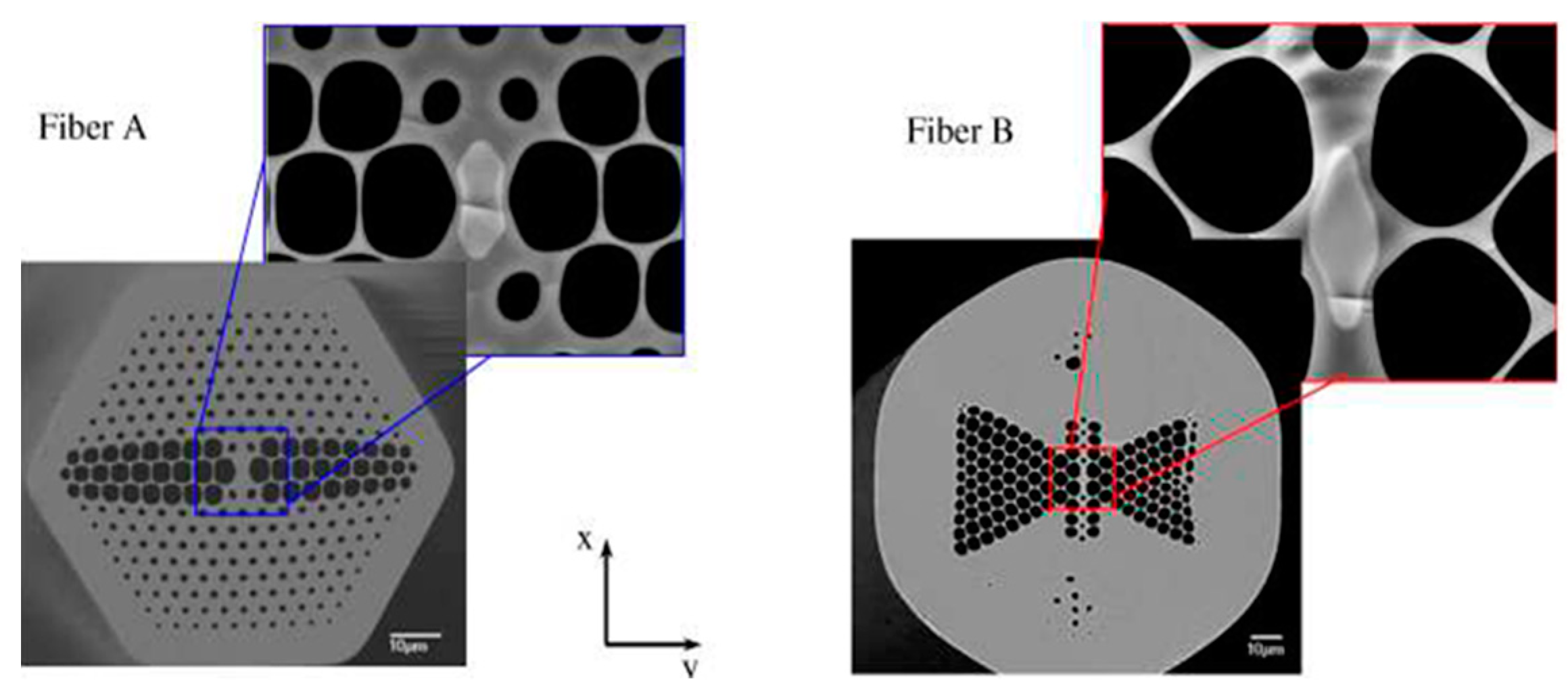
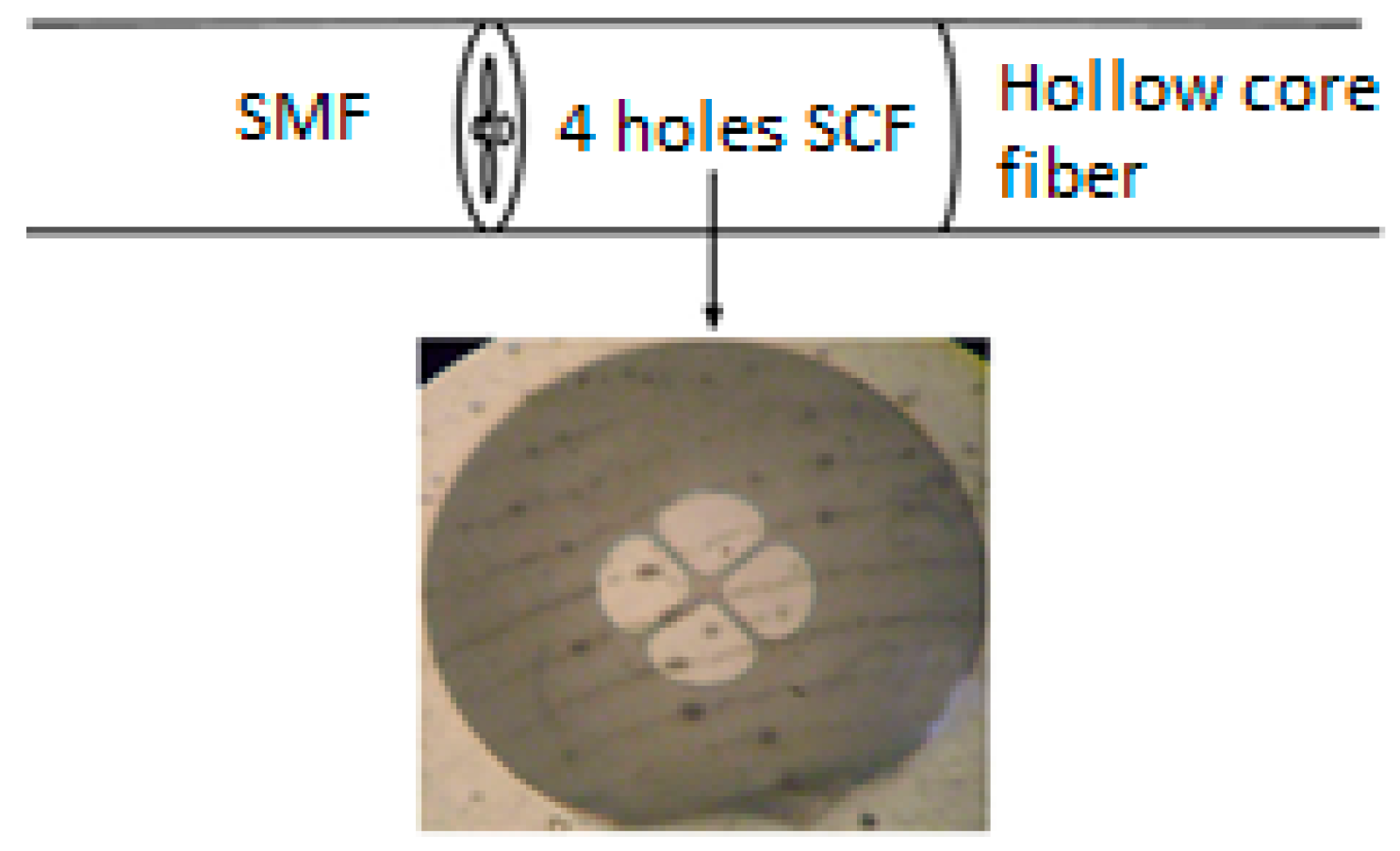
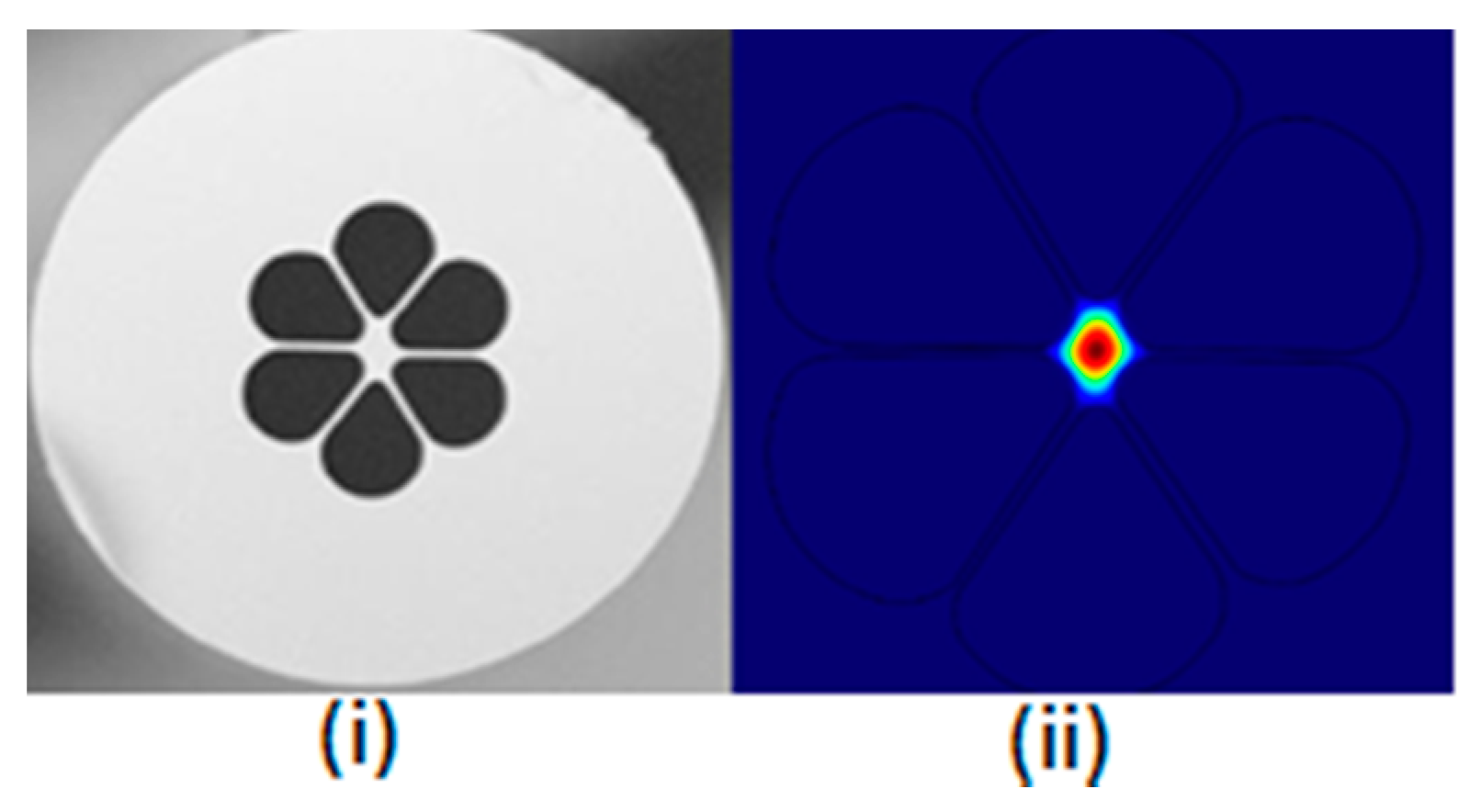
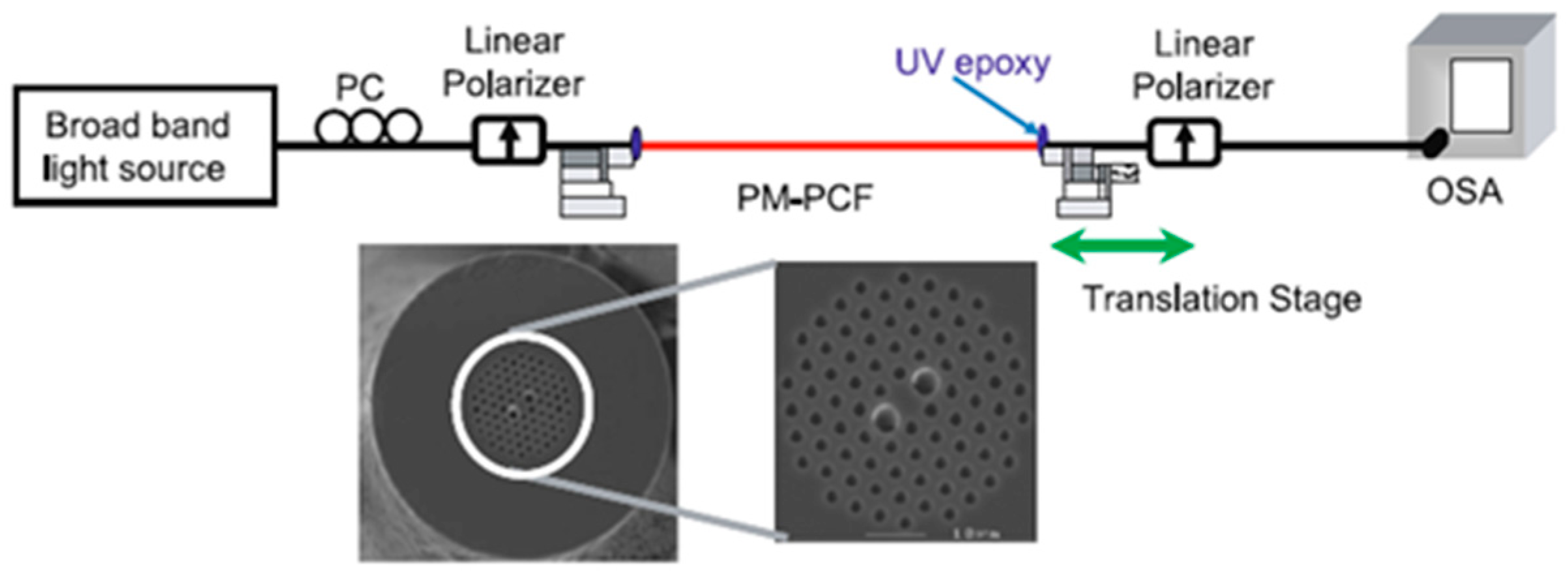
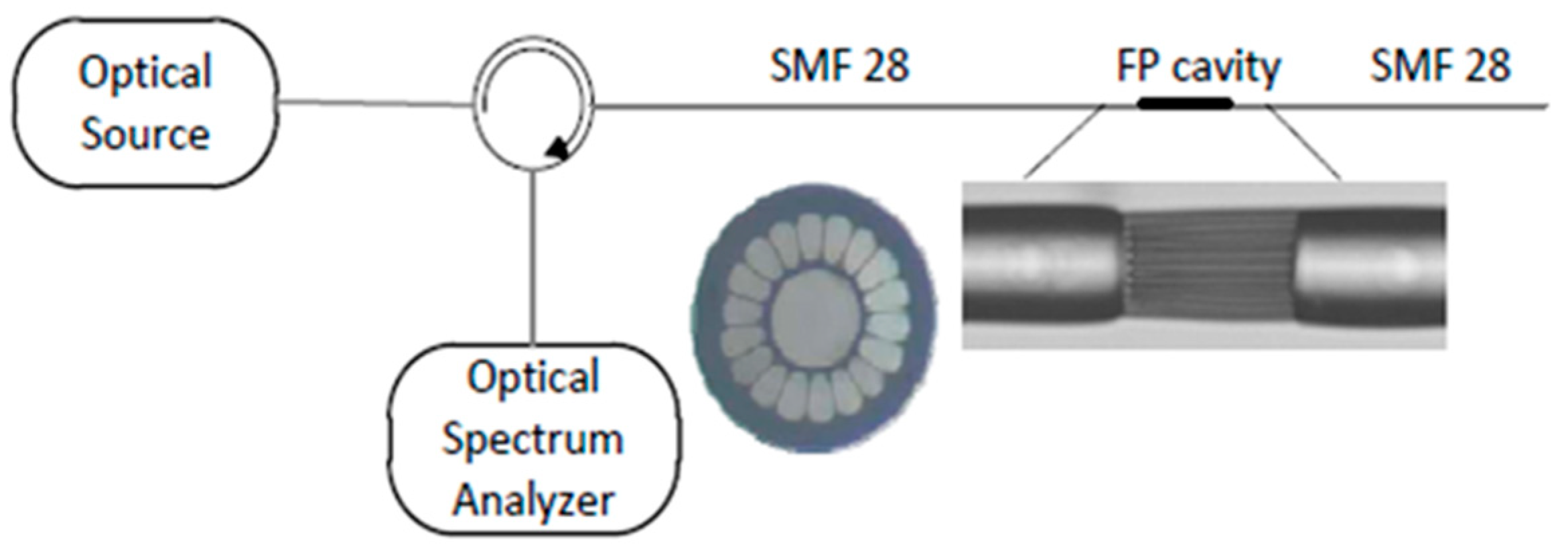


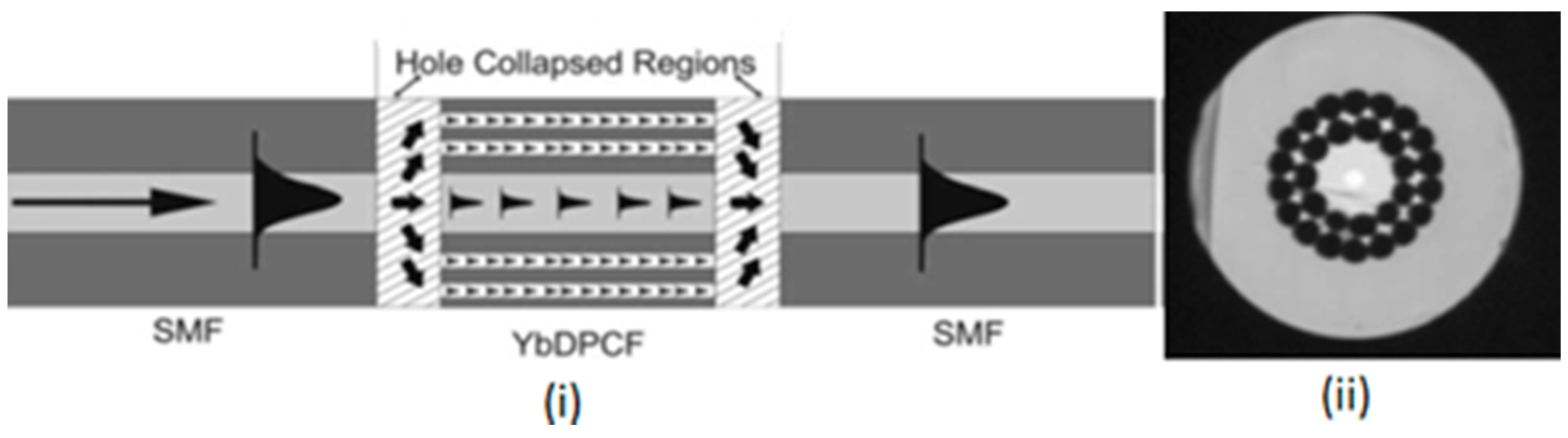


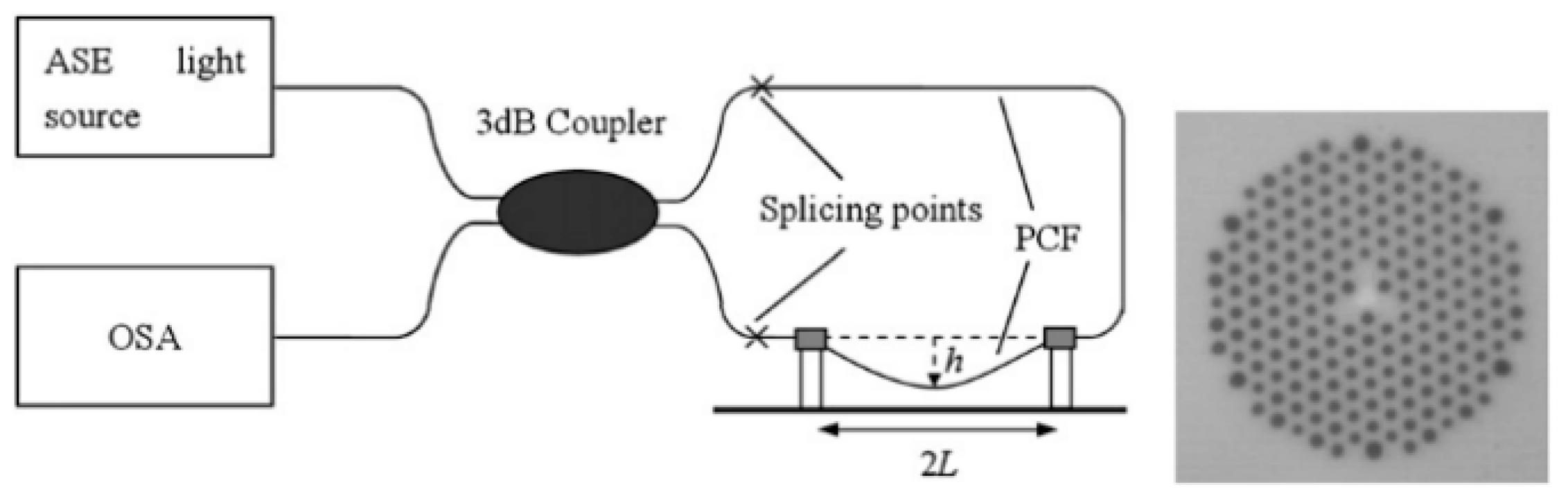

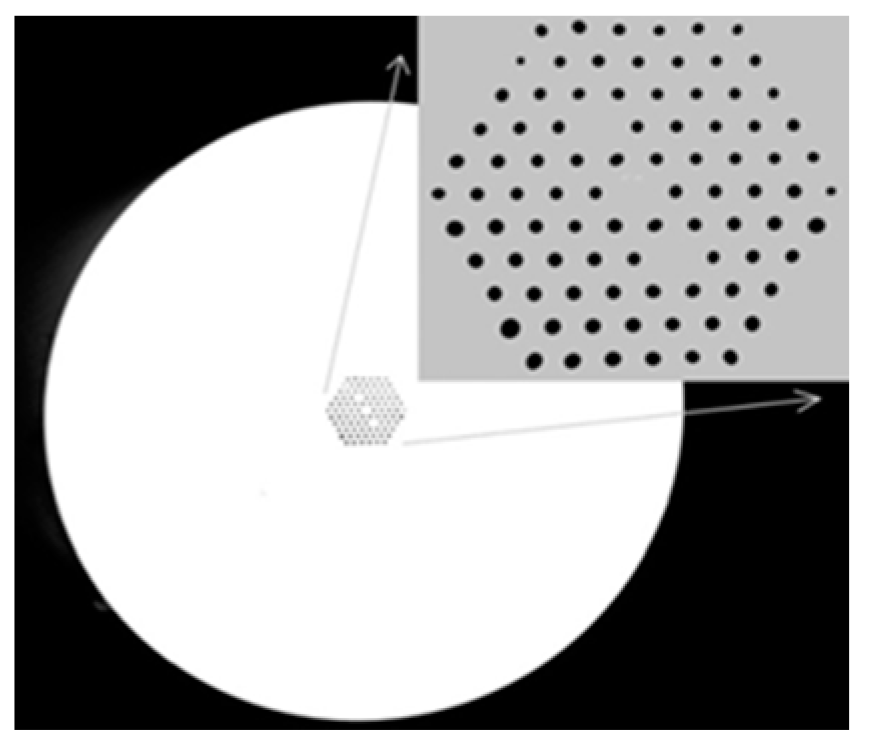



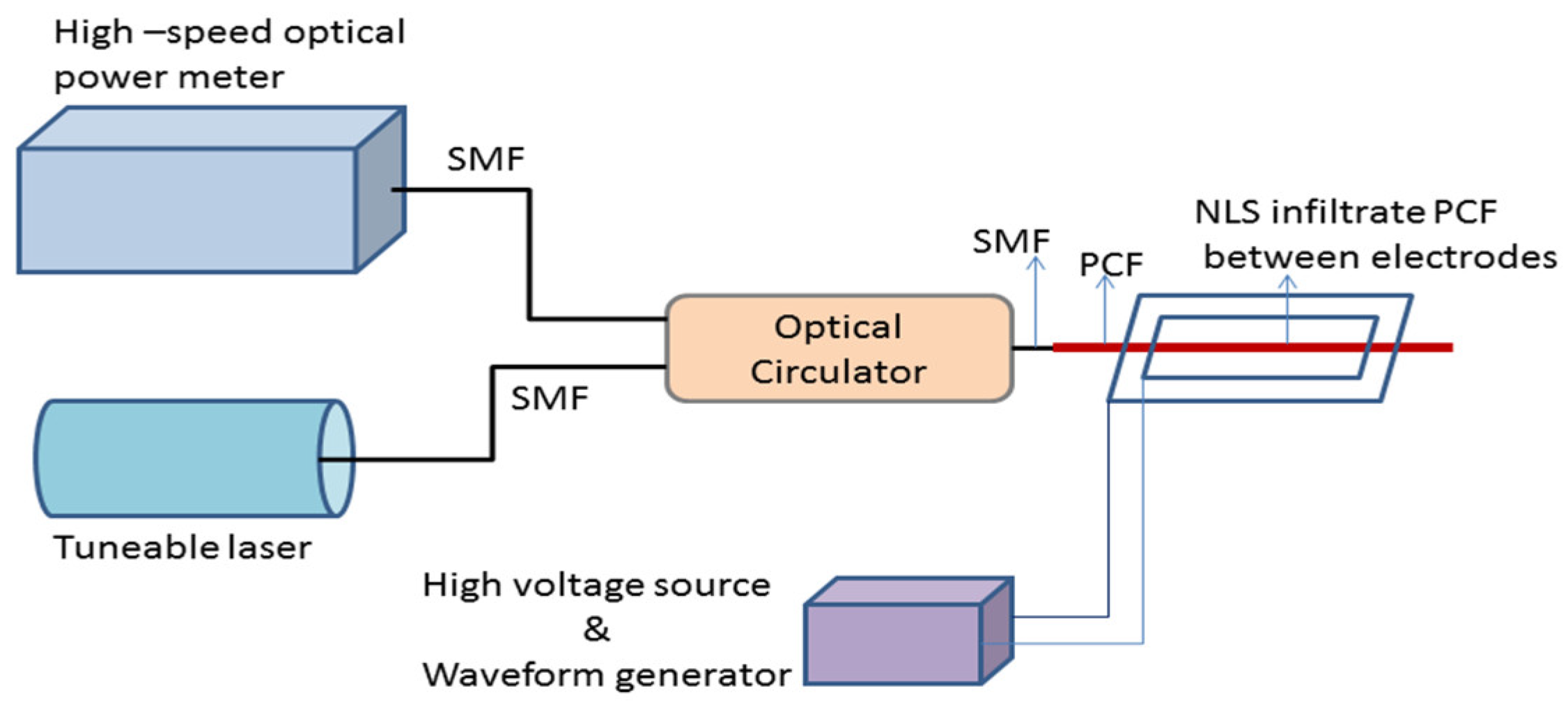

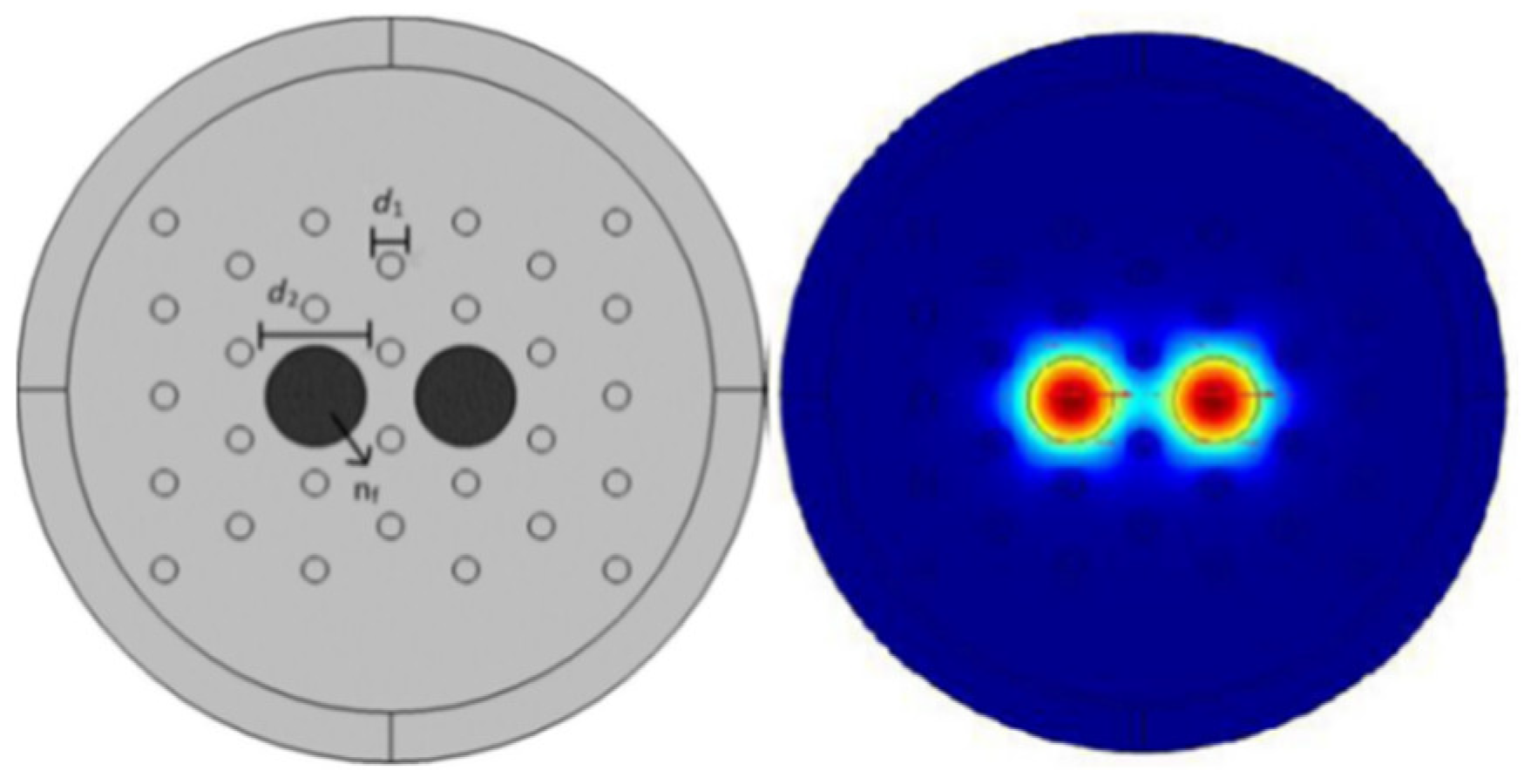
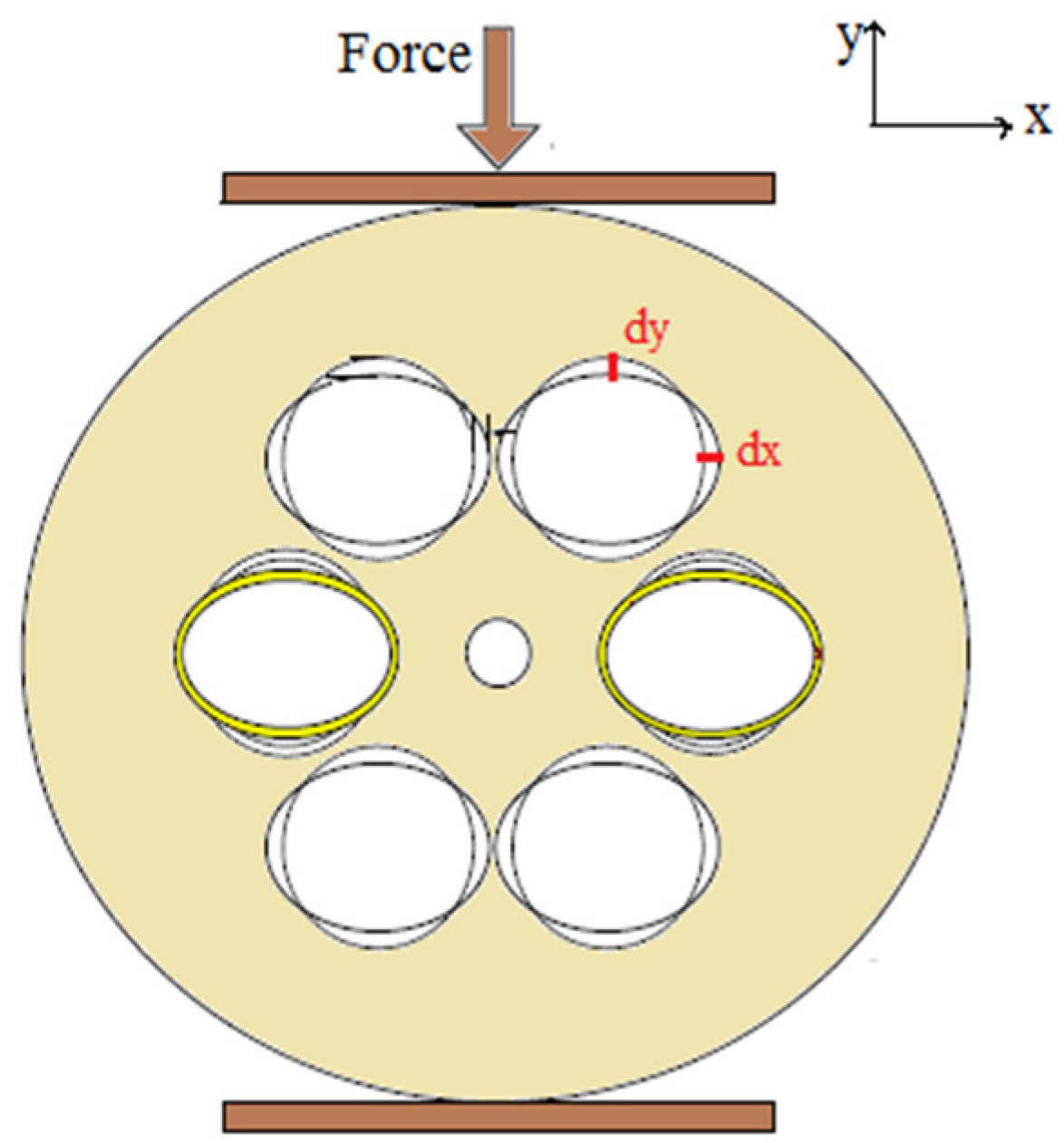
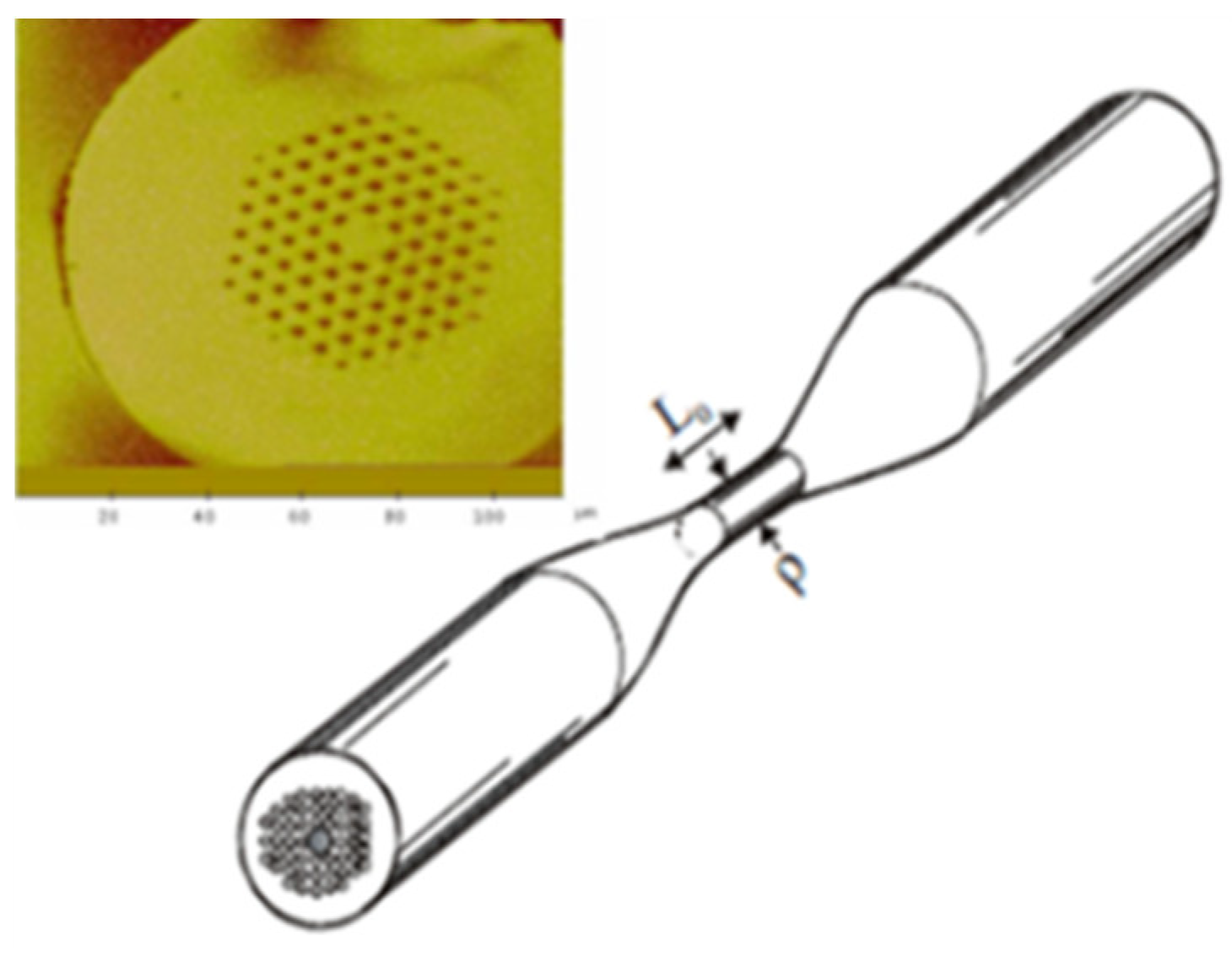


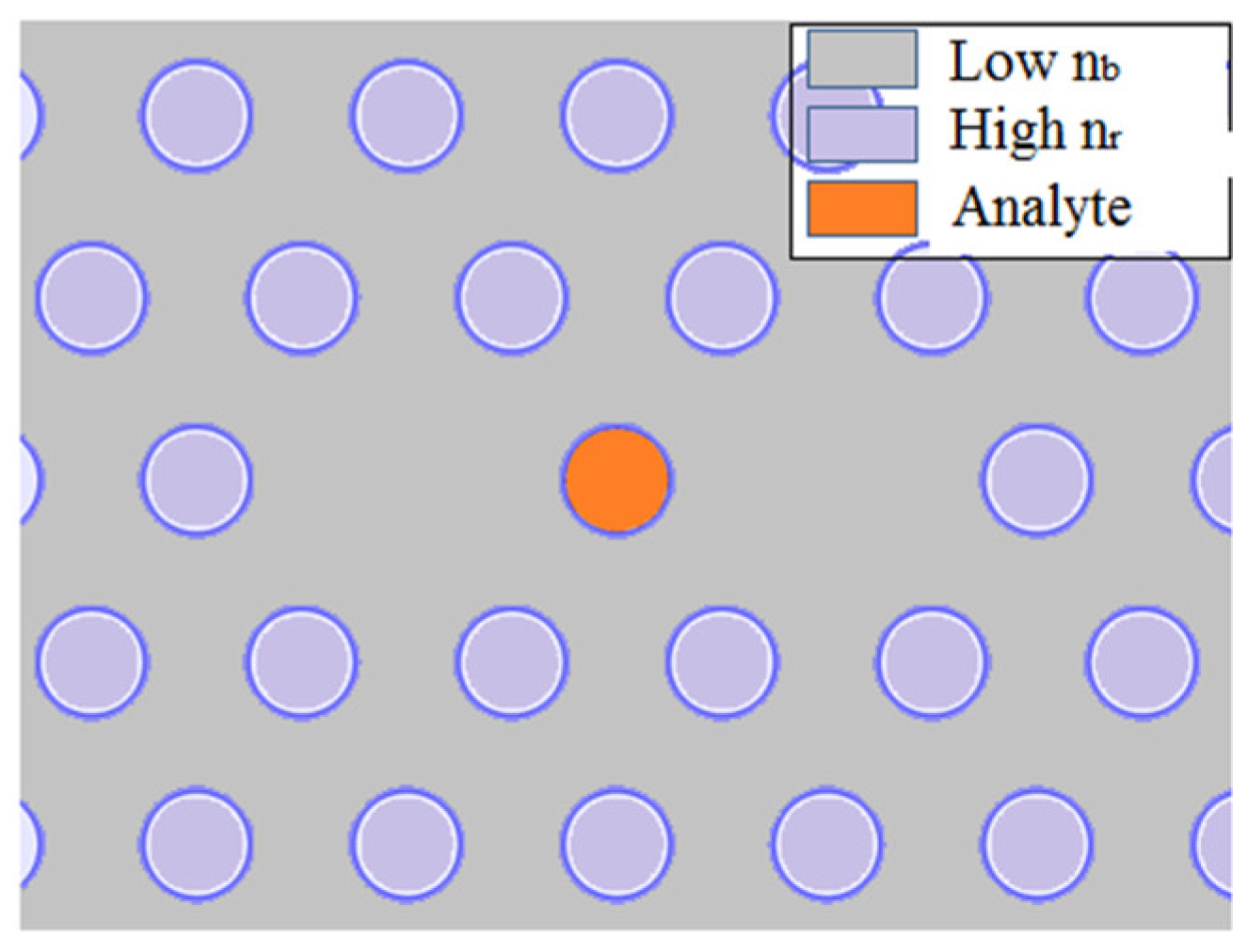
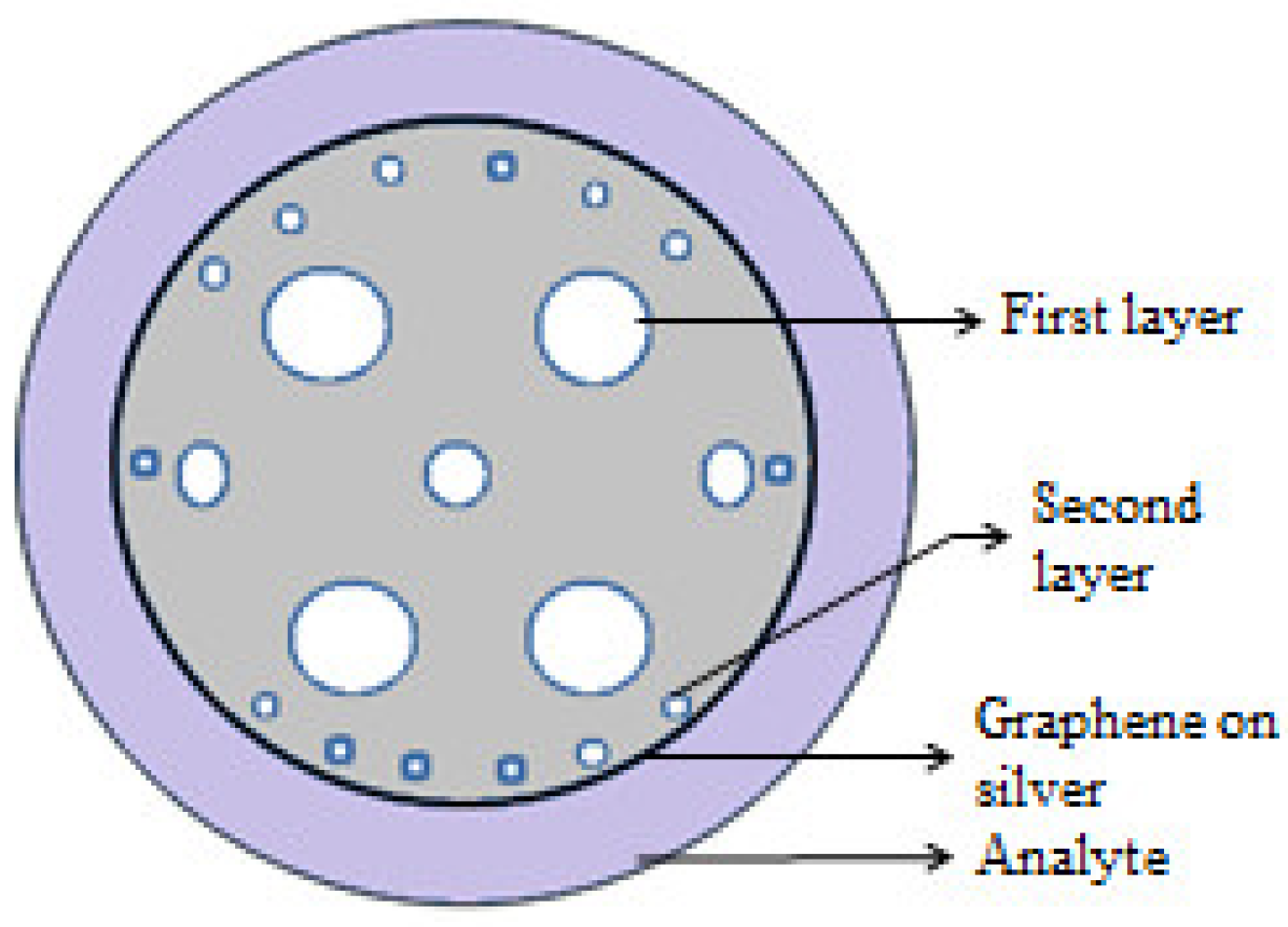
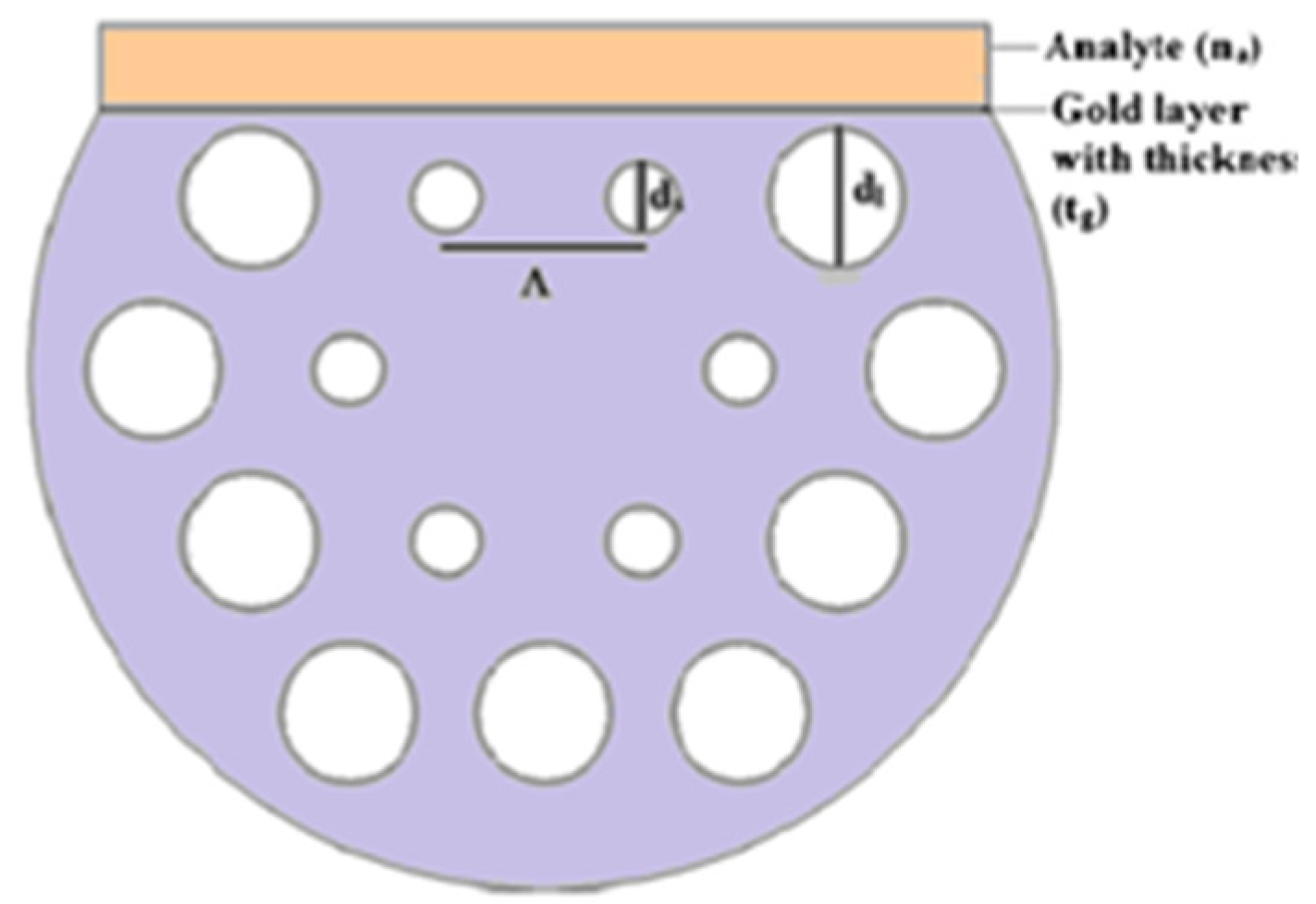

| Reported Structure | Sensing Temperature Range (°C) | Observed Quantity | Sensitivity | Ref. |
|---|---|---|---|---|
| TOPAS polymer optical fiber Bragg grating | 21–33 | Wavelength | −78 pm/°C | [46] |
| Tip interferometer using PCF spliced with SMF | 20–100 | Wavelength | 10 pm/°C | [47] |
| Mach–Zehnder interference technique combined with PCF spliced with MMF | 30–120 | Phase shift/length | 0.4272 radian/°C/cm | [48] |
| Fabry–Perot interferometer-based PCF containing inline microcavity and spliced with SMF | 26–103 | Wavelength | 12 pm/°C | [49] |
| Plasmon resonance-based liquid crystal PCF containing gold nanowire | 30–50 | Wavelength | 10 nm/°C | [50] |
| Microcavity incorporated solid core PCF concatenated with tapered SMF | 40–80 | Power | 0.21 dBm/°C | [51] |
| Compact and liquid infiltrated asymmetric dual elliptical core PCF | 30–34 | Wavelength | 42.99 nm/°C | [52] |
| Multibeam Mach–Zehnder interferometer using a PCF with two asymmetric cores | 25–500 | wavelength | 1.24 pm/°C | [53] |
| Isopropanol-filled PCF long period grating | 20–50 | Wavelength | 1.356 nm/°C | [54] |
| Selectively filled solid core PCF consisting a central air bore | −80 to 90 | Wavelength | −6.02 nm/°C | [55] |
| Reported Structure | More about These Sensors | Sensitivity | Ref. |
|---|---|---|---|
| Periodically tapered long-period gratings combined with PCF | Can measure pressure up to 180 bar | 11.2 pm/bar | [61] |
| Modal interferometer based high birefringence PCF | - | 3.36 nm/MPa | [62] |
| Polarization-maintaining PCF-based Sagnac interferometer for downhole application | Measured at 1320 nm | 4.21 nm/MPa | [63] |
| Side-hole polarization-maintaining PCF | - | −2.30 × 10−5/MPa | [64] |
| Bragg grating based highly birefringent microstructured optical fiber | Measured at 1550 nm | 33 pm/MPa | [65] |
| Reported Structure | Strain Range (µε) | Sensitivity | Ref. |
|---|---|---|---|
| PCF-based long-period fiber-grating | 0–800 | −7.6 pm/µε | [73] |
| PCF-based Mach–Zehnder type interferometers introducing coupling point | 0–3250 | ~2.2 pm/µε | [74] |
| Fiber Bragg gratings photo-written in PCF having refractive index-neutral germanium/fluorine codoped core | 0–3500 | 1.166 pm/με | [75] |
| In-line fiber Mach–Zehnder interferometer using solid core large mode area PCF | 0–2500 | −3 pm/µε | [76] |
| Modified PCF-based Mach–Zehnder interferometer | 0–1300 | 11.22 dB/mε | [77] |
| Fiber ring cavity laser with a photonic crystal fiber PCF in-line Mach–Zehnder interferometer structure | 0–2100 | 2.1 pm/µε | [78] |
| PCF with two asymmetric cores | 0–4000 | −1.59 pm/µε | [53] |
| Reported Structure | Spectral Range (nm) | RI Range | Observed Quantity | Sensitivity | Resolution (RIU) | Ref. |
|---|---|---|---|---|---|---|
| Stable photonic crystal fiber modal interferometer | 1250–1340 | 1.33–1.45 | Interference pattern shift | - | 7 × 10−5 | [113] |
| Surface long-period gratings incorporated D-shaped photonic crystal fiber | 1250–1650 | 1.00–1.45 | Wavelength | 585.3 nm/RIU | - | [114] |
| Extrinsic cavity formed by a micromirror and a photonic crystal fiber tip which contains a bifunctional lens with large radius of curvature | 1260–1350 | 1.328–1.357 | Intensity | - | 2.60 × 10−5 | [115] |
| Directional coupler based on PCF polymer fiber | 400–900 | 1.337–1.344 | Wavelength | 1.66 × 103 nm/RIU | ~2 × 10−6 | [116] |
| SPR based multicore flat fiber | 1000–1500 | 1.470–1.475 | Wavelength | 23,000 nm/RIU | 4.35 × 10−6 | [117] |
| Four channel containing PCF combined with gold wire | 1600–2000 | 1.30–1.79 | Wavelength | 3233 nm/RIU | 3.09 × 10−5 | [118] |
| D shaped PCF combined with metamaterials | 755–830 | 1.34–1.36 | Wavelength | 3700 nm/RIU | 2.70 × 10−5 | [119] |
| Gold nanowire consisting solid core PCF | 600–1100 | 1.27–1.36 | Wavelength | 2350 nm/RIU | 2.8 × 10−5 | [120] |
| SPR based dual polarized spiral PCF | 550–850 | 1.33–1.38 | Wavelength | 4600 nm/RIU | - | [121] |
| Dual core based microstructured optical fiber | 500–900 | 1.35–1.51 | Wavelength | 7000 nm/RIU | 7 × 10−6 | [122] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De, M.; Gangopadhyay, T.K.; Singh, V.K. Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview. Sensors 2019, 19, 464. https://doi.org/10.3390/s19030464
De M, Gangopadhyay TK, Singh VK. Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview. Sensors. 2019; 19(3):464. https://doi.org/10.3390/s19030464
Chicago/Turabian StyleDe, Moutusi, Tarun Kumar Gangopadhyay, and Vinod Kumar Singh. 2019. "Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview" Sensors 19, no. 3: 464. https://doi.org/10.3390/s19030464
APA StyleDe, M., Gangopadhyay, T. K., & Singh, V. K. (2019). Prospects of Photonic Crystal Fiber as Physical Sensor: An Overview. Sensors, 19(3), 464. https://doi.org/10.3390/s19030464





