Underwater gliders constitute autonomous robots designed to perform multi-sensor oceanographic sampling, for long periods in large regions. They represent a valid alternative to expensive research vessels campaigns for a wide range of applications, including water quality monitoring, detection of algae bloom hazards, ocean structure characterization, pollution source identification or sea-floor mapping, to name just a few [
1,
2]. However, their operation nowadays still require human supervision, both for short- and long-term missions. This scheme can be suitable for simple applications, but when dealing with more complex multi-objective missions, automatic path planning tools are required; this is the main motivation of our work, contributing to the development of underwater gliders with higher autonomy and better operational capabilities for multi-objective applications.
The paper first introduces, in
Section 1.1 and
Section 1.2, the concepts of the main areas our work aims to contribute to, which are underwater glider path planning and multi-objective optimization; then
Section 1.3 presents the literature review regarding multi-objective path planning. The proposal is presented in
Section 2, including the problem definition, in
Section 2.1, and methodology, in
Section 2.2, applied to address the problem of glider path planning using multi-objective optimization.
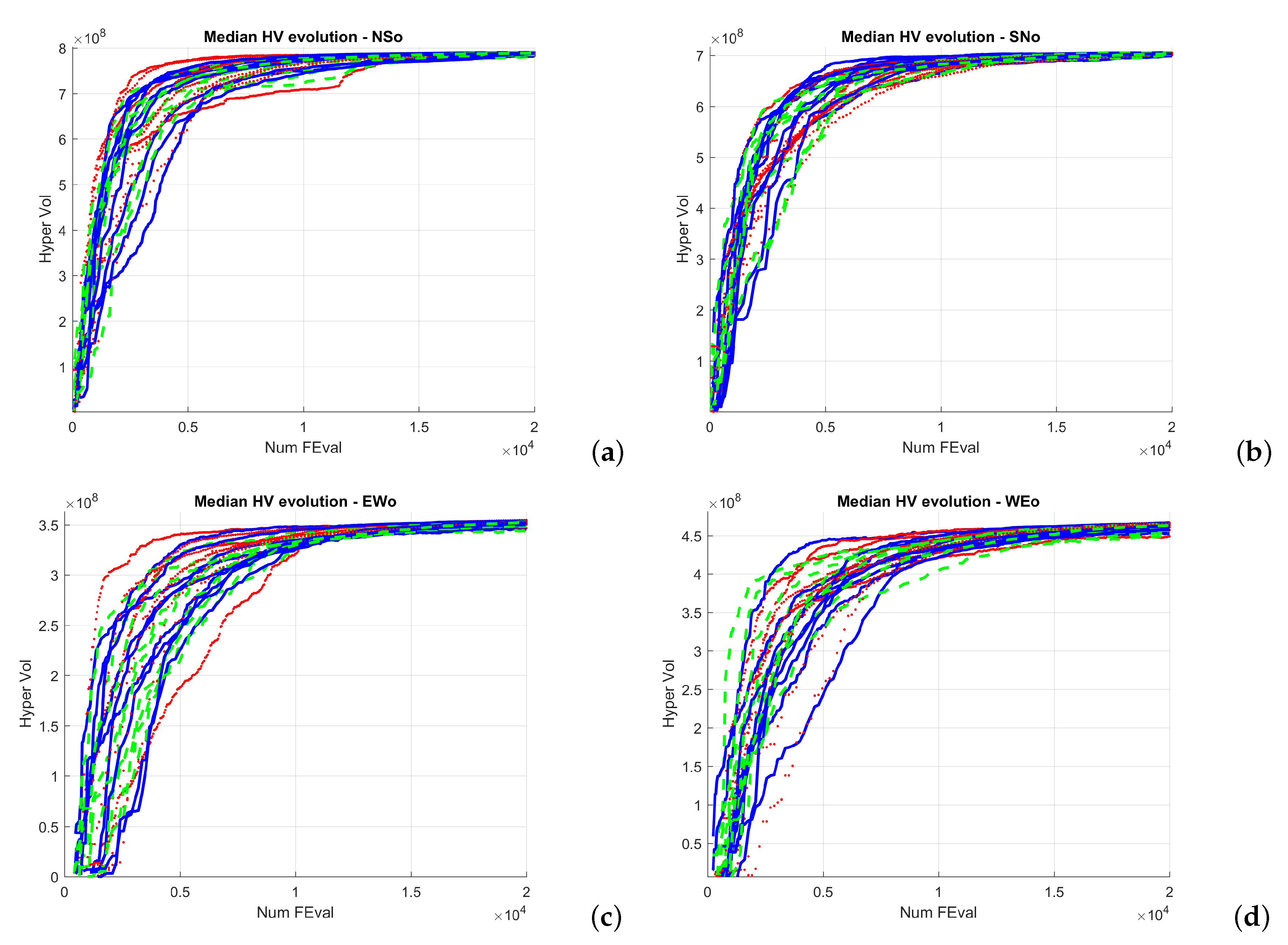
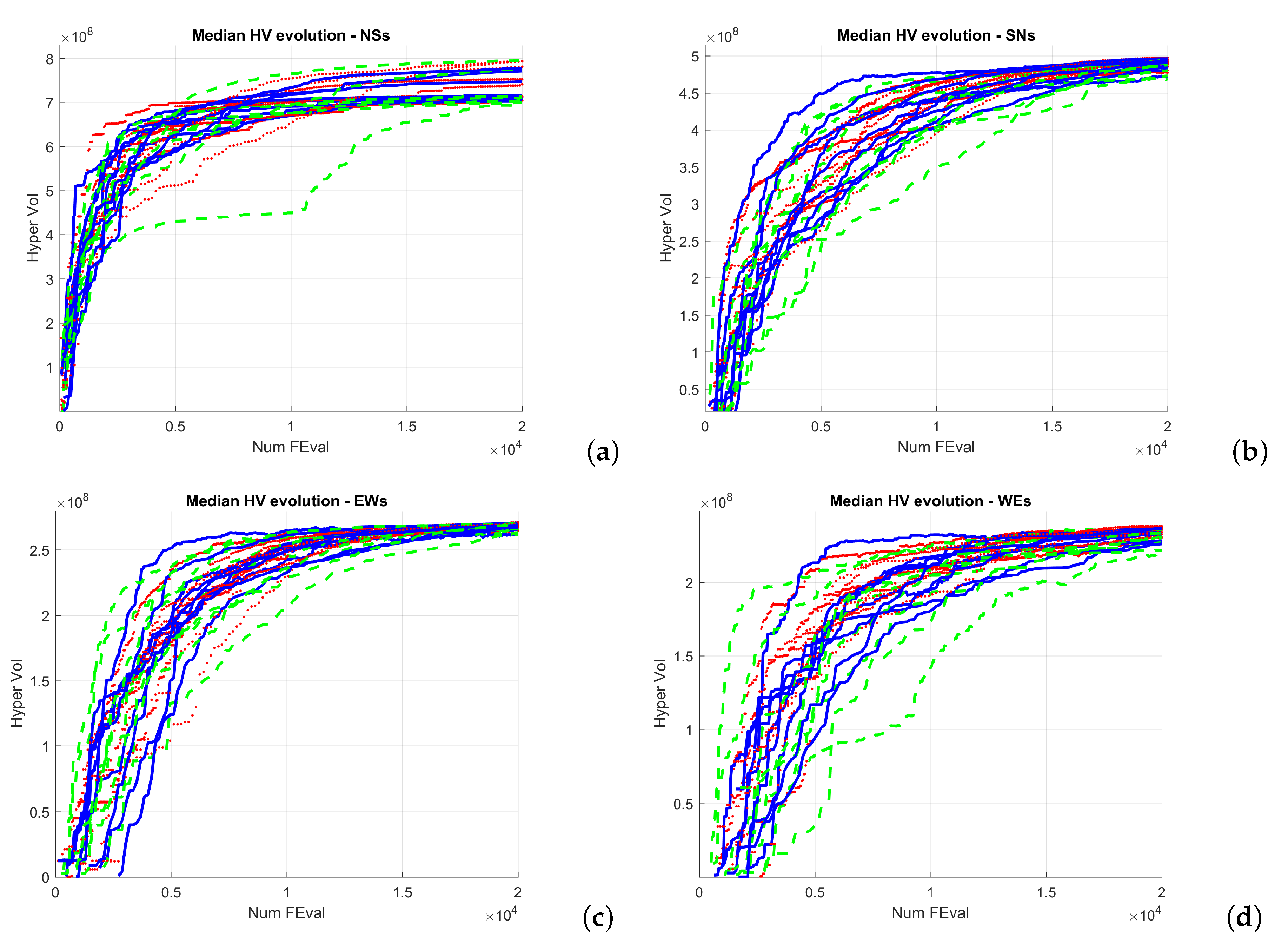
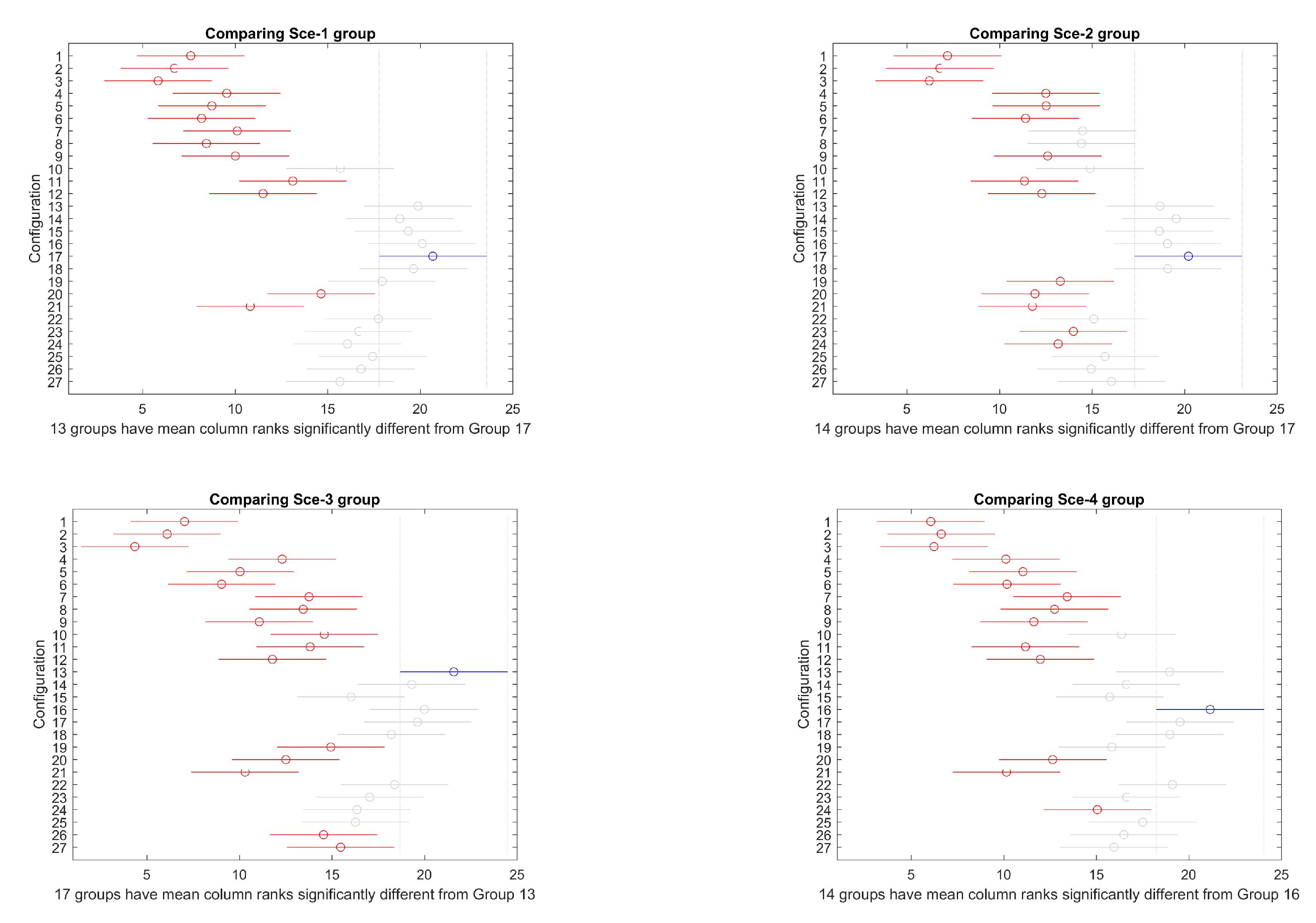
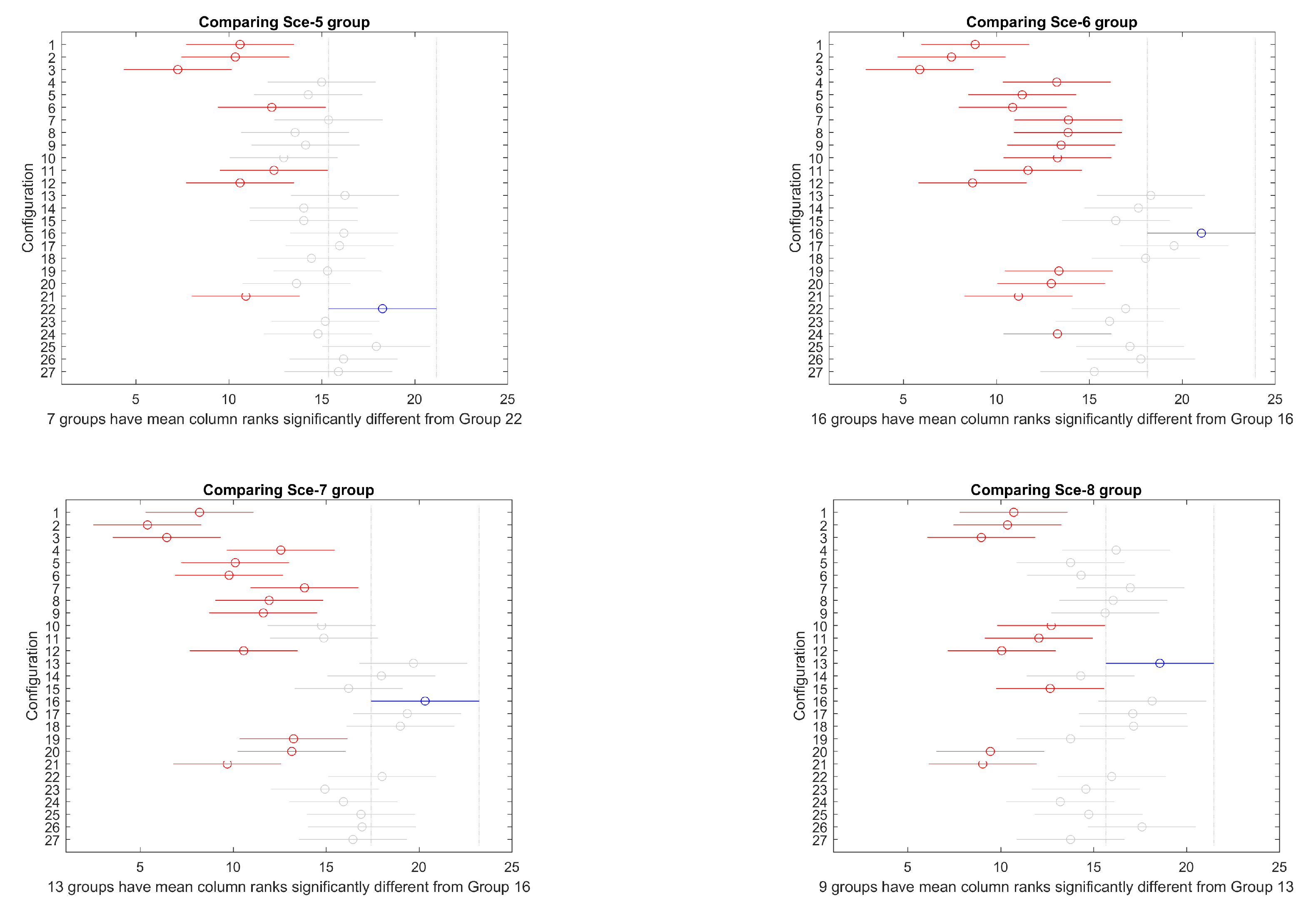
Section 3 describes the simulator, test scenarios, and algorithm configurations.
Section 4 presents the experiments carried out and the results obtained, which are discussed in
Section 5. Finally, the conclusions and some future work are outlined in
Section 6.
1.1. Underwater Glider Path Planning
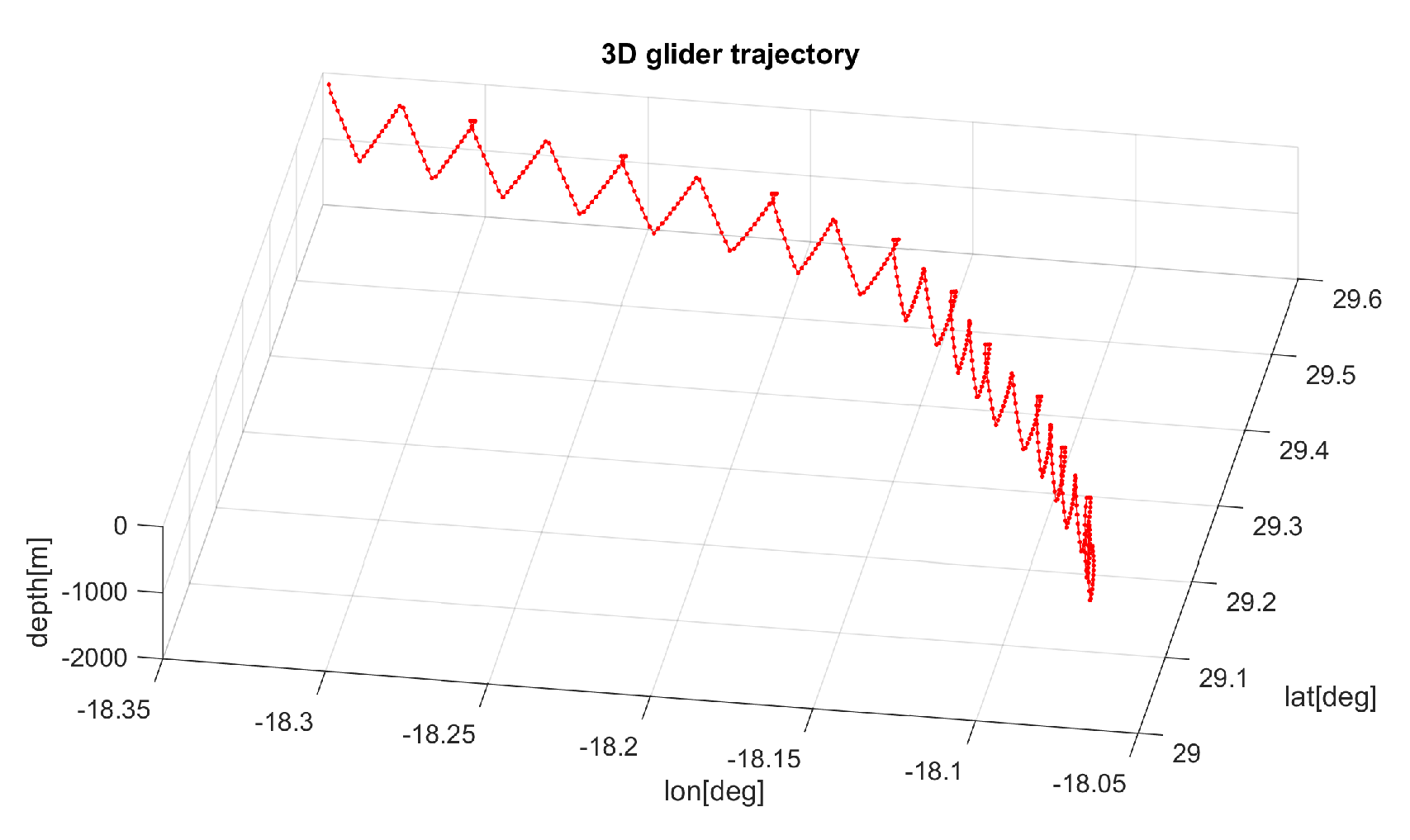
Ocean gliders are torpedo-shaped vehicles that make use of a highly energy efficient propulsion system: They modify their buoyancy and pitch angle by means of an artificial swim bladder operation combined with internal batteries displacement. The induced descend–ascend movement is transformed into effective horizontal displacement by the interaction between the water column and the vehicle hydrodynamics, resulting in a saw-tooth like trajectory profile similar to the one shown in
Figure 1. Typically, the vehicle performs two or three down-up cycles, called
yo-yo’s, between pre-defined max- and min-depths before returning to surface to start a new sequence or
stint each 6–8 h. As energy consumption is mainly associated with the activation of the electric pump, which is responsible for the buoyancy control at inflection points, extremely long-term missions are possible with these vehicles.
During a glider mission, the control centre relies on satellite communication to upload commands to the glider when at the surface, including target waypoints or depth limits, for example. The surfacing period has to be kept as short as possible to avoid collisions with surface vessels, reduce biofouling, and decrease vehicle’s drift. After the surfacing, the glider submerges again to perform another set of stints. Although major deviations from expected trajectories occur generally at surface (due to strong currents), when the glider dives, its location can only be estimated using its on-board sensors, producing errors that grow with time. In order to reduce this uncertainty, as the ocean is a very dynamic and unknown environment, researchers have developed different strategies. Woithe et al. [
4], for example, use a doppler velocity log with promising results on predicting glider position underwater; Wang et al. [
5] propose a dynamic model-aided localization scheme that proved to be able to improve significantly the precision in the estimation of the vehicle position.
The main drawback of (passive) ocean gliders is that they can only reach low horizontal speeds (around 0.25 m/s). To optimize their operation, factors such as bathymetry, marine traffic or, remarkably, ocean currents, have to be anticipated, so that suitable paths are well planned in advance. As this constitutes a 4D problem (latitude, longitude, depth, and time), with variable environment conditions, the process is not so trivial.
From the traditional path planning, the strategies to achieve the best path for gliders kept evolving. An A* search procedure was done by Garau et al. [
6], in areas with different length scale eddies and currents with varying intensities. However, the authors considered the usage of constant thrust power to navigate the vehicle. They also tested different start and end points across the simulation area, to find the best paths and best locations to achieve their objectives.
The usage of Lagrangian coherent structures carried out by [
7] showed how those can be used to find near optimal trajectories in dynamic environments, considering a 2D glider kinematic model. They used ocean current velocities collected with an HF radar system to calculate the optimal trajectories for the vehicle.
A fast marching based approach (called FM*) was used by Petres et al. [
8] in order to extract a continuous path from a discrete representation of the environment. The authors considered underwater currents, with the vehicle turning radius being added as a constraint.
The backward study of a particle tracking equation provided an optimal path in [
9], with the authors stating that the system can easily handle forbidden regions (such as strong currents areas) and real obstacles that affect the ocean flow and consequently the vehicle pathway.
Further strategies to address underwater glider path planning (UGPP) under complex scenarios (static and dynamic obstacles) are discussed in [
10], as the classical path planning might not be adequate. Those strategies include pointing the vehicle to the destination and make small adjustments during the mission or in adverse zones position the vehicle across the current, in order to reach a place with weaker and/or more favourable currents. The same work suggests some metrics to evaluate performance, in order to determine how well defined the path-planning arrays are, considering the mission objectives.
The work presented by [
11] concluded that adequate path planning contributes to a substantial energy saving set of solutions compared to straight line trajectories, in cases when ocean currents and vehicle’s speed are comparable. The authors also point out that a straight line trajectory from start to end can only be an optimum path when the currents’ velocity does not exceed half of the vehicle’s velocity. Energy and time saved with path planned missions can be used to either increase the distance travelled and/or add more sensors.
A stochastic optimization methodology was carried out by Subramani et al. [
12], focused on obtaining the best paths from the viewpoint of energy-optimal missions. They also concluded that vehicles that can change their displacement speeds can reach the programmable locations by using favourable currents, saving energy for crossing areas with unfavourable conditions.
UGPP challenge has also been tackled using evolutionary techniques, like in Zamuda et al. works [
13,
14], including eddy sampling applications [
15].
1.2. Multi-Objective Optimization
In early days, due to the lack of methodologies, multi-objective optimization problems (MOOP) in general were solved by casting all objectives in one and solving it as a single objective problem [
16]. Currently, MOOP are solved differently by optimizing a group of two or more fitness functions (usually in conflict [
17]), without prejudice among them, until no more improvements to the current solution set could be achieved. MOOP results are (usually) a set of optimal solutions that minimize all the objective functions at the same time, or either maximize all the functions or a combination of maximization and minimization of different functions [
16,
18]. The set of optimal solutions is designated as Pareto front, on which a point
is called Pareto optimal IFF there does not exist another point,
, such that
, and
for at least one fitness function [
19]. Also, on the Pareto front, all the solutions yield the same optimal value [
20].
One way to tackle MOOP and obtain solutions that converge to a Pareto front is through the usage of evolutionary algorithms (EA), very popular among researchers because of its flexibility and easy adaptation to different problems. Also, as EA are population-based algorithms, they are well suited to be used to solve MOOP in form of multi-objective evolutionary algorithms (MOEA). Currently, the usage of MOEA can be found on multiple areas [
21], integrating diverse selection and estimation mechanisms.
A recent review of evolutionary multi-objective methods can be found in [
22], including some that became standards when dealing with MOOP, such as the NSGA-II algorithm. The work considers three types of MOEA: Pareto-based (such as NSGA-II [
23]), indicator-based (such as SMS-EMOA [
24]), and decomposition-based (such as MOEA/D [
25]), exposing their advantages and disadvantages. Also, choosing the right method depends on the dimension of the objective space, how many solutions should be generated, the distribution of solutions, and an a priori knowledge about the location and shape of the Pareto front.
Considering real problems of engineering, EA are currently being used for energy, electrical, structural and civil engineering, scheduling, transport, combinatorial optimization, and more, as described by Greiner et al. in [
26]. However, these are just some examples, as many other problems that need to do multi-objective optimizations are using EA.
1.3. Multi-Objective Path Planning
One area in which multi-objective optimization is important is in path planning. Multi-objective path planning (MOPP) problems will be introduced here, including different techniques and applications discussed in the scientific literature.
MOPP is the way of finding a feasible path for a vehicle that requires travelling from a staring point A to a final point B, and accomplishes all the objectives planned for the mission. Considering the most common objective—reaching a target—other objectives for the mission might include (but are not limited to), verifying several path properties, limiting battery consumption, and crossing or avoiding specified areas [
10]. Previous studies solved MOPP in different ways, for diverse types of vehicles and different environments. In [
27,
28], the authors used genetic algorithms (GA) to optimize both length and difficulty of the path, adding a basic path repair mechanism to make non-valid paths usable, on a 2D realm.
The genetic algorithm NSGA-II was used by Mittal and Deb [
29] to perform offline path planning for an unmanned aerial vehicle, with the fitness functions being avoid collisions, no abrupt changes to the path, and not flying above a specified altitude. Also, Lee et al. [
30], worked on path planning optimization for unmanned aerial vehicles, using NSGA-II combined with Nash-equilibrium to decrease the time for searching one global solution, showing that a hybridization with game theory is a valid choice to solve MOPP.
The usage of particle swarm optimization (PSO) to solve a MOPP was proposed in [
31], to find smooth and shorter paths, with parameter tuning, using a 2D map. Another work using PSO was carried out by Gong et al. [
32] to solve path planning on a 2D environment, incorporating previously known danger locations, and similarly in [
33], where path planning in a 2D uncertain environment, with danger sources and obstacles were concurrently being considered also using PSO. A spline approach is discussed in [
34], to perform MOPP with fitness functions being “path length and potential”, “obstacle hindrance”, and “visibility” of the robot. Davoodi et al. [
17] described a MOPP accounting for length and clearance of the path, using path refiner operators based on geometry parameters.
Later, Bopardikar et al. [
20] tried to find a path that minimizes a primary cost function subject to a bound on a secondary cost function, handling collision avoidance in all the vertexes along the path. The same work described planning in belief space, with collision probability and multi-objective, proposing one algorithm that is more accurate but with higher computation costs and another that sacrifices accuracy but is more efficient. Using the Mars Rover scenario (3D), Ref [
35] developed a MOPP using A* search with real objectives (minimize difficulty, danger, elevation, and length). Usage of the Pareto front and the Pareto optimal in every step of A* was proposed by [
36,
37] using memetic algorithms in order to optimize both path length and smoothness.
A survey of 2016 [
38], about applying nature inspired algorithms to solve MOPP, analysed the usage of particle swarm optimization, ant colony optimization, and artificial bee colony. In addition, Hidalgo et al. [
39] presented a firefly-based approach to pursue MOPP considering path safety, length, and smoothness, pointing to the path planning as one of the most researched topics in robotics.
One year later, in 2017 another publication [
40] reviews robot path planning techniques, with soft computing and heuristic approaches (artificial neural networks, fuzzy logic, wavelets, and genetic algorithms) replacing the classical methods (potential fields, roadmap, and cell decomposition). In same year, another work [
41] addressed the path planning for the problem of an aircraft climbing using PSO and a two-level optimization scheme, in order to improve search performance, with results showing 15% faster climbs saving 20% more fuel.
Later, in 2018, and also using PSO, Ref. [
42] compared their improved PSO algorithm against other evolutionary algorithms, showing better results finding collision free and feasible paths along with minimum length and terrain roughness for a car-like mobile robot. Using an adapted version of NSGA-II, Ref. [
43] was able to optimize three objectives and study the influence of the input parameters, when applying it to mobile robots on a 2D plane, obtaining fast optimization speeds and a good convergence of solutions. Also applied to mobile robotics, Ref. [
44] proposed a multi-objective evolutionary algorithm, tested using five scenarios and quality metrics.
Using a combination of ant colony and PSO on different optimization levels was studied by [
45], to find the best energy-efficient path for underwater vehicles on an eddy field, using uncertainty levels. An algorithm to do multi-objective path planning using PSO was proposed by [
46] applied to mobile sink in wireless sensor networks, employing the concept of Pareto front to select the global and local best solutions, outperforming other algorithms in several performance metrics.
Considering aerial vehicles, Ref. [
47] used a genetic algorithm to do collision-free shortest path planning, testing their proposal with and without restrictions to the path of aerial vehicles, stating that their solution can be applied to 3D environments. Another solution for multi-objective path planning for aerial vehicles was proposed by [
48], combining a genetic algorithm with ant colony and using maps of height, risk, quantity, and value of sensing information. Authors used small population sizes and generations and were able to obtain dynamic environmental adaptability and high utility paths. Ref. [
49] used an improved genetic algorithm to do multi-objective path planning, applied to a free-form surface milling, with three fitness functions (efficiency, energy, and carbon footprint) being converted to one single fitness function and replicating the travelling salesman problem. Another approach to multi-objective path planning using a genetic algorithm was done by [
50], by using both dynamic and static 2D environments and concluding that their matrix-binary codes approach is more efficient and robust than random search algorithms.
The usage of hybrid algorithms, was detailed later in [
51], applying hybrid particle-swarm optimization–modified frequency bat optimization algorithm to tackle 2D path planning. The fitness functions were collision-free path, path-smoothness, and shortest-distance, assuming some simplifications to ease the process, such as no kinematic constraints, circular obstacles, and the addition of the robot size to the obstacle size.
More recently, in 2019, Ref. [
52] combined the concepts of robust optimization and the integration of multiple scenarios as a multi-objective function, in order to investigate the relation between dominance and robustness.
Using a parallel genetic approach, Ref. [
53] tackled optimal path planning for single and multiple underwater vehicles, avoiding upstream currents in multi-objective optimizations by developing a new crossover operator in order to raise the diversity of the solution. Authors state two aspects when dealing with underwater vehicles: the importance of path planning tools and the usage of simulations to validate solutions before real tests.
The usage of a multi-objective firefly algorithm was proposed by [
54], which saves elite particles obtained on each generation to ensure a higher ability to escape local optima results, increases the convergence speed and precision of the solution, being suitable for high-complexity multi-objective optimization problems.