High Precision Dimensional Measurement with Convolutional Neural Network and Bi-Directional Long Short-Term Memory (LSTM)
Abstract
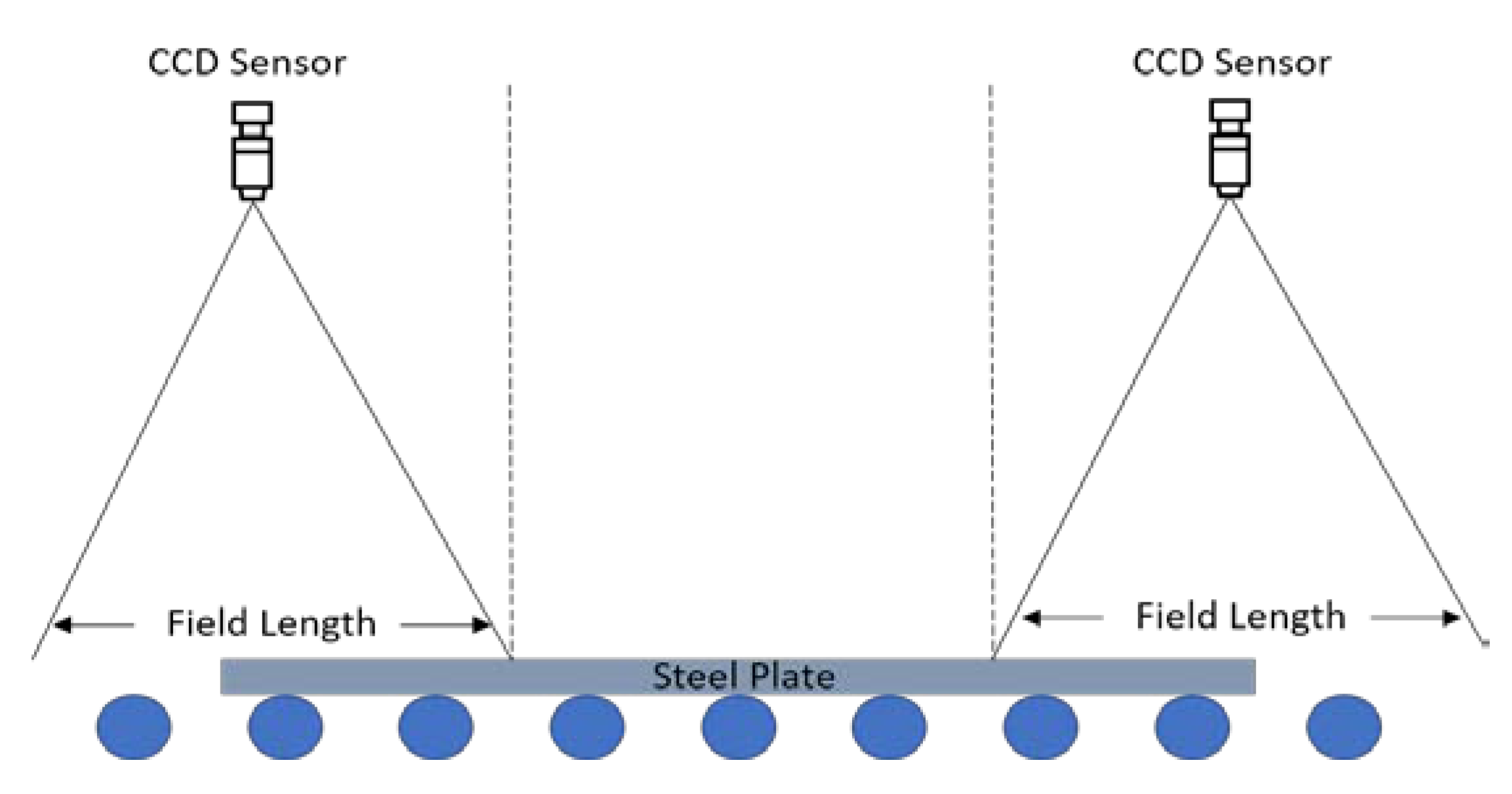
1. Introduction
- We propose a sub-pixel edge detection method based on deep learning for high precision dimensional measurements.
- We adopt CNN to extract features from images and introduce the anti-noise ability by adding bi-directional LSTM.
- We offer a sub-pixel edge detection dataset of steel plate used in training and testing sub-pixel edge detection methods.
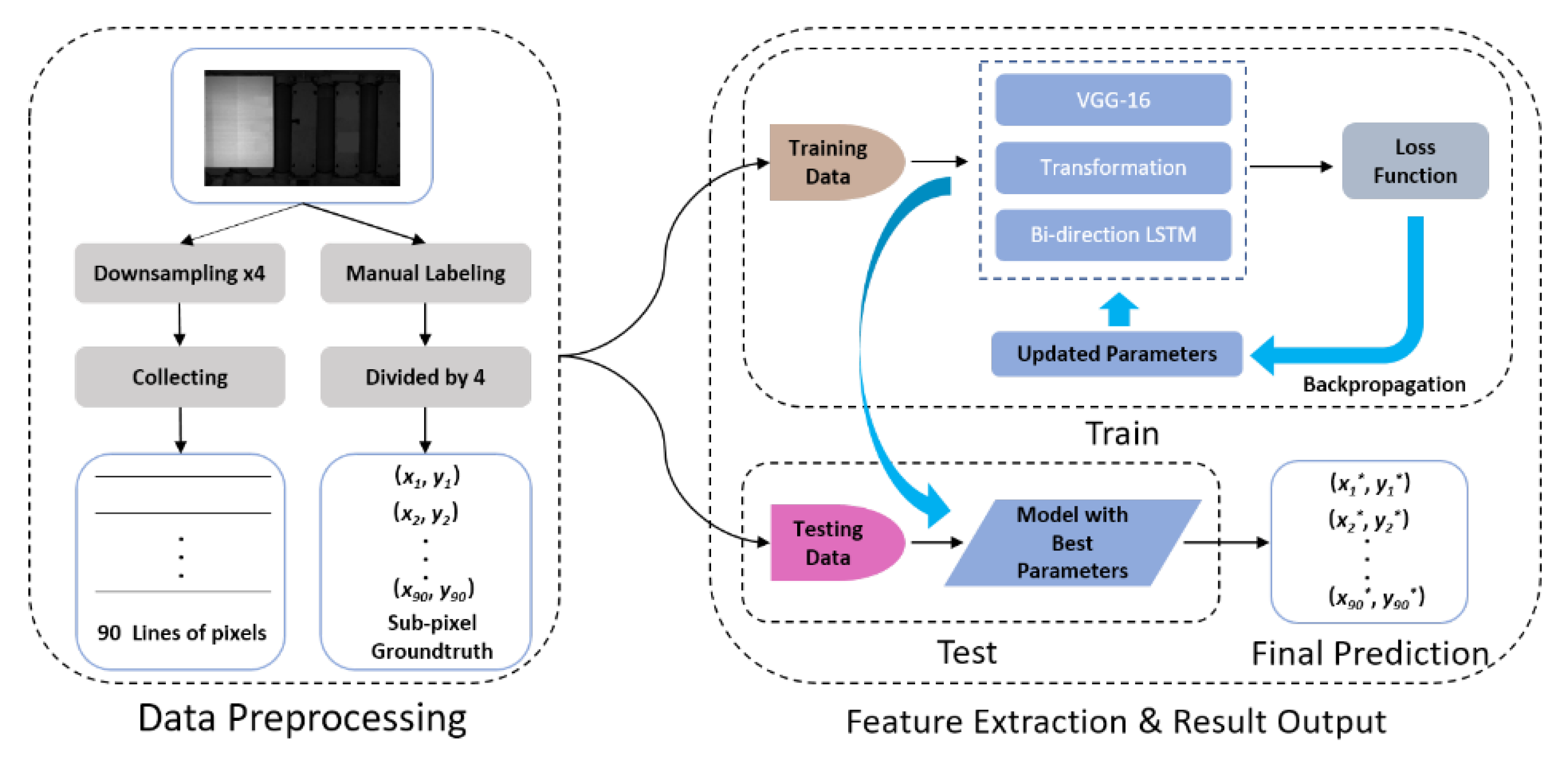
2. Methods
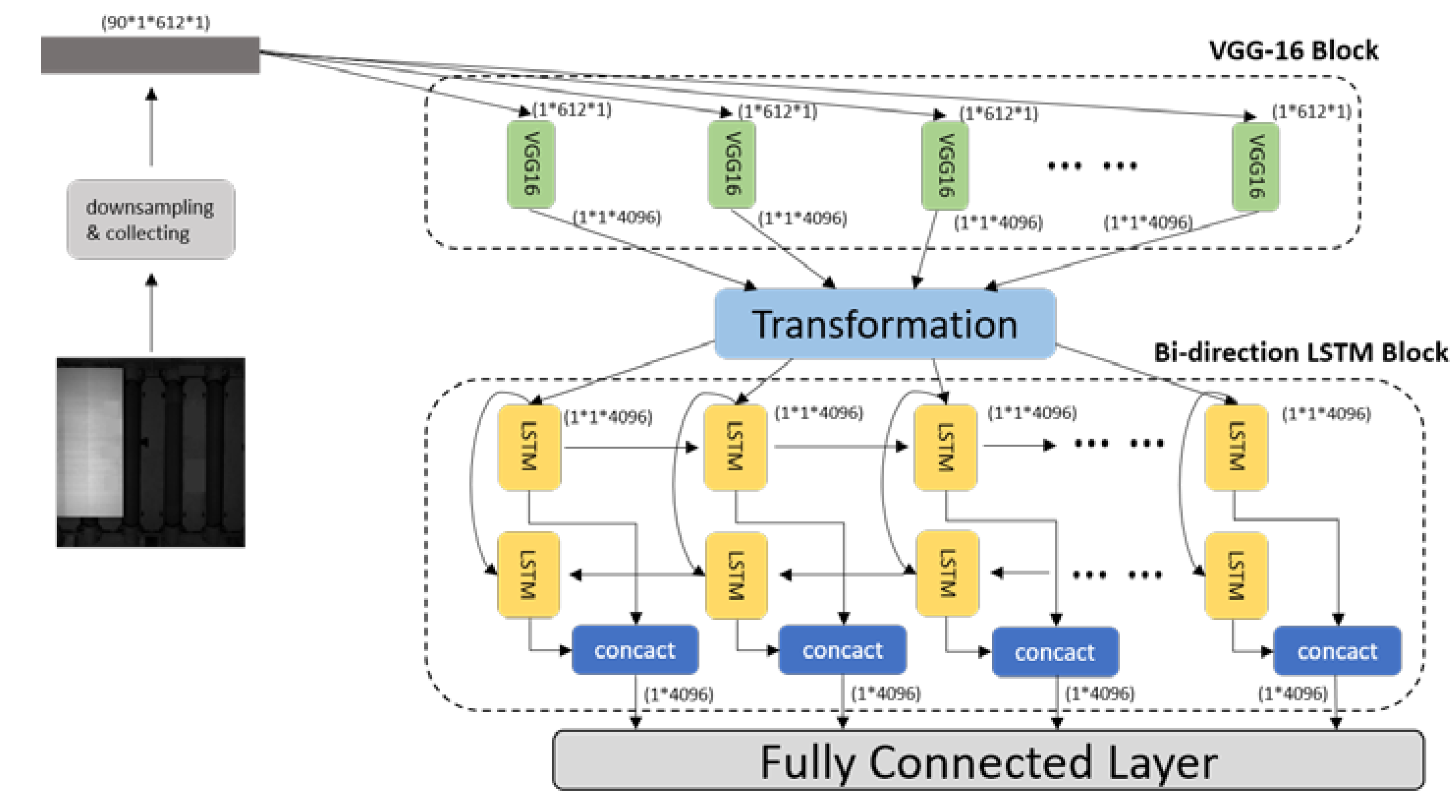
2.1. Building Blocks
2.1.1. VGG-16 as Feature Extractor
2.1.2. Transformation Module
| Algorithm 1. The Process of the Transformation Operation |
| 1. All the outputs from VGG-16 are denoted as , the form is , where , is the width and height of the feature map, and is the number of channel. Expand the dimension of at first axis, the new form of is . |
| 2. Concat all the at first axis, the output is denoted as , and the form is . |
| 3. Expand the dimension of , the new form is . |
| 4. Compress the width, height, and channel to one dimension, the form of the final output is . |
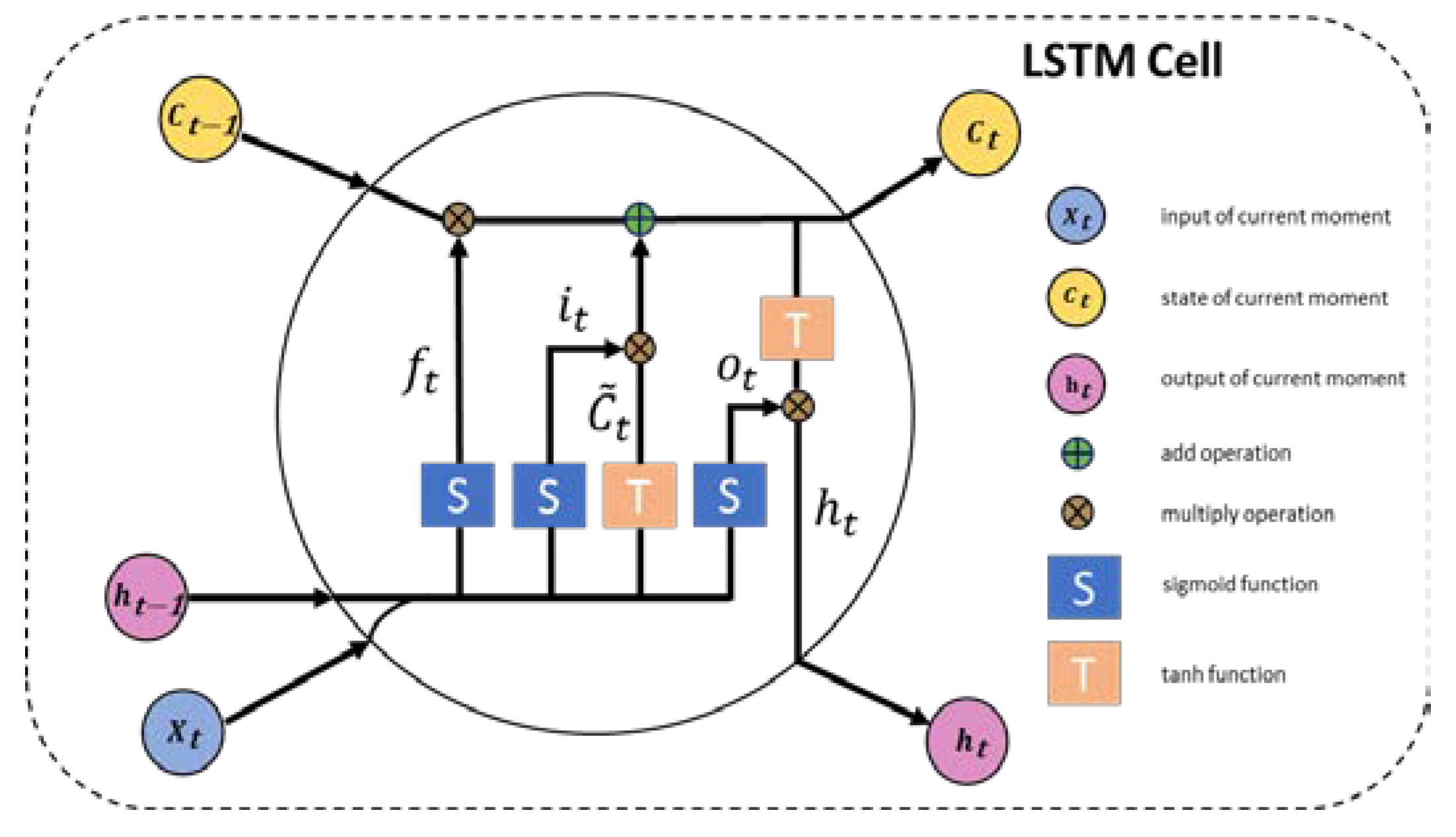
2.1.3. Bi-Directional LSTM
2.2. MSE as Loss Function
3. Results
3.1. Dataset
3.2. Preprocessing the Dataset
3.3. Training Protocol and Metrics
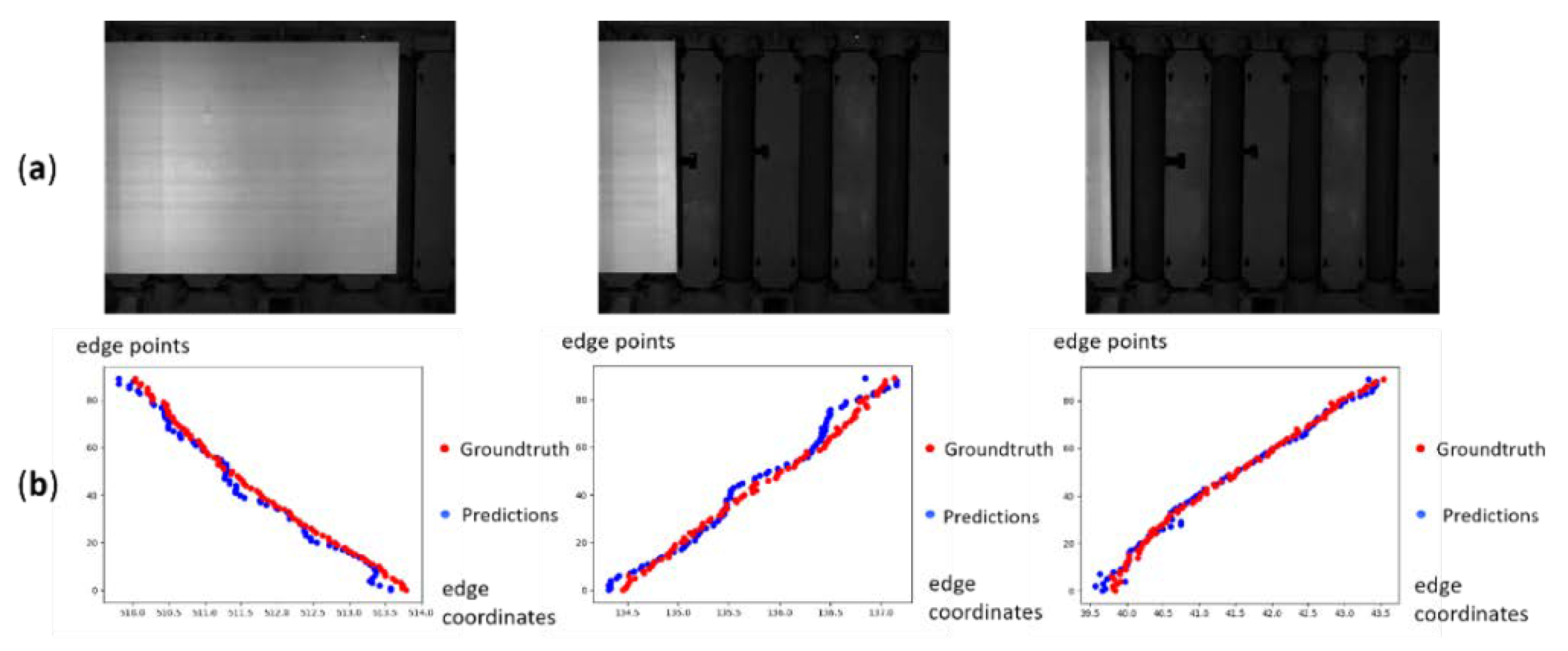
3.4. Experimental Results
4. Evaluation and Discussion
4.1. The Selection of Feature Extraction Block
4.2. The Effect of the Fully Connected Layers in VGG-16
4.3. The Importance of Bi-Directional LSTM
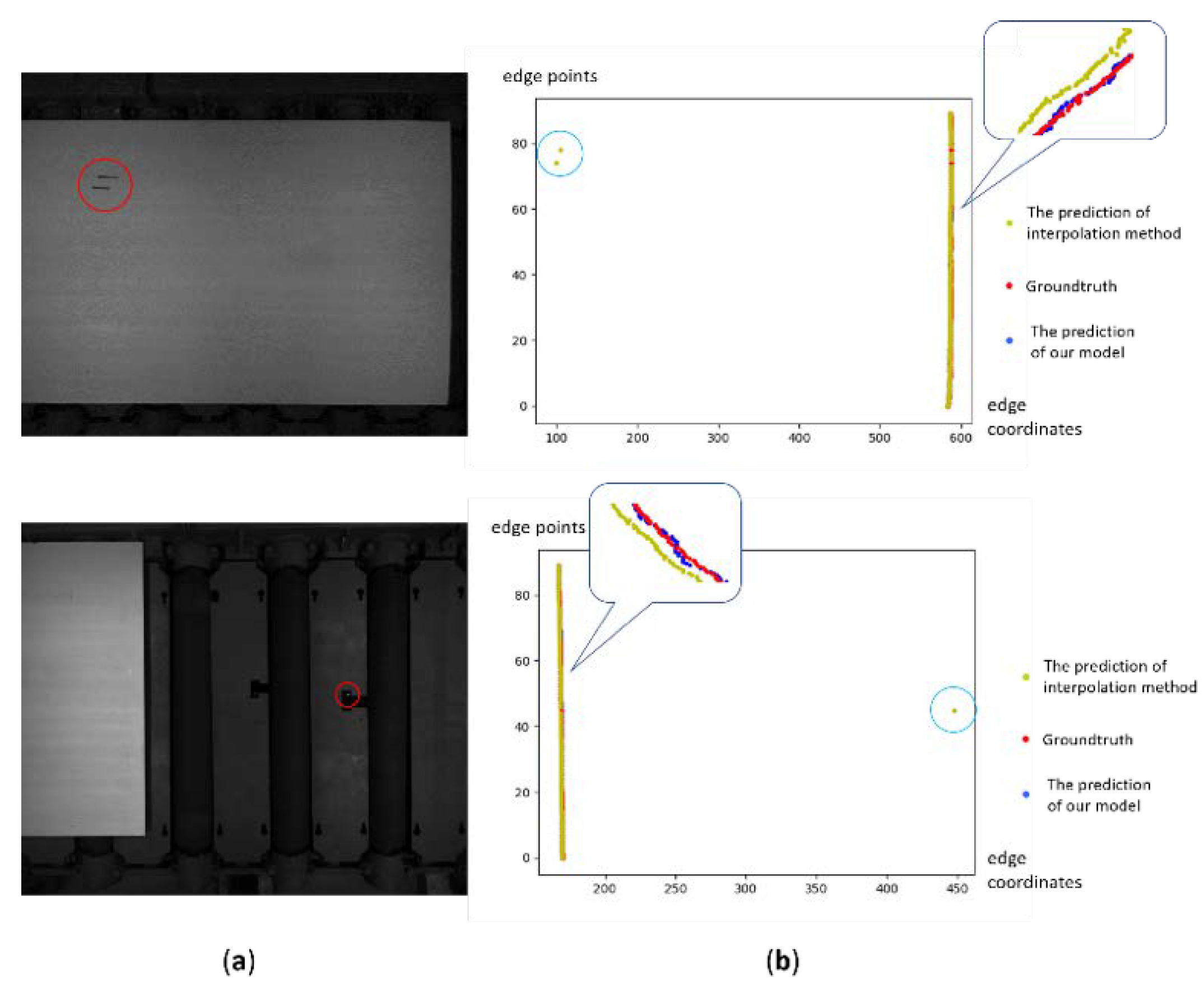
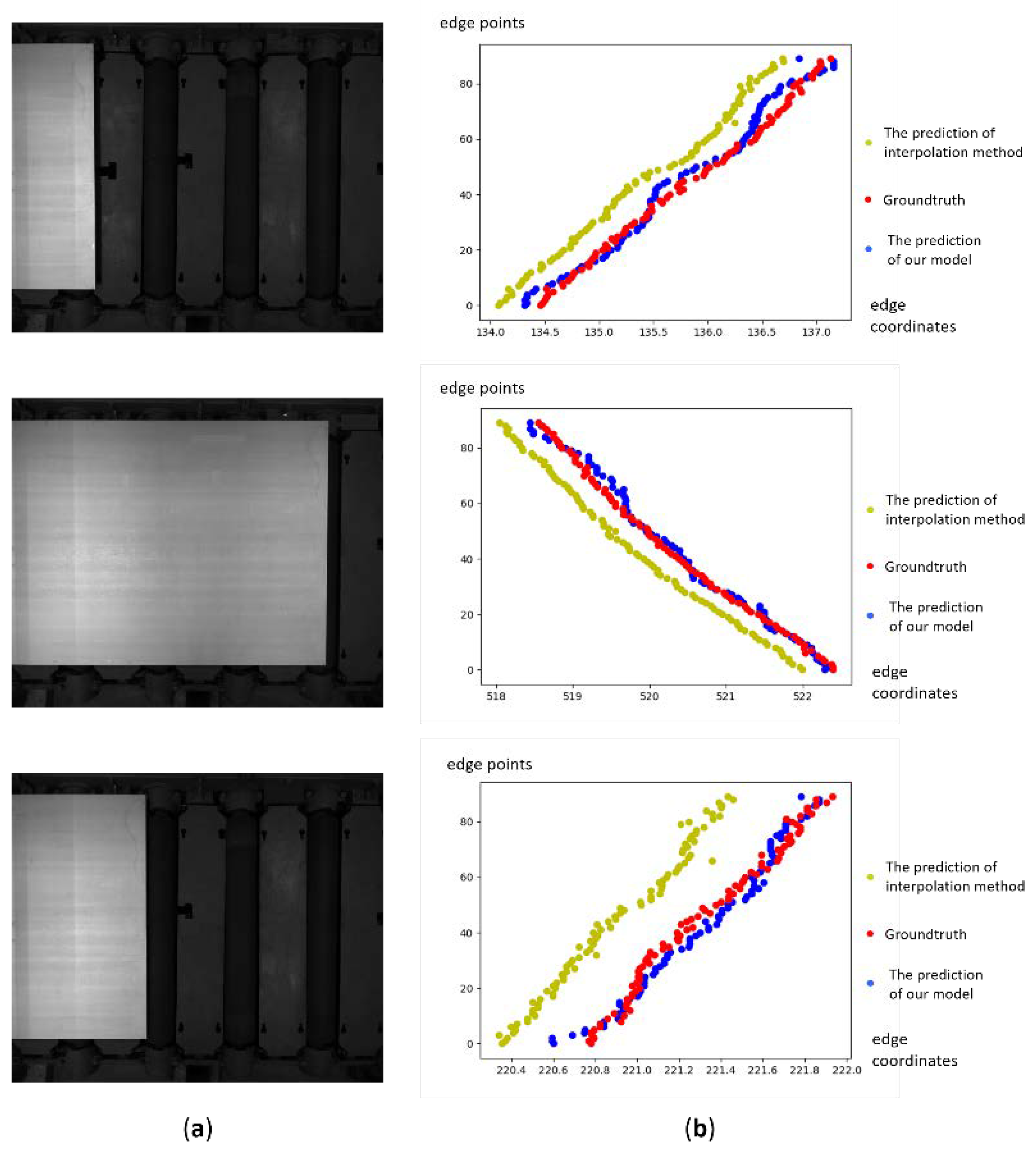
4.4. The Comparison to Other Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pangrazio, J.G.; Pangrazio, J.A.; Pangrazio, R.T.; Brey, K.L.; Pena-Gutierrez, C. Dimensional Detection System and Associated Method. U.S. Patent 8,134,717, 13 March 2012. [Google Scholar]
- Lyvers, E.; Mitchell, O.; Akey, M.; Reeves, A. Subpixel measurements using a moment-based edge operator. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 1293–1309. [Google Scholar] [CrossRef]
- Wang, Y.P.; Ye, A. Sub-Pixel Dataform Reader with Dynamic Noise Margins. U.S. Patent 5,979,763, 9 November 1999. [Google Scholar]
- Rösgen, T. Optimal subpixel interpolation in particle image velocimetry. Exp. Fluid. 2003, 35, 252–256. [Google Scholar] [CrossRef][Green Version]
- Nalwa, V.S. Edge-Detector Resolution Improvement by Image Interpolation. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 446–451. [Google Scholar] [CrossRef] [PubMed]
- Pap, L.; Zou, J.J. Sub-pixel edge detection for photogrammetry using laplace difference of Gaussian and 4th order ENO interpolation. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 2841–2844. [Google Scholar]
- Ghosal, S.; Mehrotra, R. Detection of composite edges. IEEE Trans. Image Process. 1994, 3, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, S.; Mehrotra, R. Orthogonal moment operators for subpixel edge detection. Pattern Recognit. 1993, 26, 295–306. [Google Scholar] [CrossRef]
- Da, F.; Zhang, H. Sub-pixel edge detection based on an improved moment. Image Vis. Comput. 2010, 28, 1645–1658. [Google Scholar] [CrossRef]
- Yang, H.; Pei, L. Fast algorithm of subpixel edge detection based on Zernike moments. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; Volume 3, pp. 1236–1240. [Google Scholar]
- Xie, X.; Ge, S.; Xie, M.; Hu, F.; Jiang, N. An improved industrial sub-pixel edge detection algorithm based on coarse and precise location. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Pdf ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L.; Shetty, S.; Leung, T. Large-Scale Video Classification with Convolutional Neural Networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 1725–1732. [Google Scholar]
- Hu, B.; Lu, Z.; Li, H.; Chen, Q. Convolutional Neural Network Architectures for Matching Natural Language Sentences. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, Canada, 8–13 December 2014; pp. 2042–2050. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In European Conference on Computer Vision; Springer Science and Business Media LLC: Cham, Switzerland, 2016; Volume 9908, pp. 525–542. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep Convolutional Neural Network for Inverse Problems in Imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Zhang, W.; Liao, P.; Li, K.; Zhou, J.; Wang, G. Low-dose CT via convolutional neural network. Biomed. Opt. Express 2017, 8, 679–694. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, L.; Yan, Q.; Deng, S. Scene classification with improved AlexNet model. In Proceedings of the 2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), NanJing, China, 24–26 November 2017; pp. 1–6. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In European Conference on Computer Vision; Springer Science and Business Media LLC: Cham, Switzerland, 2014; Volume 8689, pp. 818–833. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 3–7 December 2015; pp. 1–9. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Sun, Y.; Liang, D.; Wang, X.; Tang, X. DeepID3: Face Recognition with Very Deep Neural Networks. arXiv 2015, arXiv:1502.00873. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, L.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional LSTM-CRF Models for Sequence Tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar]
- Ordóñez, F.J.; Roggen, D. Deep Convolutional and LSTM Recurrent Neural Networks for Multimodal Wearable Activity Recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef]
- Chiu, J.P.; Nichols, E. Named Entity Recognition with Bidirectional LSTM-CNNs. Trans. Assoc. Comput. Linguist. 2016, 4, 357–370. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, M.; Dong, S.; Lin, L.; Liu, Y. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
- Ma, C.-Y.; Chen, M.-H.; Kira, Z.; AlRegib, G. TS-LSTM and temporal-inception: Exploiting spatiotemporal dynamics for activity recognition. Signal Process. Image Commun. 2019, 71, 76–87. [Google Scholar] [CrossRef]
- Zhang, P.; Ouyang, W.; Zhang, P.; Xue, J.; Zheng, N. SR-LSTM: State Refinement for LSTM towards Pedestrian Trajectory Prediction. arXiv 2019, arXiv:1903.02793. [Google Scholar]
- Paliwal, K.; Schuster, M. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar]
- Graves, A.; Mohamed, A.-R.; Hinton, G.; Graves, A. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent Neural Network Regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Chen, T.; Xu, R.; He, Y.; Wang, X. Improving sentiment analysis via sentence type classification using BiLSTM-CRF and CNN. Expert Syst. Appl. 2017, 72, 221–230. [Google Scholar] [CrossRef]
- Luo, L.; Yang, Z.; Yang, P.; Zhang, Y.; Wang, L.; Lin, H.; Wang, J. An attention-based BiLSTM-CRF approach to document-level chemical named entity recognition. Bioinformatics 2017, 34, 1381–1388. [Google Scholar] [CrossRef]
- Talman, A.; Yli-Jyrä, A.; Tiedemann, J. Natural Language Inference with Hierarchical BiLSTM Max Pooling Architecture. arXiv 2018, arXiv:1808.08762. [Google Scholar]
- Chen, Z.; Zhao, R.; Zhu, Q.; Masood, M.K.; Soh, Y.C.; Mao, K. Building occupancy estimation with environmental snesors via CDBLSTM. IEEE Trans. Ind. Electron. 2017, 64, 9549–9559. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Zhang, M.; Chen, X.; Li, J. Improving Stockline Detection of Radar Sensor Array Systems in Blast Furnaces Using a Novel Encoder–Decoder Architecture. Sensors 2019, 19, 3470. [Google Scholar] [CrossRef]

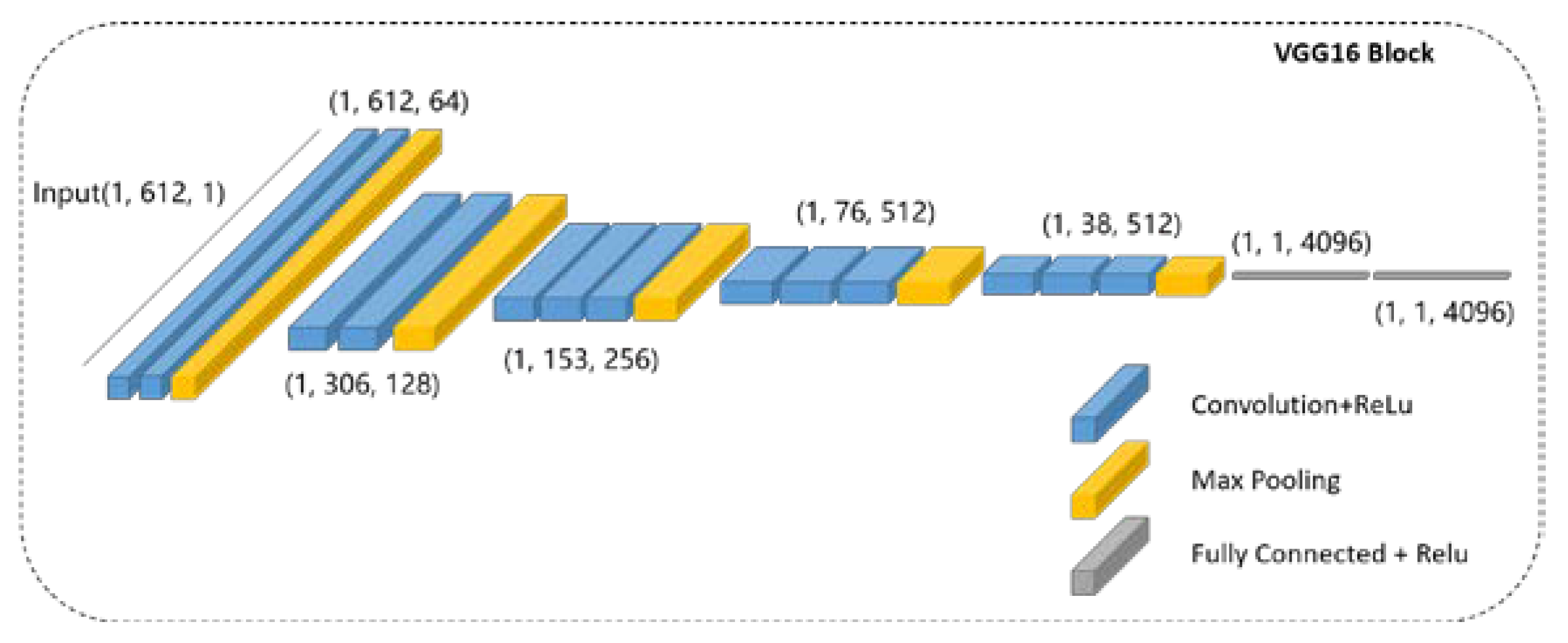

| Layer | Type | Kernel Size | Resolution | |
|---|---|---|---|---|
| VGG-16 | conv1_1 | convolution | 1 × 3, 64 | 1 × 612 |
| conv1_2 | convolution | 1 × 3, 64 | 1 × 612 | |
| pool_1 | max_pooling | 1 × 2, 64, stride 2 | 1 × 306 | |
| conv2_1 | convolution | 1 × 3, 128 | 1 × 306 | |
| conv2_2 | convolution | 1 × 3, 128 | 1 × 306 | |
| pool_2 | max_pooling | 1 × 2, 128, stride 2 | 1 × 153 | |
| conv3_1 | convolution | 1 × 3, 256 | 1 × 153 | |
| conv3_2 | convolution | 1 × 3, 256 | 1 × 153 | |
| conv3_3 | convolution | 1 × 3, 256 | 1 × 153 | |
| pool_3 | max_pooling | 1 × 2, 256, stride 2 | 1 × 76 | |
| conv4_1 | convolution | 1 × 3, 512 | 1 × 76 | |
| conv4_2 | convolution | 1 × 3, 512 | 1 × 76 | |
| conv4_3 | convolution | 1 × 3, 512 | 1 × 76 | |
| pool_4 | max_pooling | 1 × 2, 512, stride 2 | 1 × 38 | |
| conv5_1 | convolution | 1 × 3, 512 | 1 × 38 | |
| conv5_2 | convolution | 1 × 3, 512 | 1 × 38 | |
| conv5_3 | convolution | 1 × 3, 512 | 1 × 38 | |
| pool_5 | max_pooling | 1 × 2, 512, stride 2 | 1 × 19 | |
| fc_1 | fully_connected | -, 4096 | - | |
| fc_2 | fully_connected | -, 4096 | - | |
| Bi-directional LSTM | block1 | - | -, 4096 | - |
| Output | fc_3 | fully_connected | -, 90 | - |
| Method | MAE | MSE | RMSE |
|---|---|---|---|
| Proposed model (VGG-16 + Bi-LSTM) | 0.112 | 0.0406 | 0.202 |
| Method | MAE | MSE | RMSE |
|---|---|---|---|
| VGG-19 + Bi-LSTM | 0.121 | 0.0436 | 0.209 |
| ResNet + Bi-LSTM | 0.124 | 0.0438 | 0.209 |
| DenseNet + Bi-LSTM | 0.117 | 0.0450 | 0.212 |
| Proposed Model (VGG-16 + Bi-LSTM) | 0.112 | 0.0406 | 0.202 |
| Method | MAE | MSE | RMSE |
|---|---|---|---|
| Conv with 4096 | 0.118 | 0.0423 | 0.206 |
| FC with 2048 | 0.116 | 0.0418 | 0.204 |
| Ours (FC with 4096) | 0.112 | 0.0406 | 0.202 |
| Model | VGG-16 | Vanilla LSTM | Bi-directional LSTM | MAE | MSE | RMSE |
| √ | × | × | 0.183 | 0.0610 | 0.247 | |
| √ | √ | × | 0.134 | 0.0482 | 0.220 | |
| √ | × | √ | 0.112 | 0.0406 | 0.202 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, Q.; Ding, M.; Li, J. High Precision Dimensional Measurement with Convolutional Neural Network and Bi-Directional Long Short-Term Memory (LSTM). Sensors 2019, 19, 5302. https://doi.org/10.3390/s19235302
Wang Y, Chen Q, Ding M, Li J. High Precision Dimensional Measurement with Convolutional Neural Network and Bi-Directional Long Short-Term Memory (LSTM). Sensors. 2019; 19(23):5302. https://doi.org/10.3390/s19235302
Chicago/Turabian StyleWang, Yuhao, Qibai Chen, Meng Ding, and Jiangyun Li. 2019. "High Precision Dimensional Measurement with Convolutional Neural Network and Bi-Directional Long Short-Term Memory (LSTM)" Sensors 19, no. 23: 5302. https://doi.org/10.3390/s19235302
APA StyleWang, Y., Chen, Q., Ding, M., & Li, J. (2019). High Precision Dimensional Measurement with Convolutional Neural Network and Bi-Directional Long Short-Term Memory (LSTM). Sensors, 19(23), 5302. https://doi.org/10.3390/s19235302






