Laboratory Calibration and Field Validation of Soil Water Content and Salinity Measurements Using the 5TE Sensor
Abstract
1. Introduction
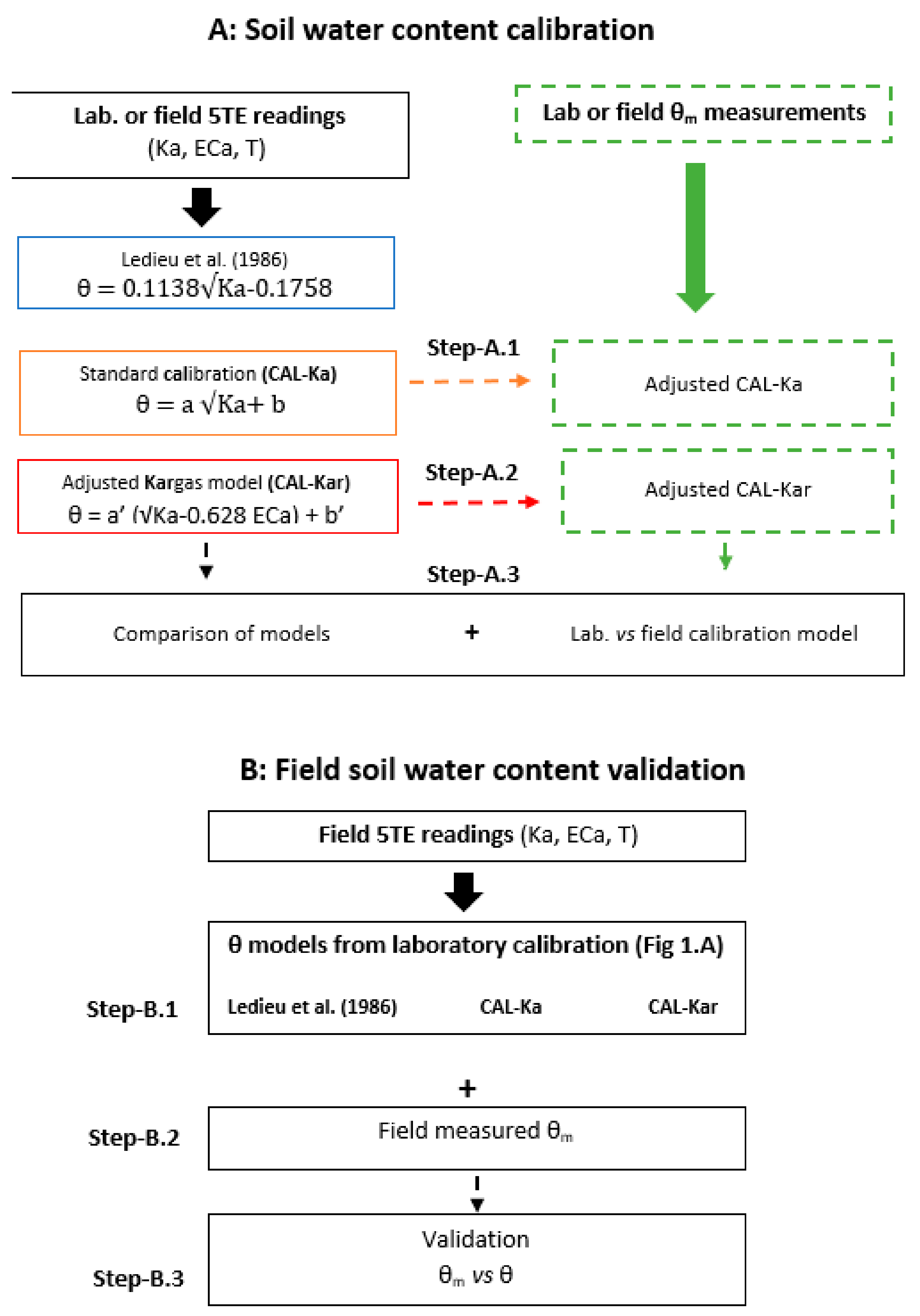
2. Materials and Methods
2.1. Theoretical Considerations
2.1.1. Permittivity-Corrected Linear Model
2.1.2. Water Content Model
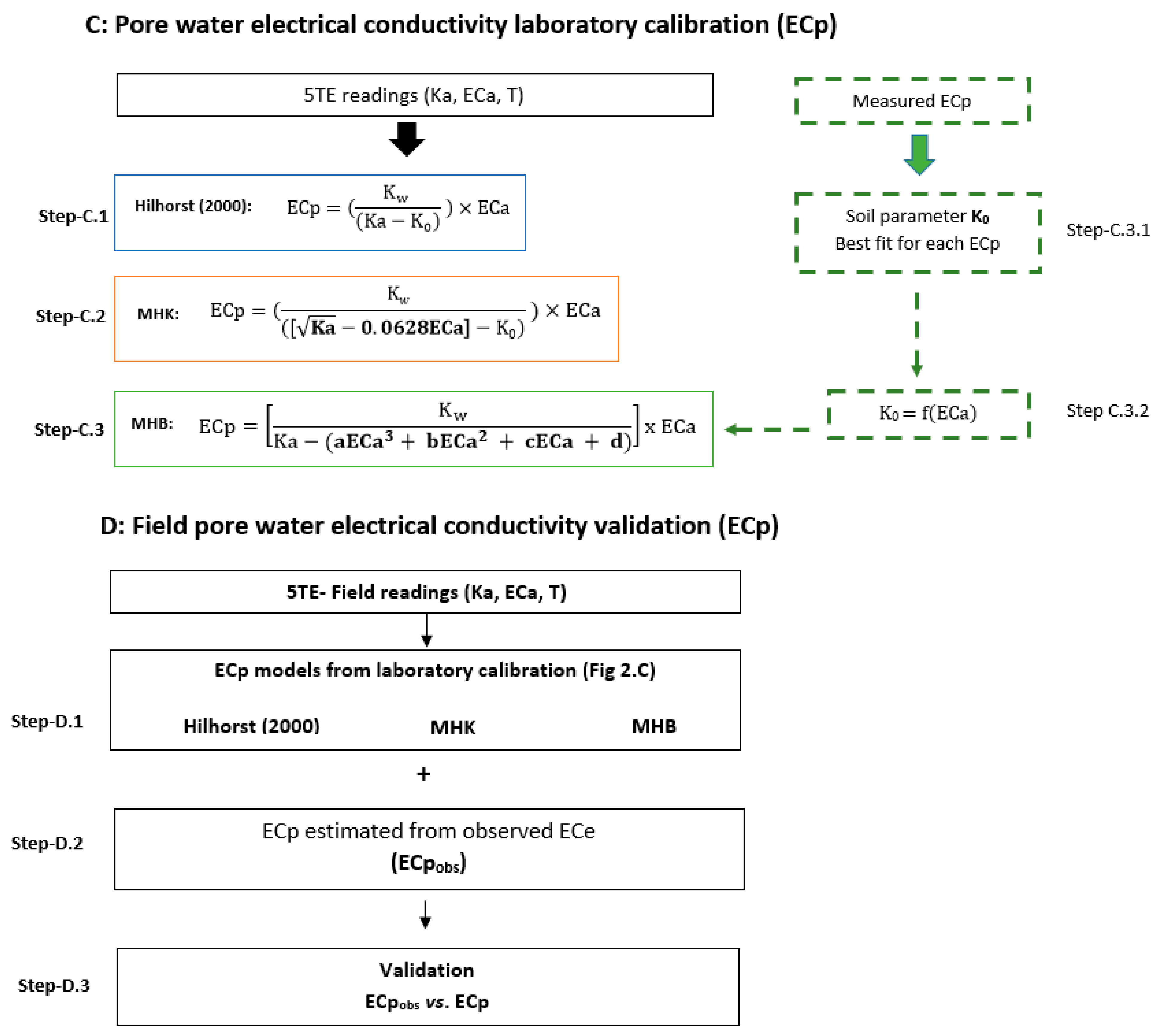
2.1.3. Pore Water Electrical Conductivity Model
2.2. Study Area
2.3. Laboratory Experiments
2.4. Field Measurements
3. Results
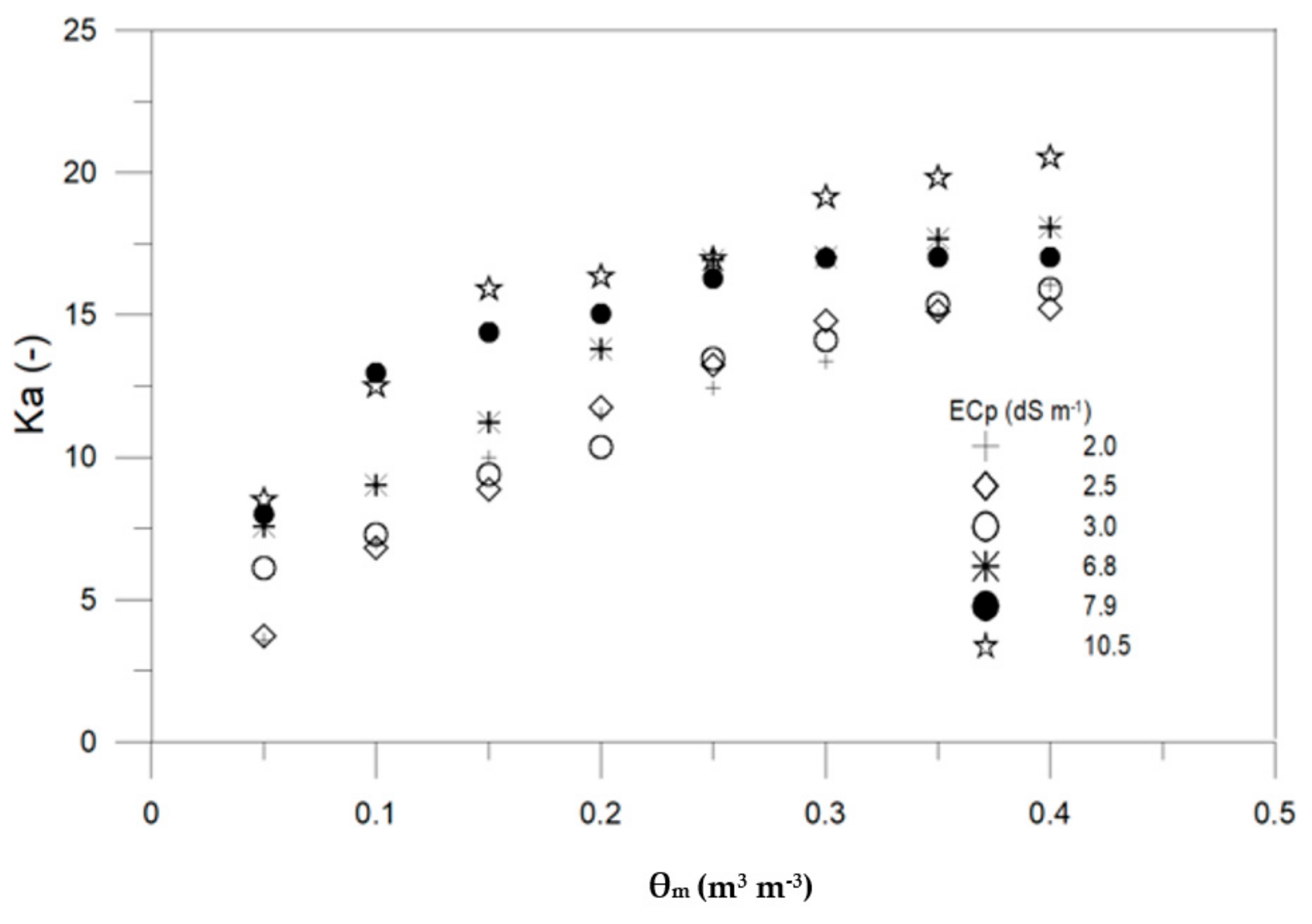
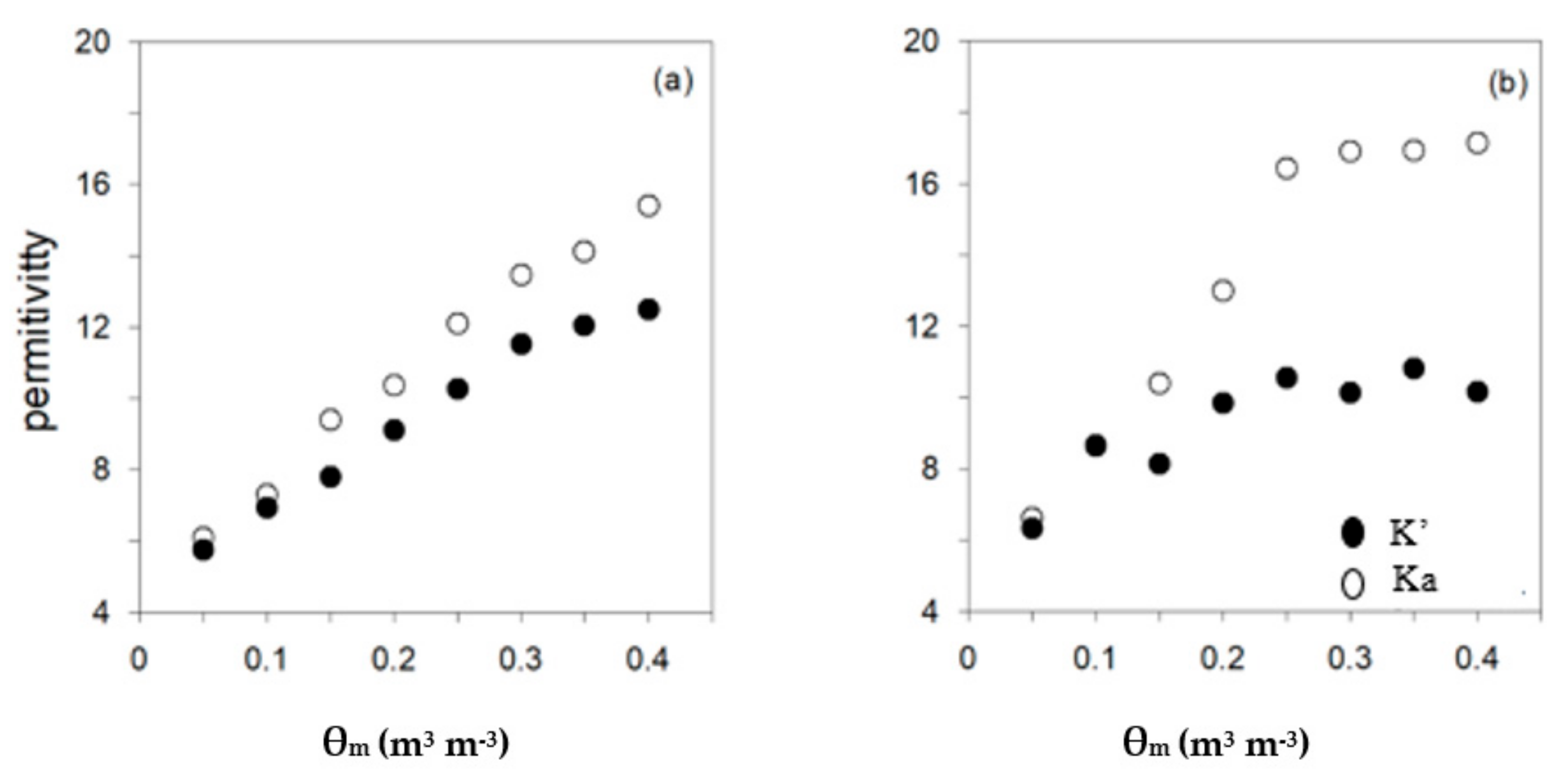
3.1. Soil Water Content
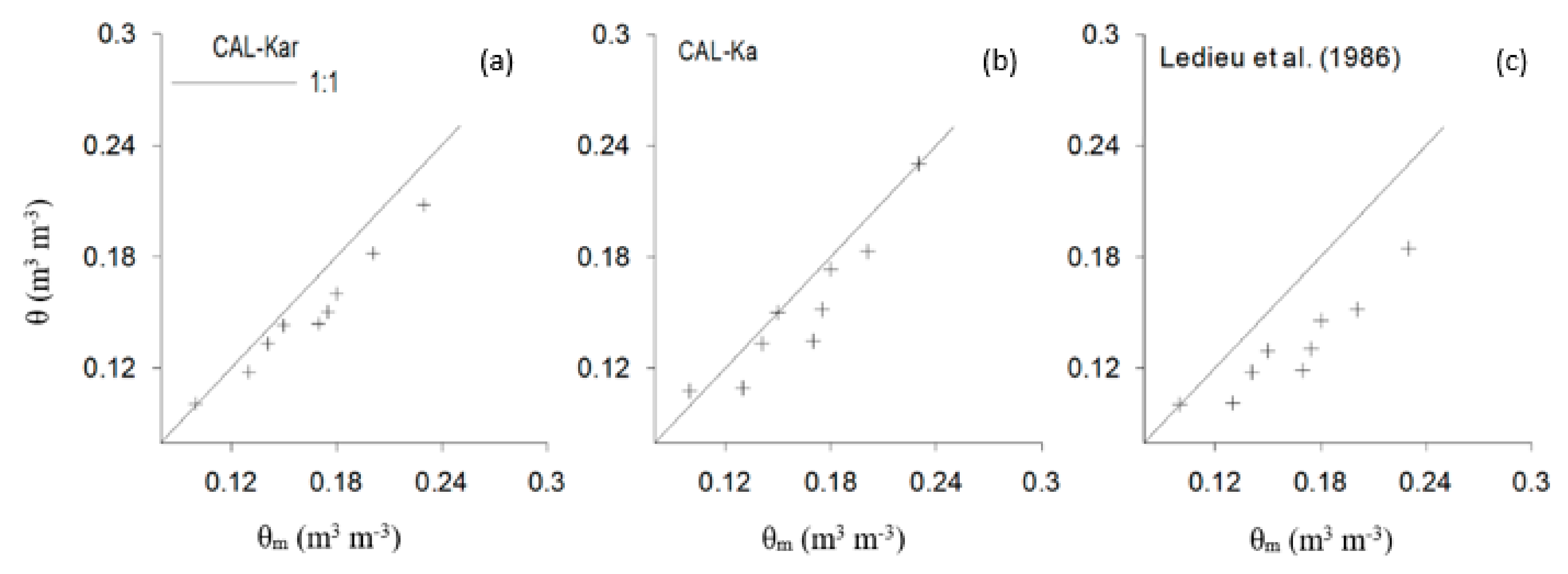
3.2. Field Validation of Soil Water Content Models
3.3. Soil Pore Electrical Conductivity (ECp)
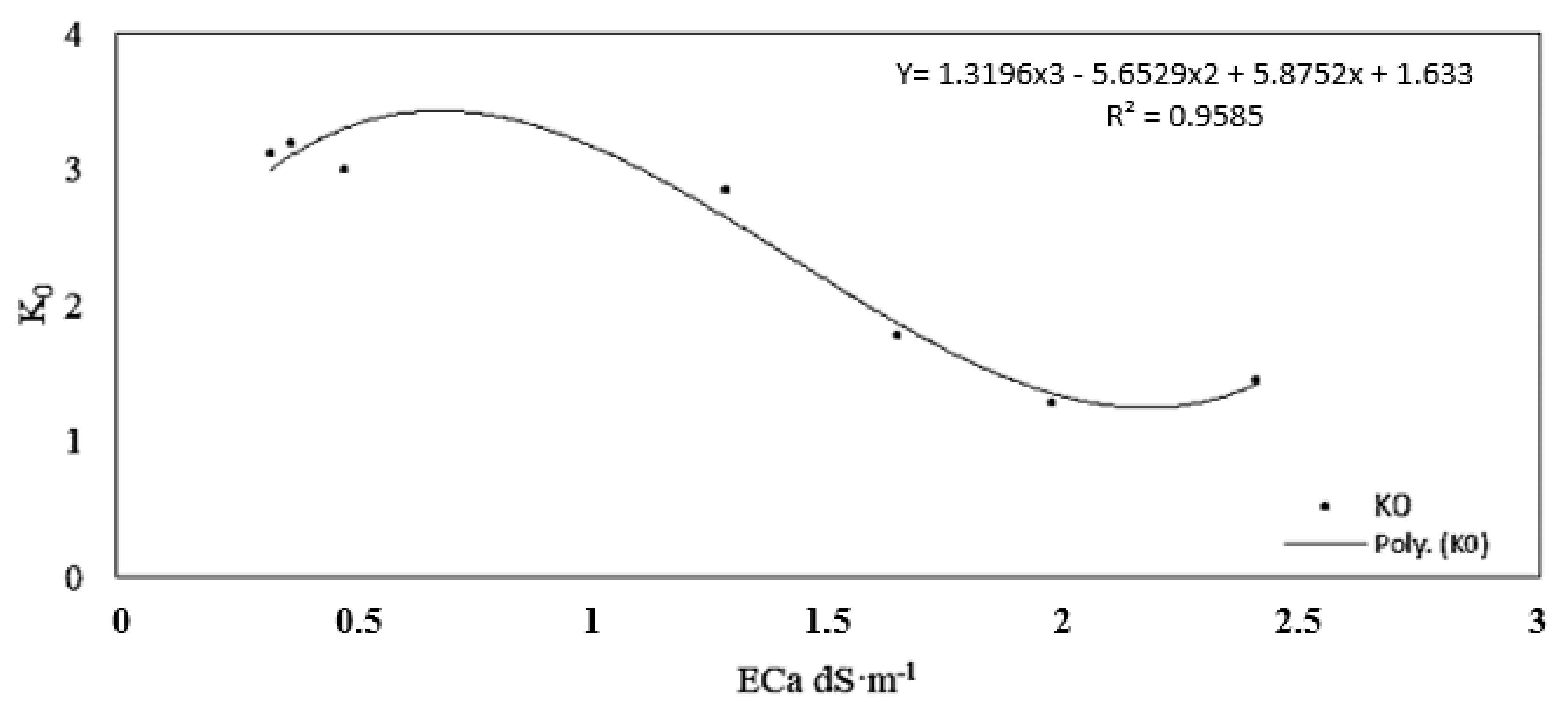
3.3.1. ECp Laboratory Calibration
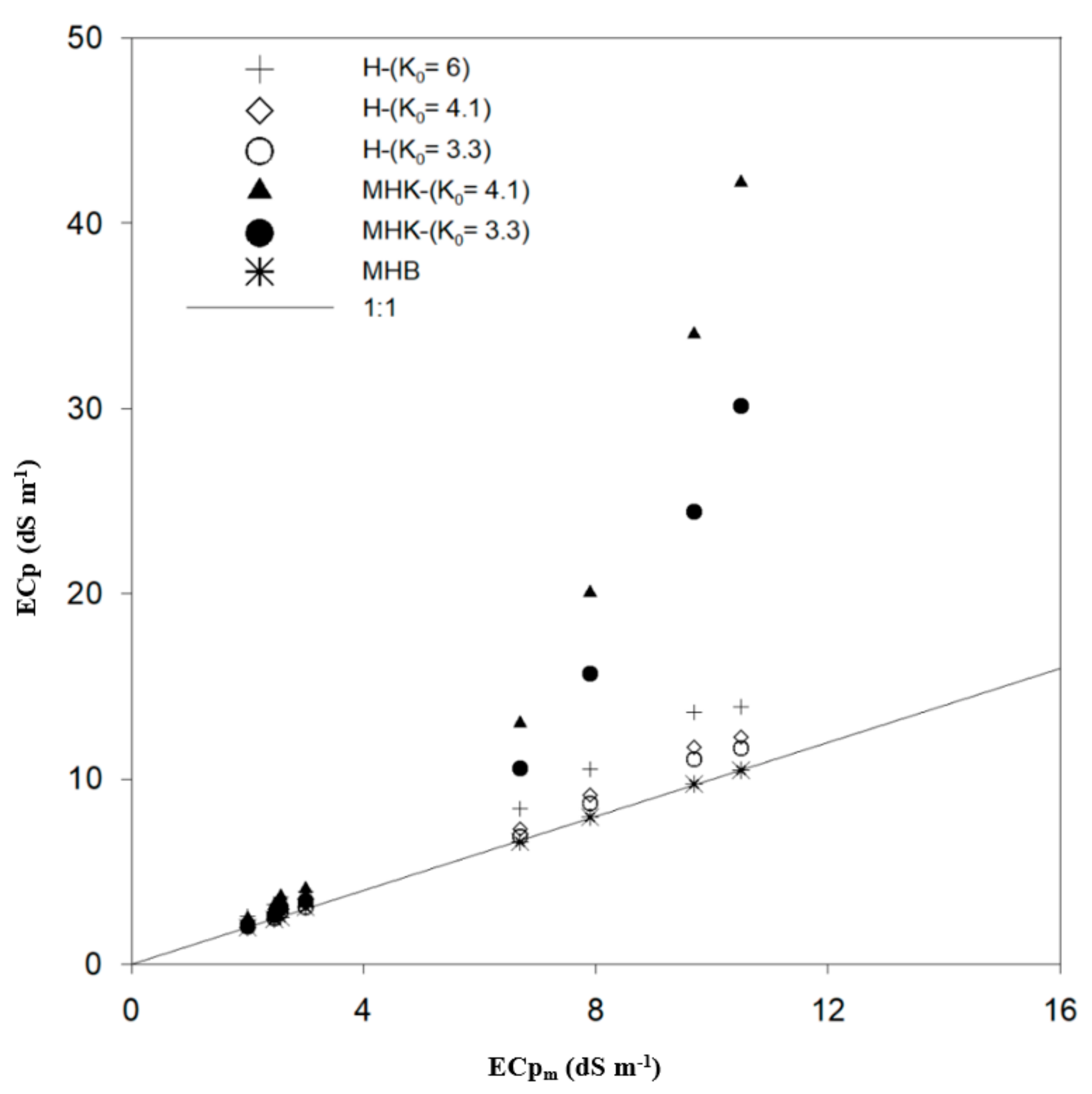
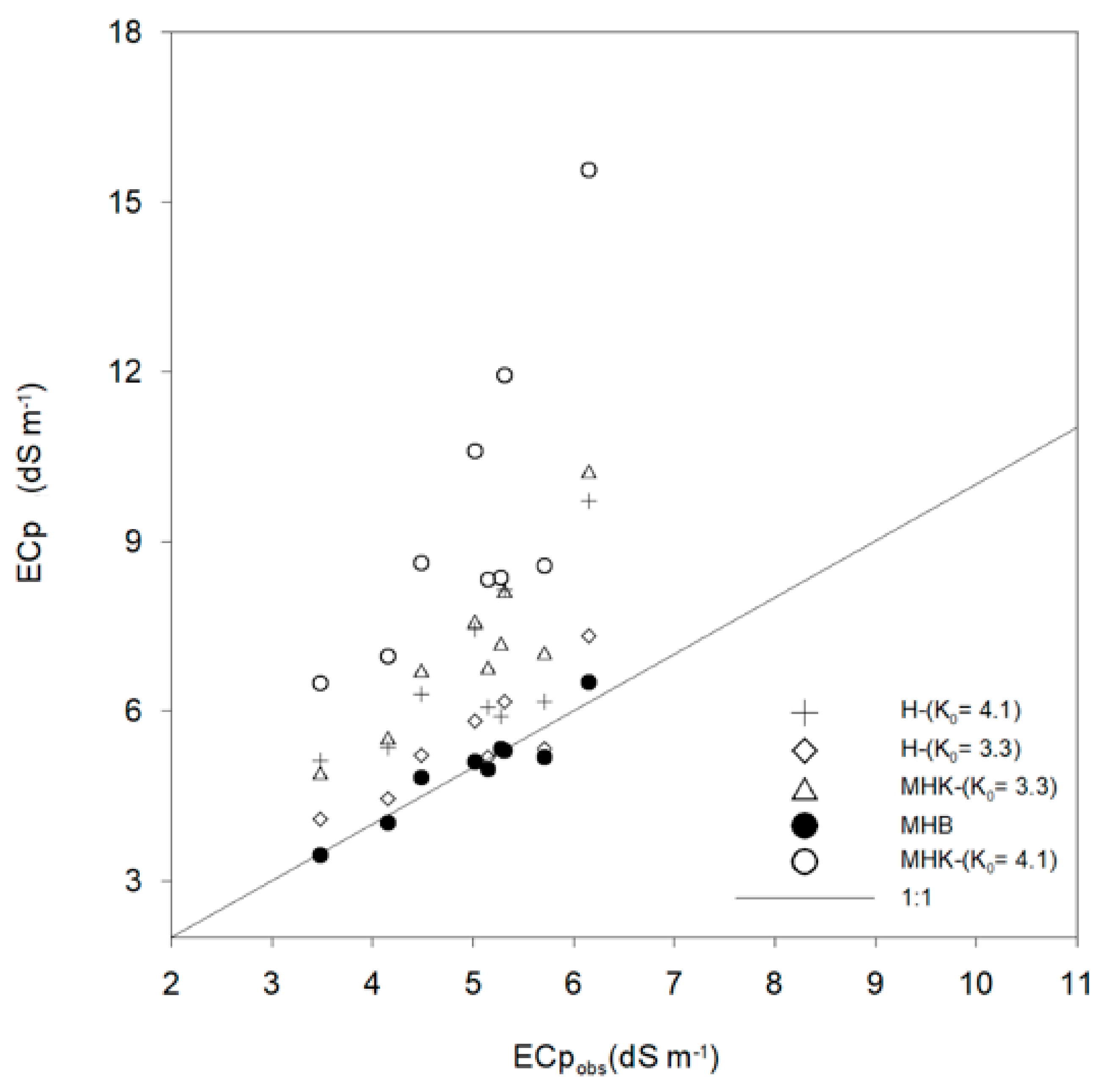
3.3.2. Field Validation of ECp Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Soil Parameter | Acronym | Data Source | Sensor/Method |
|---|---|---|---|
| Soil dry bulk density | Bd | Measured | Cylinder method- United States Department of Agriculture (USDA) |
| Soil pH | pH | Measured | pH-meter |
| Apparent soil permittivity | Ka | Measured | 5TE-probe |
| Soil parameter | K0 | Estimated | 5TE-probe |
| Dielectric constant of pore water | Kw | Estimated | 5TE-probe |
| Corrected apparent soil permittivity | K’ | Estimated | 5TE-probe |
| Soil temperature | T | Measured | 5TE-probe |
| Electrical conductivity of saturated soil paste extract | ECe | Measured | EC-meter/USDA method |
| Soil apparent electrical conductivity | ECa | Measured | 5TE-probe |
| Irrigation water electrical conductivity | ECiw | Measured | EC-meter |
| Measured soil water content | Measured | Gravimetric method-USDA | |
| Estimated volumetric water content | Estimated | –Models (see Figure 1) | |
| Laboratory measured pore water electrical conductivity | ECpm | Measured | EC-meter |
| Field observed pore water electrical conductivity | ECpobs | Measured | ECpobs = a ECe + b (see Figure 2) |
| Pore water electrical conductivity | ECp | Estimated | ECp-Models (see Figure 2) |
| 5TE sensor specification | |||
| Type | Specifics | ||
| Sensor type | FDR (Frequency Domain Reflectometry) | ||
| Power supply | +3.6 to +15 V | ||
| Frequency | 70 MHz | ||
| Size | Length 10.9 cm (4.3 in) Width 3.4 cm (1.3 in) Height 1.0 cm (0.4 in) | ||
| Measurement volume | 300 cm3 | ||
| Direct output data | Ka, ECa, and T | ||
| Indirect output data | |||
| Range (Ka, ECa) | 1–80, 0–7 dS m−1 | ||
| Resolution (Ka, ECa) | 0.1, 0.01 dS m−1 | ||
| Accuracy (Ka, ECa) | ±3%, ±10% | ||
| Models | |||
| CAL-Ka (see Figure 1) | Calibration of soil water content model without permittivity correction | ||
| CAL-Kar (see Figure 1) | Calibration of soil water content model with permittivity correction according to Kargas et al. (2017) | ||
| H (see Figure 2) | Standard Hilhorst (2000) model for ECp prediction | ||
| MHK (see Figure 2) | Modified Hilhorst model according to Kargas et al. (2017) for ECp prediction | ||
| MHB (see Figure 2) | Modified Hilhorst model according to Bouksila et al. (2008) for ECp prediction | ||
| Model performance statistic tool | |||
| RMSE | Root Mean Square Error | ||
| R2 | Coefficient of determination | ||
| MRE | Mean Relative Error | ||
| CV | Coefficient of Variation | ||
References
- Selim, T.; Bouksila, F.; Berndtsson, R.; Persson, M. Soil Water and Salinity Distribution under Different Treatments of Drip Irrigation. Soil Sci. Soc. Am. J. 2013, 77, 1144–1156. [Google Scholar] [CrossRef]
- Slama, F.; Zemni, N.; Bouksila, F.; De Mascellis, R.; Bouhlila, R. Modelling the Impact on Root Water Uptake and Solute Return Flow of Different Drip Irrigation Regimes with Brackish Water. Water 2019, 11, 425. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Manteghi, N.A.; Shouse, P.J.; Alves, W.J. Soil Electrical Conductivity and Soil Salinity: New Formulations and Calibrations. Soil Sci. Soc. Am. J. 1989, 53, 433–439. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Robinson, D.A.; Gardner, C.M.K.; Cooper, J.D. Measurement of relative permittivity in sandy soils using TDR, capacitance and theta probes: Comparison, including the effects of bulk soil electrical conductivity. J. Hydrol. 1999, 223, 198–211. [Google Scholar] [CrossRef]
- Kargas, G.; Persson, M.; Kanelis, G.; Markopoulou, I.; Kerkides, P. Prediction of Soil Solution Electrical Conductivity by the Permittivity Corrected Linear Model Using a Dielectric Sensor. J. Irrig. Drain. Eng. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Ledieu, J.; Ridder, P.D.; Clerck, P.D.; Dautrebande, S. A method of measuring soil moisture by time-domain reflectometry. J. Hydrol. 1986, 88, 319–328. [Google Scholar] [CrossRef]
- Hilhorst, M.A. A Pore Water Conductivity Sensor. Soil Sci. Soc. Am. J. 2000, 64, 1922–1925. [Google Scholar] [CrossRef]
- Malicki, M.A.; Walczak, R.T. Evaluating soil salinity status from bulk electrical conductivity and permittivity. Eur. J. Soil Sci. 1999, 50, 505–514. [Google Scholar] [CrossRef]
- Mualem, Y.; Friedman, S.P. Theoretical Prediction of Electrical Conductivity in Saturated and Unsaturated Soil. Water Resour. Res. 1991, 27, 2771–2777. [Google Scholar] [CrossRef]
- Dalton, F.N. Development of Time-Domain Reflectometry for Measuring Soil Water Content and Bulk Soil Electrical Conductivity. In Advances in Measurement of Soil Physical Properties: Bringing Theory into Practice; Topp, G.C., Reynolds, W.D., Green, R.E., Eds.; Soil Science Society of America: Madison, WI, USA, 1992; pp. 143–167. [Google Scholar] [CrossRef]
- Nadler, A.; Gamliel, A.; Peretz, I. Practical Aspects of Salinity Effect on TDR-Measured Water Content A Field Study Contribution from the Agricultural Research Organization, Volcani Center, Bet Dagan, 50-250, Israel; No 611/98 1998 series. Soil Sci. Soc. Am. J. 1999, 63, 1070–1076. [Google Scholar] [CrossRef]
- Persson, M. Evaluating the linear dielectric constant-electrical conductivity model using time-domain reflectometry. Hydrol. Sci. J. 2000, 47, 269–277. [Google Scholar] [CrossRef]
- Hamed, Y.; Samy, G.; Persson, M. Evaluation of the WET sensor compared to time domain reflectometry. Hydrol. Sci. J. 2006, 51, 671–681. [Google Scholar] [CrossRef]
- Inoue, M.; Ould Ahmed, B.A.; Saito, T.; Irshad, M.; Uzoma, K.C. Comparison of three dielectric moisture sensors for measurement of water in saline sandy soil. Soil Use Manag. 2008, 24, 156–162. [Google Scholar] [CrossRef]
- Kargas, G.; Soulis, K.X. Performance Analysis and Calibration of a New Low-Cost Capacitance Soil Moisture Sensor. J. Irrig. Drain. Eng. 2012, 138, 632–641. [Google Scholar] [CrossRef]
- Regalado, C.M.; Ritter, A.; Rodríguez-González, R.M. Performance of the Commercial WET Capacitance Sensor as Compared with Time Domain Reflectometry in Volcanic Soils. Vadose Zone J. 2007, 6, 244–254. [Google Scholar] [CrossRef]
- Bouksila, F.; Persson, M.; Berndtsson, R.; Bahri, A. Soil water content and salinity determination using different dielectric methods in saline gypsiferous soil. Hydrol. Sci. J. 2008, 53, 253–265. [Google Scholar] [CrossRef]
- Visconti, F.; de Paz, J.M.; MartÃnez, D.; Molina, M.J. Laboratory and field assessment of the capacitance sensors Decagon 10HS and 5TE for estimating the water content of irrigated soils. Agric. Water Manag. 2014, 132, 111–119. [Google Scholar] [CrossRef]
- Nimmo, J.R. Porosity and Pore Size Distribution. Encycl. Soils Environ. 2004, 3, 295–303. [Google Scholar]
- Iwata, Y.; Miyamoto, T.; Kameyama, K.; Nishiya, M. Effect of sensor installation on the accurate measurement of soil water content. Eur. J. Soil Sci. 2017, 68, 817–828. [Google Scholar] [CrossRef]
- Pardossi, A.; Incrocci, L.; Incrocci, G.; Malorgio, F.; Battista, P.; Bacci, L.; Rapi, B.; Marzialetti, P.; Hemming, J.; Balendonck, J. Root Zone Sensors for Irrigation Management in Intensive Agriculture. Sensors 2009, 9, 2809–2835. [Google Scholar] [CrossRef] [PubMed]
- Baram, S.; Couvreurd, V.; Harter, T.; Read, M.; Brown, P.H.; Kandelous, M.; Smart, D.R.; Hopmans, J.W. Estimating Nitrate Leaching to Groundwater from Orchards: Comparing Crop Nitrogen Excess, Deep Vadose Zone Data-Driven Estimates, and HYDRUS Modeling. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Gamage, D.N.V.; Biswas, A.; Strachan, I.B. Field Water Balance Closure with Actively Heated Fiber-Optics and Point-Based Soil Water Sensors. Water 2019, 11, 135. [Google Scholar] [CrossRef]
- Evett, S.R.; Tolk, J.A.; Howell, T.A. Soil Profile Water Content Determination. Vadose Zone J. 2006, 5, 894–907. [Google Scholar] [CrossRef]
- Schwartz, R.C.; Casanova, J.J.; Pelletier, M.G.; Evett, S.R.; Baumhardt, R.L. Soil Permittivity Response to Bulk Electrical Conductivity for Selected Soil Water Sensors. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Varble, J.L.; Chavez, J.L. Performance evaluation and calibration of soil water content and potential sensors for agricultural soils in eastern Colorado. Agric. Water Manag. 2011, 101, 93–106. [Google Scholar] [CrossRef]
- Jae-Kwon, S.; Won-Tae, S.; Jae-Young, C. Laboratory and Field Assessment of the Decagon 5TE and GS3 Sensors for Estimating Soil Water Content in Saline-Alkali Reclaimed Soils. Commun. Soil Sci. Plant Anal. 2017, 48, 2268–2279. [Google Scholar]
- Campbell, J.E. Dielectric Properties and Influence of Conductivity in Soils at One to Fifty Megahertz. Soil Sci. Soc. Am. J. 1990, 54, 332–341. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Verma, A.K. Measured and Modeled Dielectric Properties of Soils at 50 Megahertz. Soil Sci. Soc. Am. J. 2010, 74, 744–752. [Google Scholar] [CrossRef]
- Jones, S.B.; Blonquist, J.M.J.; Robinson, D.A.; Philip Rasmussen, V.; Or, D. Standardizing Characterization of Electromagnetic Water Content Sensors: Part 1. Methodology. Vadose Zone J. 2005, 4, 1048–1058. [Google Scholar] [CrossRef]
- Whalley, W.R. Considerations on the use of time-domain reflectometry (TDR) for measuring soil water content. J. Soil Sci. 1993, 44, 1–9. [Google Scholar] [CrossRef]
- Persson, M. Soil Solution Electrical Conductivity Measurements under Transient Conditions Using Time Domain Reflectometry. Soil Sci. Soc. Am. J. 1997, 61, 997–1003. [Google Scholar] [CrossRef]
- Rhoades, J.D.; van Schilfgaarde, J. An Electrical Conductivity Probe for Determining Soil Salinity. Soil Sci. Soc. Am. J. 1976, 40, 647–651. [Google Scholar] [CrossRef]
- Malicki, M.W.R.; Walczak, R.; Koch, S.; Fluhler, H. Determining soil salinity from simultaneous readings of its electrical conductivity and permittivity using TDR. In Proceedings of the Time Domain Reflectometry in Environmental, Infrastructure, and Mining Applications United States Department of Interior Bureau of Mines, the Time Domain Reflectometry in Environmental, Infrastructure, and Mining Applications United States Department of Interior Bureau of Mines, 7–9 September 1994; Northwestern University: Evanston, IL, USA; pp. 328–336. [Google Scholar]
- 5TE. Sensor Manual. 5TE- Water Content, Electrical Conductivity (EC) and Temperature sensor; Decagon Devices Inc.: Pullman, WA, USA, 2016; Available online: https://www.decagon.com/ (accessed on 15 March 2016).
- WET. Sensor Manual-UTM-1.6; Delta-T Devices Ltd.: Cambridge, UK, 2019; Available online: https://www.delta-t.co.uk/ (accessed on 10 July 2019).
- Zammouri, M.; Siegfried, T.; El-Fahem, T.; Kriaca, S.; Kinzelbach, W. Salinization of groundwater in the Nefzawa oases region, Tunisia: Results of a regional-scale hydrogeologic approach. Hydrogeol. J. 2007, 15, 1357–1375. [Google Scholar] [CrossRef]
- USDA. Diagnostic and improvement of saline and alkali soil. In Agriculture Handbook No. 60; US Department of Agriculture: Washington, DC, USA, 1954. Available online: https://www.ars.usda.gov (accessed on 20 September 2019).
- Scudiero, E.; Berti, A.; Teatini, P.; Morari, F. Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe. Sensors 2012, 12, 17588–17607. [Google Scholar] [CrossRef]
- Bircher, S.; Demontoux, F.O.; Razafindratsima, S.; Zakharova, E.; Drusch, M.; Wigneron, J.-P.; Kerr, Y. L-Band relative permittivity of organic soil surface layers: A new dataset of resonant cavity measurements and model evaluation. Remote Sens. 2016, 8, 1–17. [Google Scholar] [CrossRef]
- Parvin, N.; Degra, A. Soil-specific calibration of capacitance sensors considering clay content and bulk density. Soil Res. 2016, 54, 111–119. [Google Scholar] [CrossRef]
- Cardenas-Lailhacar, B.; Dukes, M.D. Precision of soil moisture sensor irrigation controllers under field conditions. Agric. Water Manag. 2010, 97, 666–672. [Google Scholar] [CrossRef]
- Kassaye, K.; Boulange, J.; Saito, H.; Watanabe, H. Calibration of capacitance sensor for Andosol under field and laboratory conditions in the temperate monsoon climate. Soil Tillage Res. 2019, 189, 52–63. [Google Scholar] [CrossRef]
- Kinzli, K.-D.; Manana, N.; Oad, R. Comparison of Laboratory and Field Calibration of a Soil-Moisture Capacitance Probe for Various Soils. J. Irrig. Drain. Eng. 2012, 138, 310–321. [Google Scholar] [CrossRef]
- Heimovaara, T.J.; Focke, A.G.; Bouten, W.; Verstraten, J.M. Assessing Temporal Variations in Soil Water Composition with Time Domain Reflectometry. Soil Sci. Soc. Am. J. 1995, 59, 689–698. [Google Scholar] [CrossRef]
| Depth (m) | Clay (%) | Fine Silt (%) | Coarse Silt (%) | Fine Sand (%) | Coarse Sand (%) | pH | ECe (dS m−1) |
|---|---|---|---|---|---|---|---|
| 0–0.5 | 5 | 3 | 4 | 22 | 65 | 8.5 | 1.8 |
| Laboratory Calibration | ||||
|---|---|---|---|---|
| ECp (dS m−1) | Ledieu et al. (1986) | CAL-Ka | CAL-Kar | |
| Fit | Equation (4) | θ = 0.16 √Ka1−0.30 | θ = 0.18√K’2−0.33 | |
| ECp ≤ 3 | RMSE | 0.06 | 0.05 | 0.04 |
| R2 | 0.93 | 0.95 | 0.95 | |
| ECp = 6.8 | RMSE | 0.08 | 0.06 | 0.10 |
| R2 | 0.73 | 0.87 | 0.50 | |
| 6.8 < ECp ≤ 10.5 | RMSE | 0.09 | 0.07 | 0.13 |
| R2 | 0.77 | 0.85 | 0.39 | |
| Mean RMSE | 0.08 | 0.06 | 0.09 | |
| Mean R2 | 0.8 | 0.9 | 0.6 | |
| CV (%) | 26.5 | 20 | 19.8 | |
| Field calibration | ||||
| Fit | θ = 0.15 √Ka−0.26 | θ = 0.20√K’−0.37 | ||
| ECa3 ≤ 0.7 and 1.7 ≤ ECe4 ≤ 4.1 | RMSE (m3 m−3) | - | 0.04 | 0.03 |
| R2 | - | 0.94 | 0.97 | |
| CV (%) | - | 23 | 24 | |
| Field validation | ||||
| ECa ≤ 0.7 and 1.7 ≤ ECe ≤ 4.1 | RMSE (m3 m−3) | 0.1 | 0.060 | 0.060 |
| R2 | 0.80 | 0.88 | 0.97 | |
| CV (%) | 27 | 21 | 24 | |
| ECp (dS m−1) | Hilhorst (2000) | MHK | MHB | |||
|---|---|---|---|---|---|---|
| Soil Parameter-K0 | K0 = 4.1 | K0 = 3.3 1 | K0 = 6 | K0 = 4.1 | K0 = 3.3 1 | Best Fit K0 = f (ECa2) |
| ECp ≤ 3 | 0.29 | 0.14 | 0.83 | 0.88 | 0.34 | 0.044 |
| ECp = 6.8 | 0.57 | 0.21 | 1.7 | 6.3 | 3.8 | 0.050 |
| 6.8 < ECp ≤ 10.5 | 1.48 | 0.99 | 3.06 | - | - | 0.054 |
| Hilhorst (2000) | MHK | MHB | ||||
|---|---|---|---|---|---|---|
| ECa2 ≤ 0.7 and 1.7 ≤ ECe3 ≤ 4.1 | K0 = 4.1 | K0 = 3.31 | K0 = 6 | K0 = 4.1 | K0 = 3.31 | Best Fit K0 = f (ECa) |
| RMSE (dS m−1) | 0.82 | 0.70 | 10 | 1.8 | 1.34 | 0.30 |
| R2 | 0.53 | 0.73 | 0.26 | 0.56 | 0.77 | 0.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zemni, N.; Bouksila, F.; Persson, M.; Slama, F.; Berndtsson, R.; Bouhlila, R. Laboratory Calibration and Field Validation of Soil Water Content and Salinity Measurements Using the 5TE Sensor. Sensors 2019, 19, 5272. https://doi.org/10.3390/s19235272
Zemni N, Bouksila F, Persson M, Slama F, Berndtsson R, Bouhlila R. Laboratory Calibration and Field Validation of Soil Water Content and Salinity Measurements Using the 5TE Sensor. Sensors. 2019; 19(23):5272. https://doi.org/10.3390/s19235272
Chicago/Turabian StyleZemni, Nessrine, Fethi Bouksila, Magnus Persson, Fairouz Slama, Ronny Berndtsson, and Rachida Bouhlila. 2019. "Laboratory Calibration and Field Validation of Soil Water Content and Salinity Measurements Using the 5TE Sensor" Sensors 19, no. 23: 5272. https://doi.org/10.3390/s19235272
APA StyleZemni, N., Bouksila, F., Persson, M., Slama, F., Berndtsson, R., & Bouhlila, R. (2019). Laboratory Calibration and Field Validation of Soil Water Content and Salinity Measurements Using the 5TE Sensor. Sensors, 19(23), 5272. https://doi.org/10.3390/s19235272







