An Imaging Plane Calibration Method for MIMO Radar Imaging
Abstract
:1. Introduction
2. Problem Formulation of Imaging Plane Mismatch
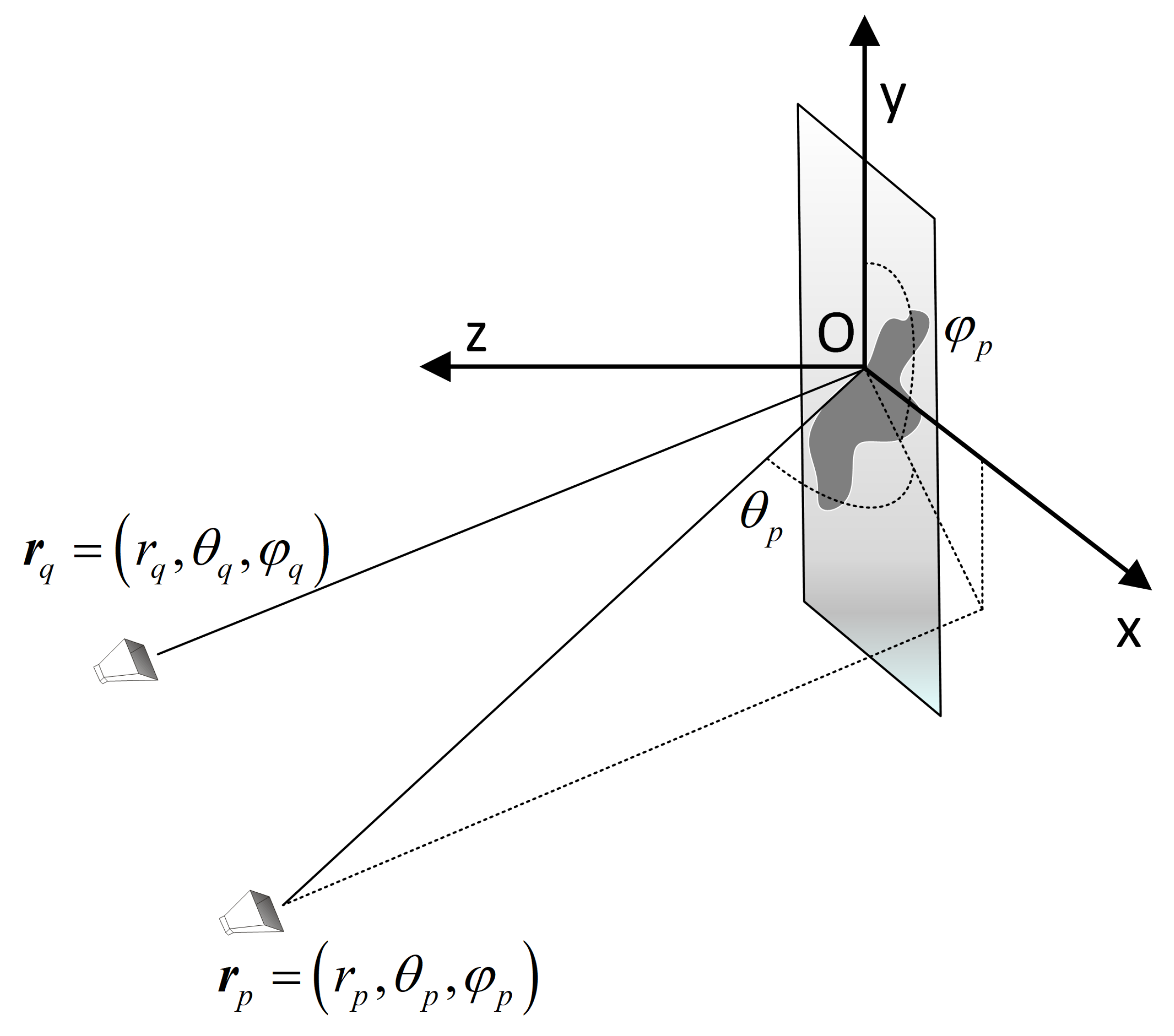
2.1. Space Spectral Imaging Model of Multiple-Input Multiple-Output (MIMO) Radar
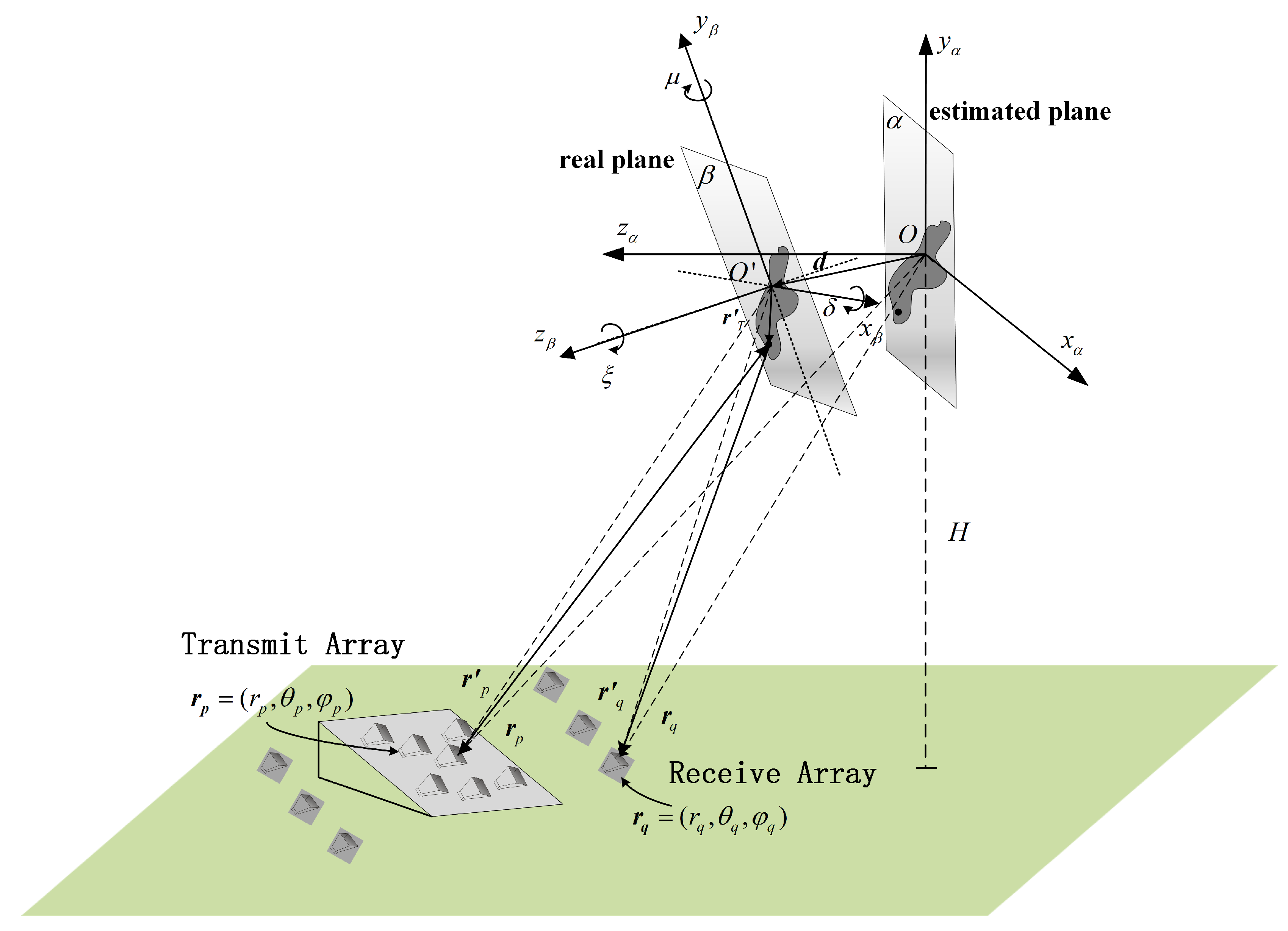
2.2. Analysis of Model Mismatch Problem Caused by Imaging Plane Mismatch
2.3. The Calibration Operation
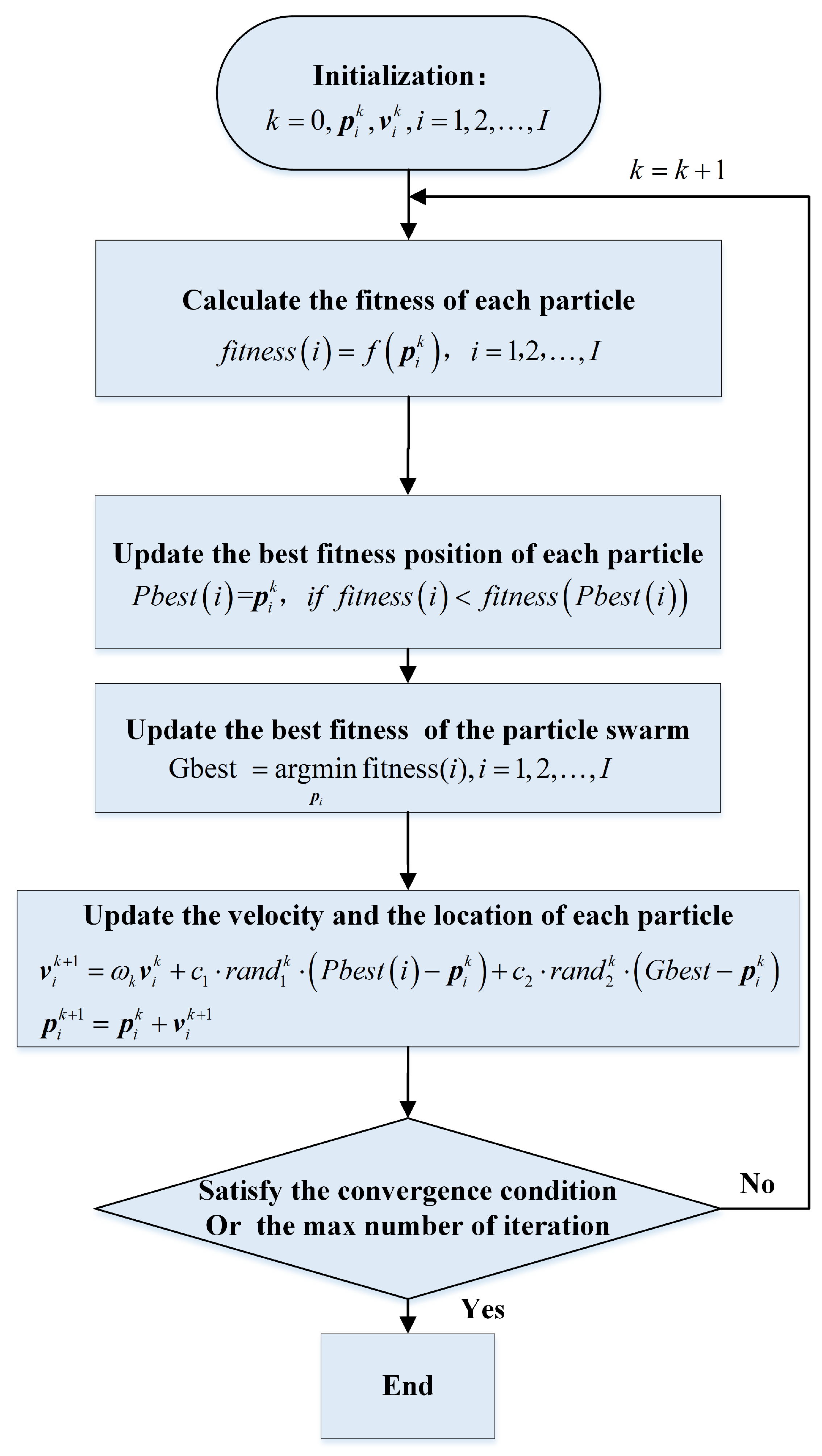
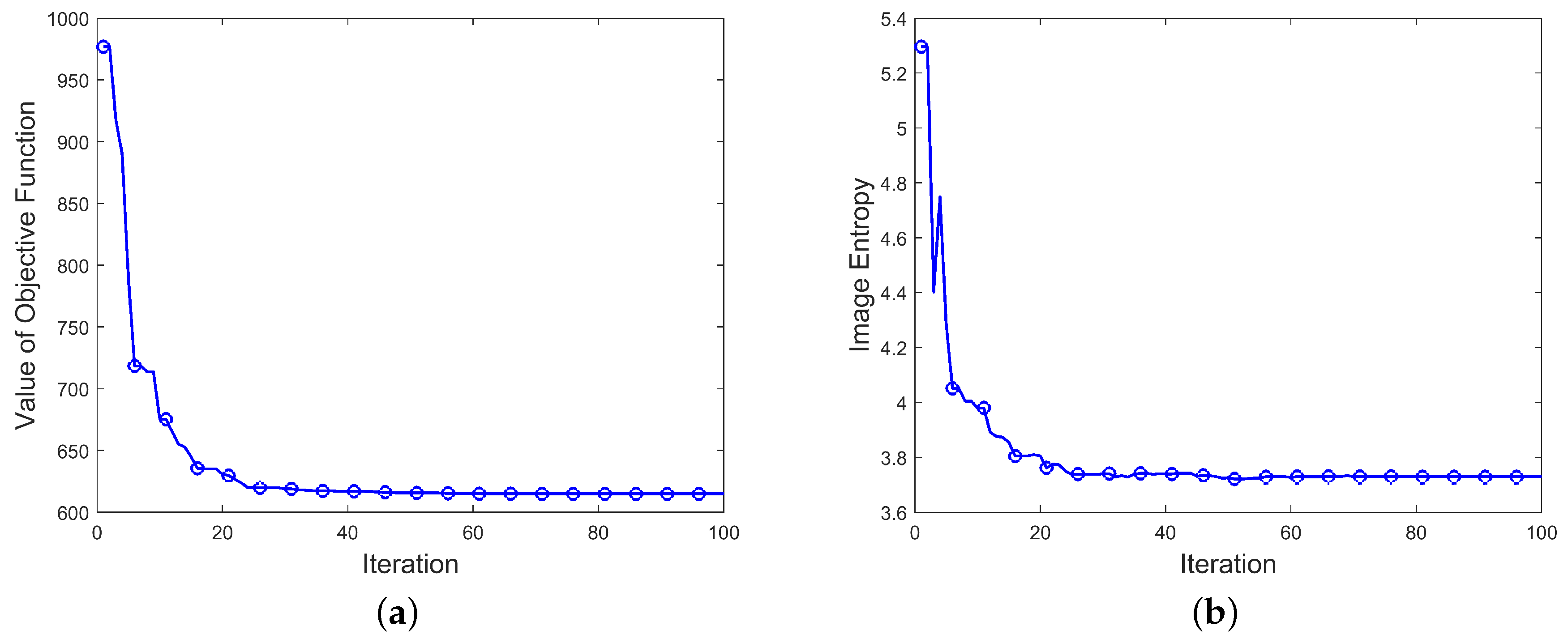
3. The Proposed Imaging Plane Calibration Algorithm (IPCA)
| Algorithm 1: IPCA |
 |
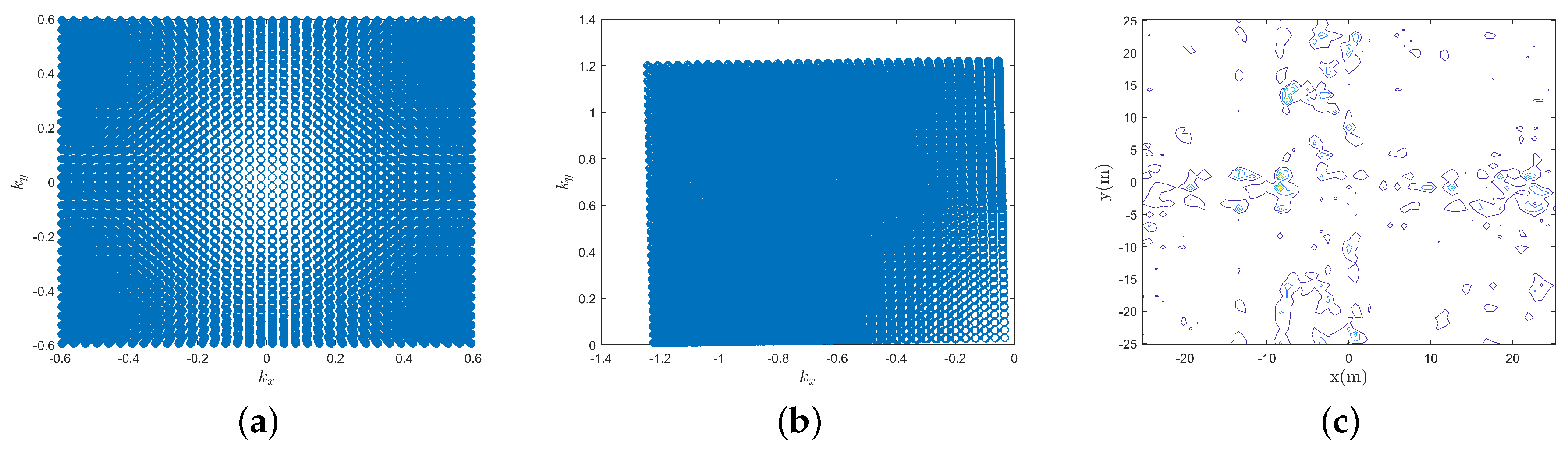
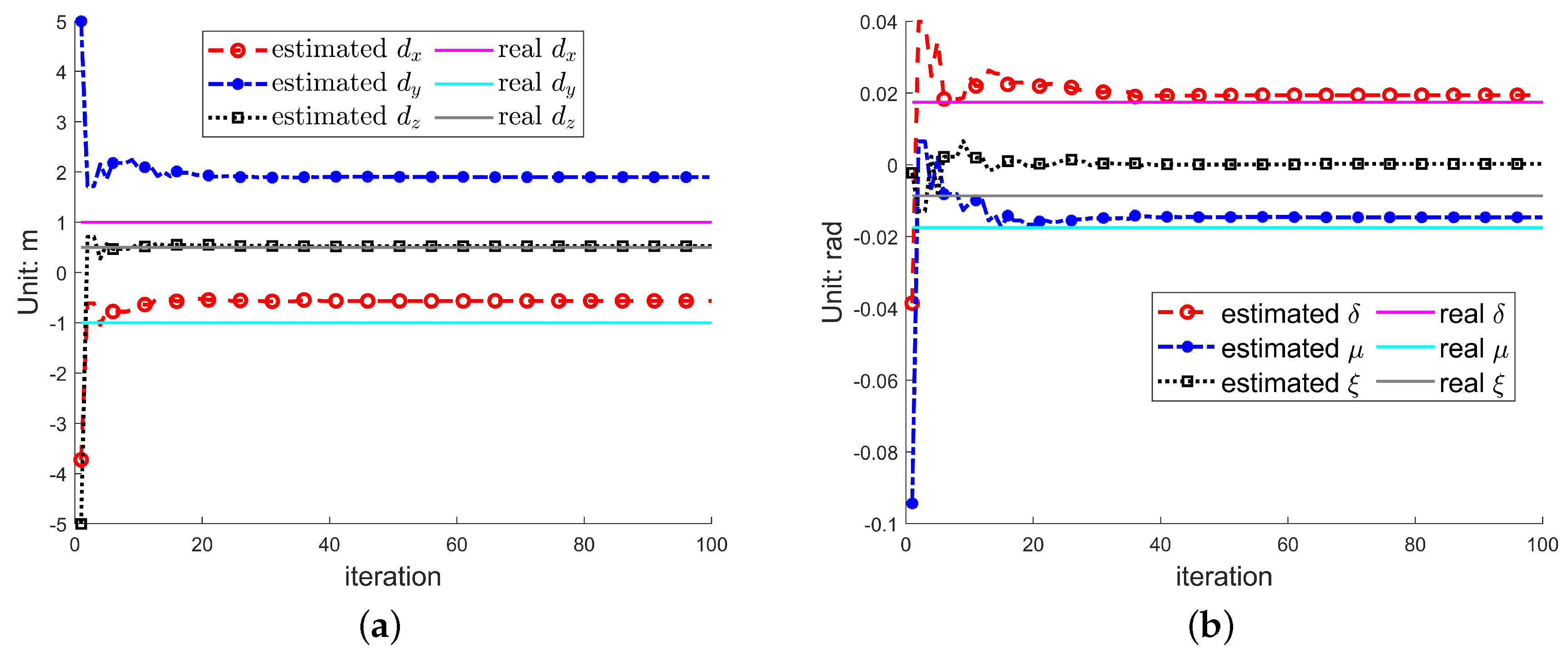
4. Simulations
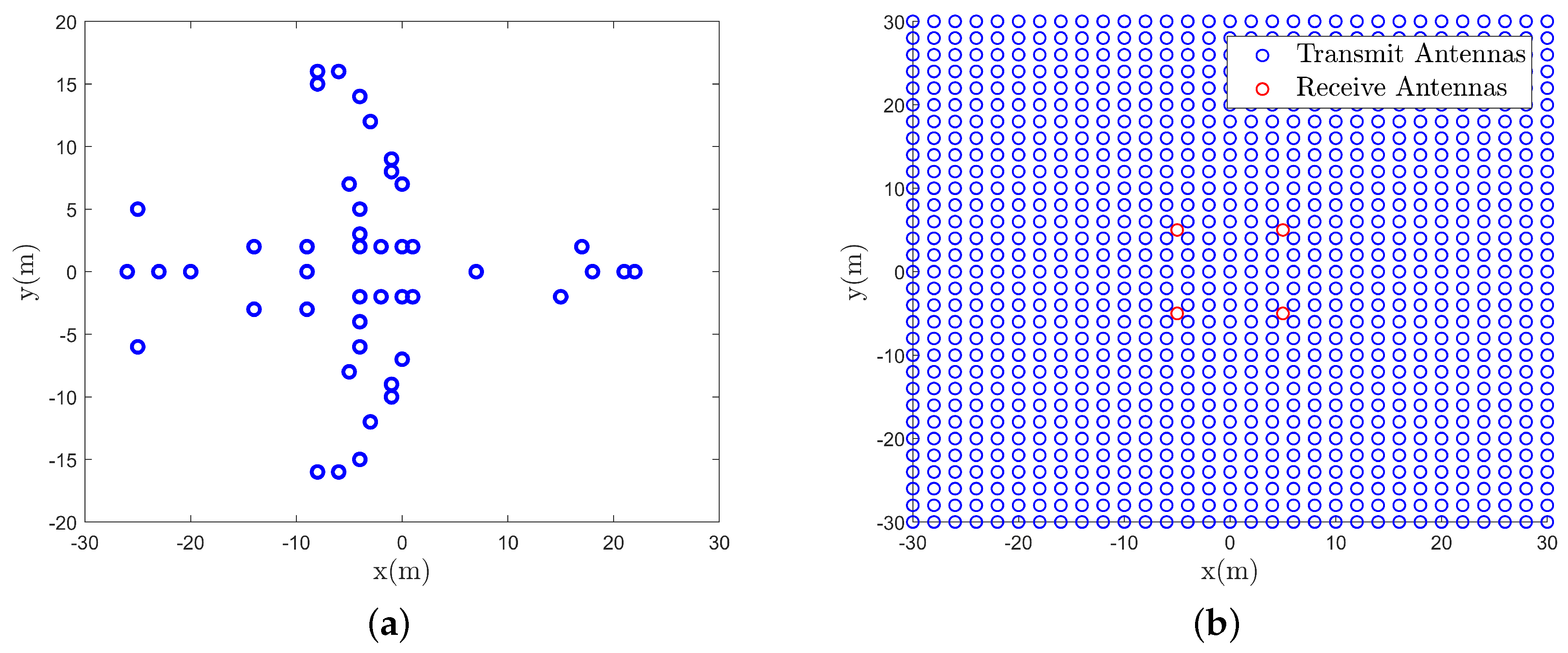
4.1. Imaging Simulation
4.2. Simulations with Different Tunable Parameter
4.3. Simulations under Different Signal-to-Noise Ratios (SNRs)
4.4. Simulations under Different Parameter Ranges
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Constancias, L.; Cattenoz, M.; Brouard, P.; Brun, A. Coherent collocated MIMO radar demonstration for air defence applications. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–6. [Google Scholar]
- Chen, X.P.; Zeng, X.N. Superiority Analysis of MIMO Radar in Aerial Defence and Anti-missile Battle. Telecommun. Eng. 2009, 10. [Google Scholar]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 26–29 April 2004; pp. 71–78. [Google Scholar]
- Li, X.R.; Zhang, Z.; Mao, W.X.; Wang, X.M.; Lu, J.; Wang, W.S. A study of frequency diversity MIMO radar beamforming. In Proceedings of the IEEE International Conference on Signal Processing, Beijing, China, 24–28 October 2010. [Google Scholar]
- Wang, D.W.; Ma, X.Y.; Su, Y. Two-dimensional imaging via a narrowband MIMO radar system with two perpendicular linear arrays. IEEE Trans. Image Process. 2009, 19, 1269–1279. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Tong, N.; Song, B.; Ding, S.; Zhao, X. Joint sparsity-driven three-dimensional imaging method for multiple-input multiple-output radar with sparse antenna array. IET Radar Sonar Navig. 2016, 11, 709–720. [Google Scholar] [CrossRef]
- Sakamoto, T.; Sato, T.; Aubry, P.J.; Yarovoy, A.G. Ultra-wideband radar imaging using a hybrid of Kirchhoff migration and Stolt FK migration with an inverse boundary scattering transform. IEEE Trans. Antennas Propag. 2015, 63, 3502–3512. [Google Scholar] [CrossRef]
- Wang, J.; Cetinkaya, H.; Yarovoy, A. NUFFT based frequency-wavenumber domain focusing under MIMO array configurations. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1–5. [Google Scholar]
- Savelyev, T.; Yarovoy, A. 3D imaging by fast deconvolution algorithm in short-range UWB radar for concealed weapon detection. Int. J. Microw. Wirel. Technol. 2013, 5, 381–389. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A.G.; Savelyev, T.; Ligthart, L. Modified Kirchhoff migration for UWB MIMO array-based radar imaging. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2692–2703. [Google Scholar] [CrossRef]
- Roberts, W.; Stoica, P.; Li, J.; Yardibi, T.; Sadjadi, F.A. Iterative adaptive approaches to MIMO radar imaging. IEEE J. Sel. Top. Signal Process. 2010, 4, 5–20. [Google Scholar] [CrossRef]
- Tan, X.; Roberts, W.; Li, J.; Stoica, P. Sparse learning via iterative minimization with application to MIMO radar imaging. IEEE Trans. Signal Process. 2010, 59, 1088–1101. [Google Scholar] [CrossRef]
- Ding, L.; Chen, W. MIMO radar sparse imaging with phase mismatch. IEEE Geosci. Remote Sens. Lett. 2014, 12, 816–820. [Google Scholar] [CrossRef]
- Yun, L.; Zhao, H.; Du, M. A MIMO radar quadrature and multi-channel amplitude-phase error combined correction method based on cross-correlation. In Proceedings of the Ninth International Conference on Graphic and Image Processing (ICGIP 2017), Qingdao, China, 13–15 October 2017; International Society for Optics and Photonics: Bellingham, DC, USA, 2018; Volume 10615, p. 1061555. [Google Scholar]
- Ding, L.; Chen, W.; Zhang, W.; Poor, H.V. MIMO radar imaging with imperfect carrier synchronization: A point spread function analysis. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2236–2247. [Google Scholar] [CrossRef]
- Liu, C.; Yan, J.; Chen, W. Sparse self-calibration by MAP method for MIMO radar imaging. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2469–2472. [Google Scholar]
- Tan, Z.; Nehorai, A. Sparse direction of arrival estimation using co-prime arrays with off-grid targets. IEEE Signal Process. Lett. 2014, 21, 26–29. [Google Scholar] [CrossRef]
- He, X.; Liu, C.; Liu, B.; Wang, D. Sparse frequency diverse MIMO radar imaging for off-grid target based on adaptive iterative MAP. Remote Sens. 2013, 5, 631–647. [Google Scholar] [CrossRef]
- Duan, G.Q.; Dang, W.W.; Xiao, Y.M.; Yi, S. Three-Dimensional Imaging via Wideband MIMO Radar System. IEEE Geosci. Remote Sens. Lett. 2010, 7, 445–449. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; pp. 760–766. [Google Scholar]
- Gao, C.; Teh, K.C.; Liu, A. Orthogonal Frequency Diversity Waveform with Range-Doppler Optimization for MIMO Radar. IEEE Signal Process. Lett. 2014, 21, 1201–1205. [Google Scholar] [CrossRef]
- Chen, A.L.; Wang, D.W.; Ma, X.Y. An improved BP algorithm for high-resolution MIMO imaging radar. In Proceedings of the 2010 International Conference on Audio, Language and Image Processing, Shanghai, China, 23–25 November 2010; pp. 1663–1667. [Google Scholar]
- Yang, X.S. Metaheuristic optimization: Algorithm analysis and open problems. In Proceedings of the 10th International Conference on Experimental Algorithms, Crete, Greece, 5–7 May 2011; pp. 21–32. [Google Scholar]
- Liu, L.; Zhou, F.; Tao, M.; Zhang, Z. A Novel Method for Multi-Targets ISAR Imaging Based on Particle Swarm Optimization and Modified CLEAN Technique. IEEE Sens. J. 2015, 16, 97–108. [Google Scholar] [CrossRef]
- Luo, C.; Wang, G.; Lu, G.; Wang, D. Recovery of moving targets for a novel super-resolution imaging radar with PSO-SRC. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 Octorber 2016. [Google Scholar]
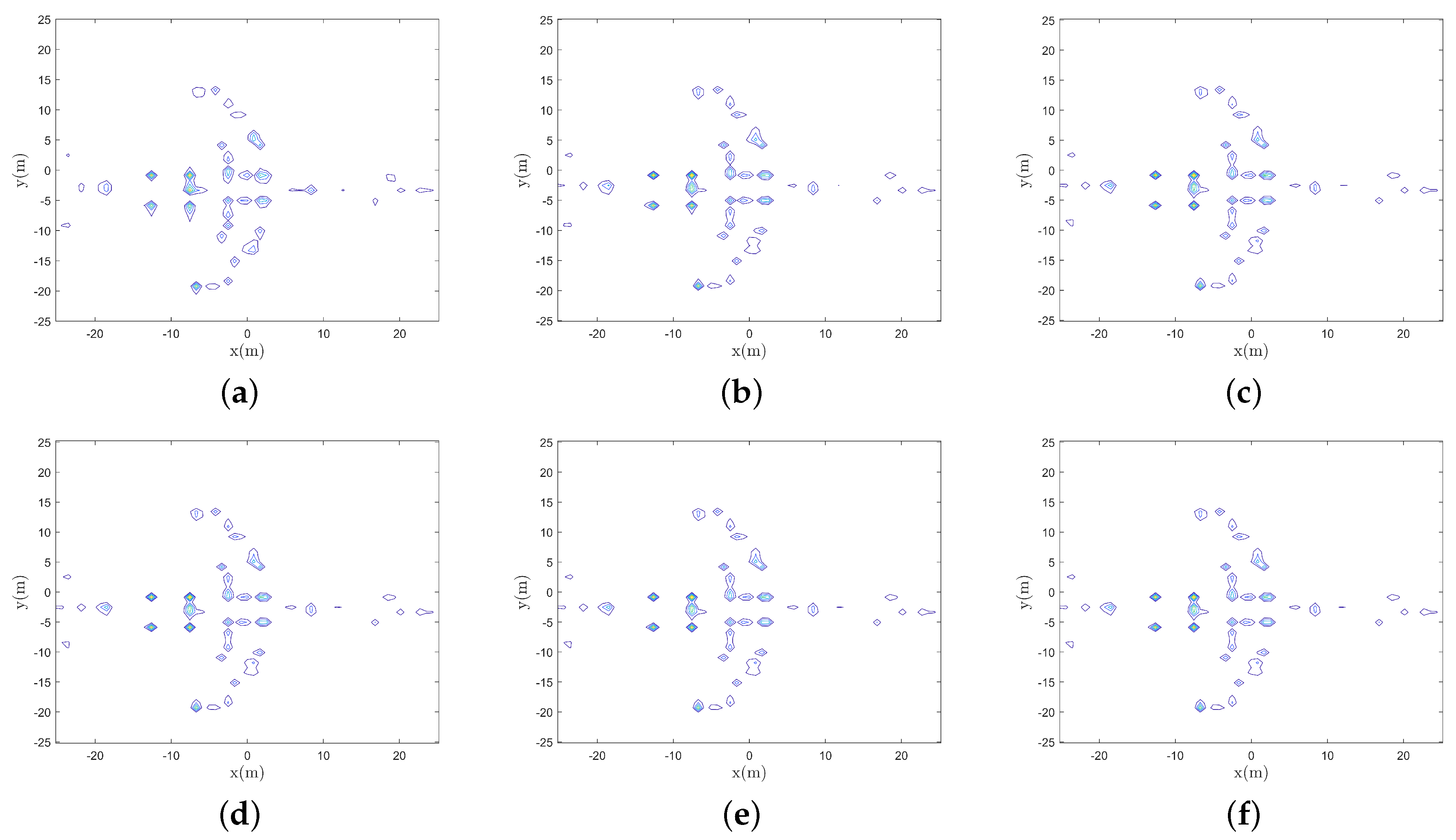
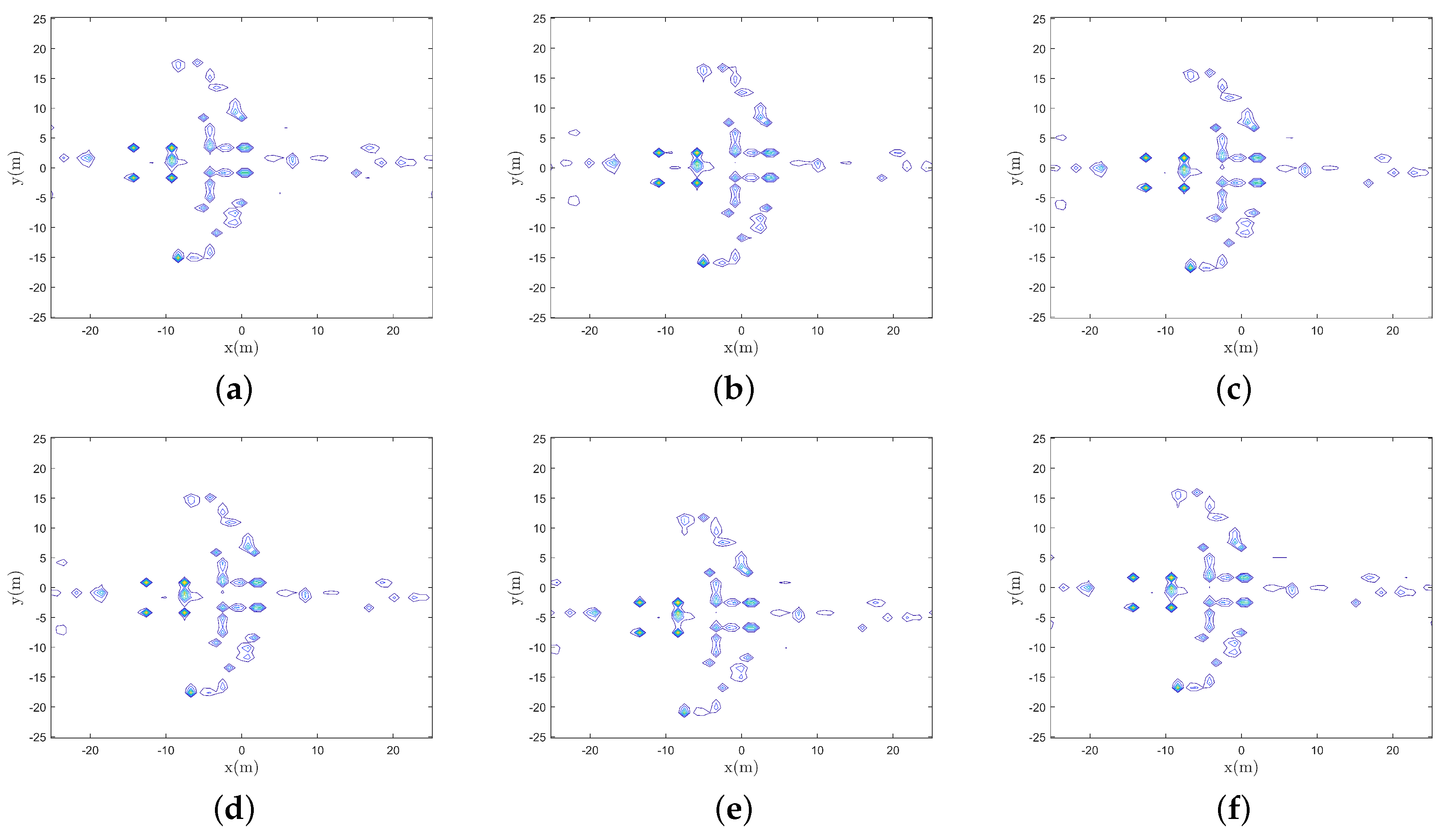
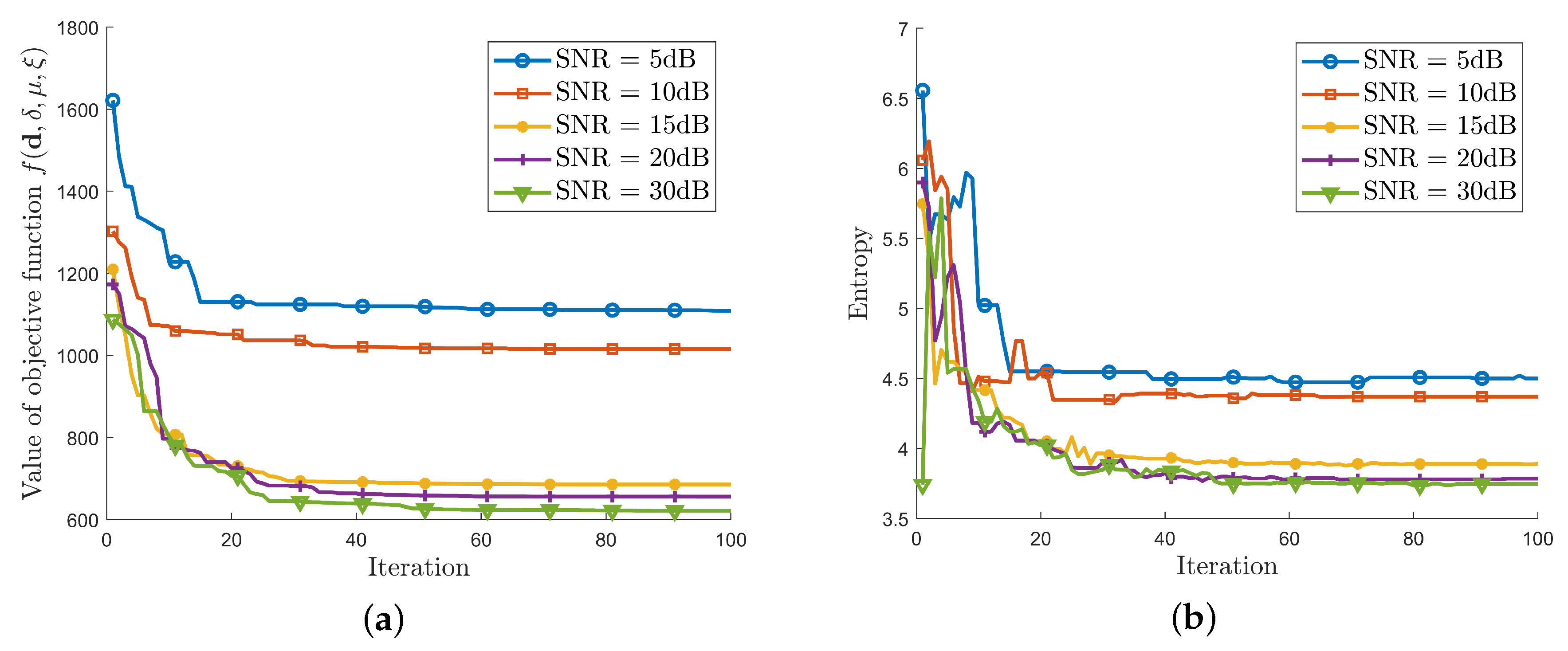
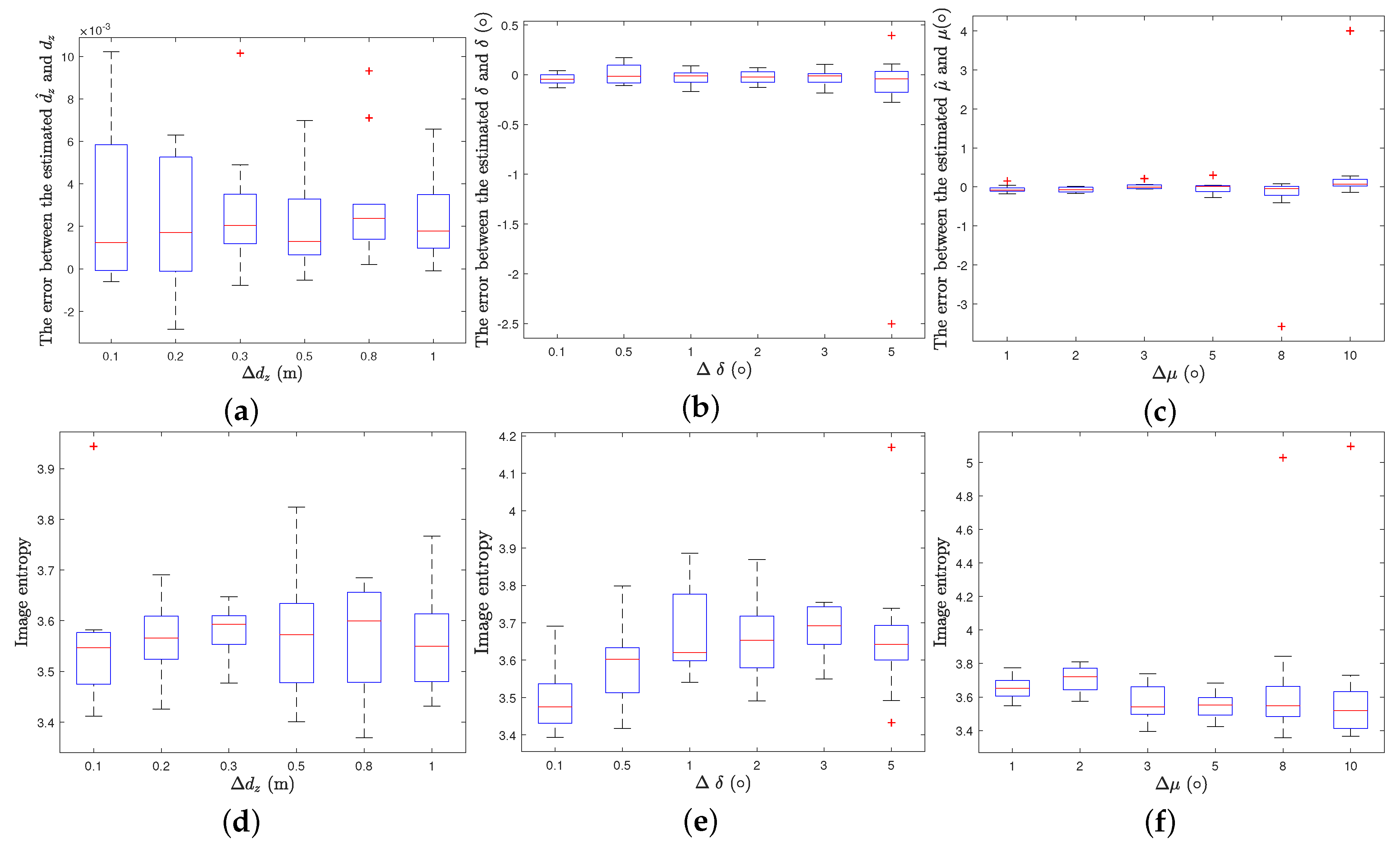
| Parameter | Value |
|---|---|
| Imaging distance | 1 km |
| The size of the imaging plane | 60 m m |
| The size of the radar antenna array | 60 m m |
| Number of transmitters | |
| Number of receivers | 4 |
| Carrier frequency | 5 GHz |
| Bandwidth | 200 MHz |
| Parameter | Value |
|---|---|
| Deviation of the center of the imaging plane | |
| Deviation of the posture angle of the imaging plane |
| Adopted Algorithm | IFFT | The Proposed IPCA |
|---|---|---|
| Image entropy | 5.66 | 3.729 |
| 0.1 | 0.5 | 1 | 3 | 5 | 10 | 50 | |
|---|---|---|---|---|---|---|---|
| Image entropy | 3.76 | 3.70 | 3.63 | 3.73 | 3.73 | 3.74 | 3.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Yuan, B.; Wang, Z.; Xia, R. An Imaging Plane Calibration Method for MIMO Radar Imaging. Sensors 2019, 19, 5261. https://doi.org/10.3390/s19235261
Guo Y, Yuan B, Wang Z, Xia R. An Imaging Plane Calibration Method for MIMO Radar Imaging. Sensors. 2019; 19(23):5261. https://doi.org/10.3390/s19235261
Chicago/Turabian StyleGuo, Yuanyue, Bo Yuan, Zhaohui Wang, and Rui Xia. 2019. "An Imaging Plane Calibration Method for MIMO Radar Imaging" Sensors 19, no. 23: 5261. https://doi.org/10.3390/s19235261
APA StyleGuo, Y., Yuan, B., Wang, Z., & Xia, R. (2019). An Imaging Plane Calibration Method for MIMO Radar Imaging. Sensors, 19(23), 5261. https://doi.org/10.3390/s19235261





