Efficacy of Msplit Estimation in Displacement Analysis
Abstract
1. Introduction and Motivation
2. Theoretical Foundations
3. Empirical Analyses
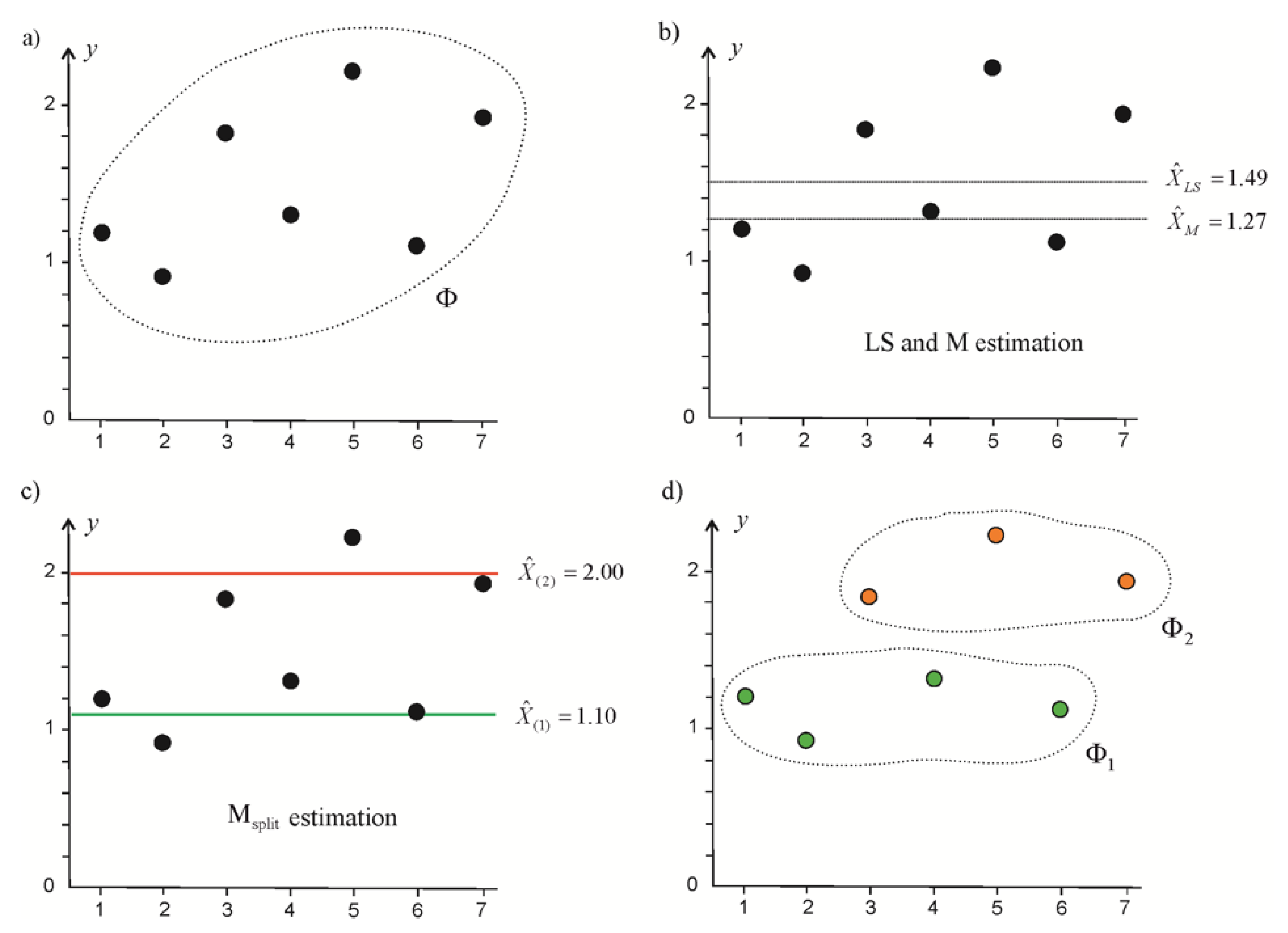
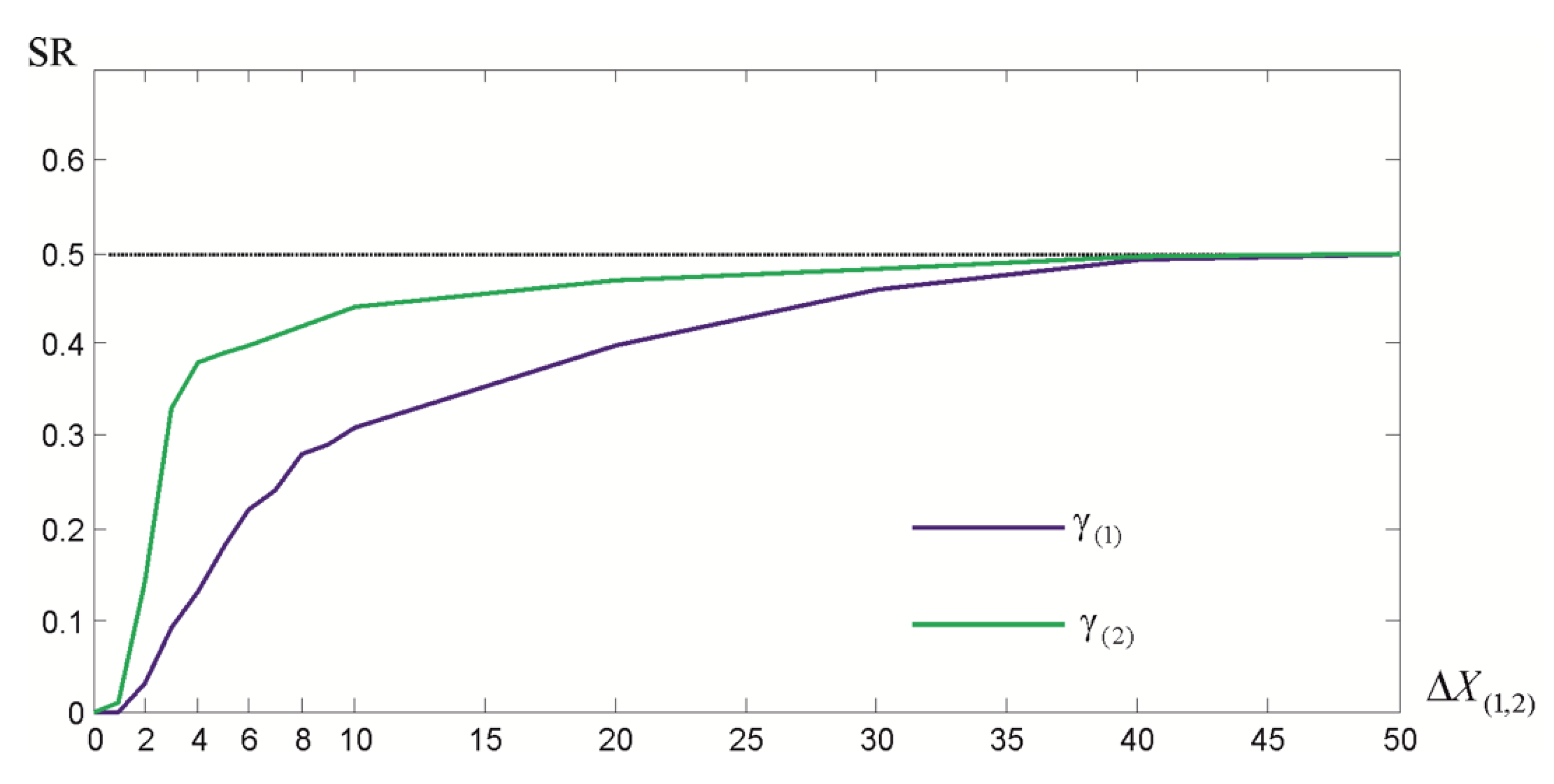
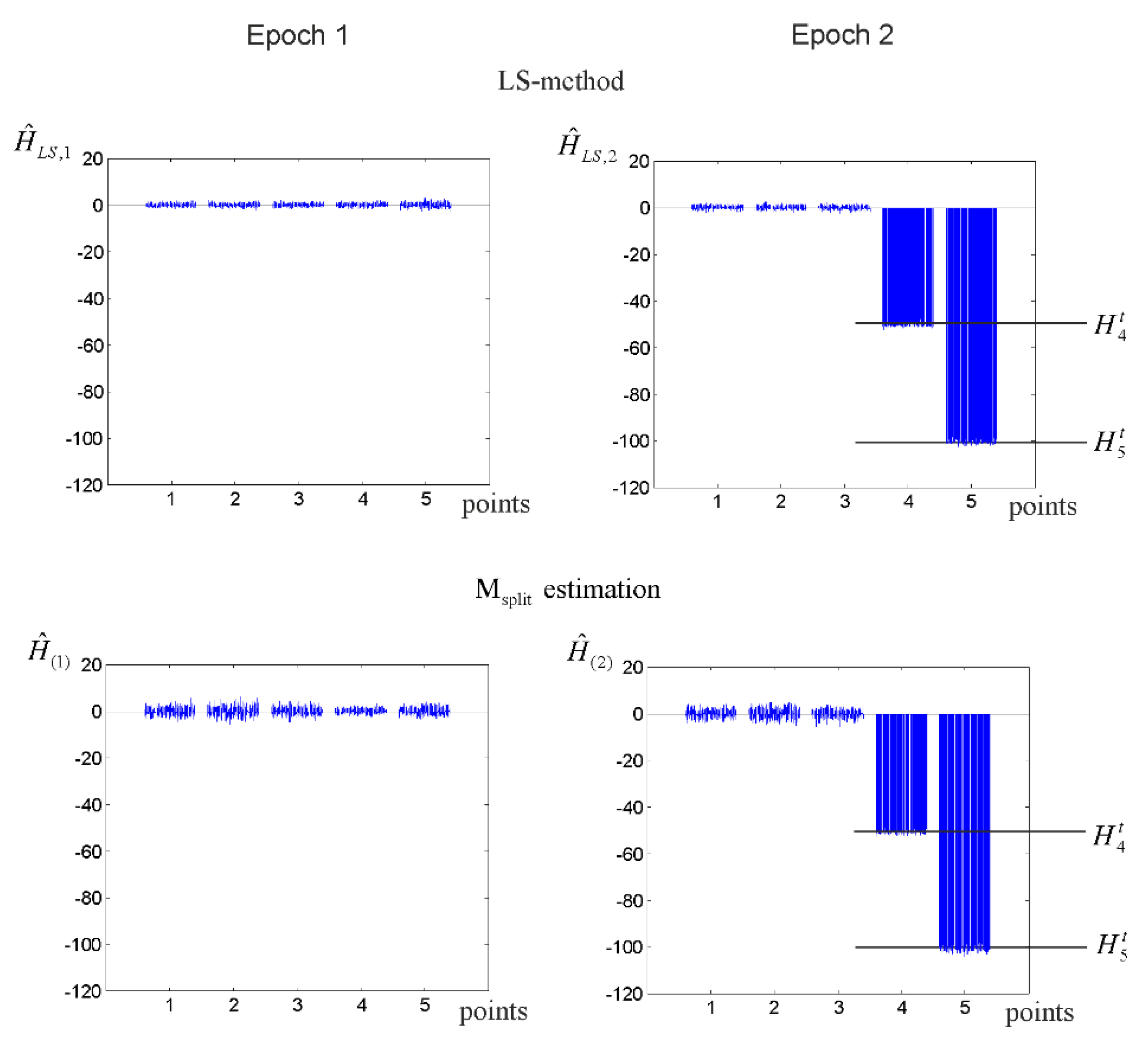
3.1. Elementary Tests
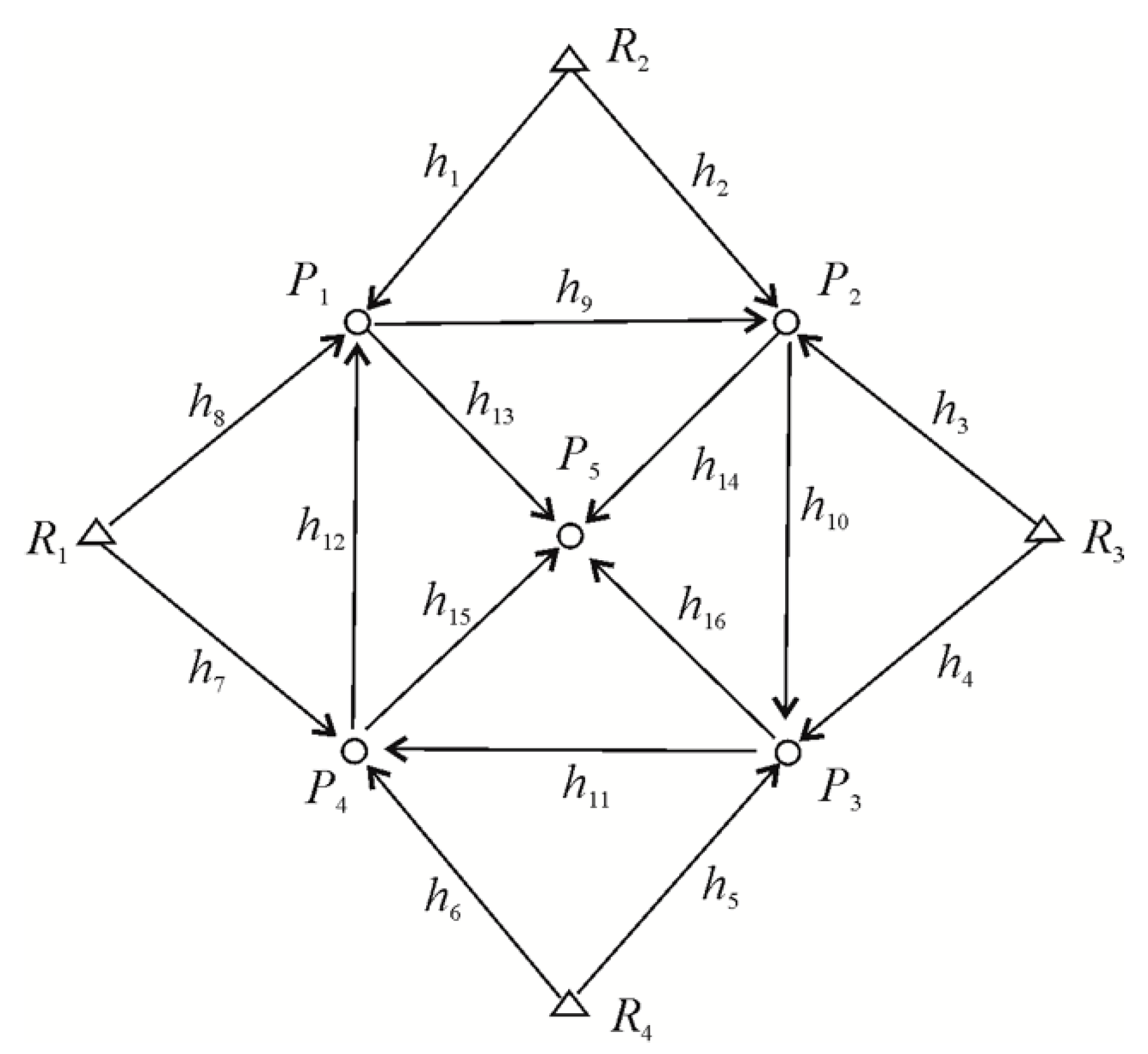
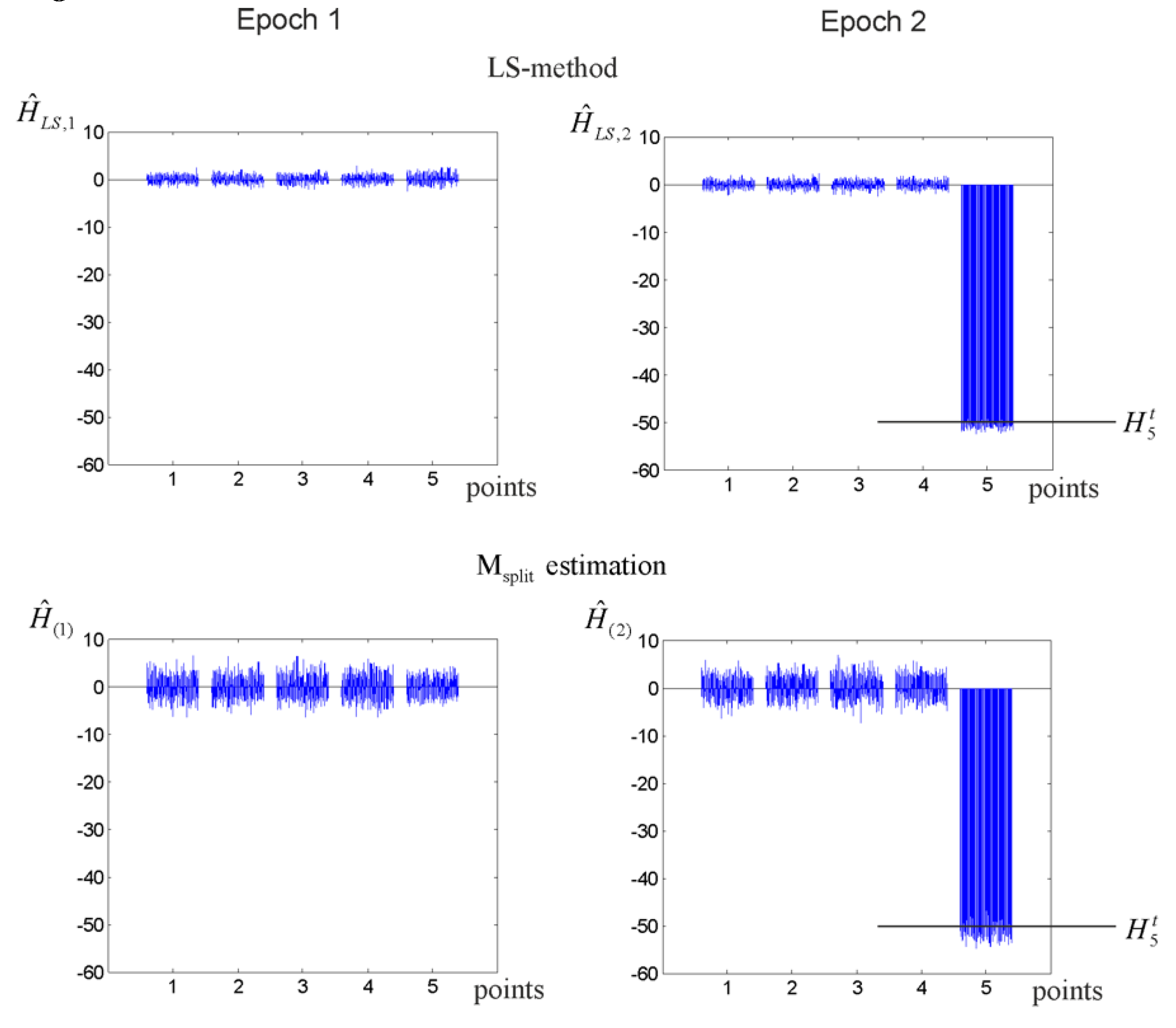
3.2. Vertical Displacement Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pelzer, H. Zur Analyse Geodätischer Deformationsmessungen; Deutsche Geodätische Kommission: Munich, Germany, 1971. [Google Scholar]
- Caspary, W.F.; Haen, W.; Borutta, H. Deformation analysis by statistical methods. Technometrics 1990, 32, 49–57. [Google Scholar] [CrossRef]
- Hekimoglu, S.; Erdogan, B.; Butterworth, S. Increasing the efficacy of the conventional deformation analysis methods: Alternative strategy. J. Surv. Eng. 2010, 136, 1–8. [Google Scholar] [CrossRef]
- Niemeier, W. Statistical tests for detecting movements in repeatedly measured geodetic networks. In Developments in Geotectonics; Elsevier: Amsterdam, The Netherlands, 1981; Volume 71, pp. 335–351. [Google Scholar]
- Setan, H.; Singh, R. Deformation analysis of a geodetic monitoring network. Geomatica 2001, 55, 333–346. [Google Scholar]
- Denli, H.H.; Deniz, R. Global congruency test methods for GPS networks. J. Surv. Eng. 2003, 129, 95–98. [Google Scholar] [CrossRef]
- Chen, Y.Q. Analysis of Deformation Surveys—A Generalized Method; Technical Report; UNB Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 1983. [Google Scholar]
- Caspary, W.F.; Borutta, H. Robust estimation in deformation models. Surv. Rev. 1987, 29, 29–45. [Google Scholar] [CrossRef]
- Duchnowski, R. Median-based estimates and their application in controlling reference mark stability. J. Surv. Eng. 2010, 136, 47–52. [Google Scholar] [CrossRef]
- Duchnowski, R. Hodges–Lehmann estimates in deformation analyses. J. Geod. 2013, 87, 873–884. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Comparison of two unconventional methods of estimation applied to determine network point displacement. Surv. Rev. 2014, 46, 401–405. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Accuracy of the Hodges-Lehmann estimates computed by applying Monte Carlo simulations. Acta Geod. Geophys. 2017, 52, 511–525. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Msplit and Mp estimation. A wider range of robustness. In Proceedings of the International Conference on Environmental Engineering, Vilnius, Lithuania, 27–28 April 2017; pp. 1–6. [Google Scholar]
- Wyszkowska, P.; Duchnowski, R. Subjective breakdown points of R-estimators applied in deformation analysis. In Proceedings of the International Conference on Environmental Engineering, Vilnius, Lithuania, 27–28 April 2017; pp. 1–6. [Google Scholar]
- Erdogan, B.; Hekimoglu, S. Effect of subnetwork configuration design on deformation analysis. Surv. Rev. 2014, 46, 142–148. [Google Scholar] [CrossRef]
- Nowel, K.; Kamiński, W. Robust estimation of deformation from observation differences for free control networks. J. Geod. 2014, 88, 749–764. [Google Scholar] [CrossRef][Green Version]
- Nowel, K. Robust M-Estimation in analysis of control network deformations: classical and new method. J. Surv. Eng. 2015, 141, 04015002. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Alaei-Tabatabaei, S.M.; Zangeneh-Nejad, F.; Voosoghi, B. Stability analysis of deformation-monitoring network points using simultaneous observation adjustment of two epochs. J. Surv. Eng. 2017, 143, 04016020. [Google Scholar] [CrossRef]
- Wiśniewski, Z. Estimation of parameters in a split functional model of geodetic observations (Msplit estimation). J. Geod. 2009, 83, 105–120. [Google Scholar] [CrossRef]
- Wiśniewski, Z. Msplit(q) estimation: Estimation of parameters in a multi split functional model of geodetic observations. J. Geod. 2010, 84, 355–372. [Google Scholar] [CrossRef]
- Janowski, A.; Rapiński, J. M–Split Estimation in Laser Scanning Data Modeling. J Indian Soc. Remote Sens. 2013, 41, 15–19. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Estimation of the shift between parameters of functional models of geodetic observations by applying Msplit estimation. J. Surv. Eng. 2011, 138, 1–8. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H. Application of Msplit estimation to determine control points displacements in networks with unstable reference system. Surv. Rev. 2015, 47, 174–180. [Google Scholar] [CrossRef]
- Wiśniewski, Z.; Zienkiewicz, M.H. Shift- estimation in deformation analyses. J. Surv. Eng. 2016, 142, 04016015. [Google Scholar] [CrossRef]
- Velsink, H. Testing methods for adjustment models with constraints. J. Surv. Eng. 2018, 144, 04018009. [Google Scholar] [CrossRef]
- Li, J.; Wang, A.; Wang, X. Msplit estimate the relationship between LS and its application in gross error detection. Mine Surv. (China) 2013, 2, 57–59. [Google Scholar]
- Huber, P.J. Robust estimation of location parameter. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Huber, P.J. Robust Statistics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wyszkowska, P.; Duchnowski, R. Msplit estimation based on L1 norm condition. J. Surv. Eng. 2019, 145, 04019006. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H. Determination of an adequate number of competitive functional models in the square Msplit(q) estimation with the use of a modified Baarda’s approach. Surv. Rev. 2018, 1–11. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Robustness of Msplit(q) estimation: A theoretical approach. Stud. Geophys. Geod. 2019, 63, 390–417. [Google Scholar] [CrossRef]
- Sebert, D.M.; Montgomery, D.C.; Rollier, D.A. A clustering algorithm for identifying multiple outliers in linear regression. Comput. Stat. Data Anal. 1998, 27, 461–484. [Google Scholar] [CrossRef]
- Soto, J.; Vigo Aguiar, M.I.; Flores-Sintas, A. A fuzzy clustering application to precise orbit determination. J. Comput. Appl. Math. 2007, 204, 137–143. [Google Scholar] [CrossRef][Green Version]
- Spurr, B.D. On estimating the parameters in mixtures of circular normal distributions. J. Int. Assoc. Math. Geol. 1981, 13, 163–173. [Google Scholar] [CrossRef]
- Hsu, J.S.; Walker, J.J.; Orgen, D.E. A stepwise method for determining the number of component distributions in a mixture. Math. Geol. 1986, 18, 153–160. [Google Scholar] [CrossRef]
- Hekimoglu, S.; Koch, K.R. How can reliability of the test for outliers be measured? Allg. Vermes. Nachr. 2000, 7, 247–253. [Google Scholar]


| 0.2 | −3.1 | 0.4 | 2.9 | −0.5 | −1.1 | −0.6 | 0.6 | 0.9 | −1.8 | −0.7 | −0.4 |
| 1.4 | −1.2 | −1.0 | 0.9 | −0.4 | −1.3 | 0.7 | 2.9 | 0.5 | 0.7 | 0.5 | −0.8 |
| 2.1 | −0.6 | −0.6 | −0.6 | 0.1 | −0.6 | 0.5 | 1.3 | −0.3 | −2.8 | −0.1 | 1.1 |
| -0.8 | −3.6 | −0.6 | 0.6 | 1.1 | −0.9 | −1.0 | 1.2 | 0.0 | −0.4 | −1.5 | 1.5 |
| 0.8 | −1.9 | −50.4 | −49.1 | 0.3 | −1.2 | −99.8 | −98.7 | 0.8 | −0.8 | −200.1 | −199.7 |
| −0.2 | −0.5 | −0.3 | 0.6 | −0.5 | 0.1 | −0.4 | 0.3 | 0.0 | −1.3 | −0.3 | −1.1 |
| −0.4 | −2.0 | −0.1 | −0.1 | 0.2 | 0.5 | −0.2 | −0.4 | 0.0 | −0.2 | −0.1 | 0.9 |
| −0.4 | −0.4 | −0.9 | 0.2 | 0.1 | −0.3 | 0.2 | −0.3 | −0.2 | −0.2 | −0.3 | −0.4 |
| −0.1 | −0.3 | −50.5 | −50.1 | 0.4 | 0.5 | −49.9 | −49.6 | −0.1 | −0.4 | −50.0 | −50.1 |
| −0.5 | −1.4 | −50.1 | −50.2 | −0.6 | −0.4 | −100.1 | −99.8 | −0.5 | −0.8 | −200.3 | −200.2 |
| Variant A: Correct Order | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 2.2 | 0.3 | −1.1 | 0.4 | −1.5 | −6.8 | 0.3 | −0.8 | 0.4 | −4.5 | −5.2 |
| 0.4 | −0.1 | 1.1 | 0.4 | −0.5 | −1.5 | 2.1 | 1.8 | −0.2 | −0.8 | −5.3 | −7.7 |
| 0.6 | 0.8 | 0.3 | −1.5 | −0.6 | −3.6 | 3.4 | 1.6 | −0.1 | −1.0 | 4.9 | 7.4 |
| −0.7 | −0.9 | 0.0 | 1.0 | 0.3 | −1.4 | 2.0 | 2.4 | −1.3 | −0.6 | 5.2 | 7.1 |
| −0.2 | 0.5 | −49.8 | −50.3 | 0.4 | −1.5 | −36.2 | −46.5 | −2.0 | −1.0 | 25.3 | −42.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiśniewski, Z.; Duchnowski, R.; Dumalski, A. Efficacy of Msplit Estimation in Displacement Analysis. Sensors 2019, 19, 5047. https://doi.org/10.3390/s19225047
Wiśniewski Z, Duchnowski R, Dumalski A. Efficacy of Msplit Estimation in Displacement Analysis. Sensors. 2019; 19(22):5047. https://doi.org/10.3390/s19225047
Chicago/Turabian StyleWiśniewski, Zbigniew, Robert Duchnowski, and Andrzej Dumalski. 2019. "Efficacy of Msplit Estimation in Displacement Analysis" Sensors 19, no. 22: 5047. https://doi.org/10.3390/s19225047
APA StyleWiśniewski, Z., Duchnowski, R., & Dumalski, A. (2019). Efficacy of Msplit Estimation in Displacement Analysis. Sensors, 19(22), 5047. https://doi.org/10.3390/s19225047





