Detection of Structural Vibration with High-Rate Precise Point Positioning: Case Study Results Based on 100 Hz Multi-GNSS Observables and Shake-Table Simulation
Abstract
1. Introduction
2. Methodology
2.1. Multi-GNSS PPP Functional and Stochastic Model
- is the wavelength on selected frequency signal;
- is the phase observable in cycles;
- is the pseudorange in meters;
- l and i represent station and satellite, respectively;
- is the geometric range between satellite and station;
- and are the receiver and satellite clock corrections in seconds, respectively;
- is the speed of light in meters per second;
- and denote the frequency-dependent receiver and satellite phase delays in cycles, respectively, which include initial and hardware phase biases;
- and are the frequency-dependent receiver and satellite code biases in meters, respectively;
- α refers to the troposphere mapping function coefficient;
- ZTD denotes the zenith tropospheric delay;
- denotes ionospheric delay;
- is the phase ambiguity term;
- denotes the observational noise.
2.2. Filtration of PPP Coordinate Time Series for the Extraction of the High-Rate Dynamic Displacements
3. Experiment Design and Results
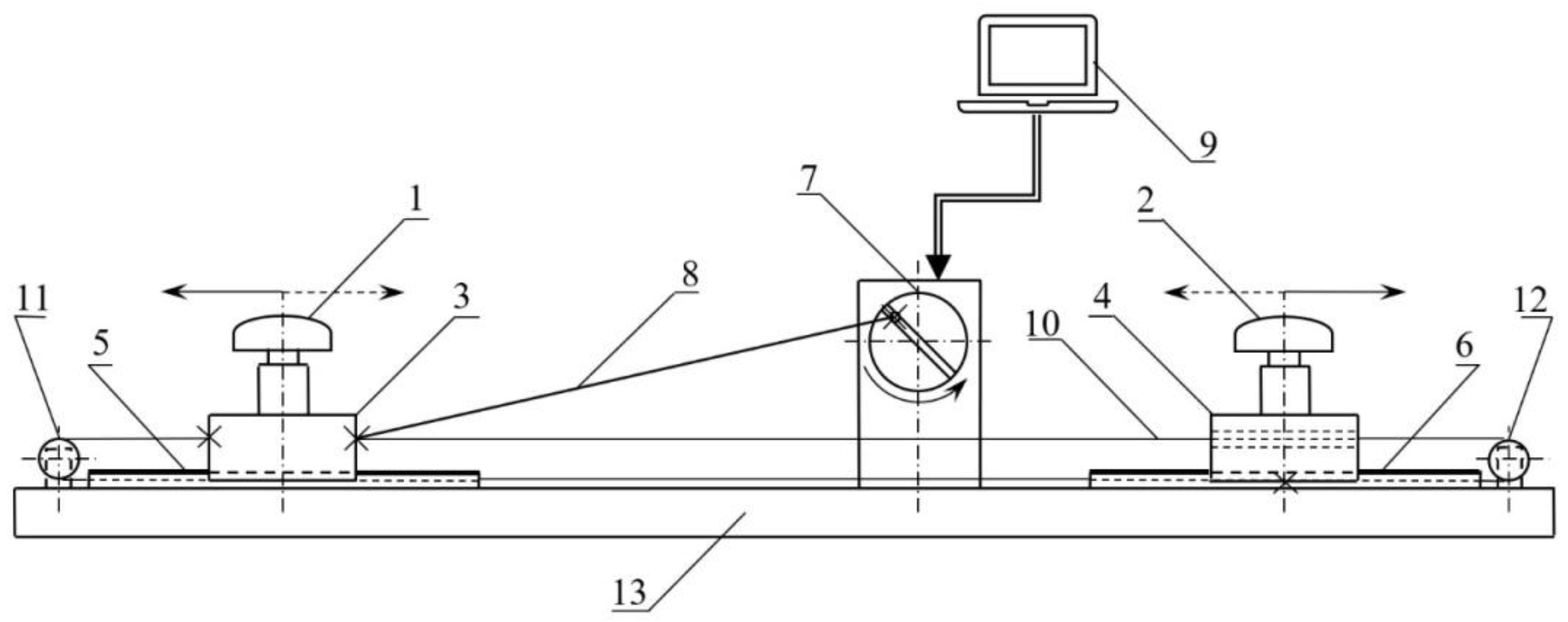
3.1. Shake-Table System
3.2. Experiment Design and Data Collection
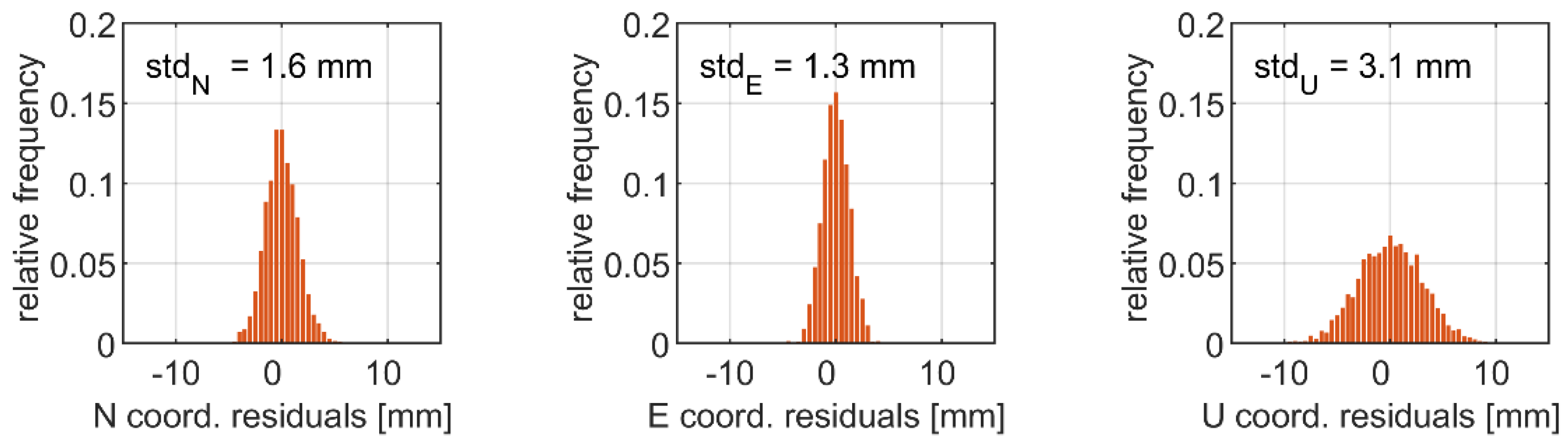
3.3. Initial Evaluation of the High-Rate PPP Displacement Time Series Noise
3.4. Applicability of High-Rate PPP to the Detection of Dynamic Displacements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Psimoulis, P.A.; Pytharouli, S.; Karambalis, D.; Stiros, S.C. Potential of global positioning system (GPS) to measure frequencies of oscillations of engineering structures. J. Sound Vib. 2008, 318, 606–623. [Google Scholar] [CrossRef]
- Avallone, A.; Marzario, M.; Cirella, A.; Piatanesi, A.; Rovelli, A.; Di Alessandro, C.; D’Anastasio, E.; D’Agostino, N.; Giuliani, R.; Mattone, M. Very high rate (10 Hz) GPS seismology for moderate magnitude earthquakes: The case of the Mw 6.3 L’Aquila (central Italy) event. J. Geophys. Res. 2011, 116, B02305. [Google Scholar] [CrossRef]
- Geng, T.; Xie, X.; Fang, R.; Su, X.; Zhao, Q.; Liu, G.; Li, H.; Shi, C.; Liu, J. Real-time capture of seismic waves using high-rate multi-GNSS observations: Application to the 2015 Mw 7.8 Nepal earthquake. Geophys. Res. Lett. 2016, 43, 161–167. [Google Scholar] [CrossRef]
- Hirahara, K.; Nakano, T.; Hoso, Y. An experiment for GPS strain seismometer. In Proceedings of the Japanese Symposium on GPS, Tokyo, Japan, 15–16 December 1994; pp. 67–75. [Google Scholar]
- Nickitopoulou, A.; Protopsalti, K.; Stiros, S. Monitoring dynamic and quasi-static deformations of large flexible engineering structures with GPS: Accuracy, limitations, and promises. Eng. Struct. 2006, 28, 1471–1482. [Google Scholar] [CrossRef]
- Li, X.; Ge, L.; Ambikairajah, E.; Rizos, C.; Tamura, Y.; Yoshida, A. Full-scale structural monitoring using an integrated GPS and accelerometer system. GPS Solut. 2006, 10, 233–247. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge. Measurement 2013, 46, 420–432. [Google Scholar] [CrossRef]
- Yu, J.; Meng, X.; Shao, X.; Yan, B.; Yang, L. Identification of dynamic displacements and modal frequencies of a medium-span suspension bridge using multimode GNSS processing. Eng. Struct. 2014, 8, 432–443. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Multi-GNSS high-rate RTK, PPP and novel direct phase observation processing method: Application to precise dynamic displacements detection. Meas. Sci. Technol. 2018, 29, 035002. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Liu, J.; Wang, L.; Tao, T.; Wu, D.; Chen, R. A Review of Global Navigation Satellite System (GNSS)-Based Dynamic Monitoring Technologies for Structural Health Monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef]
- Dong, D.N.; Bock, Y. Global Positioning System network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Plag, H.P.; Stein, S.; Okal, E. Rapid determination of earthquake magnitude using GPS for tsunami warning systems. Geophys. Res. Lett. 2006, 33, L11309. [Google Scholar] [CrossRef]
- Kogan, M.G.; Kim, W.Y.; Bock, Y.; Smyth, A.W. Load response on the Verrazano Narrows Bridge during the NYC Marathon revealed by GPS and accelerometers. Seismol. Res. Lett. 2008, 79, 12–19. [Google Scholar] [CrossRef]
- Crowell, B.; Bock, Y.; Squibb, M. Demonstration of earthquake early warning using total displacement waveforms from real time GPS networks. Seismol. Res. Lett. 2009, 80, 772–782. [Google Scholar] [CrossRef]
- Ohta, Y.; Kobayashi, T.; Tsushima, H.; Miura, S.; Hino, R.; Takasu, T.; Fujimoto, H.; Iinuma, T.; Tachibana, K.; Demachi, T.; et al. Quasi real-time fault model estimation for near-field tsunami forecasting based on RTK-GPS analysis: Application to the 2011 Tohoku-Oki earthquake (Mw 9.0). J. Geophys. Res. 2012, 117, B02311. [Google Scholar] [CrossRef]
- Melgar, D.; Bock, Y.; Sanchez, D.; Crowell, B.W. On robust and reliable automated baseline corrections for strong motion seismology. J. Geophys. Res. Solid Earth 2013, 118, 1177–1187. [Google Scholar] [CrossRef]
- Elnabwy, M.T.; Kaloop, M.R.; Elbeltagi, E. Talkha steel highway bridge monitoring and movement identification using RTK-GPS technique. Measurement 2013, 46, 4282–4292. [Google Scholar] [CrossRef]
- Yu, J.; Yan, B.; Meng, X.; Shao, X.; Ye, H. Measurement of bridge dynamic responses using network-based real-time kinematic GNSS technique. J. Surv. Eng. 2016, 142, 04015013. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W. Dynamic Performance Analysis of the Towers of a Long-Span Bridge Based on GPS Monitoring Technique. J. Sens. 2016, 2016, 7494817. [Google Scholar] [CrossRef]
- Colosimo, G.; Crespi, M.; Mazzoni, A. Real-time GPS seismology with a stand-alone receiver: A preliminary feasibility demonstration. J. Geophys. Res. Solid Earth 2011, 116, B11302. [Google Scholar] [CrossRef]
- Schaal, R.E.; Larocca, A.P.C. A Methodology for Monitoring Vertical Dynamic Sub-Centimeter Displacments with GPS. GPS Solut. 2002, 5, 15–18. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Deo, M.; Rizos, C. On biases in Precise Point Positioning with multi-constellation and multi-frequency GNSS data. Meas. Sci. Technol. 2016, 27, 035102. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, X.; Zhang, Y.; Guo, B.; Wang, R.; Klotz, J.; Wickert, J. Real-time high-rate co-seismic displacement from ambiguity fixed precise point positioning: Application to earthquake early warning. Geophys. Res. Lett. 2013, 40, 295–300. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y.; Melgar, D.; Crowell, B.W.; Haase, J. A new seismogeodetic approach applied to GPS and accelerometer observations of the 2012 Brawley seismic swarm: Implications for earthquake early warning. Geochem. Geophys. Geosyst. 2013, 14, 2124–2142. [Google Scholar] [CrossRef]
- Paziewski, J. Precise GNSS single epoch positioning with multiple receiver configuration for medium-length baselines: Methodology and performance analysis. Meas. Sci. Technol. 2015, 26, 035002. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.; Ge, M.; Teferle, F. Rapid reconvergences to ambiguity-fixed solutions in precise point positioning. J. Geod. 2010, 84, 705–714. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Brocca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. In Proceedings of the 2008 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 28–30 January 2008; pp. 720–732. [Google Scholar]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. PLL bandwidth and noise in 100 Hz GPS measurements. GPS Solut. 2015, 19, 173–185. [Google Scholar] [CrossRef]
- Shu, Y.; Fang, R.; Liu, J. Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations. Remote Sens. 2017, 9, 1188. [Google Scholar] [CrossRef]
- Choy, S.; Bisnath, S.; Rizos, C. Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut. 2017, 21, 13–22. [Google Scholar] [CrossRef]
- Kudlacik, I.; Kaplon, J.; Bosy, J.; Lizurek, G. Seismic phenomena in the light of high-rate GPS Precise Point Positioning results. Acta Geodyn. Geomater. 2019, 16, 99–112. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Galileo status: Orbits, clocks, and positioning. GPS Solut. 2017, 21, 319–331. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Xia, F.; Ye, S.; Xia, P.; Zhao, L.; Jiang, N.; Chen, D.; Hu, G. Assessing the latest performance of Galileo-only PPP and the contribution of Galileo to Multi-GNSS PPP. Adv. Space Res. 2019, 63, 2784–2795. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Wielgosz, P. On the Applicability of Galileo FOC Satellites with Incorrect Highly Eccentric Orbits: An Evaluation of Instantaneous Medium-Range Positioning. Remote Sens. 2018, 10, 208. [Google Scholar] [CrossRef]
- Jiao, G.; Song, S.; Ge, Y.; Su, K.; Liu, Y. Assessment of BeiDou-3 and Multi-GNSS Precise Point Positioning Performance. Sensors 2019, 19, 2496. [Google Scholar] [CrossRef]
- Yigit, C.O.; Gurlek, E. Experimental testing of high-rate GNSS precise point positioning (PPP) method for detecting dynamic vertical displacement response of engineering structures. Geomat. Nat. Hazards Risk 2017, 8, 893–904. [Google Scholar] [CrossRef]
- Tang, X.; Roberts, G.W.; Li, X.; Hancock, C.M. Real-time kinematic PPP GPS for structure monitoring applied on the Severn Suspension Bridge, UK. Adv. Space Res. 2017, 60, 925–937. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Li, P.; Li, X.; Ge, M.; Guo, F.; Sang, J.; Schuh, H. Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning. J. Geod. 2019. [Google Scholar] [CrossRef]







| Option | Setting |
|---|---|
| Signals | Phase and code GPS L1/L2, BDS B1/B2, and Galileo E1/E5a |
| Sampling rate | 0.01 s (100 Hz) |
| Observable combination | Undifferenced ionosphere-free linear combination (IF-LC) |
| Weighting scheme | Elevation-dependent weighting |
| Elevation cutoff angle | 10° |
| Troposphere delay modelling | Estimation of the residual ZTD, a priori modified Hopfield model + global mapping function |
| Ionosphere delay modelling | First order of ionospheric delay eliminated taking advantage of IF-LC |
| Type of the solution | Float kinematic |
| Stochastic modelling: a priori standard deviation of observations | 0.3 m/0.003 m for code/phase of GPS and Galileo signals, respectively; BDS signals down-weighted by the value of 20%. |
| Satellite orbits and clocks | Precise CODE (interval: orbits 5 min; clocks 30 s) |
| Parameter estimation method | Sequential least squares with a priori parameter constraining and equivalent elimination |
| Feature | Value |
|---|---|
| Dimensions | 1.34 m length, 0.23 width, 0.18 m height (without antenna) |
| Total mass | 10 kg |
| Number of GNSS antennas that can be set in motion | 2 |
| Maximum load weight | 4 kg |
| Number of motion axes | single |
| Characteristics of the motion | Linear, periodical in selected horizontal direction |
| Maximum frequency of the oscillations | Up to 25 Hz |
| Amplitude range | 1–85 mm |
| Precision of dedicated amplitude | −0.5 mm |
| Control system | dedicated software running under a PC |
| Engine | Stepper motor |
| Type of Solution | stdN [mm] | stdE [mm] | stdU [mm] |
|---|---|---|---|
| RTK G + E + C | 1.6 | 1.3 | 3.1 |
| PPP G | 2.8 | 2.4 | 4.5 |
| PPP G + E + C | 3.4 | 3.4 | 5.7 |
| Detected Values | Benchmark Values | ||||
|---|---|---|---|---|---|
| FN [Hz] | FE [Hz] | A [mm] | F [Hz] | A [mm] | |
| RTK G + E + C | 3.775 | 3.775 | 9.1 | 3.800 | 9.0 |
| PPP G | 3.778 | 3.778 | 10.0 | ||
| PPP G + E + C | 3.778 | 3.778 | 10.0 | ||
| Detected Values | Benchmark Values | ||||
|---|---|---|---|---|---|
| FN [Hz] | FE [Hz] | A [mm] | F [Hz] | A [mm] | |
| RTK G + E + C | 3.777 | 3.777 | 7.6 | 3.800 | 6.0 |
| PPP G | 3.777 | 3.777 | 6.9 | ||
| PPP G + E + C | 3.777 | 3.777 | 6.9 | ||
| Detected Values | Benchmark Values | ||||
|---|---|---|---|---|---|
| FN [Hz] | FE [Hz] | A [mm] | F [Hz] | A [mm] | |
| RTK G + E + C | 3.773 | 3.773 | 3.1 | 3.800 | 1.5 |
| PPP G | 3.774 | 3.774 | 2.0 | ||
| PPP G + E + C | 3.774 | 3.774 | 2.8 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paziewski, J.; Sieradzki, R.; Baryla, R. Detection of Structural Vibration with High-Rate Precise Point Positioning: Case Study Results Based on 100 Hz Multi-GNSS Observables and Shake-Table Simulation. Sensors 2019, 19, 4832. https://doi.org/10.3390/s19224832
Paziewski J, Sieradzki R, Baryla R. Detection of Structural Vibration with High-Rate Precise Point Positioning: Case Study Results Based on 100 Hz Multi-GNSS Observables and Shake-Table Simulation. Sensors. 2019; 19(22):4832. https://doi.org/10.3390/s19224832
Chicago/Turabian StylePaziewski, Jacek, Rafal Sieradzki, and Radoslaw Baryla. 2019. "Detection of Structural Vibration with High-Rate Precise Point Positioning: Case Study Results Based on 100 Hz Multi-GNSS Observables and Shake-Table Simulation" Sensors 19, no. 22: 4832. https://doi.org/10.3390/s19224832
APA StylePaziewski, J., Sieradzki, R., & Baryla, R. (2019). Detection of Structural Vibration with High-Rate Precise Point Positioning: Case Study Results Based on 100 Hz Multi-GNSS Observables and Shake-Table Simulation. Sensors, 19(22), 4832. https://doi.org/10.3390/s19224832






