A Monocular SLAM-based Controller for Multirotors with Sensor Faults under Ground Effect
Abstract
:1. Introduction
2. Related Work
3. Methods and Materials
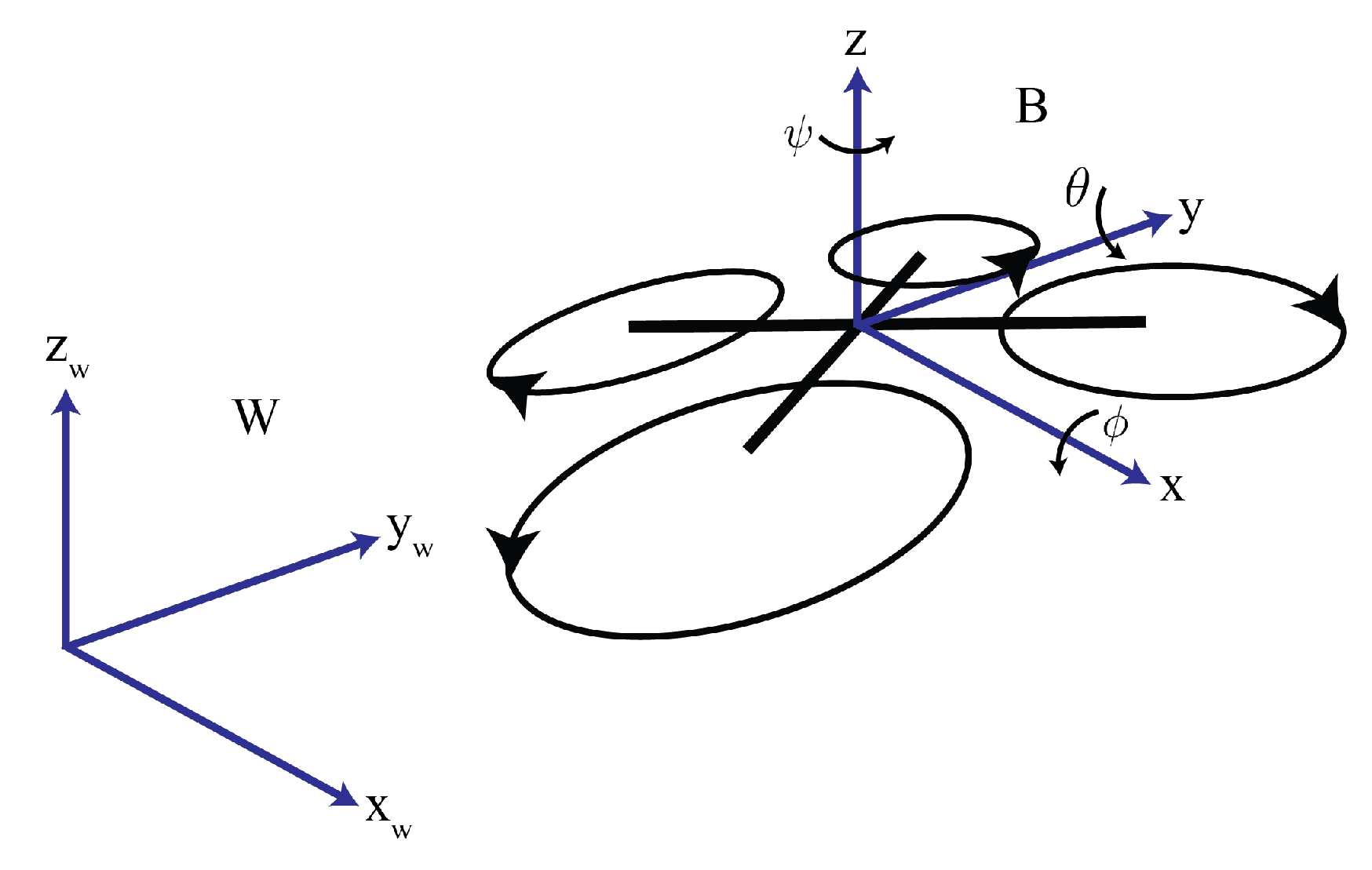
3.1. Multirotor Dynamics
3.2. Altitude Control
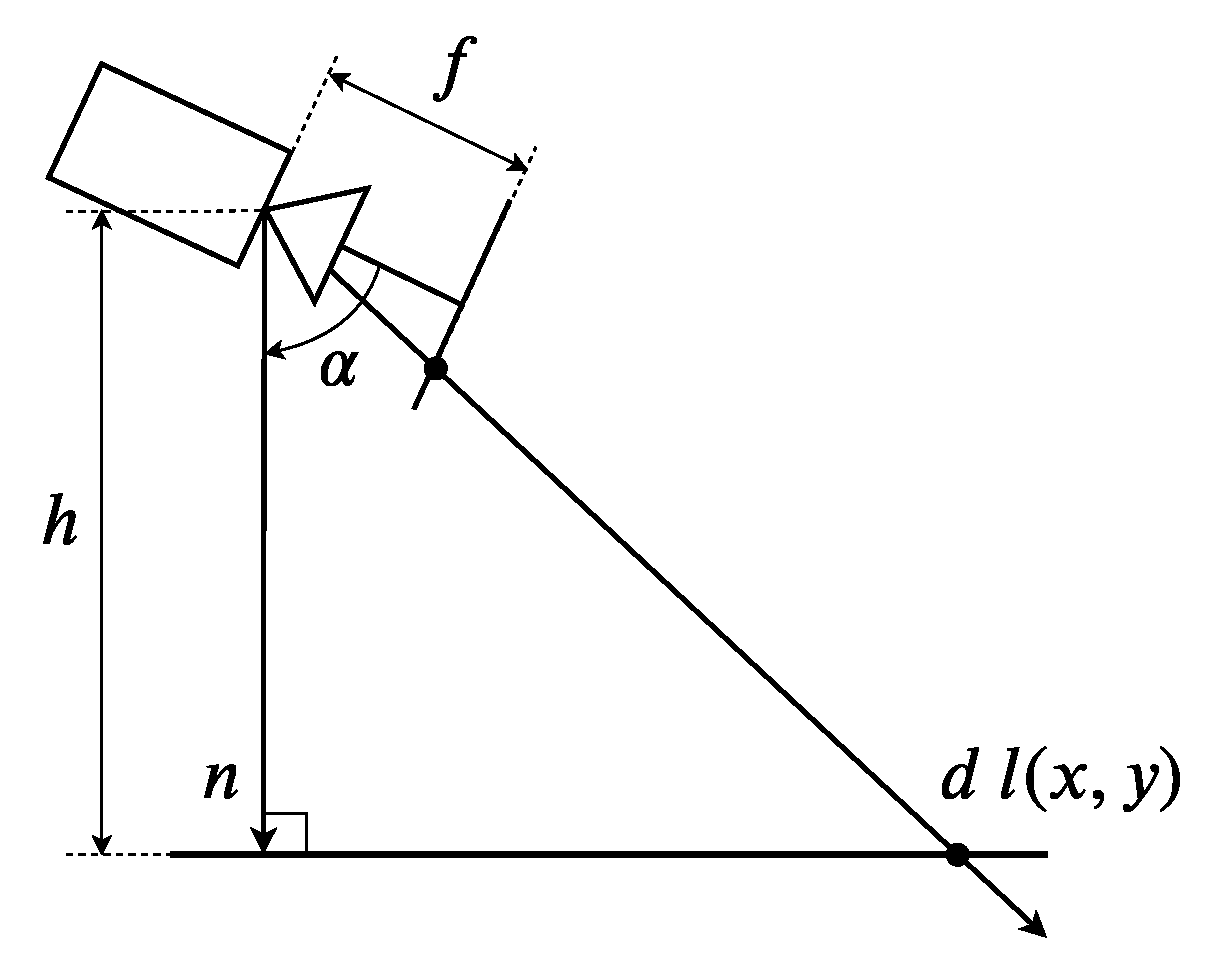
3.3. Metric Monocular SLAM
3.4. Fault-tolerant Control
3.5. Equipment
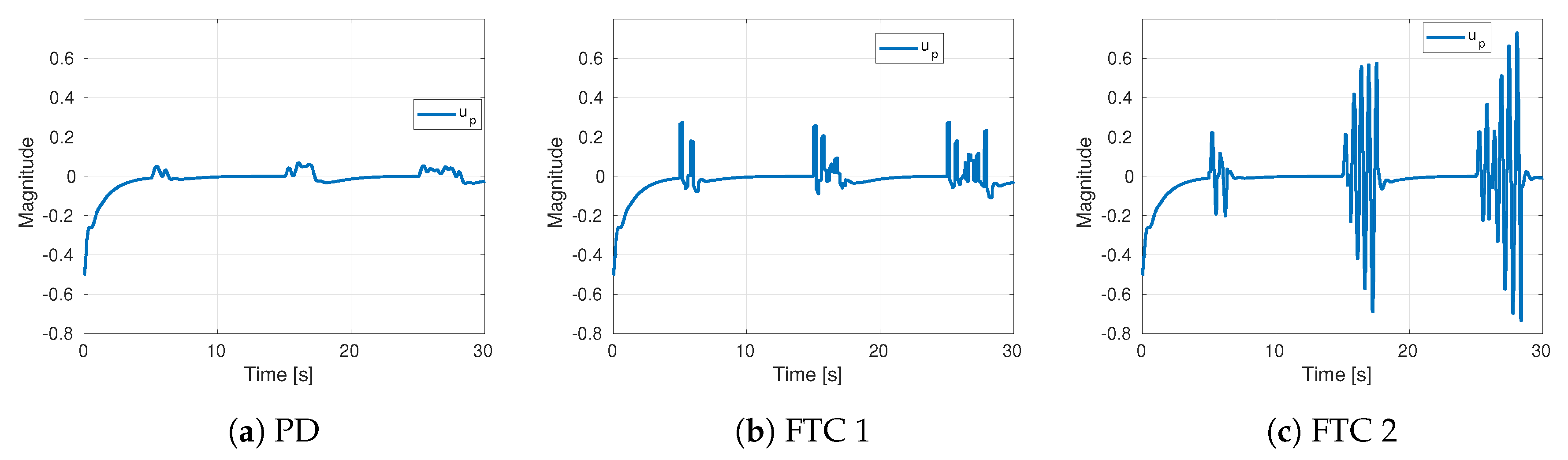
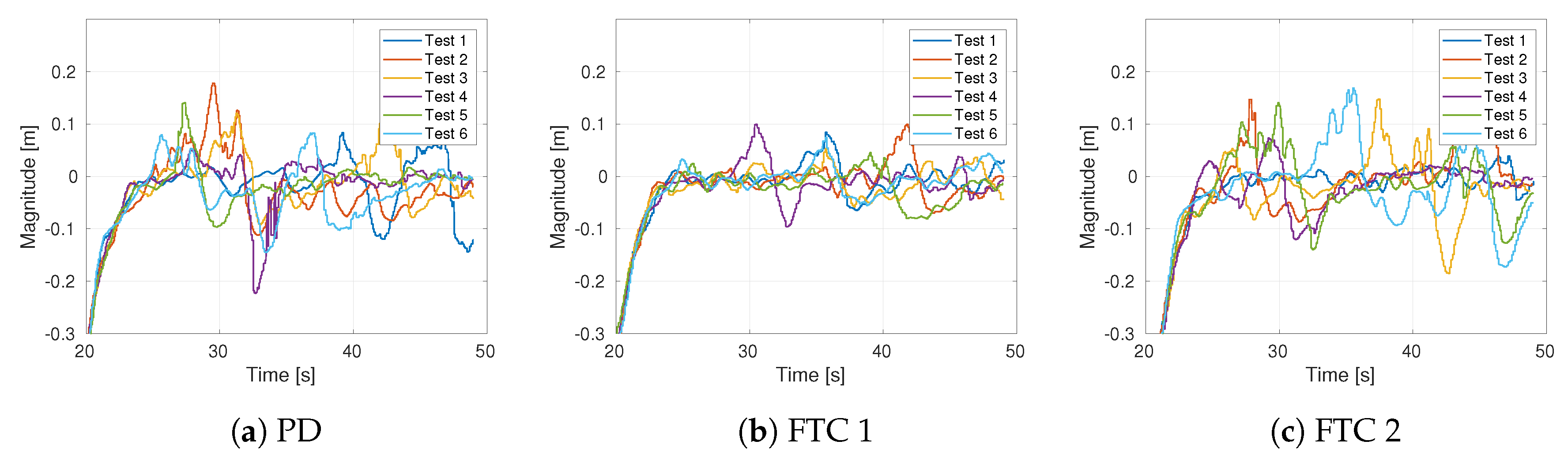
4. Results and Discussion
4.1. Altitude Sensor Faults
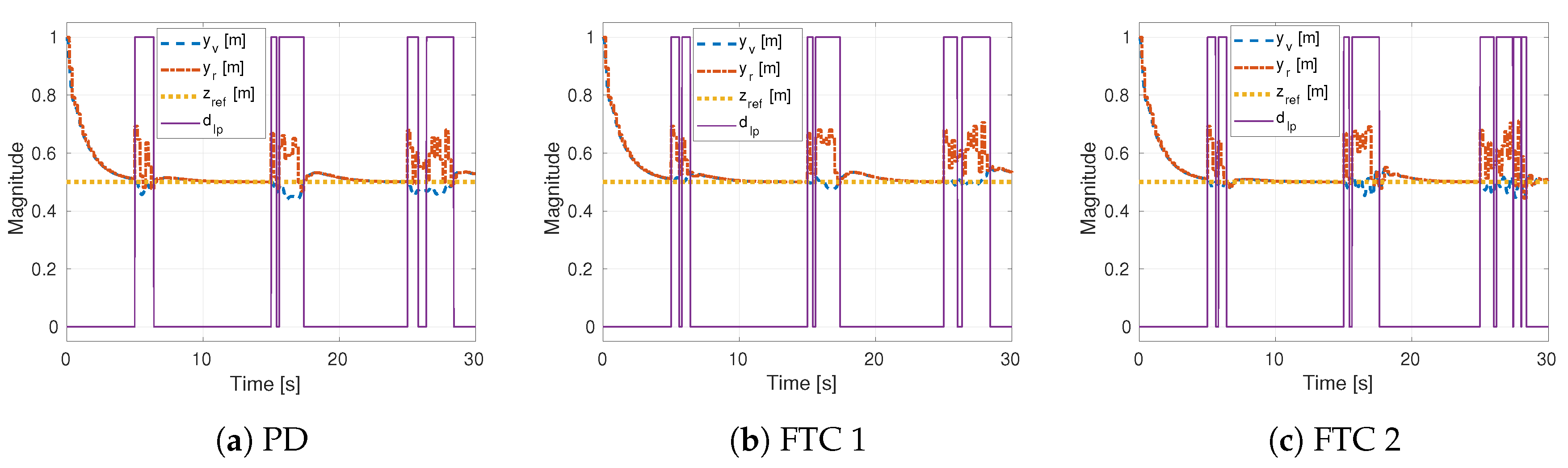
4.2. Simulation
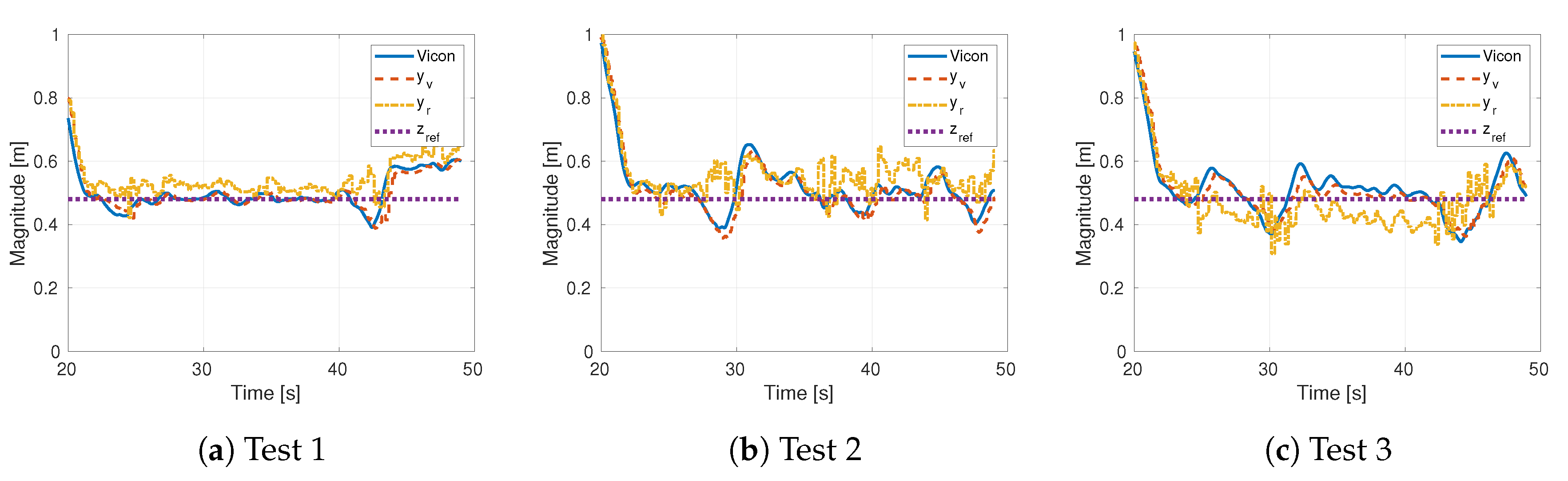
4.3. Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols
| x, y, z | Position in the world-fixed frame |
| , , | Roll, pitch, and yaw angles |
| Velocity of the z axis | |
| m | Mass of the multirotor |
| g | Gravitational acceleration |
| , , | Diagonal elements of the inertia matrix |
| Thrust force | |
| , , | Input torques |
| , | Control inputs of acceleration and velocity |
| , | Position and velocity references of the z axis |
| , | Position and velocity errors of the z axis |
| , | Parameters of the external controller |
| , , | Parameter of the internal controller |
| h | Height above ground of the camera |
| Angle of the camera | |
| f | Focal length of the camera |
| l | Vector from the camera’s optical center through a pixel to the ground |
| n | Vector perpendicular to the ground from the camera’s optical center to the ground |
| d | Distance at which l intersects the ground |
| Sensor fault | |
| , | Range-based and vision-based measurements of the altitude |
| Inertial-based measurement | |
| r | Residual vector |
| Residual evaluation function | |
| , | Fault detection threshold and logical variable |
| , | Sampling periods of the external and internal loops |
| , | Control input of velocity in normal case and fault case |
| Additive control term | |
| Control gain (for positive and negative disturbances) of FTC 1 | |
| c, C | Composite disturbance term and its bound |
| s, | Sliding surface and its parameter |
| Sliding mode control gain of FTC 2 |
References
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Camera-IMU-based localization: Observability analysis and consistency improvement. Int. J. Rob. Res. 2013, 33, 182–201. [Google Scholar] [CrossRef]
- Moon, H.; Martinez-Carranza, J.; Cieslewski, T.; Faessler, M.; Falanga, D.; Simovic, A.; Scaramuzza, D.; Li, S.; Ozo, M.; Wagter, C.D.; et al. Challenges and implemented technologies used in autonomous drone racing. Intell. Serv. Rob. 2019, 12, 137–148. [Google Scholar] [CrossRef]
- Nakanishi, H.; Kanata, S.; Sawaragi, T. Measurement model of barometer in ground effect of unmanned helicopter and its application to estimate terrain clearance. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 232–237. [Google Scholar]
- Cheeseman, I.; Bennet, W. The Effect of the Ground on a Helicopter Rotor in Forward Flight. Aeronaut. Rese. Counc. Rep. Memo 1957, 3021, 1–10. [Google Scholar]
- Hayden, J.S. The Effect of the Ground on Helicopter Hovering Power Required. In Proceedings of the 32nd Annual Forum of the American Helicopter Society, Washington, WA, USA, 10–12 May 1976; Available online: https://vtol.org/store/product/the-effect-of-the-ground-on-helicopter-hovering-power-required-9877.cfm (accessed on 11 November 2019).
- Lee, T.E.; Leishman, J.G.; Ramasamy, M. Fluid Dynamics of Interacting Blade Tip Vortices with a Ground Plane. J. Am. Helicopter Soc. 2010, 55, 22005. [Google Scholar] [CrossRef]
- Nonaka, K.; Sugizaki, H. Integral sliding mode altitude control for a small model helicopter with ground effect compensation. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 202–207. [Google Scholar]
- Ryan, T.; Kim, H.J. Modelling of Quadrotor Ground Effect Forces via Simple Visual Feedback and Support Vector Regression. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; pp. 1–12. [Google Scholar]
- Lee, D.; Kim, H.J.; Sastry, S. Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter. Int. J. Control Autom. Syst. 2009, 7, 419–428. [Google Scholar] [CrossRef]
- Mirzaei, M.; Nia, F.S.; Mohammadi, H. Applying adaptive fuzzy sliding mode control to an underactuated system. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation, Shiraz, Iran, 27–29 December 2011; pp. 654–659. [Google Scholar]
- Matus-Vargas, A.; Rodriguez-Gomez, G.; Martinez-Carranza, J. Aerodynamic Disturbance Rejection Acting on a Quadcopter Near Ground. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1516–1521. [Google Scholar]
- Robinson, D.C. Modelling and Estimation of Aerodynamic Disturbances Acting on a Hovering Micro Helicopter in Close Proximity to Planar Surfaces. Ph.D. Thesis, Monash University, Melbourne, Australia, 2016. [Google Scholar]
- Lakshminarayan, V.K.; Kalra, T.S.; Baeder, J.D. Detailed Computational Investigation of a Hovering Microscale Rotor in Ground Effect. AIAA J. 2013, 51, 893–909. [Google Scholar] [CrossRef]
- Kalra, T.S. CFD Modeling and Analysis of Rotor Wake in Hover Interacting with a Ground Plane. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2014. [Google Scholar]
- Guenard, N.; Hamel, T.; Eck, L. Control Laws For The Tele Operation of An Unmanned Aerial Vehicle Known as An X4-flyer. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3249–3254. [Google Scholar]
- Powers, C.; Mellinger, D.; Kushleyev, A.; Kothmann, B.; Kumar, V. Influence of Aerodynamics and Proximity Effects in Quadrotor Flight. In Experimental Robotics; Springer: Heidelberg, Germany, 2013; pp. 289–302. [Google Scholar] [CrossRef]
- Sharf, I.; Nahon, M.; Harmat, A.; Khan, W.; Michini, M.; Speal, N.; Trentini, M.; Tsadok, T.; Wang, T. Ground effect experiments and model validation with Draganflyer X8 rotorcraft. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1158–1166. [Google Scholar]
- Sanchez-Cuevas, P.; Heredia, G.; Ollero, A. Characterization of the Aerodynamic Ground Effect and Its Influence in Multirotor Control. Int. J. Aerosp. Eng. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Nobahari, H.; Sharifi, A. Continuous ant colony filter applied to online estimation and compensation of ground effect in automatic landing of quadrotor. Eng. Appl. Artif. Intell. 2014, 32, 100–111. [Google Scholar] [CrossRef]
- Hu, B.; Lu, L.; Mishra, S. Fast, safe and precise landing of a quadrotor on an oscillating platform. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 3836–3841. [Google Scholar]
- Danjun, L.; Yan, Z.; Zongying, S.; Geng, L. Autonomous landing of quadrotor based on ground effect modelling. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 5647–5652. [Google Scholar]
- Bartholomew, J.; Calway, A.; Mayol-Cuevas, W. Learning to predict obstacle aerodynamics from depth images for Micro Air Vehicles. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4967–4973. [Google Scholar]
- Bartholomew, J.; Calway, A.; Mayol-Cuevas, W. Improving MAV control by predicting aerodynamic effects of obstacles. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4826–4873. [Google Scholar]
- Tomic, T.; Haddadin, S. A unified framework for external wrench estimation, interaction control and collision reflexes for flying robots. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4197–4204. [Google Scholar]
- Du, H.; Pu, Z.; Yi, J.; Qian, H. Advanced quadrotor takeoff control based on incremental nonlinear dynamic inversion and integral extended state observer. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 1881–1886. [Google Scholar]
- Robinson, D.C.; Ryan, K.; Chung, H. Helicopter hovering attitude control using a direct feedthrough simultaneous state and disturbance observer. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, NSW, Australia, 21–23 September 2015; pp. 633–638. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A New Disturbance Attenuation Control Scheme for Quadrotor Unmanned Aerial Vehicles. IEEE Trans. Ind. Inf. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- McKinnon, C.D.; Schoellig, A.P. Unscented external force and torque estimation for quadrotors. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, South Korea, 9–14 October 2016; pp. 5651–5657. [Google Scholar]
- Zhang, Y.; Chamseddine, A.; Rabbath, C.; Gordon, B.; Su, C.Y.; Rakheja, S.; Fulford, C.; Apkarian, J.; Gosselin, P. Development of advanced FDD and FTC techniques with application to an unmanned quadrotor helicopter testbed. J. Franklin Inst. 2013, 350, 2396–2422. [Google Scholar] [CrossRef]
- Berbra, C.; Lesecq, S.; Martinez, J. A Multi-observer Switching Strategy for Fault-Tolerant Control of a Quadrotor Helicopter. In Proceedings of the 2016 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 1094–1099. [Google Scholar]
- Rafaralahy, H.; Richard, E.; Boutayeb, M.; Zasadzinski, M. Simultaneous observer based sensor diagnosis and speed estimation of Unmanned Aerial Vehicle. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2938–2943. [Google Scholar]
- Nguyen, H.; Berbra, C.; Lesecq, S.; Gentil, S.; Barraud, A.; Godin, C. Diagnosis of an Inertial Measurement Unit based on set membership estimation. In Proceedings of the 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 211–216. [Google Scholar]
- Qin, L.; He, X.; Yan, R.; Zhou, D. Active Fault-Tolerant Control for a Quadrotor with Sensor Faults. J. Intell. Rob. Syst. 2017, 88, 449–467. [Google Scholar] [CrossRef]
- Cook, M.V. Systems of Axes and Notation. In Flight Dynamics Principles; Elsevier: Oxford, UK, 2013; pp. 13–32. [Google Scholar]
- Bouabdallah, S.; Siegwart, R. Full control of a quadrotor. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Bresciani, T. Modelling, Identification and Control of a Quadrotor Helicopter. Master’s Thesis, Lund University, Lund, Sweden, 2008. [Google Scholar]
- Xuan-Mung, N.; Hong, S.K. Improved Altitude Control Algorithm for Quadcopter Unmanned Aerial Vehicles. Appl. Sci. 2019, 9, 2122. [Google Scholar] [CrossRef]
- Khan, H.S.; Kadri, M.B. Attitude and altitude control of quadrotor by discrete PID control and non-linear model predictive control. In Proceedings of the 2015 International Conference on Information and Communication Technologies (ICICT), Karachi, Pakistan, 12–13 December 2015; pp. 1–11. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Rob. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Noura, H.; Theilliol, D.; Ponsart, J.C.; Chamseddine, A. Fault-tolerant Control Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Tan, C.P.; Edwards, C. Sliding mode observers for robust detection and reconstruction of actuator and sensor faults. Int. J. Robust Nonlinear Control 2003, 13, 443–463. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Cocquempot, V. Adaptive Observer-based Fast Fault Estimation. Int. J. Control Autom. Syst. 2008, 6, 320–326. [Google Scholar]
- Griffiths, D.A.; Ananthan, S.; Leishman, J.G. Predictions of Rotor Performance in Ground Effect Using a Free-Vortex Wake Model. J. Am. Helicopter Soc. 2005, 50, 302–314. [Google Scholar] [CrossRef]
- Raine, A.; Aslam, N.; Underwood, C.; Danaher, S. Development of an Ultrasonic Airflow Measurement Device for Ducted Air. Sensors 2015, 15, 10705–10722. [Google Scholar] [CrossRef] [PubMed]
- Davies, D.G.; Bolam, R.C.; Vagapov, Y.; Excell, P. Ultrasonic sensor for UAV flight navigation. In Proceedings of the 2018 25th International Workshop on Electric Drives: Optimization in Control of Electric Drives (IWED), Moscow, Russia, 31 January–2 February 2018; pp. 1–7. [Google Scholar]



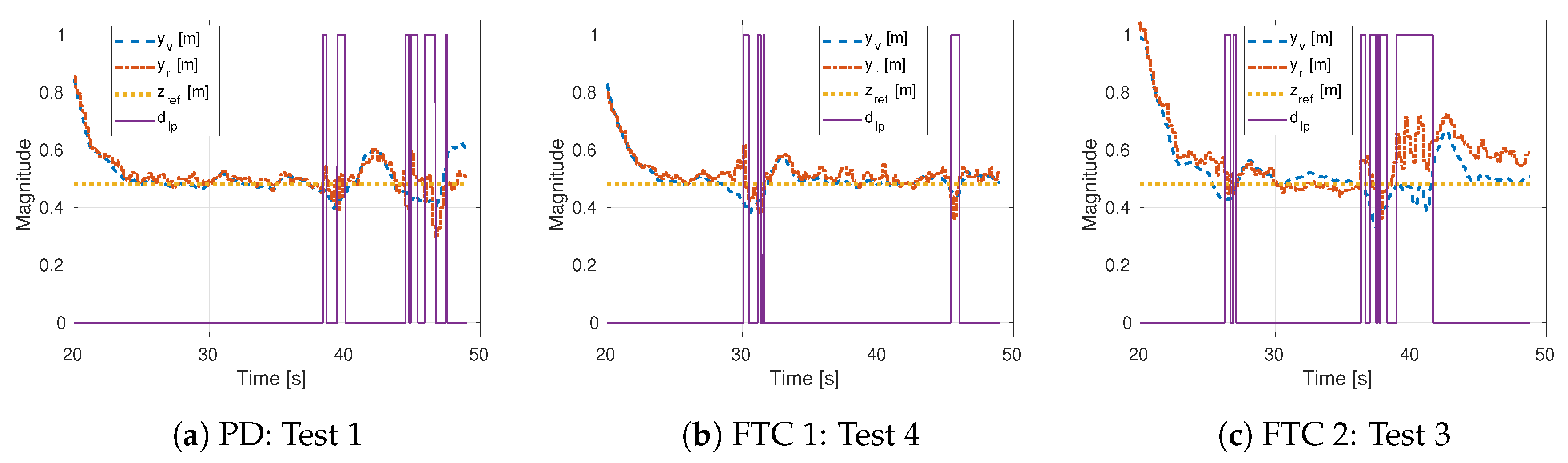

| PD | FTC 1 | FTC 2 | |
|---|---|---|---|
| RMSE | 0.0214 | 0.0172 | 0.0155 |
| RMSE | Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | Average |
|---|---|---|---|---|---|---|
| PD | 0.0492 | 0.0591 | 0.0479 | 0.0460 | 0.0549 | 0.0514 |
| FTC 1 | 0.0266 | 0.0304 | 0.0249 | 0.0317 | 0.0247 | 0.0277 |
| FTC 2 | 0.0215 | 0.0576 | 0.0579 | 0.0417 | 0.0582 | 0.0474 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matus-Vargas, A.; Rodriguez-Gomez, G.; Martinez-Carranza, J. A Monocular SLAM-based Controller for Multirotors with Sensor Faults under Ground Effect. Sensors 2019, 19, 4948. https://doi.org/10.3390/s19224948
Matus-Vargas A, Rodriguez-Gomez G, Martinez-Carranza J. A Monocular SLAM-based Controller for Multirotors with Sensor Faults under Ground Effect. Sensors. 2019; 19(22):4948. https://doi.org/10.3390/s19224948
Chicago/Turabian StyleMatus-Vargas, Antonio, Gustavo Rodriguez-Gomez, and Jose Martinez-Carranza. 2019. "A Monocular SLAM-based Controller for Multirotors with Sensor Faults under Ground Effect" Sensors 19, no. 22: 4948. https://doi.org/10.3390/s19224948
APA StyleMatus-Vargas, A., Rodriguez-Gomez, G., & Martinez-Carranza, J. (2019). A Monocular SLAM-based Controller for Multirotors with Sensor Faults under Ground Effect. Sensors, 19(22), 4948. https://doi.org/10.3390/s19224948






