Kinetic Energy Harvesting for Wearable Medical Sensors
Abstract
1. Introduction
- -
- To address this problem by using coupled numerical analyses, experimental characterizations and novel excitation modalities;
- -
- To propose a modular design of a harvester that enables increasing the attainable specific power outputs while overcoming the limitations induced by the random nature of excitations generated by human motion, and;
- -
- To suggest a generalized scheme of electrical circuitry necessary for the corresponding energy management.
2. Power Requirements of Wearable Medical Sensors
- Medicine: patient health monitoring and early detection of disorders allowing timely medical interventions;
- Risky Professions: monitoring of the workers´ state to prevent dangerous situations or potential injuries, particularly common in construction, mining or shipbuilding;
- Education: stress level and health condition monitoring can provide a suitable foundation for the development of personalized learning plans, time management recommendations, or for scheduling of classroom activities;
- Office Environment and Industry: Occupational stress can cause the deterioration of health conditions, implying that the monitoring of the health parameters of the employees can be beneficial in preventing such occurrences;
- Sports and Recreation: Monitoring of parameters related to training activities and health conditions allows the prevention of injuries, achieving optimal fitness levels or assessing sleep quality.
3. Materials and Methods in Modeling the Behavior of Piezoelectric Kinetic Energy Harvesters
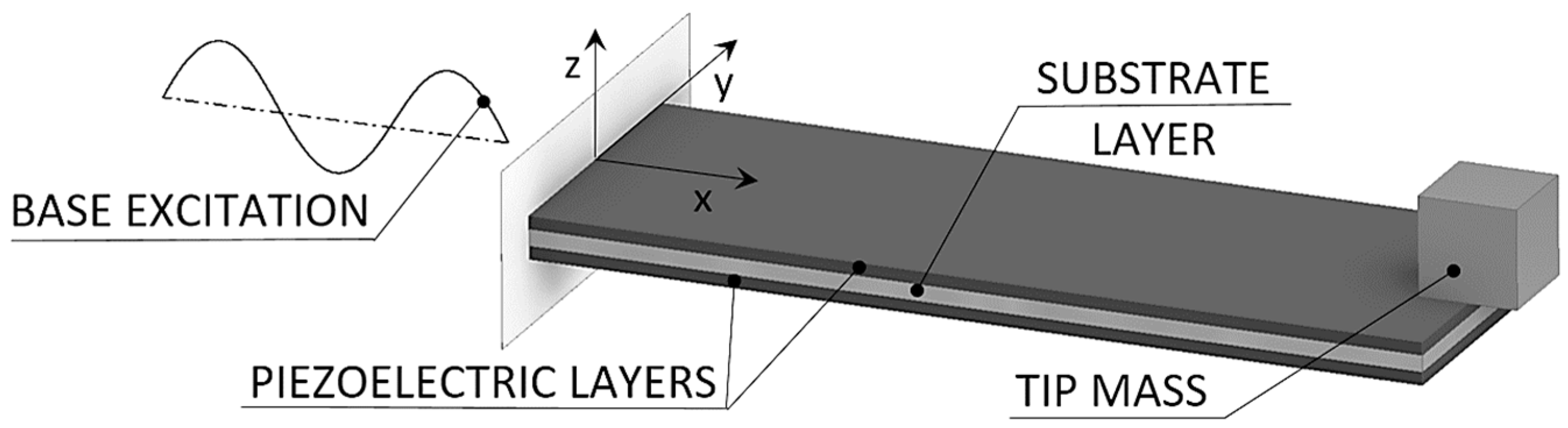
3.1. Coupled Electromechanical Approach
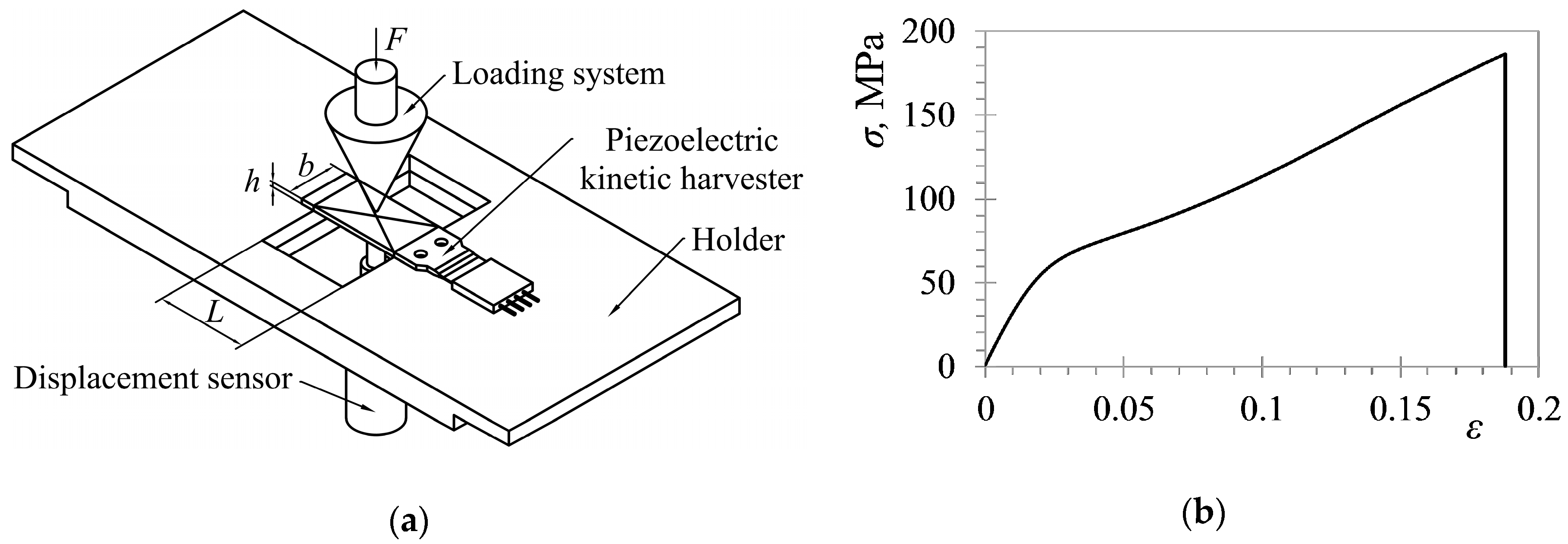
3.2. Finite Element Approach
- Modal analysis allowing the determination of the mechanical dynamical response and the respective eigenfrequencies of the harvester;
- Coupled harmonic analysis resulting in coupled FRFs, and;
- Coupled linear and nonlinear transient analysis resulting in dynamical responses under forced excitation at discrete time steps, including geometrical nonlinearities.
- SOLID226 prismatic elements with 20 nodes and five degrees of freedom (DOFs) per node, enabling the simulation of piezoelectric material properties;
- SOLID186 prismatic elements with 20 nodes and three DOFs per node used to model the substrate and the tip mass;
- CIRCU94 element used in the harmonic and the transient analyses for the simulation of the electrical loads.
3.2.1. Modal Analysis
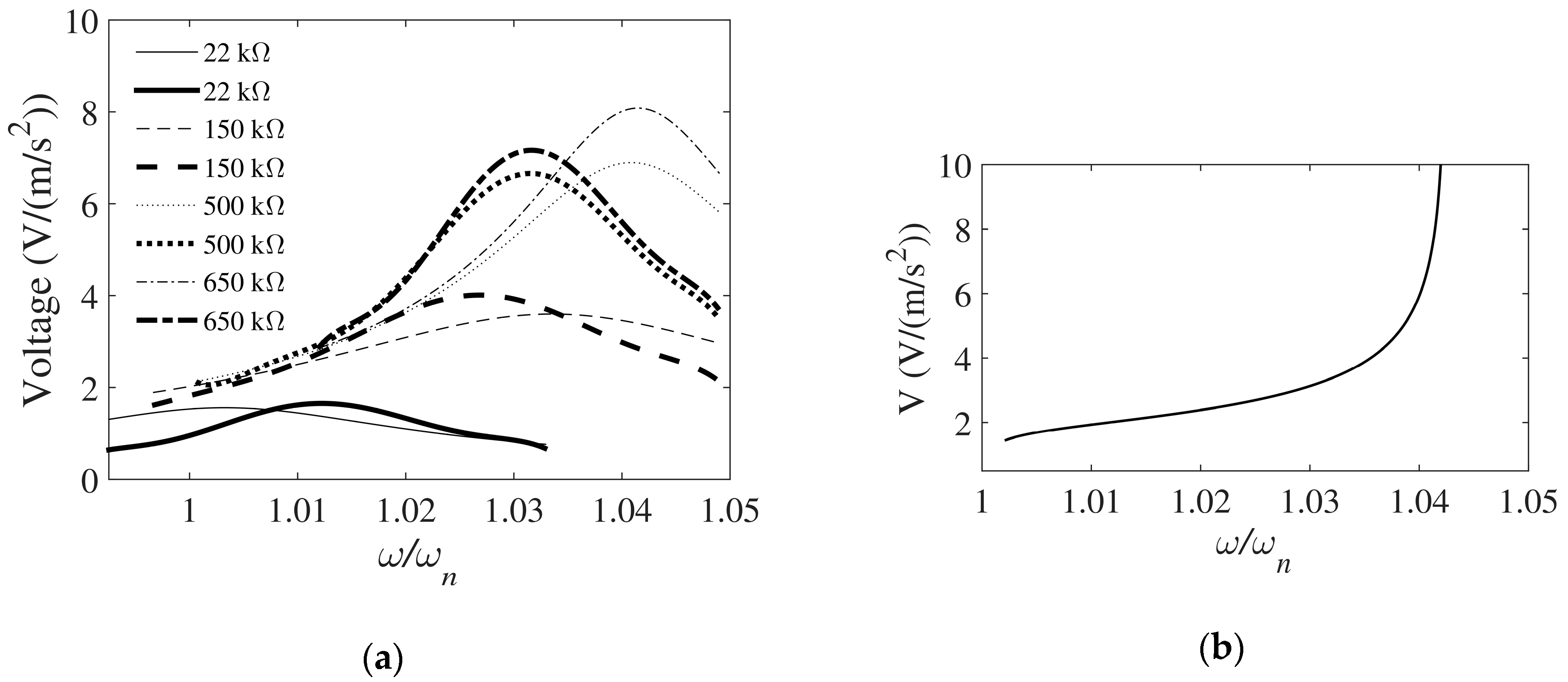
3.2.2. Harmonic Analysis
3.2.3. Linear and Nonlinear Transient Analyses
4. Piezoelectric Kinetic Energy Harvesters for Wearable Medical Monitoring Systems
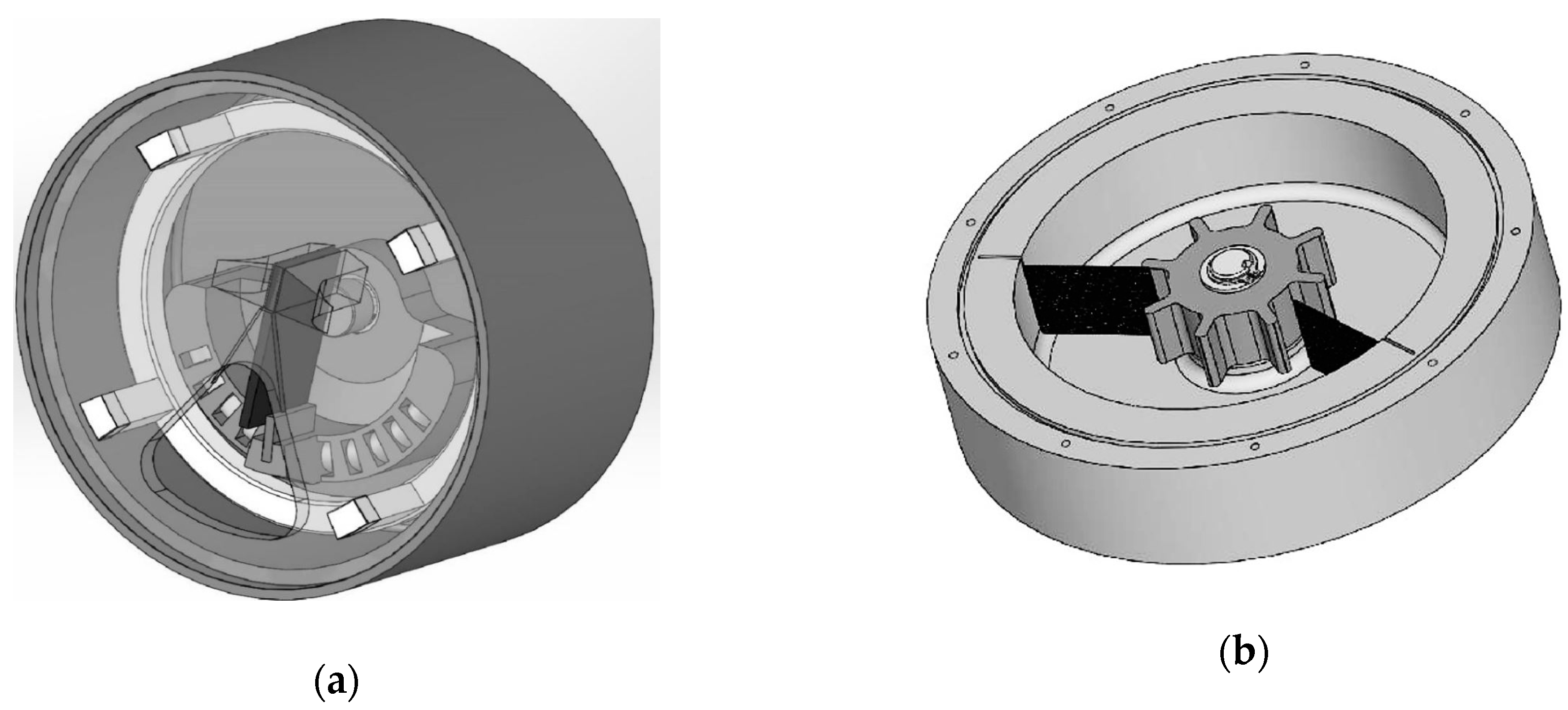
4.1. Frequency Up-Conversion
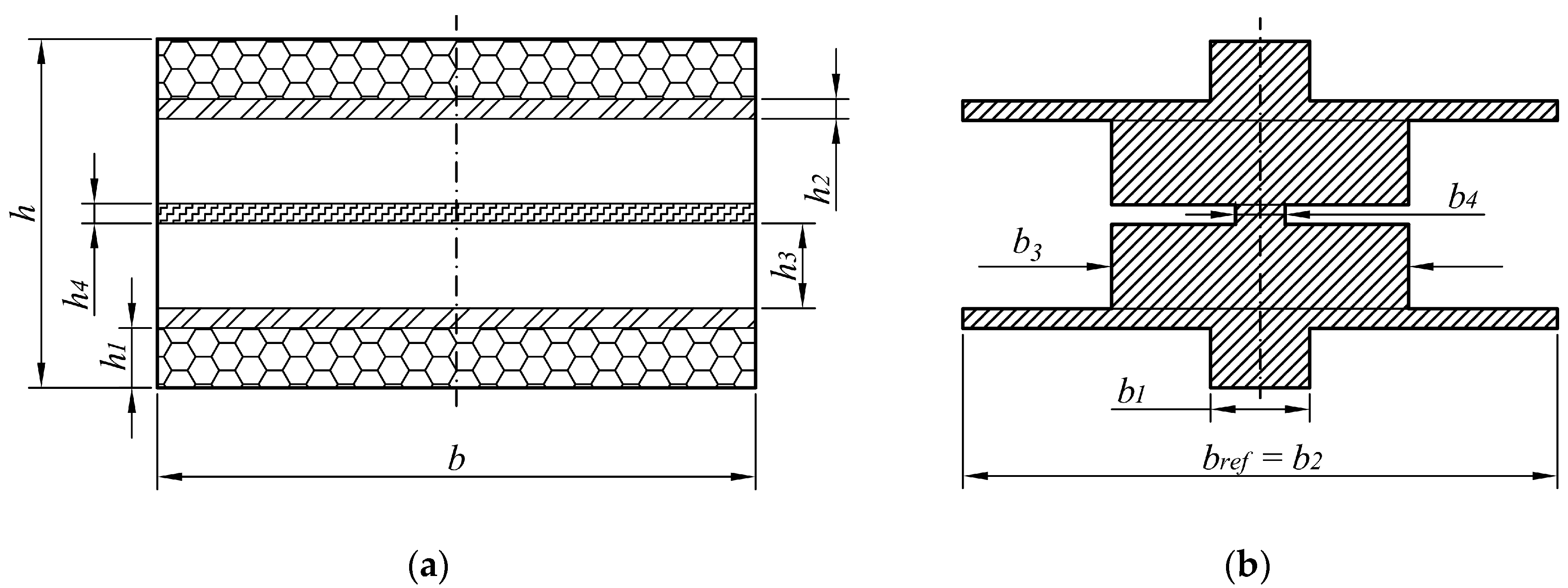
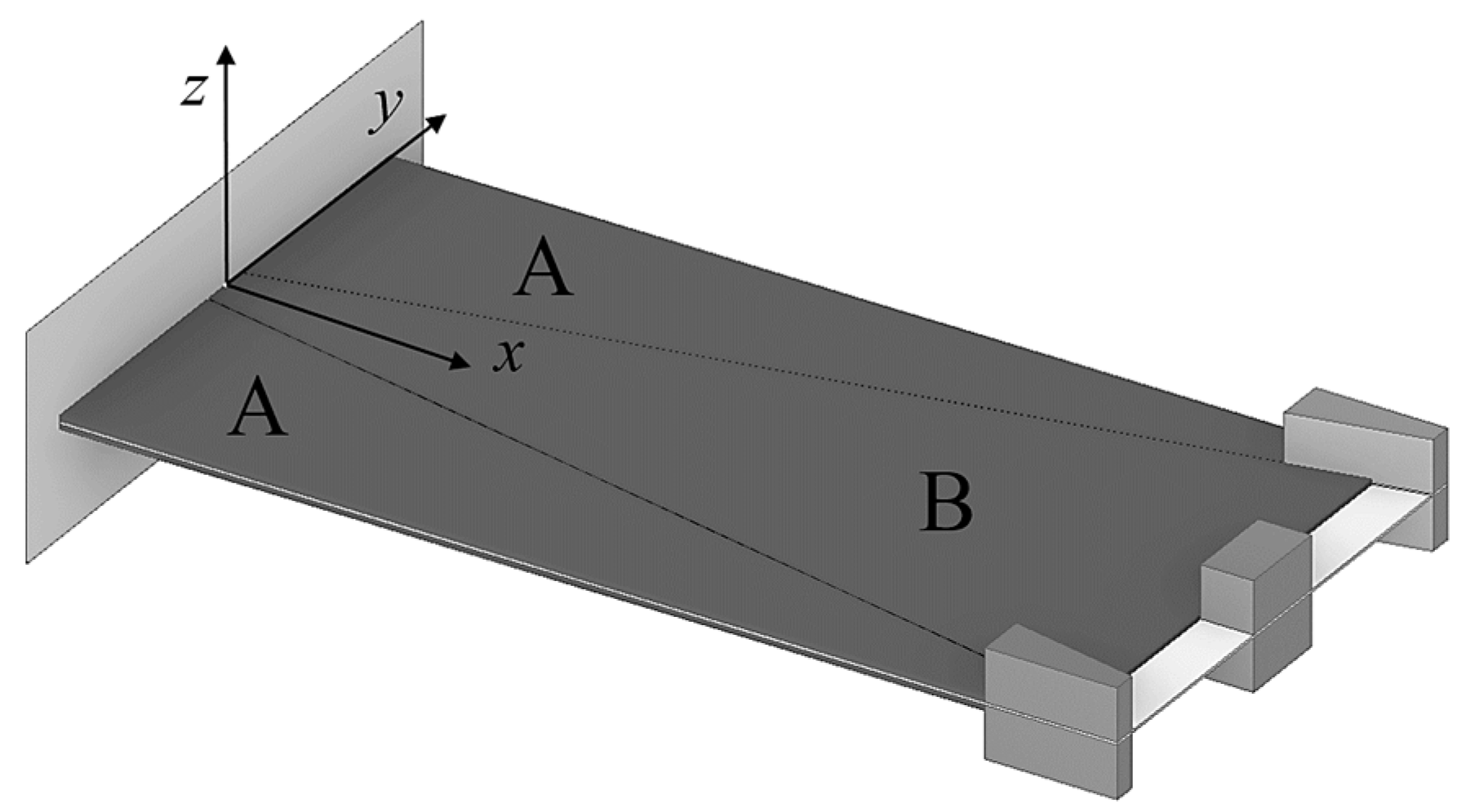
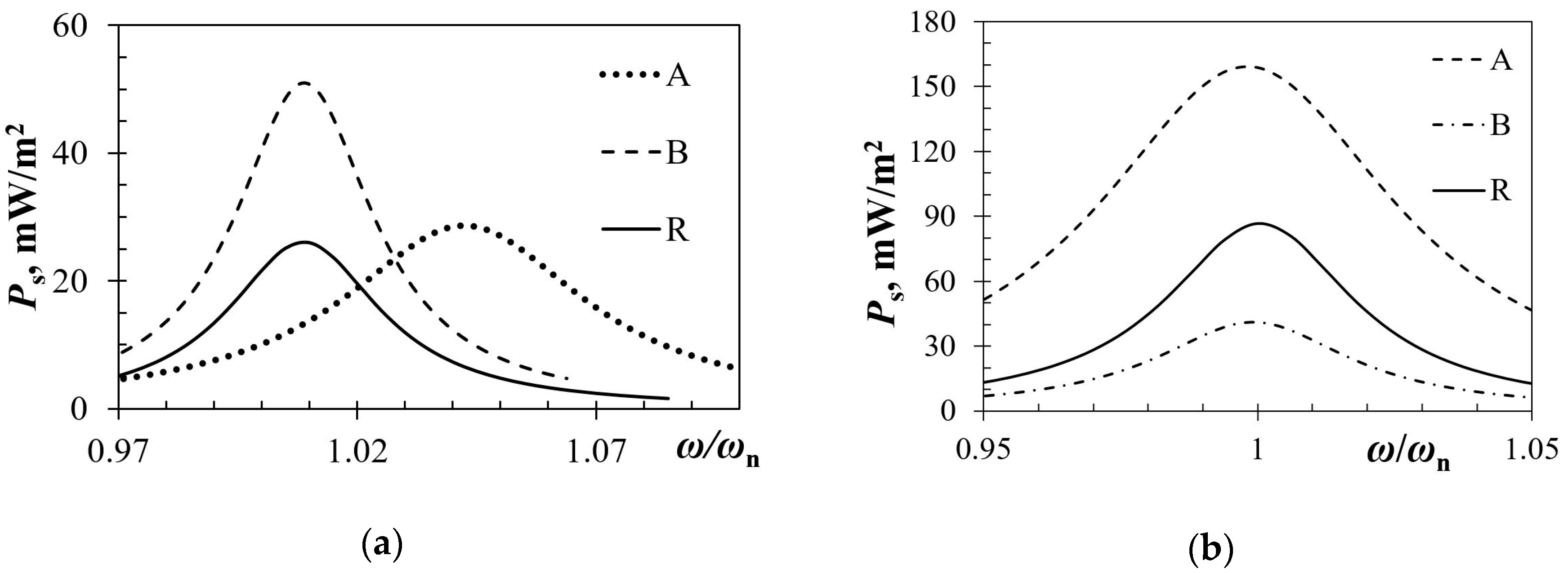
4.2. Geometry Optimization
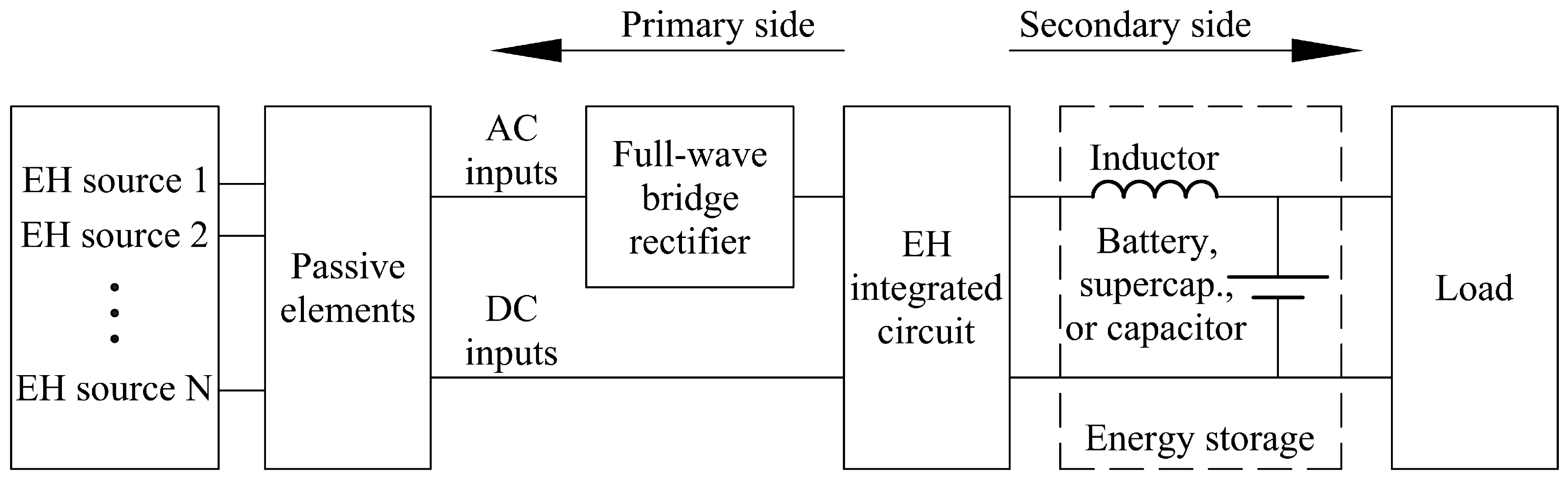
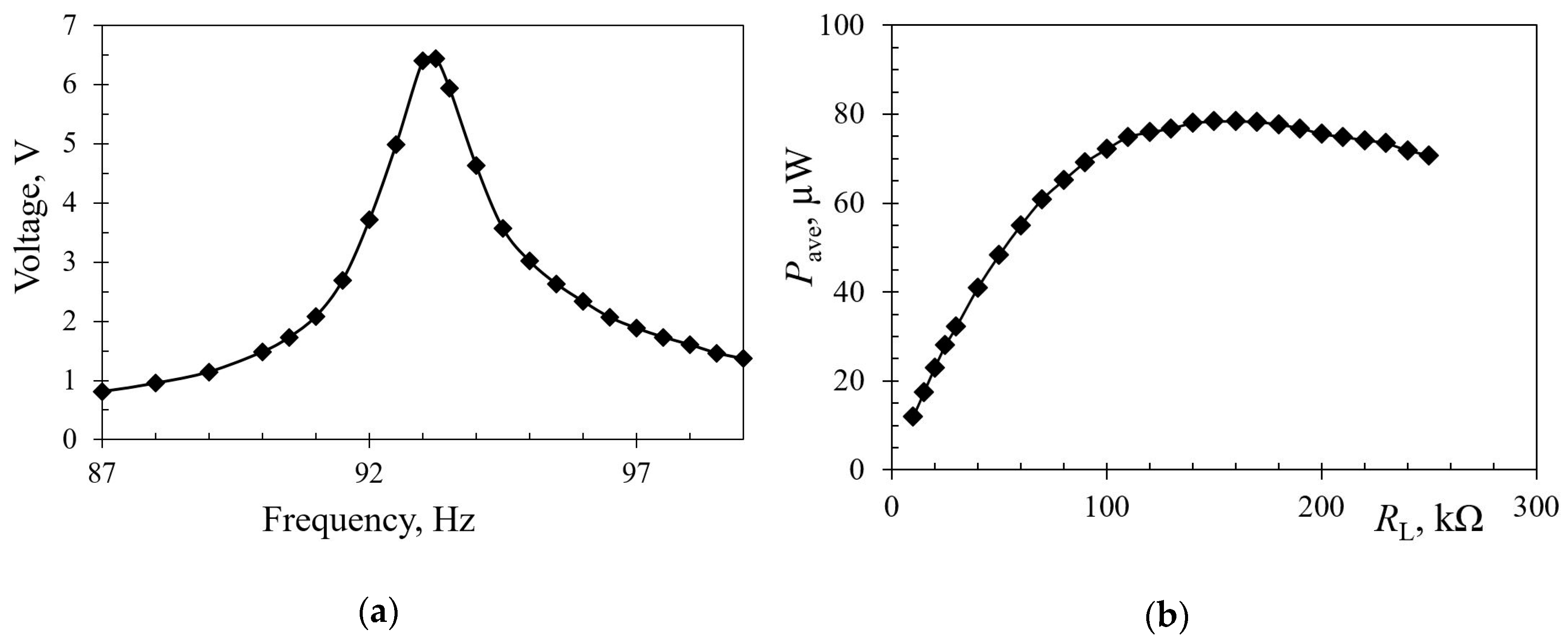
4.3. Power Management in Wearable Medical Monitoring Systems
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kazmierski, T.J.; Beeby, S. Energy Harvesting Systems: Principles Modeling and Applications; Kaźmierski, T.J., Ed.; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-7565-2. [Google Scholar]
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: New York, NY, USA, 2009; ISBN 978-0-387-76463-4. [Google Scholar]
- Tan, Y.K. Energy Harvesting Autonomous Sensor Systems: Design, Analysis, and Practical Implementation; CRC Press: Boca Raton, IL, USA, 2013; ISBN 978-1-4398-9273-2. [Google Scholar]
- Angelopoulou, T.; Tziolas, N.; Balafoutis, A.; Zalidis, G.; Bochtis, D. Remote Sensing Techniques for Soil Organic Carbon Estimation: A Review. Remote Sens. 2019, 11, 676. [Google Scholar] [CrossRef]
- Shakoor, N.; Northrup, D.; Murray, S.; Mockler, T.C. Big Data Driven Agriculture: Big Data Analytics in Plant Breeding, Genomics, and the Use of Remote Sensing Technologies to Advance Crop Productivity. TPPJ 2019, 2. [Google Scholar] [CrossRef]
- Pandey, K.K.; Gupta, A.K. On Detection of Critical Events in a Finite Forest Using Randomly Deployed Wireless Sensors. arXiv 2019, arXiv:190409543. [Google Scholar]
- Muminov, A.; Na, D.; Lee, C.; Kang, H.; Jeon, H. Modern Virtual Fencing Application: Monitoring and Controlling Behavior of Goats Using GPS Collars and Warning Signals. Sensors 2019, 19, 1598. [Google Scholar] [CrossRef] [PubMed]
- Qing, X.; Li, W.; Wang, Y.; Sun, H. Piezoelectric Transducer-Based Structural Health Monitoring for Aircraft Applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Jia, Y.; Arroyo, E.; Fernandez, S.; Riches, S.T.; Seshia, A.A. MEMS Piezoelectric Energy Harvester Powered Wireless Sensor Module Driven by Noisy Base Excitation. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 350–353. [Google Scholar]
- Blažević, D.; Kamenar, E.; Zelenika, S. Load optimised piezoelectric generator for powering battery-less TPMS. In Proceedings of the Smart Sensors, Actuators, and MEMS VI, Grenoble, France, 24–26 April 2013; Schmid, U., de R. Aldavero, J.L.S., Leester-Schaedel, M., Eds.; SPIE: Bellingham, WA, USA, 2013; Volume 8763, pp. 385–394. [Google Scholar]
- Kamenar, E.; Zelenika, S.; Blažević, D.; Maćešić, S.; Gregov, G.; Marković, K.; Glažar, V. Harvesting of river flow energy for wireless sensor network technology. Microsyst. Technol. 2016, 22, 1557–1574. [Google Scholar] [CrossRef]
- Sun, W.; Cai, Z.; Li, Y.; Liu, F.; Fang, S.; Wang, G. Security and Privacy in the Medical Internet of Things: A Review. Secur. Commun. Netw. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Gljušćić, P.; Zelenika, S.; Kamenar, E. Characterisation of performances of thermoelectric generators for energy harvesting applications. In DAAAM Proceedings; Katalinic, B., Ed.; DAAAM International Vienna: Vienna, Austria, 2018; Volume 1, pp. 0025–0030. ISBN 978-3-902734-20-4. [Google Scholar]
- Benasciutti, D.; Moro, L.; Zelenika, S.; Brusa, E. Vibration energy scavenging via piezoelectric bimorphs of optimized shapes. Microsyst. Technol. 2010, 16, 657–668. [Google Scholar] [CrossRef]
- Kamišalić, A.; Fister, I.; Turkanović, M.; Karakatič, S. Sensors and Functionalities of Non-Invasive Wrist-Wearable Devices: A Review. Sensors 2018, 18, 1714. [Google Scholar] [CrossRef] [PubMed]
- Oletic, D.; Bilas, V. System-Level Power Consumption Analysis of the Wearable Asthmatic Wheeze Quantification. J. Sens. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- ROHM Semiconductor—ROHM Co., Ltd. Available online: https://www.rohm.com/ (accessed on 14 October 2019).
- Maxim Integrated—Analog, Linear, & Mixed-Signal Devices. Available online: https://www.maximintegrated.com/en.html (accessed on 14 October 2019).
- Home|Microchip Technology. Available online: https://www.microchip.com/ (accessed on 14 October 2019).
- Aras, S.; Johnson, T.; Cabulong, K.; Gniady, C. Green Monitor: Extending battery life for continuous heart rate monitoring in smartwatches. In Proceedings of the 2015 17th International Conference on E-health Networking, Application & Services (HealthCom), Boston, MA, USA, 14–17 October 2015; pp. 317–322. [Google Scholar]
- Wang, C.; Li, X.; Hu, H.; Zhang, L.; Huang, Z.; Lin, M.; Zhang, Z.; Yin, Z.; Huang, B.; Gong, H.; et al. Monitoring of the central blood pressure waveform via a conformal ultrasonic device. Nat. Biomed. Eng. 2018, 2, 687–695. [Google Scholar] [CrossRef] [PubMed]
- Salo, T.; Kirstein, K.-U.; Sedivy, J.; Grunenfelder, J.; Vancura, T.; Zund, G.; Baltes, H. Continuous blood pressure monitoring utilizing a CMOS tactile sensor. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; Volume 3, pp. 23226–23229. [Google Scholar]
- Asano, S.; Muroyama, M.; Nakayama, T.; Hata, Y.; Nonomura, Y.; Tanaka, S. 3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer. Sensors 2017, 17, 2451. [Google Scholar] [CrossRef] [PubMed]
- Gia, T.N.; Ali, M.; Dhaou, I.B.; Rahmani, A.M.; Westerlund, T.; Liljeberg, P.; Tenhunen, H. IoT-based continuous glucose monitoring system: A feasibility study. Procedia Comput. Sci. 2017, 109, 327–334. [Google Scholar] [CrossRef]
- Hayashi, K.; Arata, S.; Xu, G.; Murakami, S.; Bui, C.D.; Kobayashi, A.; Niitsu, K. A 385 × 385 µm2 0.165 V 0.27n W Fully-Integrated Supply-Modulated OOK Transmitter in 65n m CMOS for Glasses-Free, Self-Powered, and Fuel-Cell-Embedded Continuous Glucose Monitoring Contact Lens. IEICE Trans. Electron. 2019, E102.C, 590–594. [Google Scholar] [CrossRef]
- Xiao, Z.; Tan, X.; Chen, X.; Chen, S.; Zhang, Z.; Zhang, H.; Wang, J.; Huang, Y.; Zhang, P.; Zheng, L.; et al. An Implantable RFID Sensor Tag toward Continuous Glucose Monitoring. IEEE J. Biomed. Health Inform. 2015, 3, 910–919. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kim, E.; Lee, Y.; Kim, H.; Lee, J.; Kim, M.; Yoo, H.-J.; Yoo, S. Toward all-day wearable health monitoring: An ultralow-power, reflective organic pulse oximetry sensing patch. Sci. Adv. 2018, 4, eaas9530. [Google Scholar] [CrossRef] [PubMed]
- Tavakoli, M.; Turicchia, L.; Sarpeshkar, R. An Ultra-Low-Power Pulse Oximeter Implemented with an Energy-Efficient Transimpedance Amplifier. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 27–38. [Google Scholar] [CrossRef] [PubMed]
- Majumder, S.; Mondal, T.; Deen, M. Wearable Sensors for Remote Health Monitoring. Sensors 2017, 17, 130. [Google Scholar] [CrossRef] [PubMed]
- Antonin, B. Propedeutika Interne Medicine; Jumena: Zagreb, Croatia, 1989; ISBN 86-7111-057-5. [Google Scholar]
- Blažević, D.; Zelenika, S. Nonlinear numerical modelling and experimental validation of multilayer piezoelectric vibration energy scavengers. In Proceedings of the Smart Sensors, Actuators, and MEMS VII; and Cyber Physical Systems, Barcelona, Spain, 4–6 May 2015; Sánchez-Rojas, J.L., Brama, R., Eds.; SPIE: Bellingham, WA, USA, 2015; Volume 9517, pp. 342–354. [Google Scholar]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 25009. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill: Boston, MA, USA, 2001; ISBN 978-0-07-041345-0. [Google Scholar]
- Blažević, D.; Zelenika, S. Sensitivity Analysis of Piezoelectric Scavenging of Vibration Energy. In Proceedings of the 11th International Conference of the European Society for Precision Engineering and Nanotechnology (EUSPEN), Como, Italy, 23–26 May 2011; Spaan, H., Shore, P., Van Brussel, H., Burke, T., Eds.; Delft: Sieca Repro, The Netherlands, 2011; Volume 2, pp. 454–457. [Google Scholar]
- Zelenika, S.; Blažević, D. Issues in validation of performances of piezoelectric vibration-based energy harvesters. In Proceedings of the Smart Sensors, Actuators, and MEMS V, Prague, Czech Republic, 18–20 April 2011; Schmid, U., Sánchez-Rojas, J.L., Leester-Schaedel, M., Eds.; SPIE: Bellingham, WA, USA, 2011; Volume 8066, pp. 346–356. [Google Scholar]
- Blažević, D. Analiza Mehaničkih Čimbenika pri Konstrukciji Uređaja za Prikupljanje Niskorazinske Energije Vibracija iz Okoliša. Ph.D. Thesis, University of Rijeka, Rijeka, Croatia, 2014. [Google Scholar]
- Gljušćić, P.; Zelenika, S. Coupled Electromechanical Numerical Modelling of Piezoelectric Vibration Energy Harvesters. In DAAAM Proceedings; Katalinic, B., Ed.; DAAAM International Vienna: Vienna, Austria, 2018; Volume 1, pp. 0009–0015. ISBN 978-3-902734-20-4. [Google Scholar]
- Laboratorij za Precizno Inženjerstvo|Precision Engineering Laboratory. Available online: http://precenglab.riteh.uniri.hr/ (accessed on 14 October 2019).
- De Bona, F.; Zelenika, S.; Munteanu, M.G. Mechanical properties of microcantilevers: Influence of the anticlastic effect. Sens. Actuators A Phys. 2011, 165, 431–438. [Google Scholar] [CrossRef]
- De Bona, F.; Zelenika, S. A generalized Elastica-type approach to the analysis of large displacements of spring-strips. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 509–517. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, L. Equivalent Circuit Modeling of Piezoelectric Energy Harvesters. J. Intell. Mater. Syst. Struct. 2009, 20, 2223–2235. [Google Scholar] [CrossRef]
- Moro, L.; Benasciutti, D. Harvested power and sensitivity analysis of vibrating shoe-mounted piezoelectric cantilevers. Smart Mater. Struct. 2010, 19, 115011. [Google Scholar] [CrossRef]
- Takács, G.; Rohal’-Ilkiv, B. Model Predictive Vibration Control: Efficient Constrained MPC Vibration Control for Lightly Damped Mechanical Structures; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-1-4471-2333-0. [Google Scholar]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.-W.; Lin, L. A comprehensive review on piezoelectric energy harvesting technology: Materials, mechanisms, and applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef]
- Smilek, J.; Hadas, Z.; Vetiska, J.; Beeby, S. Rolling mass energy harvester for very low frequency of input vibrations. Mech. Syst. Signal Process. 2019, 125, 215–228. [Google Scholar] [CrossRef]
- Bai, Y.; Tofel, P.; Hadas, Z.; Smilek, J.; Losak, P.; Skarvada, P.; Macku, R. Investigation of a cantilever structured piezoelectric energy harvester used for wearable devices with random vibration input. Mech. Syst. Signal Process. 2018, 106, 303–318. [Google Scholar] [CrossRef]
- Xu, Z.; Shan, X.; Chen, D.; Xie, T. A Novel Tunable Multi-Frequency Hybrid Vibration Energy Harvester Using Piezoelectric and Electromagnetic Conversion Mechanisms. Appl. Sci. 2016, 6, 10. [Google Scholar] [CrossRef]
- Pozzi, M.; Aung, M.S.H.; Zhu, M.; Jones, R.K.; Goulermas, J.Y. The pizzicato knee-joint energy harvester: Characterization with biomechanical data and the effect of backpack load. Smart Mater. Struct. 2012, 21, 075023. [Google Scholar] [CrossRef]
- Xue, T.; Roundy, S. On magnetic plucking configurations for frequency up-converting mechanical energy harvesters. Sens. Actuators A Phys. 2017, 253, 101–111. [Google Scholar] [CrossRef]
- Gljušćić, P.; Zelenika, S.; Franulović, M. Miniaturized wearable broadband energy harvesters. In Proceedings of the 36th Danubia-Adria Symposium on Advances in Experimental Mechanics, Plzeň, Czech Republic, 24–27 September 2019; Zemčík, R., Krystek, J., Eds.; University of West Bohemia: Plzeň, Czech Republic, 2019; pp. 17–18. [Google Scholar]
- Mixed-Signal and Digital Signal Processing ICs|Analog Devices. Available online: https://www.analog.com/en/index.html# (accessed on 14 October 2019).



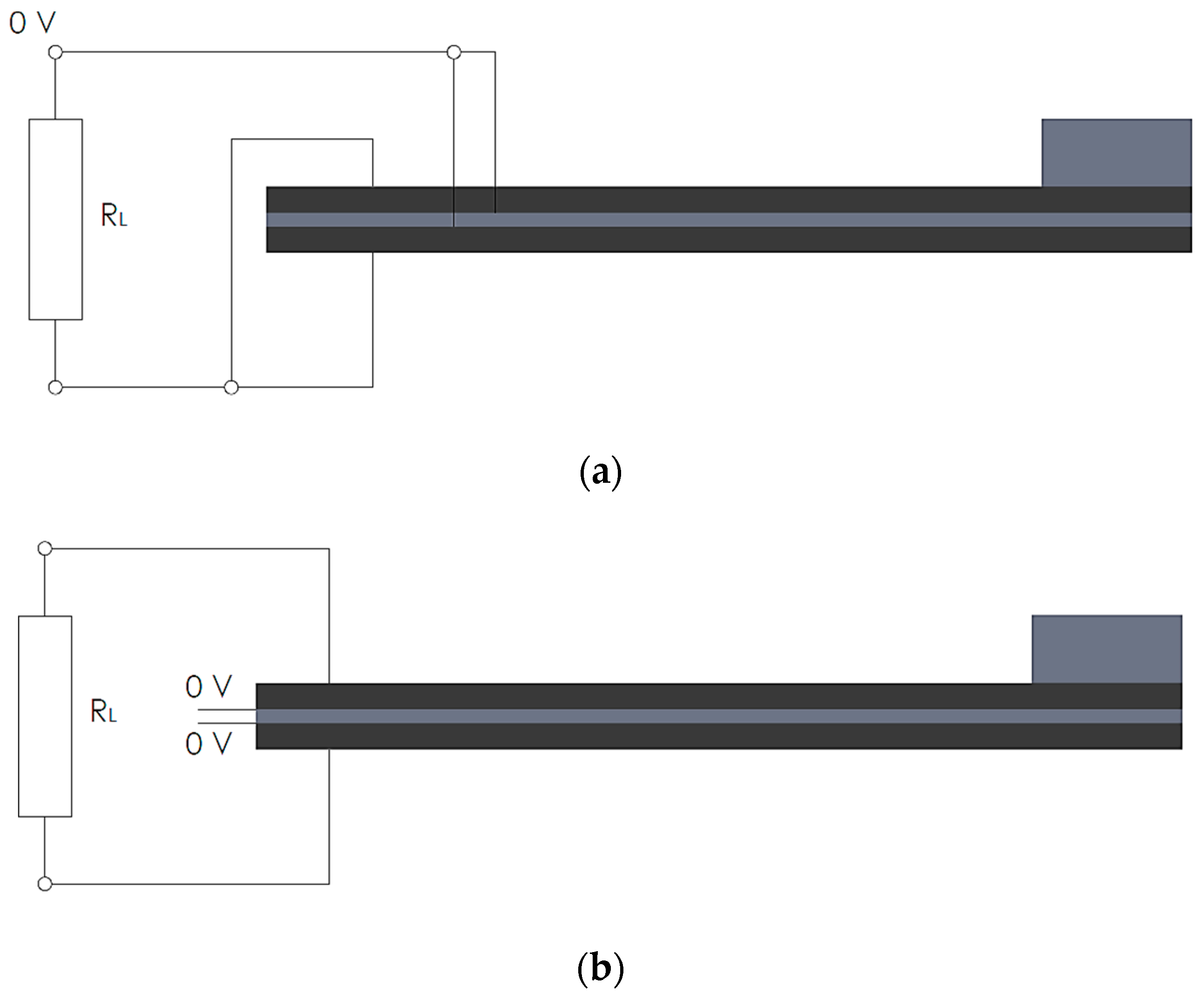
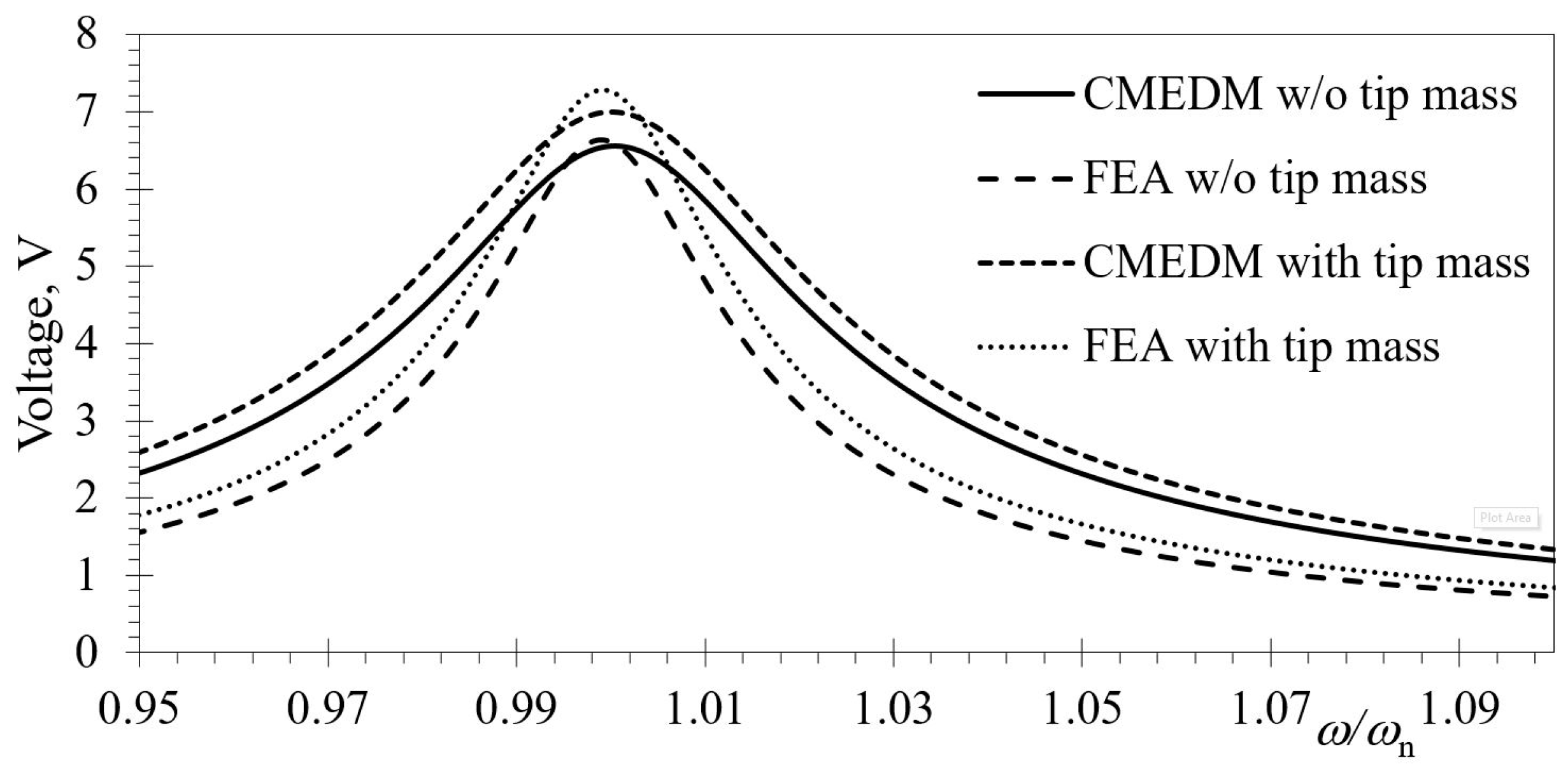
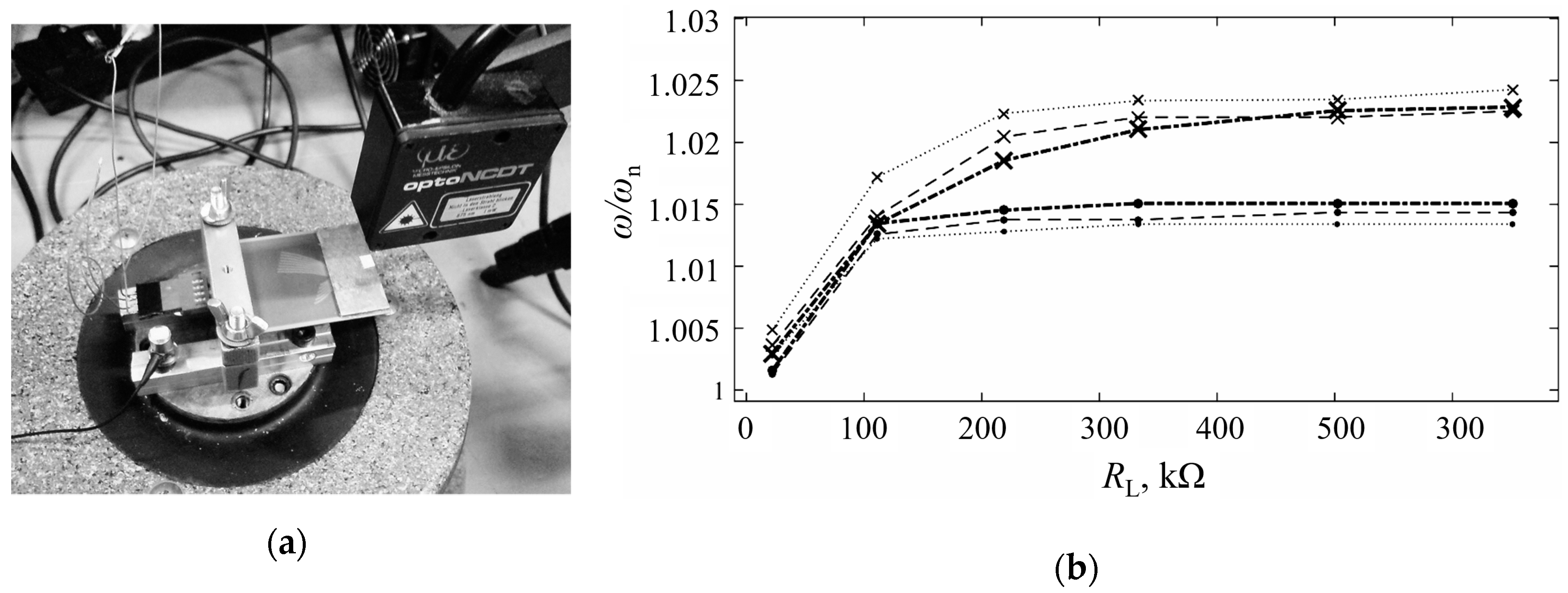

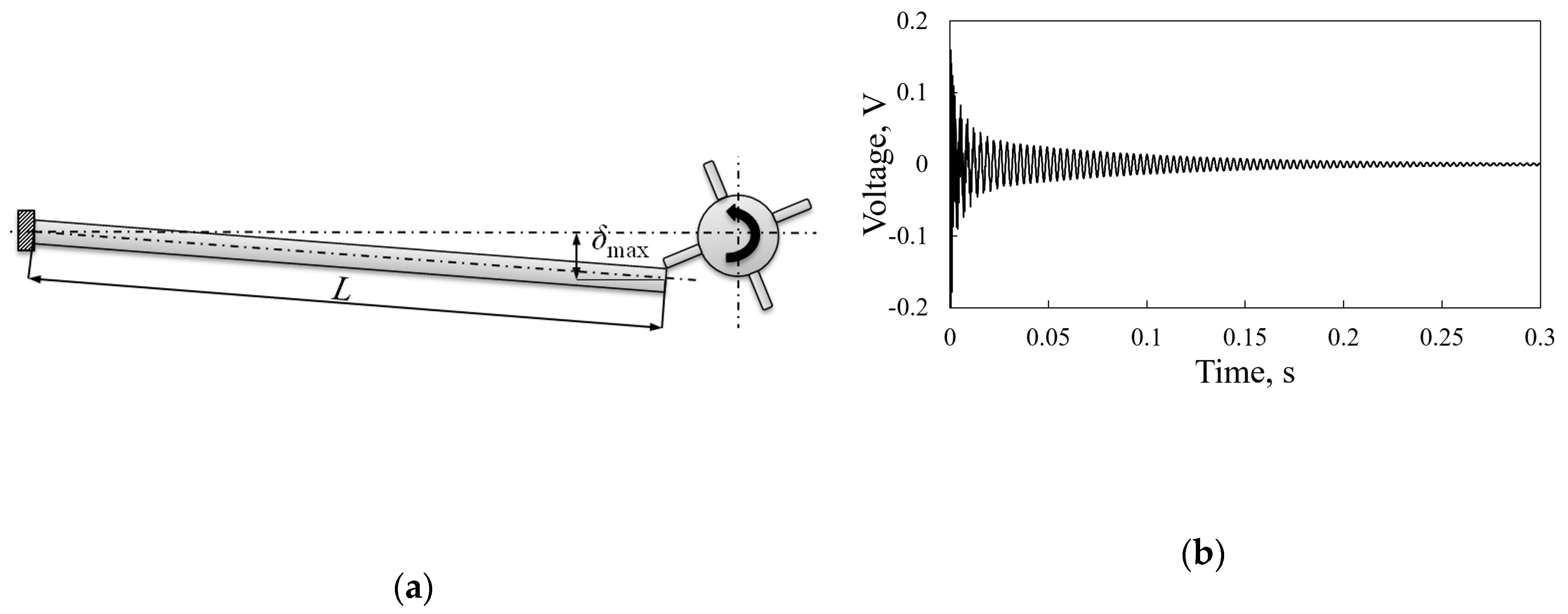


| Device Device | Voltage | Power Consumption | Ref. |
|---|---|---|---|
| Accelerometers | |||
| Analog, 300 mV/g, ADXL337 | 3.0 V | 900 μW | [16] |
| Digital, 3.9 mg/LSB, ADXL345 | 2.5 V | 350 μW | [16] |
| KX022 tri-axis (*—low power mode) | 1.8–3.6 V | 522 (36*) μW | [17] |
| Temperature sensors | |||
| BD1020HFV −30 °C to +100 °C | 2.4–5.5 V | 38.5 μW | [17] |
| MAX30208 0 °C to +70 °C | 1.7–3.6 V | 241 μW | [18] |
| MCP9700 −40 °C to +150 °C | 2.3–5.5 V | 82 μW | [19] |
| Heart rate monitors | |||
| Samsung Galaxy Gear Neo 2® component | - | ~50 mW | [20] |
| MAX30102 pulse oximetry/heart-rate monitor | 1.8–3.3 V | ˂1 mW | [18] |
| BH1790GLC optical heart rate sensor | 1.7–3.6 V | 720 μW | [17] |
| Blood pressure sensors | |||
| Conformal ultrasonic device | - | ~24 mW | [21] |
| CMOS Tactile Sensor | 5 V | 11.5 mW | [22] |
| 3-Axis Fully-Integrated Capacitive Tactile Sensor | 1.8–3.3 V | 1.2–4.6 mW | [23] |
| Blood glucose monitoring systems | |||
| IoT-based continuous glucose monitoring system | 2.0 V | 1 mW | [24] |
| Continuous glucose monitoring contact lens | ~100 mV | ˂1 μW | [25] |
| Implantable RFID continuous glucose monitoring sensor | 1.0–1.2 V | 50 μW | [26] |
| Microphones | |||
| MEMS microphone, digital, ADMP441 | 1.8 V | 2.52 mW | [16] |
| Electret condenser microphone, KEEG1542 | 2.0 V | 1 mW | [16] |
| MEMS microphone, analog, ICS-40310 | 1.0 V | 16 μW | [16] |
| Pulse oximeter sensors | |||
| Reflective organic pulse oximetry sensing patch | 3.3–5.0 V | 68–125 μW | [27] |
| MAX30102 pulse oximetry/heart-rate monitor | 1.8–3.3 V | ˂1 mW | [18] |
| Ultra-low-power pulse oximeter with amplifier | 5.0 V | 4.8 mW | [28] |
| A/D converters | |||
| AD7684 16-bit SAR 100 kS/s | 2.7–5.0 V | 15 μW | [16] |
| ADS1114 16-bit sigma-delta 0.860 kS/s | 2.0–5.5 V | 368 μW | [16] |
| DS1251 24-bit sigma-delta 20 kS/s | 3.3–5.0 V | 1.95 mW | [18] |
| Signal processors | |||
| MC56F8006 Audio DSP, 16-bit 56800E | 1.8–3.6 V | 4282 μW/MHz | [16] |
| STM32L151C8 High-perf. MCU, 32-bit ARM Cortex-M3 | 1.7–3.6 V | 540 μW/MHz | [16] |
| nRF52832 Bluetooth SoC, 32-bit ARM Cortex-M4 | 1.7–3.6 V | 100 μW/MHz | [16] |
| Wireless communication devices | |||
| RFID 13.56 MHz 860–960 MHz (range: 0–3 m) | 5.0 V | 200 mW | [29] |
| Bluetooth 2.4–2.5 GHz (range: 1–100 m) | - | 2.5–100 mW | [29] |
| MICS 402–405 MHz (range: 0–2 m) | - | 25 μW | [29] |
| Device Type | Input Voltage | Output Voltage(s) | Inputs | Ref. |
|---|---|---|---|---|
| Solar/piezoelectric kinetic/electro-magnetic energy harvesting devices | ||||
| MB39C811 | 2.6–23 V DC/AC | 1.5, 1.8, 2.5, 3.3, 3.6, 4.1, 4.5 and 5.0 V DC | 2 AC, 1 DC | [11] |
| Solar/piezoelectric kinetic/electro-magnetic energy harvesting devices | ||||
| LTC3588-1 | 2.7–20 V DC/AC | 1.8, 2.5, 3.3 and 3.6 V DC | 2 AC, 1 DC | [10] |
| LTC3588-2 | 14–20 V DC/AC | 3.45, 4.1, 4.5 and 5.0 V DC | 2 AC, 1 DC | [51] |
| Solar/thermo-electric/radio-frequency/piezoelectric kinetic energy harvesting devices | ||||
| MAX17710 | 0.75–5.3 V DC | 1.8, 2.3 and 3.3 V DC | 2 DC | [18] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gljušćić, P.; Zelenika, S.; Blažević, D.; Kamenar, E. Kinetic Energy Harvesting for Wearable Medical Sensors. Sensors 2019, 19, 4922. https://doi.org/10.3390/s19224922
Gljušćić P, Zelenika S, Blažević D, Kamenar E. Kinetic Energy Harvesting for Wearable Medical Sensors. Sensors. 2019; 19(22):4922. https://doi.org/10.3390/s19224922
Chicago/Turabian StyleGljušćić, Petar, Saša Zelenika, David Blažević, and Ervin Kamenar. 2019. "Kinetic Energy Harvesting for Wearable Medical Sensors" Sensors 19, no. 22: 4922. https://doi.org/10.3390/s19224922
APA StyleGljušćić, P., Zelenika, S., Blažević, D., & Kamenar, E. (2019). Kinetic Energy Harvesting for Wearable Medical Sensors. Sensors, 19(22), 4922. https://doi.org/10.3390/s19224922







