Paradox Elimination in Dempster–Shafer Combination Rule with Novel Entropy Function: Application in Decision-Level Multi-Sensor Fusion
Abstract
1. Introduction
- A single sensor may provide faulty, erroneous results, and there is no way to modify that other than by changing the sensor. A multi-sensor system provides results with diverse accuracy. With the help of a proper fusion algorithm, faulty sensors can be easily detected.
- A multi-sensor system receives information with wide variety and characteristics. Thus, it helps to create a more robust system with less interference.
2. Dempster–Shafer Evidence-Based Combination Rule
2.1. Frame of Discernment (FOD)
2.2. Basic Probability Assignment (BPA)/Mass Function
2.3. Dempster–Shafer Rule of Combination
2.4. Belief and Plausibility Function
3. Paradoxes (Source of Conflicts) in DS Combination Rule
3.1. Completely Conflicting Paradox:
3.2. “One Ballot Veto” Paradox
3.3. “Total Trust” Paradox
4. Eliminating the Paradoxes of DS Combination Rule
4.1. Modification of DS Combination Rule
4.2. Revision of Original Evidence before Combination
4.3. Hybrid Technique Combining Both Modification of DS Rule and Original Evidence
5. Entropy in Information Theory under DS Framework
Properties of Proposed Entropy Function
6. Proposed Steps to Eliminate Paradoxes
- Step 1: Build a multi-sensor information matrix. Assume, for a multi-sensor system, there are N evidences (sensors) in the frame (objects to be detected).
- Step 2: Measure the relative distance between evidences. Several distance function can be used to measure the relative distance. They all have their own advantages and disadvantages regarding runtime and accuracy. We have used Jousselme’s distance [28] function. Jousselme’s distance function uses cardinality in measuring distance which is an important metric when multiple elements are present in one BPA under DS framework. The effect of different distance functions (Euclidean, Jousselme, Minkowsky, Manhttan, Jffreys, and Camberra distance function) on simulation time and information fusion can be found in the literature [29]. Assuming that there are two mass functions indicated by and on the discriminant frame , the Jousselme distance between and is defined as follows:where and |.| represents cardinality.
- Step 3: Calculate sum of evidence distance for each sensor.
- Step 4: Calculate global average of evidence distance.
- Step 5: Calculate belief entropy for each sensor by using Equation (11), and normalize.
- Step 6: The evidence set is divided into two parts: the credible evidence and the incredible evidence. From Equations (14) and (15):
- Step 7: Modify the original evidences.
- Step 8: Combine modified evidence for () times (for this example, 4 times) with DS combination rule by using Equations (5) and (6). How to apply the fusion rule is important. For this example, if evidences and are fused with modified evidence, then . Now, to get , if values are fused with values using Equations (5) and (6), that would be wrong. To get , values should be fused with the original modified evidence from step 7. It is also evident that, for single elements, if that element has higher value after step 7, it will have highest value after fusing () times. The higher the value after step 7, the higher the value after fusion.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Fourati, H. Multisensor Data Fusion: From Algorithms and Architectural Design to Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jiang, W.; Luo, Y.; Qin, X.-Y.; Zhan, J. An improved method to rank generalized fuzzy numbers with different left heights and right heights. J. Intell. Fuzzy Syst. 2015, 28, 2343–2355. [Google Scholar] [CrossRef]
- Bossé, E.; Roy, J. Fusion of identity declarations from dissimilar sources using the Dempster-Shafer theory. Opt. Eng. 1997, 36, 648–657. [Google Scholar]
- Coombs, K.; Freel, D.; Lampert, D.; Brahm, S.J. Sensor Fusion: Architectures, Algorithms, and Applications III. Int. Soc. Opt. Photonics 1999, 3719, 103–113. [Google Scholar]
- Yager, R.R.; Liu, L. Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer: Berlin/Heidelberg, Germany, 2008; Volume 219. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping, in Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. [Google Scholar]
- Deng, Y. Deng Entropy: A Generalized Shannon Entropy to Measure Uncertainty. 2015. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.678.2878&rep=rep1&type=pdf (accessed on 30 October 2019).
- Guo, K.; Li, W. Combination rule of D–S evidence theory based on the strategy of cross merging between evidences. Expert Syst. Appl. 2011, 38, 13360–13366. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Tian, Y. A Robust DS Combination Method Based on Evidence Correction and Conflict Redistribution. J. Sens. 2018, 2018, 6526018. [Google Scholar] [CrossRef]
- Smets, P. Data fusion in the transferable belief model. In Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000. [Google Scholar]
- Yager, R.R. On the Dempster-Shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Bicheng, L.; Jie, H.; Hujun, Y. Two efficient combination rules for conflicting belief functions. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009. [Google Scholar]
- Inagaki, T. Interdependence between safety-control policy and multiple-sensor schemes via Dempster-Shafer theory. IEEE Trans. Reliab. 1991, 40, 182–188. [Google Scholar] [CrossRef]
- Zhang, L. Representation, independence, and combination of evidence in the Dempster-Shafer theory. In Advances in the Dempster-Shafer Theory of Evidence; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1994; pp. 51–69. [Google Scholar]
- Li, Y.; Chen, J.; Feng, L. Dealing with uncertainty: A survey of theories and practices. IEEE Trans. Knowl. Data Eng. 2013, 52, 449–460. [Google Scholar] [CrossRef]
- Chen, S.; Deng, Y.; Wu, J. Fuzzy sensor fusion based on evidence theory and its application. Appl. Artif. Intell. 2013, 27, 235–248. [Google Scholar] [CrossRef]
- Sun, S.; Gao, J.; Chen, M.; Xu, B.; Ding, Z. FS-DS based Multi-sensor Data Fusion. JSW 2013, 8, 1157–1161. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Xie, C.; Zhou, D. An evidential sensor fusion method in fault diagnosis. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Murphy, R.R. Dempster-Shafer theory for sensor fusion in autonomous mobile robots. IEEE Trans. Robot. Autom. 1998, 14, 197–206. [Google Scholar] [CrossRef]
- Jiang, W.; Zhuang, M.; Qin, X.; Tang, Y. Conflicting Evidence Combination Based on Uncertainty Measure and Distance of Evidence; SpringerPlus: Berlin/Heidelberg, Germany, 2016; Volume 5. [Google Scholar]
- Xiao, F. An improved method for combining conflicting evidences based on the similarity measure and belief function entropy. Int. J. Fuzzy Syst. 2018, 20, 1256–1266. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Ma, C.; Dou, Z.; Ma, X. A new combination method for multisensor conflict information. J. Supercomput. 2018, 72, 2874–2890. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Henderson, T.C. Multisensor data fusion. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 585–610. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y. A new belief entropy to measure uncertainty of basic probability assignments based on belief function and plausibility function. J. Entropy 2018, 20, 842. [Google Scholar] [CrossRef]
- Jousselme, A.-L.; Grenier, D.; Bossé, É. A new distance between two bodies of evidence. Inf. Fusion 2001, 2, 91–101. [Google Scholar] [CrossRef]
- Chen, J.; Fang, Y.; Tao, J. Numerical analyses of modified DS combination methods based on different distance functions. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium - Fall (PIERS - FALL), Singapore, 19–22 November 2017; pp. 2169–2175. [Google Scholar]
- Deng, Y.; Shi, W.; Zhu, Z.; Liu, Q. Combining belief functions based on distance of evidence. Decis. Support Syst. 2004, 38, 489–493. [Google Scholar]
- Han, D.Q.; Deng, Y.; Han, C.Z.; Hou, Z. Weighted evidence combination based on distance of evidence and uncertainty measure. J. Infrared Millim. Waves 2011, 30, 396–400. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, F.; Deng, X.; Fei, L.; Deng, Y. Weighted evidence combination based on distance of evidence and entropy function. Int. J. Distrib. Sens. Netw. 2016, 12, 3218784. [Google Scholar] [CrossRef]

| A | B | C | A,B | A,C | B,C | A,B,C | |
|---|---|---|---|---|---|---|---|
| Bel(.) | 0.48 | 0.24 | 0.08 | 0.72 | 0.56 | 0.32 | 1.0 |
| Pl(.) | 0.68 | 0.44 | 0.28 | 0.92 | 0.76 | 0.52 | 1.0 |
| a | b | c | a,b | a,c | b,c | a,b,c | |
|---|---|---|---|---|---|---|---|
| Bel(.) | 1/7 | 1/7 | 1/7 | 3/7 | 3/7 | 3/7 | 1.0 |
| Pl(.) | 4/7 | 4/7 | 4/7 | 6/7 | 6/7 | 6/7 | 1.0 |
| m(A) | m(B) | m(C) | m(A,C) | |
|---|---|---|---|---|
| Bel = 0.42, Pl = 0.41 | Bel = 0.29, Pl = 0.29 | Bel = 0.3, Pl = 0.3 | Bel = 0, Pl = 0 | |
| Bel = 0, Pl = 0 | Bel = 0.9, Pl = 0.9 | Bel = 0.1, Pl = 0.1 | Bel = 0, Pl = 0 | |
| Bel = 0.93, Pl = 0.93 | Bel = 0.07, Pl = 0.07 | Bel = 0, Pl = 0.35 | Bel = 0.93, Pl = 0.93 | |
| Bel = 0.9, Pl = 0.9 | Bel = 0.1, Pl = 0.1 | Bel = 0, Pl = 0.35 | Bel = 0.9, Pl = 0.9 | |
| Bel = 0.9, Pl = 0.9 | Bel = 0.1, Pl = 0.1 | Bel = 0, Pl = 0.3 | Bel = 0.9, Pl = 0.9 |
| Combination Rule | ||||
|---|---|---|---|---|
| Dempster [8] | m(A) = 0, m(B) = 0.8969, m(C) = 0.1031 | m(A) = 0, m(B) = 0.8969, m(C) = 0.1031 | m(A) = 0, m(B) = 0.8969, m(C) = 0.1031 | m(A) = 0, m(B) = 0.8969, m(C) = 0.1031 |
| Murphy [21] | m(A) = 0.0964, m(B) = 0.8119, m(C) = 0.0917, m(AC) = 0 | m(A) = 0.4619, m(B) = 0.4497, m(C) = 0.0794, m(AC) = 0.0090 | m(A) = 0.8362, m(B) = 0.1147, m(C) = 0.0410, m(AC) = 0.0081 | m(A) = 0.9620, m(B) = 0.0210, m(C) = 0.0138, m(AC) = 0.0032 |
| Deng [30] | m(A) = 0.0964, m(B) = 0.8119, m(C) = 0.0917, m(AC) = 0 | m(A) = 0.4974, m(B) = 0.4054, m(C) = 0.0888, m(AC) = 0.0084 | m(A) = 0.9089, m(B) = 0.0444, m(C) = 0.0379, m(AC) = 0.0089 | m(A) = 0.9820, m(B) = 0.0039, m(C) = 0.0107, m(AC) = 0.0034 |
| Han [31] | m(A) = 0.0964, m(B) = 0.8119, m(C) = 0.0917, m(AC) = 0 | m(A) = 0.5188, m(B) = 0.3802, m(C) = 0.0926, m(AC) = 0.0084 | m(A) = 0.9246, m(B) = 0.0300, m(C) = 0.0362, m(AC) = 0.0092 | m(A) = 0.9844, m(B) = 0.0023, m(C) = 0.0099, m(AC) = 0.0034 |
| Wang [32] recalculated | m(A) = 0.0964, m(B) = 0.8119, m(C) = 0.0917, m(AC) = 0 | m(A) = 0.6495, m(B) = 0.2367, m(C) = 0.1065, m(AC) = 0.0079 | m(A) = 0.9577, m(B) = 0.0129, m(C) = 0.0200, m(AC) = 0.0094 | m(A) = 0.9867, m(B) = 0.0008, m(C) = 0.0087, m(AC) = 0.0035 |
| Jiang [20] | m(A) = 0.0964, m(B) = 0.8119, m(C) = 0.0917, m(AC) = 0 | m(A) = 0.7614, m(B) = 0.1295, m(C) = 0.0961, m(AC) = 0.0130 | m(A) = 0.9379, m(B) = 0.0173, m(C) = 0.0361, m(AC) = 0.0087 | m(A) = 0.9837, m(B) = 0.0021, m(C) = 0.0110, m(AC) = 0.0032 |
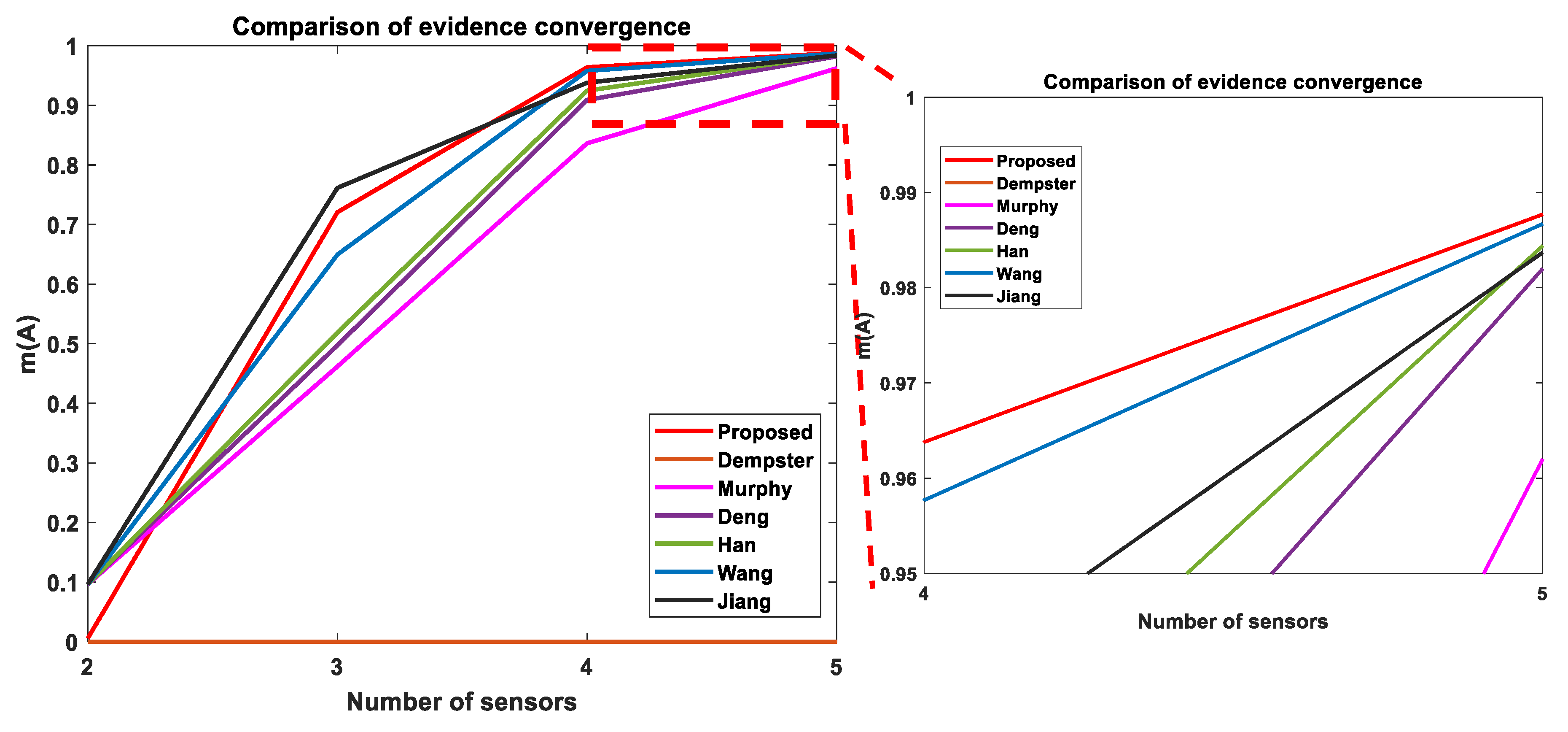
| Proposed | m(A) = 0.00573, m(B) = 0.96906, m(C) = 0.02522, m(AC) = 0 | m(A) = 0.7207, m(B) = 0.1541, m(C) = 0.1178, m(AC) = 0.007 | m(A) = 0.9638, m(B) = 0.0019, m(C) = 0.0224, m(AC) = 0.0117 | m(A) = 0.9877, m(B) = 0.0002, m(C) = 0.0087, m(AC) = 0.0034 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.N.; Anwar, S. Paradox Elimination in Dempster–Shafer Combination Rule with Novel Entropy Function: Application in Decision-Level Multi-Sensor Fusion. Sensors 2019, 19, 4810. https://doi.org/10.3390/s19214810
Khan MN, Anwar S. Paradox Elimination in Dempster–Shafer Combination Rule with Novel Entropy Function: Application in Decision-Level Multi-Sensor Fusion. Sensors. 2019; 19(21):4810. https://doi.org/10.3390/s19214810
Chicago/Turabian StyleKhan, Md Nazmuzzaman, and Sohel Anwar. 2019. "Paradox Elimination in Dempster–Shafer Combination Rule with Novel Entropy Function: Application in Decision-Level Multi-Sensor Fusion" Sensors 19, no. 21: 4810. https://doi.org/10.3390/s19214810
APA StyleKhan, M. N., & Anwar, S. (2019). Paradox Elimination in Dempster–Shafer Combination Rule with Novel Entropy Function: Application in Decision-Level Multi-Sensor Fusion. Sensors, 19(21), 4810. https://doi.org/10.3390/s19214810






