The Influence of Air Pressure on the Dynamics of Flexural Ultrasonic Transducers
Abstract
1. Introduction
2. Materials and Methods
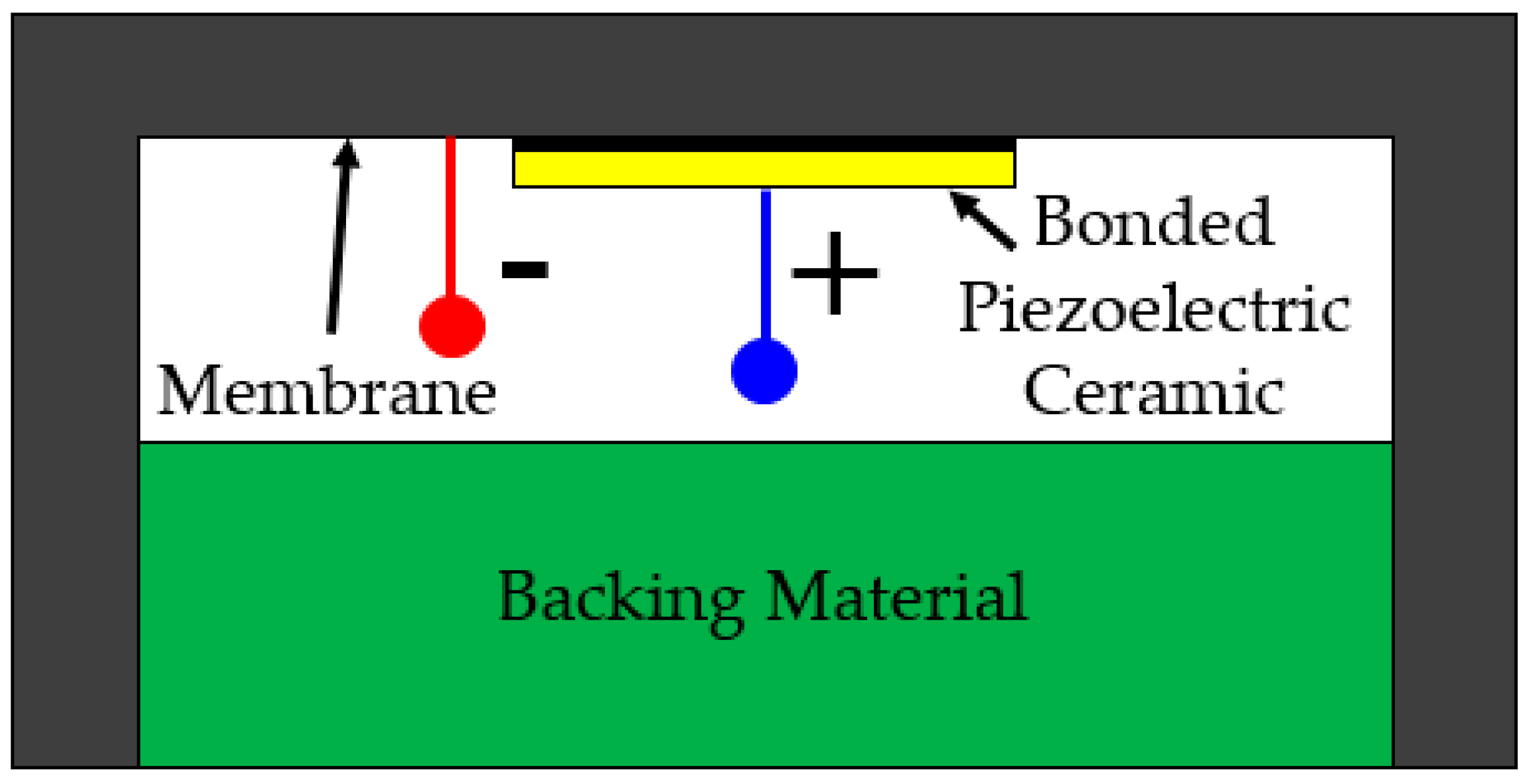
2.1. Transducer Specifications
2.2. Characterization Process
2.2.1. Analysis of Resonance Characteristics
2.2.2. Pitch-Catch Ultrasound Measurement
3. Results
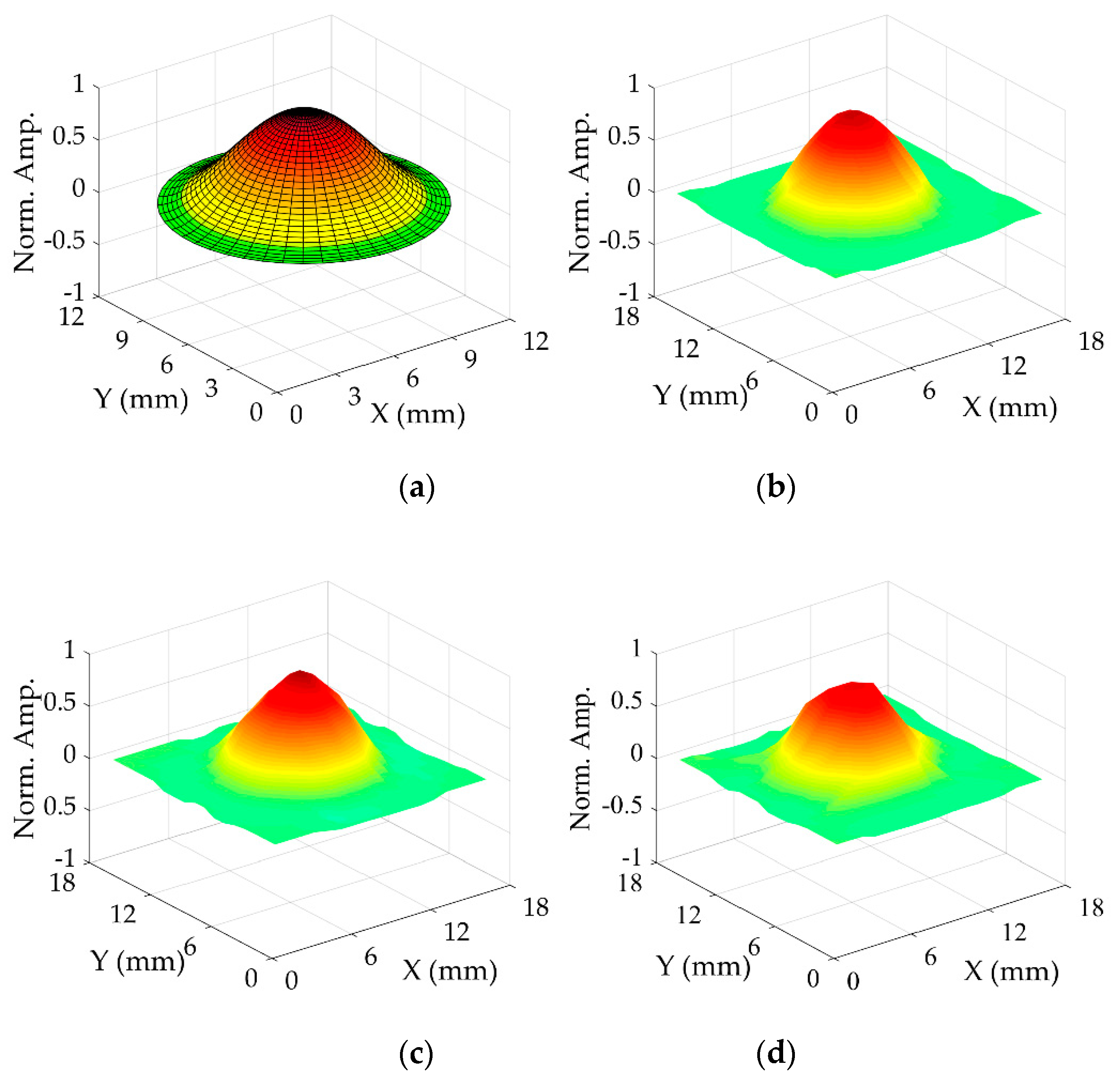
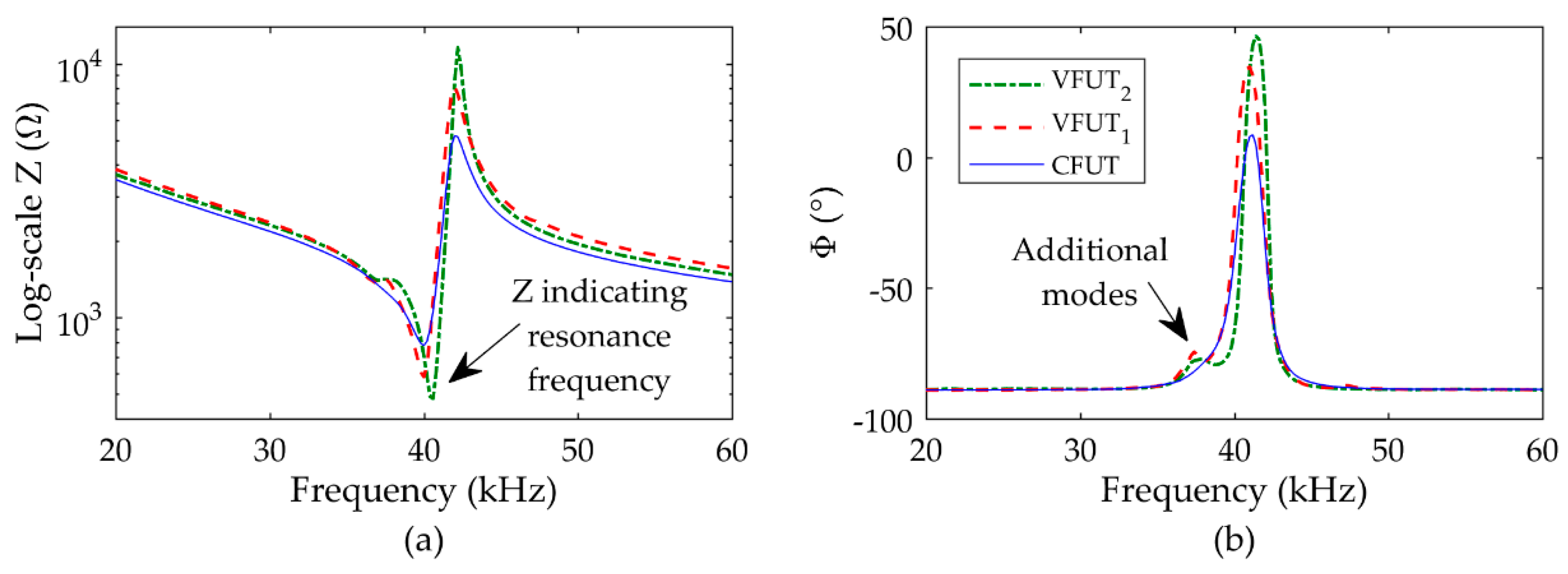
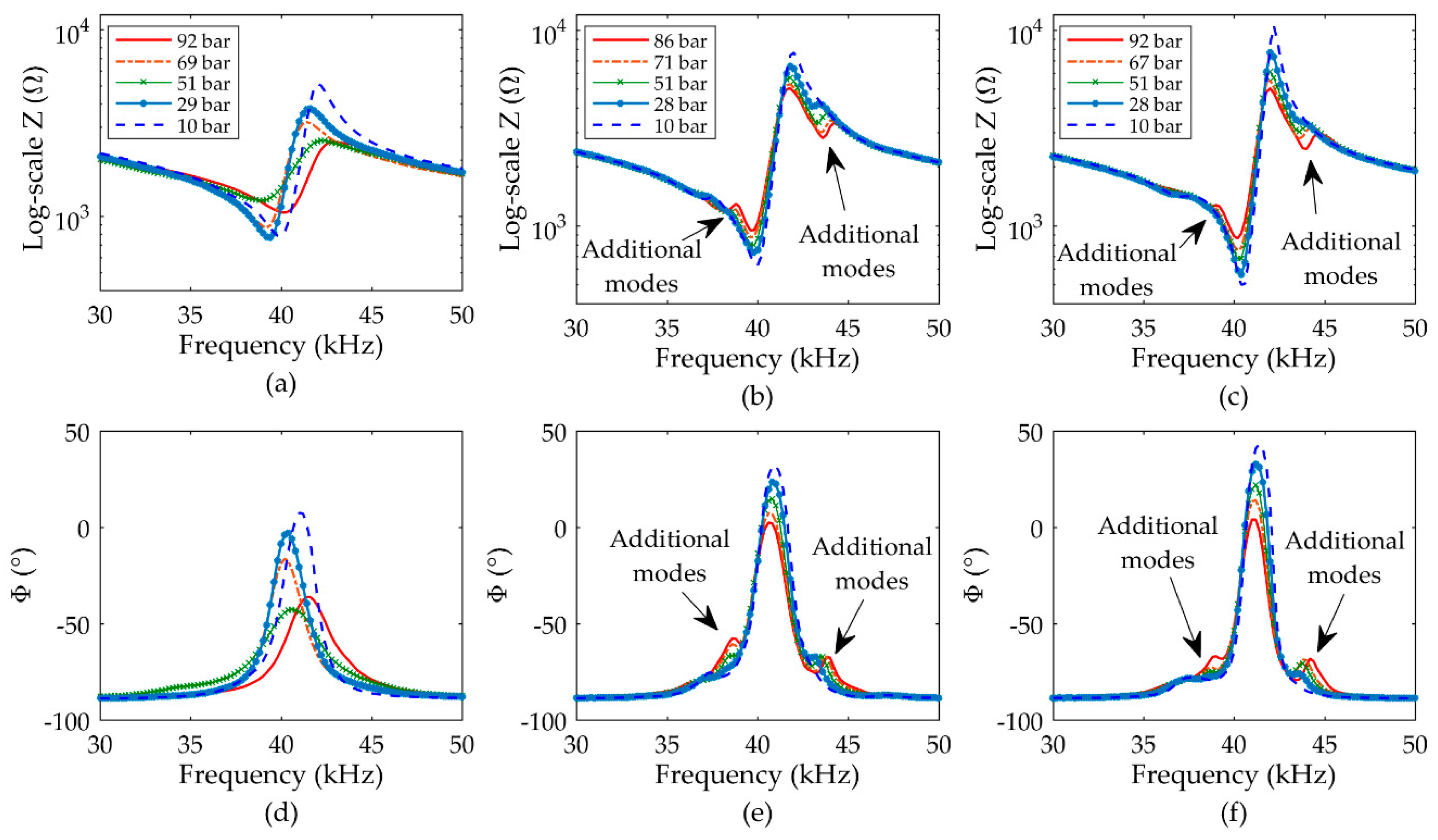
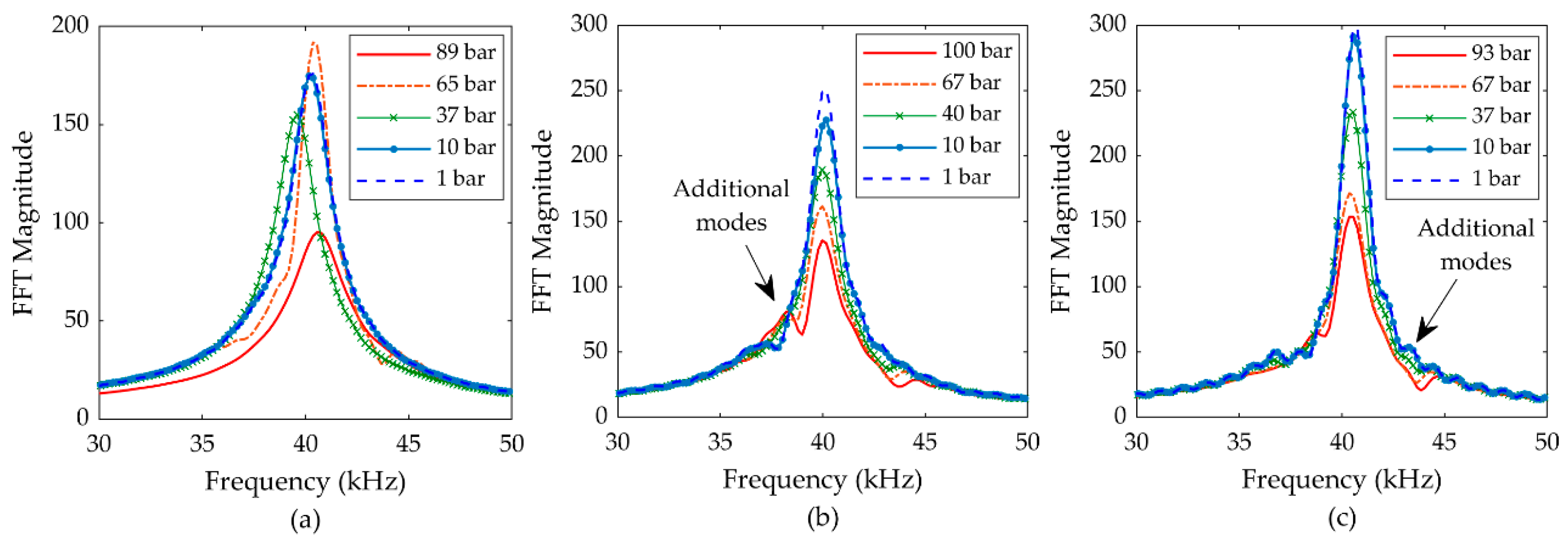
3.1. Resonance Characteristics
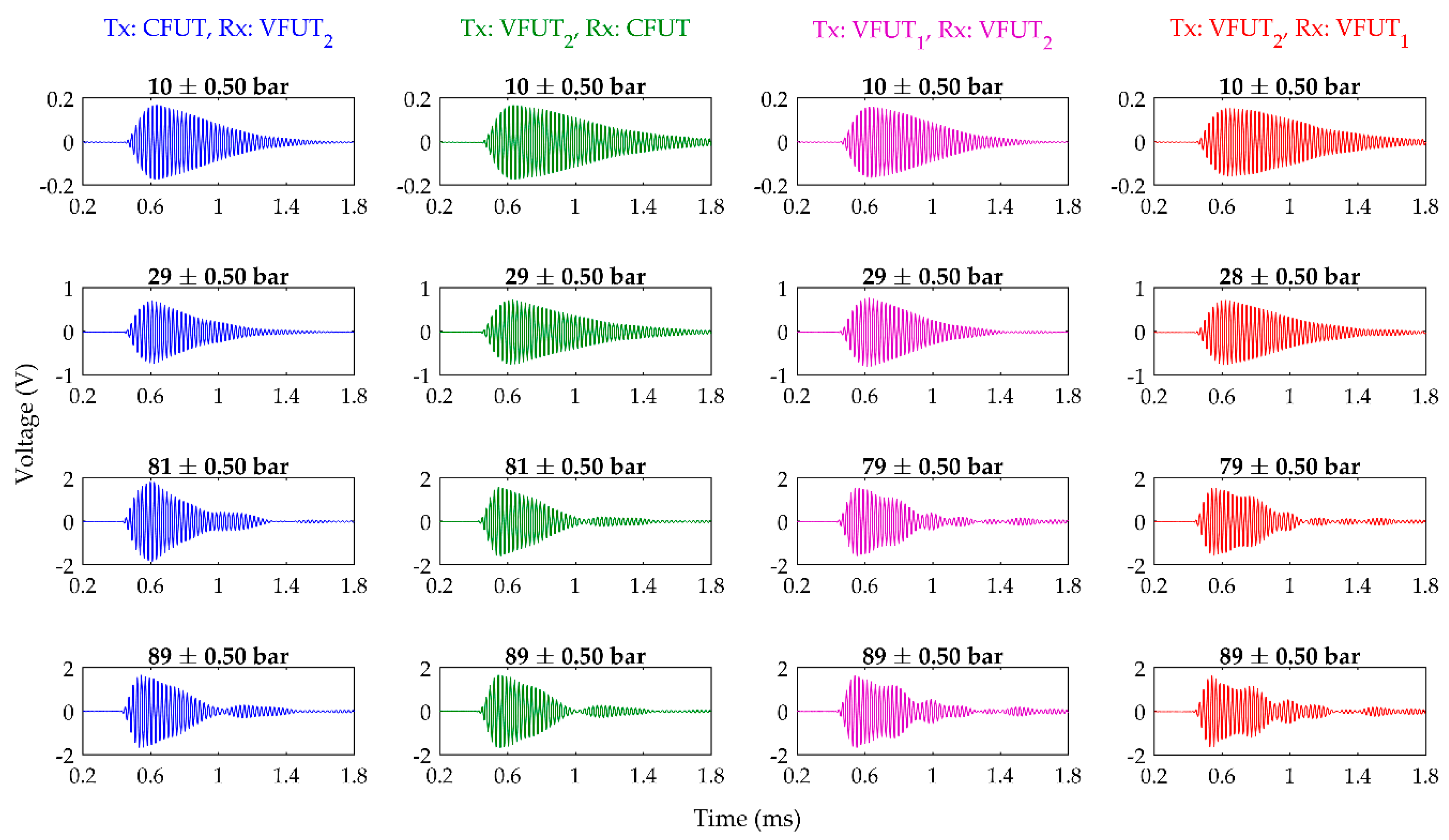
3.2. Pitch-Catch Ultrasound Measurement
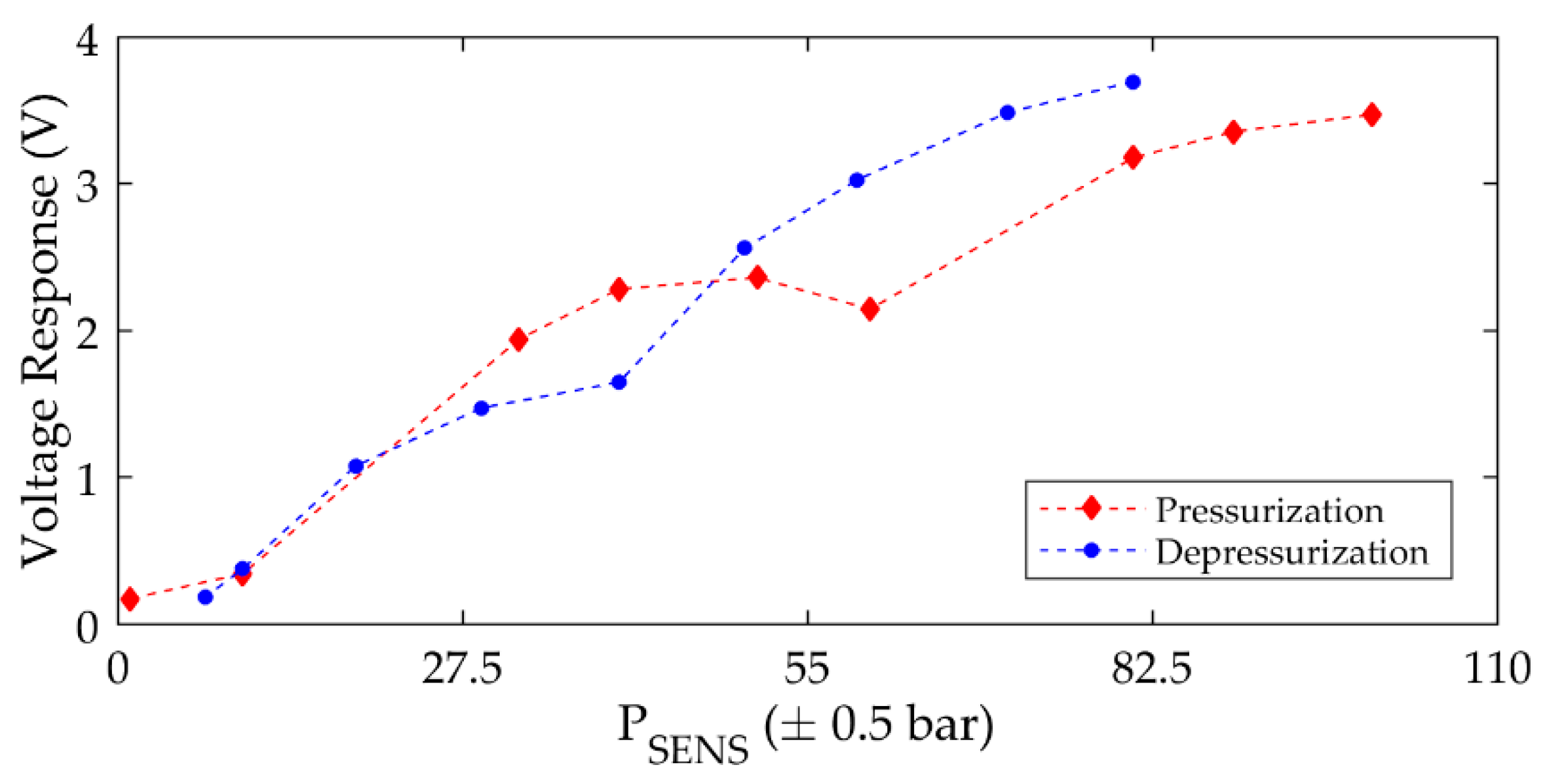
3.2.1. Influence of Air Pressure Level on Voltage Response
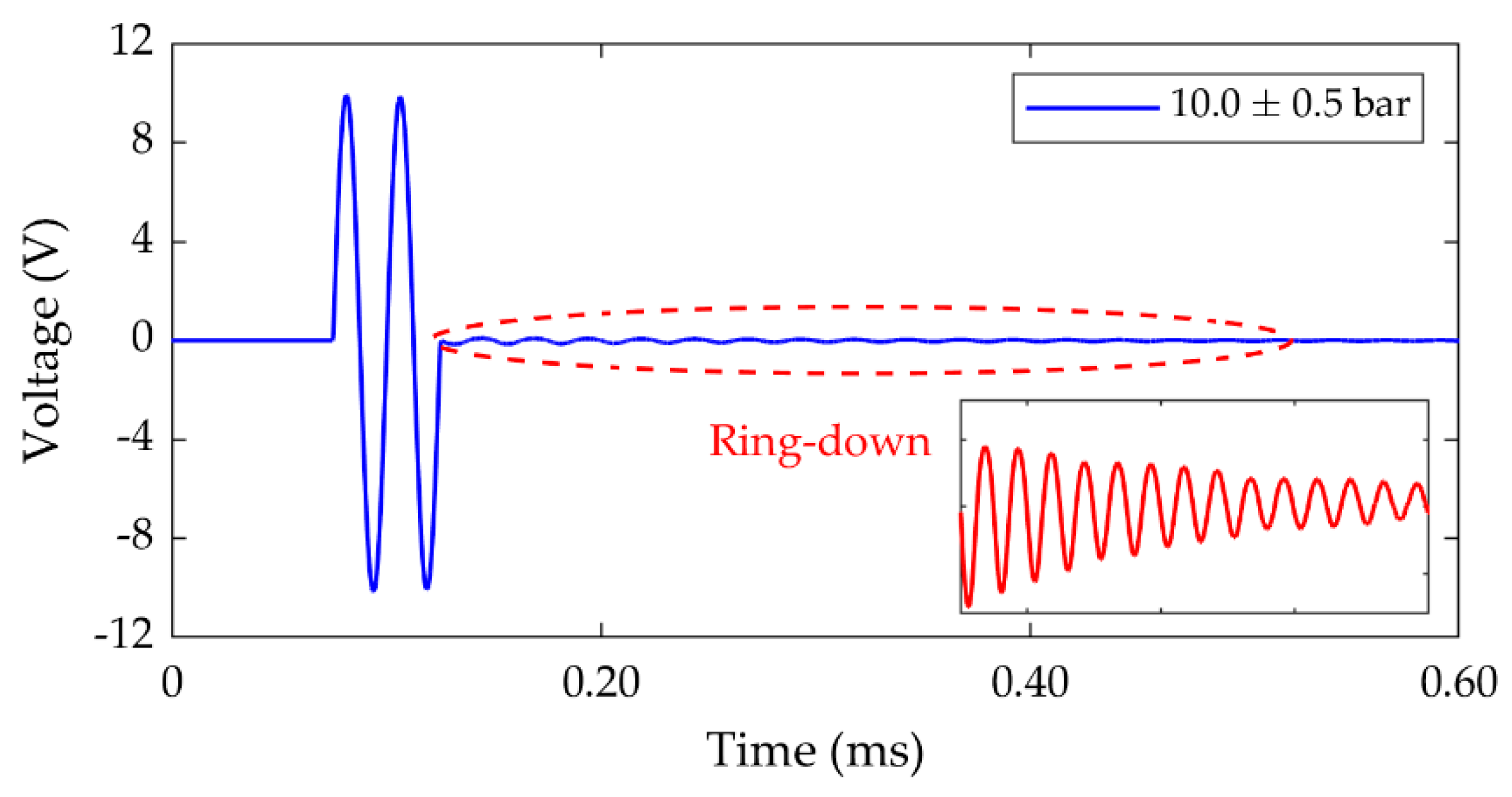
3.2.2. Analysis of the Resonant Ring-Down Response
4. Conclusions
5. Patents
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chimenti, D. Review of air-coupled ultrasonic materials characterization. Ultrason. 2014, 54, 1804–1816. [Google Scholar] [CrossRef] [PubMed]
- Stansfield, D. Underwater Electroacoustic Transducers; Peninsula Publishing: Newport Beach, CA, USA, 1991. [Google Scholar]
- Baker, R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications; Cambridge University Press: Cambridge, UK, 2016; pp. 312–356. [Google Scholar]
- Sherman, C.H.; Butler, J.L. Transducers and Arrays for Underwater Sound; Springer Science and Business Media LLC: Berlin, Germany, 2007; pp. 1–30. [Google Scholar]
- Park, E.J.; Werner, J.; Smith, N.B. Ultrasound Mediated Transdermal Insulin Delivery in Pigs Using a Lightweight Transducer. Pharm. Res. 2007, 24, 1396–1401. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Gigliotti, J.V.; Wallace, M.; Griggio, F.; DeMore, C.E.M.; Cochran, S.; Mc Kinstry, S.T. Piezoelectric Micromachined Ultrasound Transducer (PMUT) Arrays for Integrated Sensing, Actuation and Imaging. Sensors 2015, 15, 8020–8041. [Google Scholar] [CrossRef] [PubMed]
- Pun, S.H.; Yu, Y.; Zhang, J.; Wang, J.; Cheng, C.-H.; Lei, K.F.; Yuan, Z.; Mak, P.U. Monolithic Multiband CMUTs for Photoacoustic Computed Tomography With In Vivo Biological Tissue Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2018, 65, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Yoon, I.; Lee, S.; Kim, H.; Seo, J.W.; Chung, Y.; Unger, A.; Kupnik, M.; Lee, H.J. CMUT-based resonant gas sensor array for VOC detection with low operating voltage. Sens. Actuators B Chem. 2018, 273, 1556–1563. [Google Scholar] [CrossRef]
- Eriksson, T.; Ramadas, S.; Dixon, S. Experimental and simulation characterisation of flexural vibration modes in unimorph ultrasound transducers. Ultrason. 2016, 65, 242–248. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Feeney, A.; Dixon, S. Analysis of influence of inconsistent performances of array elements on flexural ultrasonic phased array for measurement of ultrasound in fluids. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Ding, Z.S.; Boned, C.; Xans, P.; Alliez, J. Automation of an ultrasound velocity measurement system in high-pressure liquids. Meas. Sci. Technol. 1997, 8, 154–161. [Google Scholar] [CrossRef]
- Dell’Isola, M.; Cannizzo, M.; Diritti, M. Measurement of high-pressure natural gas flow using ultrasonic flowmeters. Meas. 1997, 20, 75–89. [Google Scholar] [CrossRef]
- Apte, N.; Park, K.K.; Khuri-Yakub, B.T. Experimental evaluation of CMUTs with vented cavities under varying pressure. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 1–4. [Google Scholar]
- Apte, N.; Park, K.K.; Nikoozadeh, A.; Khuri-Yakub, B.T. Effect of fluid losses and acoustic resonances in CMUTs with vented cavities. In Proceedings of the 2015 Transducers: 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 682–685. [Google Scholar]
- Leissa, A.W. Vibration of Plates; U.S. Government Press: Washington, DC, USA, 1969; pp. 1–8.
- Remillieux, M.C.; Anderson, B.E.; Le Bas, P.Y.; Ulrich, T. Improving the air coupling of bulk piezoelectric transducers with wedges of power-law profiles: A numerical study. Ultrason. 2014, 54, 1409–1416. [Google Scholar] [CrossRef] [PubMed]
- Dixon, S.; Kang, L.; Ginestier, M.; Wells, C.; Rowlands, G.; Feeney, A. The electro-mechanical behaviour of flexural ultrasonic transducers. Appl. Phys. Lett. 2017, 110, 223502. [Google Scholar] [CrossRef]
- Feeney, A.; Kang, L.; Rowlands, G.; Dixon, S. The Dynamic Performance of Flexural Ultrasonic Transducers. Sensors 2018, 18, 270. [Google Scholar] [CrossRef] [PubMed]
- Feeney, A.; Kang, L.; Dixon, S. High-Frequency Measurement of Ultrasound Using Flexural Ultrasonic Transducers. IEEE Sensors J. 2018, 18, 5238–5244. [Google Scholar] [CrossRef]
- Feeney, A.; Kang, L.; Rowlands, G.; Zhou, L.; Dixon, S. Dynamic Nonlinearity in Piezoelectric Flexural Ultrasonic Transducers. IEEE Sensors J. 2019, 19, 6056–6066. [Google Scholar] [CrossRef]
- Gao, J.; Altintas, Y. Development of a Three-Degree-of-Freedom Ultrasonic Vibration Tool Holder for Milling and Drilling. IEEE/ASME Trans. Mechatronics 2019, 24, 1238–1247. [Google Scholar] [CrossRef]
- Feeney, A.; Kang, L.; Dixon, S. Nonlinearity in the dynamic response of flexural ultrasonic transducers. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]



| Nom. (bar) | CFUT | VFUT1 | VFUT2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
(kHz) | (kHz) | (kHz) | |||||||
| 10 | 779.53 | −35.68 | 40.00 | 625.67 | −20.08 | 40.00 | 498.67 | −34.49 | 40.40 |
| 30 | 767.65 | −40.26 | 39.40 | 729.57 | −32.65 | 39.80 | 562.72 | −22.55 | 40.40 |
| 50 | 1212.85 | −63.56 | 38.80 | 792.18 | −28.64 | 39.80 | 678.32 | −40.02 | 40.20 |
| 70 | 869.07 | −49.84 | 39.20 | 872.84 | −41.54 | 39.60 | 747.12 | −38.33 | 40.20 |
| 90 | 1043.67 | −59.25 | 40.20 | 946.63 | −43.47 | 39.60 | 859.16 | −38.49 | 40.20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feeney, A.; Kang, L.; Somerset, W.E.; Dixon, S. The Influence of Air Pressure on the Dynamics of Flexural Ultrasonic Transducers. Sensors 2019, 19, 4710. https://doi.org/10.3390/s19214710
Feeney A, Kang L, Somerset WE, Dixon S. The Influence of Air Pressure on the Dynamics of Flexural Ultrasonic Transducers. Sensors. 2019; 19(21):4710. https://doi.org/10.3390/s19214710
Chicago/Turabian StyleFeeney, Andrew, Lei Kang, William E. Somerset, and Steve Dixon. 2019. "The Influence of Air Pressure on the Dynamics of Flexural Ultrasonic Transducers" Sensors 19, no. 21: 4710. https://doi.org/10.3390/s19214710
APA StyleFeeney, A., Kang, L., Somerset, W. E., & Dixon, S. (2019). The Influence of Air Pressure on the Dynamics of Flexural Ultrasonic Transducers. Sensors, 19(21), 4710. https://doi.org/10.3390/s19214710






