Characteristics of a Magnetic Field Sensor with a Concentrating-Conducting Magnetic Flux Structure
Abstract
:1. Introduction
2. Structure and Principle
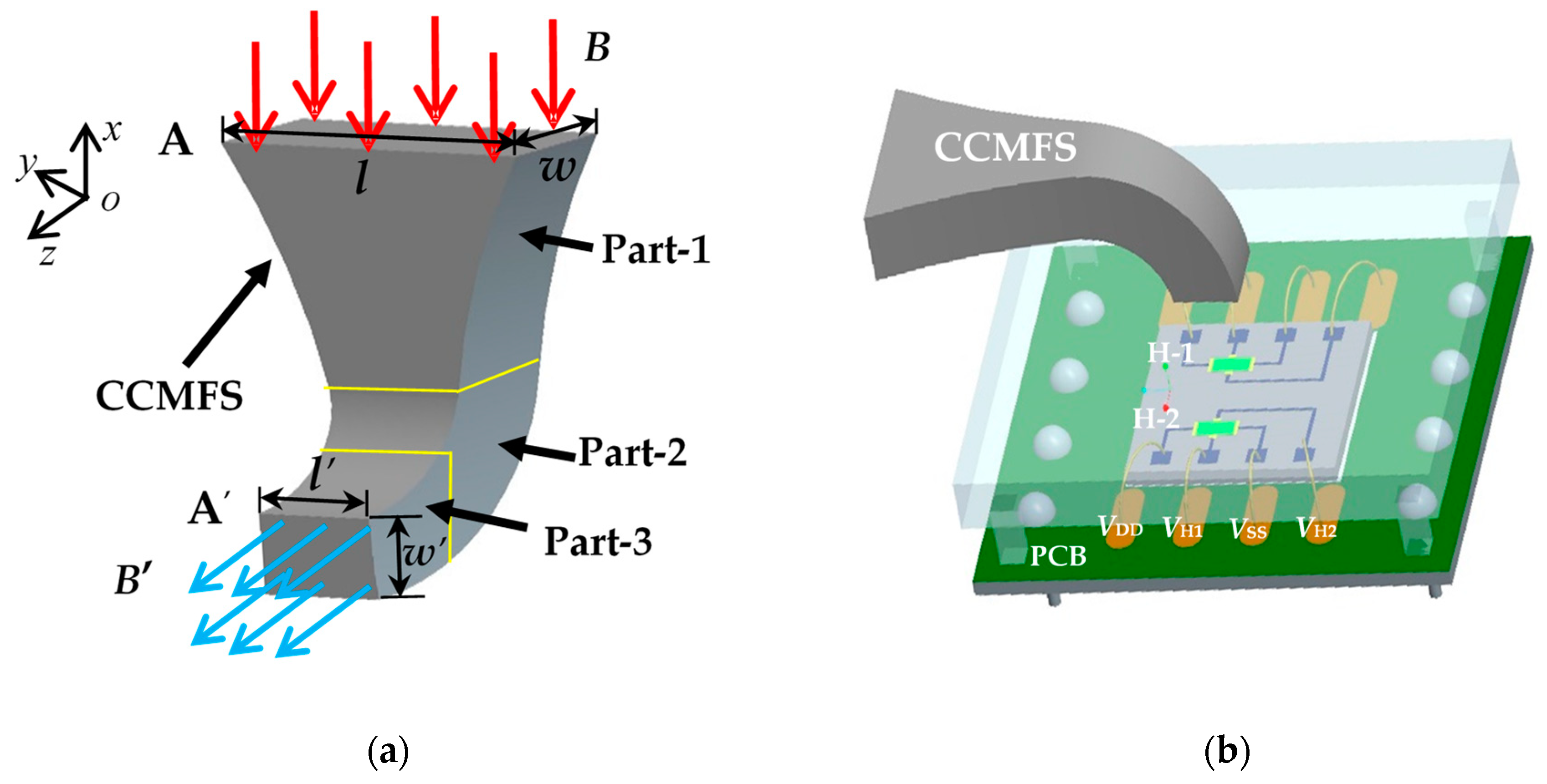
2.1. Basic Structure
2.2. Theoretical Analysis of CCMFS
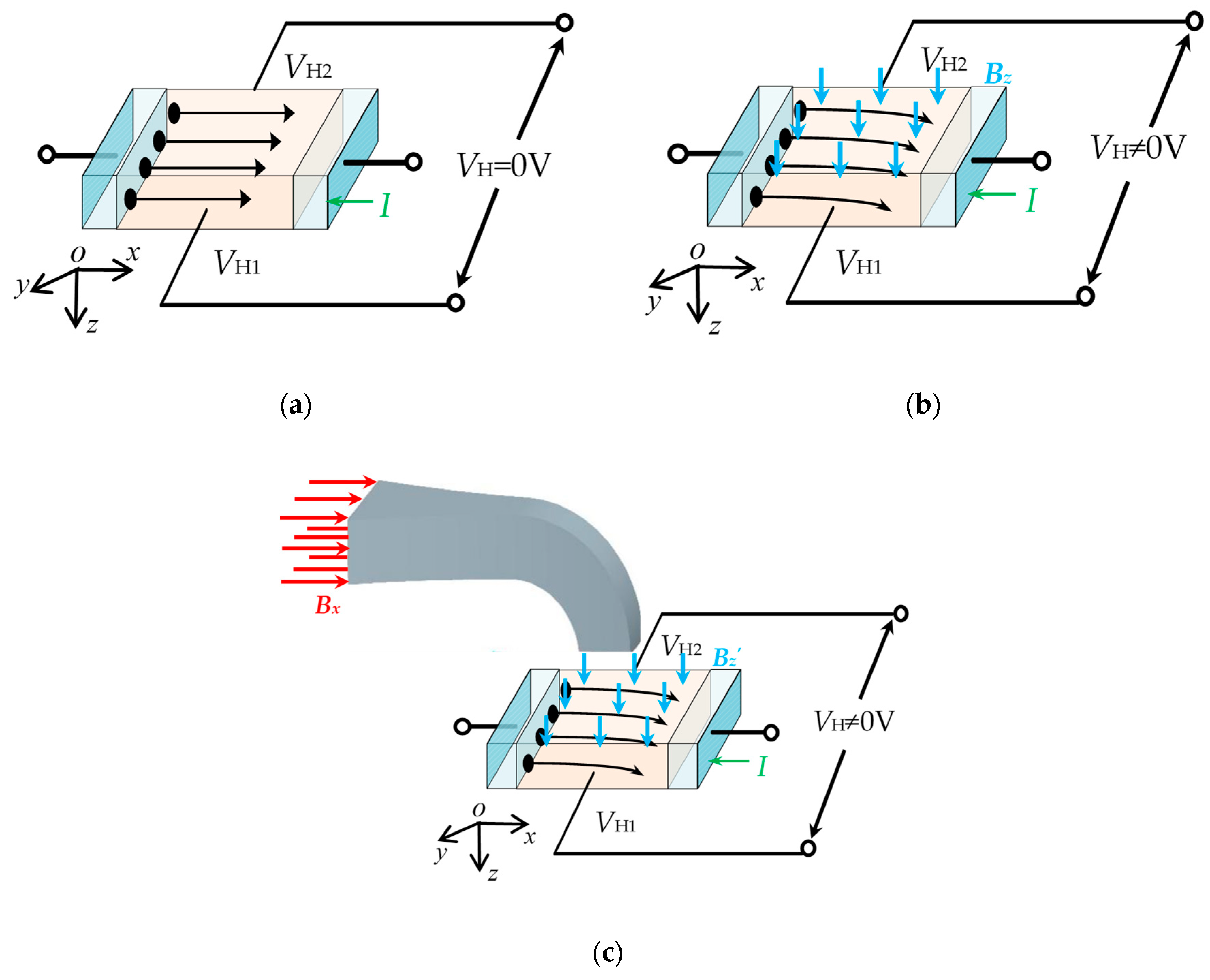
2.3. Operating Principle of Magnetic Field Sensor
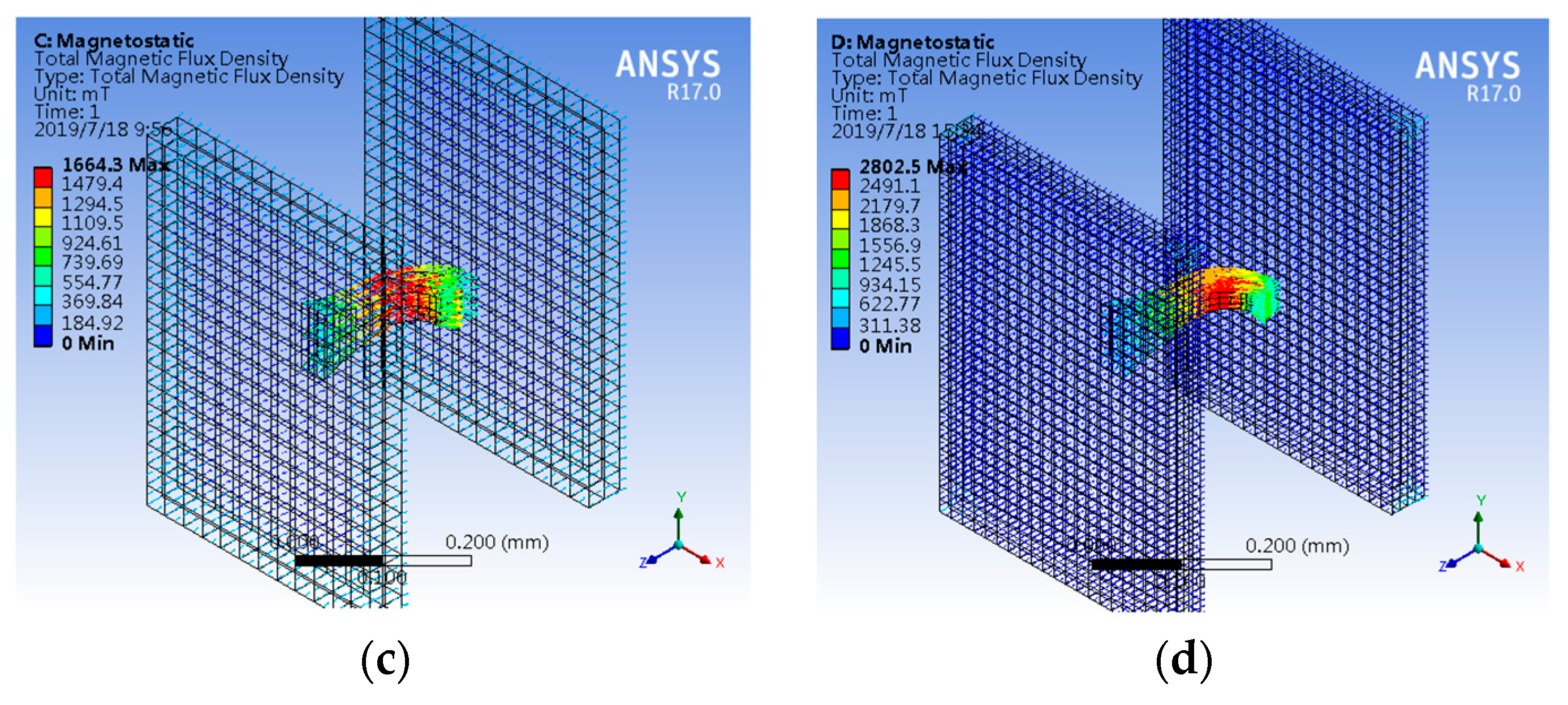
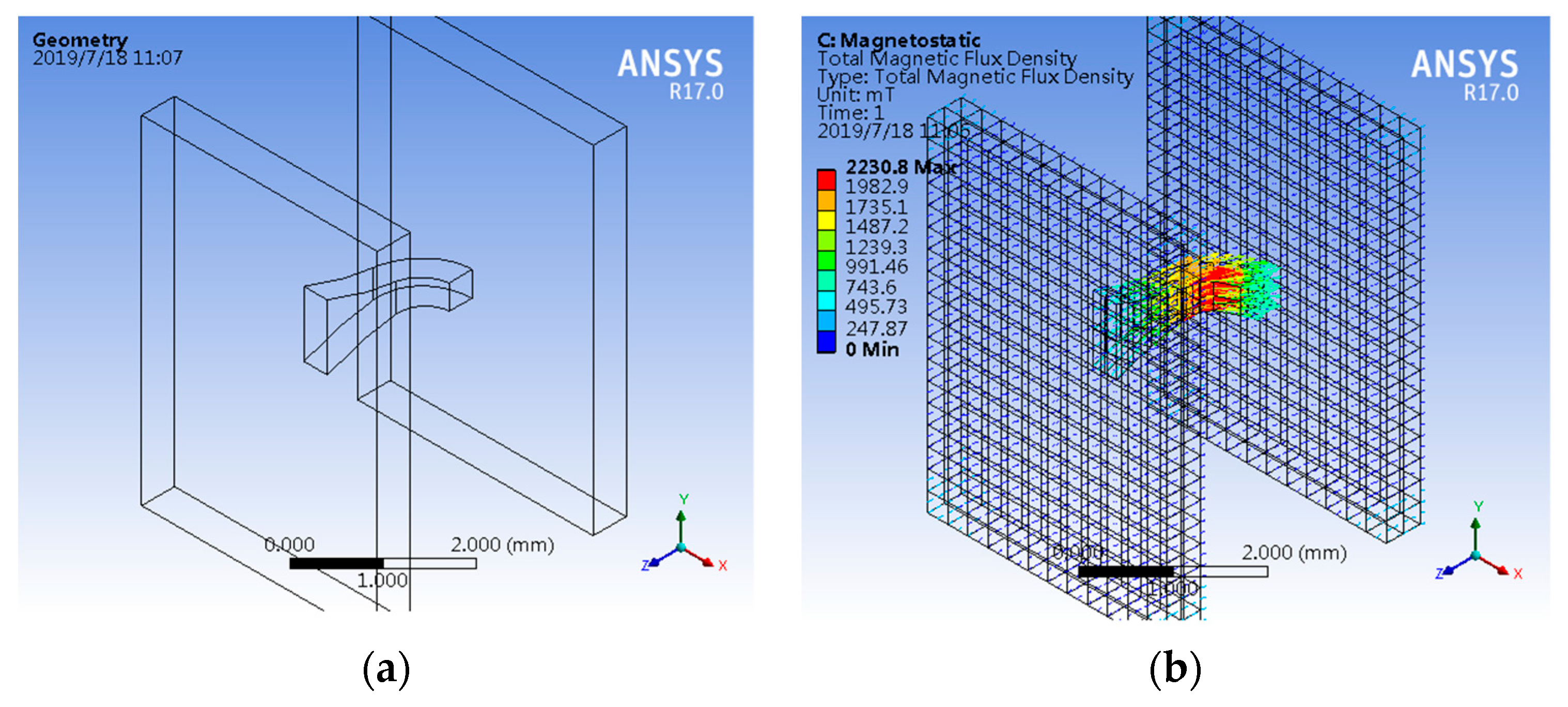
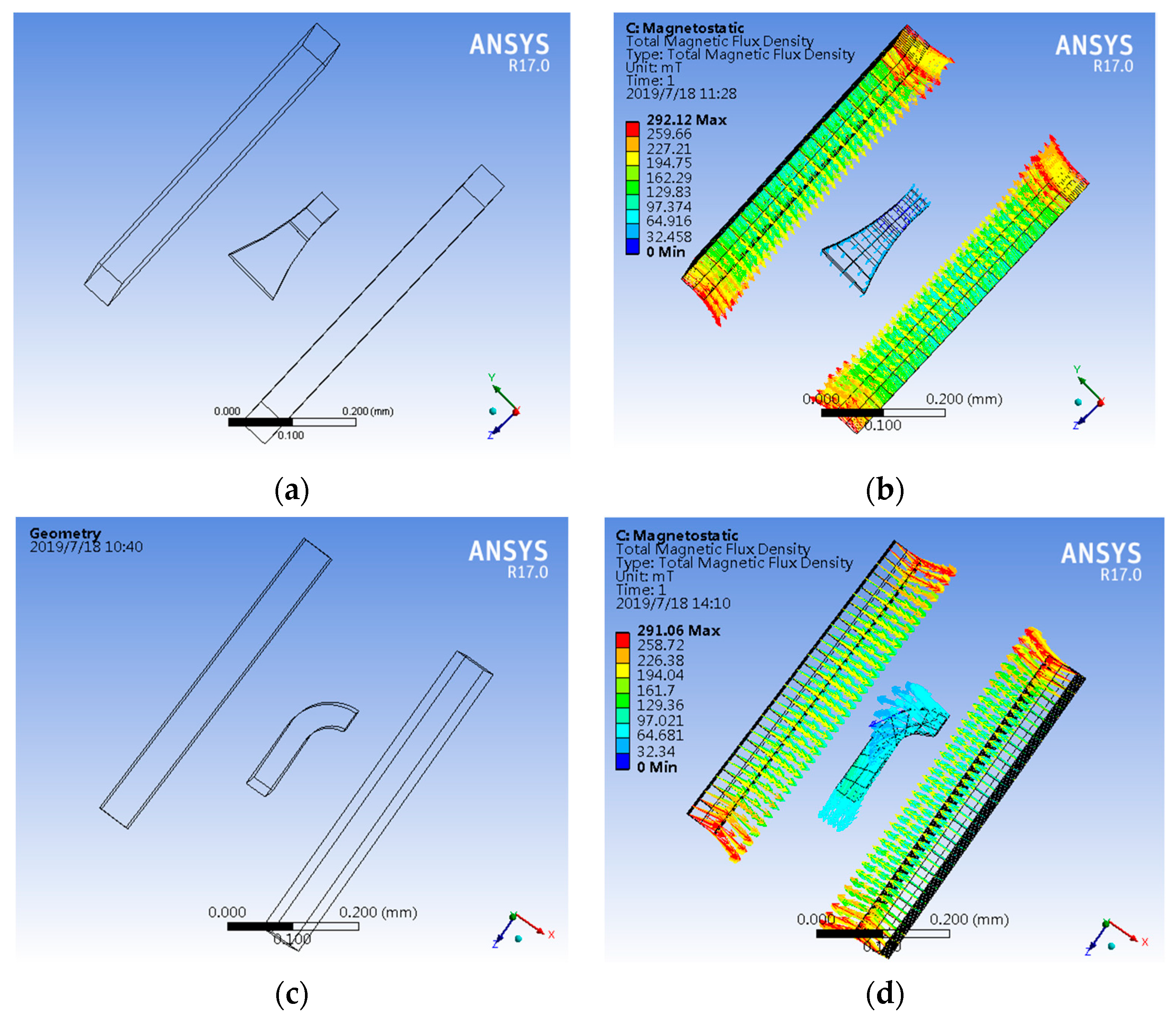
3. Simulation Analysis and Fabrication Technology
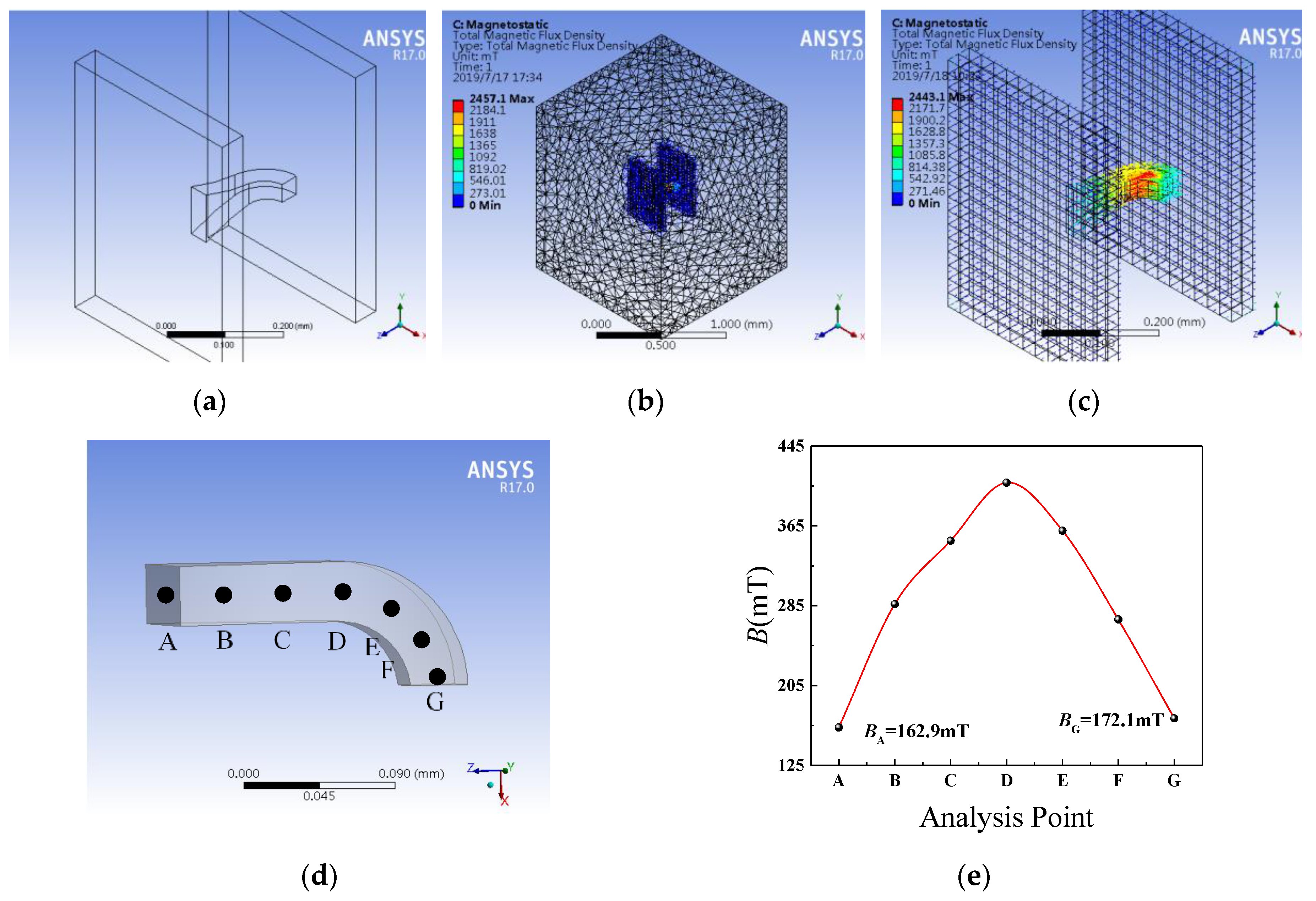
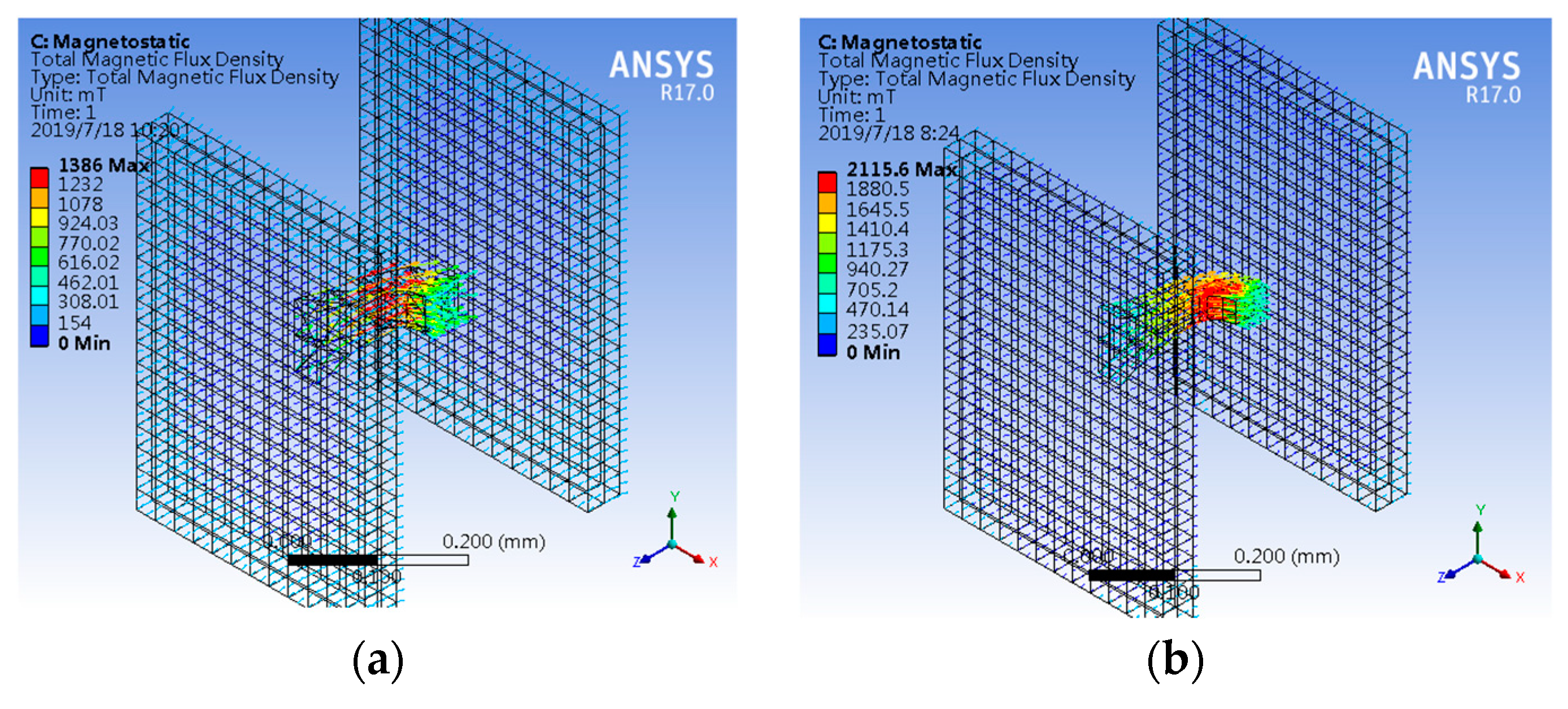
3.1. Characteristics Simulation of CCMFS
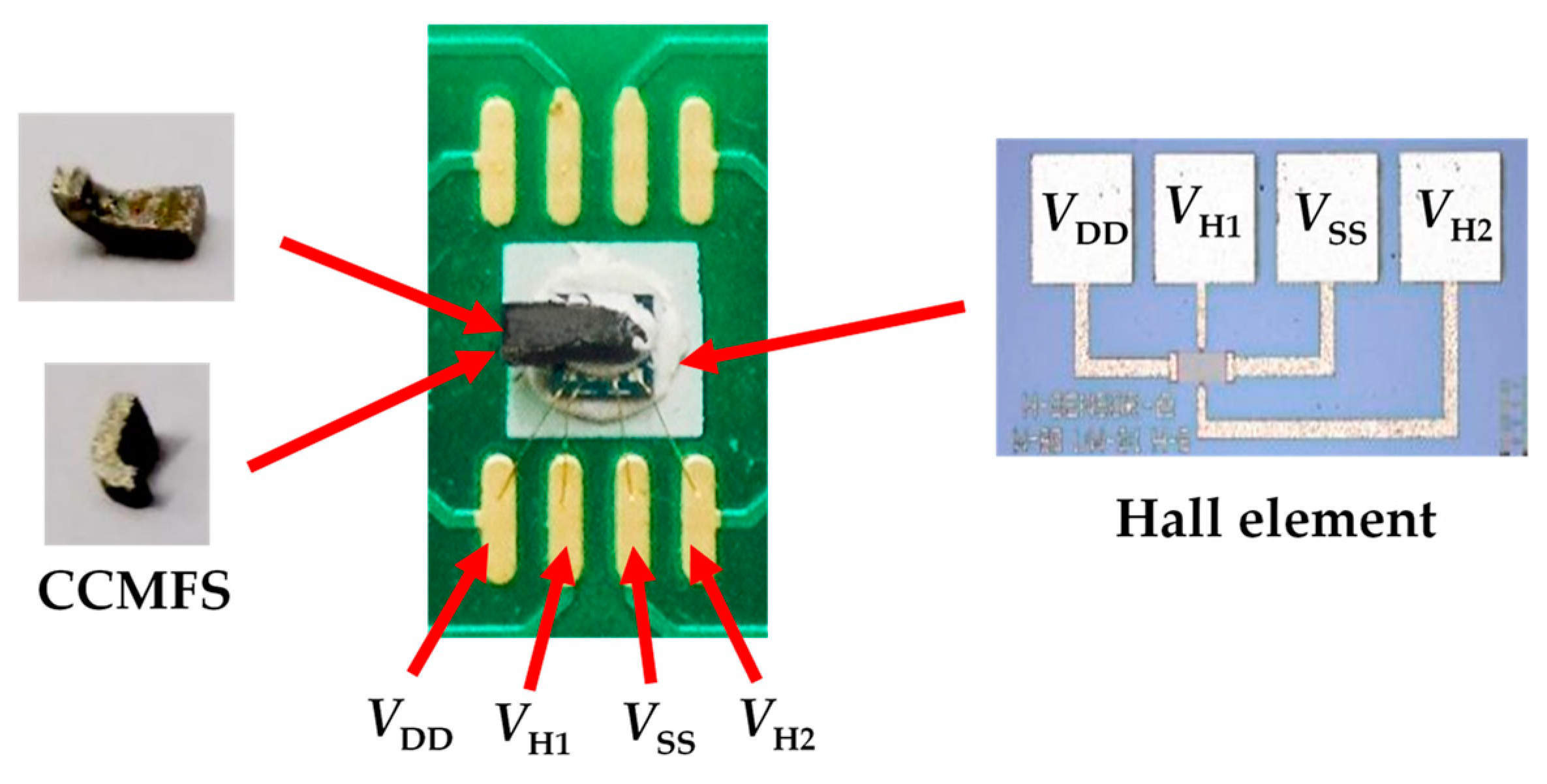
3.2. Fabrication Technology
4. Results and Discussion
4.1. Magnetic Sensitive Characteristic of Hall Elements
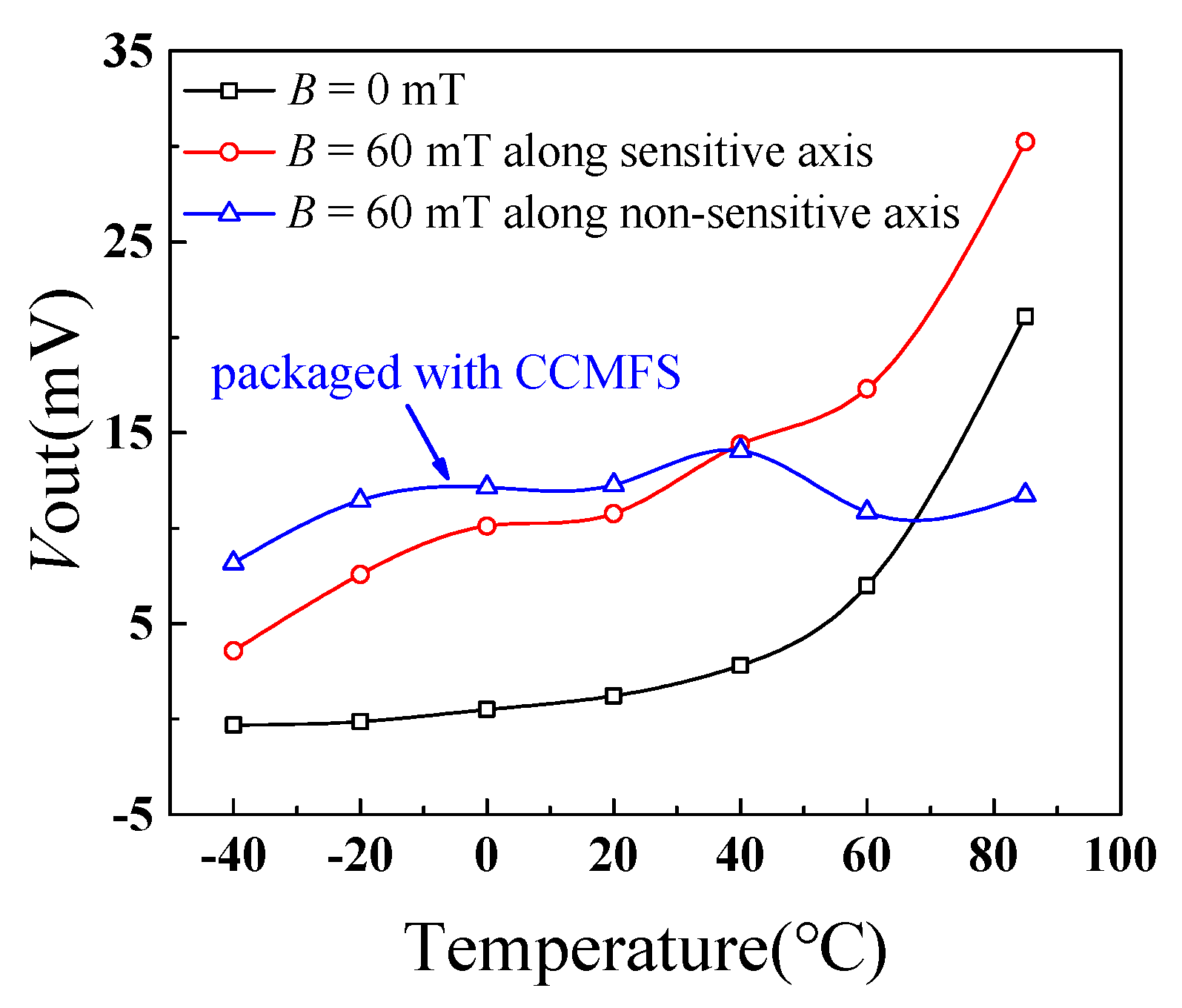
4.2. Characteristic Detection of the Magnetic Field Sensor along the Non-Sensitive Axis
4.3. Temperature Characteristic of the Magnetic Field Sensor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, X.F.; Jin, C.C.; Deng, Q.; Lv, M.W.; Wen, D.Z. Fabrication Technology and Characteristics Research of a Monolithically Integrated 2D Magnetic Field Sensor Based on Silicon Magnetic Sensitive Transistors. Sensors 2018, 18, 2551. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.F.; Yang, X.H.; Li, B.Z.; Wen, D.Z. Characteristics Research of the Three Dimensional Hall Magnetic Field Sensor Based on Packaging Technology. Sens. Transducers 2016, 197, 14–19. [Google Scholar]
- Zhao, X.F.; Bai, Y.J.; Deng, Q.; Ai, C.P.; Yang, X.H.; Wen, D.Z. Research of the Monolithic Integrated 3-D Magnetic Field Sensor Based on MEMS Technology. IEEE Sens. J. 2017, 17, 5849–5856. [Google Scholar] [CrossRef]
- Chen, J.; Wurz, M.C.; Belski, A.; Rissing, L. Designs and Characterizations of Soft Magnetic Flux Guides in a 3-D Magnetic Field Sensor. IEEE Trans. Magn. 2012, 48, 1481–1484. [Google Scholar] [CrossRef]
- Schott, C.; Racz, R.; Manco, A.; Simonne, N. CMOS Single Chip Electronic Compass with Microcontroller. IEEE J. Solid-State Circuits 2007, 42, 2923–2933. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, J.; Tian, W.; Hu, J.; Pan, M. Designs of Novel Magnetic Flux Guides for Three-Axis Magnetic Sensor. IEEE Trans. Magn. 2015, 51, 1–6. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, W.; Zhang, Q.; Pan, M.; Hu, J.; Chen, D.; Luo, F. Designs of Slope Magnetic Flux Guides for Three-Axis Magnetic Sensor. IEEE Trans. Magn. 2013, 49, 5301–5303. [Google Scholar] [CrossRef]
- Schott, C.; Huber, S. Modern CMOS Hall Sensors with Integrated Magnetic Concentrators. Lect. Notes Electr. Eng. 2008, 4, 3–21. [Google Scholar]
- Leroy, P.; Coillot, C.; Roux, A.F.; Chanteur, G.M. High Magnetic Field Amplification for Improving the Sensitivity of Hall Sensors. IEEE Sens. J. 2006, 6, 707–713. [Google Scholar] [CrossRef]
- Wang, S.; He, T.; Zhang, Y. Research on a Superconducting Magnetic Flux Concentrator for a GMI-Based Mixed Sensor. IEEE Trans. Appl. Supercond. 2014, 24, 1–5. [Google Scholar]
- Sun, X.; Jiang, L.; Pong, P.W.T. Magnetic Flux Concentration at Micrometer Scale. Microelectron. Eng. 2013, 111, 77–81. [Google Scholar] [CrossRef]
- Brugger, S.; Paul, O. Field Concentrator Based Resonant Magnetic Sensor with Integrated Planar Coils. J. Microelectromech. Syst. 2009, 18, 1432–1443. [Google Scholar] [CrossRef]
- Brugger, S.; Paul, O. Magnetic Field Amplification by Slender Cuboid Shaped Magnetic Concentrators with a Single Gap. Sens. Actuators A Phys. 2010, 157, 135–139. [Google Scholar] [CrossRef]
- Leitao, D.C.; Gameiro, L.; Silva, A.V.; Cardoso, S.; Freitas, P.P. Field Detection in Spin Valve Sensors Using CoFeB/Ru Synthetic Antiferromagnetic Multilayers as Magnetic Flux Concentrators. IEEE Trans. Magn. 2012, 48, 3847–3850. [Google Scholar] [CrossRef]
- Bean C, P. Magnetization of Hard Superconductors. Phys. Rev. 1962, 8, 250–253. [Google Scholar] [CrossRef]
- Osborn J, A. Demagnetizing Factors of The General Ellipsoid. Phys. Rev. 1945, 67, 351–357. [Google Scholar] [CrossRef]
- Leroy, P.; Coillot, C.; Mosser, V.; Roux, A.; Chanteur, G. An ac/dc Magnetometer for Space Missions: Improvement of a Hall Sensor by the Magnetic Flux Concentration of the Magnetic Core of a Searchcoil. Sens. Actuators A Phys. 2008, 142, 503–510. [Google Scholar] [CrossRef]
- Hall, E.H. The Hall Effect. Science 1884, 4, 351. [Google Scholar] [CrossRef] [PubMed]
- Beran, P.; Stahl-Offergeld, M.; Peters, V.; Krause, D.; Hohe, H.P. Impact of Contact Misalignment on Magnetic Cross Sensitivity of Integrated Vertical Hall Sensors. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
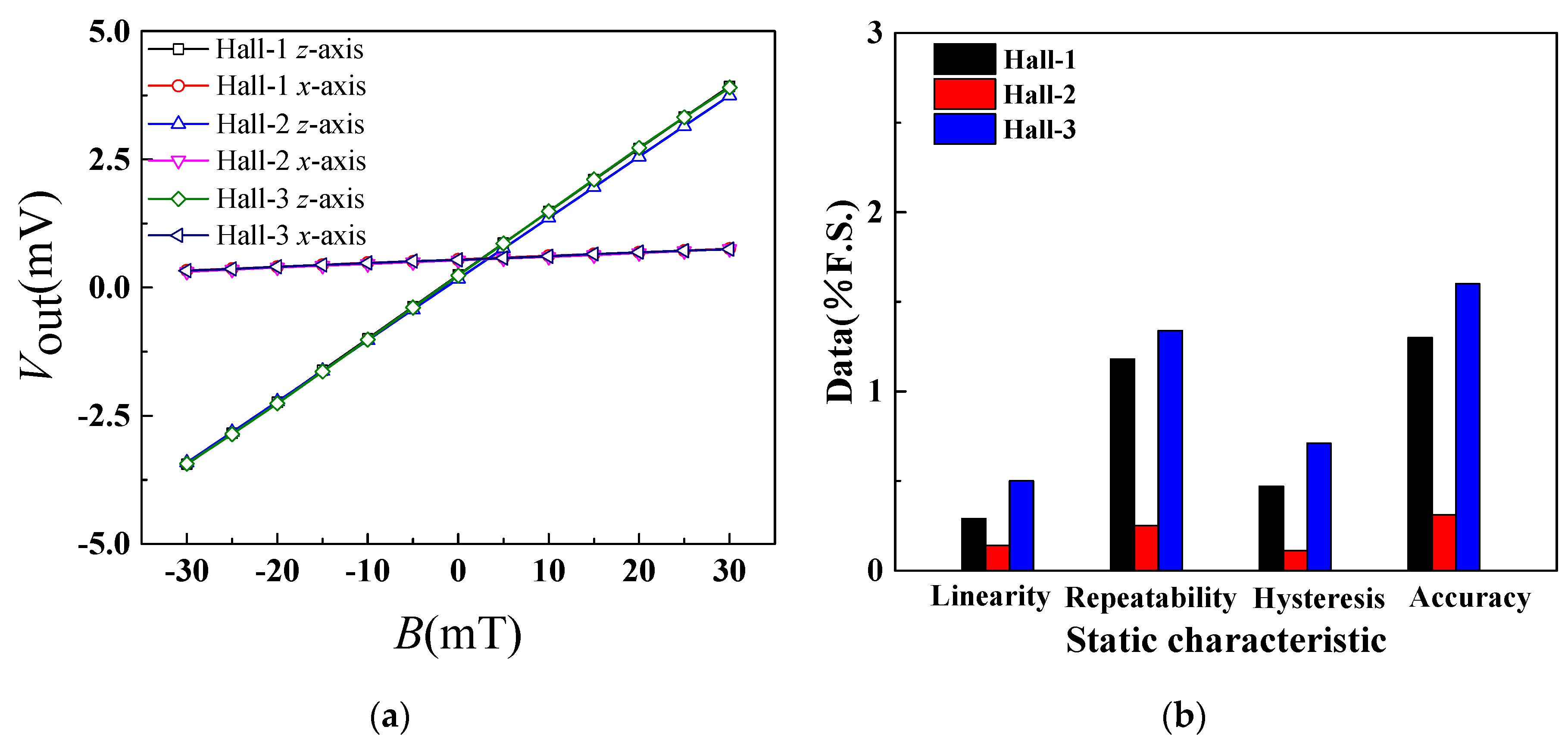
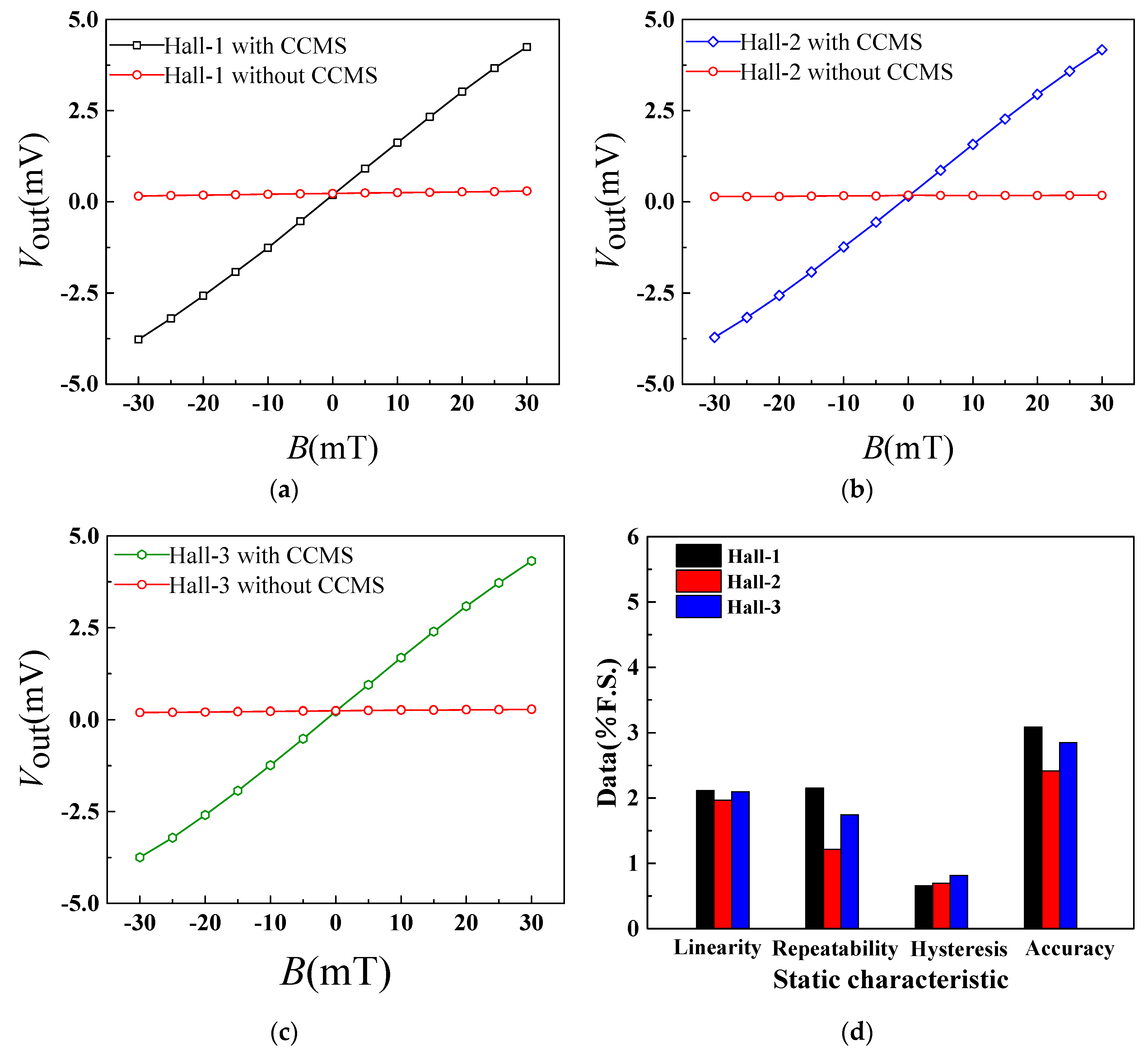
| Sensitivity | Linearity | Repeatability | Hysteresis | Accuracy | |
|---|---|---|---|---|---|
| Hall-1 | 122.8 mV/T | 0.29% F.S | 1.18% F.S | 0.47% F.S | 1.30% F.S |
| Hall-1 (CCMFS) | 133.7 mV/T | 2.11% F.S | 2.15% F.S | 0.65% F.S | 3.09% F.S |
| Hall-2 | 119.4 mV/T | 0.14% F.S | 0.25% F.S | 0.11% F.S | 0.31% F.S |
| Hall-2 (CCMFS) | 132.0 mV/T | 1.97% F.S | 1.21% F.S | 0.69% F.S | 2.41% F.S |
| Hall-3 | 122.3 mV/T | 0.50% F.S | 1.34% F.S | 0.71% F.S | 1.60% F.S |
| Hall-3 (CCMFS) | 132.9 mV/T | 2.09% F.S | 1.74% F.S | 0.81% F.S | 2.84% F.S |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhao, X.; Wen, D. Characteristics of a Magnetic Field Sensor with a Concentrating-Conducting Magnetic Flux Structure. Sensors 2019, 19, 4498. https://doi.org/10.3390/s19204498
Li X, Zhao X, Wen D. Characteristics of a Magnetic Field Sensor with a Concentrating-Conducting Magnetic Flux Structure. Sensors. 2019; 19(20):4498. https://doi.org/10.3390/s19204498
Chicago/Turabian StyleLi, Xuelei, Xiaofeng Zhao, and Dianzhong Wen. 2019. "Characteristics of a Magnetic Field Sensor with a Concentrating-Conducting Magnetic Flux Structure" Sensors 19, no. 20: 4498. https://doi.org/10.3390/s19204498
APA StyleLi, X., Zhao, X., & Wen, D. (2019). Characteristics of a Magnetic Field Sensor with a Concentrating-Conducting Magnetic Flux Structure. Sensors, 19(20), 4498. https://doi.org/10.3390/s19204498




