Aerial Cooperative Jamming for Cellular-Enabled UAV Secure Communication Network: Joint Trajectory and Power Control Design
Abstract
:1. Introduction
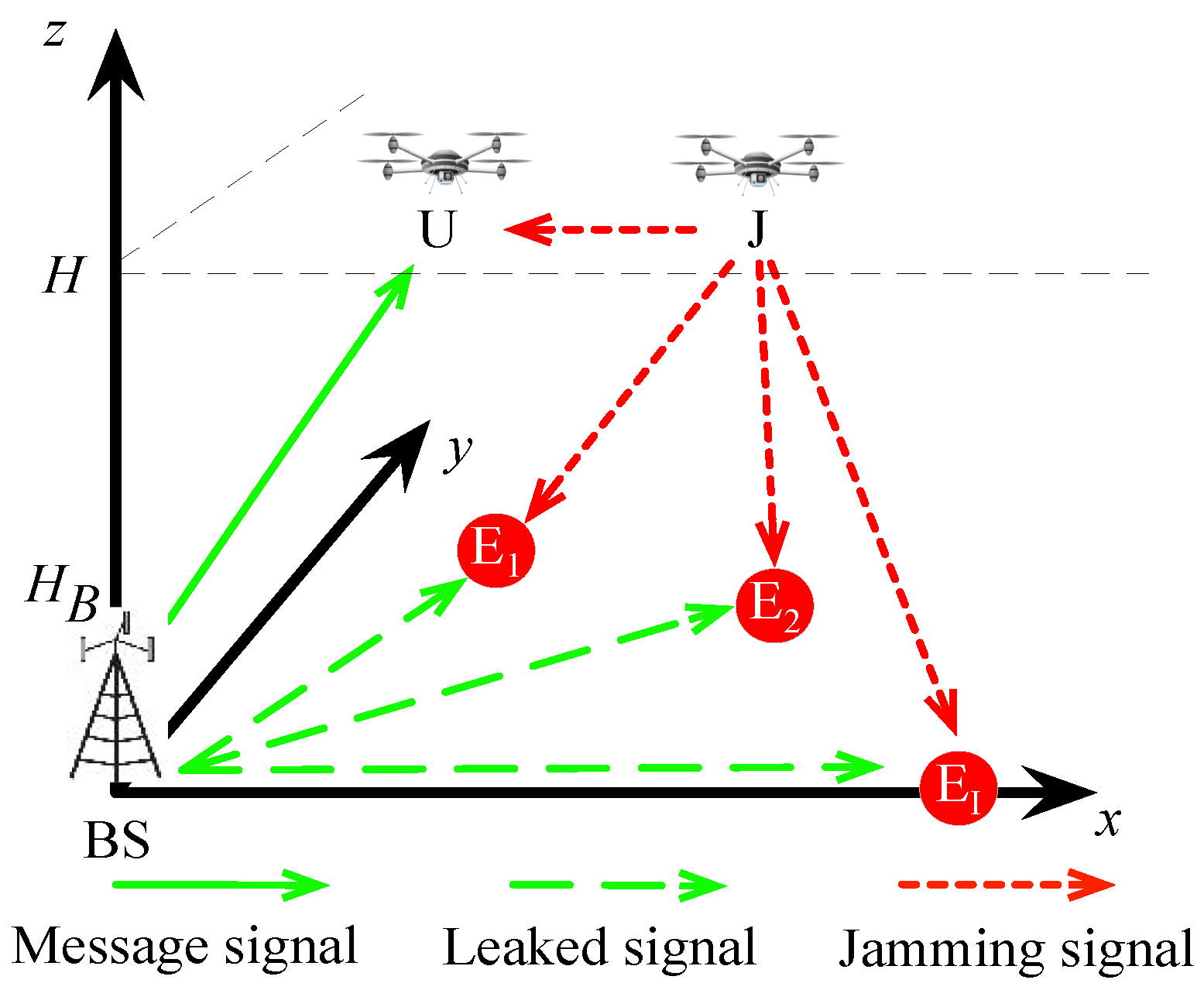
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Joint Trajectory and Power Control Algorithm
3.1. Transmit Power Optimization
3.2. Jamming Power Optimization
3.3. Trajectory Optimization of the UAV U
3.4. Trajectory Optimization of the UAV J
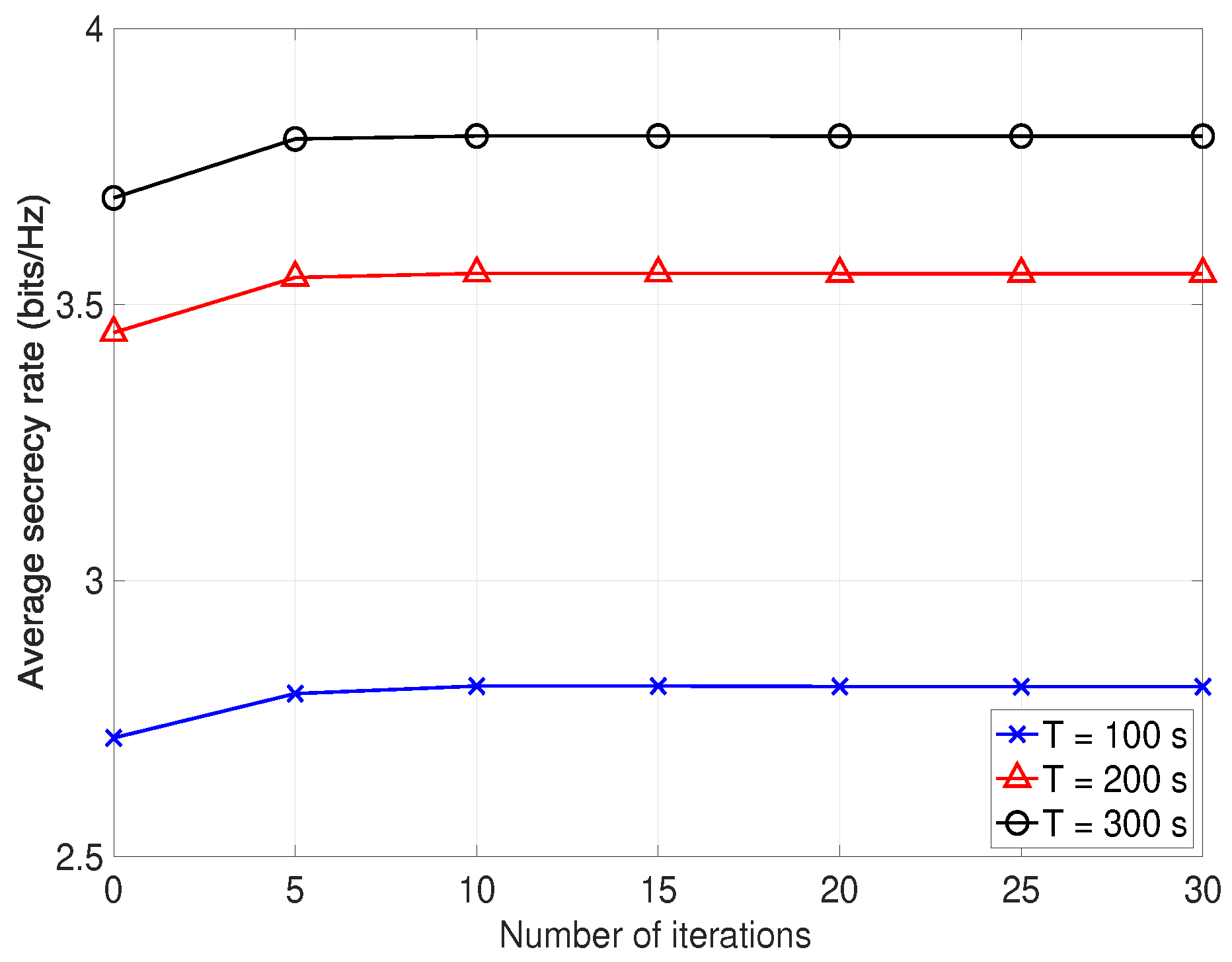
3.5. Overall Algorithm
| Algorithm 1 Proposed algorithm for solving problem (13) |
| 1: Initial , , , , and . Let . 2: repeat 3: Solve problem (14) with given , , and , and denote by the optimal solution. 4: Solve problem (17) with given , , and , and denote by the optimal solution. 5: Solve problem (23) with given , , , and , and denote by the optimal solution. 6: Solve problem (31) with given , , , and , and denote by the optimal solution. 7: Update . 8: until Converge to a pre-specified precision . |
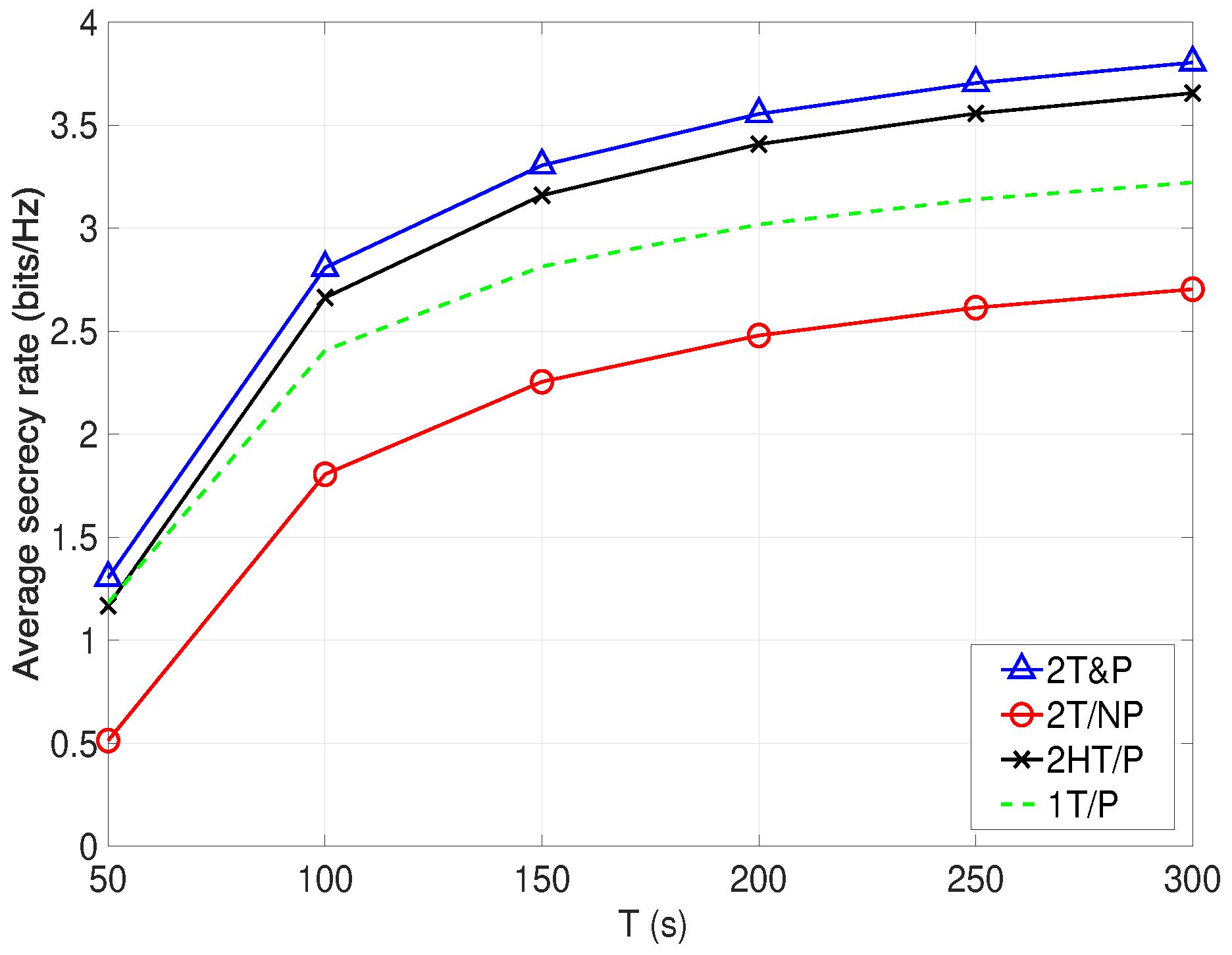
4. Numerical Results
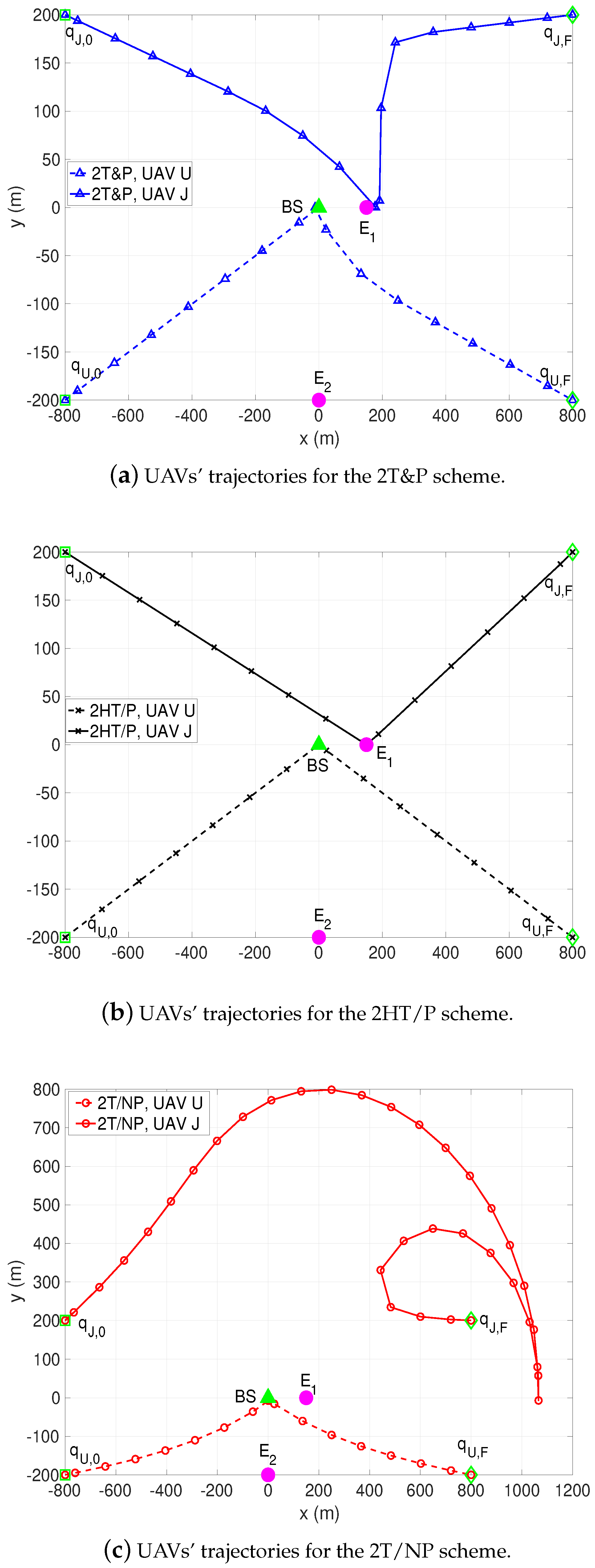
- UAVs’ trajectories optimization without power control (denoted as 2T/NP);
- heuristic UAVs’ trajectories with power control (2HT/P);
- joint optimization of the UAV U’s trajectory and BS’s power control without aerial cooperative jamming from the UAV J (denoted as 1T&P), which is identical with the algorithm proposed in [18].
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Appendix
References
- Moon, J.; Lee, H.; Song, C.; Lee, S.; Lee, I. Proactive eavesdropping with full-duplex relay and cooperative jamming. IEEE Trans. Wirel. Commun. 2018, 17, 6707–6719. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, H.; Dai, H.; Wu, W.; Wang, B. Proactive eavesdropping in UAV-aided suspicious communication systems. IEEE Trans. Veh. Technol. 2019, 68, 1993–1997. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Cai, L. Optimal location of supplementary node in UAV surveillance system. J. Netw. Comput. Appl. 2019, 140, 23–39. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K. UAV-assisted emergency networks in disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef]
- Tuna, G.; Nefzi, B.; Conte, G. Unmanned aerial vehicle-aided communications system for disaster recovery. J. Netw. Comput. Appl. 2014, 41, 27–36. [Google Scholar] [CrossRef]
- Peng, K.; Du, J.; Lu, F.; Sun, Q.; Dong, Y.; Zhou, P.; Hu, M. A hybrid genetic algorithm on routing and scheduling for vehicle-assisted multi-drone parcel delivery. IEEE Access 2019, 7, 49191–49200. [Google Scholar] [CrossRef]
- You, C.; Zhang, R. 3D trajectory optimization in Rician fading for UAV-enabled data harvesting. IEEE Wirel. Commun. 2019, 18, 3192–3207. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Throughput maximization for UAV-enabled mobile relaying systems. IEEE Wirel. Commun. 2016, 64, 4983–4996. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing from the Sky: A Tutorial on UAV Communications for 5G and Beyond. 2019. Available online: https://arxiv.org/abs/1903.05289 (accessed on 13 March 2019).
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Zeng, Y.; Lyu, J.; Zhang, R. Cellular-connected UAV: Potential, challenges, and promising technologies. IEEE Wirel. Commun. 2019, 26, 120–127. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Common throughput maximization in UAV-enabled OFDMA systems with delay consideration. IEEE Trans. Commun. 2018, 66, 6614–6627. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R.; Lim, T.J. Placement optimization of UAV-mounted mobile base stations. IEEE Commun. Lett. 2017, 21, 604–607. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Zhang, R. Cellular-enabled UAV communication: A connectivity-constrained trajectory optimization perspective. IEEE Trans. Commun. 2019, 67, 2580–2604. [Google Scholar] [CrossRef]
- Lin, X.; Yajnanarayana, V.; Muruganathan, S.D.; Gao, S.; Asplund, H.; Maattanen, H.; Bergstrom, M.; Euler, S.; Wang, Y.E. The sky is not the Limit: LTE for unmanned aerial vehicles. IEEE Commun. Mag. 2018, 56, 204–210. [Google Scholar] [CrossRef]
- Der Bergh, B.V.; Chiumento, A.; Pollin, S. LTE in the sky: Trading off propagation benefits with interference costs for aerial nodes. IEEE Commun. Mag. 2016, 54, 44–50. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV communications via joint trajectory and power control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef]
- Cui, M.; Zhang, G.; Wu, Q.; Ng, D.W.K. Robust trajectory and transmit power design for secure UAV communications. IEEE Trans. Veh. Technol. 2018, 67, 9042–9046. [Google Scholar] [CrossRef]
- Li, A.; Wu, Q.; Zhang, R. UAV-enabled cooperative jamming for improving secrecy of ground wiretap channel. IEEE Wirel. Commun. Lett. 2019, 8, 181–184. [Google Scholar] [CrossRef]
- Duo, B.; Wu, Q.; Zhang, R. Energy Efficiency Maximization for Full-Duplex UAV Secrecy Communication. 2019. Available online: https://arxiv.org/abs/1906.07346 (accessed on 18 June 2019).
- Wang, Q.; Chen, Z.; Li, H.; Li, S. Joint power and trajectory design for physical-layer secrecy in the UAV-aided mobile relaying system. IEEE Access 2018, 6, 62849–62855. [Google Scholar] [CrossRef]
- Zhong, C.; Yao, J.; Xu, J. Secure UAV communication with cooperative jamming and trajectory control. IEEE Commun. Lett. 2019, 32, 286–289. [Google Scholar] [CrossRef]
- Cai, Y.; Cui, F.; Shi, Q.; Zhao, M.; Li, G.Y. Dual-UAV enabled secure communications: Joint trajectory design and user scheduling. IEEE J. Sel. Areas Commun. 2018, 36, 1972–1985. [Google Scholar] [CrossRef]
- Beck, A.; Tetruashvili, L. On the convergence of block coordinate descent type methods. SIAM J. Optim. 2013, 23, 2037–2060. [Google Scholar] [CrossRef]
- Hong, M.; Razaviyayn, M.; Luo, Z.; Pang, J. A unified algorithmic framework for block-structured optimization involving big data: With applications in machine learning and signal processing. IEEE Sign. Process. Mag. 2016, 33, 57–77. [Google Scholar] [CrossRef]
- Razaviyayn, M.; Hong, M.; Luo, Z. A unified convergence analysis of block successive minimization methods for nonsmooth optimization. SIAM J. Optim. 2013, 23, 1126–1153. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R. Energy-efficient UAV communication with trajectory optimization. IEEE Trans. Wirel. Commun. 2017, 16, 3747–3760. [Google Scholar] [CrossRef]
- Mukherjee, A.; Fakoorian, S.A.A.; Huang, J.; Swindlehurst, A.L. Principles of physical layer security in multiuser wireless networks: A survey. IEEE Commun. Surv. Tuts 2014, 16, 1550–1573. [Google Scholar] [CrossRef]
- You, C.; Zhang, R. Hybrid Offline-Online Design for UAV-Enabled Data Harvesting in Probabilistic LoS Channel. 2019. Available online: https://arxiv.org/abs/1907.06181v1 (accessed on 14 July 2019).
- Gopala, P.K.; Lai, L.; El Gamal, H. On the secrecy capacity of fading channels. IEEE Trans. Inf. Theory 2008, 54, 4687–4698. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.; Vandenberghe, L.; Press, C.U. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2018. Available online: http://cvxr.com/cvx (accessed on 14 October 2019).
- Ben-Tal, A.; Nemirovskiaei, A.S. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
| Notation | Physical Meaning | Simulation Value |
|---|---|---|
| Initial horizontal location of the UAV U | m | |
| Final horizontal location of the UAV U | m | |
| Initial horizontal location of the the UAV J | m | |
| Final horizontal location of the UAV J | m | |
| Horizontal location of the BS | m | |
| Location of the first eavesdropper | m, | |
| Location of the second eavesdropper | m | |
| H | Altitude of UAVs | 100 m |
| Altitude of BS | 10 m | |
| Maximum speed of UAVs | 40 m/s | |
| Minimum safe distance between UAVs | 20 m | |
| Time slot length | 1 s | |
| Channel power gain at the reference distance | −60 dB | |
| Noise power levels | −110 dBm | |
| and | Average and peak power of UAV U | 20 dBm and 26 dBm |
| and | Average and peak power of UAV J | 10 dBm and 16 dBm |
| Accuracy threshold |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Duo, B.; Wang, Z.; Lin, X.; Gao, C. Aerial Cooperative Jamming for Cellular-Enabled UAV Secure Communication Network: Joint Trajectory and Power Control Design. Sensors 2019, 19, 4440. https://doi.org/10.3390/s19204440
Sun H, Duo B, Wang Z, Lin X, Gao C. Aerial Cooperative Jamming for Cellular-Enabled UAV Secure Communication Network: Joint Trajectory and Power Control Design. Sensors. 2019; 19(20):4440. https://doi.org/10.3390/s19204440
Chicago/Turabian StyleSun, Hanming, Bin Duo, Zhengqiang Wang, Xiaochen Lin, and Changchun Gao. 2019. "Aerial Cooperative Jamming for Cellular-Enabled UAV Secure Communication Network: Joint Trajectory and Power Control Design" Sensors 19, no. 20: 4440. https://doi.org/10.3390/s19204440
APA StyleSun, H., Duo, B., Wang, Z., Lin, X., & Gao, C. (2019). Aerial Cooperative Jamming for Cellular-Enabled UAV Secure Communication Network: Joint Trajectory and Power Control Design. Sensors, 19(20), 4440. https://doi.org/10.3390/s19204440





