County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model
Abstract
1. Introduction
2. Materials and Methods
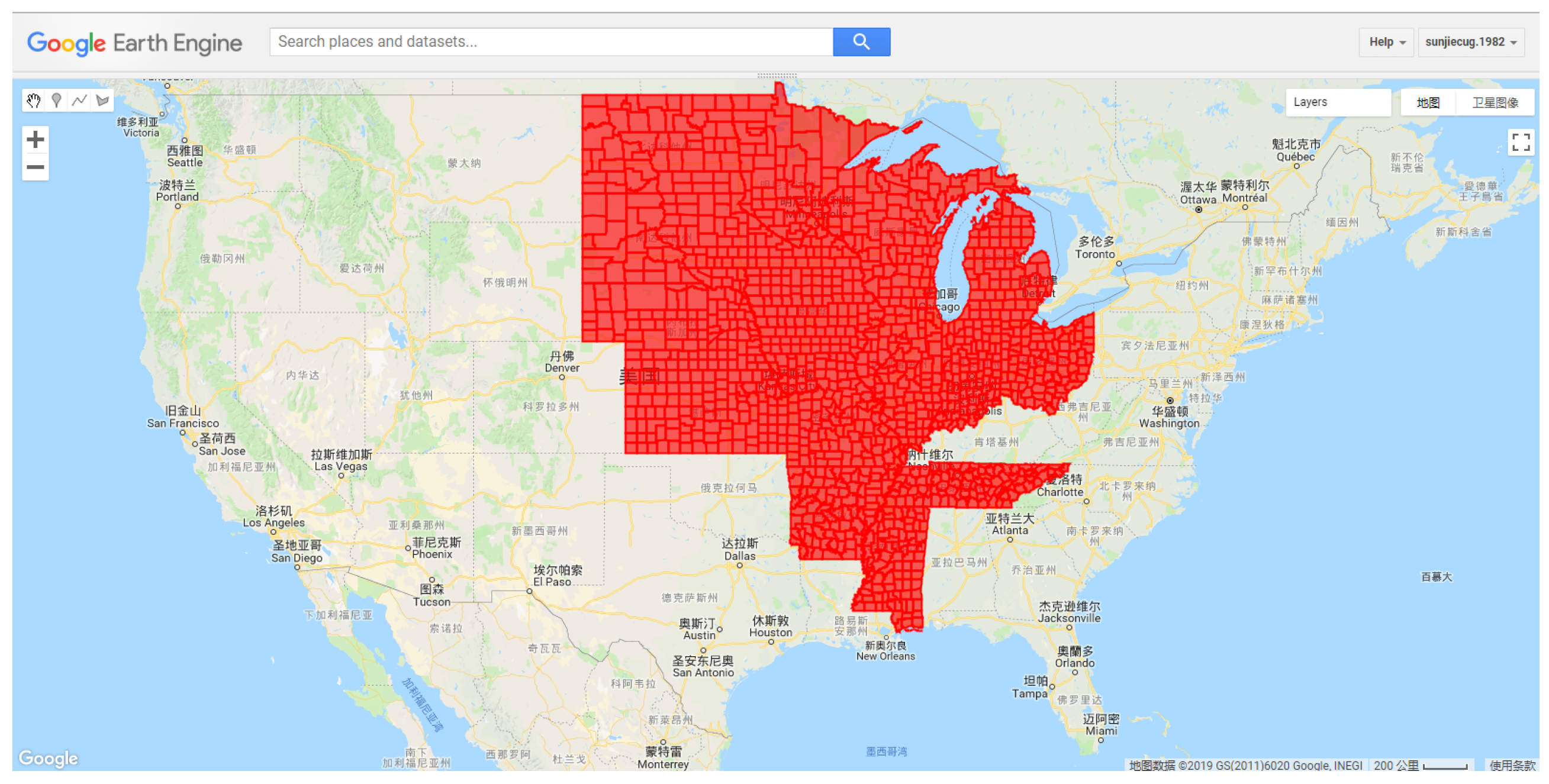
2.1. Study Area
2.2. Data
2.2.1. USDA Yield Data
2.2.2. USDA NASS Cropland Data Layers
2.2.3. U.S. County Boundaries
2.2.4. MODIS Surface Reflectance
2.2.5. MODIS Land Surface Temperature
2.2.6. Weather Data
2.3. Method
2.3.1. The Tensor Workflow in GEE
- As all the data in the GEE have been already preprocessed, ImageCollections can be made for each type of remote sensing data selected in the study according to the date range after cloud removal.
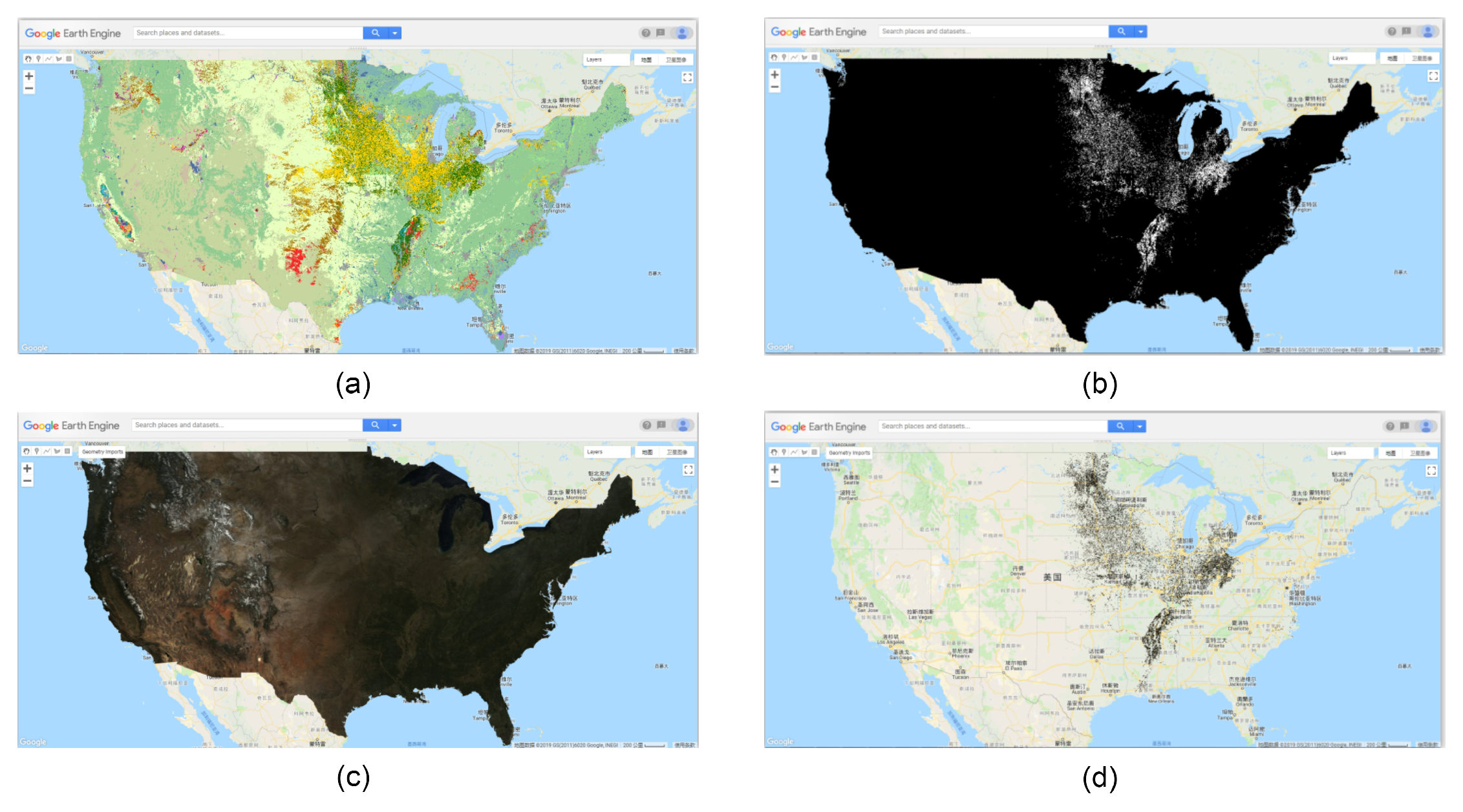
- Crop Data Layer was employed as a soybean mask for eliminating the interference of other ground objects in all ImageCollection; the process is shown in Figure A1 of Appendix A. Besides, the counties containing no soybean pixels will be excluded.
- MODIS SR data and MODIS LST data can be easily joined into a new ImageCollection by data system_time. Whereas, Daymet Daily weather data has a higher cadence. Therefore, they were aligned with MODIS ImageCollection after a mean values calculation at the 8-day interval in the GEE; after layer stacking, a (time steps × features) ImageCollection for each year was prepared.
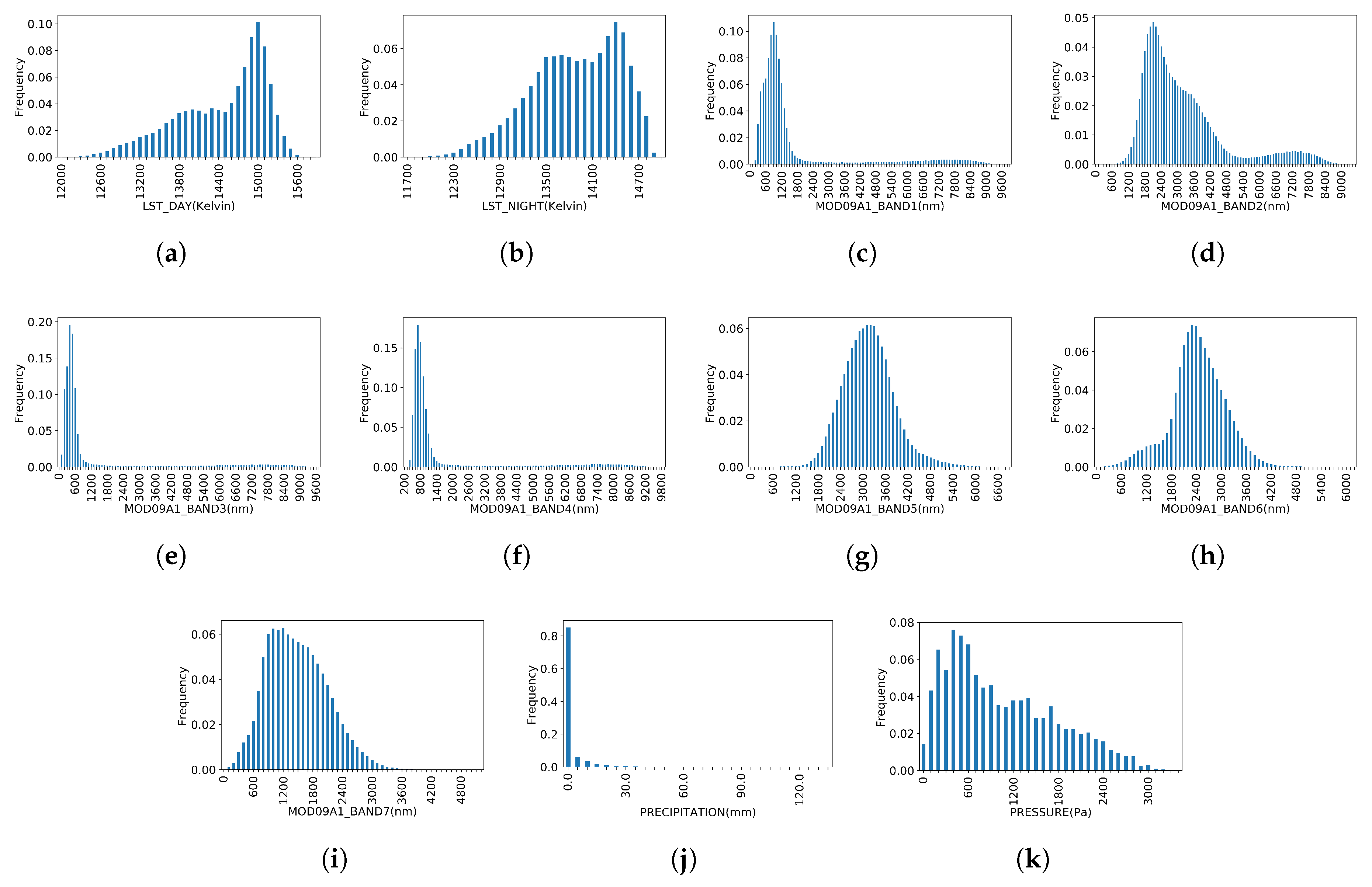
- Before the histogram transformation, actual limits should be given. However, the theoretical limits of each band are always too wide to provide a reasonable resolution for each bin. The real distribution of each band should be calculated over the study area, which can be used as a reference for final limits. The U.S. County Boundaries data was imported as a FeatureCollection in the GEE and, combined with ImageCollections, a global statistic of each featured band was calculated covering the whole study area, then the real limits of the distribution of the pixels can be determined. Considering the capacity of GEE, all the satellite data were collected from 2003-01-01 to 2012-12-31, approximately 10 years, including 460 MOD09A1 and MOD11A2 images respectively and 521 Daymet_V3 images in the study area. The distribution of different features of soybean is presented in Figure A2 of Appendix A.
- The GEE provides an efficient API which can transform the whole ImageCollection into a 32-bin normalized histogram by county-level. Assume t represents the number of time steps for each county during the season, in the study . Each county has an image , which has t time steps, and each time step has bands with seven MODIS surface reflectance bands, two surface temperature bands two weather bands. Each band can be transformed into a histogram with bins. Then, each will have a histogram with the shape of (time steps×bins×bands) as the tensor. Finally, each tensor will be assigned its corresponding county-level yield from USDA statistics; if no corresponding yield data was found in that year, the tensor will be abandoned.
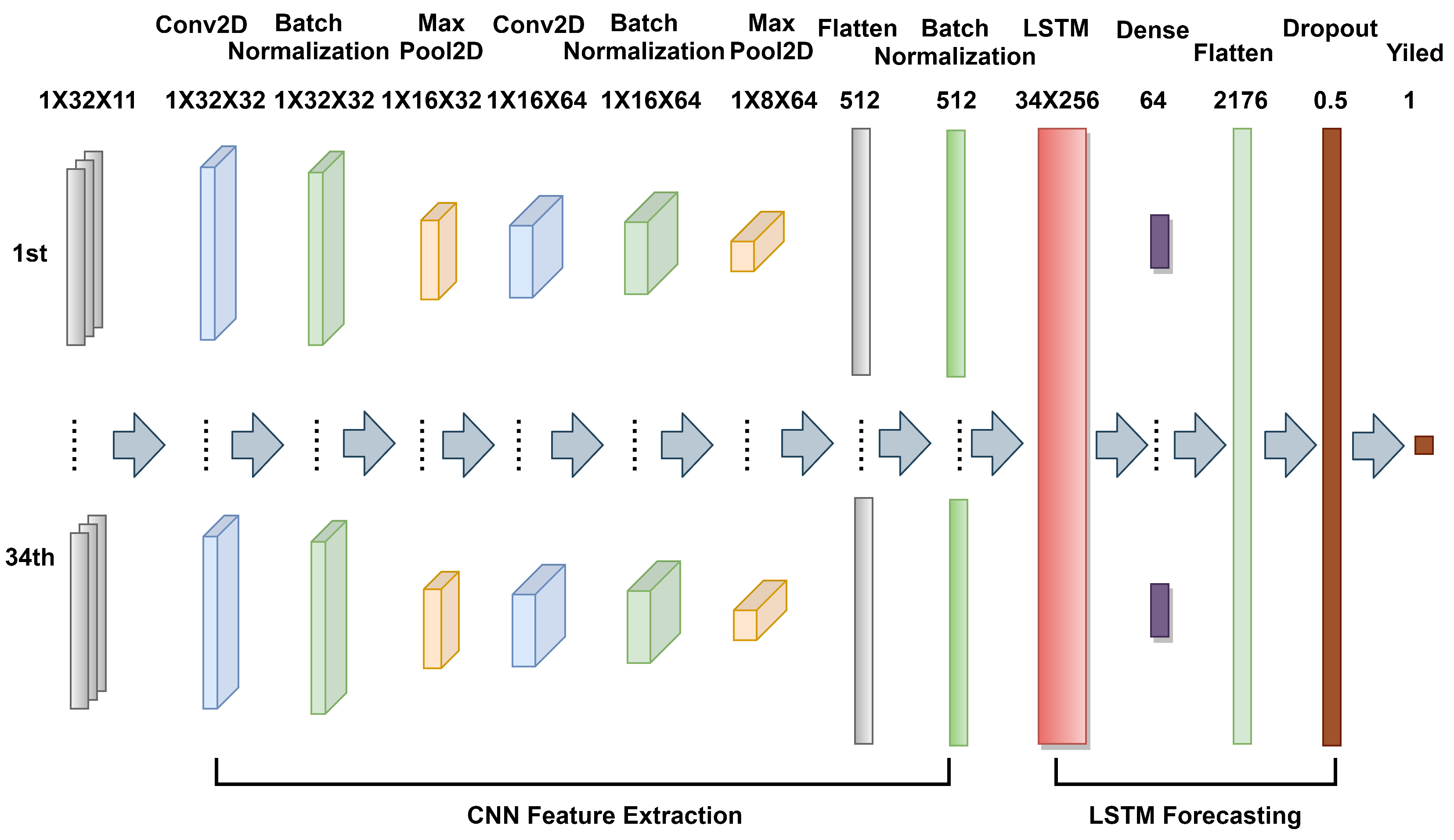
2.3.2. Model Architecture
2.3.3. End-of-Season and in-Season Yield Prediction
2.4. Evaluation
3. Results and Discussion
3.1. Tensor Generation
3.2. Model Evaluation
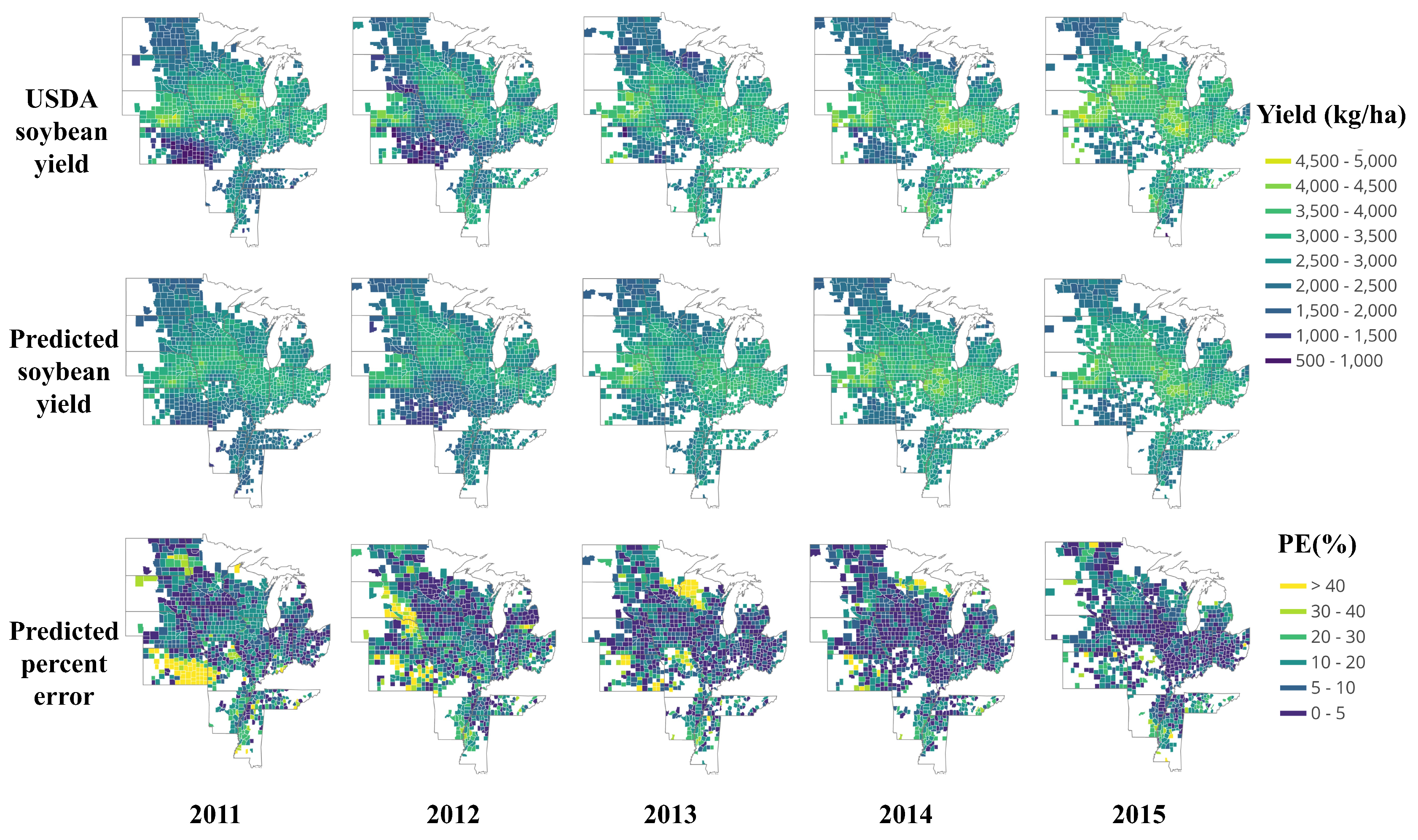
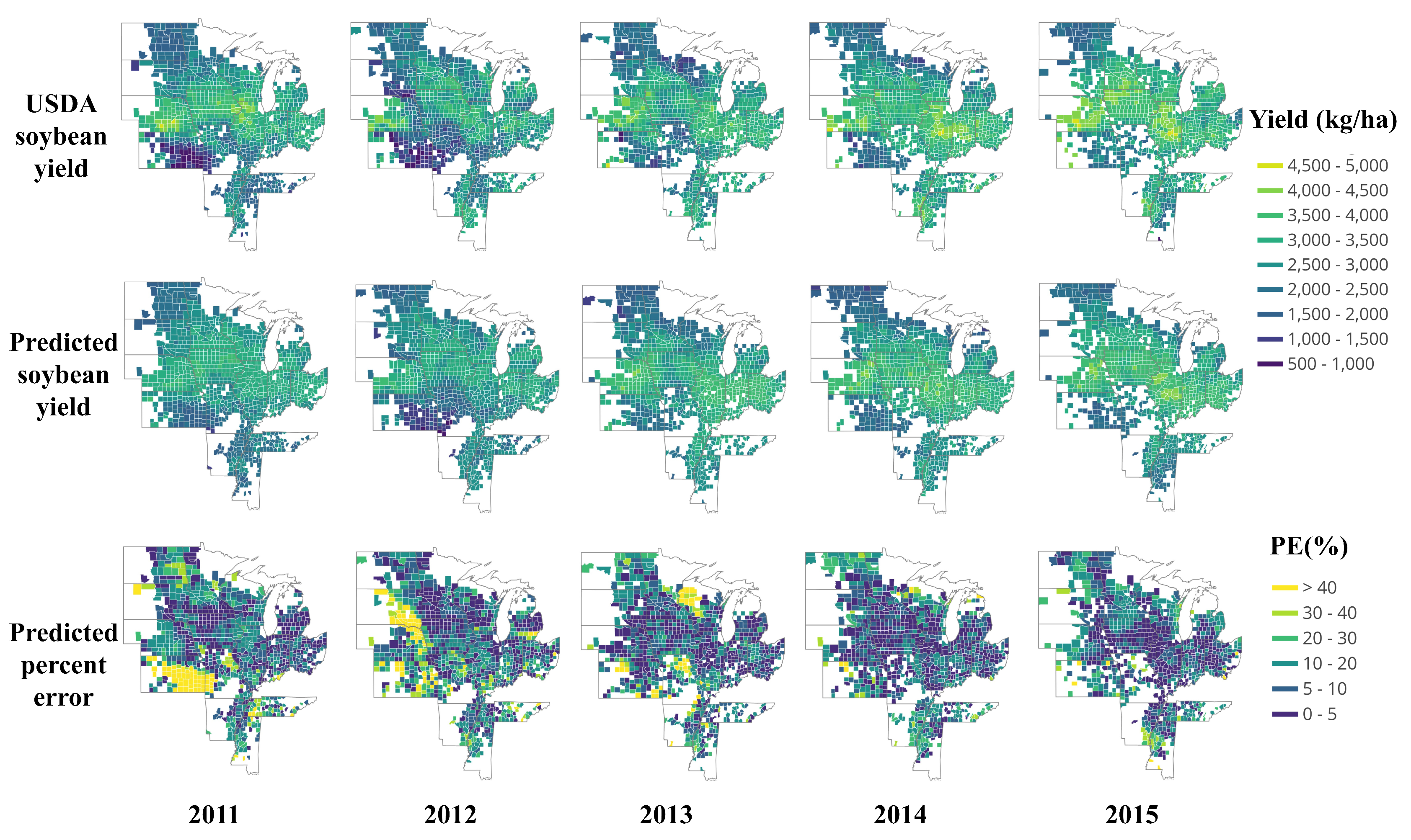
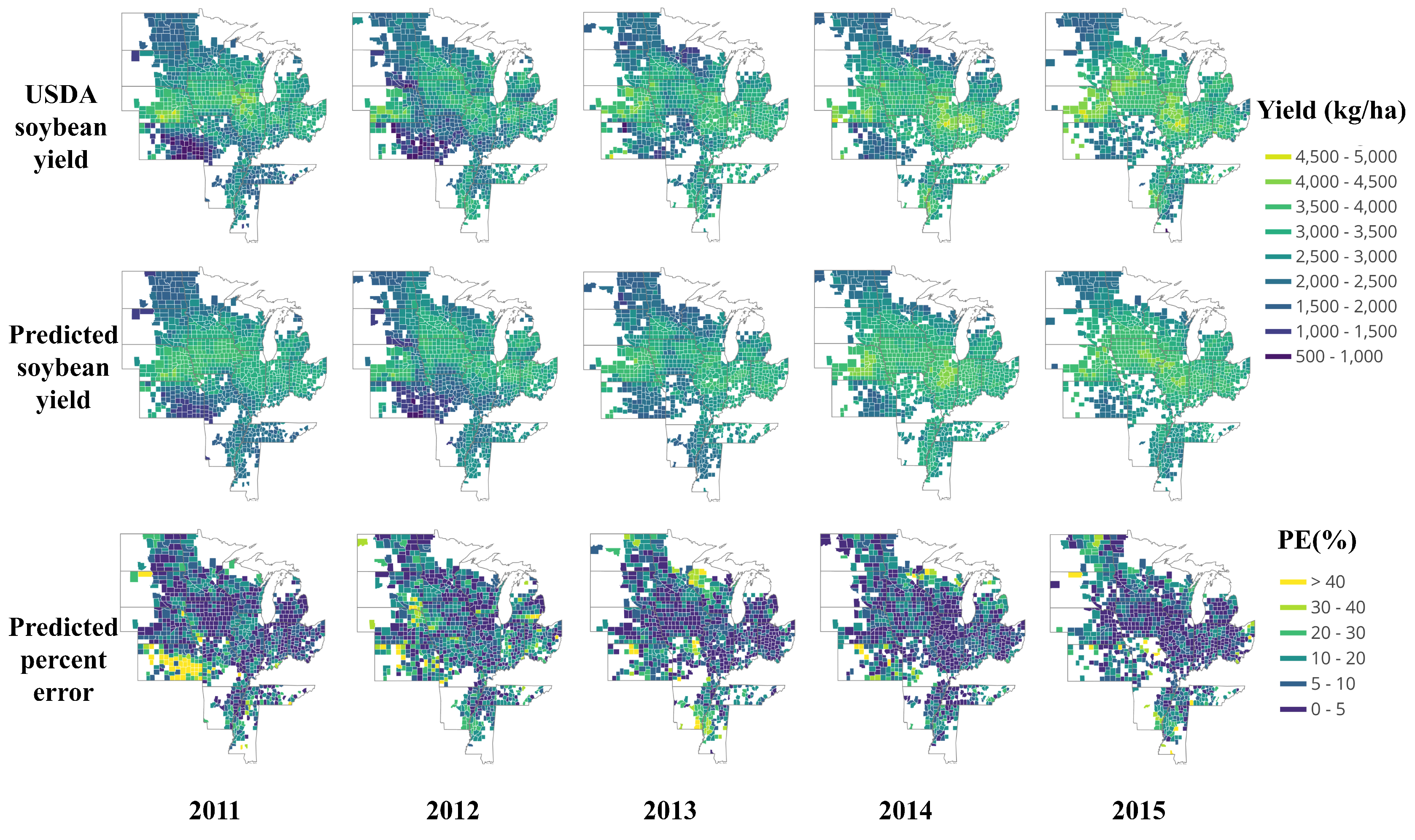
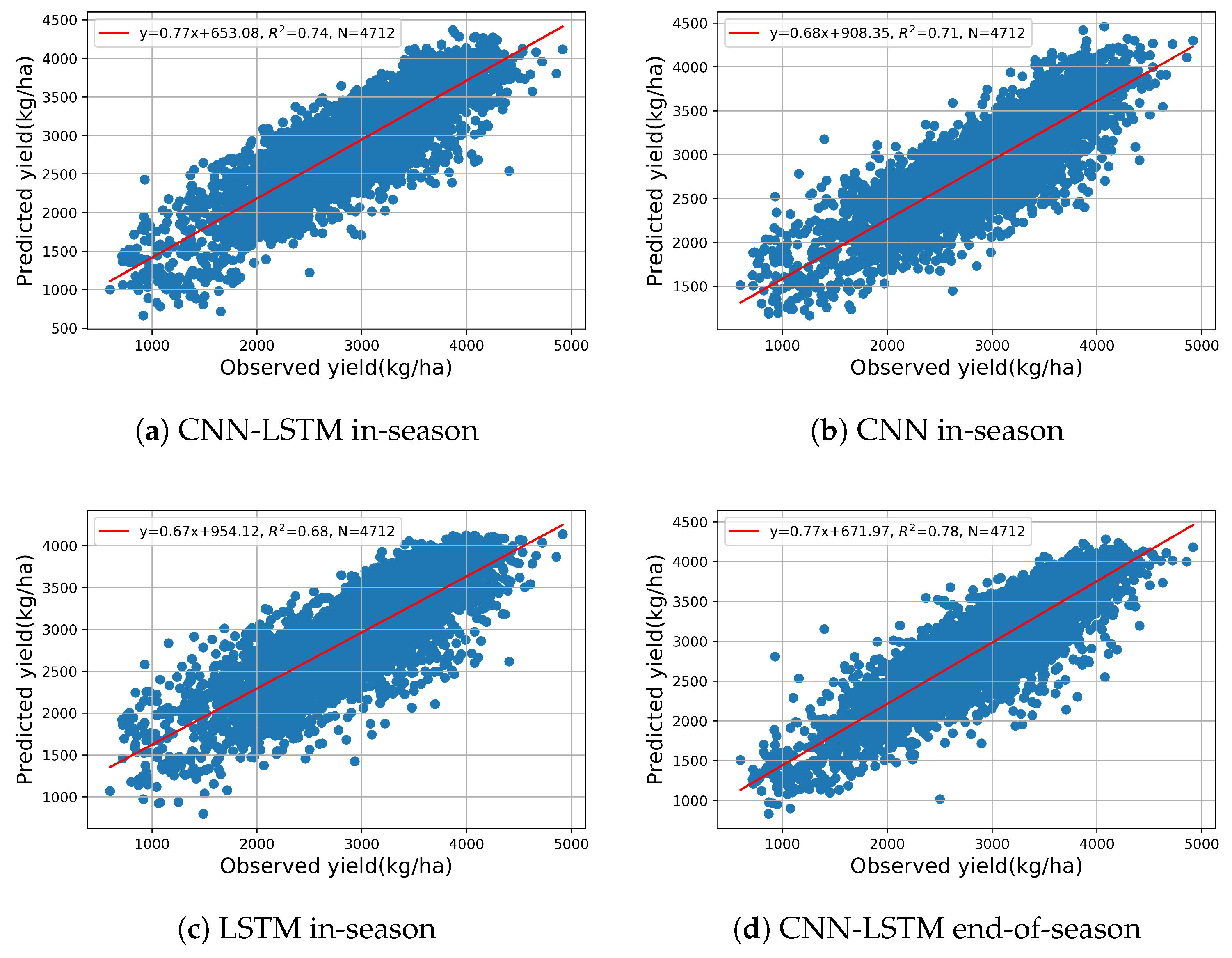
3.2.1. End-of-Season Yield Prediction
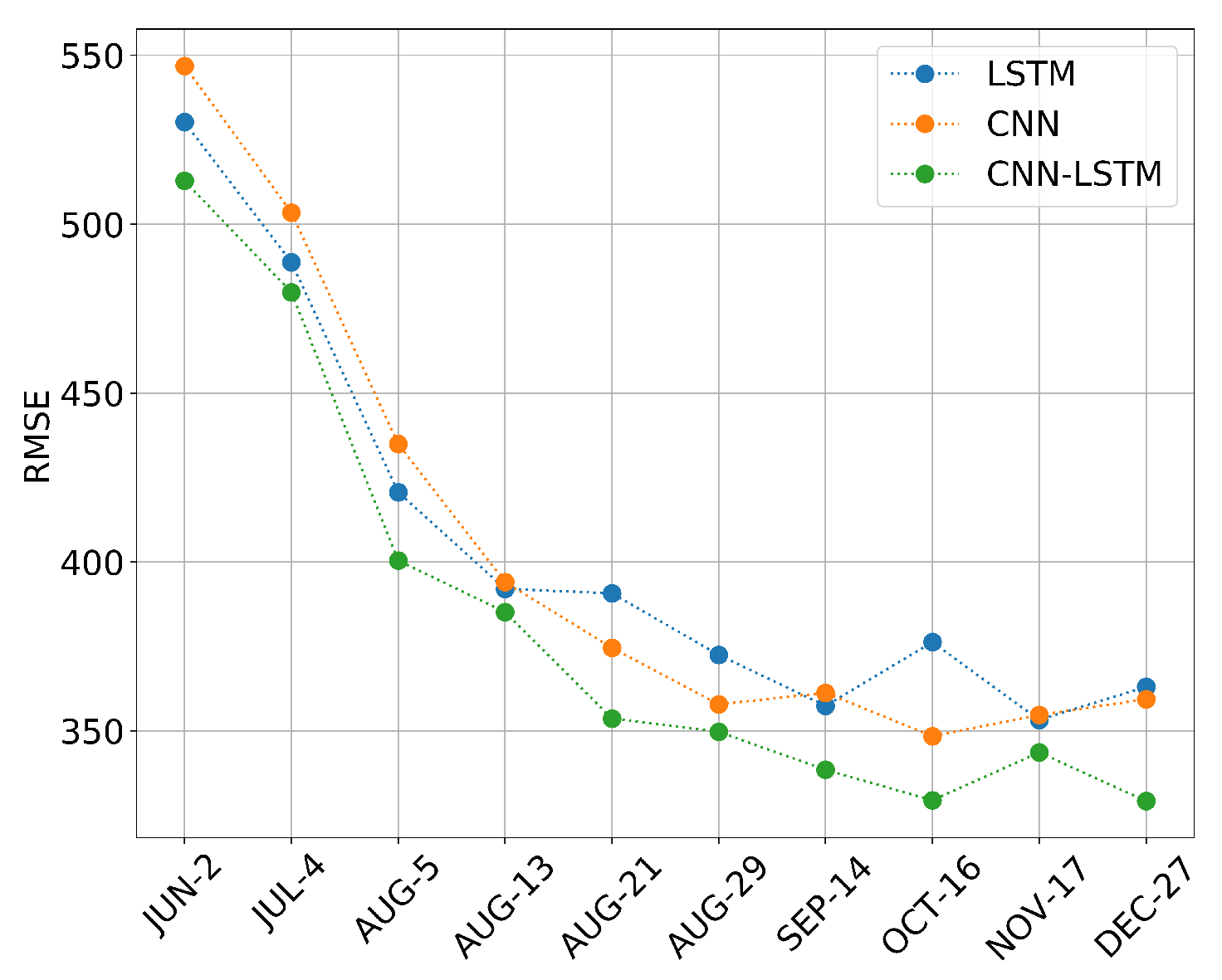
3.2.2. In-Season Yield Prediction
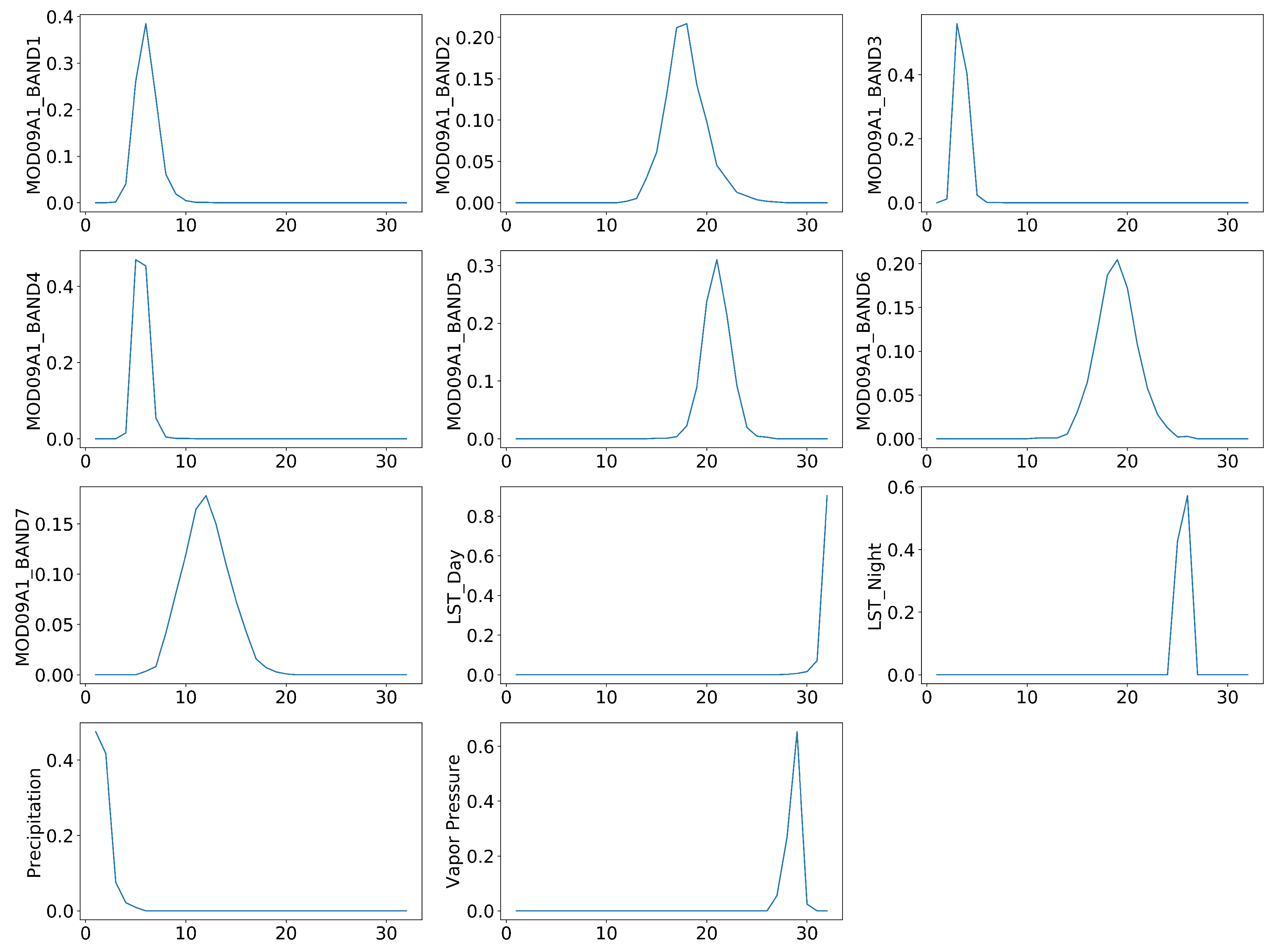
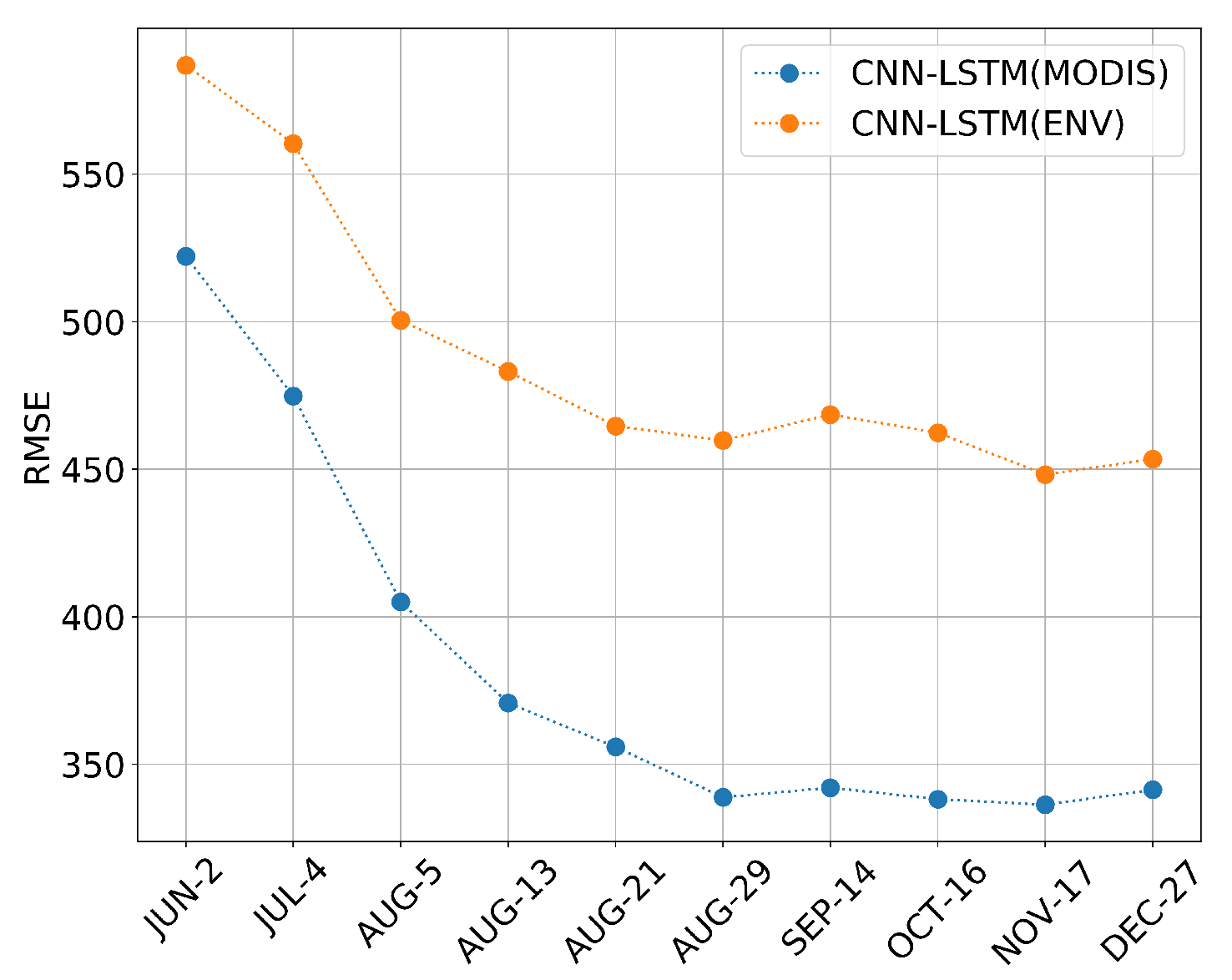
3.2.3. Feature Importance Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Liakos, K.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Shrestha, R.; Di, L.; Eugene, G.Y.; Kang, L.; Li, L.; Rahman, M.S.; Deng, M.; Yang, Z. Regression based corn yield assessment using MODIS based daily NDVI in Iowa state. In Proceedings of the 2016 Fifth International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Tianjin, China, 18–20 July 2016; pp. 1–5. [Google Scholar]
- Shrestha, R.; Di, L.; Yu, E.G.; Kang, L.; Shao, Y.Z.; Bai, Y.Q. Regression model to estimate flood impact on corn yield using MODIS NDVI and USDA cropland data layer. J. Integr. Agric. 2017, 16, 398–407. [Google Scholar] [CrossRef]
- Yu, B.; Shang, S. Multi-Year Mapping of Major Crop Yields in an Irrigation District from High Spatial and Temporal Resolution Vegetation Index. Sensors 2018, 18, 3787. [Google Scholar] [CrossRef] [PubMed]
- Lofton, J.; Tubana, B.S.; Kanke, Y.; Teboh, J.; Viator, H.; Dalen, M. Estimating Sugarcane Yield Potential Using an In-Season Determination of Normalized Difference Vegetative Index. Sensors 2012, 12, 7529–7547. [Google Scholar] [CrossRef] [PubMed]
- Duchemin, B.; Maisongrande, P.; Boulet, G.; Benhadj, I. A simple algorithm for yield estimates: Evaluation for semi-arid irrigated winter wheat monitored with green leaf area index. Environ. Model. Softw. 2008, 23, 876–892. [Google Scholar] [CrossRef]
- Ghaemi, A.; Moazed, H.; Rafie Rafiee, M.; Broomand Nasab, S. Determining CWSI to estimate eggplant evapotranspiration and yield under greenhouse and outdoor conditions. Iran Agric. Res. 2016, 34, 49–60. [Google Scholar]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Panda, S.S.; Ames, D.P.; Panigrahi, S. Application of Vegetation Indices for Agricultural Crop Yield Prediction Using Neural Network Techniques. Remote Sens. 2010, 2, 673–696. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017. [Google Scholar] [CrossRef]
- Mathieu, J.A.; Aires, F. Using Neural Network Classifier Approach for Statistically Forecasting Extreme Corn Yield Losses in Eastern United States. Earth Space Sci. 2018, 5, 622–639. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Crane-Droesch, A. Machine learning methods for crop yield prediction and climate change impact assessment in agriculture. Environ. Res. Lett. 2018, 13. [Google Scholar] [CrossRef]
- Pourmohammadali, B.; Hosseinifard, S.J.; Salehi, M.H.; Shirani, H.; Boroujeni, I.E. Effects of soil properties, water quality and management practices on pistachio yield in Rafsanjan region, southeast of Iran. Agric. Water Manag. 2019, 213, 894–902. [Google Scholar] [CrossRef]
- Bocca, F.F.; Rodrigues, L.H.A. The effect of tuning, feature engineering, and feature selection in data mining applied to rainfed sugarcane yield modelling. Comput. Electron. Agric. 2016, 128, 67–76. [Google Scholar] [CrossRef]
- Kim, N.; Lee, Y. Machine learning approaches to corn yield estimation using satellite images and climate data: A case of Iowa State. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 34, 383–390. [Google Scholar] [CrossRef]
- Niedbala, G. Simple model based on artificial neural network for early prediction and simulation winter rapeseed yield. J. Integr. Agric. 2019, 18, 54–61. [Google Scholar] [CrossRef]
- Wenzhi, Z.; Chi, X.; Zhao, G.; Jingwei, W.; Jiesheng, H. Estimation of Sunflower Seed Yield Using Partial Least Squares Regression and Artificial Neural Network Models. Pedosphere 2018, 28, 764–774. [Google Scholar] [CrossRef]
- Abrougui, K.; Gabsi, K.; Mercatoris, B.; Khemis, C.; Amami, R.; Chehaibi, S. Prediction of organic potato yield using tillage systems and soil properties by artificial neural network (ANN) and multiple linear regressions (MLR). Soil Tillage Res. 2019, 190, 202–208. [Google Scholar] [CrossRef]
- Ma, J.W.; Nguyen, C.H.; Lee, K.; Heo, J. Regional-scale rice-yield estimation using stacked auto-encoder with climatic and MODIS data: a case study of South Korea. Int. J. Remote Sens. 2019, 40, 51–71. [Google Scholar] [CrossRef]
- Kuwata, K.; Shibasaki, R. Estimating crop yields with deep learning and remotely sensed data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 858–861. [Google Scholar]
- Nevavuori, P.; Narra, N.; Lipping, T. Crop yield prediction with deep convolutional neural networks. Comput. Electron. Agric. 2019, 163. [Google Scholar] [CrossRef]
- Yang, Q.; Shi, L.; Han, J.; Zha, Y.; Zhu, P. Deep convolutional neural networks for rice grain yield estimation at the ripening stage using UAV-based remotely sensed images. Field Crop. Res. 2019, 235, 142–153. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, W.S.; Gan, H.; Peres, N.; Fraisse, C.; Zhang, Y.; He, Y. Strawberry Yield Prediction Based on a Deep Neural Network Using High-Resolution Aerial Orthoimages. Remote Sens. 2019, 11, 1584. [Google Scholar] [CrossRef]
- Russello, H. Convolutional Neural Networks for Crop Yield Prediction Using Satellite Images. Master’s Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2018. [Google Scholar]
- Jiang, Z.; Liu, C.; Hendricks, N.P.; Ganapathysubramanian, B.; Hayes, D.J.; Sarkar, S. Predicting county level corn yields using deep long short term memory models. arXiv 2018, arXiv:1805.12044. [Google Scholar]
- Kulkarni, S.; Mandal, S.N.; Sharma, G.S.; Mundada, M.R.; Meeradevi. Predictive Analysis to Improve Crop Yield using a Neural Network Model. In Proceedings of the 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; pp. 74–79. [Google Scholar] [CrossRef]
- Haider, S.A.; Naqvi, S.R.; Akram, T.; Umar, G.A.; Shahzad, A.; Sial, M.R.; Khaliq, S.; Kamran, M. LSTM Neural Network Based Forecasting Model for Wheat Production in Pakistan. Agronomy 2019, 9, 72. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. In Proceedings of the thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4559–4566. [Google Scholar]
- Alhnaity, B.; Pearson, S.; Leontidis, G.; Kollias, S. Using Deep Learning to Predict Plant Growth and Yield in Greenhouse Environments. arXiv 2019, arXiv:1907.00624. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv 2015, arXiv:1506.04214. [Google Scholar]
- Hird, J.N.; DeLancey, E.R.; McDermid, G.J.; Kariyeva, J. Google Earth Engine, Open-Access Satellite Data, and Machine Learning in Support of Large-Area Probabilistic Wetland Mapping. Remote Sens. 2017, 9, 1315. [Google Scholar] [CrossRef]
- Clinton, N.; Stuhlmacher, M.; Miles, A.; Aragon, N.U.; Wagner, M.; Georgescu, M.; Herwig, C.; Gong, P. A Global Geospatial Ecosystem Services Estimate of Urban Agriculture. Earths Future 2018, 6, 40–60. [Google Scholar] [CrossRef]
- Agapiou, A. Remote sensing heritage in a petabyte-scale: satellite data and heritage Earth Engine (c) applications. Int. J. Digit. Earth 2017, 10, 85–102. [Google Scholar] [CrossRef]
- Shelestov, A.; Lavreniuk, M.; Kussul, N.; Novikov, A.; Skakun, S. Exploring Google Earth Engine Platform for Big Data Processing: Classification of Multi-Temporal Satellite Imagery for Crop Mapping. Front. Earth Sci. 2017, 5, 1–10. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
- Azzari, G.; Jain, M.; Lobell, D.B. Towards fine resolution global maps of crop yields: Testing multiple methods and satellites in three countries. Remote Sens. Environ. 2017, 202, 129–141. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep Transfer Learning for Crop Yield Prediction with Remote Sensing Data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, Menlo Park and San Jose, CA, USA, 20–22 June 2018; pp. 50:1–50:5. [Google Scholar] [CrossRef]
- Skakun, S.; Vermote, E.; Roger, J.C.; Franch, B. Combined use of Landsat-8 and Sentinel-2A images for winter crop mapping and winter wheat yield assessment at regional scale. AIMS Geosci. 2017, 3, 163. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Kimball, J.S.; Maneta, M.P.; Maxwell, B.D.; Moreno, A.; Beguería, S.; Wu, X. Regional Crop Gross Primary Productivity and Yield Estimation Using Fused Landsat-MODIS Data. Remote Sens. 2018, 10, 372. [Google Scholar] [CrossRef]
- Goron, T.L.; Nederend, J.; Stewart, G.; Deen, B.; Raizada, M.N. Mid-Season Leaf Glutamine Predicts End-Season Maize Grain Yield and Nitrogen Content in Response to Nitrogen Fertilization under Field Conditions. Agronomy 2017, 7, 41. [Google Scholar] [CrossRef]
- Barmeier, G.; Hofer, K.; Schmidhalter, U. Mid-season prediction of grain yield and protein content of spring barley cultivars using high-throughput spectral sensing. Eur. J. Agron. 2017, 90, 108–116. [Google Scholar] [CrossRef]
- Peralta, N.R.; Assefa, Y.; Du, J.; Barden, C.J.; Ciampitti, I.A. Mid-Season High-Resolution Satellite Imagery for Forecasting Site-Specific Corn Yield. Remote Sens. 2016, 8, 848. [Google Scholar] [CrossRef]
- Leroux, L.; Castets, M.; Baron, C.; Escorihuela, M.J.; Begue, A.; Lo Seen, D. Maize yield estimation in West Africa from crop process-induced combinations of multi-domain remote sensing indices. Eur. J. Agron. 2019, 108, 11–26. [Google Scholar] [CrossRef]
- Ban, H.Y.; Kim, K.S.; Park, N.W.; Lee, B.W. Using MODIS Data to Predict Regional Corn Yields. Remote Sens. 2017, 9, 16. [Google Scholar] [CrossRef]
- USDA. Usda National Agricultural Statistics Service. Available online: https://www.nass.usda.gov/Quick_Stats/index.php/ (accessed on 19 September 2019).
- USDA. The USDA Economics, Statistics and Market Information System. Available online: https://usda.library.cornell.edu/?locale=en (accessed on 19 September 2019).
- USDA-NASS. USDA National Agricultural Statistics Service Cropland Data Layer. Available online: https://nassgeodata.gmu.edu/CropScape (accessed on 19 September 2019).
- Vermote, E. MOD09A1 MODIS/Terra Surface Reflectance 8-Day L3 Global 500m SIN Grid V006. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra Land Surface Temperature/Emissivity 8-Day L3 Global 1km SIN Grid V006. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- Thornton, P.; Thornton, M.; Mayer, B.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 3. ORNL DAAC 2016. [Google Scholar] [CrossRef]
- GEE. Google Earth Engine. Available online: https://developers.google.com/earth-engine (accessed on 19 September 2019).
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Khaki, S.; Wang, L. Crop Yield Prediction Using Deep Neural Networks. arXiv 2019, arXiv:1902.02860. [Google Scholar] [CrossRef] [PubMed]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Rippey, B.R. The U.S. drought of 2012. Weather Clim. Extrem. 2015, 10, 57–64. [Google Scholar] [CrossRef]
- NDMC. National Drought Mitigation Center. Available online: https://droughtmonitor.unl.edu/ (accessed on 19 September 2019).
- Cogato, A.; Meggio, F.; Migliorati, M.; Marinello, F. Extreme Weather Events in Agriculture: A Systematic Review. Sustainability 2019, 11, 2547. [Google Scholar] [CrossRef]
- Saeed, U.; Dempewolf, J.; Becker-Reshef, I.; Khan, A.; Ahmad, A.; Wajid, S. Forecasting wheat yield from weather data and MODIS NDVI using Random Forests for Punjab province, Pakistan. Int. J. Remote Sens. 2017, 38, 4831–4854. [Google Scholar] [CrossRef]


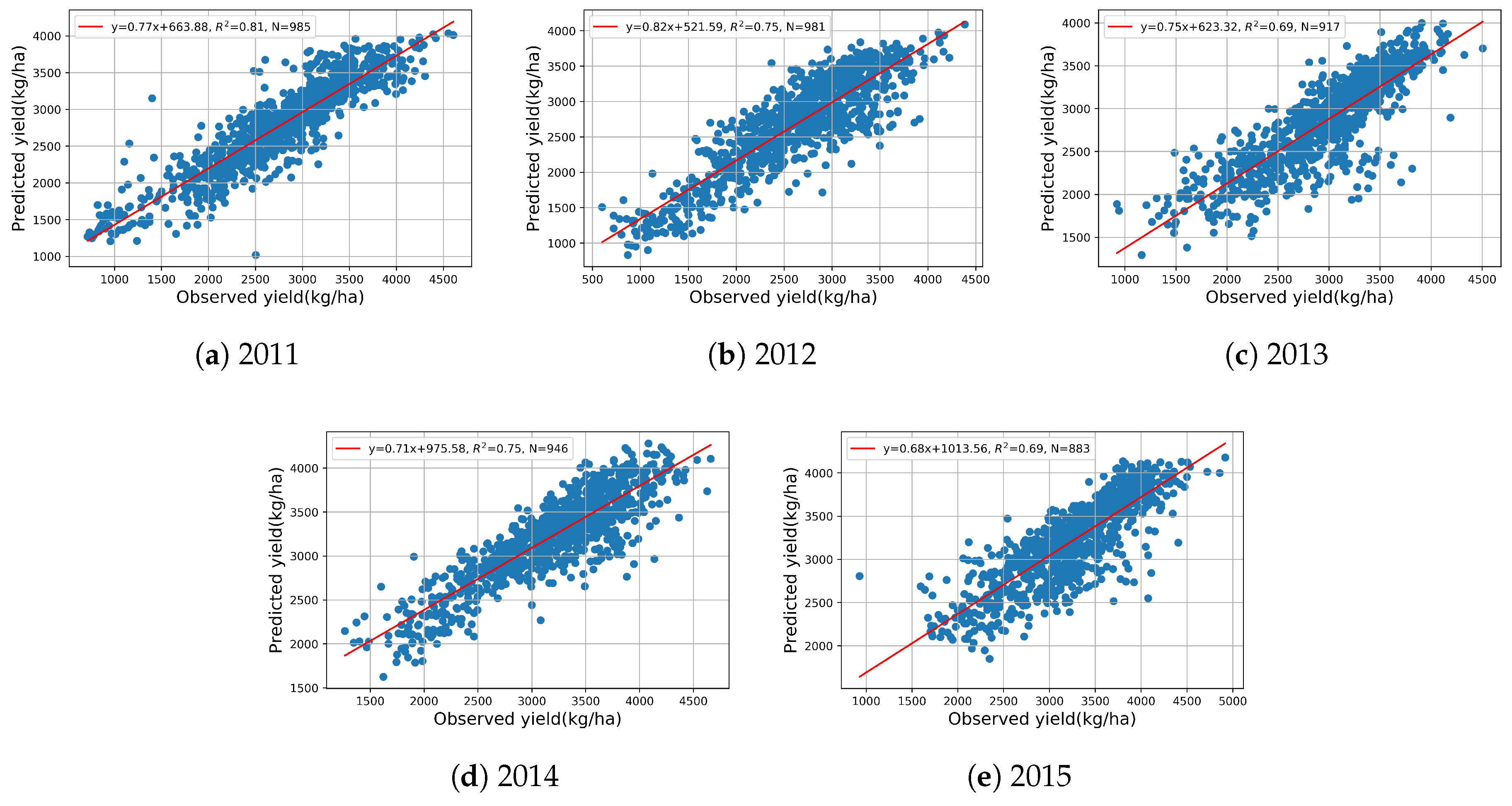
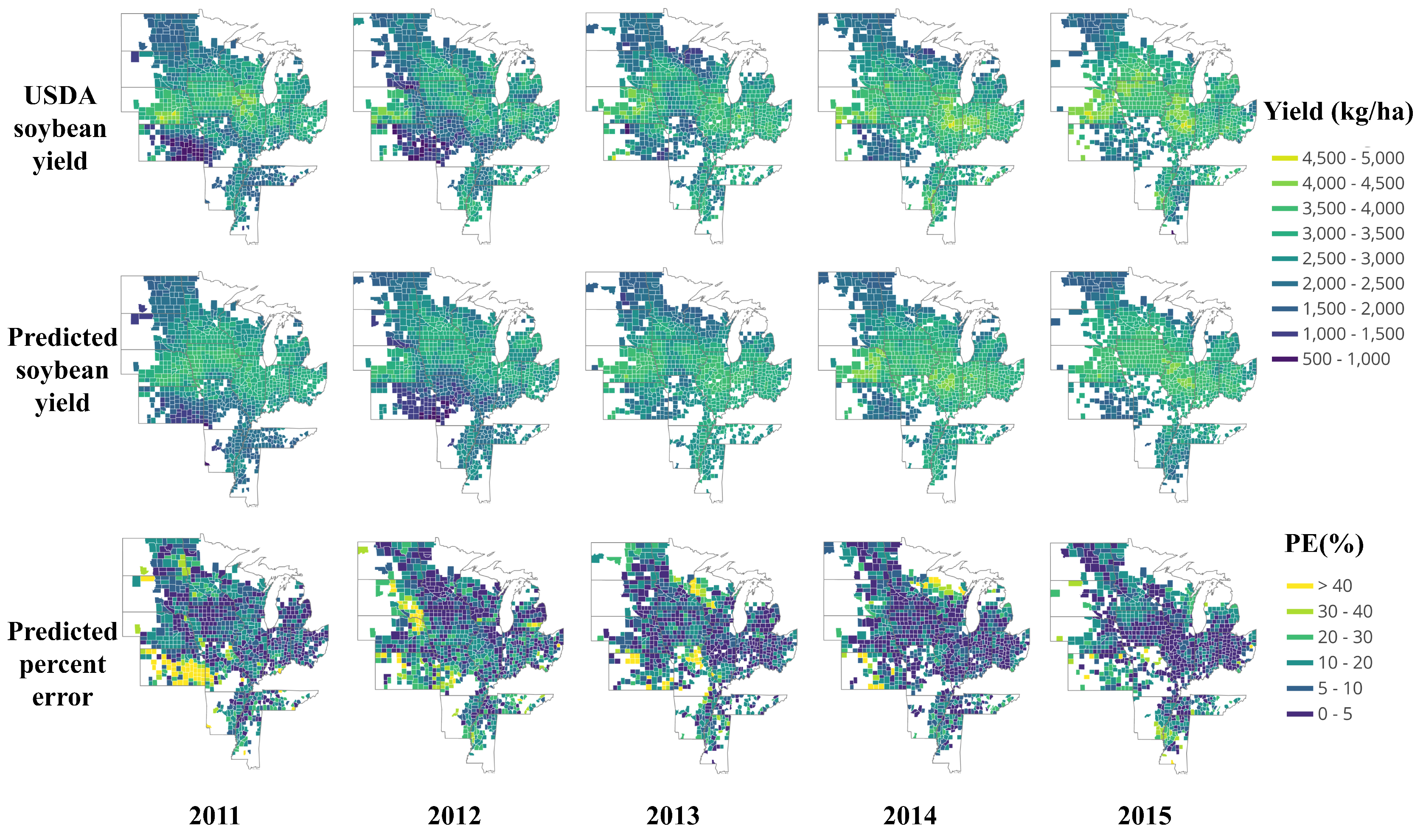
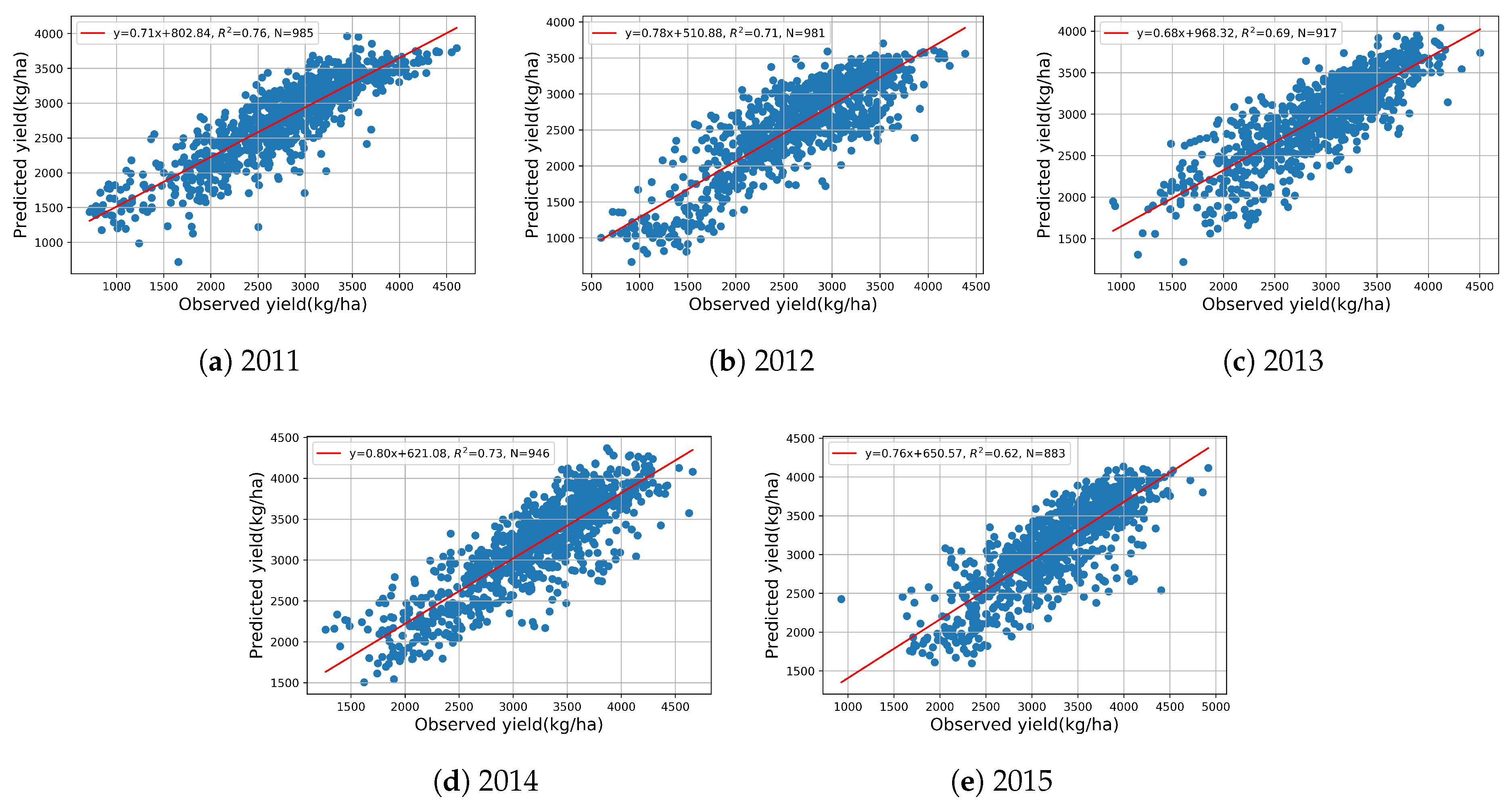
| Feature | Original Min | Original Max | New Min | New Max |
|---|---|---|---|---|
| MOD09A1 | −100 | 16,000 | 1 | 5000 |
| MOD11A2 | 7500 | 65,535 | 12,400 | 15,600 |
| PRECIPITATION | 0 | 200 | 0 | 35 |
| PRESSURE | 0 | 10,000 | 0 | 3200 |
| Year | CNN | LSTM | CNN-LSTM |
|---|---|---|---|
| 2011 | 337.60 | 372.57 | 312.72 |
| 2012 | 345.67 | 384.67 | 349.03 |
| 2013 | 357.10 | 359.12 | 338.27 |
| 2014 | 351.72 | 357.10 | 307.34 |
| 2015 | 404.85 | 341.63 | 338.94 |
| Avg | 359.12 | 363.15 | 329.53 |
| Year | JUN-2 | JUL-4 | AUG-5 | AUG-13 | AUG-21 | AUG-29 | SEP-14 | OCT-16 | NOV-17 | DEC-27 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 558.85 | 526.57 | 395.44 | 434.44 | 408.89 | 355.76 | 347.01 | 346.34 | 334.91 | 337.60 |
| 2012 | 599.21 | 560.20 | 471.43 | 371.90 | 386.69 | 370.55 | 350.38 | 353.74 | 363.15 | 345.67 |
| 2013 | 507.74 | 455.29 | 453.94 | 397.45 | 355.08 | 351.72 | 342.31 | 321.46 | 341.63 | 357.10 |
| 2014 | 504.38 | 480.17 | 412.92 | 381.98 | 349.03 | 346.34 | 343.65 | 319.44 | 323.48 | 351.72 |
| 2015 | 563.56 | 494.97 | 440.49 | 384.00 | 373.24 | 363.83 | 423.68 | 400.82 | 410.90 | 404.85 |
| Year | JUN-2 | JUL-4 | AUG-5 | AUG-13 | AUG-21 | AUG-29 | SEP-14 | OCT-16 | NOV-17 | DEC-27 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 538.68 | 497.66 | 405.52 | 411.58 | 412.92 | 393.42 | 379.97 | 391.40 | 375.93 | 372.57 |
| 2012 | 618.04 | 594.50 | 509.09 | 442.51 | 418.30 | 412.92 | 374.59 | 415.61 | 375.93 | 384.67 |
| 2013 | 524.56 | 429.06 | 390.73 | 386.02 | 367.19 | 340.29 | 332.89 | 373.91 | 338.94 | 359.12 |
| 2014 | 468.74 | 430.41 | 365.17 | 361.81 | 357.77 | 322.80 | 357.77 | 322.13 | 340.29 | 357.10 |
| 2015 | 501.02 | 492.28 | 433.10 | 357.77 | 396.78 | 393.42 | 341.63 | 377.95 | 334.24 | 341.63 |
| Year | JUN-2 | JUL-4 | AUG-5 | AUG-13 | AUG-21 | AUG-29 | SEP-14 | OCT-16 | NOV-17 | DEC-27 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 511.11 | 484.21 | 388.71 | 396.11 | 351.72 | 340.96 | 342.31 | 348.36 | 335.58 | 312.72 |
| 2012 | 597.86 | 574.99 | 449.91 | 435.11 | 377.28 | 359.79 | 343.65 | 353.74 | 347.01 | 349.03 |
| 2013 | 496.98 | 445.87 | 385.35 | 358.45 | 337.60 | 347.01 | 320.79 | 305.32 | 316.75 | 338.27 |
| 2014 | 464.03 | 435.11 | 377.95 | 343.65 | 321.46 | 311.37 | 305.32 | 298.59 | 305.99 | 307.34 |
| 2015 | 494.29 | 459.32 | 400.14 | 393.42 | 379.97 | 389.38 | 379.97 | 340.96 | 412.92 | 338.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Di, L.; Sun, Z.; Shen, Y.; Lai, Z. County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors 2019, 19, 4363. https://doi.org/10.3390/s19204363
Sun J, Di L, Sun Z, Shen Y, Lai Z. County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors. 2019; 19(20):4363. https://doi.org/10.3390/s19204363
Chicago/Turabian StyleSun, Jie, Liping Di, Ziheng Sun, Yonglin Shen, and Zulong Lai. 2019. "County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model" Sensors 19, no. 20: 4363. https://doi.org/10.3390/s19204363
APA StyleSun, J., Di, L., Sun, Z., Shen, Y., & Lai, Z. (2019). County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors, 19(20), 4363. https://doi.org/10.3390/s19204363




