Quantitative Analysis of Soil Total Nitrogen Using Hyperspectral Imaging Technology with Extreme Learning Machine
Abstract
1. Introduction
2. Materials and Methods
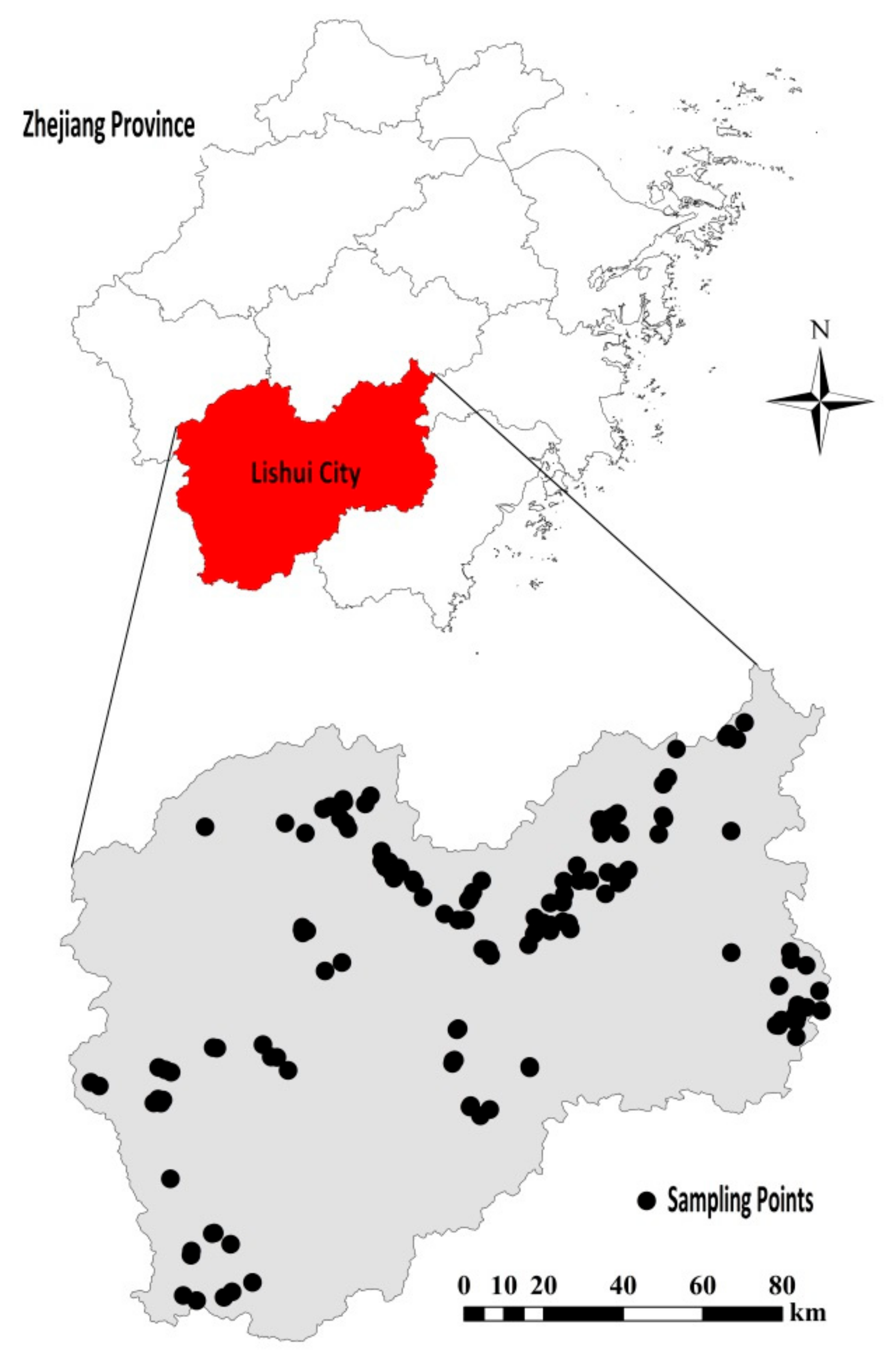
2.1. Soil Samples
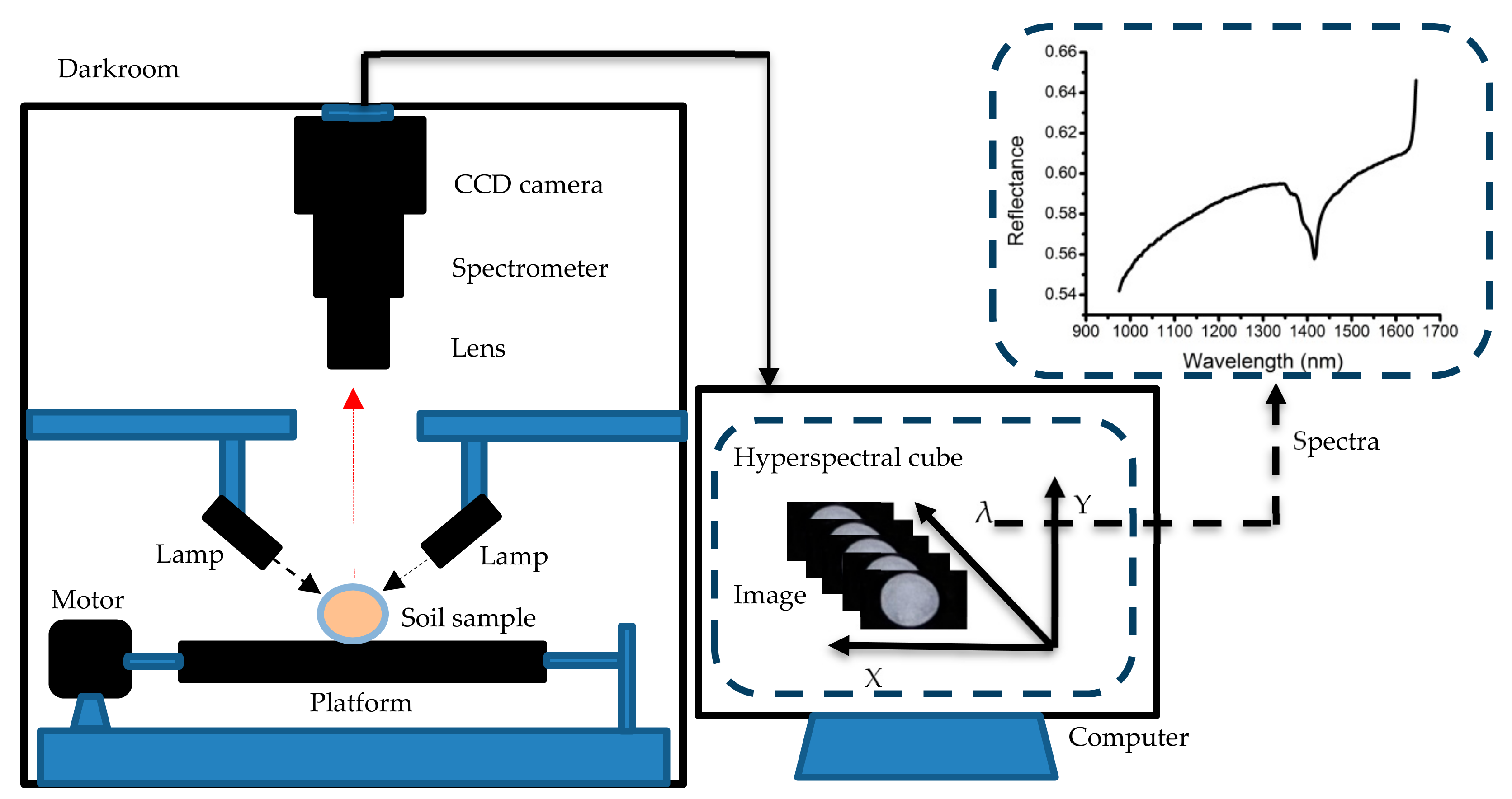
2.2. Hyperspectral Imaging System
2.3. Image Preprocessing
2.4. Multivariate Data Analysis
2.4.1. Modeling Methods
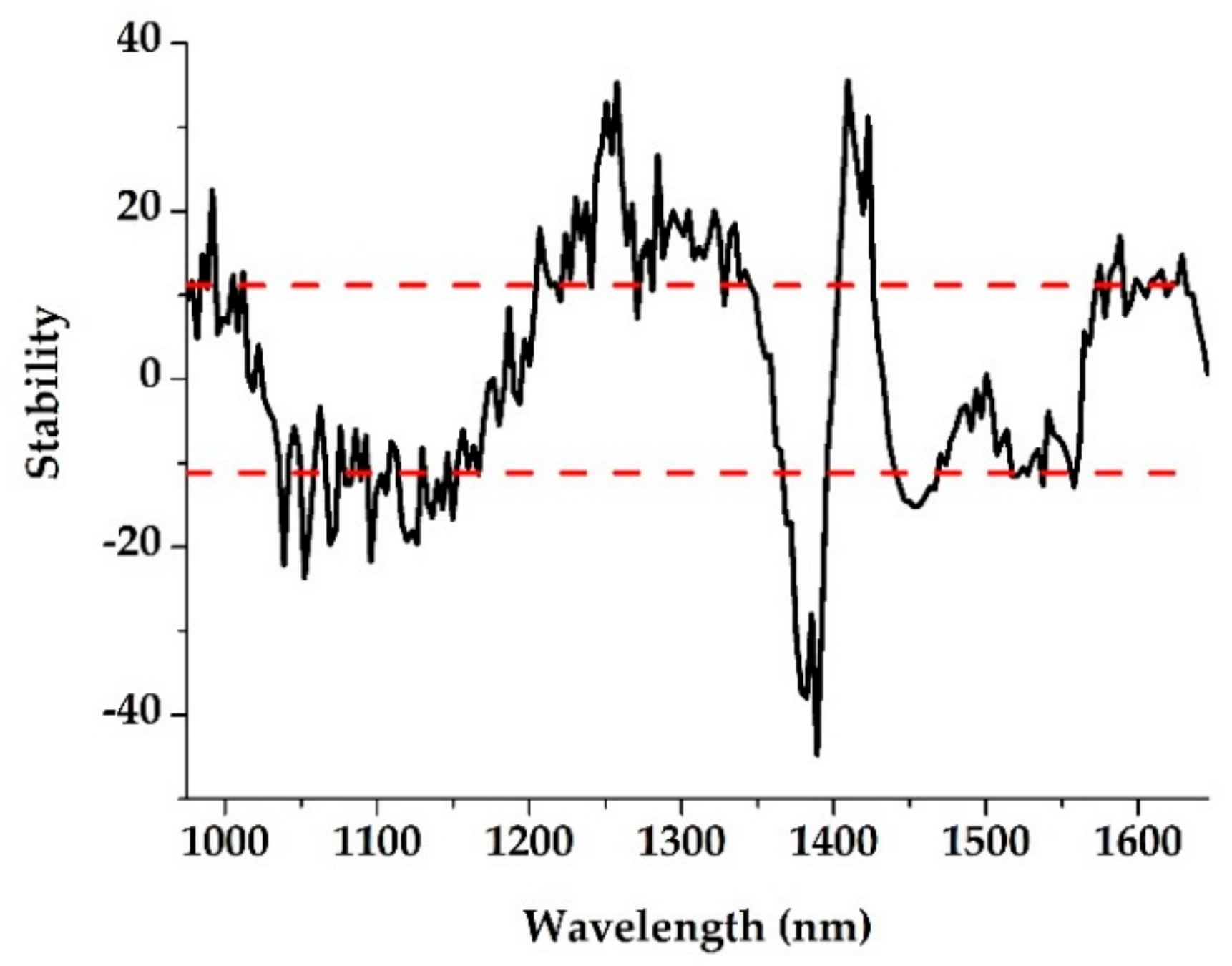
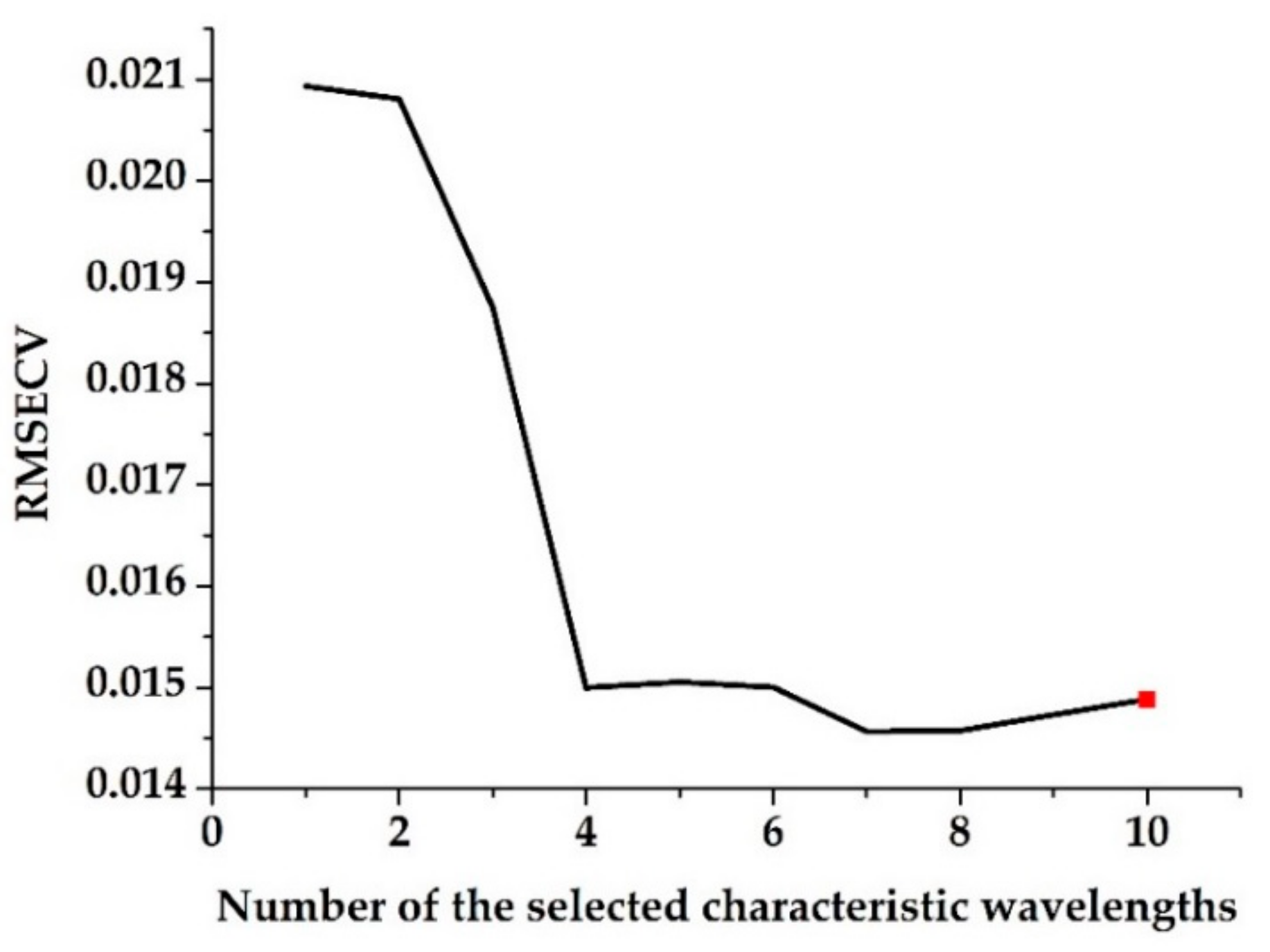
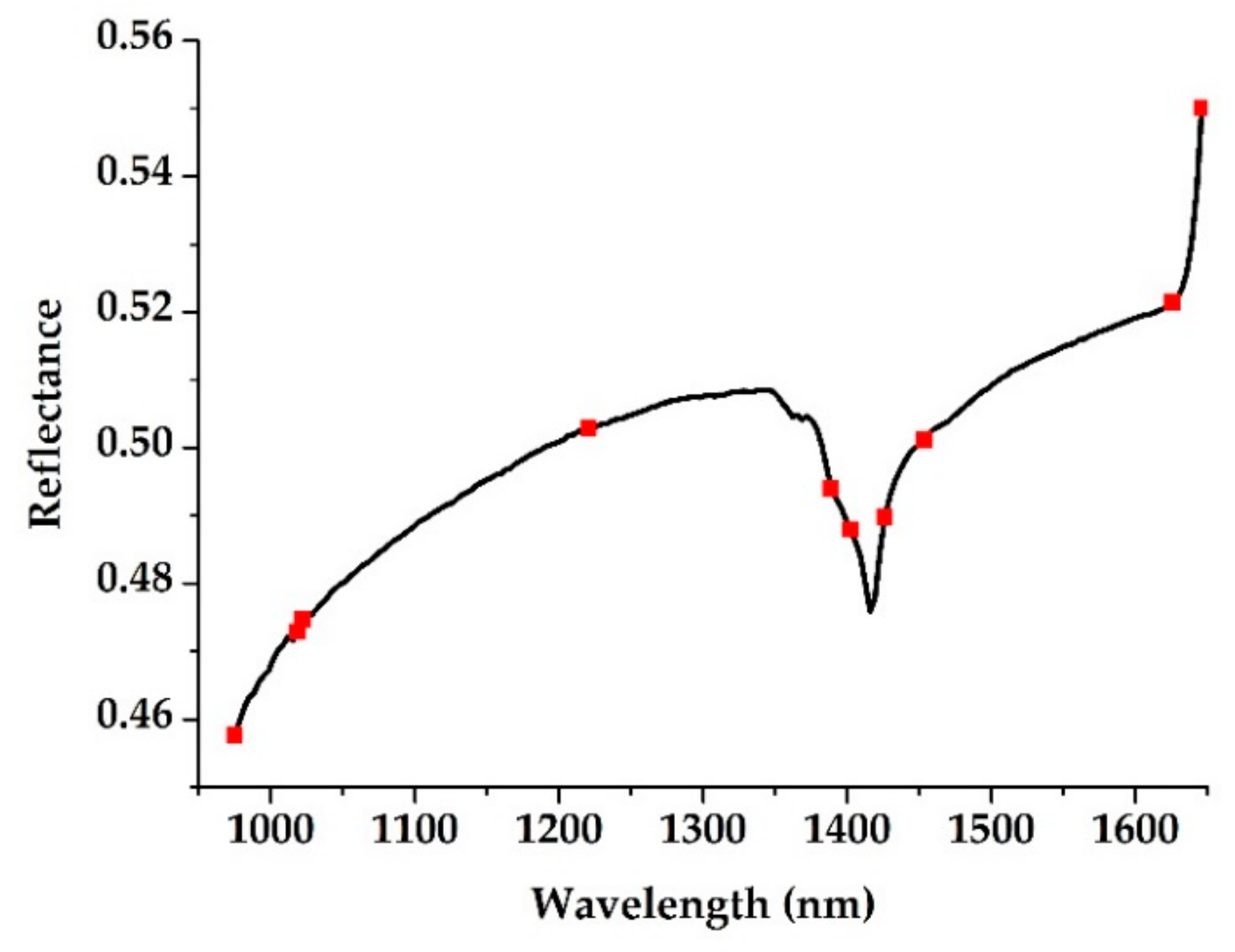
2.4.2. Characteristic Wavelength Selection
2.4.3. Model Assessment and Software
2.5. Image Processing
3. Results and Discussion
3.1. Models with Full Spectra
3.2. Characteristic Wavelength Selection
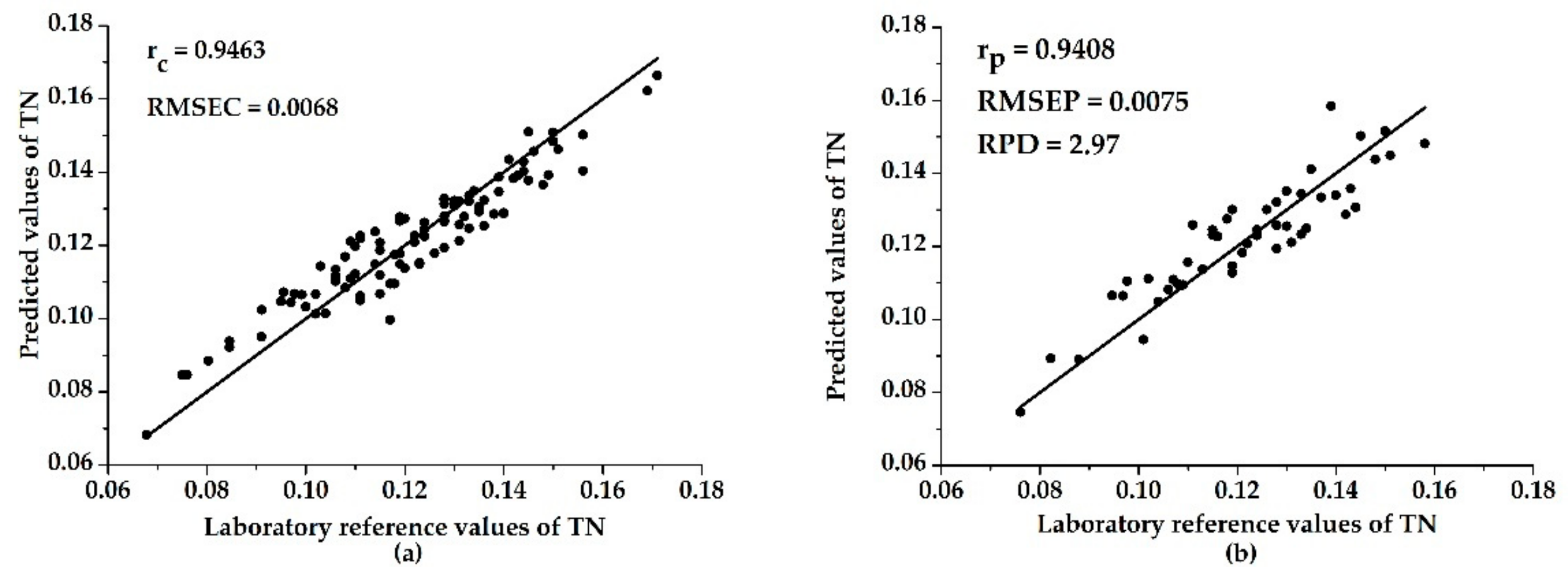
3.3. Models with Characteristic Wavelengths
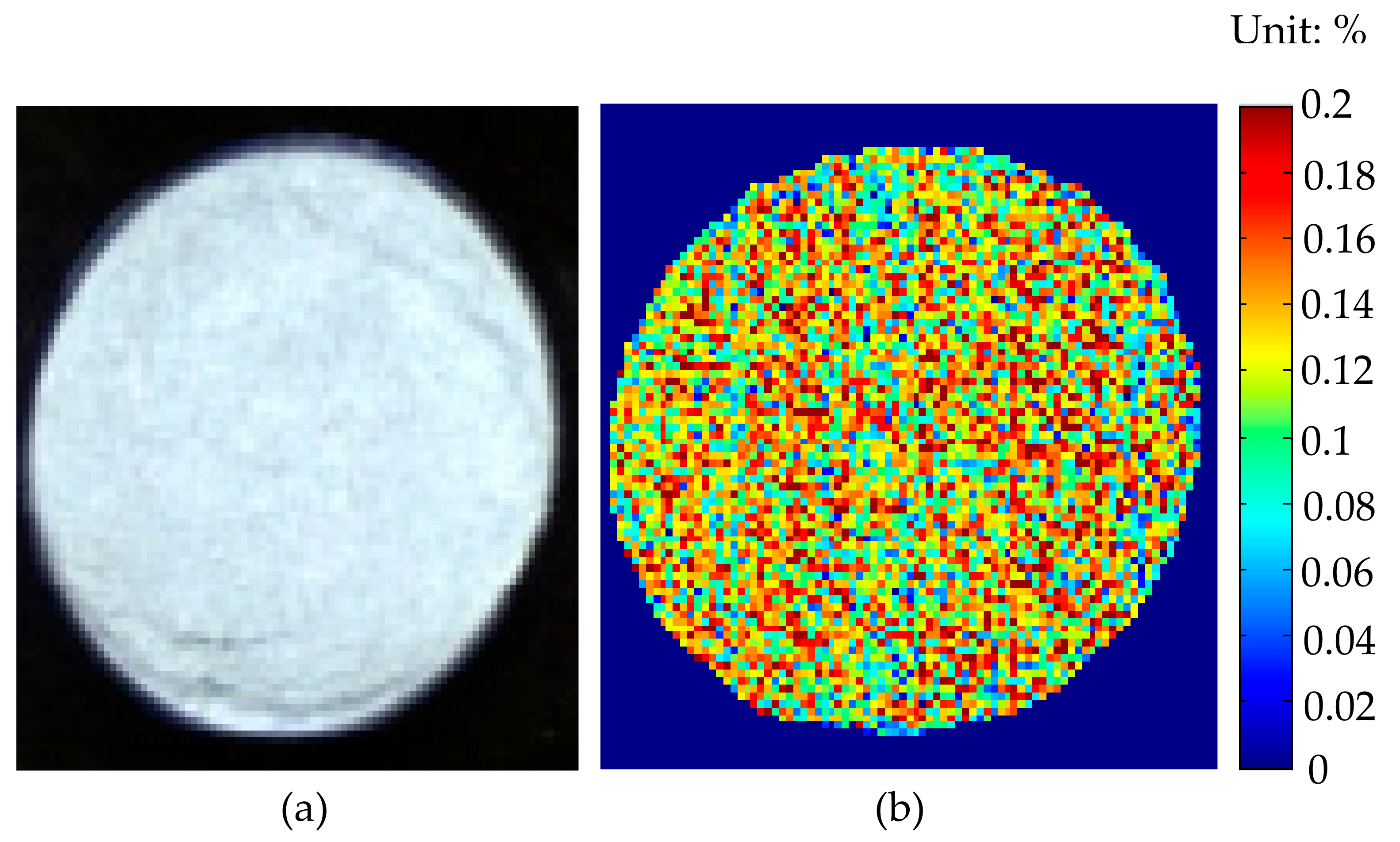
3.4. Image Visualization
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Lu, S.; Zhang, Z.; Zhao, X.; Li, X.; Ning, P.; Liu, M. Environmentally friendly fertilizers: A review of materials used and their effects on the environment. Sci. Total Environ. 2018, 613, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Song, S.; Wang, R.; Liu, Z.; Meng, J.; Sweetman, A.J.; Jenkins, A.; Ferrier, R.C.; Li, H.; Luo, W.; et al. Impacts of soil and water pollution on food safety and health risks in China. Environ. Int. 2015, 77, 5–15. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Liu, X.; Lv, Y.; Liu, F.; Peng, J.; Shen, T.; Zhao, Y.; Tang, Y.; Luo, S. Quantitative Analysis of Nutrient Elements in Soil Using Single and Double-Pulse Laser-Induced Breakdown Spectroscopy. Sensors 2018, 18, 1526. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Yang, Z.; Wang, X.; Shi, Y.; Zhang, Y. Response characteristics and efficiency of variable rate fertilization based on spectral reflectance. Int. J. Agric. Biol. Eng. 2018, 11, 152–158. [Google Scholar] [CrossRef]
- Liu, Y.; Pu, H.; Sun, D.-W. Hyperspectral imaging technique for evaluating food quality and safety during various processes: A review of recent applications. Trends Food Sci. Technol. 2017, 69, 25–35. [Google Scholar] [CrossRef]
- He, Y.; Huang, M.; García, A.; Hernández, A.; Song, H. Prediction of soil macronutrients content using near-infrared spectroscopy. Comput. Electron. Agric. 2007, 58, 144–153. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Basterretxea, K.; Martinez-Corral, U.; Finker, R.; del Campo, I. ELM-based hyperspectral imagery processor for onboard real-time classification. In Proceedings of the 2016 Conference on Design and Architectures for Signal and Image Processing (DASIP), Rennes, France, 12–14 October 2016; pp. 43–50. [Google Scholar]
- Guo, W.; Wang, M.; Gu, J.-S.; Zhu, X. Identification of bruised kiwifruits during storage by near infrared spectroscopy and extreme learning machine. Opt. Precis. Eng. 2013, 21, 2720–2727. [Google Scholar]
- Prasad, R.; Deo, R.; Li, Y.; Maraseni, T. Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition. Geoderma 2018, 330, 136–161. [Google Scholar] [CrossRef]
- Nahvi, B.; Habibi, J.; Mohammadi, K.; Shamshirband, S.; Al Razgan, O. Using self-adaptive evolutionary algorithm to improve the performance of an extreme learning machine for estimating soil temperature. Comput. Electron. Agric. 2016, 124, 150–160. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Zhang, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Cheng, H.; Liu, Y. Rapid identification of soil organic matter level via visible and near-infrared spectroscopy: Effects of two-dimensional correlation coefficient and extreme learning machine. Sci. Total Environ. 2018, 644, 1232–1243. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Yang, L.; Meng, L.; Wang, J.; Li, S.; Fu, X.; Du, X.; Wu, D. Potential of Visible and Near-Infrared Hyperspectral Imaging for Detection of Diaphania pyloalis Larvae and Damage on Mulberry Leaves. Sensors 2018, 18, 2077. [Google Scholar] [CrossRef] [PubMed]
- O’Rourke, S.M.; Holden, N.M. Determination of Soil Organic Matter and Carbon Fractions in Forest Top Soils using Spectral Data Acquired from Visible–Near Infrared Hyperspectral Images. Soil Sci. Soc. Am. J. 2012, 76, 586. [Google Scholar] [CrossRef]
- Jiang, X.; Zou, B.; Tu, Y.; Feng, H.; Chen, X. Quantitative Estimation of Cd Concentrations of Type Standard Soil Samples Using Hyperspectral Data. Spectrosc. Spectral Anal. 2018, 38, 3254–3260. [Google Scholar]
- Cheng, W.; Sun, D.; Pu, H.; Liu, Y. Integration of spectral and textural data for enhancing hyperspectral prediction of K value in pork meat. LWT Food Sci. Technol. 2016, 72, 322–329. [Google Scholar] [CrossRef]
- Zhang, C.; Ye, H.; Liu, F.; He, Y.; Kong, W.; Sheng, K. Determination and Visualization of pH Values in Anaerobic Digestion of Water Hyacinth and Rice Straw Mixtures Using Hyperspectral Imaging with Wavelet Transform Denoising and Variable Selection. Sensors 2016, 16, 244. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.R.; Li, X.; Yu, K.Q.; Cheng, F.; He, Y. Hyperspectral Imaging for Determining Pigment Contents in Cucumber Leaves in Response to Angular Leaf Spot Disease. Sci. Rep. 2016, 6, 27790. [Google Scholar] [CrossRef]
- Hesse, P.R. A Textbook of Soil Chemical Analysis; John Murray: London, UK, 1971. [Google Scholar]
- Dong, J.; Guo, W.; Wang, Z.; Liu, D.; Zhao, F. Nondestructive Determination of Soluble Solids Content of ‘Fuji’ Apples Produced in Different Areas and Bagged with Different Materials During Ripening. Food Anal. Methods 2015, 9, 1087–1095. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Q.; Shi, A.; Yang, Y.; Liu, L.; Hu, H.; Liu, H. Visualization of Protein in Peanut Using Hyperspectral Image with Chemometrics. Spectrosc. Spectral Anal. 2017, 37, 853–858. [Google Scholar]
- Cheng, J.; Sun, D. Partial Least Squares Regression (PLSR) Applied to NIR and HSI Spectral Data Modeling to Predict Chemical Properties of Fish Muscle. Food Eng. Rev. 2017, 9, 36–49. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Y.; Liu, H.; Wang, J.; Wu, G. Soil Organic Carbon Content Estimation with Laboratory-Based Visible-Near-Infrared Reflectance Spectroscopy: Feature Selection. Appl. Spectrosc. 2014, 68, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Aredo, V.; Velásquez, L.; Siche, R. Prediction of beef marbling using Hyperspectral Imaging (HSI) and Partial Least Squares Regression (PLSR). Scientia Agropecuaria 2017, 8, 169–174. [Google Scholar] [CrossRef]
- Lahoz, D.; Lacruz, B.; M.Mateo, P. A multi-objective micro genetic ELM algorithm. Neurocomputing 2013, 111, 90–103. [Google Scholar] [CrossRef]
- Khoshnoudi-Nia, S.; Moosavi-Nasab, M.; Nassiri, S.M.; Azimifar, Z. Determination of Total Viable Count in Rainbow-Trout Fish Fillets Based on Hyperspectral Imaging System and Different Variable Selection and Extraction of Reference Data Methods. Food Anal. Methods 2018, 11, 3481–3494. [Google Scholar] [CrossRef]
- Yang, H.; Kuang, B.; Mouazen, A.M. Quantitative analysis of soil nitrogen and carbon at a farm scale using visible and near infrared spectroscopy coupled with wavelength reduction. Eur. J. Soil Sci. 2012, 63, 410–420. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, H.; Liu, F.; He, Y. Application of Near-Infrared Hyperspectral Imaging with Variable Selection Methods to Determine and Visualize Caffeine Content of Coffee Beans. Food Bioprocess Technol. 2016, 10, 213–221. [Google Scholar] [CrossRef]
- Wu, W.; Chen, G.Y.; Kang, R.; Xia, J.C.; Huang, Y.P.; Chen, K.J. Successive Projections Algorithm - Multivariate Linear Regression Classifier for the Detection of Contaminants on Chicken Carcasses in Hyperspectral Images. J. Appl. Spectrosc. 2017, 84, 535–541. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, F.; Kong, W.; He, Y. Application of Visible and Near-Infrared Hyperspectral Imaging to Determine Soluble Protein Content in Oilseed Rape Leaves. Sensors 2015, 15, 16576–16588. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; ElMasry, G.; Sun, D.; Allen, P. Prediction of some quality attributes of lamb meat using near-infrared hyperspectral imaging and multivariate analysis. Anal. Chim. Acta 2012, 714, 57–67. [Google Scholar] [CrossRef]
- Kotwal, K.; Chaudhuri, S. Visualization of Hyperspectral Images Using Bilateral Filtering. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2308–2316. [Google Scholar] [CrossRef]
- Shao, Y.; He, Y. Nitrogen, phosphorus, and potassium prediction in soils, using infrared spectroscopy. Soil Res. 2011, 49, 166–172. [Google Scholar] [CrossRef]
- Cai, L.; Ding, J. Prediction for Soil Water Content Based on Variable Preferred and Extreme Learning Machine Algorithm. Spectrosc. Spectral Anal. 2018, 38, 2209–2214. [Google Scholar]
- Liu, D.; Sun, D.-W.; Zeng, X.-A. Recent Advances in Wavelength Selection Techniques for Hyperspectral Image Processing in the Food Industry. Food Bioprocess Technol. 2013, 7, 307–323. [Google Scholar] [CrossRef]
- Jia, S.; Yang, X.; Zhang, J.; Li, G. Quantitative Analysis of Soil Nitrogen, Organic Carbon, Available Phosphorous, and Available Potassium Using Near-Infrared Spectroscopy Combined With Variable Selection. Soil Sci. 2014, 179, 211–219. [Google Scholar] [CrossRef]
- Shen, Z.; Lu, B.; Shan, Y.; Xu, H. Study on Soil Carbon Estimation by On-the-Go Near-Infrared Spectra and Partial Least Squares Regression with Variable Selection. Spectrosc. Spectral Anal. 2013, 33, 1775–1780. [Google Scholar]
- Yang, M.H.; Zhao, X.M.; Fang, Q.; Xie, B.Y. Study on Soil Total N Estimation by Vis-NIR Spectra with Variable Selection. Sci. Agric. Sin. 2014, 47, 2374–2383. [Google Scholar]
- Yuan, S.; Ma, T.; Song,, T.; He, Y.; Bao, Y. Real-time Analysis of Soil Total N and P with Near Infrared Reflectance Spectroscopy. Trans. Chin. Soc. Agric. Mach. 2009, 40, 150–153. [Google Scholar]
| Sample Set | Number | Range (%) | Mean (%) | SD 1 (%) |
|---|---|---|---|---|
| Calibration set | 100 | 0.0678–0.1710 | 0.1216 | 0.0201 |
| Prediction set | 50 | 0.0760–0.1580 | 0.1197 | 0.0223 |
| Model | LVs 1/HLNs 2 | Calibration | Prediction | |||
|---|---|---|---|---|---|---|
| rc | RMSEC (%) | rp | RMSEP (%) | RPD | ||
| PLS | 6 | 0.9276 | 0.0077 | 0.9218 | 0.0086 | 2.59 |
| ELM | 24 | 0.9383 | 0.0072 | 0.9347 | 0.0079 | 2.82 |
| Model | Calibration | Prediction | |||
|---|---|---|---|---|---|
| rc | RMSEC (%) | rp | RMSEP (%) | RPD | |
| UVE–PLS | 0.9293 | 0.0074 | 0.9266 | 0.0083 | 2.69 |
| SPA–PLS | 0.9310 | 0.0076 | 0.9150 | 0.0089 | 2.51 |
| UVE–ELM | 0.9463 | 0.0068 | 0.9408 | 0.0075 | 2.97 |
| SPA–ELM | 0.9346 | 0.0074 | 0.9196 | 0.0087 | 2.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jia, S.; Le, Z. Quantitative Analysis of Soil Total Nitrogen Using Hyperspectral Imaging Technology with Extreme Learning Machine. Sensors 2019, 19, 4355. https://doi.org/10.3390/s19204355
Li H, Jia S, Le Z. Quantitative Analysis of Soil Total Nitrogen Using Hyperspectral Imaging Technology with Extreme Learning Machine. Sensors. 2019; 19(20):4355. https://doi.org/10.3390/s19204355
Chicago/Turabian StyleLi, Hongyang, Shengyao Jia, and Zichun Le. 2019. "Quantitative Analysis of Soil Total Nitrogen Using Hyperspectral Imaging Technology with Extreme Learning Machine" Sensors 19, no. 20: 4355. https://doi.org/10.3390/s19204355
APA StyleLi, H., Jia, S., & Le, Z. (2019). Quantitative Analysis of Soil Total Nitrogen Using Hyperspectral Imaging Technology with Extreme Learning Machine. Sensors, 19(20), 4355. https://doi.org/10.3390/s19204355





