In-Fiber Collimator-Based Fabry-Perot Interferometer with Enhanced Vibration Sensitivity
Abstract
1. Introduction
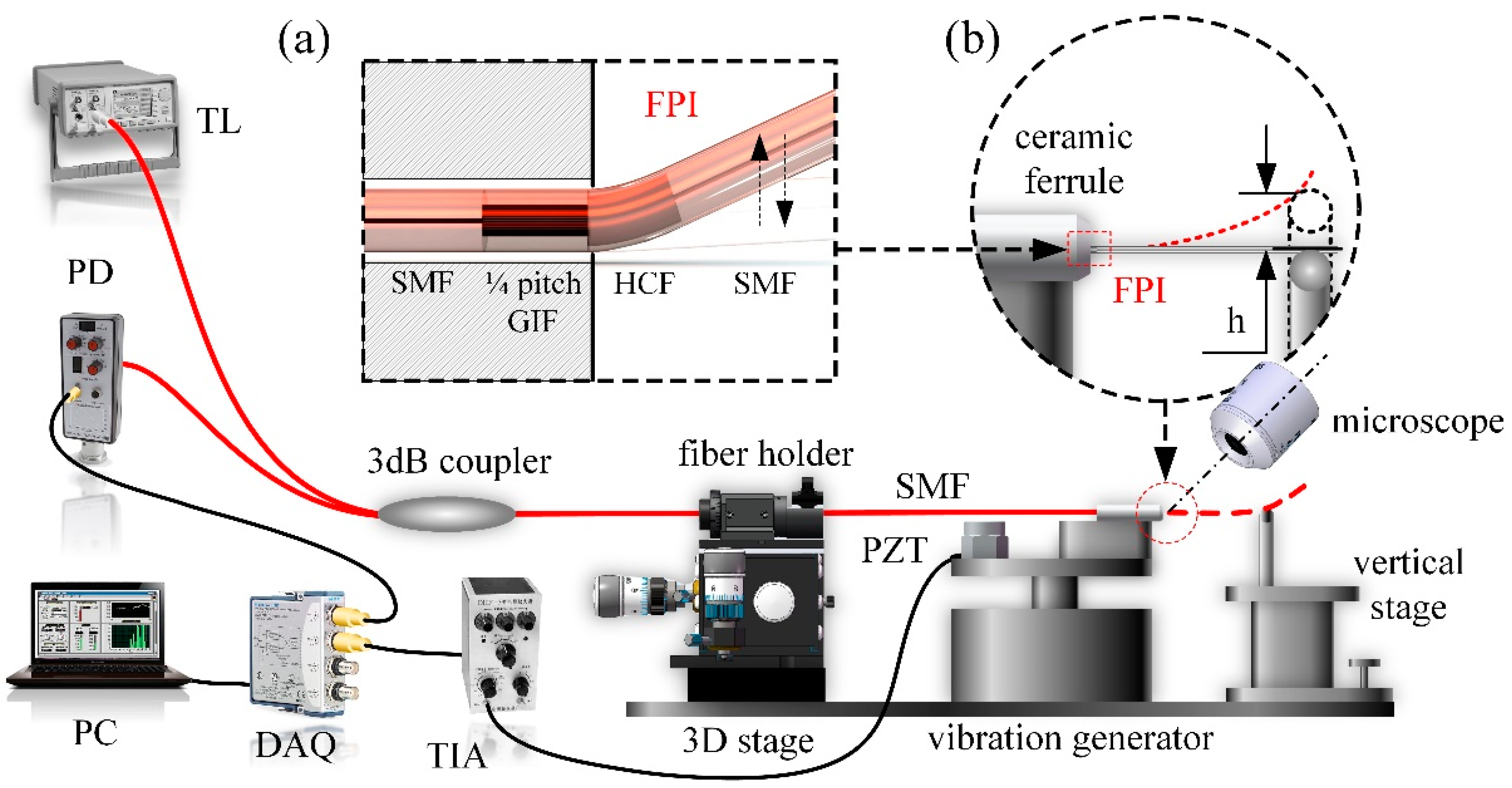
2. Vibration Sensor System
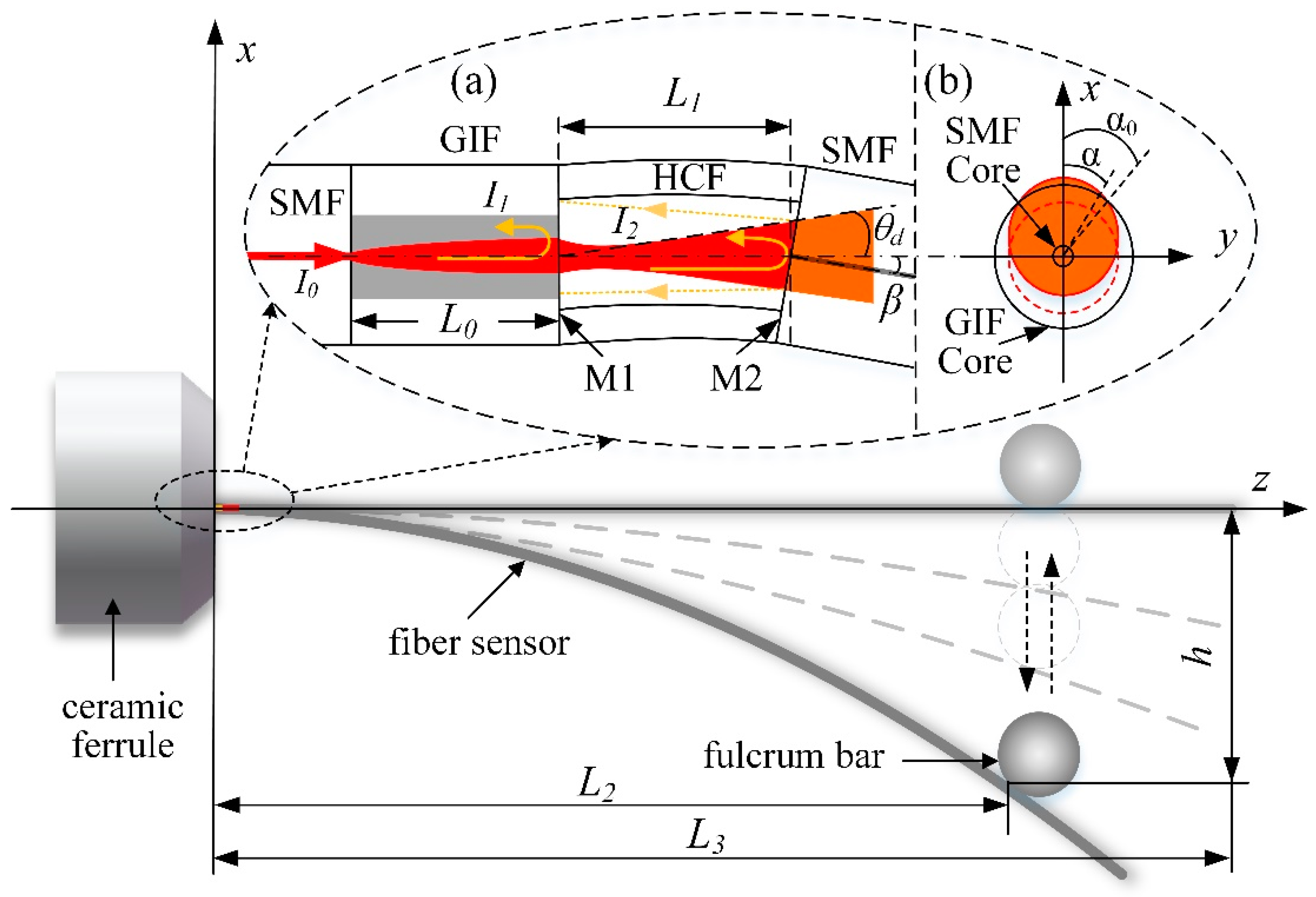
3. Principle of Operation
3.1. Divergence Angle of the Fiber Collimator
3.2. Displacement Response of the Enhanced Fabry-Perot Interferometer
3.3. Natural Frequency of the Device
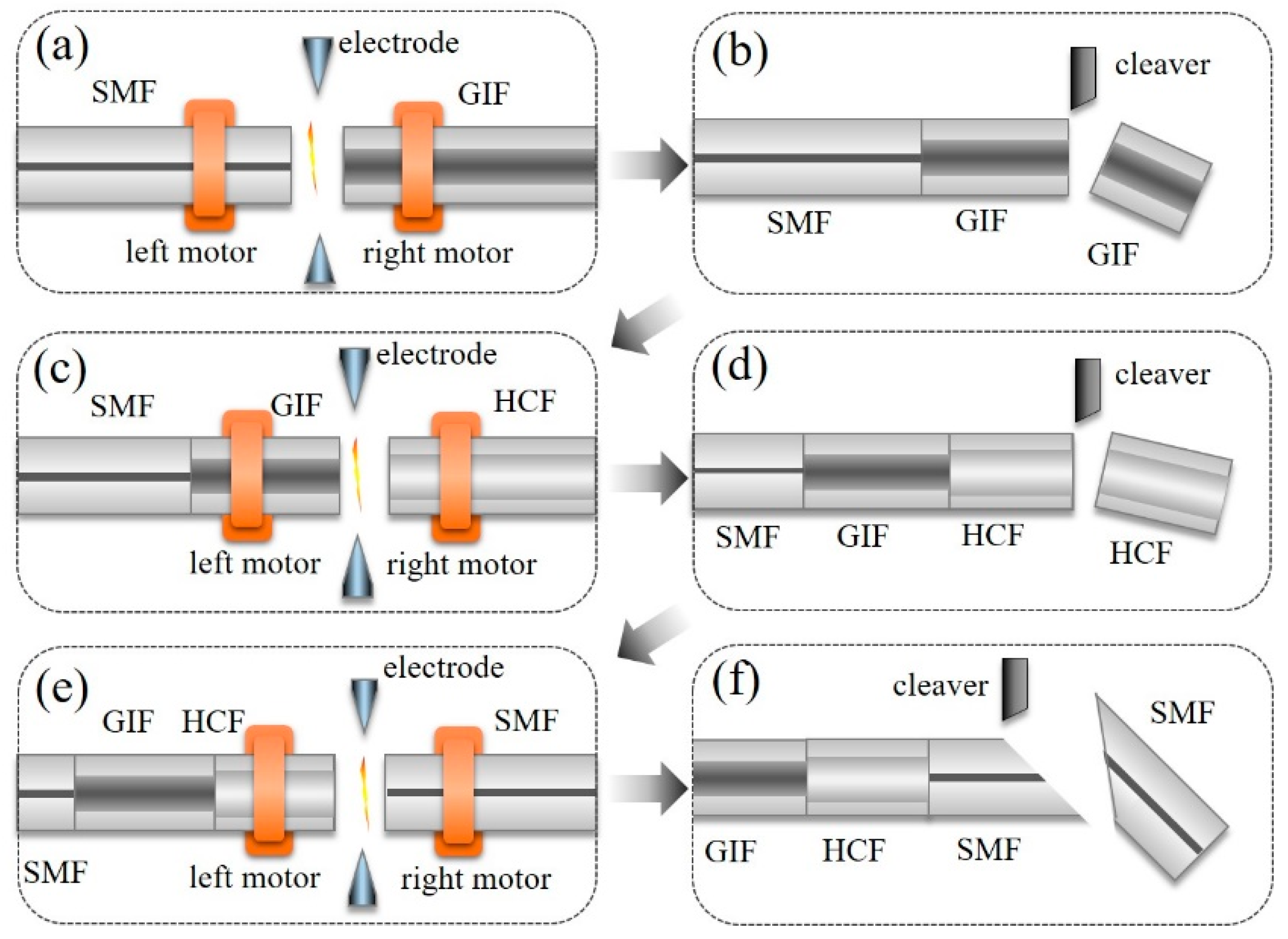
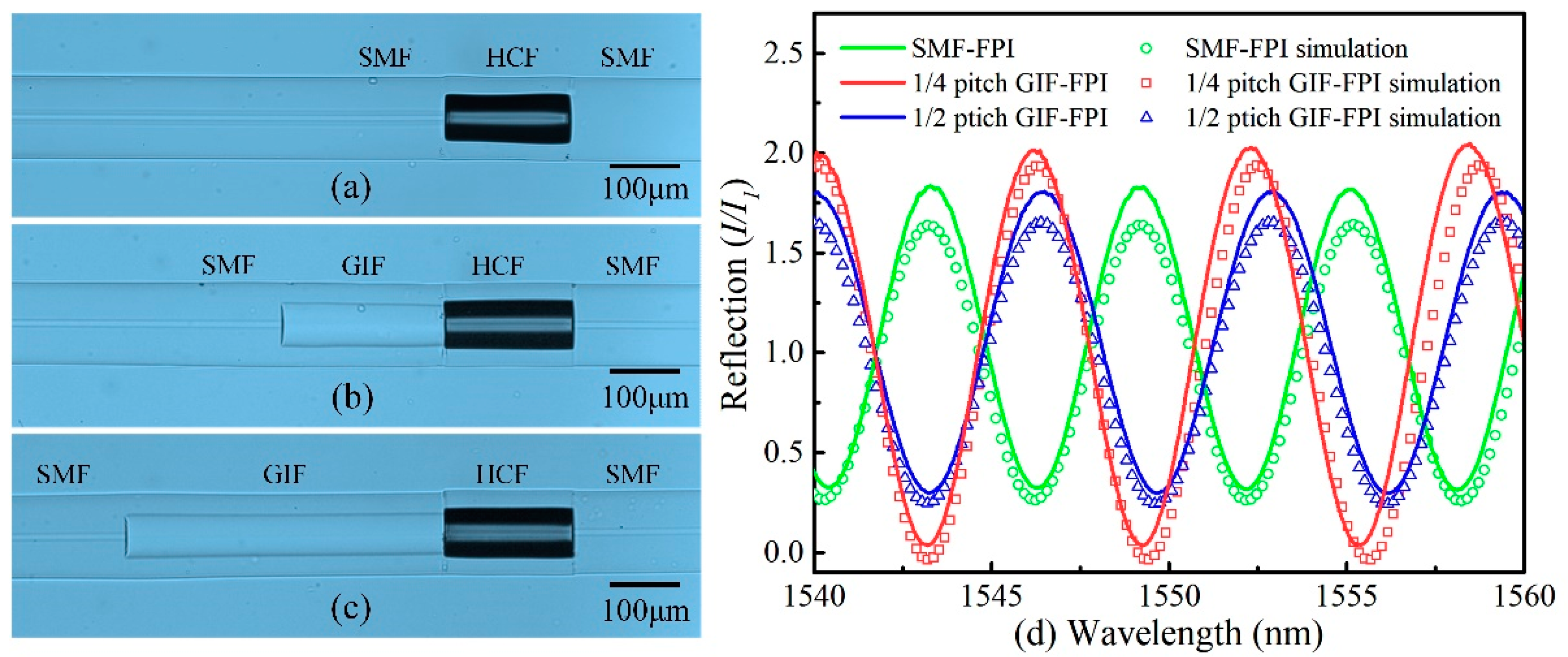
4. Device Fabrication
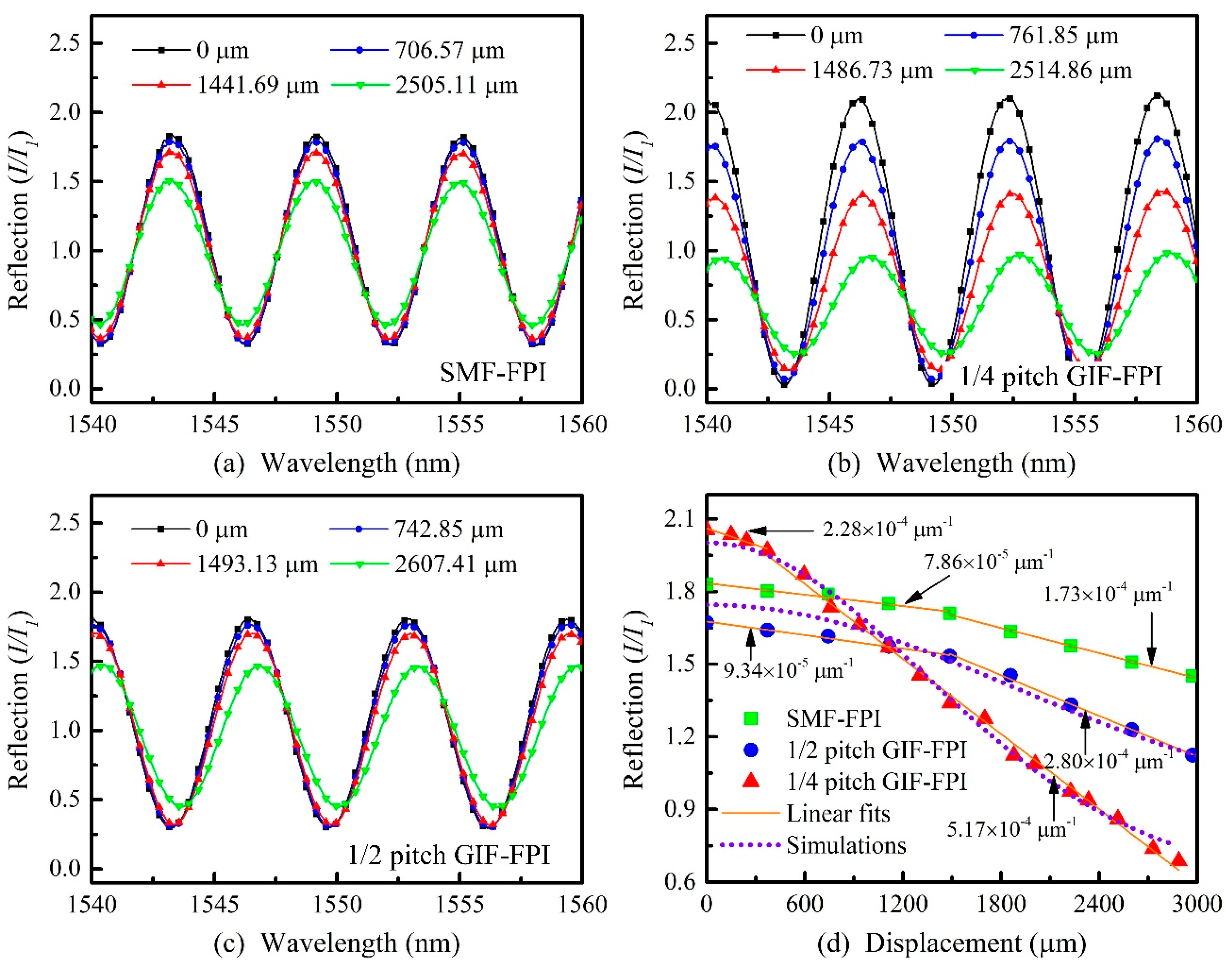
5. Static Displacement Measurement
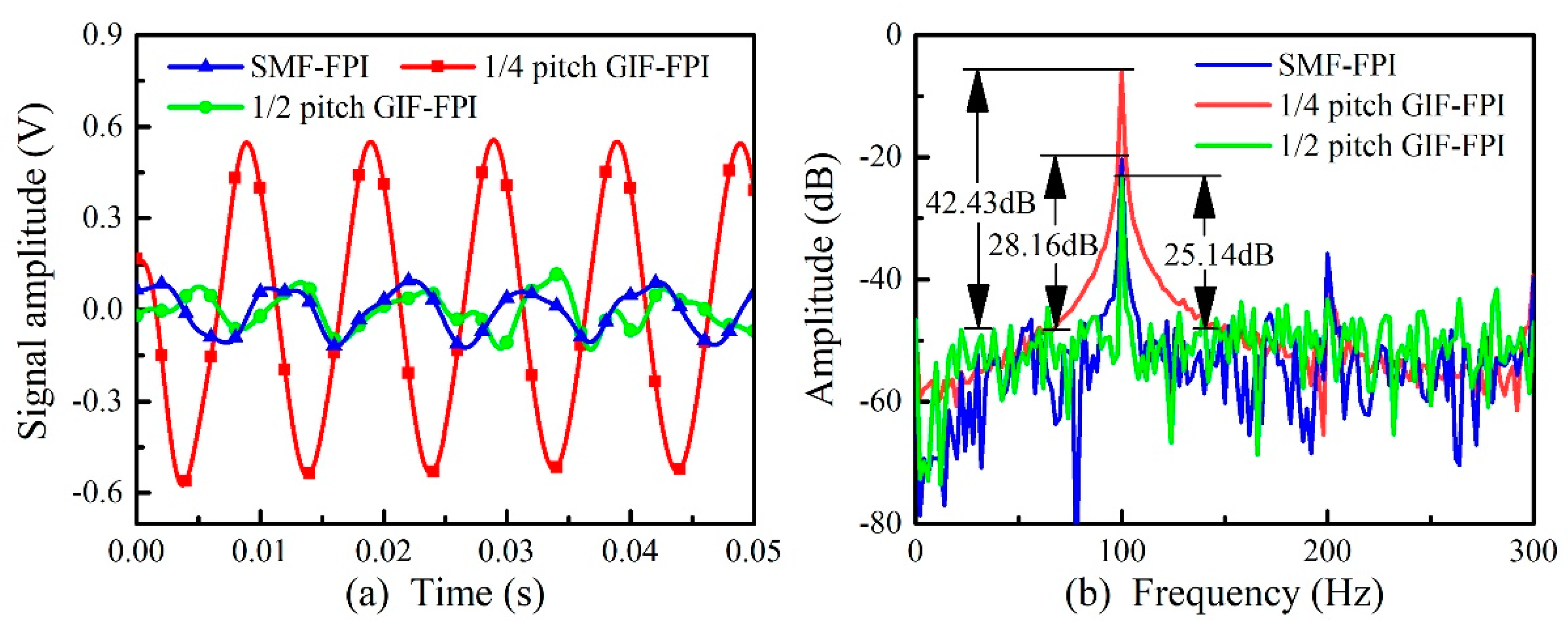
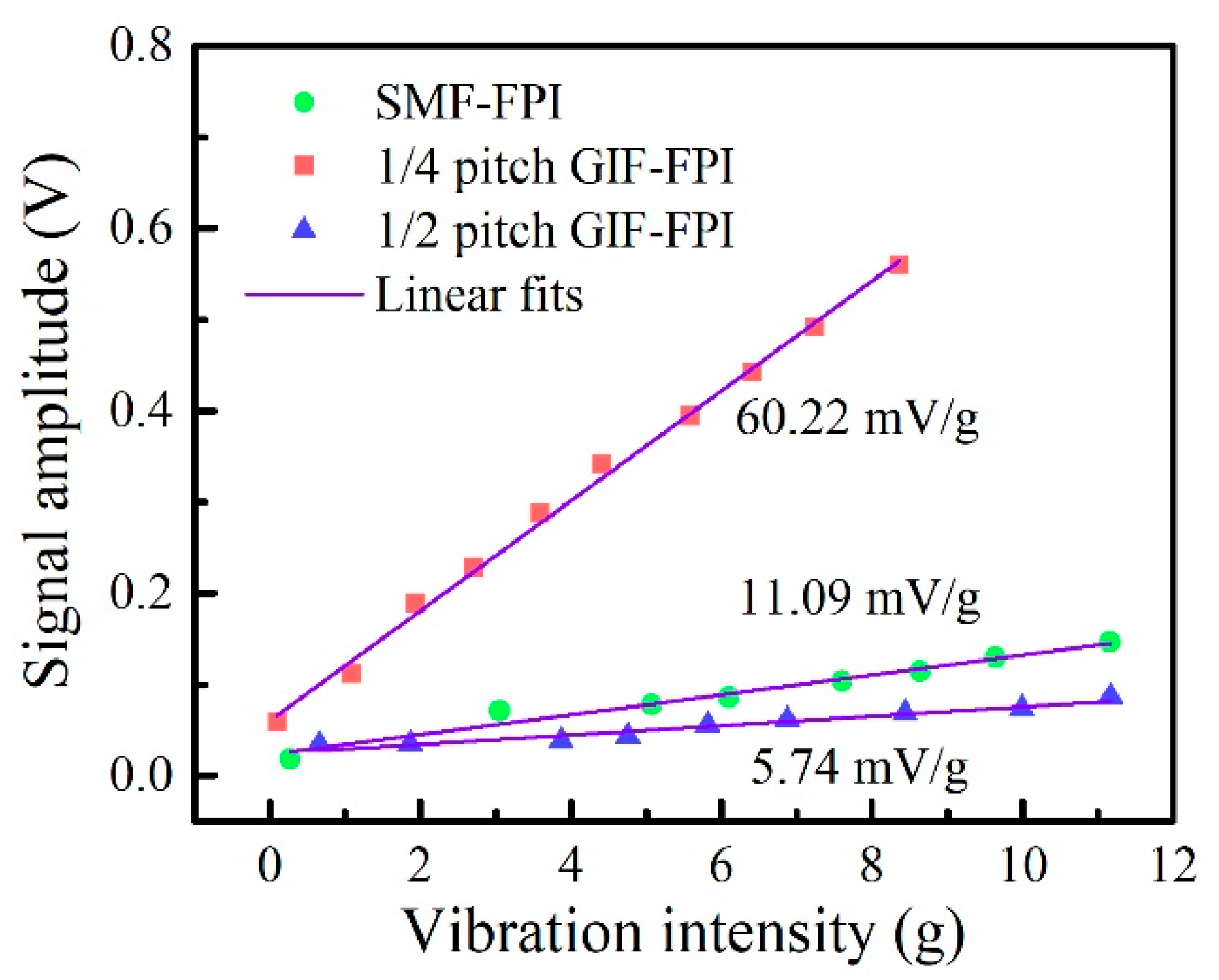
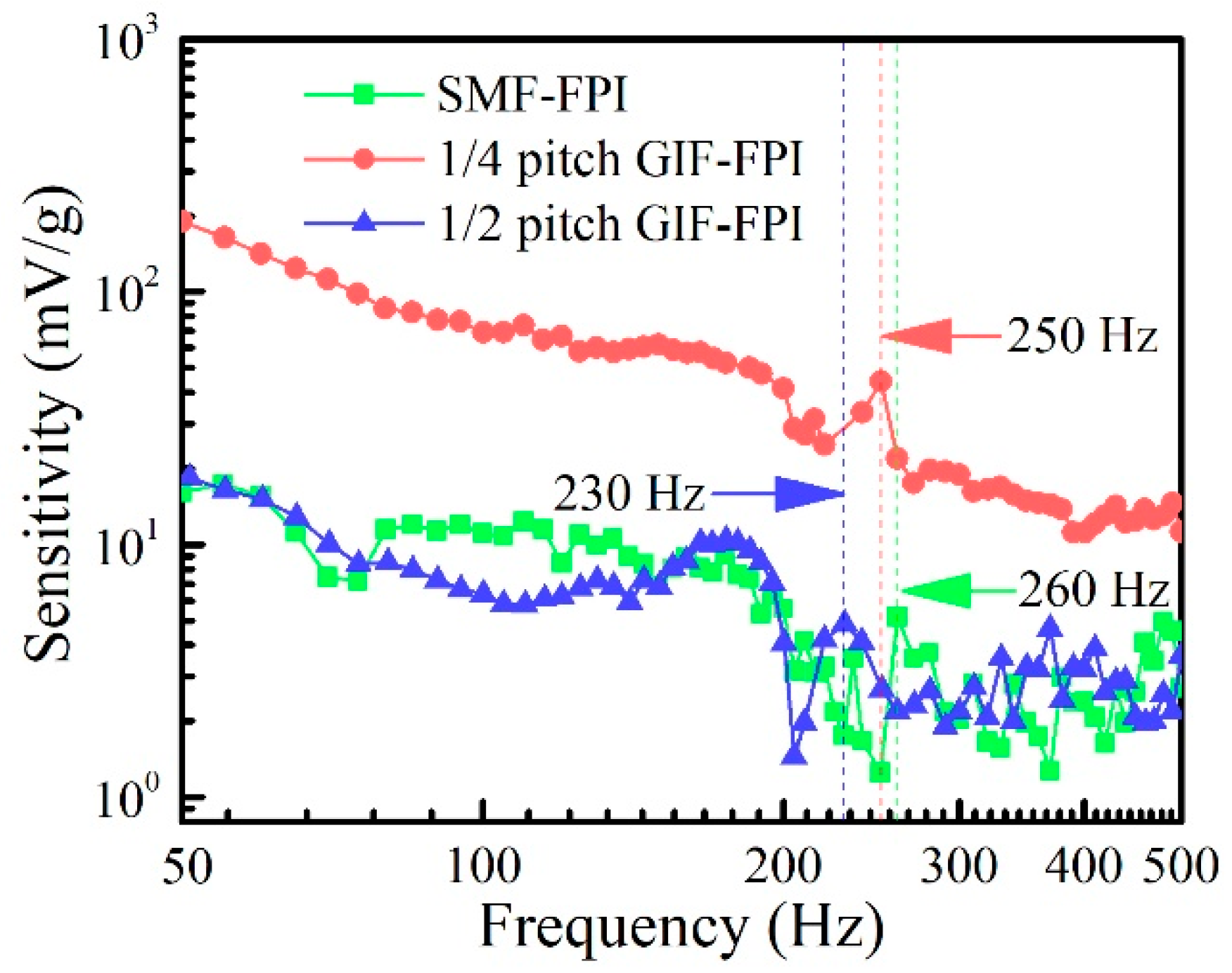
6. Vibration Response
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Colchester, R.J.; Zhang, E.Z.; Mosse, C.A.; Beard, P.C.; Papakonstantinou, I.; Desjardins, A.E. Broadband miniature optical ultrasound probe for high resolution vascular tissue imaging. Biomed. Opt. Express 2015, 6, 1502–1511. [Google Scholar] [CrossRef]
- Manuel, R.M.; Shlyagin, M.G.; Miridonov, S.V.; Meyer, J. Vibration disturbance localization Using a serial array of identical low-finesse fiber Fabry-Perot interferometers. IEEE Sens. J. 2012, 12, 124–127. [Google Scholar] [CrossRef]
- Preisser, S.; Rohringer, W.; Liu, M.; Kollmann, C.; Zotter, S.; Fischer, B.; Drexler, W. All-optical highly sensitive akinetic sensor for ultrasound detection and photoacoustic imaging. Biomed. Opt. Express 2016, 7, 4171–4186. [Google Scholar] [CrossRef] [PubMed]
- Pullteap, S.; Seat, H.C. An extrinsic fiber Fabry-Perot interferometer for dynamic displacement measurement. Photonic Sens. 2014, 5, 50–59. [Google Scholar] [CrossRef]
- Wada, A.; Tanaka, S.; Takahashi, N. Optical fiber vibration sensor using FBG Fabry–Perot interferometer with wavelength scanning and Fourier analysis. IEEE Sens. J. 2012, 12, 225–229. [Google Scholar] [CrossRef]
- Xu, X.; He, J.; Hou, M.; Liu, S.; Bai, Z.; Wang, Y.; Liao, C.; Ouyang, Z.; Wang, Y. A miniature fiber collimator for highly sensitive bend measurements. J. Lightwave Technol. 2018, 36, 2827–2833. [Google Scholar] [CrossRef]
- Zhang, Z.; He, J.; Dong, Q.; Bai, Z.; Liao, C.; Wang, Y.; Liu, S.; Guo, K.; Wang, Y. Diaphragm-free gas-pressure sensor probe based on hollow-core photonic bandgap fiber. Opt. Lett. 2018, 43, 3017–3020. [Google Scholar] [CrossRef]
- Liao, C.; Liu, S.; Xu, L.; Wang, C.; Wang, Y.; Li, Z.; Wang, Q.; Wang, D.N. Sub-micron silica diaphragm-based fiber-tip Fabry-Perot interferometer for pressure measurement. Opt. Lett. 2014, 39, 2827–2830. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Liu, S.; Liao, C.; He, J.; Lian, J.; Wang, Y. Growth dynamics of ZnO nanowire on a fiber-tip air bubble. Opt. Mater. Express 2017, 7, 3433. [Google Scholar] [CrossRef]
- Majchrowicz, D.; Hirsch, M.; Wierzba, P.; Bechelany, M.; Viter, R.; Jedrzejewska-Szczerska, M. Application of thin ZnO ALD layers in fiber-optic Fabry-Perot sensing interferometers. Sensors 2016, 16, 416. [Google Scholar] [CrossRef]
- Barnes, J.; Li, S.; Goyal, A.; Abolmaesumi, P.; Mousavi, P.; Loock, H. Broadband vibration detection in tissue phantoms using a fiber Fabry–Perot cavity. IEEE Trans. Biomed. Eng. 2018, 65, 921–927. [Google Scholar] [CrossRef]
- Hirsch, M.; Majchrowicz, D.; Wierzba, P.; Weber, M.; Bechelany, M.; Jedrzejewska-Szczerska, M. Low-coherence interferometric fiber-optic sensors with potential applications as biosensors. Sensors 2017, 17, 261. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Wang, L.; Chen, X.; Zhou, B. Flexible optical fiber Fabry-Perot interferometer based acoustic and mechanical vibration sensor. J. Lightwave Technol. 2018, 36, 2216–2221. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, C.; Tang, J.; Bai, Z.; Guo, K.; Hou, M.; He, J.; Wang, Y.; Liu, S.; Zhang, F. High-sensitivity gas-pressure sensor based on fiber-tip PVC diaphragm Fabry–Pérot interferometer. J. Lightwave Technol. 2017, 35, 4067–4071. [Google Scholar] [CrossRef]
- Nishino, Z.T.; Chen, K.; Gupta, N. Power modulation-based optical sensor for high-sensitivity vibration measurements. IEEE Sens. J. 2014, 14, 2153–2158. [Google Scholar] [CrossRef]
- Bai, Z.; Gao, S.; Deng, M.; Zhang, Z.; Li, M.; Zhang, F.; Liao, C.; Wang, Y.; Wang, Y. Bidirectional bend sensor employing a microfiber-assisted U-shaped Fabry-Perot cavity. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Takamori, A.; Araya, A.; Morii, W.; Telada, S.; Uchiyama, T.; Ohashi, M. A 100-m Fabry–Pérot cavity with automatic alignment controls for long-term observations of earth’s strain. Technologies 2014, 2, 129–142. [Google Scholar] [CrossRef]
- Gardner, D.; Hofler, T.; Baker, S.; Yarber, R.; Garrett, S. A fiber-optic interferometric seismometer. J. Lightwave Technol. 1987, 5, 953–960. [Google Scholar] [CrossRef]
- Lopez-Higuera, J.M.; Morante, M.A.; Cobo, A. Simple low-frequency optical fiber accelerometer with large rotating machine monitoring applications. J. Lightwave Technol. 1997, 15, 1120–1130. [Google Scholar] [CrossRef]
- Kamenev, O.T.; Kulchin, Y.N.; Petrov, Y.S.; Khiznyak, R.V.; Romashko, R.V. Fiber-optic seismometer on the basis of Mach-Zehnder interferometer. Sensor. Actuators A Phys. 2016, 244, 133–137. [Google Scholar] [CrossRef]
- Li, T.; Shi, C.; Tan, Y.; Li, R.; Zhou, Z.; Ren, H. A diaphragm type fiber Bragg grating vibration sensor based on transverse property of optical fiber with temperature compensation. IEEE Sens. J. 2017, 17, 1021–1029. [Google Scholar] [CrossRef]
- Li, W.; Zhang, J. Distributed weak fiber Bragg grating vibration sensing system based on 3 × 3 fiber coupler. Photonic Sens. 2018, 8, 146–156. [Google Scholar] [CrossRef]
- Wang, J.; Wei, L.; Li, R.; Liu, Q.; Yu, L. A fiber Bragg grating based torsional vibration sensor for rotating machinery. Sensors 2018, 18, 2669. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Y.; Wei, T.; Lan, X.; Huang, Y.; Chen, G.; Xiao, H. Fringe visibility enhanced extrinsic Fabry–Perot interferometer using a graded index fiber collimator. IEEE Photonics J. 2010, 2, 469–481. [Google Scholar] [CrossRef]
- Wang, S.H.; Tay, C.J.; Quan, C.; Shang, H.M. Study of collimating laser diode beam by a graded-index optical fibre. Optik 2001, 112, 531–535. [Google Scholar] [CrossRef]
- Ma, C.; Dong, B.; Gong, J.; Wang, A. Decoding the spectra of low-finesse extrinsic optical fiber Fabry-Perot interferometers. Opt Express 2011, 19, 23727–23742. [Google Scholar] [CrossRef] [PubMed]
- Ghavami, P. Mechanics of Materials: An Introduction to Engineering Technology; Springer: Cham, Switzerland, 2015; pp. 237–244. [Google Scholar] [CrossRef]
- Pérennès, F.; Beard, P.C.; Mills, T.N. Analysis of a low-finesse Fabry–Perot sensing interferometer illuminated by a multimode optical fiber. Appl. Opt. 1999, 38, 7026–7034. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Xu, X.; He, J.; Guo, K.; Huang, W.; Zhang, F.; Zhang, M.; Wang, Y. In-Fiber Collimator-Based Fabry-Perot Interferometer with Enhanced Vibration Sensitivity. Sensors 2019, 19, 435. https://doi.org/10.3390/s19020435
Du B, Xu X, He J, Guo K, Huang W, Zhang F, Zhang M, Wang Y. In-Fiber Collimator-Based Fabry-Perot Interferometer with Enhanced Vibration Sensitivity. Sensors. 2019; 19(2):435. https://doi.org/10.3390/s19020435
Chicago/Turabian StyleDu, Bin, Xizhen Xu, Jun He, Kuikui Guo, Wei Huang, Fengchan Zhang, Min Zhang, and Yiping Wang. 2019. "In-Fiber Collimator-Based Fabry-Perot Interferometer with Enhanced Vibration Sensitivity" Sensors 19, no. 2: 435. https://doi.org/10.3390/s19020435
APA StyleDu, B., Xu, X., He, J., Guo, K., Huang, W., Zhang, F., Zhang, M., & Wang, Y. (2019). In-Fiber Collimator-Based Fabry-Perot Interferometer with Enhanced Vibration Sensitivity. Sensors, 19(2), 435. https://doi.org/10.3390/s19020435






