1. Introduction
Odor information is widely used by animals when searching for food, finding mates, exchanging information, and evading predators. Inspired by these olfactory search activities, in the early 1990s, researchers started trying to build mobile robots with similar olfaction abilities (or chemical sensing capabilities in general) to replace trained animals [
1,
2,
3,
4]. It is expected that mobile robots developed with such olfaction capabilities will play an increasing role in areas such as thwarting terrorist attacks, finding toxic or harmful gas-leakage locations, checking for contraband (e.g., heroin), and searching for survivors in collapsed buildings or in the water [
5,
6,
7].
Research into the use of one or more mobile robots equipped with odor/gas sensors (in some research also with wind sensors) to search for chemical source(s) was called odor source localization (OSL) [
2,
8]. To make the OSL research more general, here we call it chemical source searching (CSS for short). The research into CSS can be roughly classified into behavior-based methods and analytical-model-based methods [
7], with most works focusing on behavior-based methods. A behavior-based CSS procedure can commonly be decomposed into three subprocedures (namely, plume finding, plume traversal, and source declaration), according to Hayes et al. [
8]. During the plume finding subprocedure, the robot tries to make contact with the chemical plume. Only a few publications have discussed plume-finding methods. Hayes et al. [
8] proposed an initial outward spiral search pattern for plume finding. Recently, Marjovi et al. [
9,
10] discussed the optimal spatial configuration of swarm robotic gas sensors for plume finding. Once the plume is detected, the robot will switch to the second subprocedure, and begins tracing the chemical toward its source. Most methods for this subprocedure are biologically inspired, such as the gradient-following algorithms [
11,
12,
13,
14], the zigzagging algorithms [
2,
13], the upwind algorithms [
8,
15], adapted ant colony optimization algorithm [
16], particle swarm optimization algorithm and its variants [
17,
18,
19,
20], the SPIRAL algorithm [
21], and genetic programming algorithm [
22]. During the plume tracing procedure, how to re-contact a lost plume is also an important issue [
23]. In the final phase, the robot locates the source [
24,
25].
Conventional plume tracing methods, especially biologically inspired methods, make it quite hard for a wheeled mobile robot equipped with normal gas sensors to approach a previously unknown chemical source in outdoor airflow environments. This is because animals fundamentally differ in their sensing and actuation capabilities from state-of-the-art gas-sensitive mobile robots [
26]. The maximum driving and steering speeds of normal wheeled mobile robots are limited by many factors, such as kinematical constraints, ground conditions, and considerations for purposes of safety. Thus, outdoor plumes usually change much faster than the speed of ground mobile robots. For example, according to our measurements in real outdoor environments, the airflow speed is usually significant (typically > 0.2 m/s, always above 1 m/s in windy days), and the airflow direction often changes randomly, rapidly, and substantially. It is well known that the chemical dispersal in airflow environments depends mainly on the transportation of turbulent airflow, forming an intermittent, patchy, sparse, and even meandering plume. Furthermore, the response/recovery lag and relatively low sensitivity of widely used metal-oxide-semiconductor gas sensors make the robot trace fast-changing and sparse plume harder.
The main contribution of this paper is that an estimation-based route planning (ERP) method is proposed for controlling a single ground mobile robot to search for a chemical source according to the historical trajectory by which a chemical patch detected by the robot has passed, namely the chemical-patch path (C-PP), in the second subprocedure of CSS. Experimental results show that the ERP method allowed the robot to successfully track intermittent, sparse and random chemical plumes and finally approach the previously unknown source in two different outdoor environments of thousands of square meters. To our knowledge, most existing CSS methods were designed for indoor airflow environments, with little research involving real-robot platforms in outdoor field environments, and there is no report of successfully solving the whole CSS problem using a single wheeled mobile robot in thousands-of-square-meter outdoor environments. The ERP method not only takes into account the fact that the airflow direction can change radically in outdoor natural-airflow environments, but also has low requirements on gas sensors and the speed of robots. Thus, it can solve the primal problem of plume sparsity and fluctuation in plume traversal subprocedure, which impose great difficulties on conventional plume tracing methods.
The proposed ERP method consists of two steps. Firstly, the C-PP is estimated using historical airflow speeds and directions when a chemical patch is detected by the robot. Secondly, a search route is planned for the robot based on the estimated C-PP. In fact, the concerned chemical patch originally comes from the source. Therefore, the source should be covered by the estimated C-PP if the C-PP is correctly reckoned back enough in the time. The search route is designed by aiming to find more chemical patches and then re-calculate the C-PP, re-plan the search route, forming an iterative searching procedure, and finally making the robot arrive at the source. A rule of thumb is that it is easier to re-meet the chemical clue when the robot moves in the downwind region (than in the upwind region) of the chemical source. Thus, in our method, the search route is planned in the downwind region and close to the estimated C-PP.
The remainder of this paper is organized as follows. The proposed CSS solution, which includes a C-PP estimation method, search-route planning method, and chemical-source searching procedure, is described in
Section 2. In
Section 3, the experimental platform is introduced.
Section 4 presents the experiments I, which include the approximate uniformity test of wind field and determination of probability-density threshold. The experiments II, i.e., the chemical source searching based on online planned routes, are introduced in
Section 5. Conclusions are given in
Section 6.
2. The Proposed ERP Method
The proposed ERP solution consists of two main steps, C-PP estimation and search route planning, in which the search route is planned based on the estimated C-PP and time-varying wind.
2.1. C-PP Estimation
2.1.1. Probability Model of Chemical Transportation
Because a wheeled mobile robot mainly moves in 2D (two dimensional) ground environments to search for chemical sources, the wind field and gas dispersal are also assumed in a 2D horizontal plane. We construct a time sequence of the airflow,
, in which
denotes the airflow velocity
(i.e., the velocity components in the
x and
y directions) observed by the robot at position
at time
. Here, times
and
stand for the start time and current time, respectively. Over a short time scale, the movement of the chemical patch can be modeled as a random walk superimposed on a mean velocity [
27,
28,
29]. Let
stand for the probability density that a chemical patch detected by the robot at the position
at time
came from the position
at time
. Then
can be expressed [
29] as
where
, the variances of the airflow velocity, can be estimated online by the time sequence of the airflow,
,
, where
and
are the coordinates of the positions
and
, respectively, and
is the distance traveled by the air mass carrying the chemical patch concerned during the period from time
to
.
With the assumption of approximately uniform airflow in an open field (see the test results presented in
Section 4.1), the distance traveled by the air mass carrying the chemical patch concerned can be estimated as
where
is the sampling period of the robot system (set to 0.5 s, in our experiments). Over a short time scale, only the 20 most recent elements in the time sequence of the airflow are used in this research, with a sampling period
s. For these 20 most recent records,
, the variance of the airflow velocity
in Equation (1) can be calculated online as
where
is the subscript for the time corresponding to the earliest element in the most recent 20 airflow records and can be calculated by
2.1.2. C-PP Estimation Algorithm
When a chemical patch is detected by the mobile robot at
, its historical trajectory (i.e., the C-PP) can be estimated [
30] as
where
is the area covering the possible locations of the concerned chemical patch at time
. Therefore,
represents all the areas through which the chemical patch possibly passed from time
to time
. To cut down the calculation,
can be estimated as
where
is defined as the 2D workspace in which the robot searches for the chemical source,
is the probability-density threshold and
The center of the area
, denoted by
has the maximal probability density in
, and the sequence
forms the most likely C-PP.
2.2. Search-Route Planning
The search route is planned online based on the estimated C-PP. Theoretically, the chemical source might be somewhere in the area described by the estimated C-PP. As a rule of thumb, the chemical is more likely to be detected in a downwind location of the source than in an upwind location. Therefore, the search route is designed near and within the downwind area of the estimated C-PP, to be followed by the robot to verify the area covered by the estimated C-PP. Searching by following the online planned route is carried out in the expectation of catching the chemical plume again, to perform the next iteration of searching, guiding the robot to gradually approach the source.
2.2.1. Illustration of the Online Planned Search Route
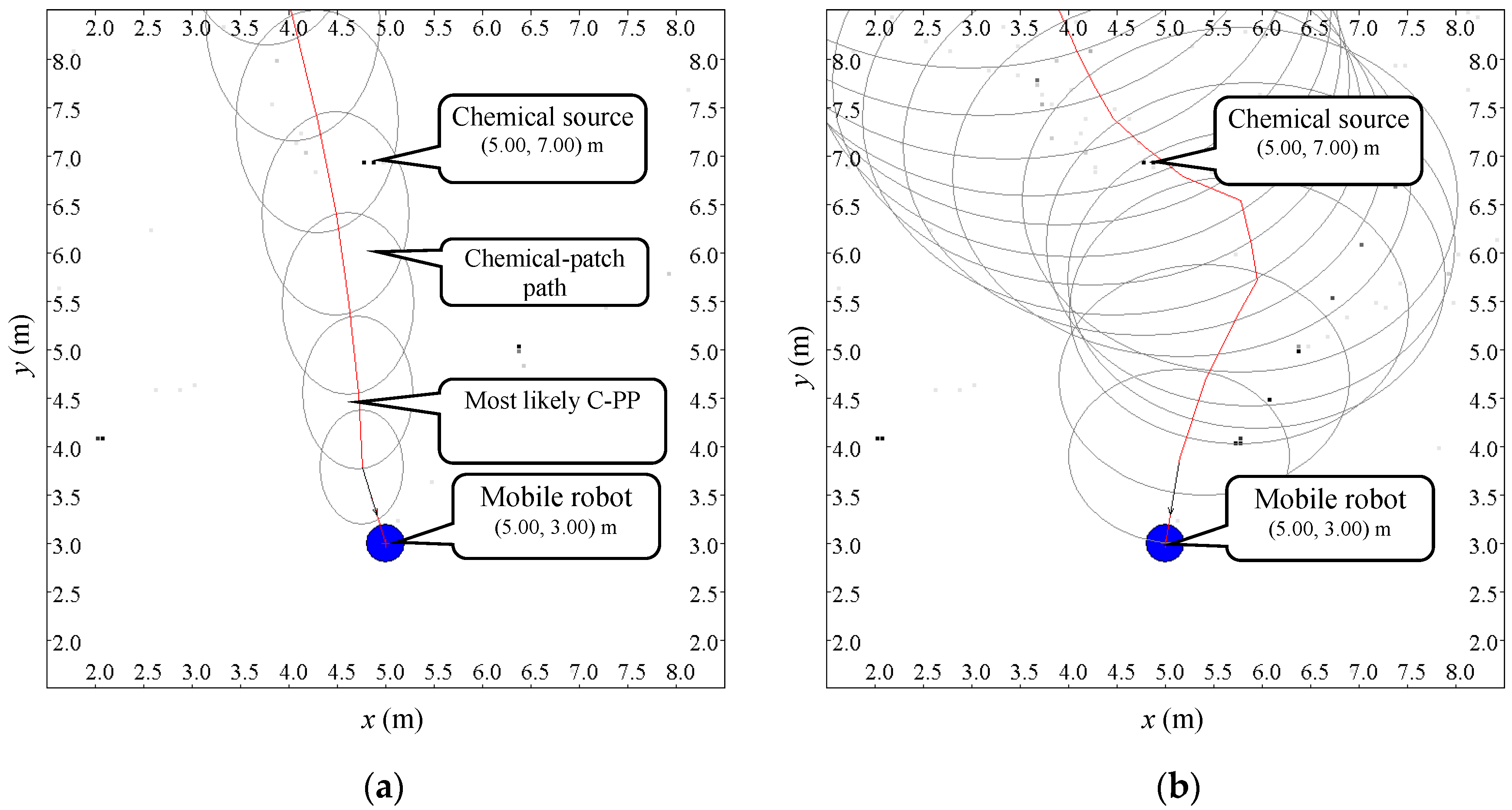
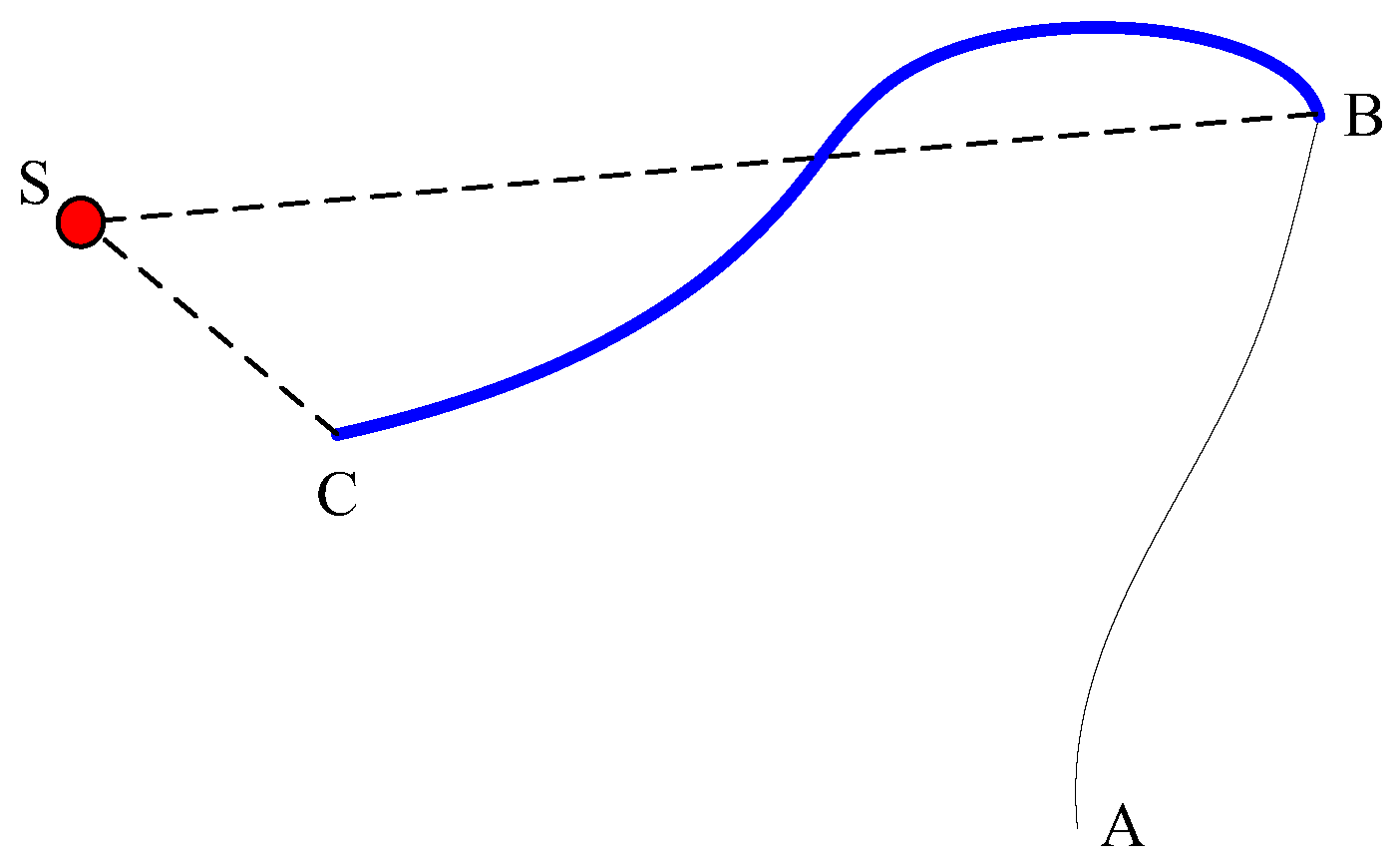
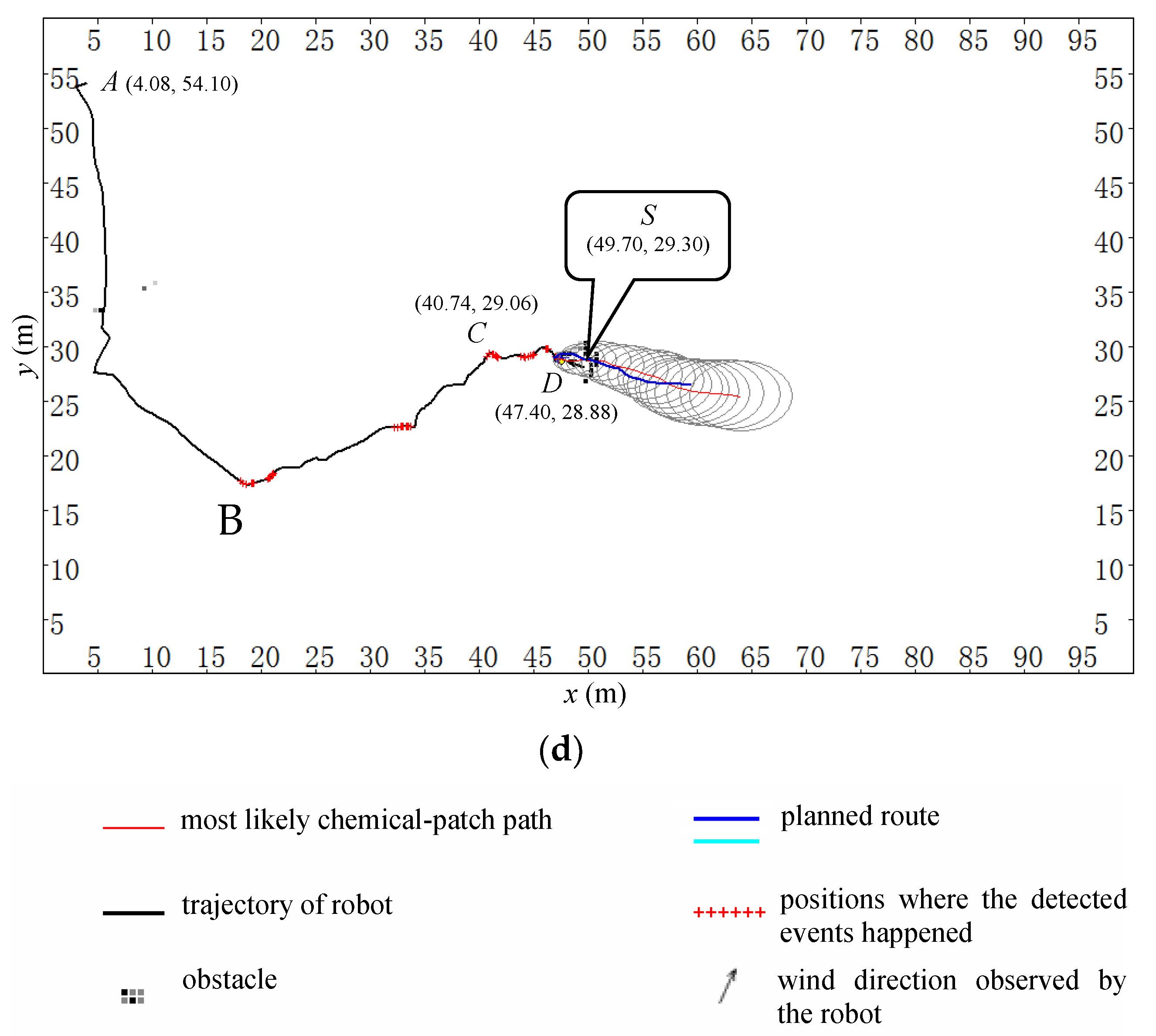
A schematic diagram of the search-route planning step is shown in
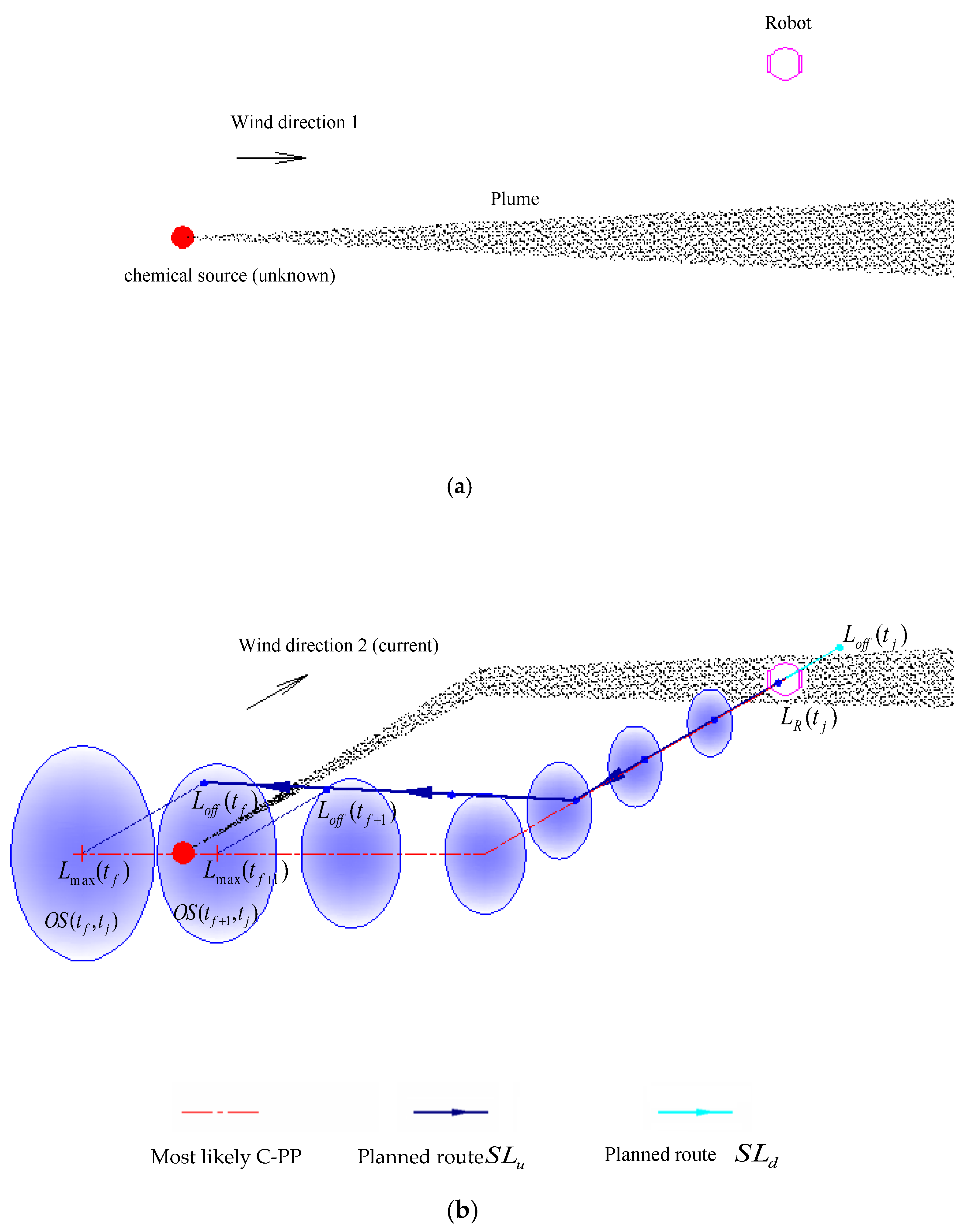
Figure 1. The gray strip originating from the chemical source indicates the plume, which is usually unknown to the robot; the ensemble of the blue ellipses denotes the estimated C-PP, and the red dash-dot line represents the most likely C-PP expressed in Equation (8).
The blue-black line and the cyan line constitute the online planned route for the robot to follow, i.e., , with the priority decreasing from left to right. and , the two parts of the online planned route deviating from the estimated C-PP in the downwind direction, are in roughly the upwind and downwind directions of the robot, respectively. The search route is planned online, aiming to make the robot re-meet the chemical clue. Normally, most areas covered by the estimated C-PP are in the roughly upwind direction of the robot. To be more likely to find chemical clues again, the robot should check these areas first. Therefore, is chosen as the first subroute for the robot to follow.
If another chemical patch is detected during the search along the planned subroutes and , a new C-PP will be estimated, and a new search route (including new subroutes and ) will be planned online for the robot to follow. If there is no chemical patch detected during the subroute , the robot has to return to the subroute to check the remaining areas covered by the estimated C-PP. Real-robot experiments show that the robot does not often follow the subroute , but it is necessary, because the subroute can be used to deal with two possible problems. One problem is that the robot might search for the chemical source in the wrong direction because of the improper estimation of the C-PP, such as in cases where the assumption of approximately uniform airflow occasionally fails. With the subroute , the robot can return to the search area where the most recent chemical-detection event occurred and try for the next possible meeting with the plume. The other problem occurs when the chemical source is near the location of the most recent chemical-detection event, but the robot passes the source, being unaware of its arrival at the source.
Through an iterative searching process (details see
Section 2.3), the robot could gradually approach the chemical source. It is worth noting that, if the airflow direction remains stable before and after a new chemical-detection event, the online planned route would be almost a straight line along the upwind direction, and in such a case, the robot would perform a searching behavior just like for a simple upwind action.
2.2.2. Mathematical Description of the Planned Search Route
As mentioned above, according to the current location of the robot and the current wind direction, the online planned route can be divided into two parts, i.e., the subroutes
and
, which are located in the roughly upwind and downwind directions of the robot, respectively. Suppose the robot has detected a chemical patch at
at time
, with the current time being
(
).
and
are expressed as
where
is a point deviating from the estimated C-PP in the downwind direction,
is the angle of the vector from
to
, and
is the short-time-average airflow direction at the current time
.
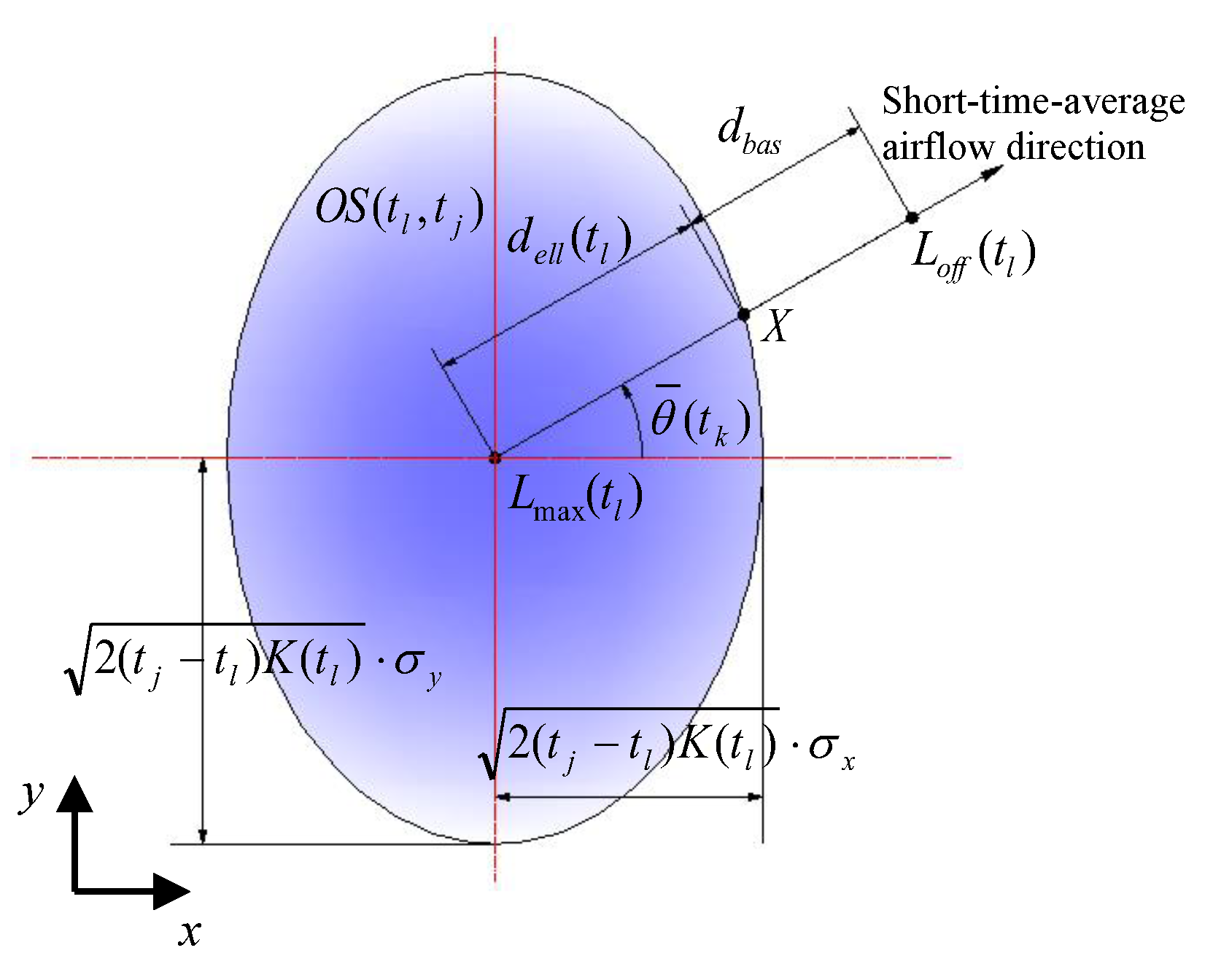
is shown in
Figure 2 and determined by
where
is the offset from
(see Equation (8)), and
is an extra offset (set to 0.1 m in our experiments). Here,
where
is the eccentric angle of the crossing point
X on the elliptical outline of
in
Figure 2, and
can be determined by
where
is the airflow velocity observed by the robot at position
at time
, and
2.3. Procedure of CSS
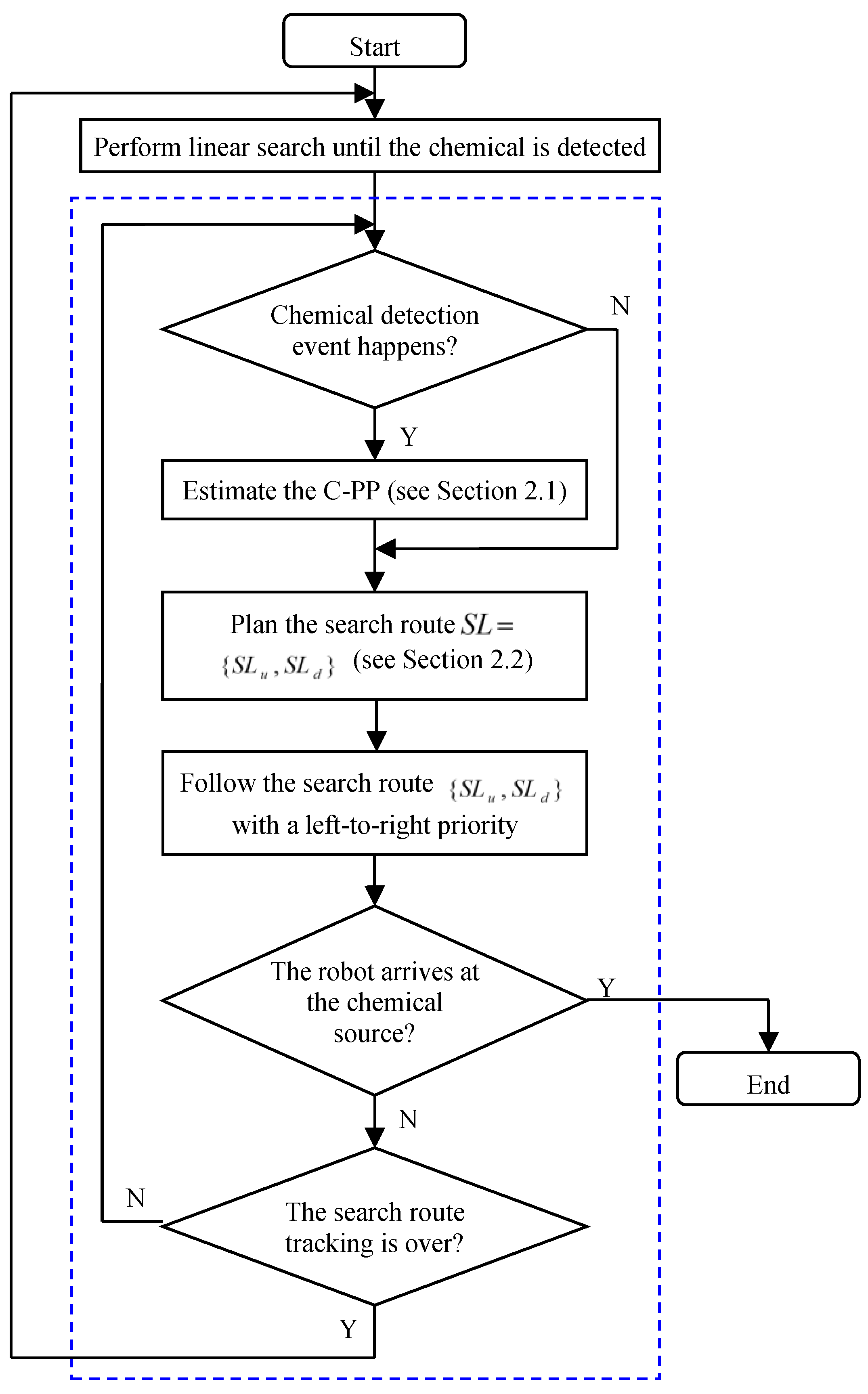
The proposed CSS is an iterative procedure, and its details are shown in
Figure 3. The linear search described in Russell et al. [
13] is adopted by the robot to find chemical clues, whereby the robot travels at an angle of 35° with respect to the upwind direction. To make the robot move smoothly in the chemical-clue-finding phase, we use the current short-time-average airflow direction as the reference of wind direction. When the robot moves near the boundaries of the search area or encounters an obstacle, it will turn back and make another linear search. When a chemical-detection event occurs, the robot switches to the ERP method to trace the two parts of the newly planned route
with a left-to-right priority. It is worth noting that the search route
will be updated at each time step according to the short-time-average airflow direction determined by Equation (12), so the route
tracked by the robot is time-varying.
During the tracking of the search route , whenever a new chemical-detection event occurs, a new C-PP is estimated, and the search route is re-planned. If there is no chemical-detection event after the robot has finished the search-route tracking, the chemical is considered to have been lost, and the robot will switch to the chemical-clue-refinding phase, which uses the same method with the chemical-clue-finding phase. When the distance between the robot and the chemical source is less than 2.5 m (an obstacle-avoidance request would arise in this case), it is considered that “the robot has arrived at the chemical source”, and the robot will be stopped manually. Here, the final stage of CSS, the chemical-source declaration, is left for future work and is not discussed in this paper.
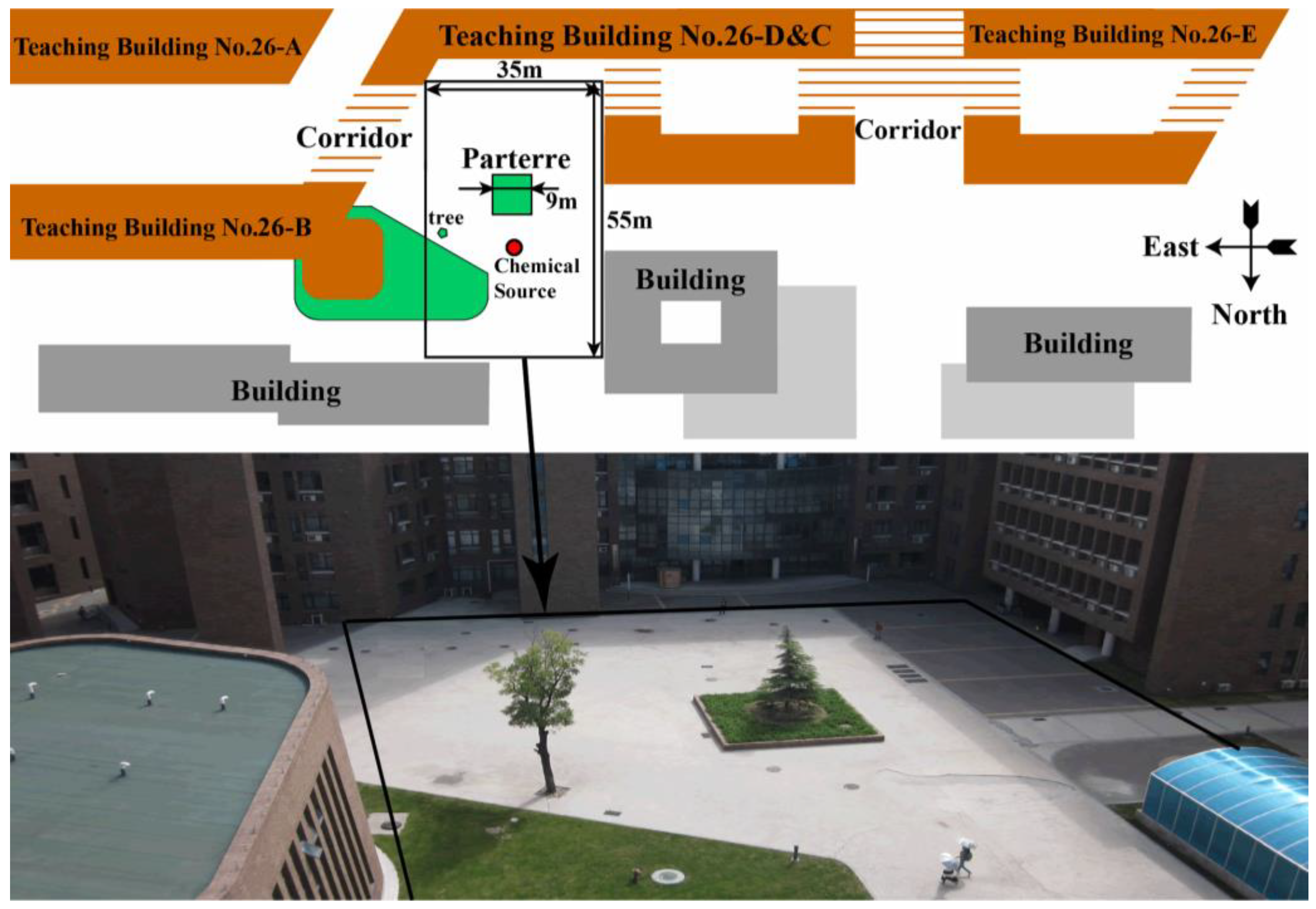
3. Experimental Platform
The experimental platform is shown in
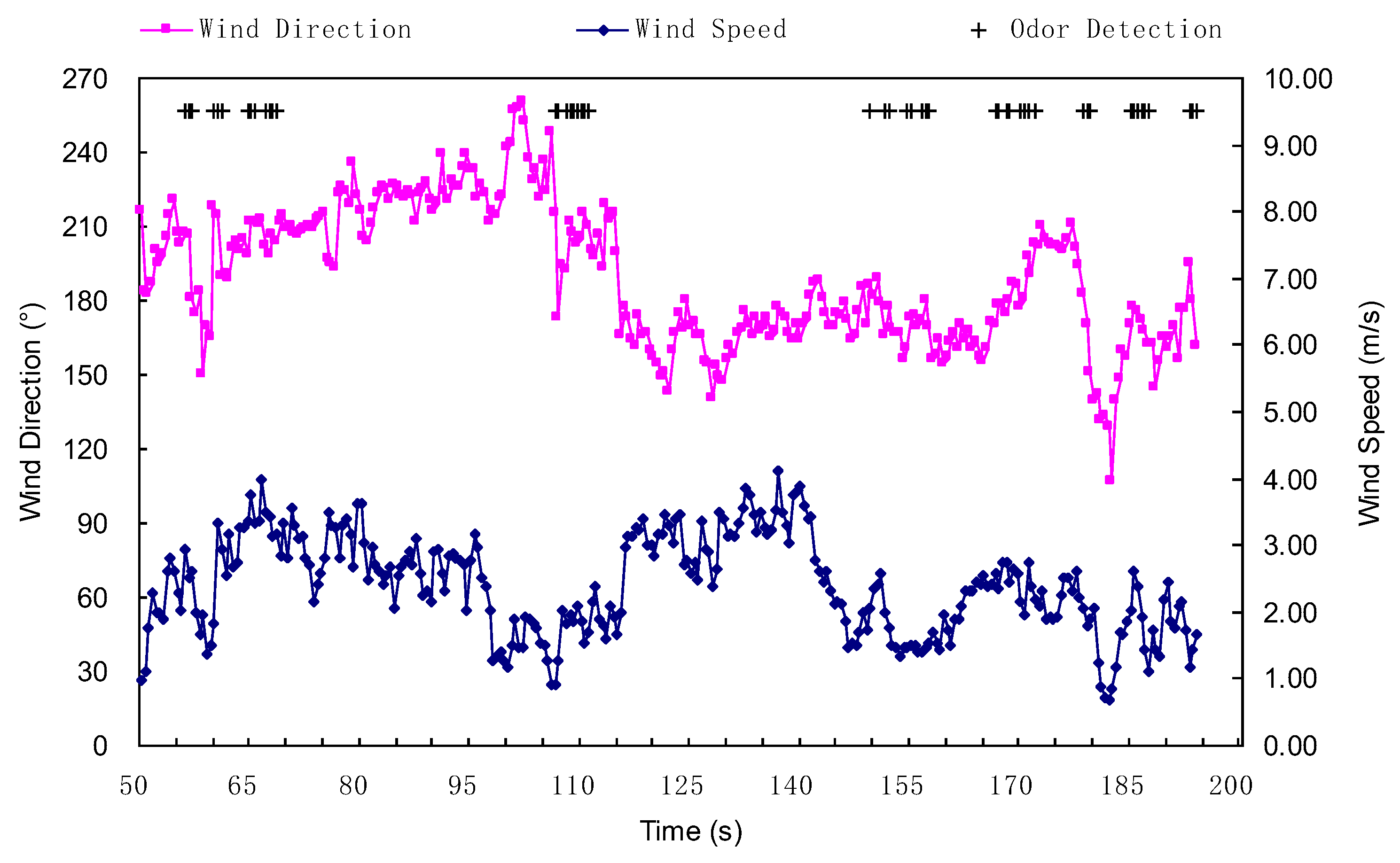
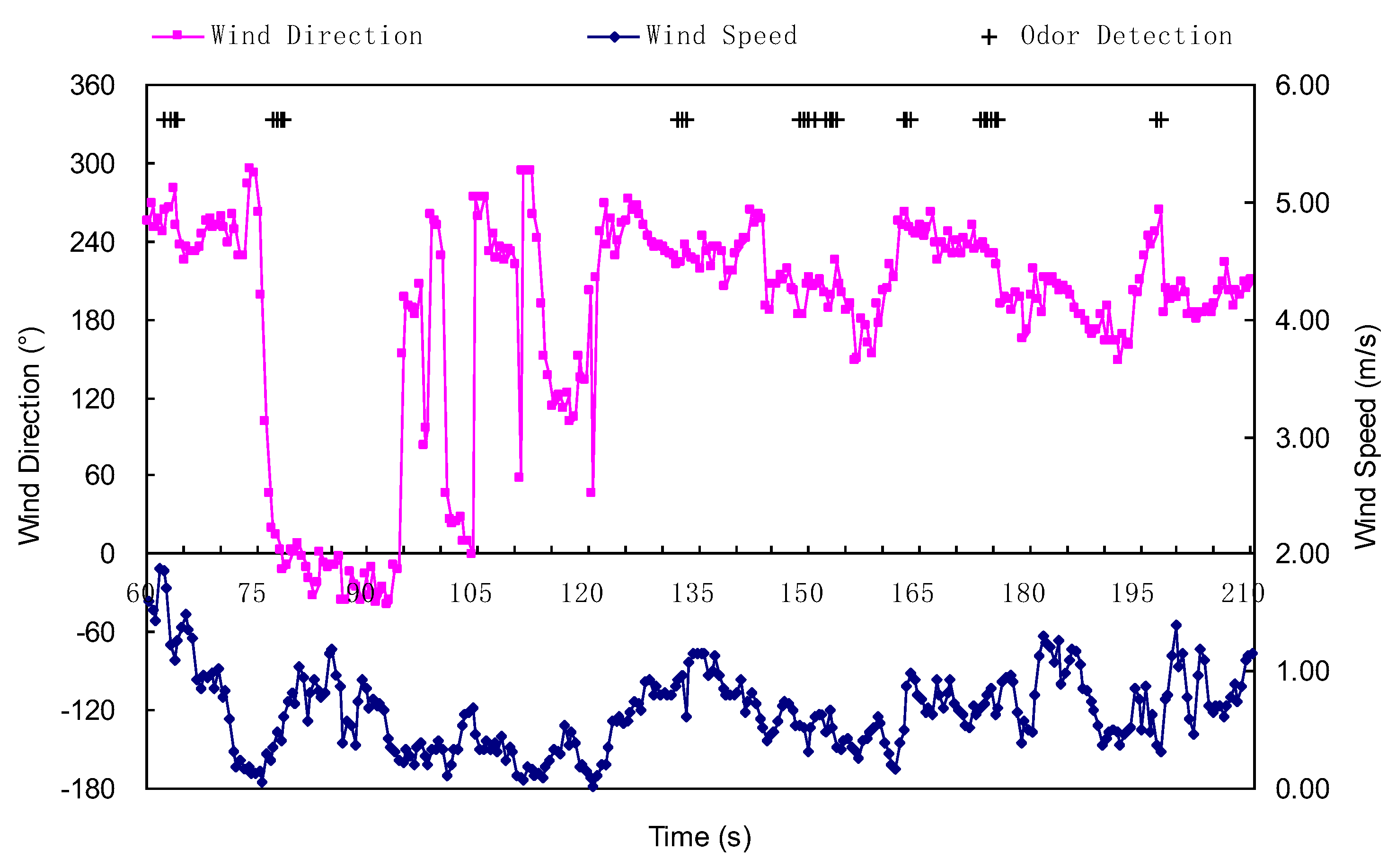
Figure 4. The robot used was a refitted Pioneer 3-AT (Adept Mobilerobots, Amherst, NH, USA) named MrSOS (Mobile Robot for Searching Odor Source), which is driven and steered differentially by four wheels, two mounted on the left and two on the right. A gas sensor (MiCS 5135, SGX sensor Technology, Co. Ltd., Chelmsford, Essex, UK), an anemometer (Windsonic, Gill Instruments Ltd., Lymington, Hampshire, UK), a laser rangefinder (LMS110, Sick AG, Waldkirch, Baden-Württemberg, Germany), an electronic compass, and a differential GPS (D-GPS) (NovAtel Inc., Calgary, Alta, Canada) module were mounted on the robot. The data from these sensors were received and processed by an onboard computer. The laser rangefinder was mounted at a height of 0.29 m above the ground. The electronic compass and the D-GPS module were used for the mobile-robot localization. Please note that the robot could measure its own speed, and the airflow speed described in this paper was a modified value, with the robot speed being deducted from the anemometer measurement.
The chemical source was a DIY humidifier containing liquid ethanol. The chemical patches were released from an outlet on the top of the humidifier while the liquid ethanol was being atomized by eight ultrasonic units at the bottom of the humidifier. The consumption rate of liquid ethanol was about 47.07 mL/min.
A binary concentration with an adaptive threshold [
30] was used in the experiments to enable the robot to respond to chemical interception quickly and reliably. If the measured concentration is above the adaptive threshold, it indicates a detection event; otherwise, a non-detection event.
6. Conclusions
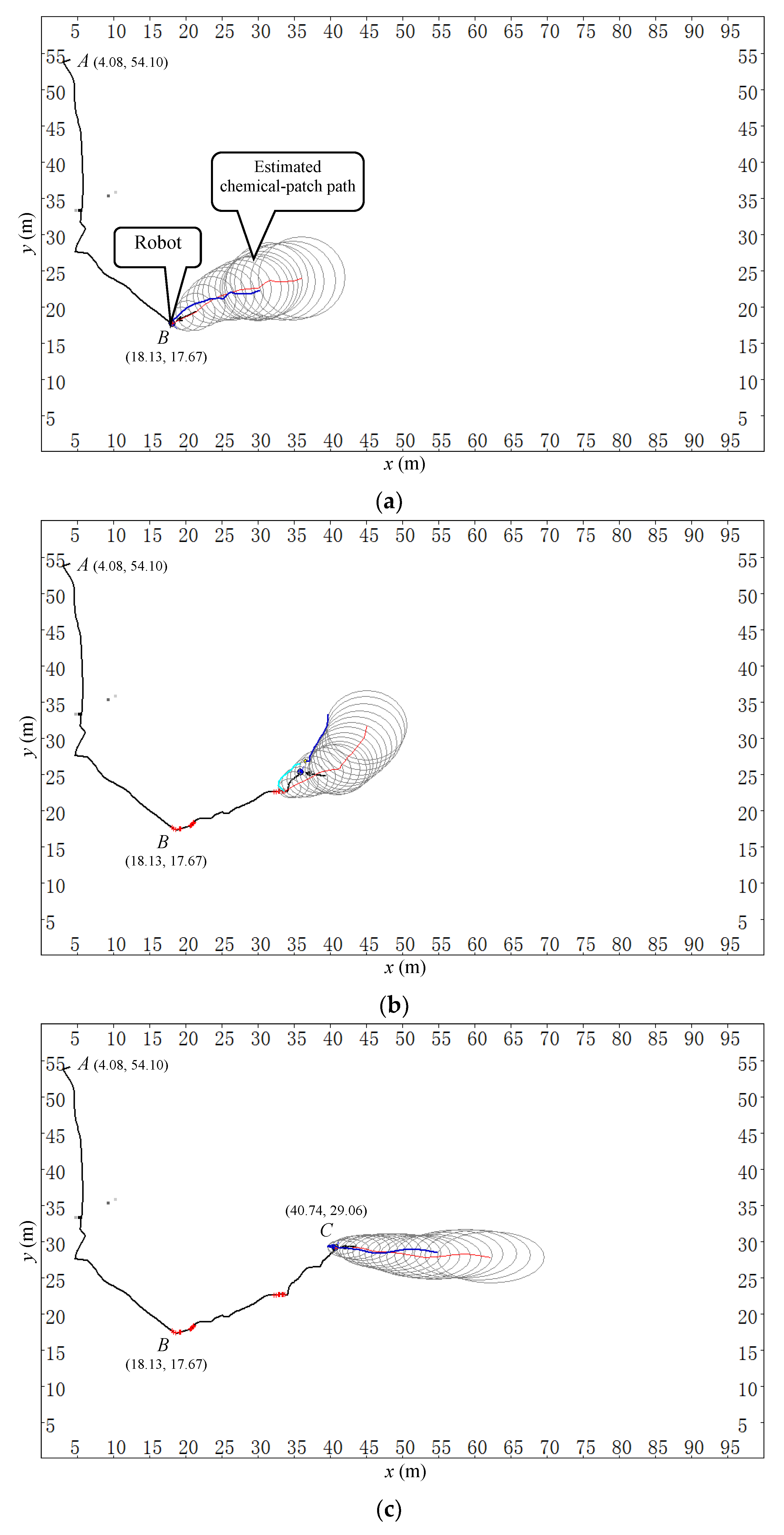
Real robot experiments in two different outdoor field environments show that searching for a chemical source according to online planned routes based on estimated C-PPs is a feasible method for a normal wheeled mobile robot moving slower than airflow/chemical plume and is equipped with slow-response gas sensors. In general, searching for a chemical source according to the proposed ERP method shows good robustness to experimental environments. This is because the current and historical flow information are both fully exploited in the proposed method, which results in highly purposive and adaptive search behavior. By following an online planned search route, the robot can systematically check the area covered by the estimated C-PP that possibly contains the chemical source, gradually approaching the chemical source and without having to consider the speed of the chemical plume. Compared with methods trying to make the robot trace chemical plume to the source by keeping contact with the plume, the proposed ERP method has less requirement on the maneuverability of the robot. Because the search route is updated at each time step to match the short-time-average airflow direction, the search behavior of the robot is able to adapt to variation of airflow direction.
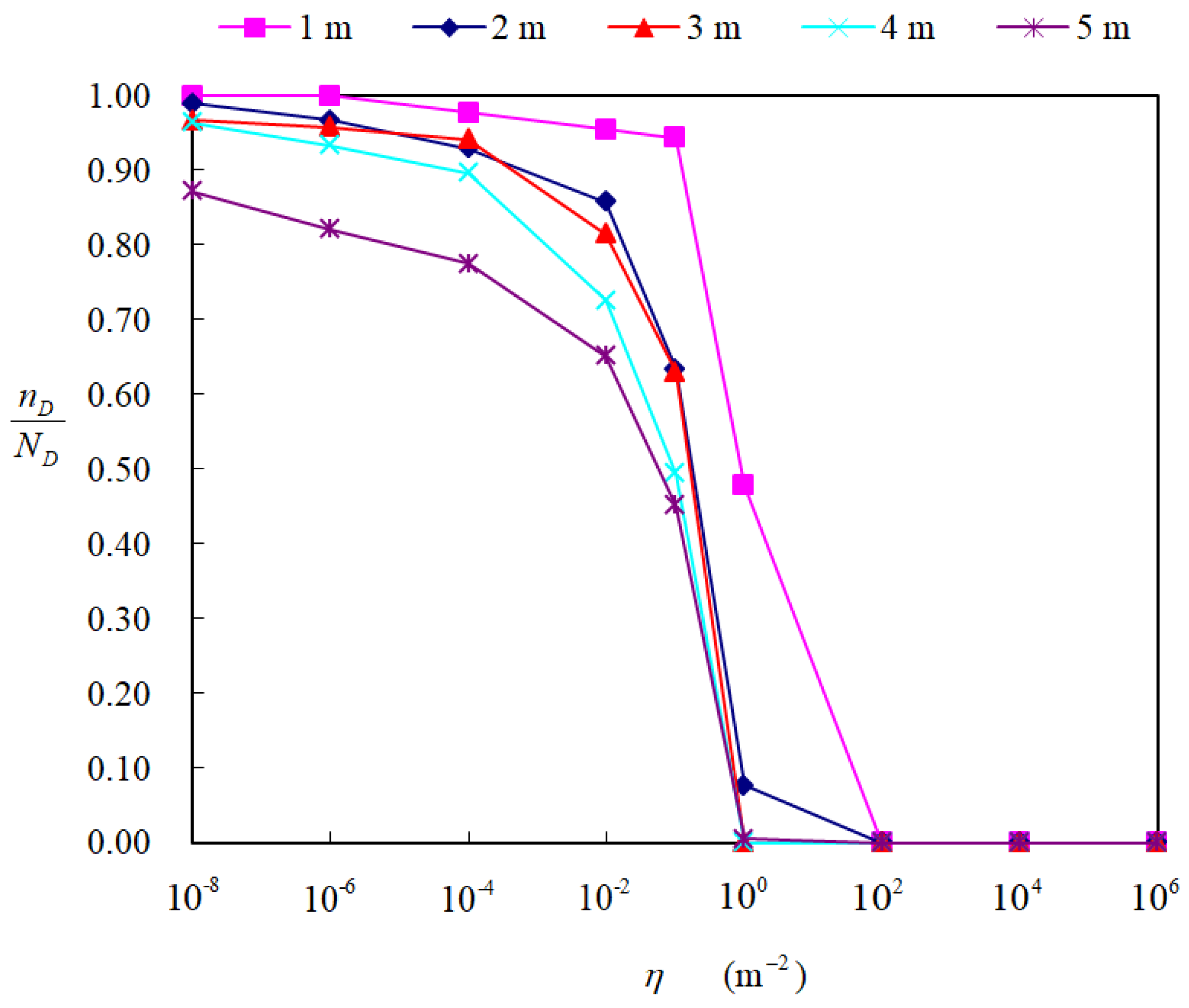
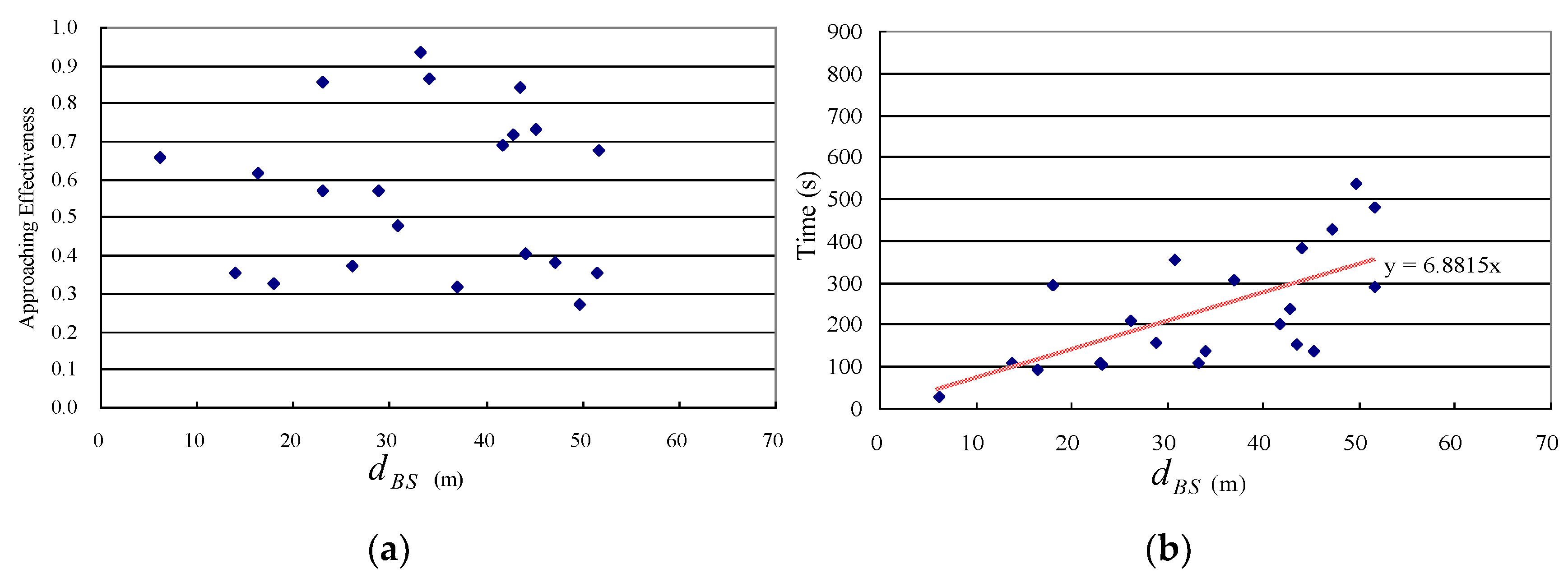
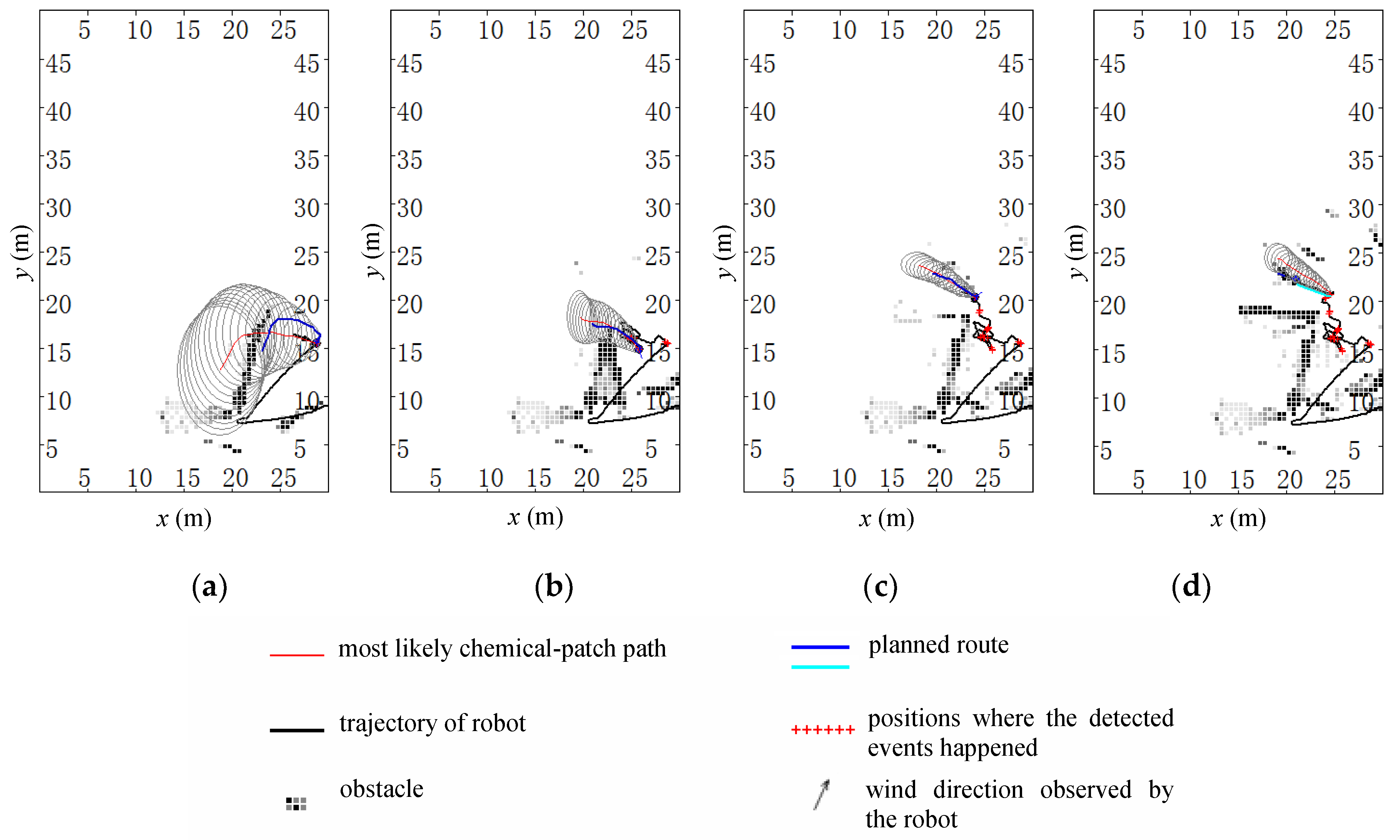
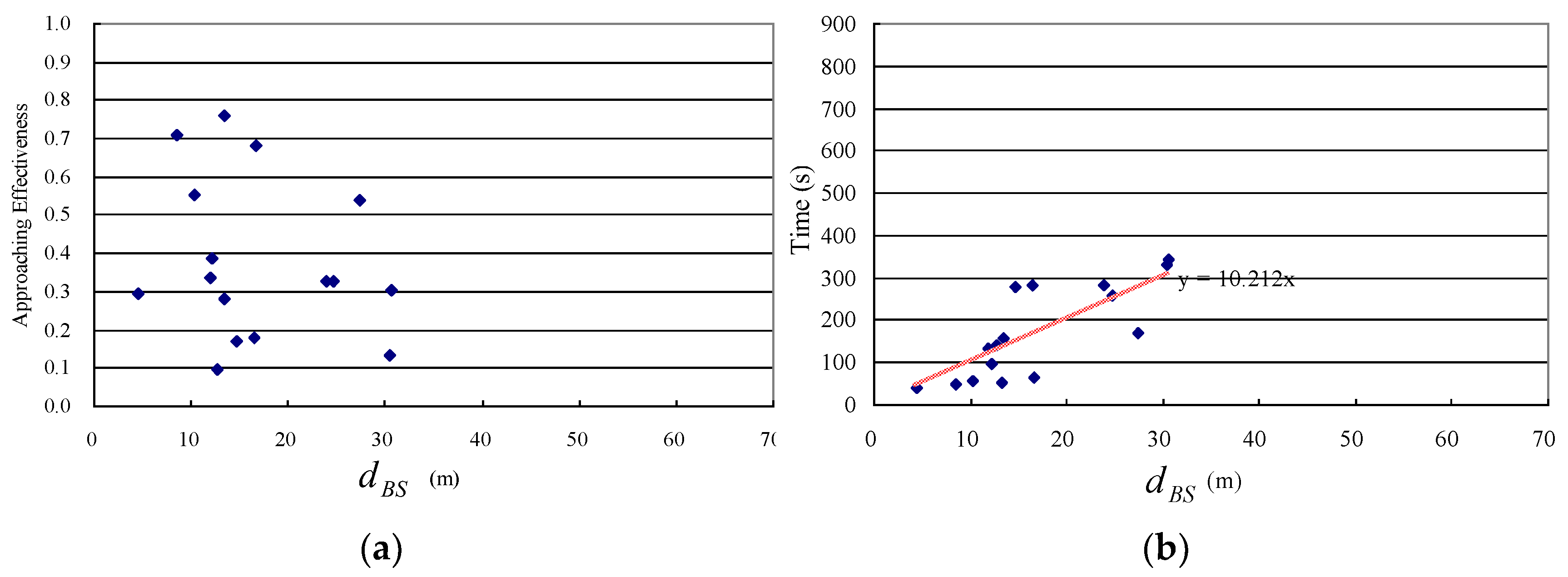
Based on the experimental results, we could further draw the following conclusions. Firstly, the uniformity of airflow field depends, inter alia, on the wind magnitude and distance. Normally, with a decrease in the wind magnitude and an increase in the distance, the uniformity of airflow field decreases. Secondly, uniformity of airflow field has an impact on searching performance. In relatively small and complex fields, since the airflow field is far from uniform, the robot might be confused by the capricious airflow and chemical measurements, leading to a difficult CSS. Thirdly, the proposed ERP method can work in environments with obstacles, although the obstacles decrease the approaching effectiveness and increase the time cost. Lastly, the approaching effectiveness of the proposed method is not sensitive to the maximum speed of the robot.