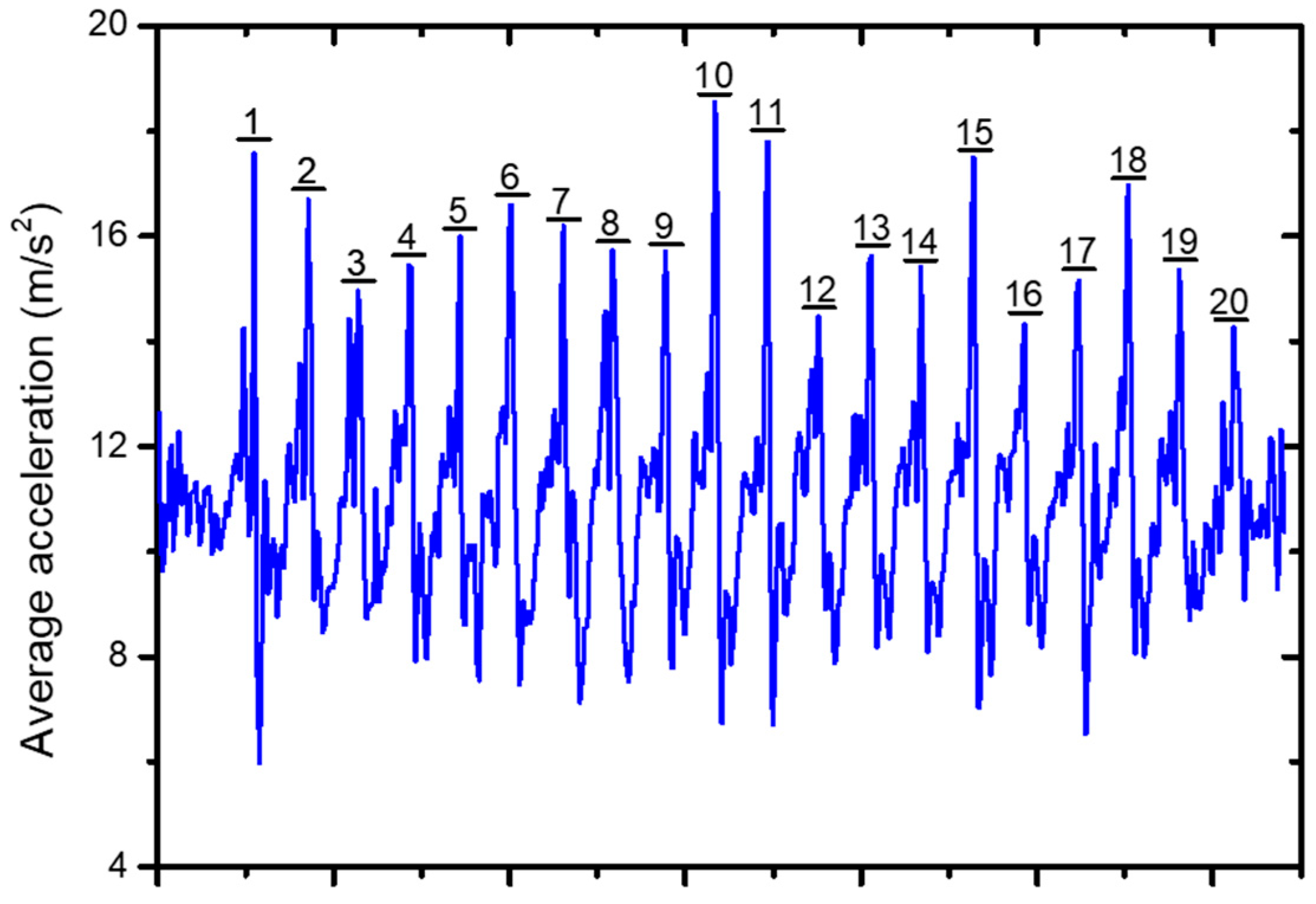
1. Introduction
Until now, the GPS-based positioning system has successfully solved the outdoor localization and navigation problems. However, people spend more than 80% to 90% of their time indoors. It is estimated that the indoor positioning market will grow to
$4.4 billion by 2019 with strong demand in healthcare, retail, hospitality, travel and other sectors [
1]. GPS, which has revolutionized outdoors localization, has proven ineffective for indoor environments due to the lack of signal coverage. Hence, several alternative approaches for indoor positioning systems were applied: Wi-Fi based positioning systems [
2], Bluetooth Low Energy (BLE) based positioning systems [
3], Radio Frequency Identification (RFID)-based positioning systems [
4], Ultra-Wide Band (UWB)-based positioning systems [
5], Visible Light Communication (VLC)-based positioning systems [
6], sensors-aided positioning systems [
7,
8]. These methods are based on different information sources like wireless communication technologies or sensor measurements. However, each of them has disadvantages, such as low precision, unreliability, high complexity or high hardware cost. For example, the Wi-Fi-based solutions have limitations due to the limited numbers of access points (APs) and their inflexibility in deployment, resulting in poor accuracy, from 5 to 15 m. In the case of RFID-based solutions, it has the best accuracy among all the technologies (error below 0.1 m) and needs no battery within its lifetime, but the short range (below 1 m) and the extensive and expensive installation of large amounts of readers restricts its use. Although UWB-based solutions have good accuracy (error below 0.3 m) and an up to 150 m range, the high-power consumption and high cost are its main disadvantages.
Besides, none of these technologies are a completed solution to fit all indoor positioning needs and there is no single technology that can provide reliable indoor positioning. Therefore, many researchers have tried to fuse two or more kinds of above technologies to design a robust and low-cost indoor localization method. In Ref. [
9] Chen et al. carried out a Wi-Fi PDR (Pedestrian Dead Reckoning) integrated method to a real-time positioning for targets in 3D scenes. A combined Wi-Fi and BLE positioning system were presented to improve the accuracy and precision of indoor positioning with low deployment density [
10]. A hybrid indoor positioning method for asset positioning by using BLE and Wi-Fi achieved 90% accuracy within 1.21 m [
11]. BLE is also integrated with PDR to achieve a positioning accuracy of less than 1 m [
12].
Most of the research and applications refer to systems using either BLE or Wi-Fi technologies, since they performed better in terms of quality and cost. BLE is a recently developed wireless technology, which improves Bluetooth technology, consumes less energy and has a long lifetime. As it is inexpensive, low-energy and easy to install, it has been widely employed for various purposes, like localization, proximity detection and interaction, active sensing, etc. [
13]. The indoor positioning is one of the most important applications of BLE and positioning by BLE can achieve sub-meter accuracy [
14]. Received Signal Strength Indicator (RSSI) is the most common way for BLE to estimate the position of the device being tracked. Generally, the most common methods of positioning are the trilateration algorithm and fingerprinting algorithm. Trilateration algorithm is the method of determining absolute or relative locations of points by measuring the distances using the geometry of circles, spheres or triangles [
15]. In Ref. [
12], Robesaat et al. proposed a positioning method based on fusing trilateration and dead reckoning with Kalman filtering as a position fusion algorithm, to achieve a positioning accuracy of less than 1 m. The fingerprinting algorithm relies on a previously-constructed radio map of BLE signals, in which measurements are collected from the environment and calibrated into specific features, called fingerprints, which describe a part of the environment [
16]. In Ref. [
17], Danis et al. developed a method to render indoor localization and tracking practical with mean of BLE RSSI fingerprinting. Generally, the fingerprinting-based positioning with dense fingerprint locations outperforms the trilateration-based positioning in terms of reliability and precision. However, compared to trilateration-based positioning, the fingerprinting-based positioning needs dense BLE deployment and high time-cost preparation work. Besides, the fingerprinting-based positioning is very susceptible to any environmental change which may cause the radio map to change [
18].
Moreover, there are a lot of Bluetooth devices for achieving intellectualized control in modern buildings such as Bluetooth lamps, Bluetooth audio, and Bluetooth transmitters. These Bluetooth devices broadcast their Bluetooth signals incessantly resulting in a dense Bluetooth environment. The environmental conditions are very variable and therefore may affect accuracy and precision in relation to the actual location [
3]. Most of the existing research has focused on the solutions that combined different supplementary means (Wi-Fi, PDR, etc.) to improve the accuracy of the BLE-based indoor positioning, since the RSSI of BLE is unreliable in distance estimation. However, few studies pay attention to the BLE-based indoor positioning in a dense Bluetooth environment, where the propagation of BLE signals become more complex and more fluctuant.
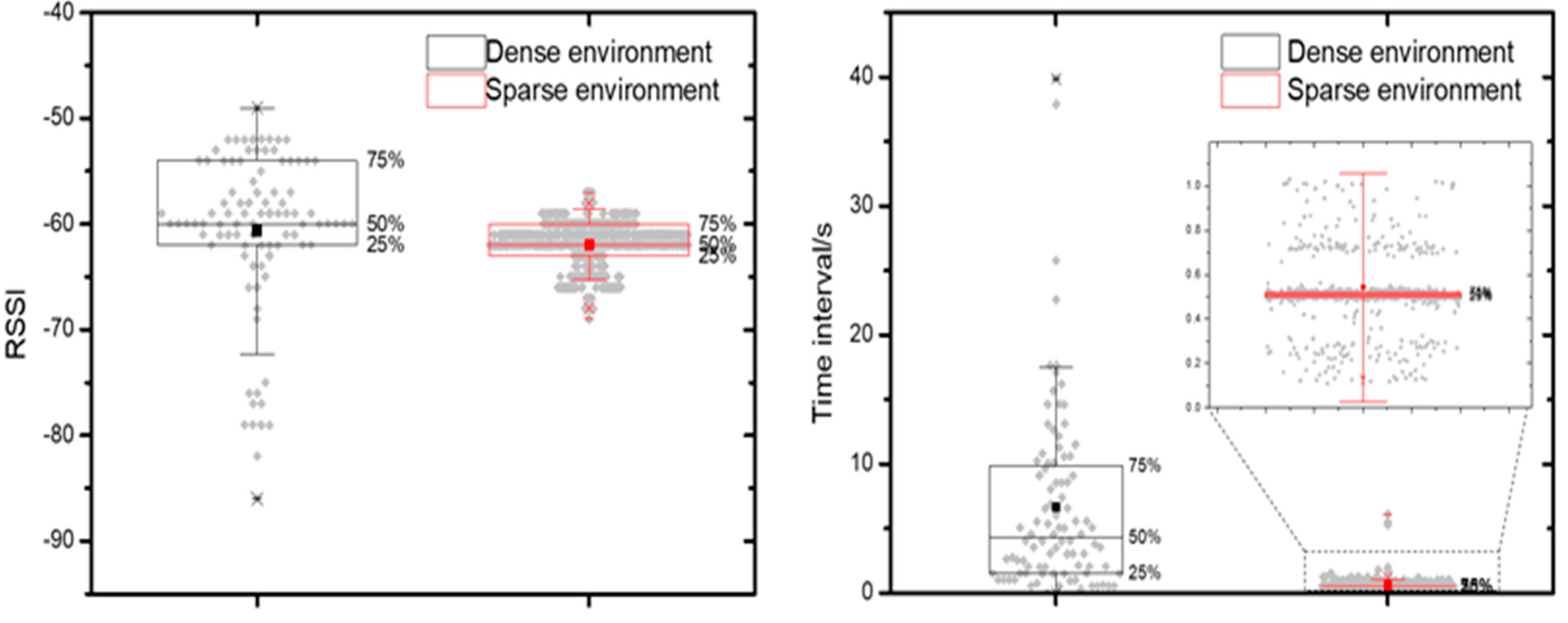
The distance estimation error and the signal timeliness become more severe when multiple Bluetooth sources are present within a small area, since a smart phone or a RSSI receiver might be unable to process all the signals within a short scanning period. It was proved that each of the 10 static beacons requires less than 1 s to be detected under a sparse environment, while the detection time can take more than 5 s under a dense environment [
13]. A long interval collection or a partial signal collection may result in a poor accuracy of indoor positioning. In addition, with the development of Bluetooth smart home devices and the spread of Bluetooth built-in consumer electronics, more and more Bluetooth signals are present in the indoor environment, forming a dense Bluetooth environment. It is important and urgent to develop a BLE-based indoor positioning solution suitable for dense Bluetooth environments.
In this work, a hybrid approach of BLE-based indoor positioning using a set of pre-deployed BLE beacons and smart mobile devices was proposed for achieving high accuracy in a real implementation of a dense Bluetooth environment. Numerous exiting indoor localization methods, namely trilateration and PDR, were applied. Moreover, Kalman filtering was adopted as a position fusion algorithm to improve accuracy, which integrates the advantage of trilateration and PDR and relives their weaknesses as well. Finally, the method to a real implementation of dense Bluetooth environment was applied and the practicability was verified.
The remainder of this paper is divided into six parts as follows.
Section 2 defines the problem resulting from the dense Bluetooth environment and the overview of our BLE-based indoor positioning system.
Section 3 elucidates the BLE propagation model and the trilateration algorithm.
Section 4 investigates the PDR method, followed by the proposed hybrid approach with Kalman filtering to improve the accuracy in a dense Bluetooth environment in
Section 5.
Section 6 illustrates the use of the hybrid approach in a real implementation of high dense environment and verifies the practicability of the method. Finally,
Section 7 draws the conclusions.
5. Hybrid Indoor Positioning
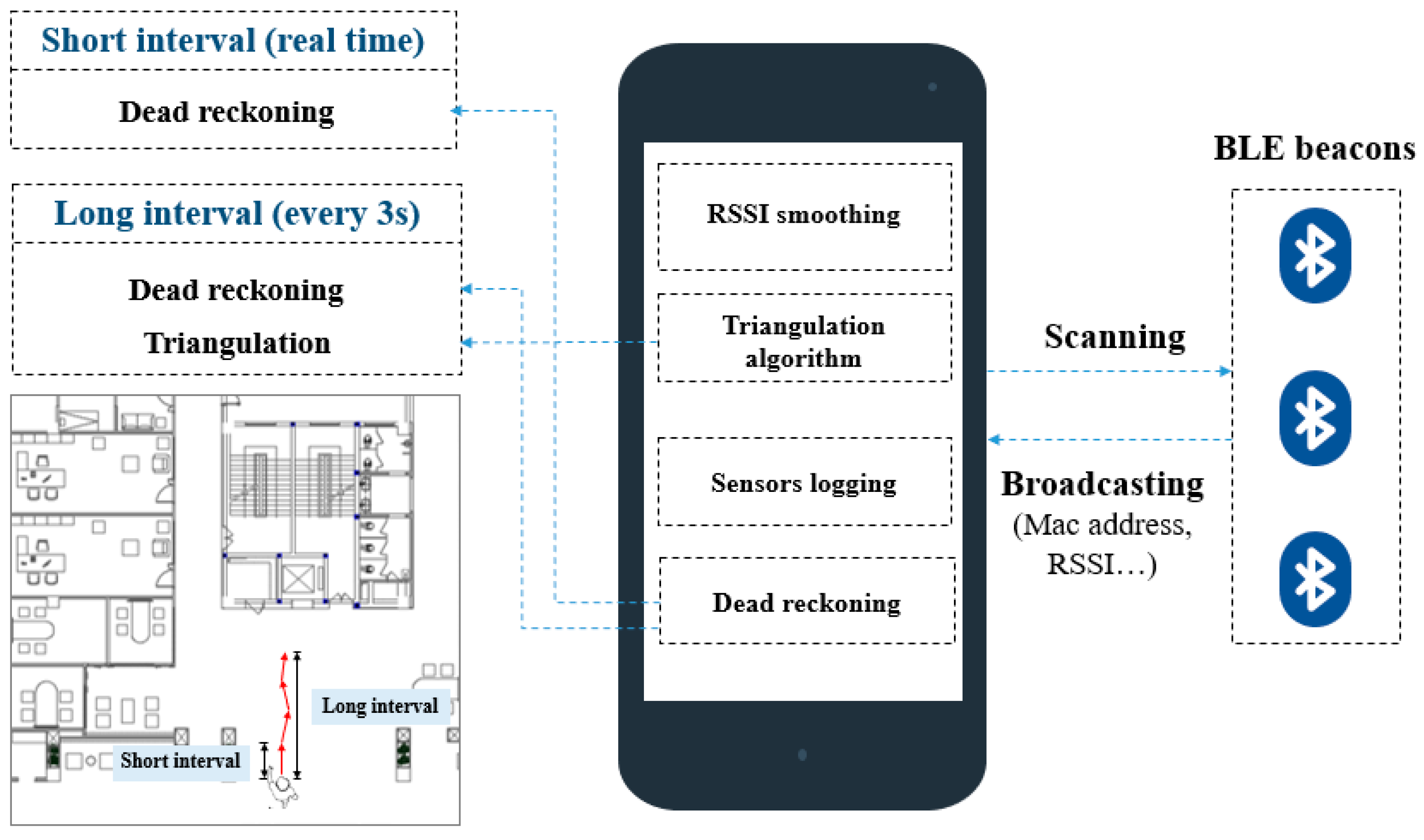
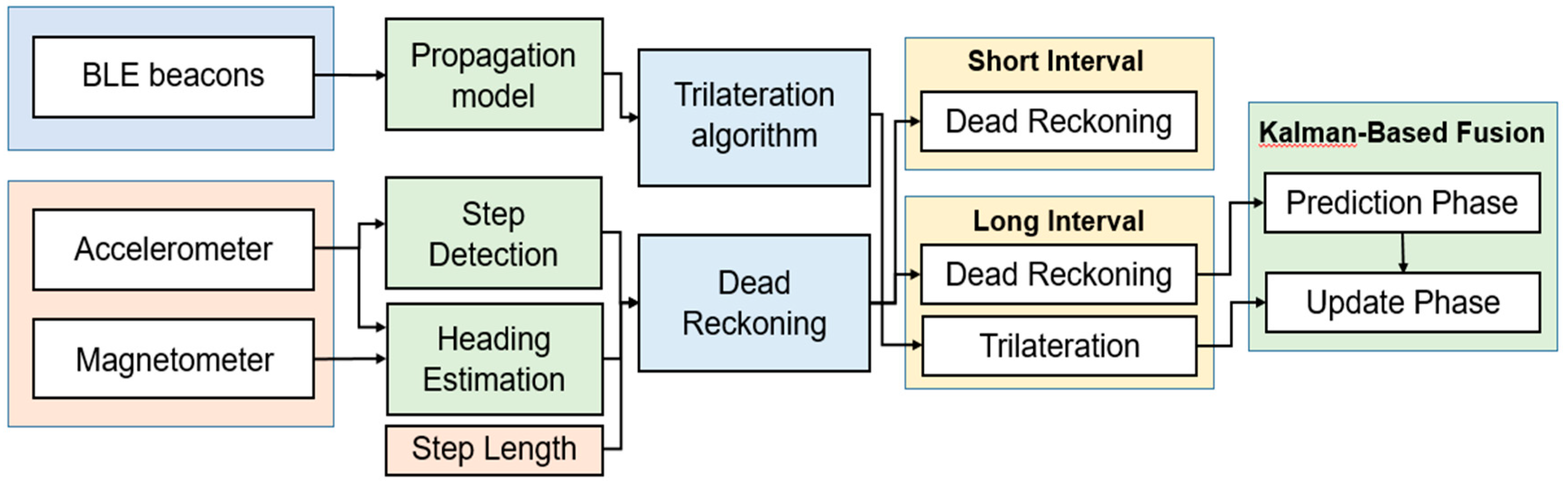
In this section, the hybrid indoor positioning method combined with Trilateration algorithm and dead reckoning is illustrated. The hybrid positioning method centered on overcoming the high RSSI variation and a long collection time interval of BLE resulting from the dense Bluetooth environment and exploiting the advantages of Trilateration algorithm and dead reckoning, but avoiding possible disadvantages, as depicted in
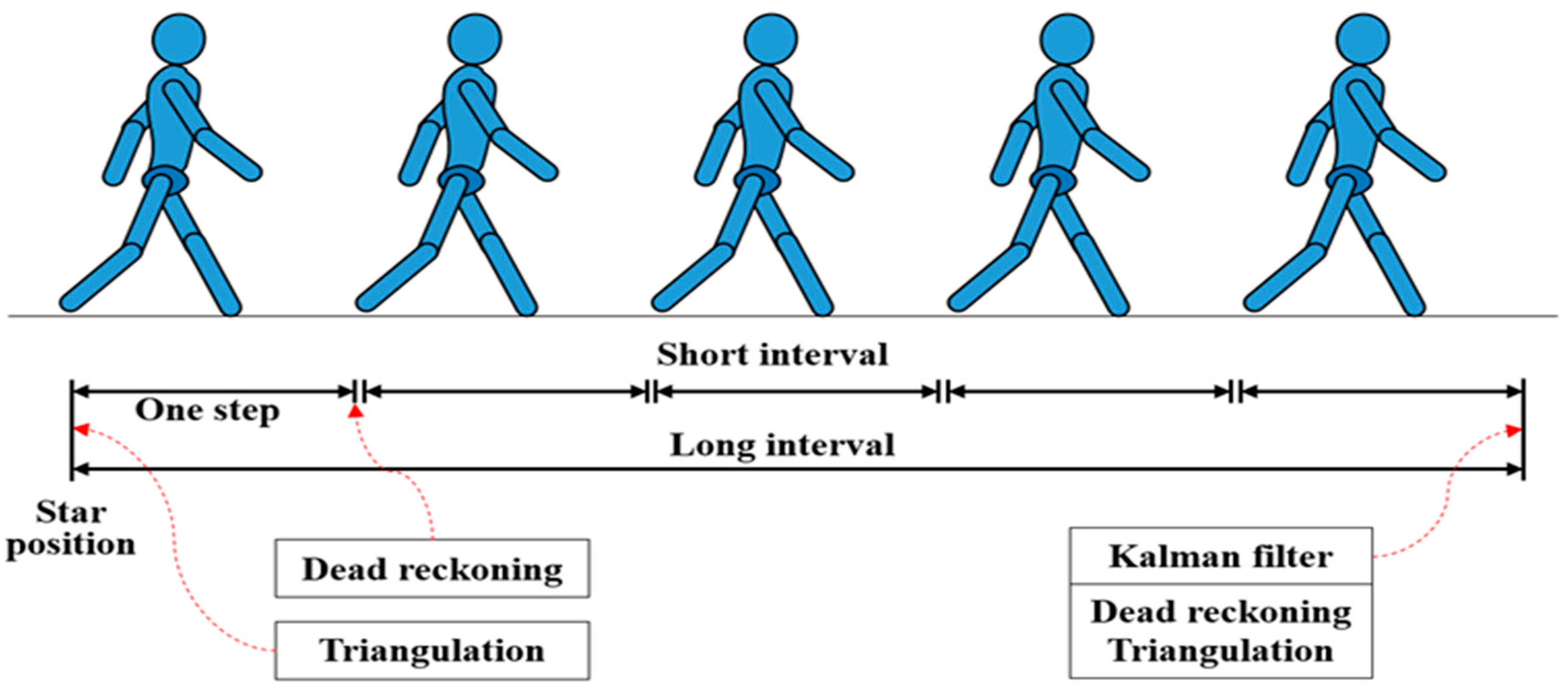
Figure 6. As mentioned before, the indoor positioning system was divided into two positioning phases, as shown in
Figure 7. During the short interval, the dead reckoning was used to determine the location of the mobile device. However, during the long interval, the triangulation algorithm was exploited to correct the deviation of the dead reckoning caused by accumulative sensing errors. To achieve that, a Kalman filter was used as a fusion center to merge the two obtained positions from the two algorithms.
5.1. Two Positioning Phases
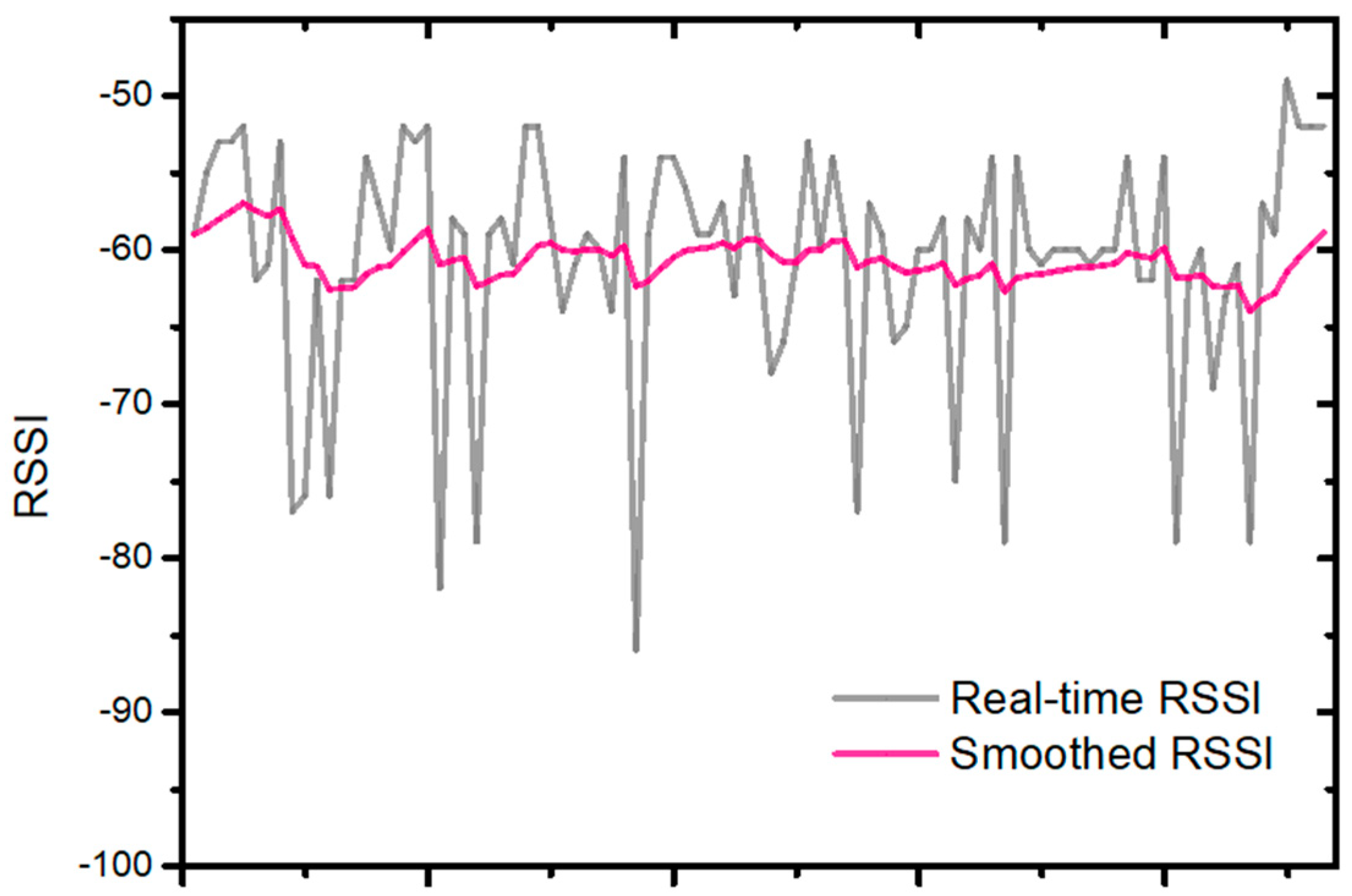
As mentioned above, a lot of the unwanted and distracted Bluetooth signals in the environment will affect the scanning of the wanted and specific BLE signals in a dense Bluetooth environment. Moreover, an average 6.652 s time interval was needed for one BLE signal collection in the dense environment, which means that the frequency of one BLE beacon signal collected by a phone was 0.15 Hz. In this indoor positioning system, there were eight BLE beacons distributed in the ceiling, which means that the frequency of the one of the eight beacons signals collected by a phone was 1.2 Hz. The trilateration algorithm took at least three BLE signals to calculate the position of the target and it would take at least 2.5 s to collect enough BLE signals feeding the trilateration algorithm to get the position. However, during the 2.5 s interval, one person possibly moves a long distance and the result from the trilateration algorithm loses timeliness leading to a wrong positioning estimation. Therefore, the dead reckoning will contribute to the real time positioning estimation. Dead reckoning produces highly accurate position fixes at the beginning of the measurements. Nevertheless, the dead reckoning performance continuously drops due to accumulative sensing errors. Consequently, it was necessary to divide the indoor positioning system into two positioning phases in a dense Bluetooth environment. During the short interval, the dead reckoning was used to determine the location of the mobile device. During the long interval, the triangulation algorithm was exploited to correct the deviation of the dead reckoning caused by accumulative sensing errors. To get the enough BLE signals for trilateration algorithm, the long interval was set to 3 s.
5.2. Kalman-Based Fusion
During the long interval phase, a Kalman filter was chosen to integrate the trilateration algorithm and dead reckoning [
12]. In the Kalman filter, the state model is obtained from the dead reckoning method and the state equation can be expressed as:
where the state vector
represents the coordinates of the target from the dead reckoning.
F and
B are identity matrices, and
N is the total amount of counted steps during the long interval phase. While,
is the coordinate change derived from
ith step. In this case,
sl is the step length and
is the heading direction. Therefore, the coordinate change resulting from the dead reckoning method during the long interval phase can be expressed as:
The measurement model is obtained from the trilateration positioning method. The measure model can be expressed as:
where
represent the coordinate of the target from the trilateration positioning, and the
H is identity matrix.
Once the time interval reaches 3 s, the Kalman filter updates the position with a prediction and an update phase. In the prediction phase, a position can be predicted as following:
where
Q is the covariance of the noise from the dead reckoning method. In the update phase, the positions from the both methods can be merged as following:
where the
K is the Kalman gain and
I is identity matrix.
R is the covariance of the noise from the trilateration positioning method, and
represents the merged position. Different values for
R and
Q were experimentally tested, and the best results were obtained by using
R = 4 and
Q = 0.1.
6. Implementation of the Hybrid Method
In this section, the performance of the proposed hybrid method was evaluated in a dense Bluetooth environment. A mobile device was used to carry out the tests.
6.1. Test Scenario
To evaluate the performance of the proposed algorithm, we conducted experiments in the middle of the office floor (the red square area), depicted in
Figure 8A. The area size was 5.6 × 8.8 m
2. There were 18 Bluetooth lights in the square area they broadcasted their Bluetooth signals incessantly resulting in a dense Bluetooth environment, as shown in
Figure 8C. Eight BLE beacons were placed in the square area, depicted in
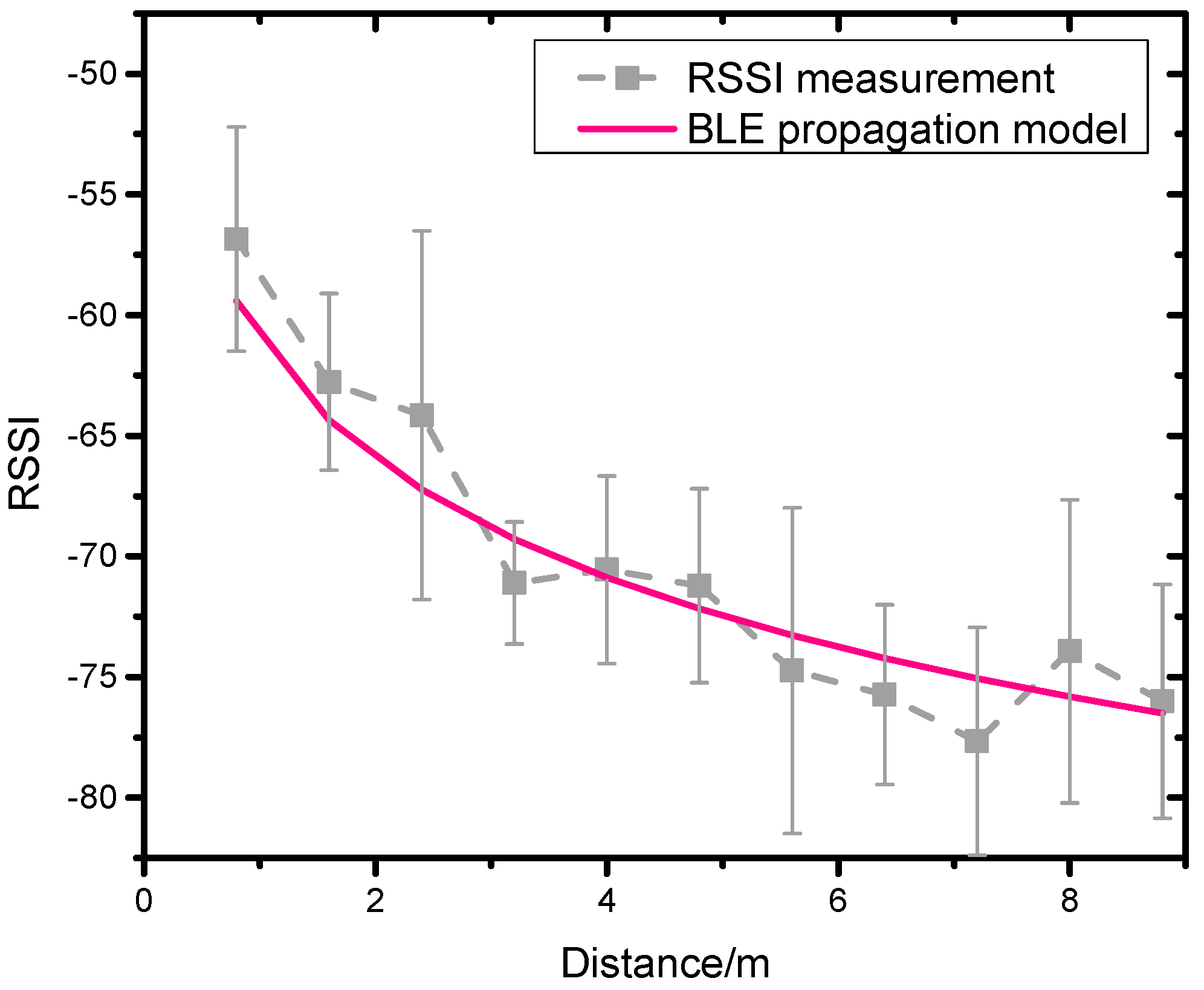
Figure 8B. Each of the beacons was placed in the ceiling, at a height of 2.7 m. The tester walked with a smartphone in the test area following the predefined path. The distance between two beacons was 4 to 6 m, such that the square was entirely covered by BLE signals. Since a 2D trilateration method was applied, the vertical distance
between the beacon and the mobile was required to get the horizontal distance
between the beacon and the mobile. Hence, the horizontal distance
in terms of measured distance
and the vertical distance
between the beacon and the mobile, as given by:
6.2. Performance Evaluation
In this section, the performance of dead reckoning, Trilateration and Hybrid method are comprehensively evaluated. It is necessary to explain that the dead reckoning method requires the coordinate of the initial position. In each test, the person holding a smart phone continued to move along the determined path with a length of 28.8 m in the area covered by the BLE modules. In the experiment, the positioning performances of the three methods in a dense Bluetooth environment were tested.
6.2.1. Dead Reckoning
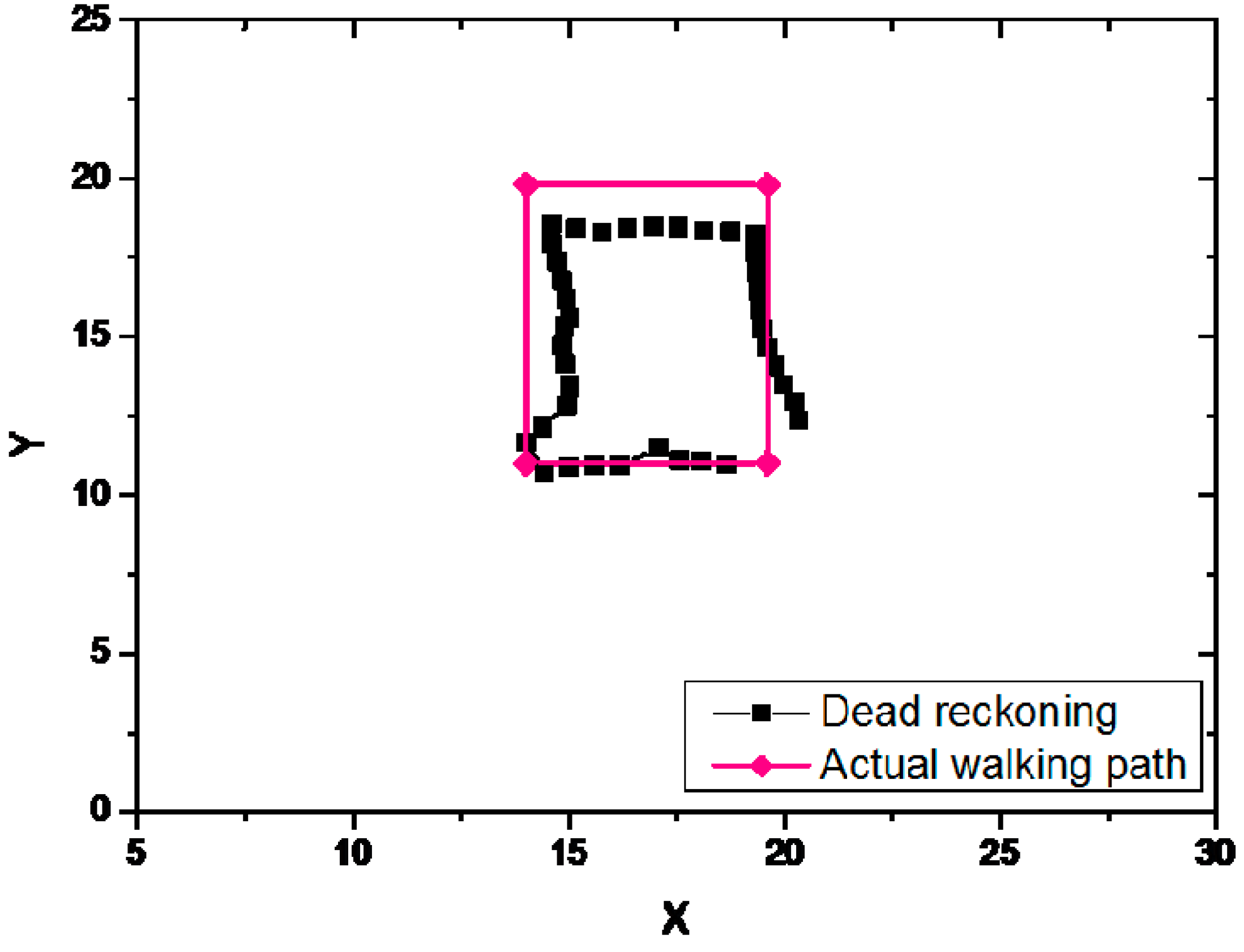
In the dead reckoning experiment, the magnetic sensor and accelerometer of the smart phone were mainly used for positioning. The dead reckoning method should get its initial coordinate at the beginning of the position, because it cannot calculate the initial coordinate by itself. The estimated path and actual walked path of the dead reckoning is shown in
Figure 9.
The estimated path of dead reckoning method was similar to the actual walked path. As the dead reckoning method requires initial coordinate to calculate the path, the cumulative error was increased with the increase of the estimated path, and a larger error appeared in the final location coordinate and the actual coordinate.
6.2.2. Trilateration
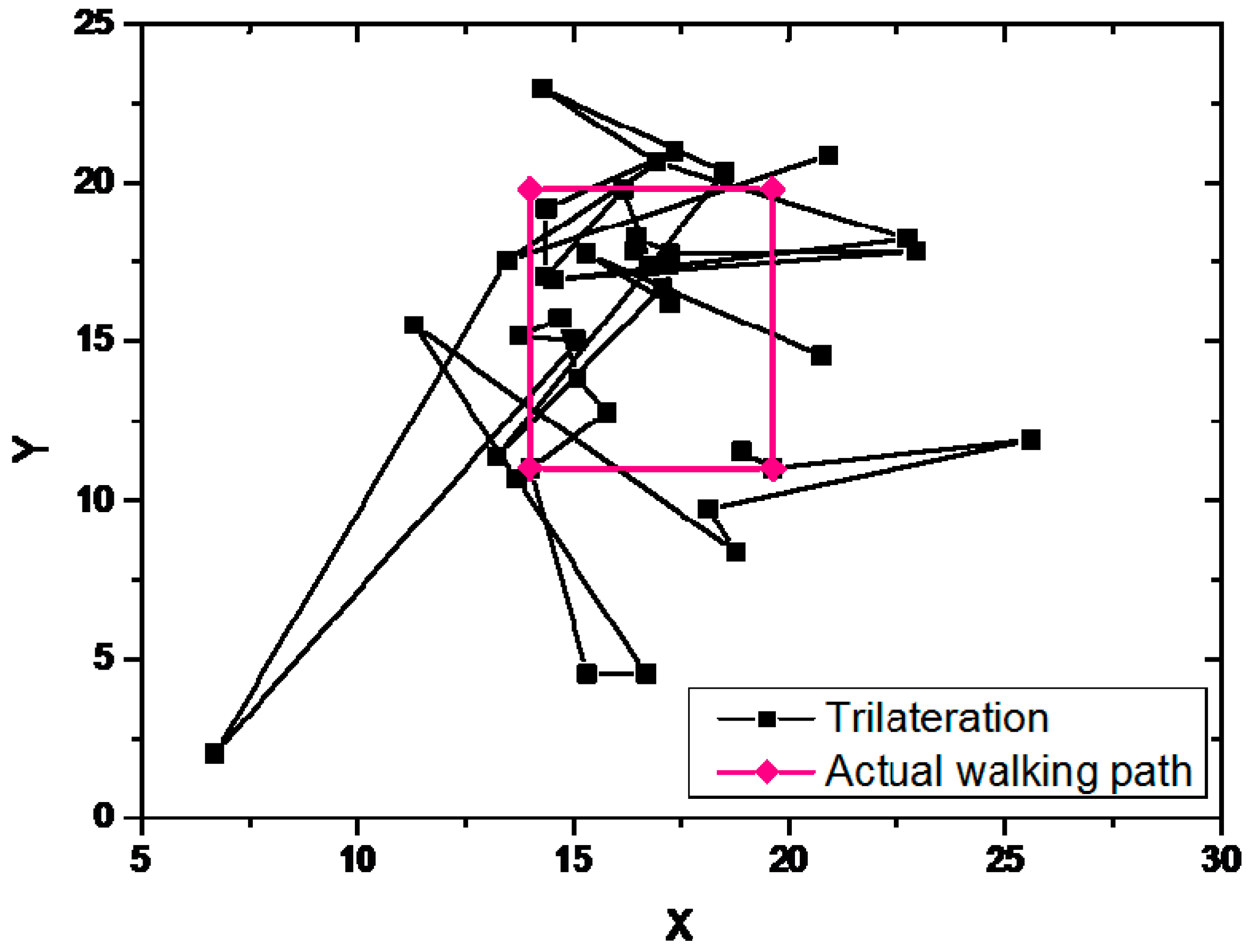
The variation of the Bluetooth signal intensity becomes larger and the scanning interval of the BLE modules become longer under a dense Bluetooth environment. It had a great influence on the positioning accuracy of trilateration method. The estimated path and actual walked path of the trilateration is shown in
Figure 10.
The estimated path of trilateration experiment was very different from the actual walked path The BLE positioning fluctuates resulting from fast fading or multipath effects in public indoor spaces. Due to the fast fading and multipath effects in the experiment environment, the trilateration method did not accurately position the actual location. The estimated path of the trilateration experiment was very different from the actual path. The experiment results showed that the trilateration method based on Bluetooth was difficult to independently complete indoor positioning with less error.
6.2.3. Hybrid Method
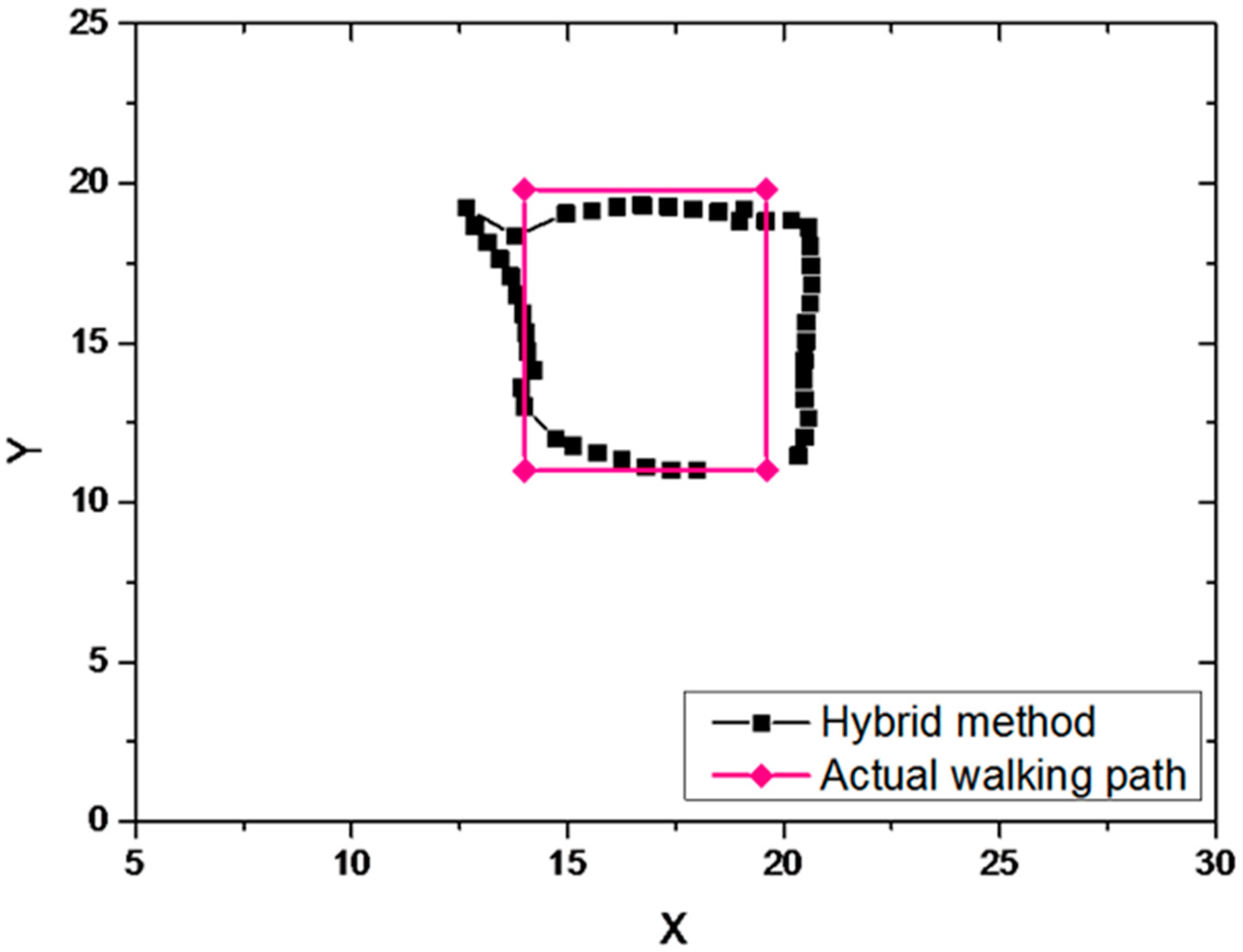
The hybrid method has the advantages of dead reckoning method and trilateration method. It can not only ensure that the estimated path has a small error with the actual walked path, but also can compensate the estimated path continuously to prevent a large cumulative error. The estimated path and actual walked path of the hybrid method is shown in
Figure 11.
The estimated path of hybrid method was basically the same as the actual walked path. Under the premise of the estimation path calculated by dead reckoning method, the Kalman-based hybrid method effectively reduces the estimated path error and achieves better positioning results.
6.2.4. Positioning Root-Mean-Square Error
The positioning root-mean-square-error (RMSE) of the above three positioning methods were calculated, as shown in Equation (23) [
26]. The RMSE was used to evaluate the closeness of the measurement trajectory to a true trajectory over
Nstep simulation steps. The results are shown in
Table 5.
where (
is the true position coordinate at step
t, (
is the measurement position,
Nstep is the number of measurements of indoor positioning.
6.3. Results
According to the results of the experiment, the estimated path of dead reckoning method is similar to the actual walked path, and the dead reckoning method can realize indoor positioning without additional hardware. However, the dead reckoning method needs initial coordinates to locate, and its cumulative error increases with the length of the walking path.
The trilateration method requires BLE module as hardware support. Moreover, the individual trilateration method is easily influenced by the dense Bluetooth environment and has great influence on its positioning accuracy. Therefore, more data needs to be calculated to get more accurate positioning coordinates.
The hybrid method combines the advantages of dead reckoning method and trilateration method. The estimated path of hybrid method is basically the same as the actual walked path. The hybrid method not only has the advantages of the smooth estimated path, but also has the advantages of real-time correction of the location path, which minimizes the positioning error.