Voltage and Deflection Amplification via Double Resonance Excitation in a Cantilever Microstructure
Abstract
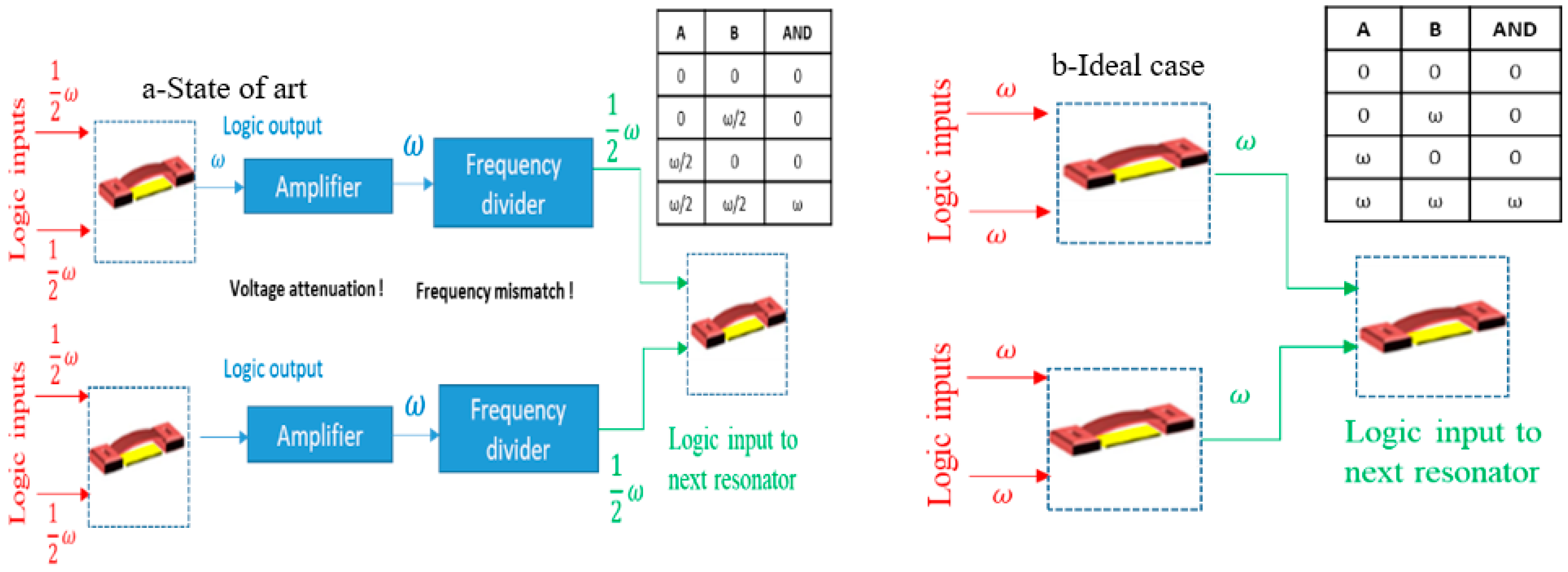
1. Introduction
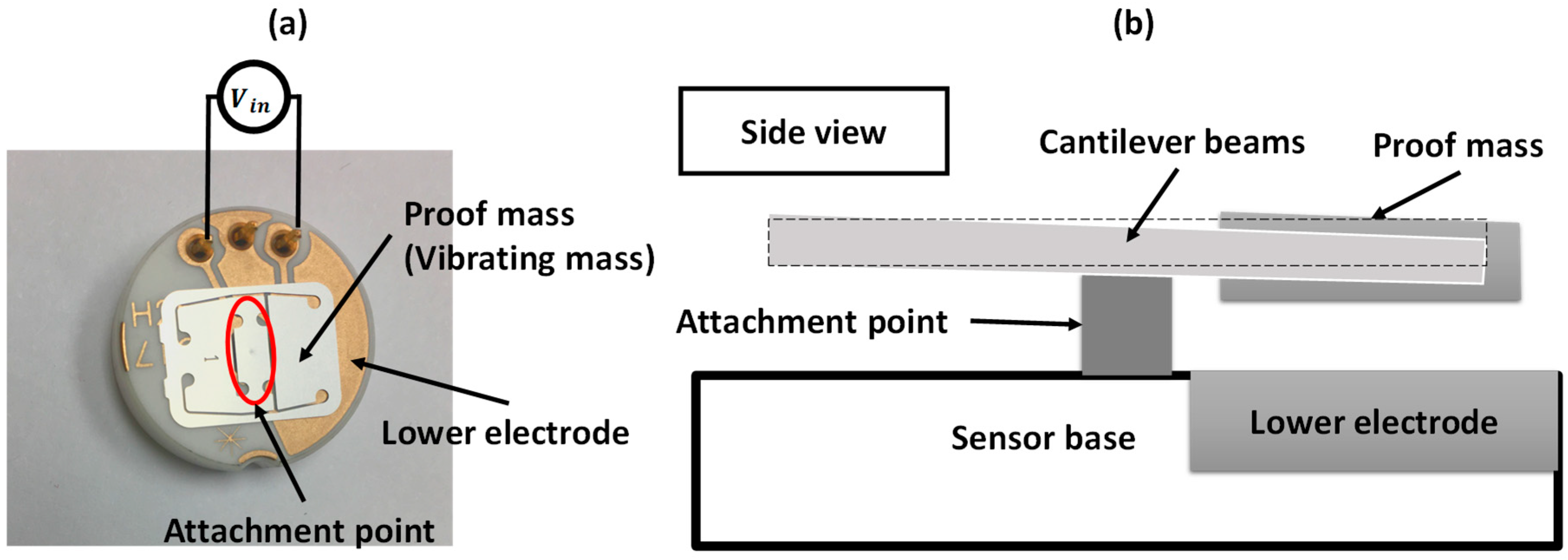
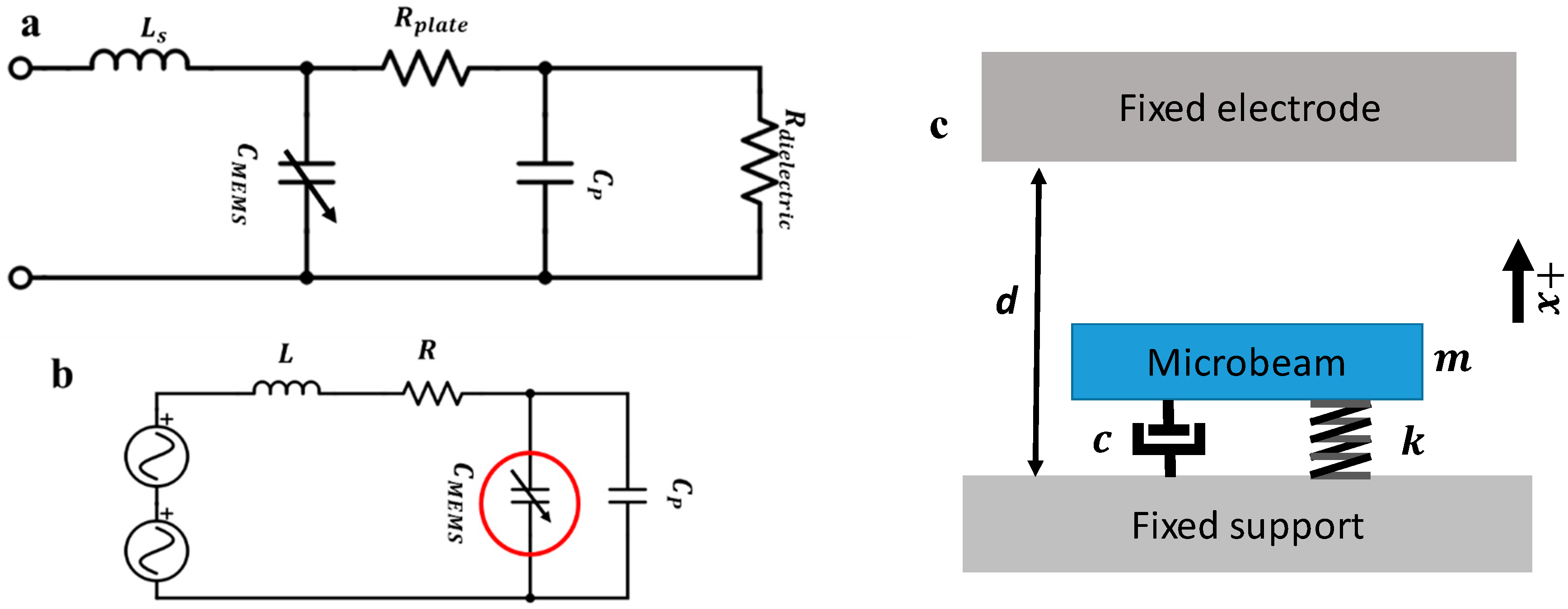
2. Device and System Modeling
2.1. Double Resonance Excitation
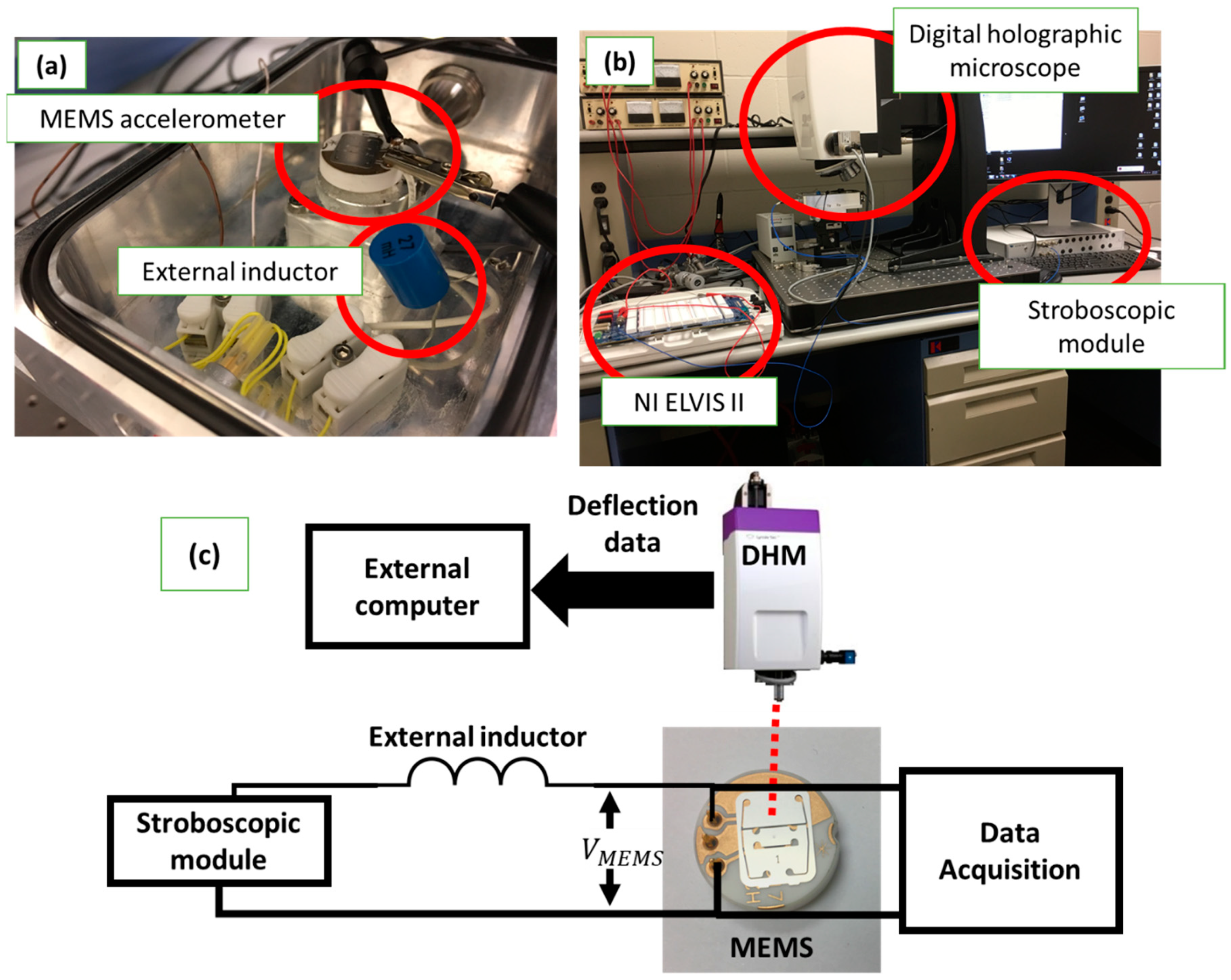
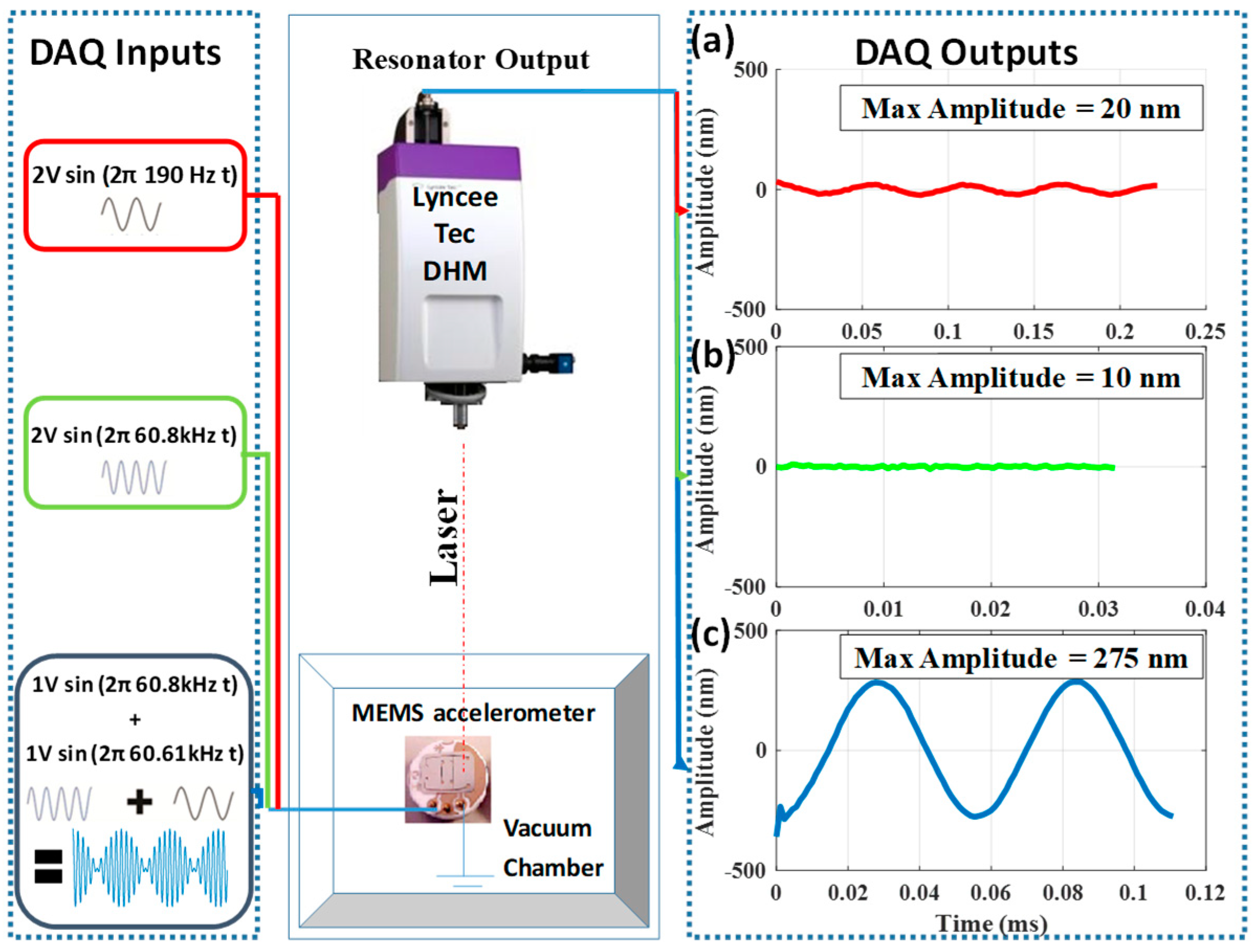
2.2. Experimental Setup
3. Results
3.1. Electrical Circuit Identification
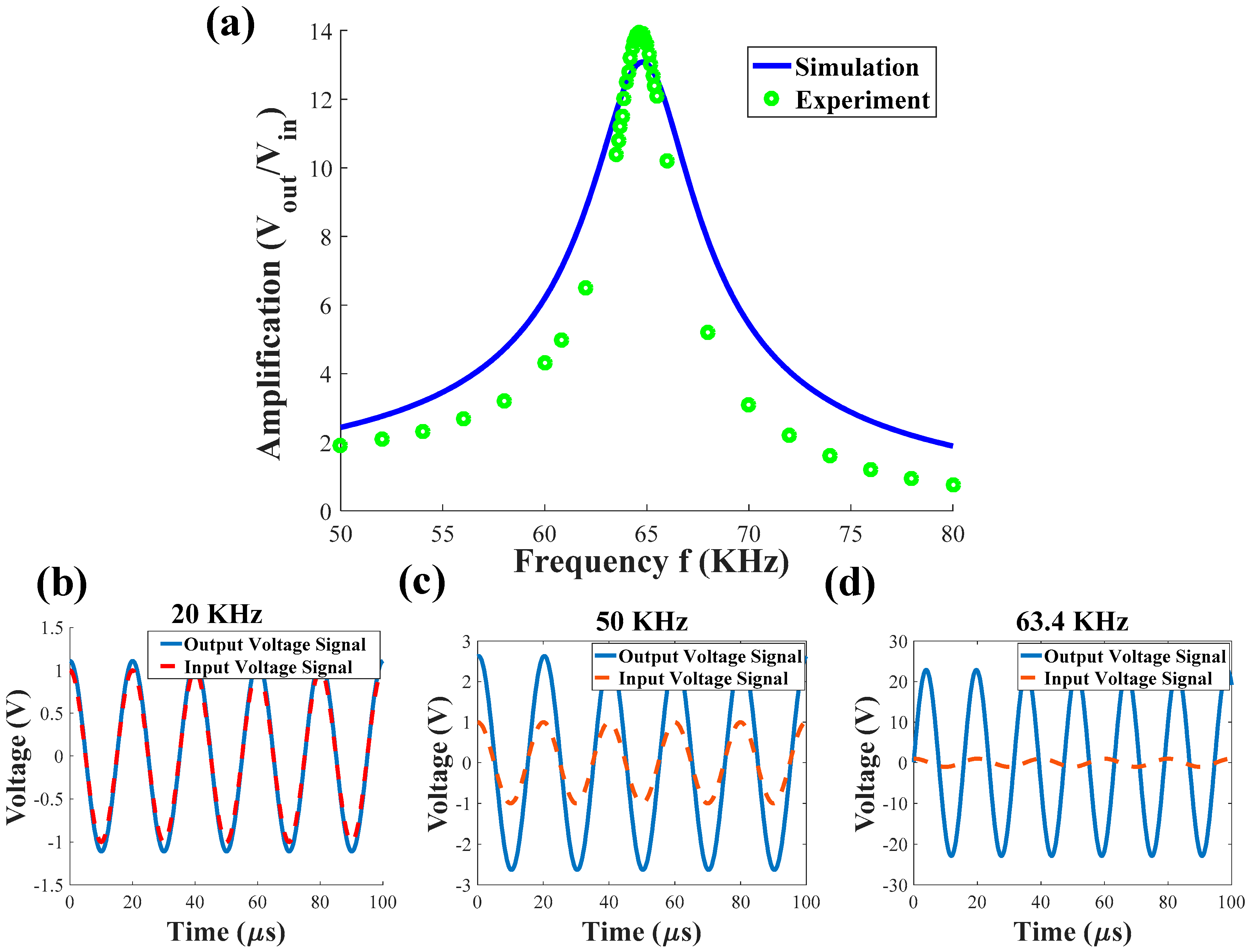
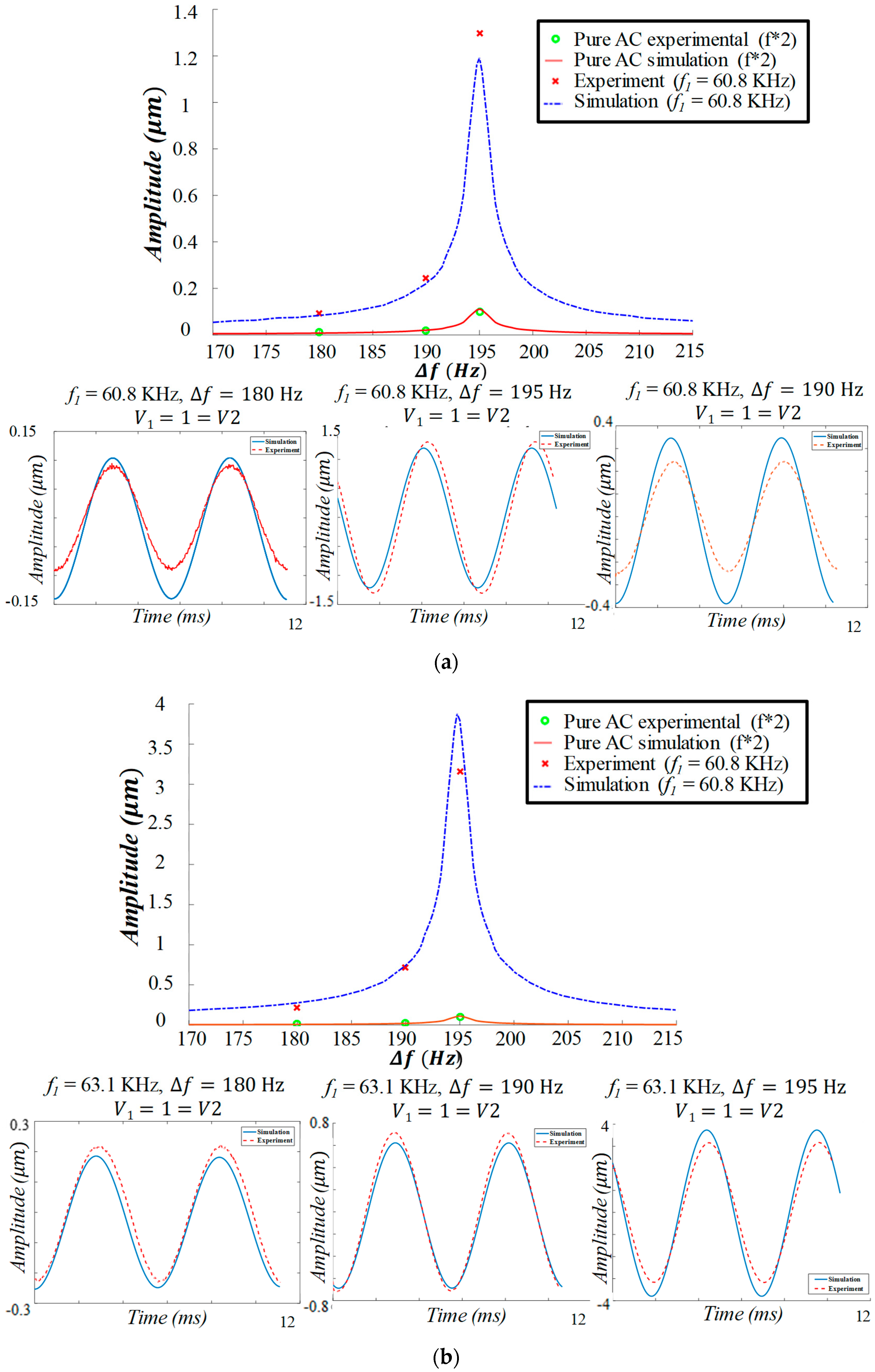
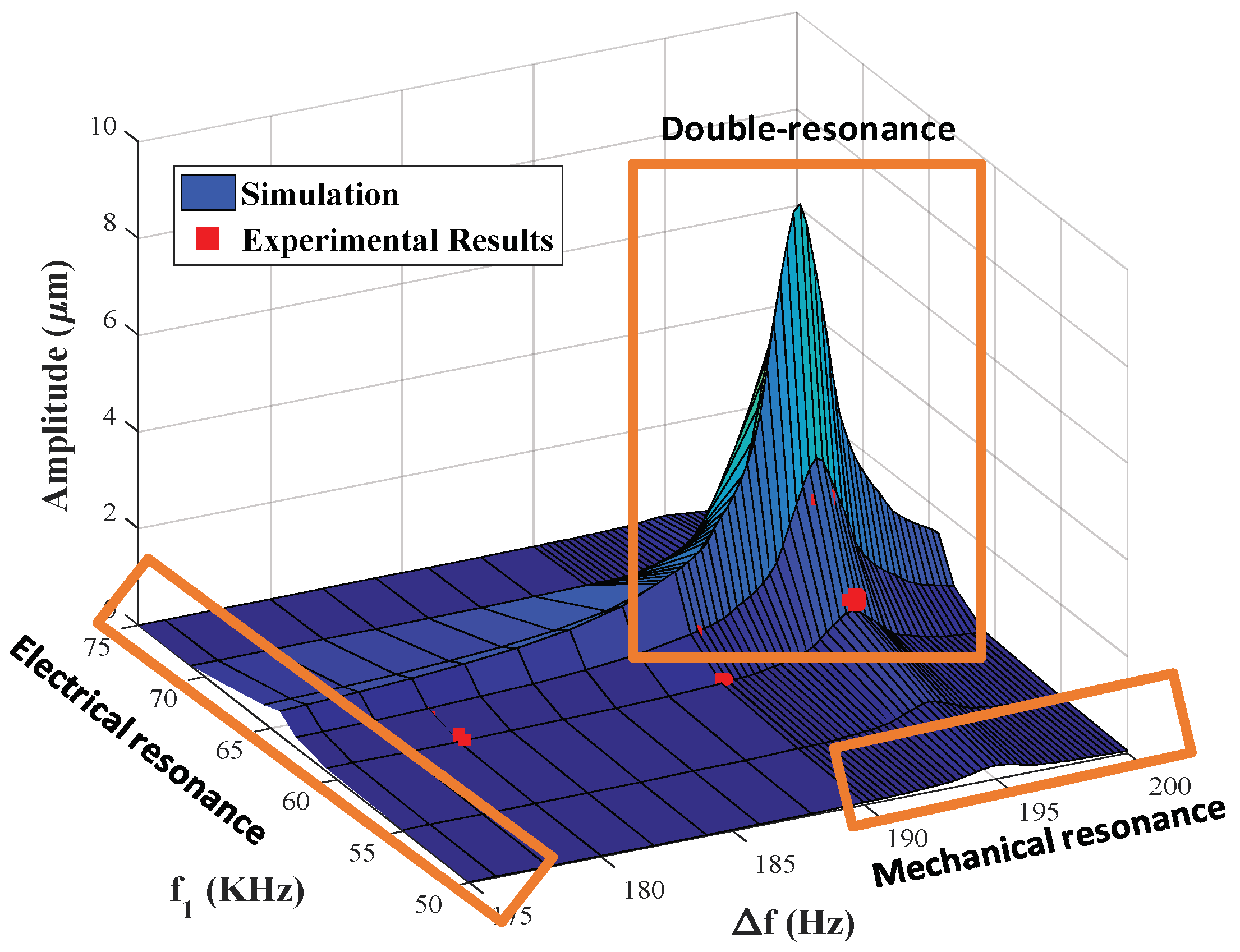
3.2. Double Resonance as a Driving Signal
3.3. Frequency Sweep When Driven Using Mixed-Frequency
4. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Intaraprasonk, V.; Fan, S. Nonvolatile bistable all-optical switch from mechanical buckling. Appl. Phys. Lett. 2011, 98, 241104. [Google Scholar] [CrossRef]
- Chowdhury, F.K.; Saab, D.; Tabib-Azar, M. Single-device “XOR” and “AND” gates for high speed, very low power LSI mechanical processors. Sens. Actuators A Phys. 2012, 188, 481–488. [Google Scholar] [CrossRef]
- Huang, X.M.H.; Manolidis, M.; Jun, S.C.; Hone, J. Nanomechanical hydrogen sensing. Appl. Phys. Lett. 2005, 86, 143104. [Google Scholar] [CrossRef]
- Ilic, B.; Yang, Y.; Aubin, K.; Reichenbach, R.; Krylov, S.; Craighead, H.G. Enumeration of DNA molecules bound to a nanomechanical oscillator. Nano Lett. 2005, 5, 925–929. [Google Scholar] [CrossRef] [PubMed]
- Southworth, D.R.; Bellan, L.M.; Linzon, Y.; Craighead, H.G.; Parpia, J.M. Stress-based vapor sensing using resonant microbridges. Appl. Phys. Lett. 2010, 96, 163503. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A bifurcation-based coupled linear-bistable system for microscale mass sensing. J. Sound Vib. 2014, 333, 2241–2252. [Google Scholar] [CrossRef]
- Wu, J.; Fedder, G.K.; Carley, L.R. A Low-Noise Low-Offset Capacitive Sensing Amplifier for a 50-mug/√ Hz Monolithic CMOS MEMS Accelerometer. IEEE J. Solid-State Circuits 2004, 39, 722–730. [Google Scholar]
- Alper, S.E.; Akin, T. Single-Crystal silicon symmetrical and decoupled MEMS gyroscope on an insulating substrate. J. Microelectromech. Syst. 2005, 14, 707–717. [Google Scholar] [CrossRef]
- Rebeiz, G.M.; Tan, G.L. Introduction: RF MEMS for Microwave Applications. In RF MEMS: Theory, Design, and Technology; Wiley: Hoboken, NJ, USA, 2003; pp. 1–20. [Google Scholar]
- Ilyas, S.; Ramini, A.; Arevalo, A.; Younis, M.I. An experimental and theoretical investigation of a micromirror under mixed-frequency excitation. J. Microelectromech. Syst. 2015, 24, 1124–1131. [Google Scholar] [CrossRef]
- Antonio, D.; Zanette, D.H.; López, D. Frequency stabilization in nonlinear micromechanical oscillators. Nat. Commun. 2012, 3, 806. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Roukes, M.L. Nanoelectromechanical systems. Rev. Sci. Instrum. 2005, 76, 061101. [Google Scholar] [CrossRef]
- Antonio, D.; Czaplewski, D.A.; Guest, J.R.; López, D.; Arroyo, S.I.; Zanette, D.H. Nonlinearity-induced synchronization enhancement in micromechanical oscillators. Phys. Rev. Lett. 2015, 114, 034103. [Google Scholar] [CrossRef] [PubMed]
- Littrell, R.J. High Performance Piezoelectric MEMS Microphones. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2010. [Google Scholar]
- Rebeiz, G.M.; Muldavin, J.B. RF MEMS switches and switch circuits. IEEE Microw. Mag. 2001, 2, 59–71. [Google Scholar] [CrossRef]
- Rebeiz, G.M. RF MEMS switches status of the technology. In Proceedings of the 12th International Conference on TRANSDUCERS, Solid-State Sensors, Actuators, and Microsystems, Boston, MA, USA, 8–12 June 2003; Volume 2, pp. 1726–1729. [Google Scholar]
- Alsaleem, F.M.; Younis, M.I.; Ouakad, H.M. On the nonlinear resonances and dynamic pull-in of electrostatically actuated resonators. J. Micromech. Microeng. 2009, 19, 045013. [Google Scholar] [CrossRef]
- Conrad, H.; Schenk, H.; Kaiser, B.; Langa, S.; Gaudet, M.; Schimmanz, K.; Lenz, M. A small-gap electrostatic micro-actuator for large deflections. Nat. Commun. 2015, 6, 10078. [Google Scholar] [CrossRef] [PubMed]
- Peroulis, D.; Pacheco, S.P.; Sarabandi, K.; Katehi, L.P. Electromechanical considerations in developing low-voltage RF MEMS switches. IEEE Trans. Microw. Theory Tech. 2003, 51, 259–270. [Google Scholar] [CrossRef]
- Huang, J.M.; Liew, K.M.; Wong, C.H.; Rajendran, S.; Tan, M.J.; Liu, A.Q. Mechanical design and optimization of the capacitive micromachined switch. Sens. Actuators A Phys. 2001, 93, 273–285. [Google Scholar] [CrossRef]
- Hosaka, H.; Itao, K.; Kuroda, S. Damping characteristics of beam-shaped micro-oscillators. Sens. Actuators A Phys. 1995, 49, 87–95. [Google Scholar] [CrossRef]
- Van Spengen, W.M.; Puers, R.; De Wolf, I. A physical model to predict stiction in MEMS. J. Micromech. Microeng. 2002, 12, 702. [Google Scholar] [CrossRef]
- Ramini, A.H.; Hajjaj, A.Z.; Younis, M.I. Tunable resonators for nonlinear modal interactions. Sci. Rep. 2016, 6, 34717. [Google Scholar] [CrossRef]
- Jaber, N.; Ramini, A.; Younis, M.I. Multifrequency excitation of a clamped-clamped microbeam: Analytical and experimental investigation. Microsyst. Nanoeng. 2016, 2, 16002. [Google Scholar] [CrossRef]
- Jaber, N.; Ramini, A.; Hennawi, Q.; Younis, M.I. Wideband MEMS resonator using multifrequency excitation. Sens. Actuators A Phys. 2016, 242, 140–145. [Google Scholar] [CrossRef]
- Ilyas, S.; Jaber, N.; Younis, M.I. Multi-function and cascadable MEMS logic device. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 877–880. [Google Scholar]
- Gallacher, B.J.; Burdess, J.S.; Harish, K.M. A control scheme for a MEMS electrostatic resonant gyroscope excited using combined parametric excitation and harmonic forcing. J. Micromech. Microeng. 2006, 16, 320. [Google Scholar] [CrossRef]
- Liu, H.; Qian, Y.; Lee, C. A multi-frequency vibration-based MEMS electromagnetic energy harvesting device. Sens. Actuators A Phys. 2013, 204, 37–43. [Google Scholar] [CrossRef]
- Marioli, D.; Sardini, E.; Serpelloni, M.; Ando, B.; Baglio, S.; Savalli, N.; Trigona, C. Hybrid telemetric MEMS for high temperature measurements into harsh industrial environments. In Proceedings of the 2009 IEEE Instrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 1423–1428. [Google Scholar]
- Park, S.; Abdel-Rahman, E. Low voltage electrostatic actuation and displacement measurement through resonant drive circuit. In Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 119–126. [Google Scholar]
- Park, S.; Pallapa, M.; Yeow, J.T.; Abdel-Rahman, E. Low voltage electrostatic actuation and angular displacement measurement of micromirror coupled with resonant drive circuit. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3976–3981. [Google Scholar]
- Chung, S.-R.; Park, S.; Abdel-Rahman, E.M.; Yeow, J.T.W.; Khater, M. Architecture for MEMS-Based Analog Demodulation. J. Micromech. Microeng. 2013, 23, 045013. [Google Scholar] [CrossRef]
- Hasan, M.H.; Alsaleem, F.M.; Jaber, N.; Hafiz, M.A.A.; Younis, M.I. Simultaneous electrical and mechanical resonance drive for large signal amplification of microresonators. AIP Adv. 2018, 8, 015312. [Google Scholar] [CrossRef]
- Sensata Technologies. Available online: https://www.sensata.com/ (accessed on 31 July 2018).
| Variable | Definition | Value |
|---|---|---|
| Le | Length of beam | 9 mm |
| b | Width of beam | 5.32 mm |
| h | Thickness of beam | 150 μm |
| d | Nominal gap | 42 μm |
| k | Linear stiffness | 215 N/m |
| fm | The primary mechanical resonance frequency | 195 Hz |
| Variable | Definition | Value |
|---|---|---|
| L | Total circuit series inductance | 25.66 mH |
| R | Total circuit series resistance | 799.2 Ω |
| C0 | Nominal capacitance | 10 pF |
| Cp | Parasitic circuit capacitance | 224.74 pF |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.H.; Alsaleem, F.; Ramini, A. Voltage and Deflection Amplification via Double Resonance Excitation in a Cantilever Microstructure. Sensors 2019, 19, 380. https://doi.org/10.3390/s19020380
Hasan MH, Alsaleem F, Ramini A. Voltage and Deflection Amplification via Double Resonance Excitation in a Cantilever Microstructure. Sensors. 2019; 19(2):380. https://doi.org/10.3390/s19020380
Chicago/Turabian StyleHasan, Mohammad H., Fadi Alsaleem, and Abdallah Ramini. 2019. "Voltage and Deflection Amplification via Double Resonance Excitation in a Cantilever Microstructure" Sensors 19, no. 2: 380. https://doi.org/10.3390/s19020380
APA StyleHasan, M. H., Alsaleem, F., & Ramini, A. (2019). Voltage and Deflection Amplification via Double Resonance Excitation in a Cantilever Microstructure. Sensors, 19(2), 380. https://doi.org/10.3390/s19020380






