Improving Angular Accuracy of a Scanning Mirror Based on Error Modeling and Correction
Abstract
1. Introduction
2. Angular Error Model
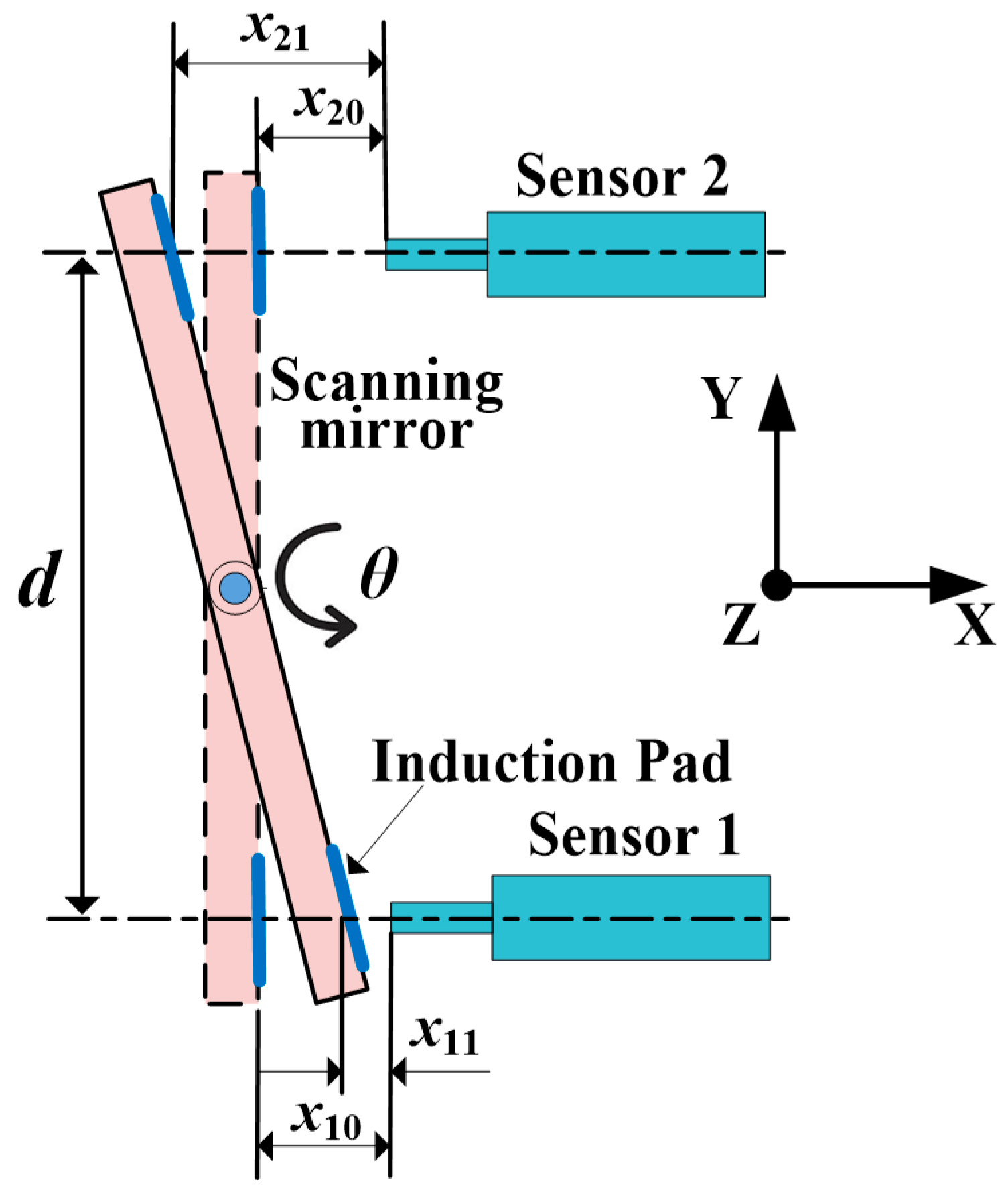
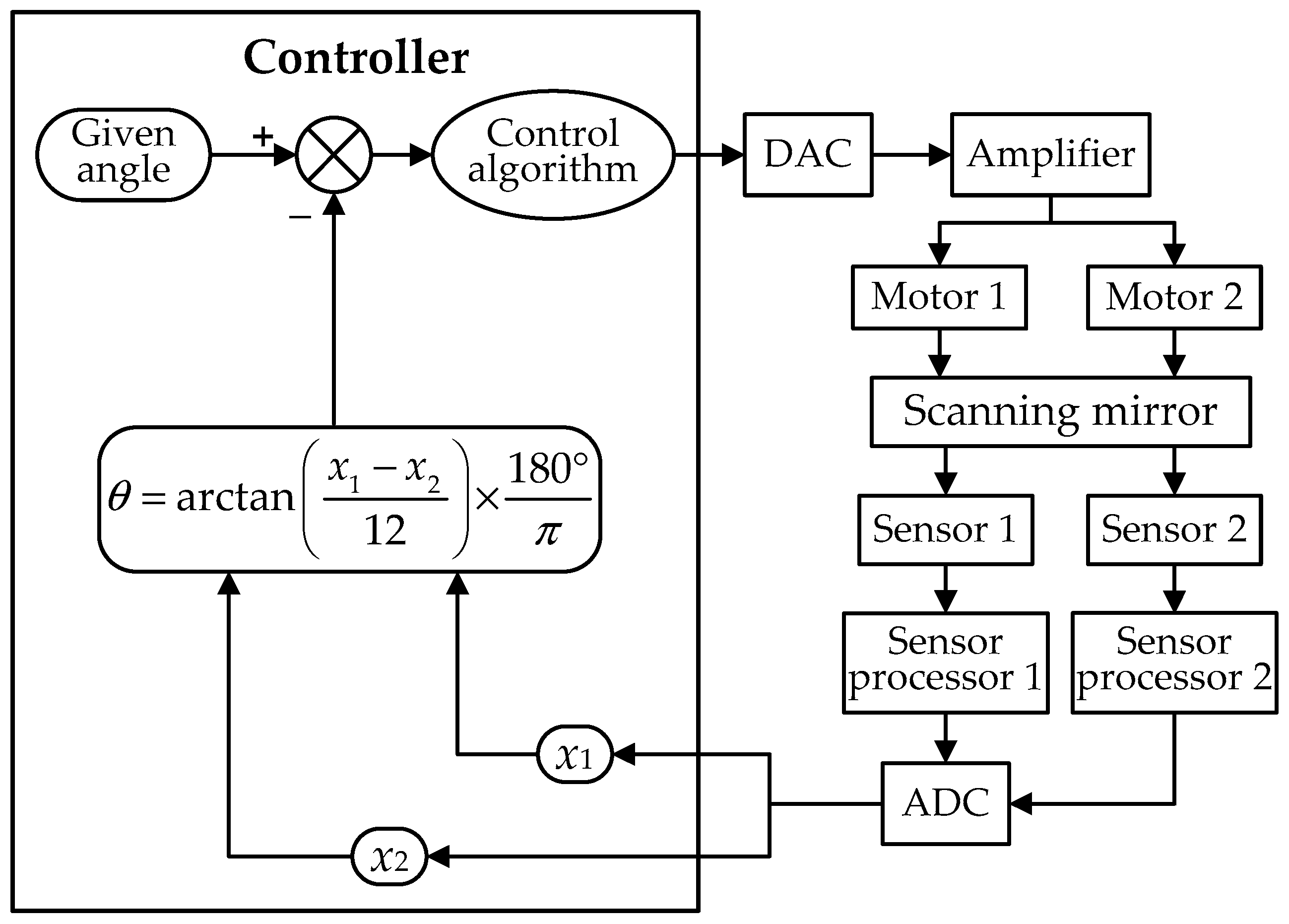
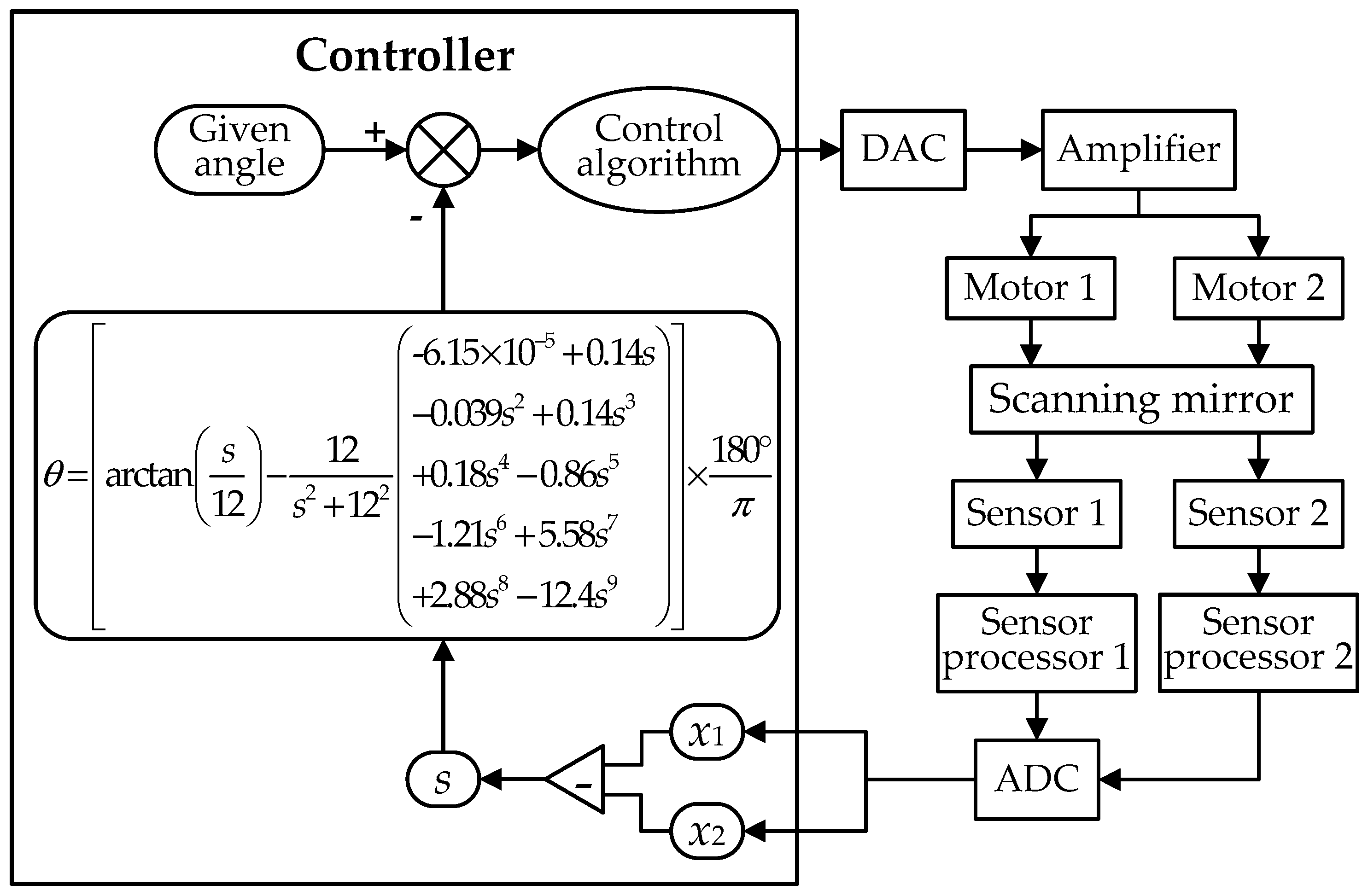
2.1. Eddy-Current Sensor-Based Angle-Measurement Principle
2.2. Error Analysis of the Angular Calculation Model
- (1)
- Nonlinearities of the eddy current displacement sensors. The linearity deviation of the Micro-Epsilon NCDT3010 eddy current sensor is less than 1.25 μm, which will cause an angular error of less than 0.01 deg;
- (2)
- Nonlinearities caused by the non-vertical relationship between the induction pads and the axes of the sensor probes during scanning. The angular error caused by tilting of the measured object relative to the sensor probe was studied by Tan et al. [22], who gave the nonlinear relationship between the angular error and the deflection angle and compensated the error by establishing the principle error equation.
- (3)
- The physical characteristic difference between the ferromagnetic material used for induction pads in our measurement system and that used for adjusting the eddy current sensor controllers in the factory, which will cause extra nonlinearity of the sensor measurements;
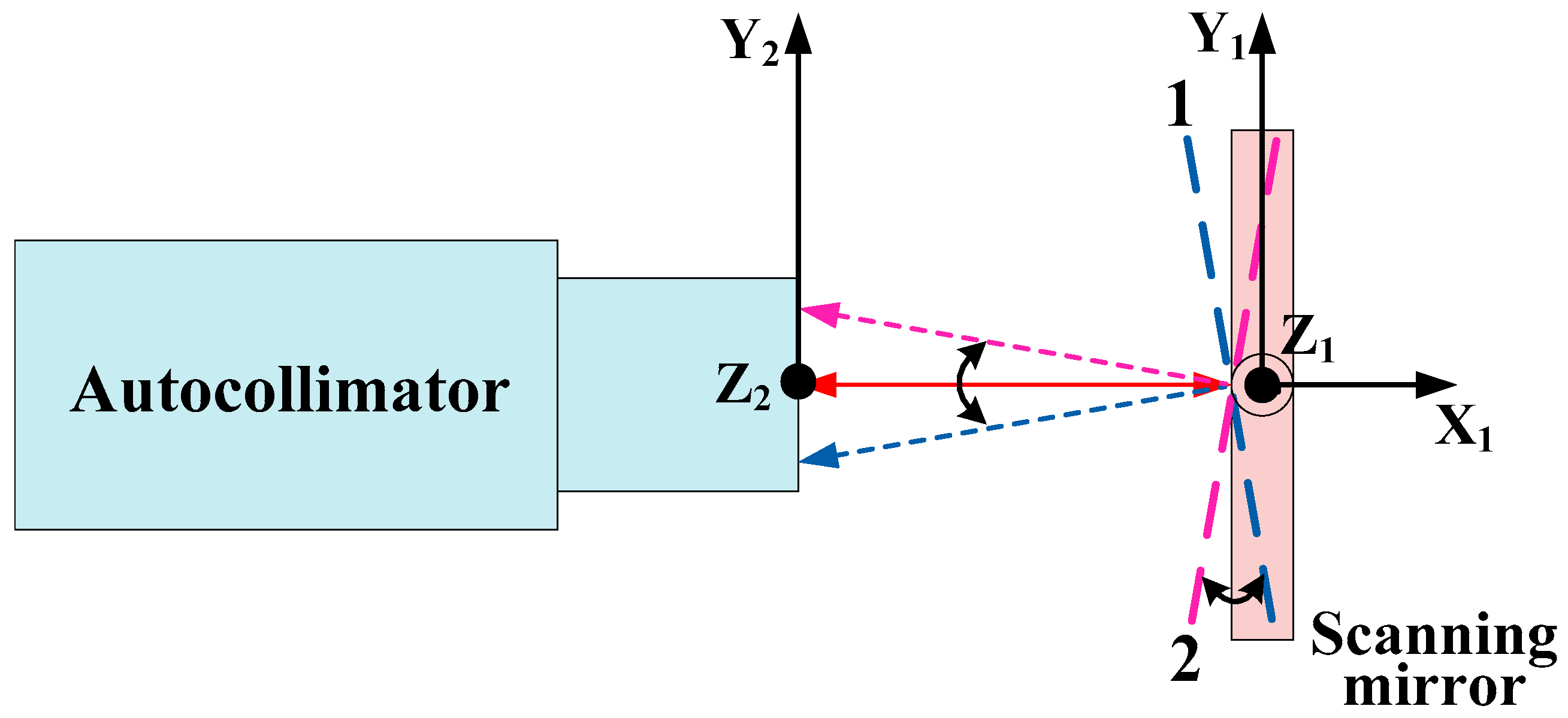
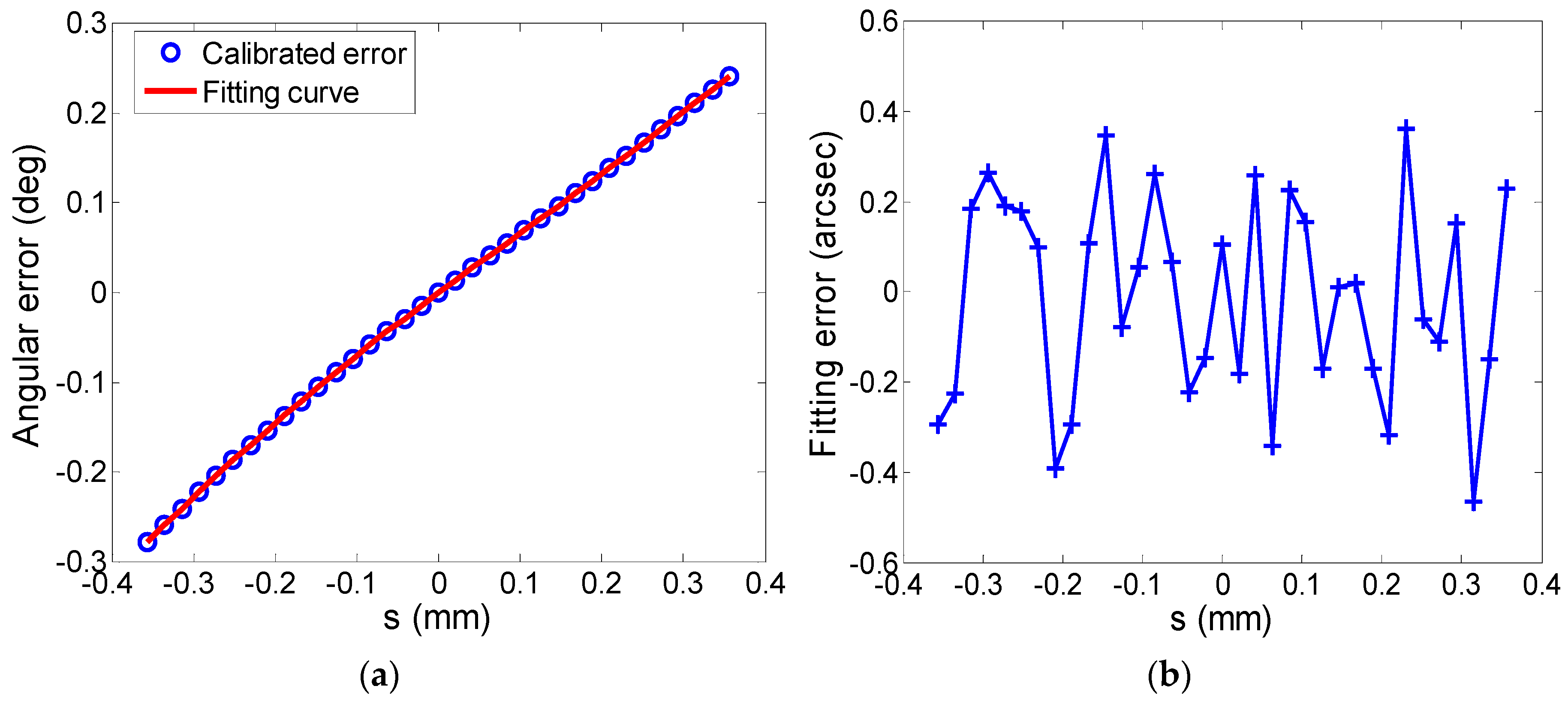
3. Calibration of Deflection Angles
4. Model Correction
4.1. Identification of Error Parameters
4.2. Correction of Angular Calculation Model
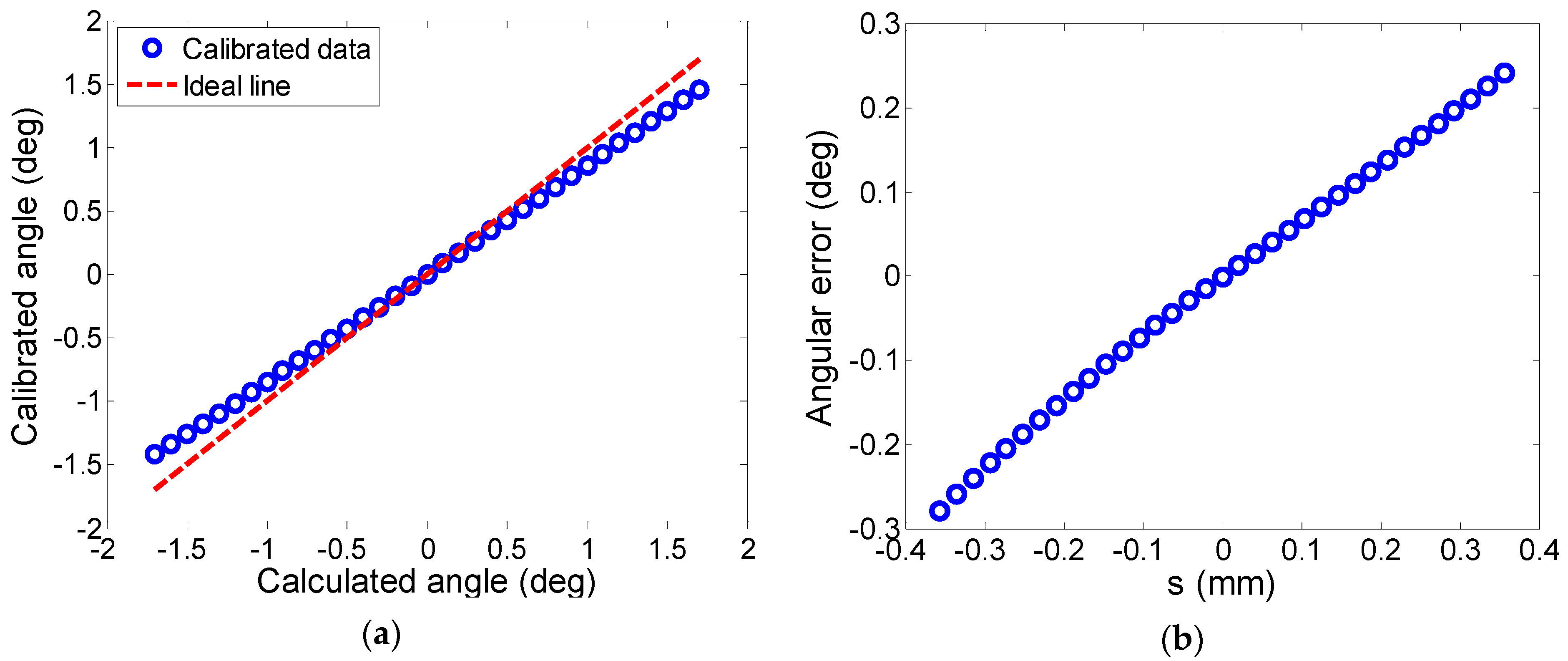
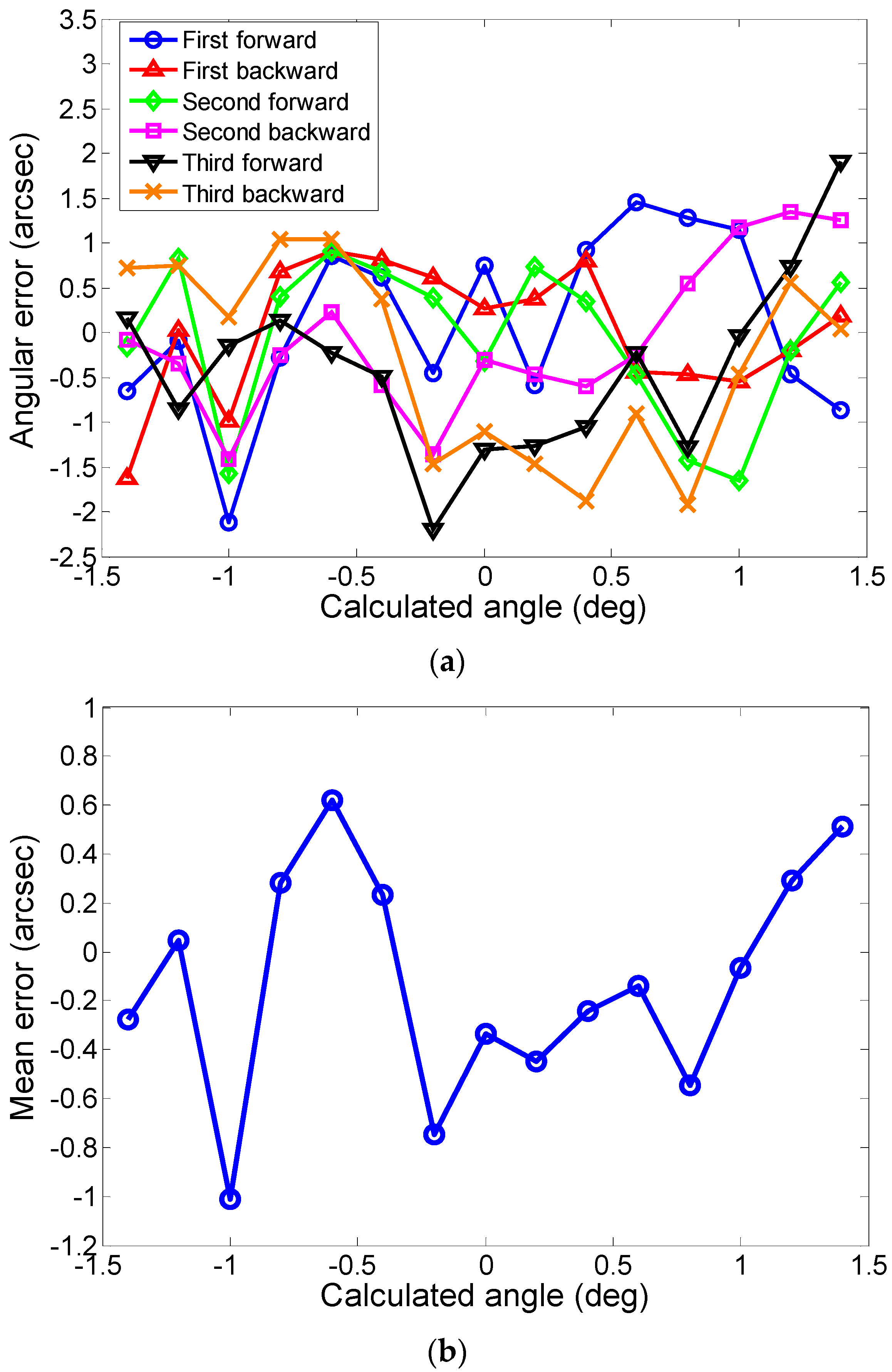
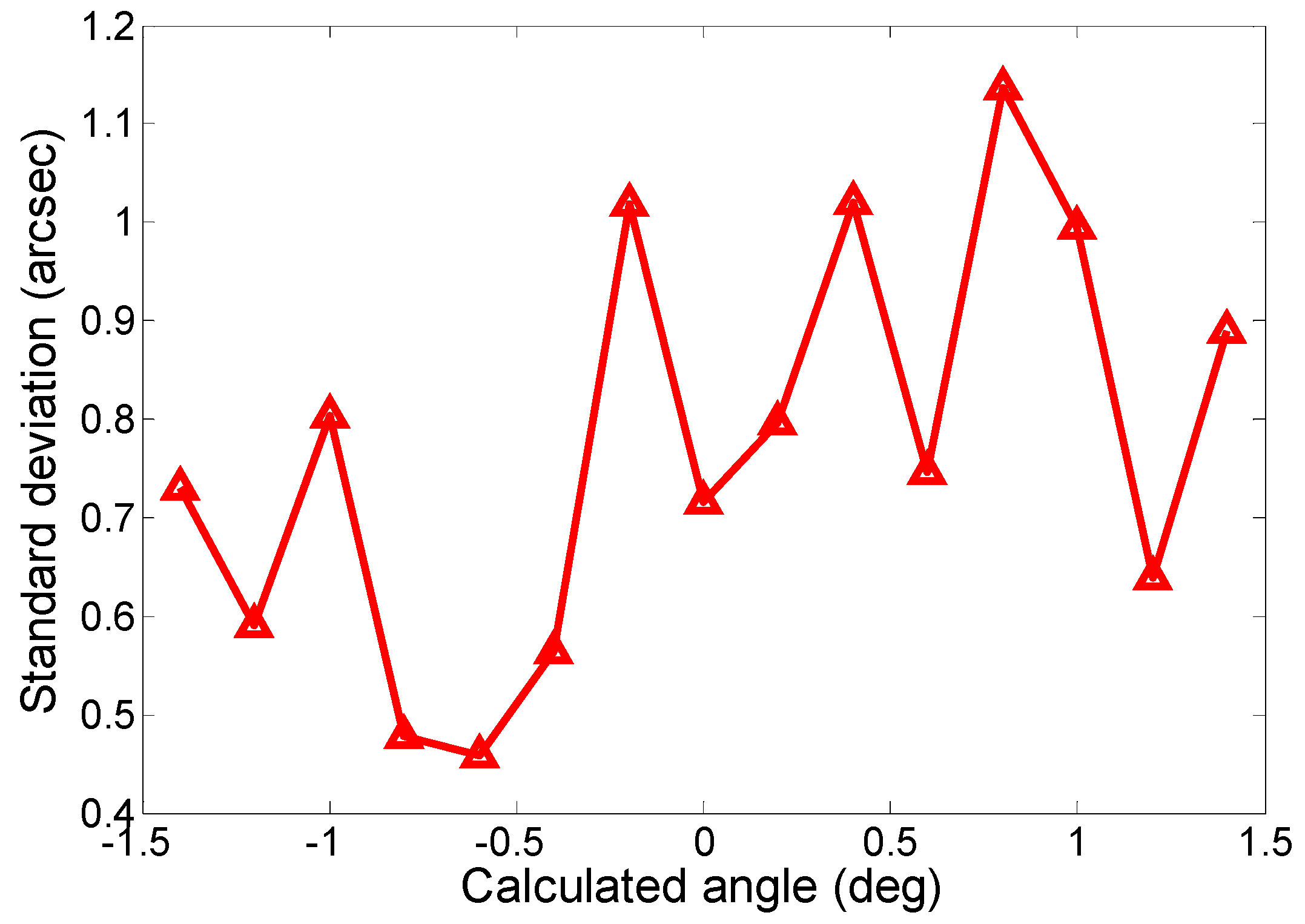
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nouguès, P.O.; Baize, P.; Roland, F.; Olivier, J.F.; Renaudat, M. Third-generation naval IRST using the step-and-stare architecture. Proc. SPIE 2008, 6940, 69401B. [Google Scholar]
- Maltese, D.; Deyla, O.; Vernet, G.; Hilt, C.G.; Nouguès, P.O. New generation of Naval IRST: Example of EOMS NG. Proc. SPIE 2010, 7660, 766004. [Google Scholar]
- Held, K.J.; Robinson, B.H. TIER II Plus Airborne EO Sensor LOS Control and Image Geolocation. In Proceedings of the 1997 IEEE Aerospace Conference, Piscataway, NJ, USA, 1–8 February 1997; IEEE: New York, NY, USA, 1997; Volume 2, pp. 377–405. [Google Scholar]
- Shin, B.H.; Oh, D.; Lee, S.Y. A Two-Dimensional Laser Scanning Mirror Using Motion-Decoupling Electromagnetic Actuators. Sensors 2013, 13, 4146–4156. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.C.; Zhang, G.F.; You, Z.V. Compatible Two-Axis PZT Driven MEMS Scanning Mirror with Mechanical Leverage Structure for Miniature LiDAR Application. Sensors 2017, 17, 521. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, L.H.; Gaines, J.D.; Newman, M.R. Line-of-Sight Stabilization and Back Scanning Using a Fast Steering Mirror and Blended Rate Sensors. AIAA 2011, 1659. [Google Scholar] [CrossRef]
- Hilkert, J.M.; Bowen, M.; Wang, J. Specifications for image stabilization systems. Proc. SPIE 1991, 1498, 24–38. [Google Scholar]
- Santhanakrishnan, T.; Ramalingam, A.; Palanisamy, P.K.; Paulpandian, S.; Banerjee, S.K.; Nayak, R.; Thomas, P.C.; Ouseph, P.P. Calibration of angular motion of a Scanning Mirror Mechanism using a Lateral-effect Position Sensitive Photodetector. Proc. SPIE 1995, 2550, 105–110. [Google Scholar]
- Korolyov, A.N.; Lukin, A.Y.; Polishchuk, G.S. Measuring the dynamic error of the angular motion of a scanning mirror. J. Opt. Technol. 2013, 80, 629–631. [Google Scholar] [CrossRef]
- Krishna, R. Improved pointing accuracy using high precision theodolite measurements. Proc. SPIE 1996, 2812, 199–209. [Google Scholar]
- Hilkert, J.M.; Kanga, G.; Kinnear, K. Line-of-sight kinematics and corrections for fast-steering mirrors used in precision pointing and tracking systems. Proc. SPIE 2014, 9076, 90760F. [Google Scholar]
- Zhang, H.; Xu, D.C.; Zhang, X.Y.; Chen, Q.; Xie, H.K.; Li, S.Q. Model-Based Angular Scan Error Correction of an Electrothermally-Actuated MEMS Mirror. Sensors 2015, 15, 30991–31004. [Google Scholar] [CrossRef] [PubMed]
- Li, J.Y.; Chen, K.; Peng, Q.; Wang, Z.K.; Jiang, Y.; Fu, C.Y.; Ren, G. Improvement of pointing accuracy for Risley prisms by parameter identification. Appl. Opt. 2017, 56, 7358–7366. [Google Scholar] [CrossRef]
- Li, K.; Kuang, C.; Liu, X. Small angular displacement measurement based on an autocollimator and a common-path compensation principle. Rev. Sci. Instrum. 2013, 84, 015108. [Google Scholar] [CrossRef] [PubMed]
- Kirsanov, A.V.; Barmashova, T.V.; Zelenogorskii, V.V.; Potemkin, A.K. Computer-aided two-coordinate autocollimator for measuring small angular deviations. Instrum. Exp. Tech. 2009, 52, 141–143. [Google Scholar] [CrossRef]
- Sasaki, O.; Togashi, C.; Suzuki, T. Two-dimensional rotation angle measurement using a sinusoidal phase-modulating laser diode interferometer. Opt. Eng. 2003, 42, 1132–1136. [Google Scholar] [CrossRef]
- Kumar, V.C.P.; Joenathan, C.; Ganesan, A.; Somasundram, U. Increasing the sensitivity for tilt measurement using a cyclic interferometer with multiple reflections. Opt. Eng. 2016, 55, 084103. [Google Scholar] [CrossRef]
- Li, W.; Jin, J.; Li, X.; Li, B. Method of rotation angle measurement in machine vision based on calibration pattern with spot array. Appl. Opt. 2010, 49, 1001–1006. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Zhao, L.; Xu, S.L. High-precision rotation angle measurement method based on monocular vision. J. Opt. Soc. Am. A 2014, 31, 1401–1407. [Google Scholar] [CrossRef]
- Cai, Y.D.; Lou, Z.F.; Ling, S.Y.; Liao, B.S.; Fan, K.C. Development of a Compact Three-Degree-of-Freedom Laser Measurement System with Self-Wavelength Correction for Displacement Feedback of a Nanopositioning Stage. Appl. Sci. 2018, 8, 2209. [Google Scholar] [CrossRef]
- Ishikawa, K.; Takamura, T.; Xiao, M.Z.; Takahashi, S.; Takamasu, K. Profile measurement of aspheric surfaces using scanning deflectometry and rotating autocollimator with wide measuring range. Meas. Sci. Technol. 2014, 25, 064008. [Google Scholar] [CrossRef]
- Tan, X.R.; Zhu, F.; Wang, C.; Yu, Y.; Shi, J.; Qi, X.; Yuan, F.; Tan, J.B. Two-Dimensional Micro-/Nanoradian Angle Generator with High Resolution and Repeatability Based on Piezo-Driven Double-Axis Flexure Hinge and Three Capacitive Sensors. Sensors 2017, 17, 2672. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Ma, W.; Jiang, P.; Huang, J.; Chen, K.; Pan, N. Improving Angular Accuracy of a Scanning Mirror Based on Error Modeling and Correction. Sensors 2019, 19, 367. https://doi.org/10.3390/s19020367
Fan Y, Ma W, Jiang P, Huang J, Chen K, Pan N. Improving Angular Accuracy of a Scanning Mirror Based on Error Modeling and Correction. Sensors. 2019; 19(2):367. https://doi.org/10.3390/s19020367
Chicago/Turabian StyleFan, Yue, Wenli Ma, Ping Jiang, Jinlong Huang, Kewei Chen, and Nian Pan. 2019. "Improving Angular Accuracy of a Scanning Mirror Based on Error Modeling and Correction" Sensors 19, no. 2: 367. https://doi.org/10.3390/s19020367
APA StyleFan, Y., Ma, W., Jiang, P., Huang, J., Chen, K., & Pan, N. (2019). Improving Angular Accuracy of a Scanning Mirror Based on Error Modeling and Correction. Sensors, 19(2), 367. https://doi.org/10.3390/s19020367



