A Strain Distribution Sensing System for Bone-Implant Interfaces Based on Digital Speckle Pattern Interferometry
Abstract
1. Introduction
2. Method and System Design
2.1. Stability Analysis of Wet-Surface Biomaterials
2.2. An Innovative Imaging Method for DSPI Technology
2.3. The Feasibility Analysis of Imaging Method
3. Experiments
3.1. Experimental Systems and Samples
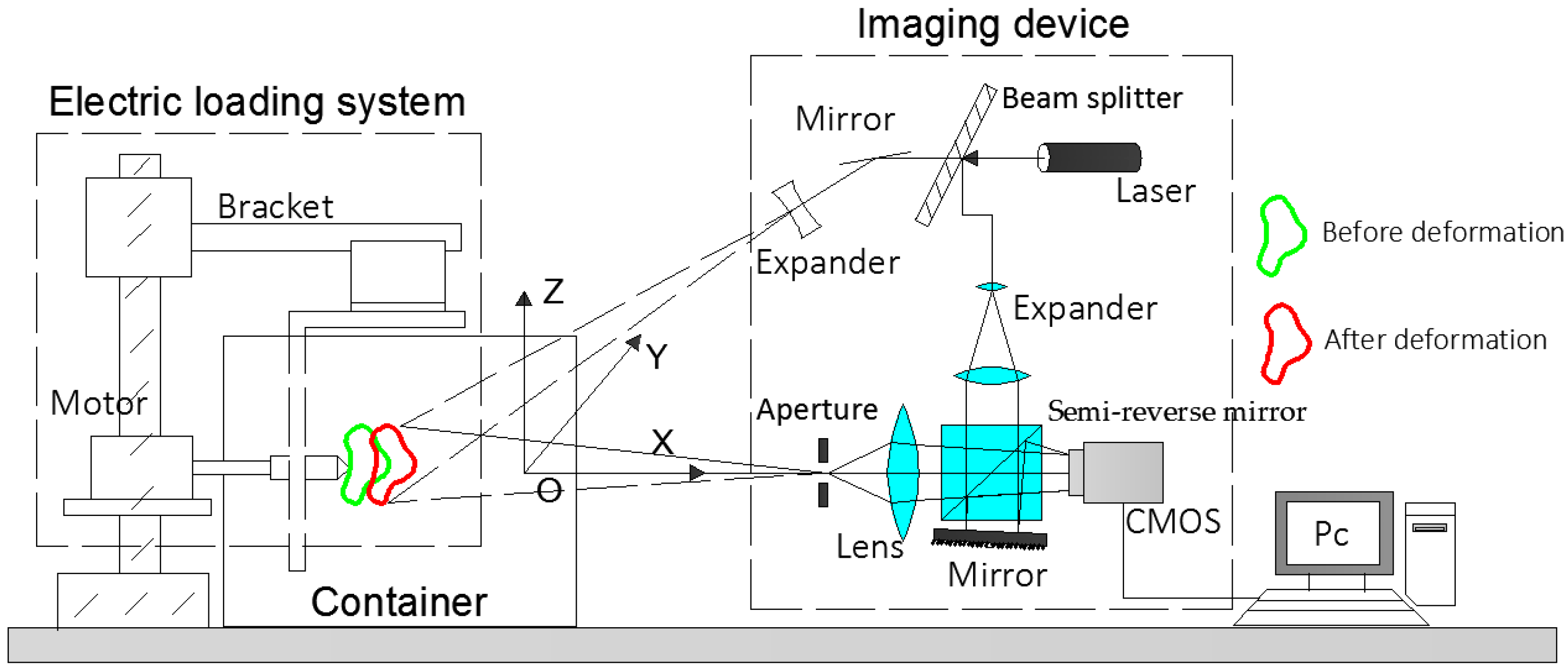
3.1.1. Design of Sensing System and Schematic Diagram
3.1.2. Set-Up
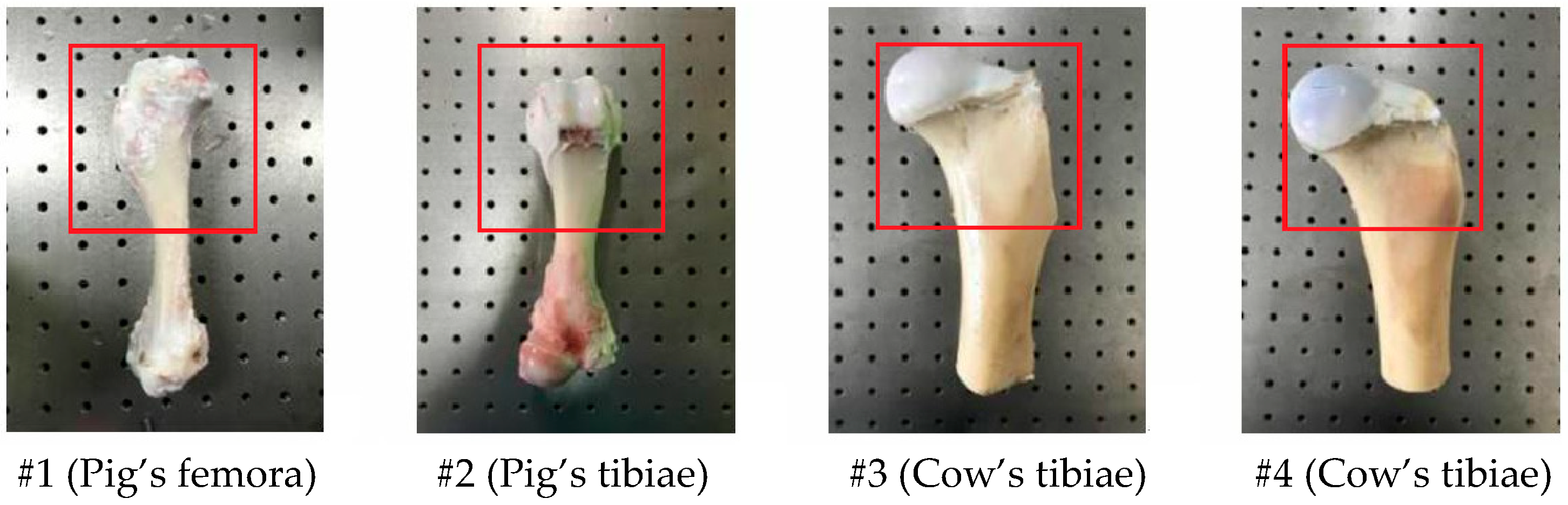
3.1.3. Wet-Surface Biological Bone Samples
3.2. Experiment Data Processing
3.2.1. Speckle Image Preprocessing
3.2.2. Phase Extraction Technique and Calculation of Out-of-Plane Deformation
3.3. Experimental Results
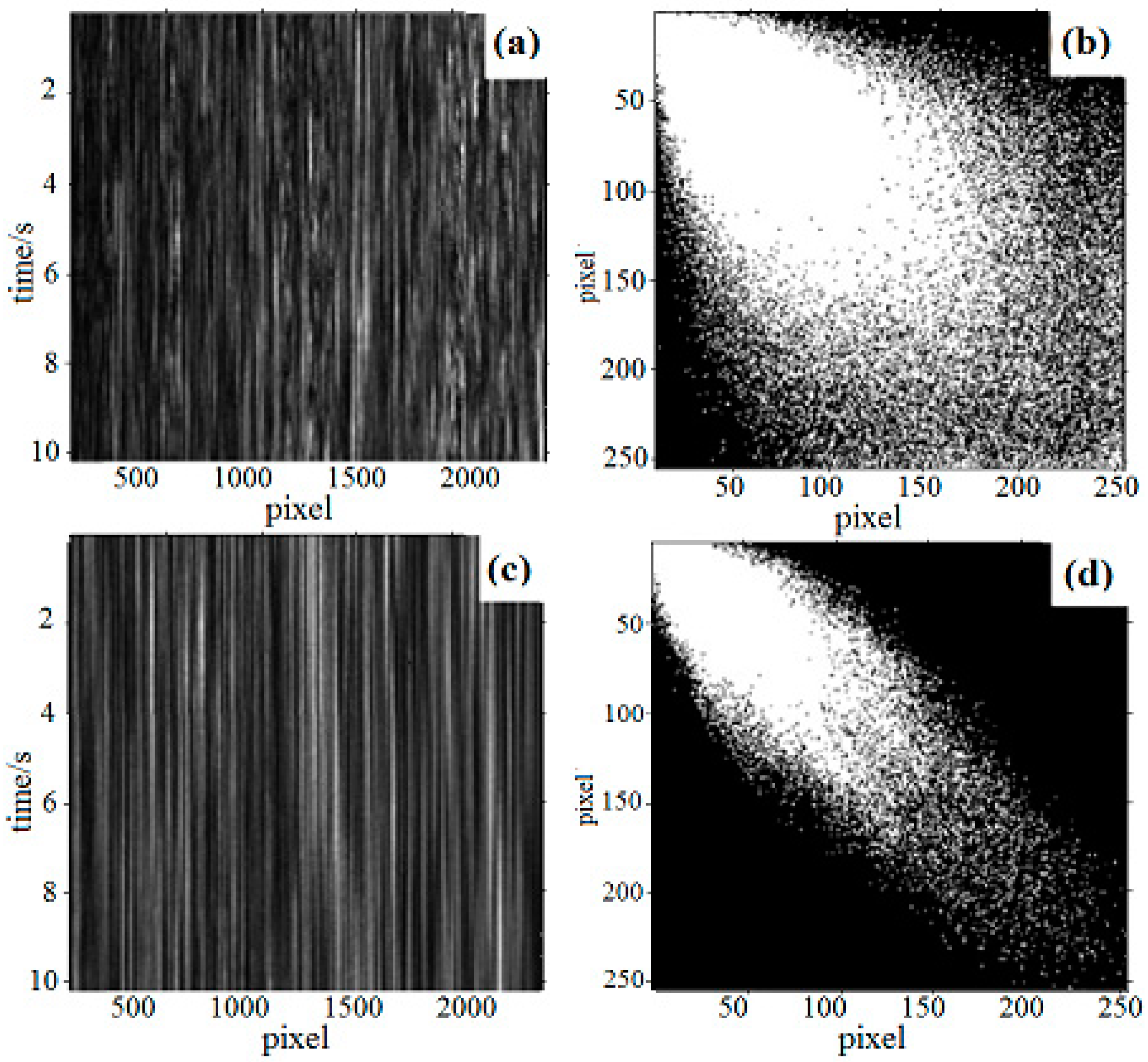
3.3.1. Contrast Experiment in Air and PBS Solution
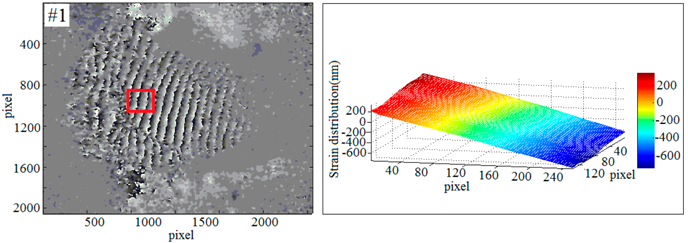
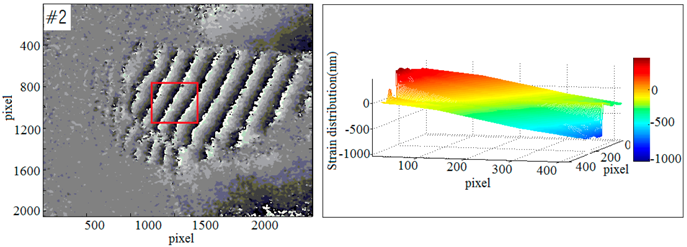
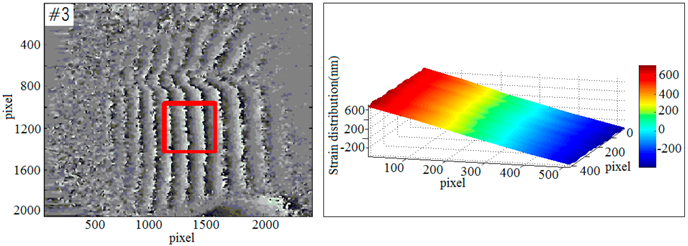
3.3.2. Multi-Sample Strain Detection Experiment
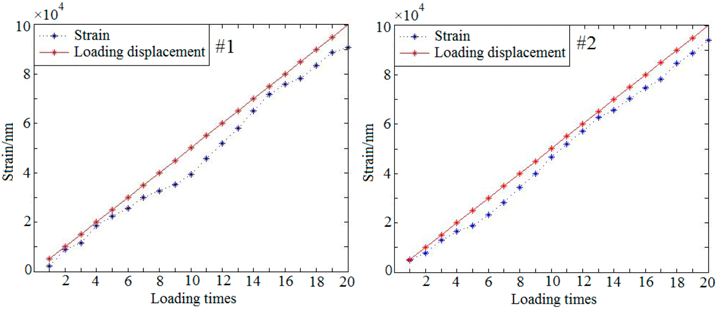
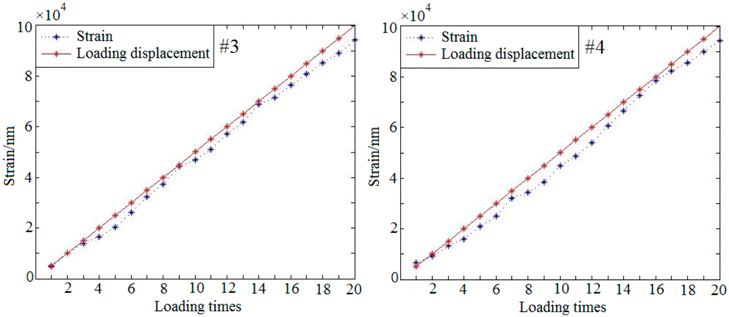
3.3.3. Quantitative Loading Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Niedernhuber, M.; Barone, D.G.; Lenggenhager, B. Prostheses as extensions of the body: Progress and challenges. Neurosci. Biobehav. Rev. 2018, 92, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Arvieux, C.; Common, H. New Diagnostic Tools for Prosthetic Joint Infection. Orthop. Traumatol. Surg. Res. 2018, 26, 1–43. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Luo, D.; Guo, C.; Rong, Q. A custom-made temporomandibular joint prosthesis for fabrication by selective laser melting: Finite element analysis. Med. Eng. Phys. 2017, 46, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Zhang, H.; Zhou, X.; Wu, W.; Zhu, Y. The Influence of Artificial Cervical Disc Prosthesis Height on the Cervical Biomechanics: A Finite Element Study. World Neurosurg. 2018, 113, e490–e498. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, Z.; Wong, D.W.-C.; Cheng, C.-K.; Zhang, M. Finite element analysis of biomechanical effects of total ankle arthroplasty on the foot. J. Orthop. Transl. 2018, 12, 55–65. [Google Scholar] [CrossRef] [PubMed]
- De Cesare, N.; Trevisan, C.; Maghin, E.; Piccoli, M.; Pavan, P.G. A finite element analysis of diaphragmatic hernia repair on an animal model. J. Mech. Behav. Biomed. Mater. 2018, 86, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Moo, E.K.; Sibole, S.C.; Han, S.K.; Herzog, W. Three-dimensional micro-scale strain mapping in living biological soft tissues. Acta Biomater. 2018, 70, 260–269. [Google Scholar] [CrossRef]
- Kerch, G. Distribution of tightly and loosely bound water in biological macromolecules and age-related diseases. Int. J. Biol. Macromol. 2018, 118, 1310–1318. [Google Scholar] [CrossRef]
- Payo, I.; Feliu, V. Strain gauges based sensor system for measuring 3-D deflections of flexible beams. Sens. Actuators A Phys. 2014, 217, 81–94. [Google Scholar] [CrossRef]
- Huang, C.Y.; Ying, K.C. Applying strain gauges to measuring thermal warpage of printed circuit boards. Measurement 2017, 110, 239–248. [Google Scholar] [CrossRef]
- Singla, D.; Veqar, Z.; Hussain, M.E. Photogrammetric Assessment of Upper Body Posture Using Postural Angles: A Literature Review. J. Chiropr. Med. 2017, 16, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Leal, J.S.; Aroeira, R.M.C.; Gressler, V.; Greco, M.; Pertence, A.E.M.; Lamounier, J.A. Accuracy of Photogrammetry for Detecting Adolescent Idiopathic Scoliosis Progression. Spine J. 2018. [Google Scholar] [CrossRef]
- Kumar, M.; Agarwal, R.; Bhutani, R.; Shakher, C. Measurement of strain distribution in cortical bone around miniscrew implants used for orthodontic anchorage using digital speckle pattern interferometry. Opt. Eng. 2016, 55, 054101. [Google Scholar] [CrossRef]
- Lychev, S.; Bychkov, P.; Saifutdinov, I. Holographic Interferometry of Thin-walled Structure Distortion During the Stereolithography Process. Procedia Iutam 2017, 23, 101–107. [Google Scholar] [CrossRef]
- Li, J.; Yang, G.; Siebert, T.; Shi, M.F.; Yang, L. A method of the direct measurement of the true stress–strain curve over a large strain range using multi-camera digital image correlation. Opt. Lasers Eng. 2018, 107, 194–201. [Google Scholar] [CrossRef]
- De la Torre, I.M.; Hernández Montes, M.d.S.; Flores-Moreno, J.M.; Santoyo, F.M. Laser speckle based digital optical methods in structural mechanics: A review. Opt. Lasers Eng. 2016, 87, 32–58. [Google Scholar] [CrossRef]
- Zhao, Y.; Zemmamouche, R.; Vandenrijt, J.F.; Georges, M.P. Accuracy concerns in digital speckle photography combined with Fresnel digital holographic interferometry. Opt. Lasers Eng. 2018, 104, 84–89. [Google Scholar] [CrossRef]
- Shang, H.; Gao, J. Theories and industrial applications of optical interferometric NDT techniques: A review. Insight Non-Destr. Test. Cond. Monit. 2009, 51, 240–251. [Google Scholar] [CrossRef]
- Gu, G.; Wang, K.; Wang, Y.; She, B. Synchronous triple-optical-path digital speckle pattern interferometry with fast discrete curvelet transform for measuring three-dimensional displacements. Opt. Laser Technol. 2016, 80, 104–111. [Google Scholar] [CrossRef]
- Dai, X.; Shao, X.; Geng, Z.; Yang, F.; Jiang, Y.; He, X. Vibration measurement based on electronic speckle pattern interferometry and radial basis function. Opt. Commun. 2015, 355, 33–43. [Google Scholar] [CrossRef]
- Song, J.; Yang, J.; Liu, F.; Lu, K. High temperature strain measurement method by combining digital image correlation of laser speckle and improved RANSAC smoothing algorithm. Opt. Lasers Eng. 2018, 111, 8–18. [Google Scholar] [CrossRef]
- Smith, G.M.; Higgins, O.; Sampath, S. In-situ observation of strain and cracking in coated laminates by digital image correlation. Surf. Coat. Technol. 2017, 328, 211–218. [Google Scholar] [CrossRef]
- Butters, J.N.; Leendertz, J.A. A double exposure technique for speckle pattern interferometry. J. Phys. E Sci. Instrum. 1971, 4, 277–279. [Google Scholar] [CrossRef]
- Sharp, B. Electronic speckle pattern interferometry (ESPI). Opt. Lasers Eng. 1989, 11, 241–255. [Google Scholar] [CrossRef]
- Ruiz, C.G.; Manuel, H.; Flores-Moreno, J.M.; Frausto-Reyes, C.; Santoyo, F.M. Cortical bone quality affectations and their strength impact analysis using holographic interferometry. Biomed. Opt. Express 2018, 10. [Google Scholar] [CrossRef]
- Aswendt, P.; Höfling, R.; Totzauer, W. Digital speckle pattern interferometry applied to thermal strain measurements of metal- ceramic compounds. Opt. Laser Technol. 1990, 22, 278–282. [Google Scholar] [CrossRef]
- An, W.; Carlsson, T.E. Speckle interferometry for measurement of continuous deformations. Opt. Lasers Eng. 2003, 40, 529–541. [Google Scholar] [CrossRef]
- Sun, P. Evaluation of two-dimensional displacement components of symmetrical deformation by phase-shifting electronic speckle pattern interferometry. Appl. Opt. 2007, 46, 2859–2862. [Google Scholar] [CrossRef]
- Kumar, M.; Khan, G.S.; Shakher, C. Measurement of lastic and thermal properties of composite materials using digital speckle attern interferometry. In Proceedings of the Speckle 2015: VI International Conference on Peckle Metrology, Guanajuato, Mexico, 24–26 August 2015; Volume 9660, p. 966011. [Google Scholar]
- Bavigadda, V.; Jallapuram, R.; Mihaylova, E.; Toal, V. Electronic speckle-pattern interferometer using holographic optical lements for vibration measurements. Opt. Lett. 2010, 35, 3273–3275. [Google Scholar] [CrossRef]
- Fang, Y.; Wu, S.J.; Yang, L.X. Synchronous Measurement of Three-Dimensional Deformations Using Tri-Channel Spatial-Carrier Digital Speckle Pattern Interferometry. Appl. Mech. Mater. 2017, 868, 316–322. [Google Scholar] [CrossRef]
- Pedrini, G.; Martínez-García, V.; Weidmann, P.; Wenzelburger, M.; Killinger, A.; Weber, U.; Osten, W. Residual Stress Analysis of Ceramic Coating by Laser Ablation and Digital Holography. Exp. Mech. 2015, 56, 683–701. [Google Scholar] [CrossRef]
- Dong, C.; Li, K.; Jiang, Y.; Arola, D.; Zhang, D. Evaluation of thermal expansion coefficient of carbon fiber reinforced composites using electronic speckle interferometry. Opt. Express 2018, 26, 531. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Shakher, C. Experimental characterization of the hygroscopic properties of wood during convective drying using digital holographic interferometry. Appl. Opt. 2016, 55, 960. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Anshu, S.B.; Sridhar, K.; Chandra, S. Measurement of initial displacement of canine and molar in human maxilla under different canine retraction methods using digital holographic interferometry. Opt. Eng. 2018, 57, 094106. [Google Scholar] [CrossRef]
- Kessler, O.; Sommers, M.; Augustin, T.; Haybaeck, J.; D’Lima, D.D.; Madey, S.M.; Bottlang, M. Higher strains in the inner region of the meniscus indicate a potential source for degeneration. J. Biomech. 2015, 48, 1377–1382. [Google Scholar] [CrossRef] [PubMed]
- Tavera, R.C.G.; De la Torre-I, M.H.; Flores-M, J.M.; Hernandez, M.M.D.S.; Mendoza-Santoyo, F.; Briones-R, M.J.; Sanchez-P, J. Surface structural damage study in cortical bone due to medical drilling. Appl. Opt. 2017, 56, F179. [Google Scholar] [CrossRef]
- Soons, J.; Lava, P.; Debruyne, D.; Dirckx, J. Full-field optical deformation measurement in biomechanics: Digital speckle pattern interferometry and 3D digital image correlation applied to bird beaks. J. Mech. Behav. Biomed. Mater. 2012, 14, 186–191. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, P.; Liu, S.; Samala, P.R.; Su, M.; Yokota, H. Measurement of strain distributions in mouse femora with 3D-digital speckle pattern interferometry. Opt. Lasers Eng. 2007, 45, 843–851. [Google Scholar] [CrossRef]
- Gaudette, G.R.; Todaro, J.; Krukenkamp, I.B.; Chiang, F.P. Computer Aided Speckle Interferometry: A Technique for Measuring Deformation of the Surface of the Heart. Ann. Biomed. Eng. 2001, 29, 775–780. [Google Scholar] [CrossRef]
- Kemper, B.; Dirksen, D.; Avenhaus, W.; Merker, A.; von Bally, G. Endoscopic double-pulse electronic-speckle-pattern interferometer for technical and medical intracavity inspection. Appl. Opt. 2000, 39, 3899. [Google Scholar] [CrossRef]
- Nandi, N.; Bagchi, B. Dielectric Relaxation of Biological Water. J. Phys. Chem. B 1997, 101, 10954–10961. [Google Scholar] [CrossRef]
- Persson, E.; Halle, B. Cell water dynamics on multiple time scales. Proc. Natl. Acad. Sci. USA 2008, 105, 6266–6271. [Google Scholar] [CrossRef] [PubMed]
- Mulji, N.; Chandra, S. Rupture and dewetting of water films on solid surfaces. J. Colloid Interface Sci. 2010, 352, 194–201. [Google Scholar] [CrossRef] [PubMed]
- Romero, G.G.; Martinez, C.C.; Alanís, E.E.; Salazar, G.A.; Broglia, V.G.; Álvarez, L. Bio-speckle activity applied to the assessment of tomato fruit ripening. Biosyst. Eng. 2009, 103, 116–119. [Google Scholar] [CrossRef]
- Ansari, M.Z.; Nirala, A.K. Assessment of bio-activity using the methods of inertia moment and absolute value of the differences. Opt. Int. J. Light Electron Opt. 2013, 124, 512–516. [Google Scholar] [CrossRef]
- Braga, R.A.; Dal Fabbro, I.M.; Borem, F.M.; Rabelo, G.; Arizaga, R.; Rabal, H.J.; Trivi, M. Assessment of Seed Viability by Laser Speckle Techniques. Biosyst. Eng. 2003, 86, 287–294. [Google Scholar] [CrossRef]
- Ansari, M.D.Z.; Nirala, A.K. Biospeckle activity measurement of Indian fruits using the methods of cross-correlation and inertia moments. Opt. Int. J. Light Electron Opt. 2013, 124, 2180–2186. [Google Scholar] [CrossRef]
- Zdunek, A.; Adamiak, A.; Pieczywek, P.M.; Kurenda, A. The biospeckle method for the investigation of agricultural crops: A review. Opt. Lasers Eng. 2014, 52, 276–285. [Google Scholar] [CrossRef]
- Gao, X.; Wu, S.; Yang, L. Dynamic measurement of deformation using Fourier transform digital holographic interferometry. In Proceedings of the Sixth International Symposium on Precision Mechanical Measurements, Guiyang, China, 8–12 August 2013. [Google Scholar] [CrossRef]
- Wolfgang, S.; Yang, L. Digital Shearography: Theroy and Application of Digital Speckle Pattern Shearing Interferometry; SPIE Press: Bellingham, DC, USA, 2003; ISBN 9780819441102. [Google Scholar]
- Jones, R.; Wykes, C. Holographic and Speckle Interferometry; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Thomson, R.E.; Emery, W.J. Digital Filters. Data Anal. Methods Phys. Oceanogr. 2014, 593–637. [Google Scholar] [CrossRef]
- Karsli, H.; Dondurur, D. A mean-based filter to remove power line harmonic noise from seismic reflection data. J. Appl. Geophys. 2018, 153, 90–99. [Google Scholar] [CrossRef]
- Zhong, C.; Gao, Z.; Wang, X.; Gao, C.; Yang, S.; Sun, X.; Wang, S. The machine learning method of phase extraction in interferometry. Opt. Lasers Eng. 2018, 110, 384–391. [Google Scholar] [CrossRef]
- Zhai, Z.; Li, Z.; Zhang, Y.; Dong, Z.; Wang, X.; Lv, Q. An accurate phase shift extraction algorithm for phase shifting interferometry. Opt. Commun. 2018, 429, 144–151. [Google Scholar] [CrossRef]
- Xie, X.; Xu, N.; Sun, J.; Wang, Y.; Yang, L. Simultaneous measurement of deformation and the first derivative with spatial phase-shift digital shearography. Opt. Commun. 2013, 286, 277–281. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, X.; Xie, X.; Wu, S.; Liu, Y.; Yang, L. Simultaneous dual directional strain measurement using spatial phase-shift digital shearography. Opt. Lasers Eng. 2016, 87, 197–203. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, H.; Zhang, R.; Xie, X.; Chen, B. A robust phase unwrapping algorithm based on reliability mask and weighted minimum least-squares method. Opt. Lasers Eng. 2019, 112, 39–45. [Google Scholar] [CrossRef]





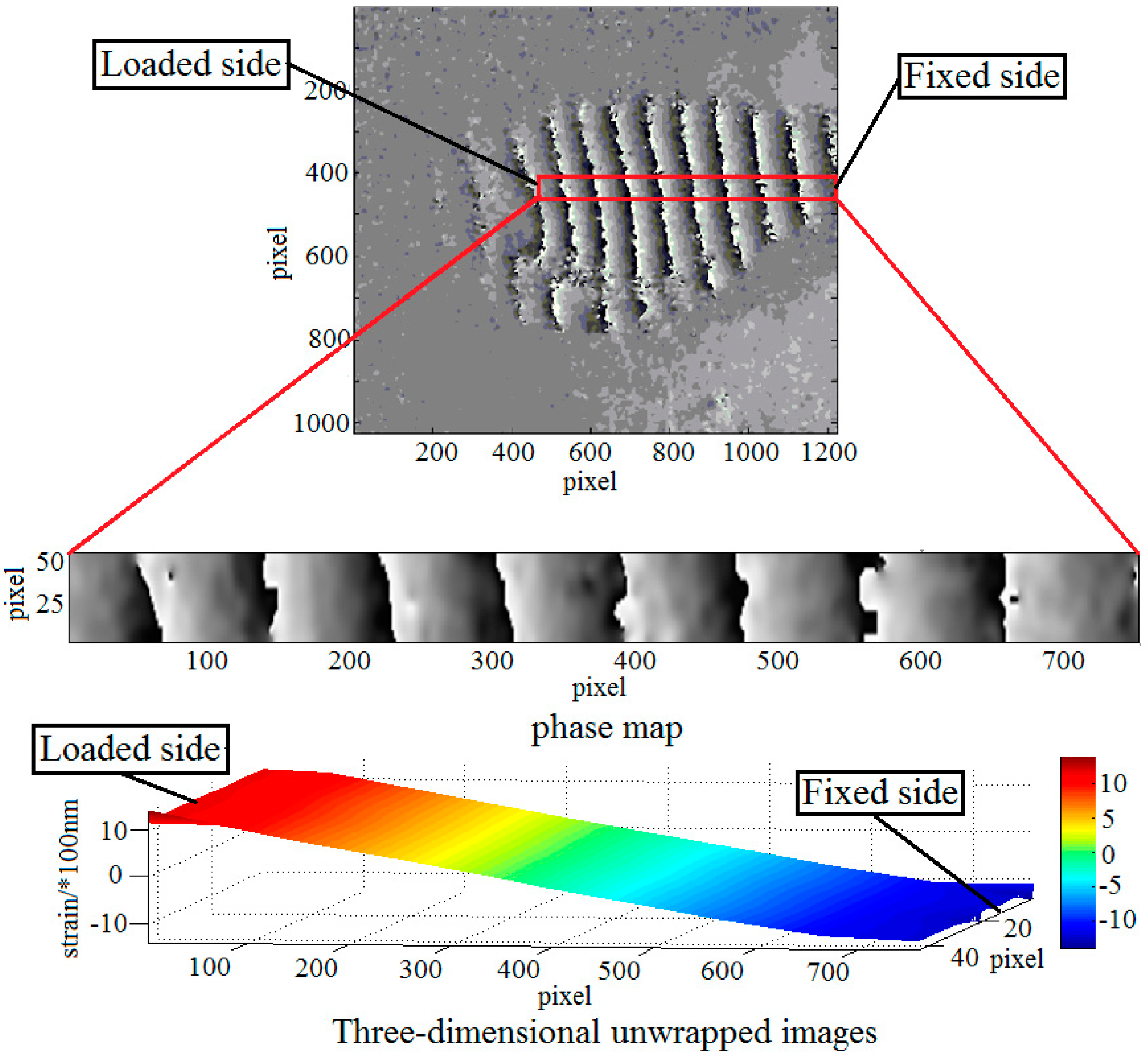
| Phase Diagrams | Three-Dimensional Reconstruction of Out-of-Plane Strain |
|---|---|
 | |
 | |
 | |
 | |
 |
 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, P.; Li, Z.; Yang, H.; Tang, X.; He, G. A Strain Distribution Sensing System for Bone-Implant Interfaces Based on Digital Speckle Pattern Interferometry. Sensors 2019, 19, 365. https://doi.org/10.3390/s19020365
Zhong P, Li Z, Yang H, Tang X, He G. A Strain Distribution Sensing System for Bone-Implant Interfaces Based on Digital Speckle Pattern Interferometry. Sensors. 2019; 19(2):365. https://doi.org/10.3390/s19020365
Chicago/Turabian StyleZhong, Ping, Zhisong Li, Huazheng Yang, Xin Tang, and Guoxing He. 2019. "A Strain Distribution Sensing System for Bone-Implant Interfaces Based on Digital Speckle Pattern Interferometry" Sensors 19, no. 2: 365. https://doi.org/10.3390/s19020365
APA StyleZhong, P., Li, Z., Yang, H., Tang, X., & He, G. (2019). A Strain Distribution Sensing System for Bone-Implant Interfaces Based on Digital Speckle Pattern Interferometry. Sensors, 19(2), 365. https://doi.org/10.3390/s19020365





