Skull’s Photoacoustic Attenuation and Dispersion Modeling with Deterministic Ray-Tracing: Towards Real-Time Aberration Correction
Abstract
1. Introduction
2. Materials and Method
2.1. Theoretical Background
2.1.1. Mathematical Modeling of the PA Wave Propagation in a Single-Layer Heterogeneous Medium
2.1.2. PA Wave Propagation at Interfaces (Interaction with Skull Tissue)
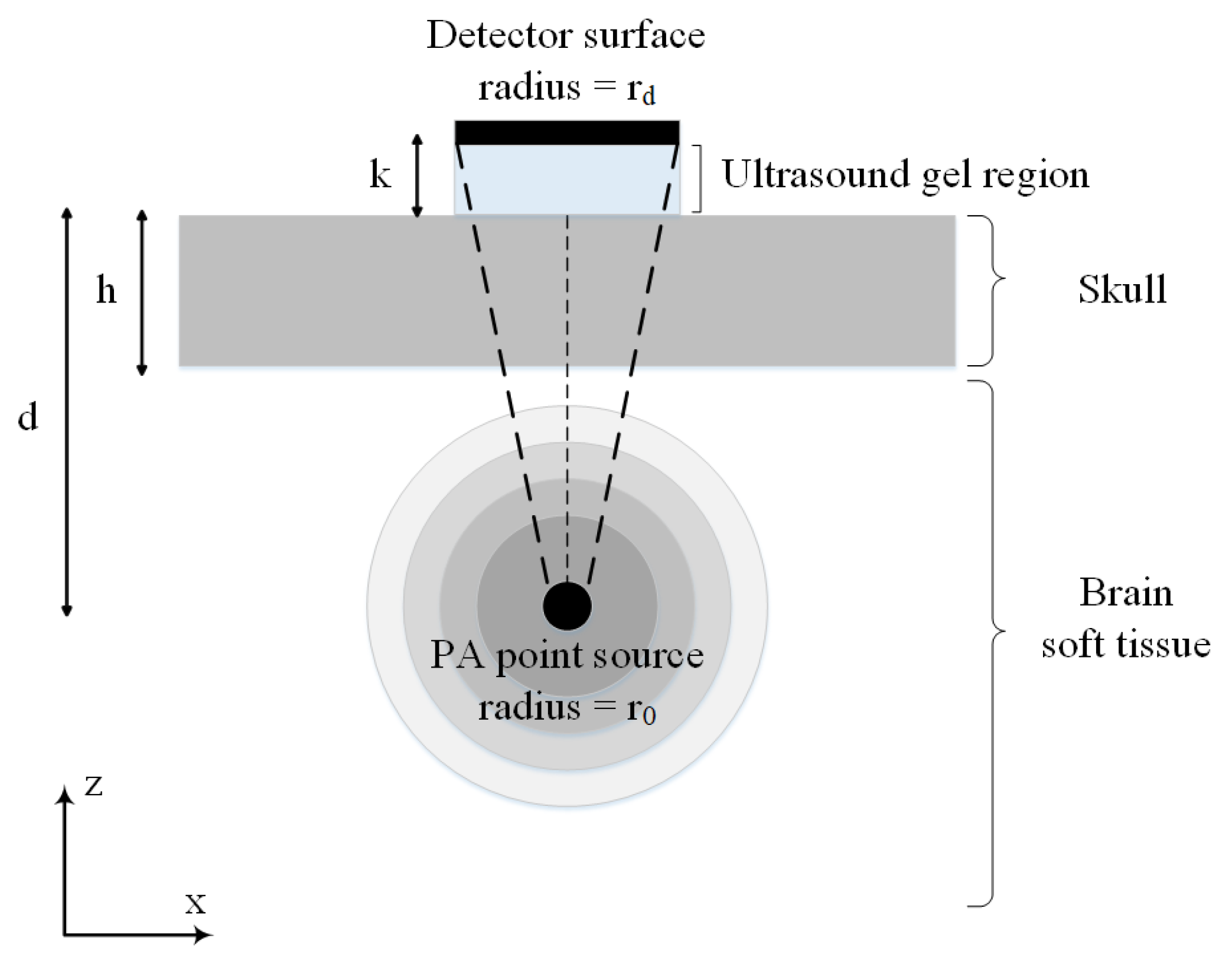
2.2. Simulation Framework
2.2.1. Ultrasound Ray Vector Space
2.2.2. Modeling of Impulse Response
2.2.3. Convolution
3. Validation
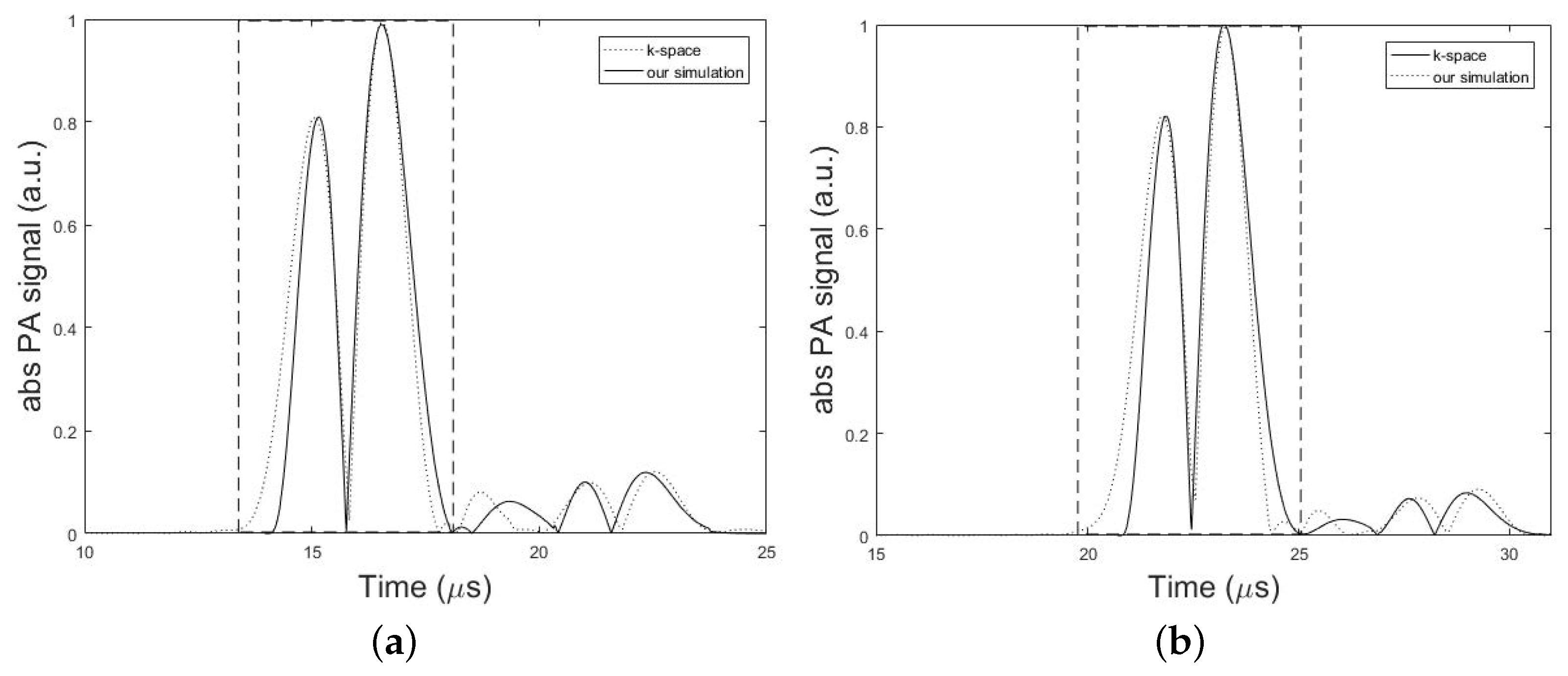
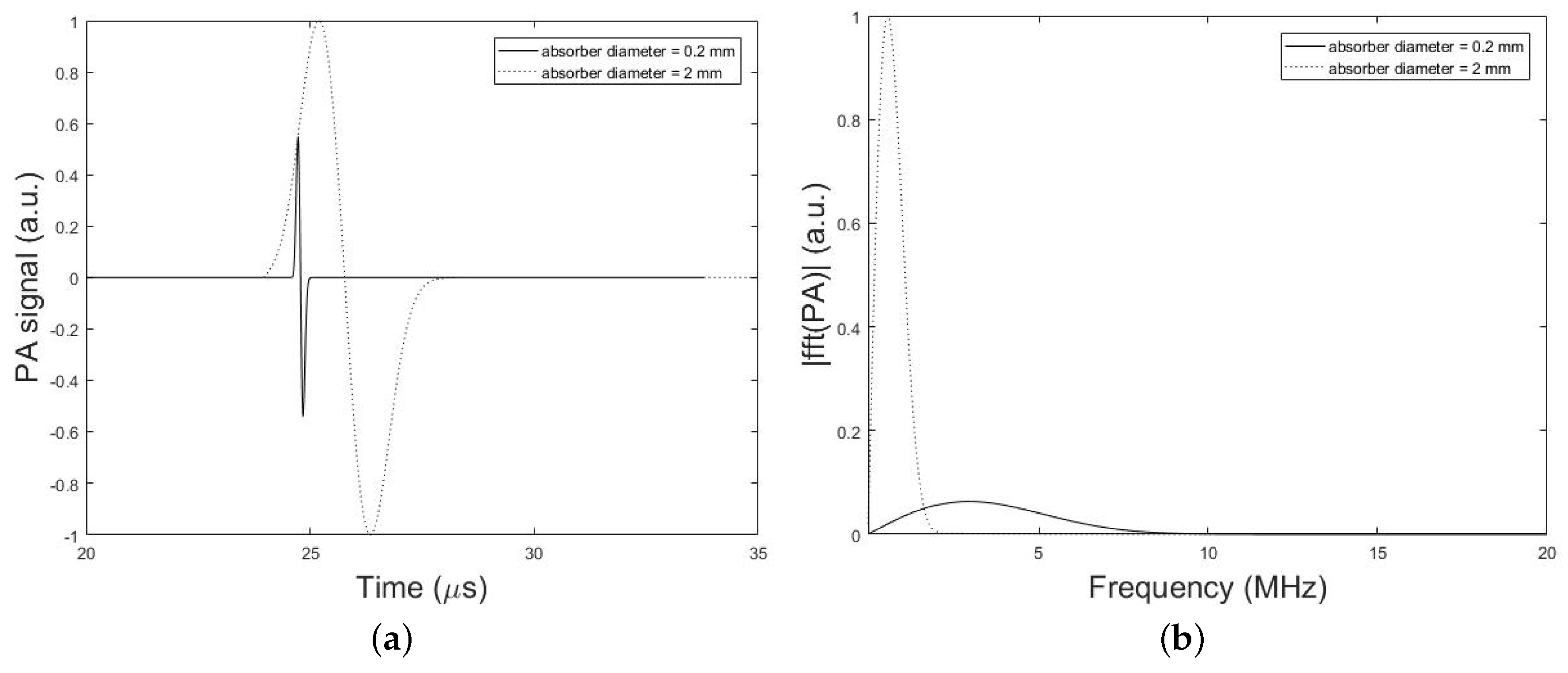
3.1. Numerical Validation
3.2. Analytical Validation
3.3. Experimental Validation
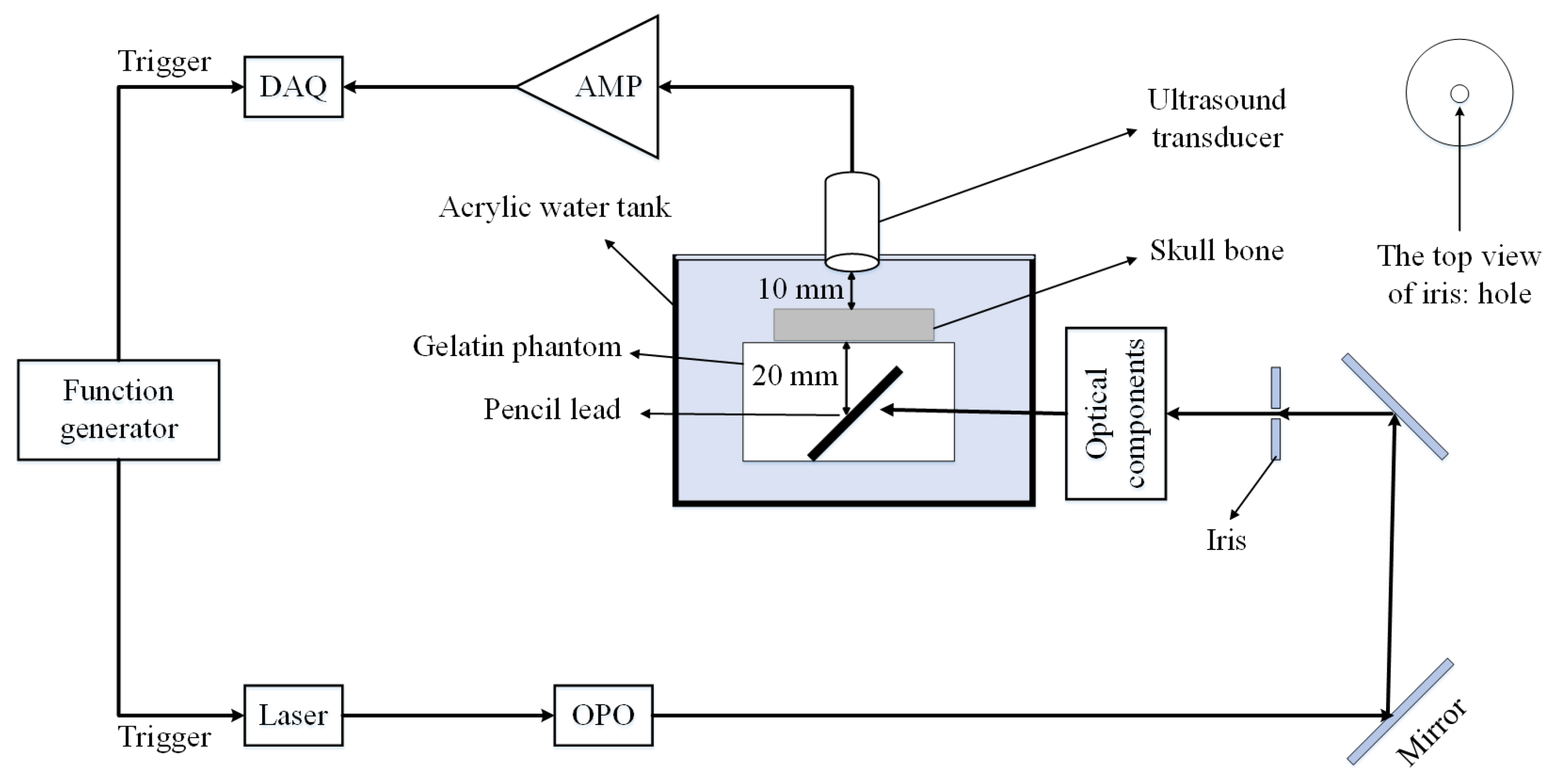
3.3.1. Experimental Setup
3.3.2. Phantom Preparation
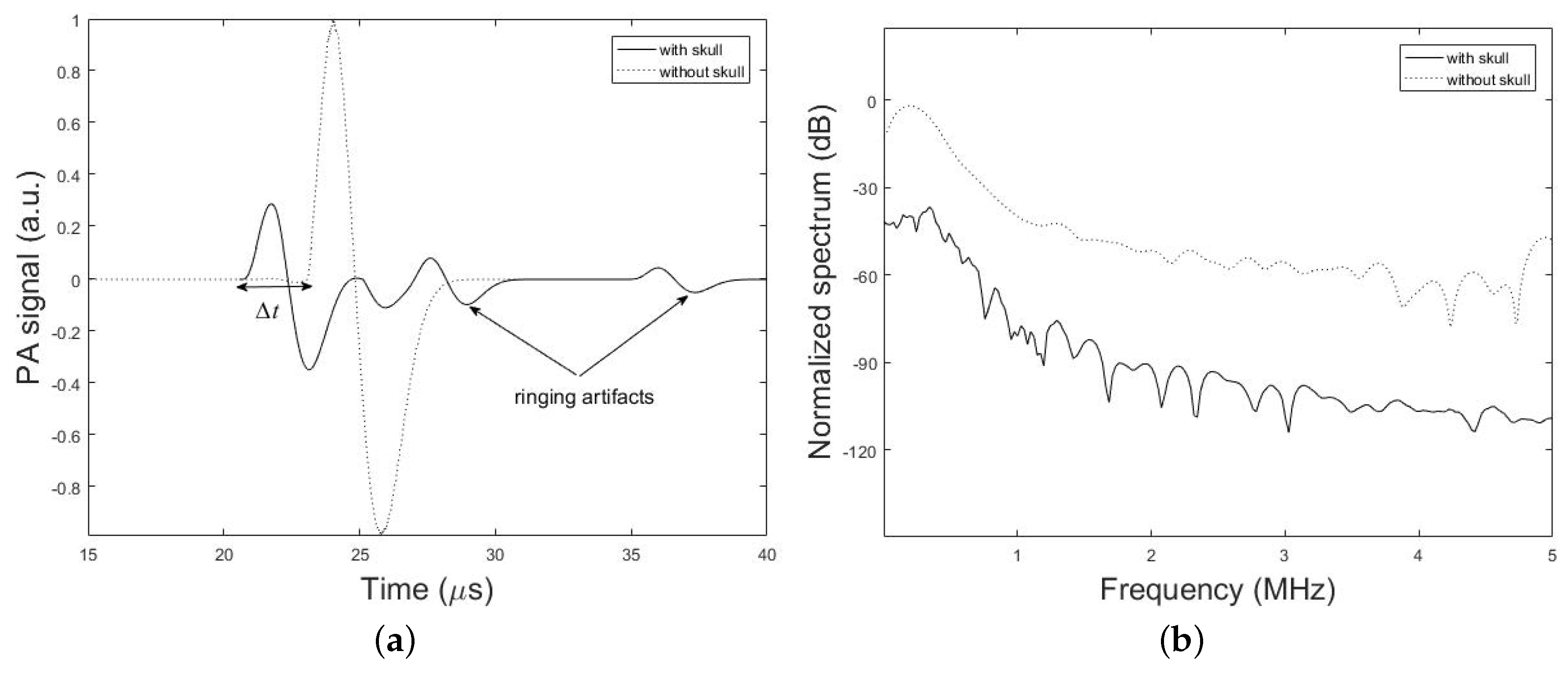
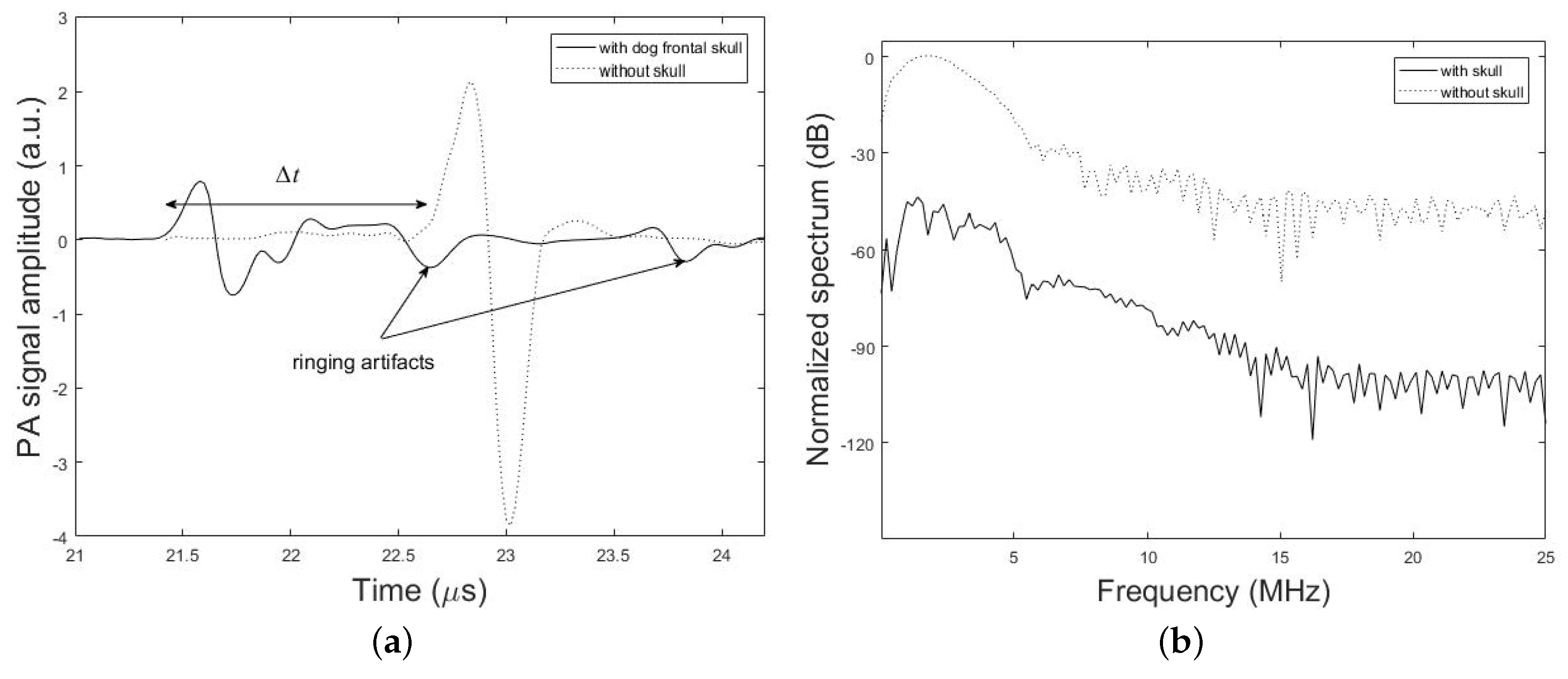
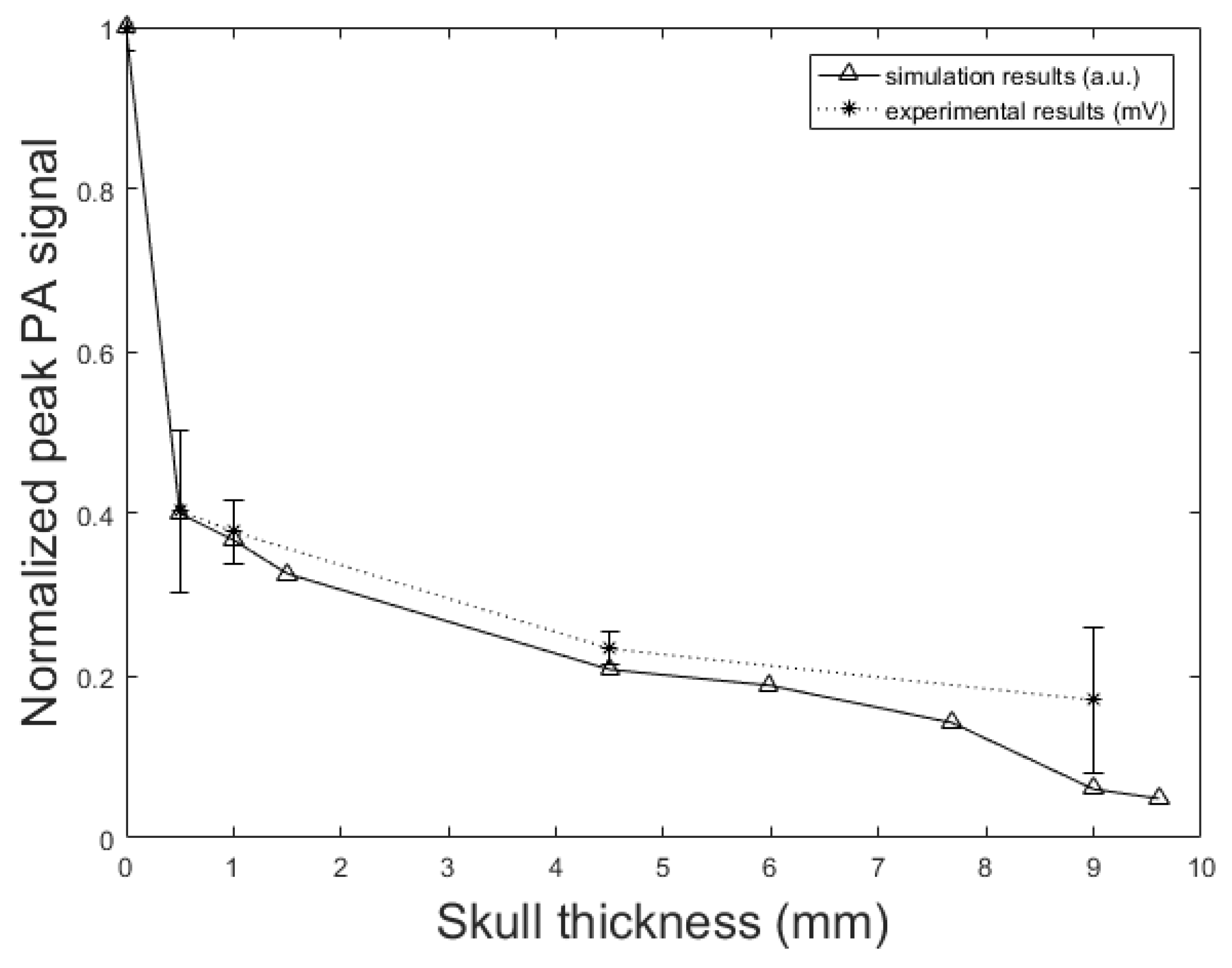
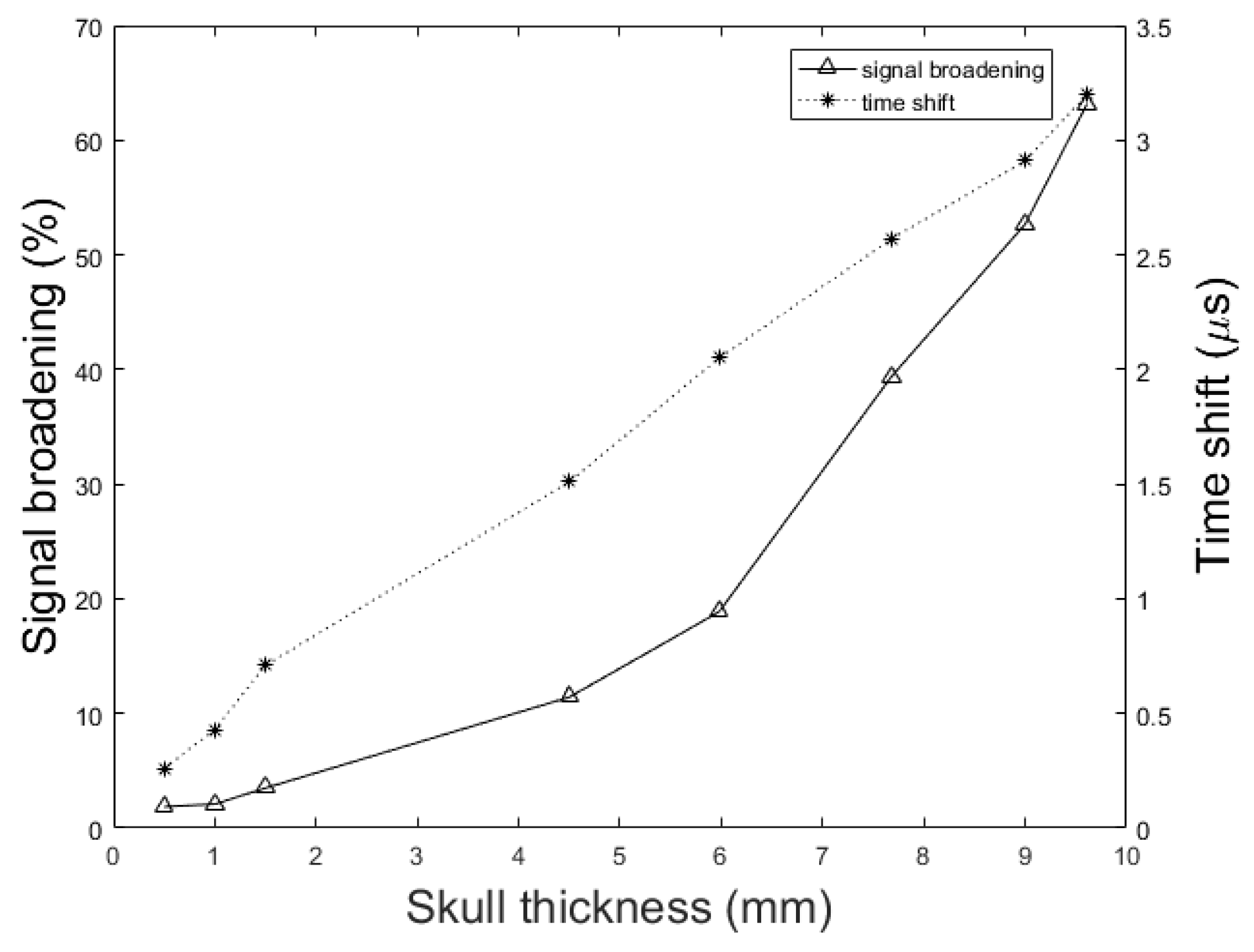
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.V.; Wu, H.I. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wang, L.V. Photoacoustic Imaging and Spectroscopy; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Brecht, H.P.; Su, R.; Fronheiser, M.; Ermilov, S.A.; Conjusteau, A.; Oraevsky, A.A. Whole-body three-dimensional optoacoustic tomography system for small animals. J. Biomed. Opt. 2009, 14, 064007. [Google Scholar] [CrossRef] [PubMed]
- Ntziachristos, V.; Razansky, D. Molecular imaging by means of multispectral optoacoustic tomography (MSOT). Chem. Rev. 2010, 110, 2783–2794. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Pang, Y.; Ku, G.; Xie, X.; Stoica, G.; Wang, L.V. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain. Nat. Biotechnol. 2003, 21, 803–806. [Google Scholar] [CrossRef]
- Burton, N.C.; Patel, M.; Morscher, S.; Driessen, W.H.; Claussen, J.; Beziere, N.; Jetzfellner, T.; Taruttis, A.; Razansky, D.; Bednar, B.; et al. Multispectral opto-acoustic tomography (MSOT) of the brain and glioblastoma characterization. Neuroimage 2013, 65, 522–528. [Google Scholar] [CrossRef]
- Mohammadi-Nejad, A.R.; Mahmoudzadeh, M.; Hassanpour, M.S.; Wallois, F.; Muzik, O.; Papadelis, C.; Hansen, A.; Soltanian-Zadeh, H.; Gelovani, J.; Nasiriavanaki, M. Neonatal brain resting-state functional connectivity imaging modalities. Photoacoustics 2018, 10. [Google Scholar] [CrossRef]
- Meimani, N.; Abani, N.; Gelovani, J.; Avanaki, M.R. A numerical analysis of a semi-dry coupling configuration in photoacoustic computed tomography for infant brain imaging. Photoacoustics 2017, 7, 27–35. [Google Scholar] [CrossRef]
- Kang, J.; Boctor, E.M.; Adams, S.; Kulikowicz, E.; Zhang, H.K.; Koehler, R.C.; Graham, E.M. Validation of Noninvasive Photoacoustic Measurements of Sagittal Sinus Oxyhemoglobin Saturation in Hypoxic Neonatal Piglets. J. Appl. Physiol. 2018, 125, 4. [Google Scholar] [CrossRef]
- Kang, J.; Zhang, H.; Rahmim, A.; Wong, D.; Kang, J.; Boctor, E. Toward high-speed transcranial photoacoustic imaging using compact near-infrared pulsed LED illumination system. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2017, San Francisco, CA, USA, 28 January–2 February 2017; p. 100643B. [Google Scholar]
- Nie, L.; Guo, Z.; Wang, L.V. Photoacoustic tomography of monkey brain using virtual point ultrasonic transducers. J. Biomed. Opt. 2011, 16, 076005. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.V. Monkey brain cortex imaging by photoacoustic tomography. J. Biomed. Opt. 2008, 13, 044009. [Google Scholar] [CrossRef]
- Yao, J.; Xia, J.; Maslov, K.I.; Nasiriavanaki, M.; Tsytsarev, V.; Demchenko, A.V.; Wang, L.V. Noninvasive photoacoustic computed tomography of mouse brain metabolism in vivo. Neuroimage 2013, 64, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Xia, J.; Li, G.; Garcia-Uribe, A.; Sheng, Q.; Anastasio, M.A.; Wang, L.V. Label-free photoacoustic tomography of whole mouse brain structures ex vivo. Neurophotonics 2016, 3, 035001. [Google Scholar] [CrossRef]
- Yao, J.; Wang, L.; Yang, J.M.; Maslov, K.I.; Wong, T.T.; Li, L.; Huang, C.H.; Zou, J.; Wang, L.V. High-speed label-free functional photoacoustic microscopy of mouse brain in action. Nat. Methods 2015, 12, 407–410. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Xia, J.; Wong, T.T.; Li, L.; Wang, L.V. In vivo deep brain imaging of rats using oral-cavity illuminated photoacoustic computed tomography. J. Biomed. Opt. 2015, 20, 016019. [Google Scholar] [CrossRef]
- Li, M.L.; Oh, J.T.; Xie, X.; Ku, G.; Wang, W.; Li, C.; Lungu, G.; Stoica, G.; Wang, L.V. Simultaneous molecular and hypoxia imaging of brain tumors in vivo using spectroscopic photoacoustic tomography. Proc. IEEE 2008, 96, 481–489. [Google Scholar]
- Hu, S.; Maslov, K.; Tsytsarev, V.; Wang, L.V. Functional transcranial brain imaging by optical-resolution photoacoustic microscopy. J. Biomed. Opt. 2009, 14, 040503. [Google Scholar] [CrossRef] [PubMed]
- Nasiriavanaki, M.; Xia, J.; Wan, H.; Bauer, A.Q.; Culver, J.P.; Wang, L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. USA 2014, 111, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Tang, Y.; Yao, J. Photoacoustic tomography of blood oxygenation: A mini review. Photoacoustics 2018, 10, 65–73. [Google Scholar] [CrossRef]
- Zhang, P.; Li, L.; Lin, L.; Hu, P.; Shi, J.; He, Y.; Zhu, L.; Zhou, Y.; Wang, L.V. High-resolution deep functional imaging of the whole mouse brain by photoacoustic computed tomography in vivo. J. Biophotonics 2018, 11, e201700024. [Google Scholar] [CrossRef] [PubMed]
- Gottschalk, S.; Felix Fehm, T.; Luís Deán-Ben, X.; Razansky, D. Noninvasive real-time visualization of multiple cerebral hemodynamic parameters in whole mouse brains using five-dimensional optoacoustic tomography. J. Cereb. Blood Flow Metab. 2015, 35, 531–535. [Google Scholar] [CrossRef]
- Gottschalk, S.; Fehm, T.F.; Deán-Ben, X.L.; Tsytsarev, V.; Razansky, D. Correlation between volumetric oxygenation responses and electrophysiology identifies deep thalamocortical activity during epileptic seizures. Neurophotonics 2016, 4, 011007. [Google Scholar] [CrossRef]
- Balasundaram, G.; Ding, L.; Li, X.; Attia, A.B.E.; Dean-Ben, X.L.; Ho, C.J.H.; Chandrasekharan, P.; Tay, H.C.; Lim, H.Q.; Ong, C.B.; et al. Noninvasive Anatomical and Functional Imaging of Orthotopic Glioblastoma Development and Therapy using Multispectral Optoacoustic Tomography. Transl. Oncol. 2018, 11, 1251–1258. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Jing, Y. A fast marching method based back projection algorithm for photoacoustic tomography in heterogeneous media. arXiv, 2015; arXiv:1501.03869. [Google Scholar]
- Kneipp, M.; Turner, J.; Estrada, H.; Rebling, J.; Shoham, S.; Razansky, D. Effects of the murine skull in optoacoustic brain microscopy. J. Biophotonics 2016, 9, 117–123. [Google Scholar] [CrossRef]
- Estrada, H.; Rebling, J.; Turner, J.; Razansky, D. Broadband acoustic properties of a murine skull. Phys. Med. Biol. 2016, 61, 1932. [Google Scholar] [CrossRef]
- Hynynen, K.; Jolesz, F.A. Demonstration of potential noninvasive ultrasound brain therapy through an intact skull. Ultrasound Med. Biol. 1998, 24, 275–283. [Google Scholar] [CrossRef]
- Hynynen, K.; Sun, J. Trans-skull ultrasound therapy: The feasibility of using image-derived skull thickness information to correct the phase distortion. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 1999, 46, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Clement, G.; Hynynen, K. A non-invasive method for focusing ultrasound through the human skull. Phys. Med. Biol. 2002, 47, 1219. [Google Scholar] [CrossRef]
- Aubry, J.F.; Tanter, M.; Pernot, M.; Thomas, J.L.; Fink, M. Experimental demonstration of noninvasive transskull adaptive focusing based on prior computed tomography scans. J. Acoust. Soc. Am. 2003, 113, 84–93. [Google Scholar] [CrossRef]
- Marquet, F.; Pernot, M.; Aubry, J.; Montaldo, G.; Marsac, L.; Tanter, M.; Fink, M. Non-invasive transcranial ultrasound therapy based on a 3D CT scan: protocol validation and in vitro results. Phys. Med. Biol. 2009, 54, 2597. [Google Scholar] [CrossRef]
- Pinton, G.; Aubry, J.F.; Fink, M.; Tanter, M. Effects of nonlinear ultrasound propagation on high intensity brain therapy. Med. Phys. 2011, 38, 1207–1216. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.M.; O’Reilly, M.A.; Hynynen, K. Transcranial passive acoustic mapping with hemispherical sparse arrays using CT-based skull-specific aberration corrections: A simulation study. Phys. Med. Biol. 2013, 58, 4981. [Google Scholar] [CrossRef] [PubMed]
- Pinton, G.; Aubry, J.F.; Bossy, E.; Muller, M.; Pernot, M.; Tanter, M. Attenuation, scattering, and absorption of ultrasound in the skull bone. Med. Phys. 2012, 39, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Cox, B. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. J. Acoust. Soc. Am. 2010, 127, 2741–2748. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Li, C.; Wang, L.V. Effects of acoustic heterogeneities on transcranial brain imaging with microwave-induced thermoacoustic tomography. Med. Phys. 2008, 35, 3205–3214. [Google Scholar] [CrossRef] [PubMed]
- Schoonover, R.W.; Wang, L.V.; Anastasio, M.A. Numerical investigation of the effects of shear waves in transcranial photoacoustic tomography with a planar geometry. J. Biomed. Opt. 2012, 17, 061215. [Google Scholar] [CrossRef] [PubMed]
- Fry, F.; Barger, J. Acoustical properties of the human skull. J. Acoust. Soc. Am. 1978, 63, 1576–1590. [Google Scholar] [CrossRef]
- Treeby, B.E. Acoustic attenuation compensation in photoacoustic tomography using time-variant filtering. J. Biomed. Opt. 2013, 18, 036008. [Google Scholar] [CrossRef]
- Deán-Ben, X.L.; Razansky, D.; Ntziachristos, V. The effects of acoustic attenuation in optoacoustic signals. Phys. Med. Biol. 2011, 56, 6129. [Google Scholar] [CrossRef]
- Roitner, H.; Burgholzer, P. Efficient modeling and compensation of ultrasound attenuation losses in photoacoustic imaging. Inverse Probl. 2010, 27, 015003. [Google Scholar] [CrossRef]
- Treeby, B.; Pan, J. A practical examination of the errors arising in the direct collocation boundary element method for acoustic scattering. Eng. Anal. Bound. Elem. 2009, 33, 1302–1315. [Google Scholar] [CrossRef]
- Mohammadi, L.; Behnam, H.; Tavakkoli, J.; Nasiriavanaki, M. Skull’s acoustic attenuation and dispersion modeling on photoacoustic signal. In Photons Plus Ultrasound: Imaging and Sensing 2018; International Society for Optics and Photonics: San Francisco, CA, USA, 2018; Volume 10494, p. 104946K. [Google Scholar]
- Huang, C.; Nie, L.; Schoonover, R.W.; Guo, Z.; Schirra, C.O.; Anastasio, M.A.; Wang, L.V. Aberration correction for transcranial photoacoustic tomography of primates employing adjunct image data. J. Biomed. Opt. 2012, 17, 0660161–0660168. [Google Scholar] [CrossRef]
- Huang, C.; Nie, L.; Schoonover, R.W.; Wang, L.V.; Anastasio, M.A. Photoacoustic computed tomography correcting for heterogeneity and attenuation. J. Biomed. Opt. 2012, 17, 0612111–0612115. [Google Scholar] [CrossRef] [PubMed]
- Schoonover, R.W.; Anastasio, M.A. Compensation of shear waves in photoacoustic tomography with layered acoustic media. JOSA A 2011, 28, 2091–2099. [Google Scholar] [CrossRef]
- Estrada, H.; Huang, X.; Rebling, J.; Zwack, M.; Gottschalk, S.; Razansky, D. Virtual craniotomy for high-resolution optoacoustic brain microscopy. Sci. Rep. 2018, 8, 1459. [Google Scholar] [CrossRef] [PubMed]
- Kyriakou, A.; Neufeld, E.; Werner, B.; Székely, G.; Kuster, N. Full-wave acoustic and thermal modeling of transcranial ultrasound propagation and investigation of skull-induced aberration correction techniques: A feasibility study. J. Ther. Ultrasound 2015, 3, 11. [Google Scholar] [CrossRef] [PubMed]
- Odabaee, M.; Odabaee, M.; Pelekanos, M.; Leinenga, G.; Götz, J. Modeling ultrasound propagation through material of increasing geometrical complexity. Ultrasonics 2018, 90, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Nagatani, Y.; Imaizumi, H.; Fukuda, T.; Matsukawa, M.; Watanabe, Y.; Otani, T. Applicability of finite-difference time-domain method to simulation of wave propagation in cancellous bone. Jpn. J. Appl. Phys. 2006, 45, 7186. [Google Scholar] [CrossRef]
- Yoon, K.; Lee, W.; Croce, P.; Cammalleri, A.; Yoo, S.S. Multi-resolution simulation of focused ultrasound propagation through ovine skull from a single-element transducer. Phys. Med. Biol. 2018, 63, 105001. [Google Scholar] [CrossRef]
- Pernot, M.; Aubry, J.F.; Tanter, M.; Thomas, J.L.; Fink, M. Experimental validation of 3D finite differences simulations of ultrasonic wave propagation through the skull. In Proceedings of the 2001 IEEE Ultrasonics Symposium, Scotland, UK, 7–10 October 2001; Volume 2, pp. 1547–1550. [Google Scholar]
- Treeby, B.E.; Cox, B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15, 021314. [Google Scholar] [CrossRef]
- Jocker, J. Ultrasonic Wave Propagation in Heterogeneous Elastic And Poroelastic Media; Delft University of Technology: Delft, The Netherlands, 2005. [Google Scholar]
- Firouzi, K.; Saffari, N. A numerical model for the study of photoacoustic imaging of brain tumours. arXiv, 2015; arXiv:1512.06792. [Google Scholar]
- Guo, X.; Zhang, D.; Gong, X. Evaluation of ultrasonic scattering in human cancellous bone by using a binary mixture model. Phys. Med. Biol. 2006, 52, 29. [Google Scholar] [CrossRef] [PubMed]
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Waters, K.R.; Hughes, M.S.; Mobley, J.; Brandenburger, G.H.; Miller, J.G. On the applicability of Kramers–Krönig relations for ultrasonic attenuation obeying a frequency power law. J. Acoust. Soc. Am. 2000, 108, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Waters, K.R.; Mobley, J.; Miller, J.G. Causality-imposed (Kramers-Kronig) relationships between attenuation and dispersion. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 822–823. [Google Scholar] [CrossRef]
- Szabo, T.L. Time domain wave equations for lossy media obeying a frequency power law. J. Acoust. Soc. Am. 1994, 96, 491–500. [Google Scholar] [CrossRef]
- Chen, W.; Holm, S. Modified Szabo’s wave equation models for lossy media obeying frequency power law. J. Acoust. Soc. Am. 2003, 114, 2570–2574. [Google Scholar] [CrossRef] [PubMed]
- White, P.; Clement, G.; Hynynen, K. Longitudinal and shear mode ultrasound propagation in human skull bone. Ultrasound Med. Biol. 2006, 32, 1085–1096. [Google Scholar] [CrossRef] [PubMed]
- Clement, G.; White, P.; Hynynen, K. Enhanced ultrasound transmission through the human skull using shear mode conversion. J. Acoust. Soc. Am. 2004, 115, 1356–1364. [Google Scholar] [CrossRef]
- Nam, K.; Rosado-Mendez, I.M.; Rubert, N.C.; Madsen, E.L.; Zagzebski, J.A.; Hall, T.J. Ultrasound attenuation measurements using a reference phantom with sound speed mismatch. Ultrason. Imaging 2011, 33, 251–263. [Google Scholar] [CrossRef]
- Hoelen, C.; De Mul, F. A new theoretical approach to photoacoustic signal generation. J. Acoust. Soc. Am. 1999, 106, 695–706. [Google Scholar] [CrossRef]
- Hayner, M.; Hynynen, K. Numerical analysis of ultrasonic transmission and absorption of oblique plane waves through the human skull. J. Acoust. Soc. Am. 2001, 110, 3319–3330. [Google Scholar] [CrossRef]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- De Greve, B. Reflections and Refractions in Ray Tracing; White Paper; Stanford University: Stanford, CA, USA, 2004. [Google Scholar]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Kratkiewicz, K.; Adabi, S.; Nasiriavanaki, M. Linear-array photoacoustic imaging using minimum variance-based delay multiply and sum adaptive beamforming algorithm. J. Biomed. Opt. 2018, 23, 026002. [Google Scholar] [CrossRef]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Adabi, S.; Nasiriavanaki, M. Double-stage delay multiply and sum beamforming algorithm: Application to linear-array photoacoustic imaging. IEEE Trans. Biomed. Eng. 2018, 65, 31–42. [Google Scholar] [CrossRef]
- Hariri, A.; Fatima, A.; Mohammadian, N.; Mahmoodkalayeh, S.; Ansari, M.A.; Bely, N.; Avanaki, M.R. Development of low-cost photoacoustic imaging systems using very low-energy pulsed laser diodes. J. Biomed. Opt. 2017, 22, 075001. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chamberland, D.L.; Xi, G. Noninvasive reflection mode photoacoustic imaging through infant skull toward imaging of neonatal brains. J. Neurosci. Methods 2008, 168, 412–421. [Google Scholar] [CrossRef] [PubMed]
- Ruan, J.; Prasad, P. The effects of skull thickness variations on human head dynamic impact responses. Stapp. Car Crash J. 2001, 45, 395–414. [Google Scholar] [PubMed]



| Symbol (Unit) | Soft Tissue | Skull | Water (Coupling Medium) |
|---|---|---|---|
| (kg/m) | 1000 [39] | 1800 [27] | 1000 [65] |
| (m/s) | 1500 [66] | 2900 [27] | 1486 [65] |
| (m/s) | — | 1444 [27] | — |
| (Np/cm) | 0.05 [66] | 1.70 [39] | 0.00 [65] |
| 1.18 [66] | 0.93 [39] | — | |
| (Np/cm) | — | 3.41 [39] | — |
| — | 0.93 [39] | — |
| Skull Thickness (mm) | NSD (%) |
|---|---|
| 1 | 0.19 |
| 4 | 0.14 |
| 7 | 0.11 |
| Target Depth (cm) | NSD (%) |
|---|---|
| 1.7 | 0.11 |
| 2.7 | 0.25 |
| 3.7 | 0.21 |
| () | (%) | (%) | ||||
|---|---|---|---|---|---|---|
| 0 | 0.414 | 0.000 | 0.421 | 0.000 | 1.69 | 0.00 |
| 15 | 0.192 | 0.026 | 0.185 | 0.025 | −3.65 | −3.85 |
| 30 | 0.133 | 0.048 | 0.139 | 0.046 | 4.51 | −4.17 |
| (MHz) | (mm) | N | (s) | (s) | |
|---|---|---|---|---|---|
| 64 Frequency | 32 Frequency | ||||
| 1 | 0.75 | 86 | 849.45 | 35.06 | 19.74 |
| 1.5 | 0.5 | 128 | 2571.89 | 40.20 | 20.16 |
| 3 | 0.25 | 256 | >18,000 | 42.66 | 22.14 |
| 5 | 0.15 | 427 | — e | 48.69 | 25.12 |
| 7.5 | 0.1 | 640 | — e | 59.14 | 27.92 |
| h (mm) | Target Depth = 1.7 cm | Target Depth = 3.7 cm | ||||||
|---|---|---|---|---|---|---|---|---|
| N | (mm) | (s) | (s) | N | (mm) | (s) | (s) | |
| 7 | 32 | 1 | 20.21 | 149.18 | 64 | 1 | 168.29 | 132.14 |
| 7.5 | 64 | 0.5 | 168.88 | 149.83 | 128 | 0.5 | 2533.10 | 135.21 |
| 7.25 | 128 | 0.25 | 2535.67 | 147.26 | 256 | 0.25 | >18,000 | 134.63 |
| 7.1 | 320 | 0.1 | — e | 146.46 | 640 | 0.1 | — e | 133.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, L.; Behnam, H.; Tavakkoli, J.; Avanaki, M.R.N. Skull’s Photoacoustic Attenuation and Dispersion Modeling with Deterministic Ray-Tracing: Towards Real-Time Aberration Correction. Sensors 2019, 19, 345. https://doi.org/10.3390/s19020345
Mohammadi L, Behnam H, Tavakkoli J, Avanaki MRN. Skull’s Photoacoustic Attenuation and Dispersion Modeling with Deterministic Ray-Tracing: Towards Real-Time Aberration Correction. Sensors. 2019; 19(2):345. https://doi.org/10.3390/s19020345
Chicago/Turabian StyleMohammadi, Leila, Hamid Behnam, Jahan Tavakkoli, and Mohammad R. N. Avanaki. 2019. "Skull’s Photoacoustic Attenuation and Dispersion Modeling with Deterministic Ray-Tracing: Towards Real-Time Aberration Correction" Sensors 19, no. 2: 345. https://doi.org/10.3390/s19020345
APA StyleMohammadi, L., Behnam, H., Tavakkoli, J., & Avanaki, M. R. N. (2019). Skull’s Photoacoustic Attenuation and Dispersion Modeling with Deterministic Ray-Tracing: Towards Real-Time Aberration Correction. Sensors, 19(2), 345. https://doi.org/10.3390/s19020345





