Algorithm Design for Edge Detection of High-Speed Moving Target Image under Noisy Environment
Abstract
1. Introduction
2. Principle of Noise-Tolerant Edge Detection Algorithm
2.1. Theoretical Basis
- (1)
- is the derivative of with respect to , if it is equal to zero at , then the wavelet transform has local extreme value in .
- (2)
- If for any point in the neighborhood of point satisfies , and in the left neighborhood or the right neighborhood strictly meet the above inequality relations, is called the maximum point of wavelet transform modulus in the scale of ; is called the maximum modulus of wavelet transform modulus on the point of .
- (3)
- On the plane of , if there is a curve that every point is a modulus maximum point of , it is called a modulus maximum curve.
- (1)
- (2)
- gets the local modulus maximum at point .
2.2. Algorithm Basis
- (1)
- Singular point of signal usually corresponds to the maximum value of the wavelet transform coefficient.
- (2)
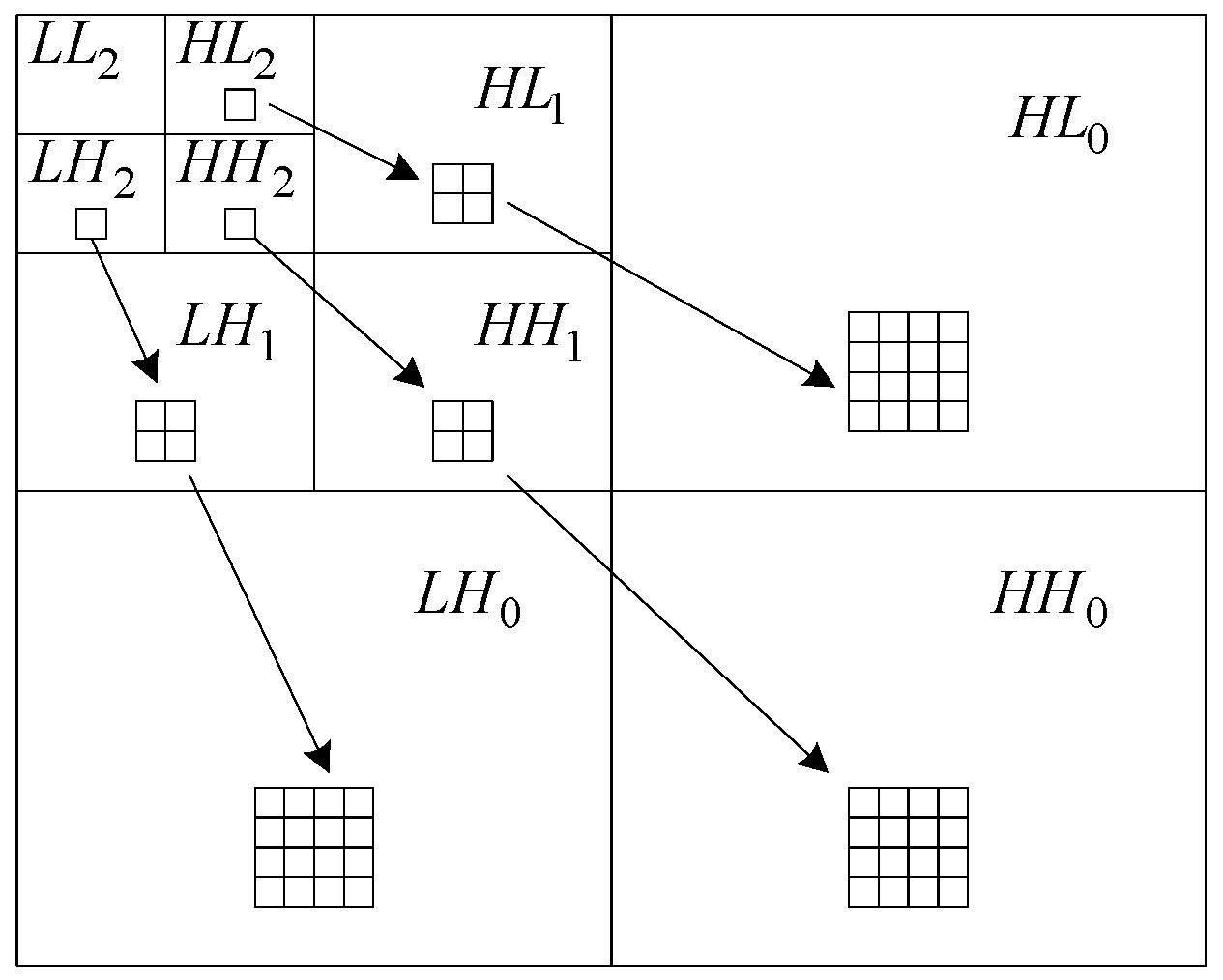
- There is a correlation relationship between wavelet coefficients in different scales, that is, when the parent coefficient has a larger value, its four sub-coefficients also have a larger value.
- (3)
- Noise and edge signal have a different Lipschitz exponent property, which means that wavelet transform modulus of noise decreases with the increase of scale, and wavelet transform modulus of image edge signal increases with the increase of scale.
- (1)
- First, select a kind of wavelet filter. The application effect of wavelet transform is closely dependent on the selection of wavelet function. Wavelet selection should comprehensively consider various performances according to the application requirements. Generally speaking, at a certain scale, the number of the detected extreme points has a linear relationship with the number of wavelet disappearing moments. The aim of this paper is to do edge detection, and a filter with small vanishing moments can be selected to get more high-frequency information in transformation domain. See Section 3 of this paper for detailed discussion.
- (2)
- Second, wavelet transform is performed at a certain scale. For digital images, the number of wavelet coefficients decreases by ration of . If the original image is small, the coefficients after several layers of wavelet transformation will become too less to support the detection and analysis algorithm. In this paper, for image with resolution of , three-layer wavelet transform is adopted for coefficients analysis.
- (3)
- The correlation relationship between wavelet transform coefficients is used for edge detection and denoising. This is composed of two steps: the first, from bottom to top, preserve the important coefficients by using the idea of activation function of neural network unit; the second, from top to bottom, eliminate unimportant coefficients by using outlier point search judgment algorithm. See Section 2.3 of this article for detailed algorithm.
- (4)
- Wavelet inverse transform is applied to the coefficients preserved after the above treatment.
- (5)
- According to the actual processing effect, some mathematical morphology algorithm can be adopted to remove the isolated noise points, so as to obtain a clearer and complete edge image.
2.3. Process of Denoising by Interlayer Correlation of Wavelet Coefficients
2.3.1. Process of Wavelet Coefficients Adopting Idea of Neural Network Activation Function
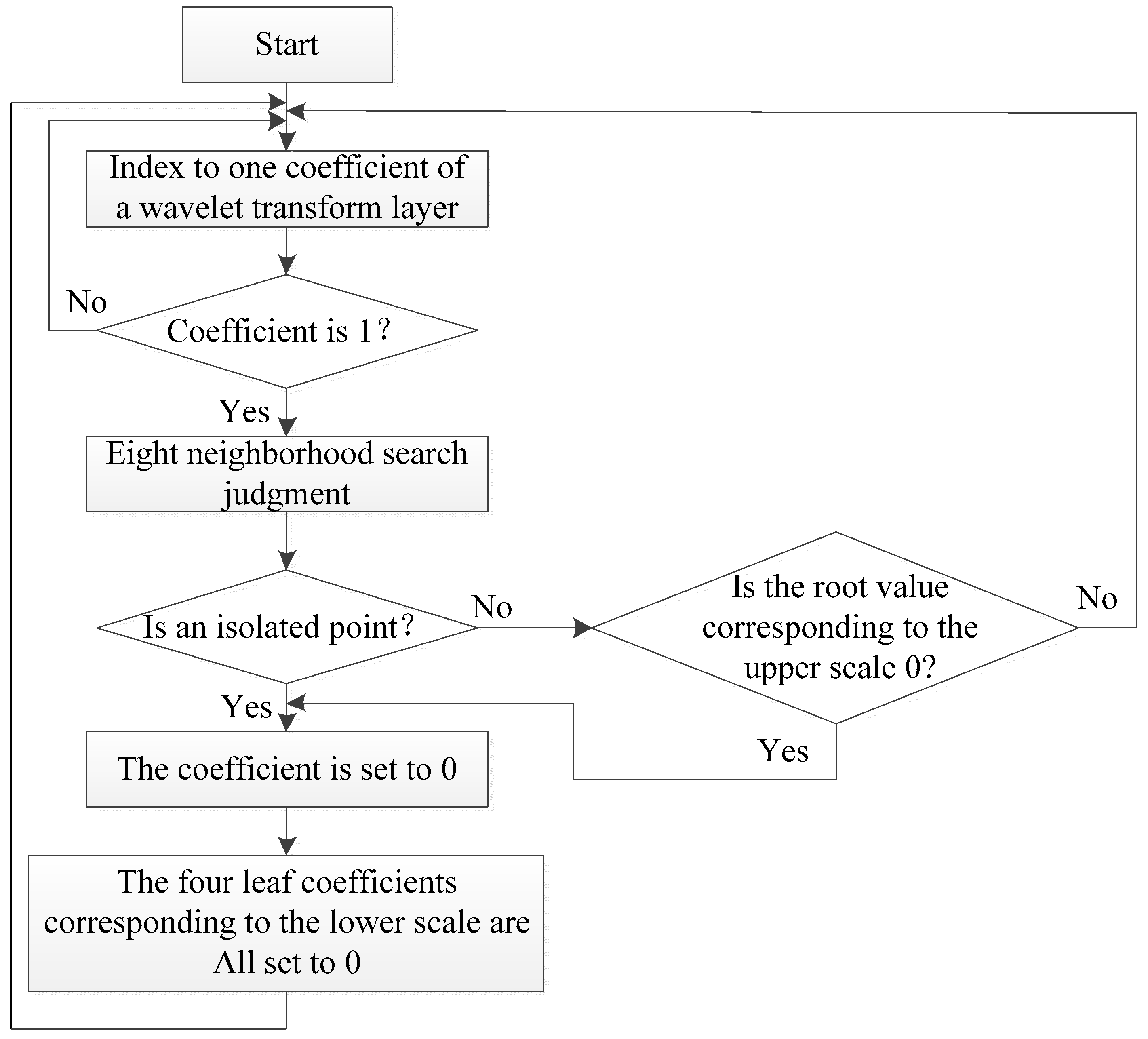
2.3.2. Judgment for Isolated Coefficients
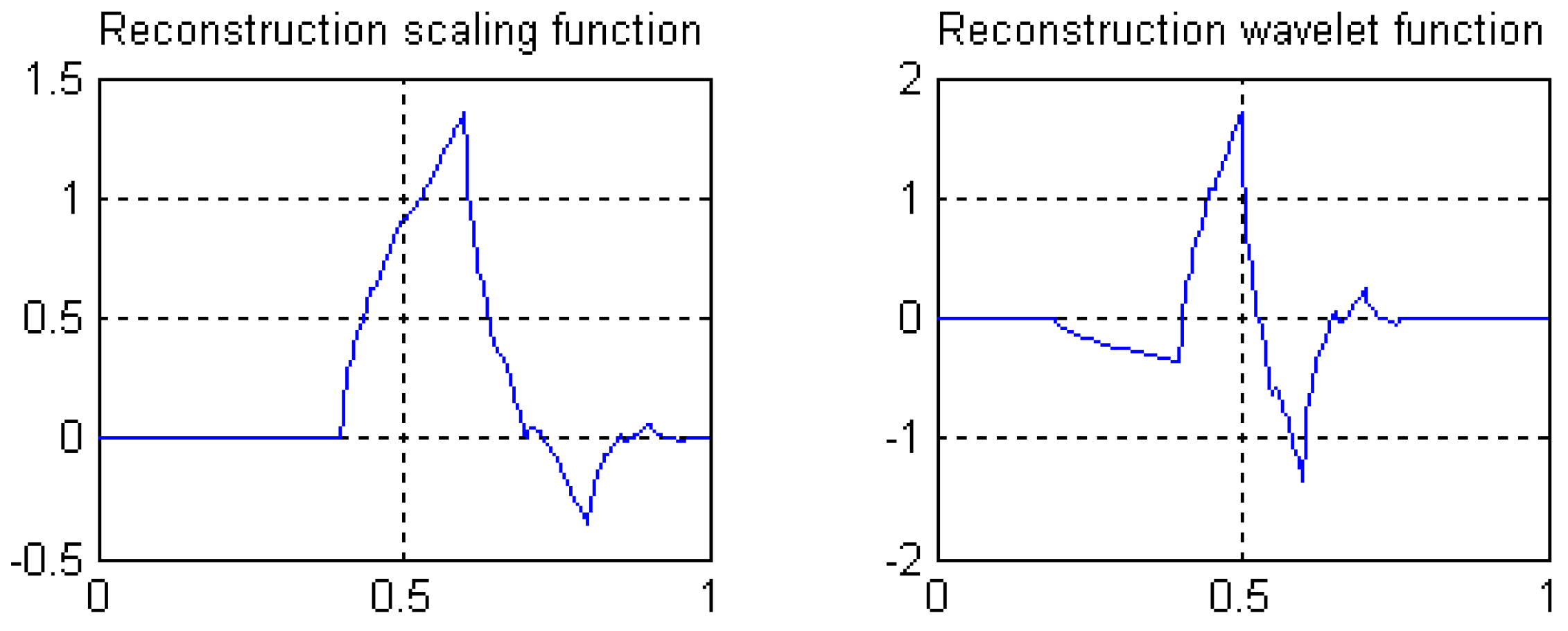
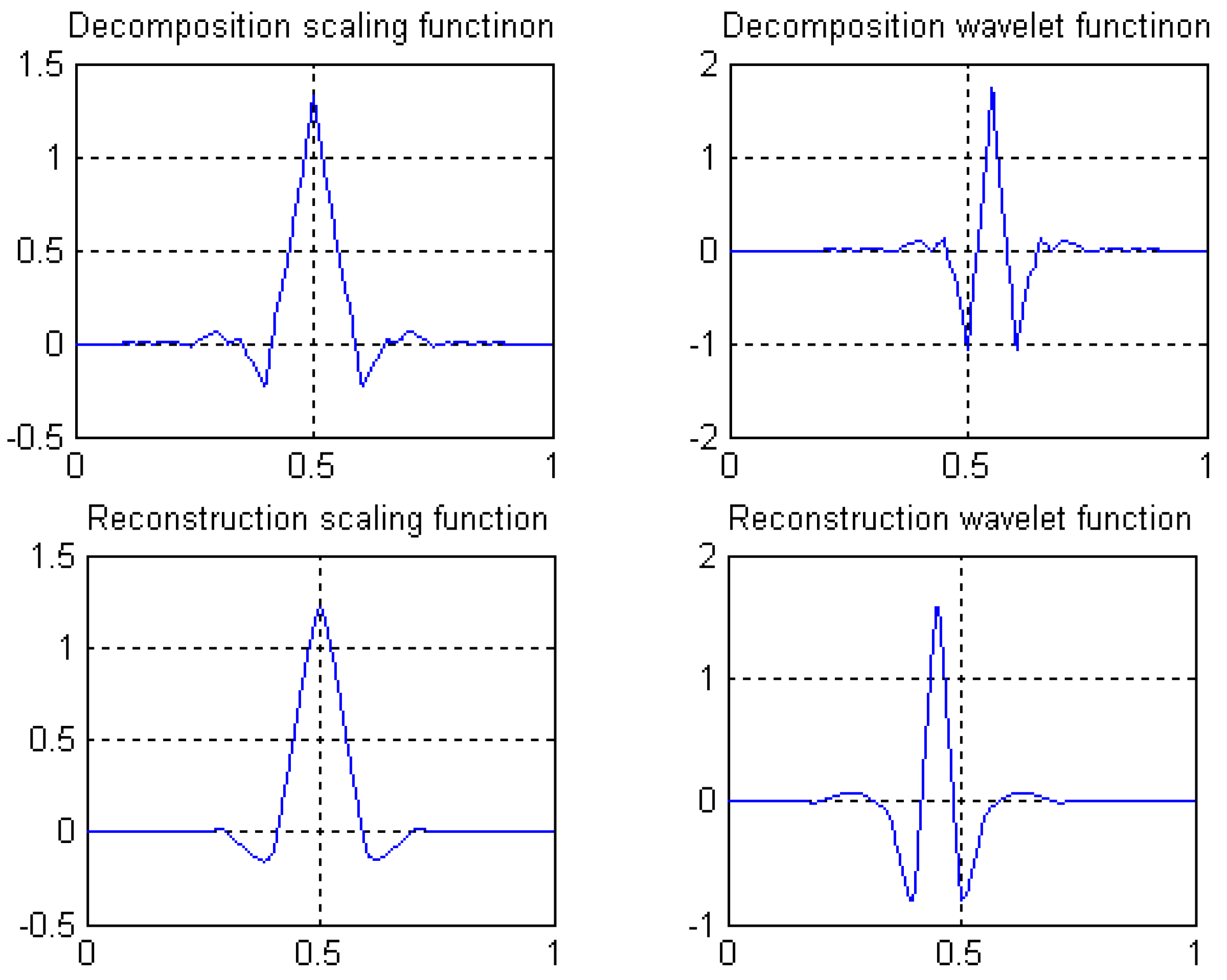
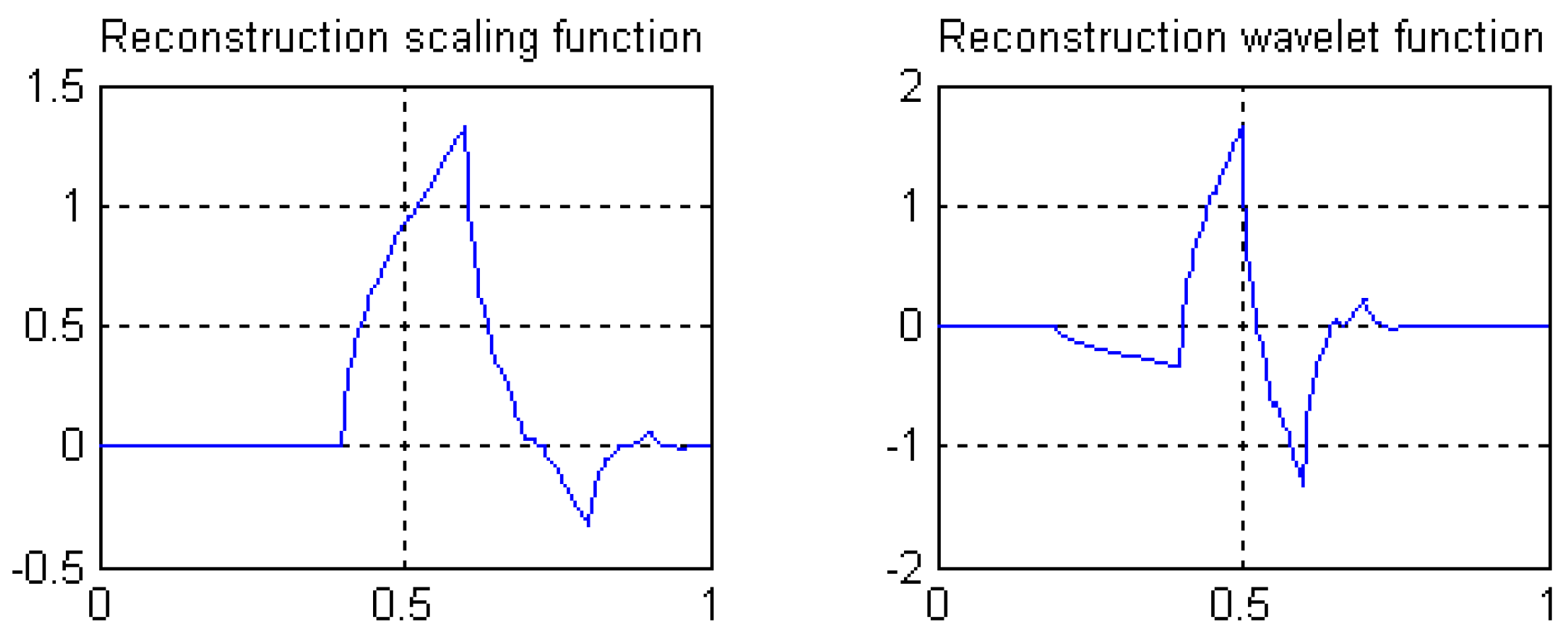
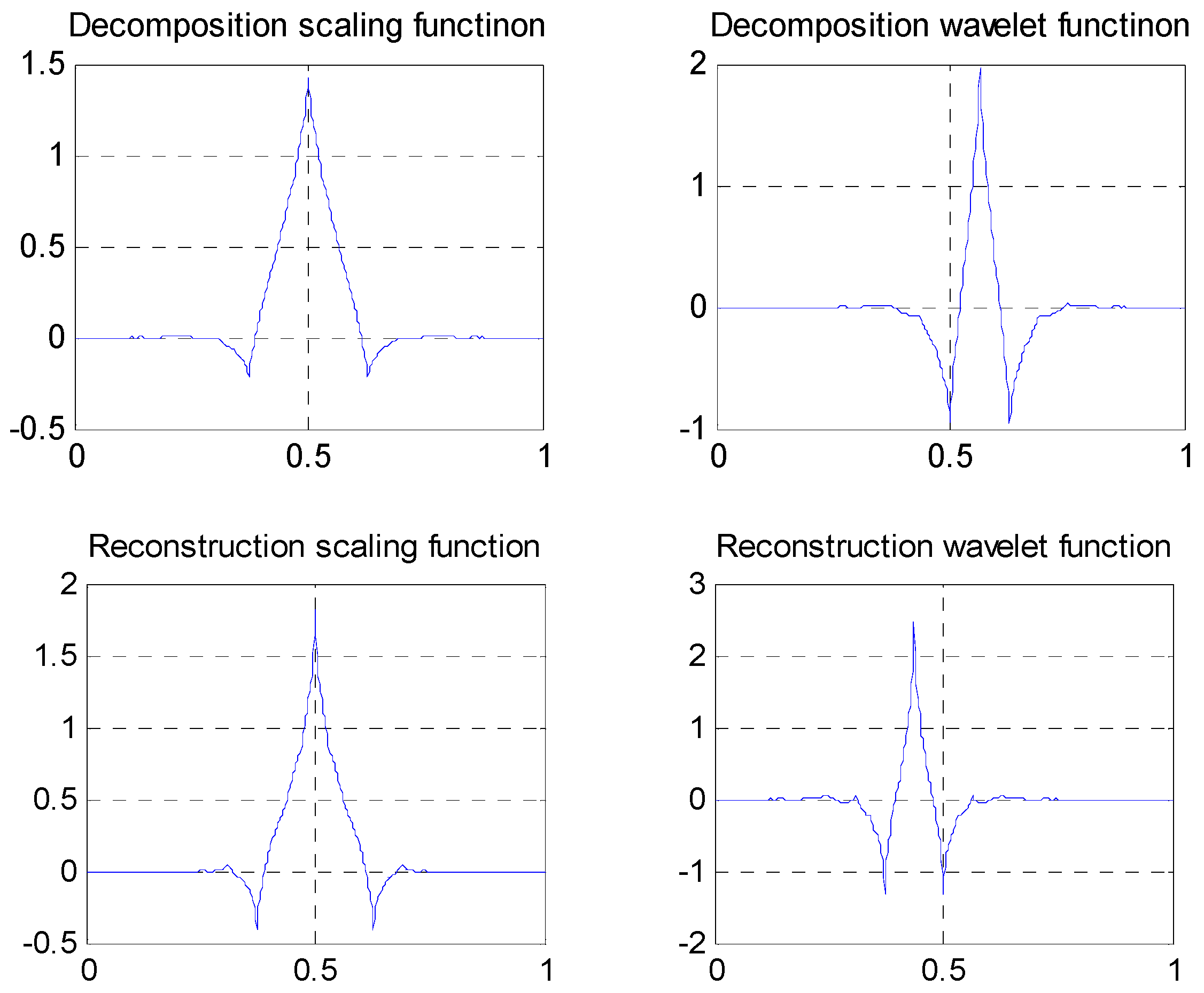
3. Design of Rational Coefficients Biorthogonal Wavelet Filters
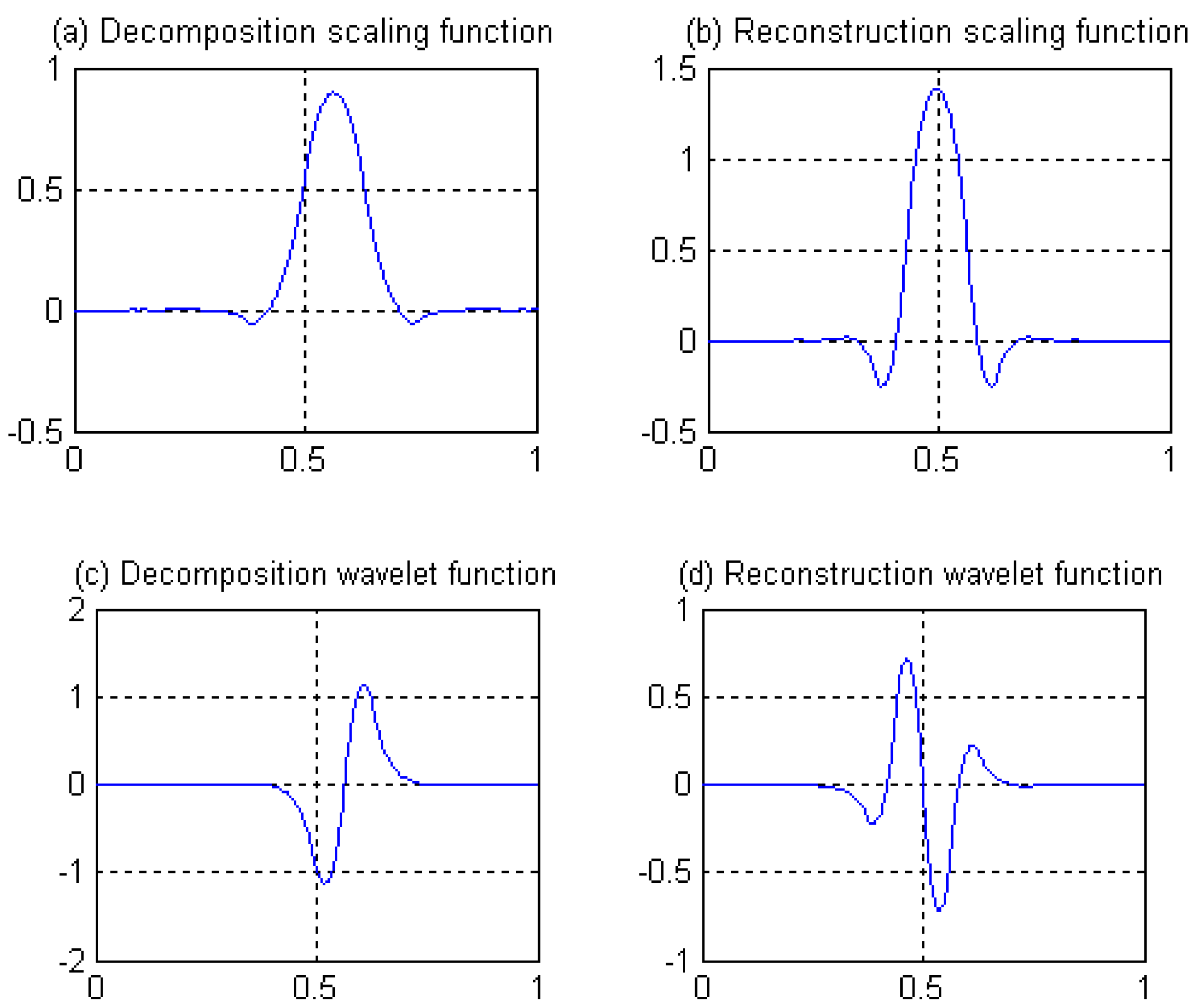
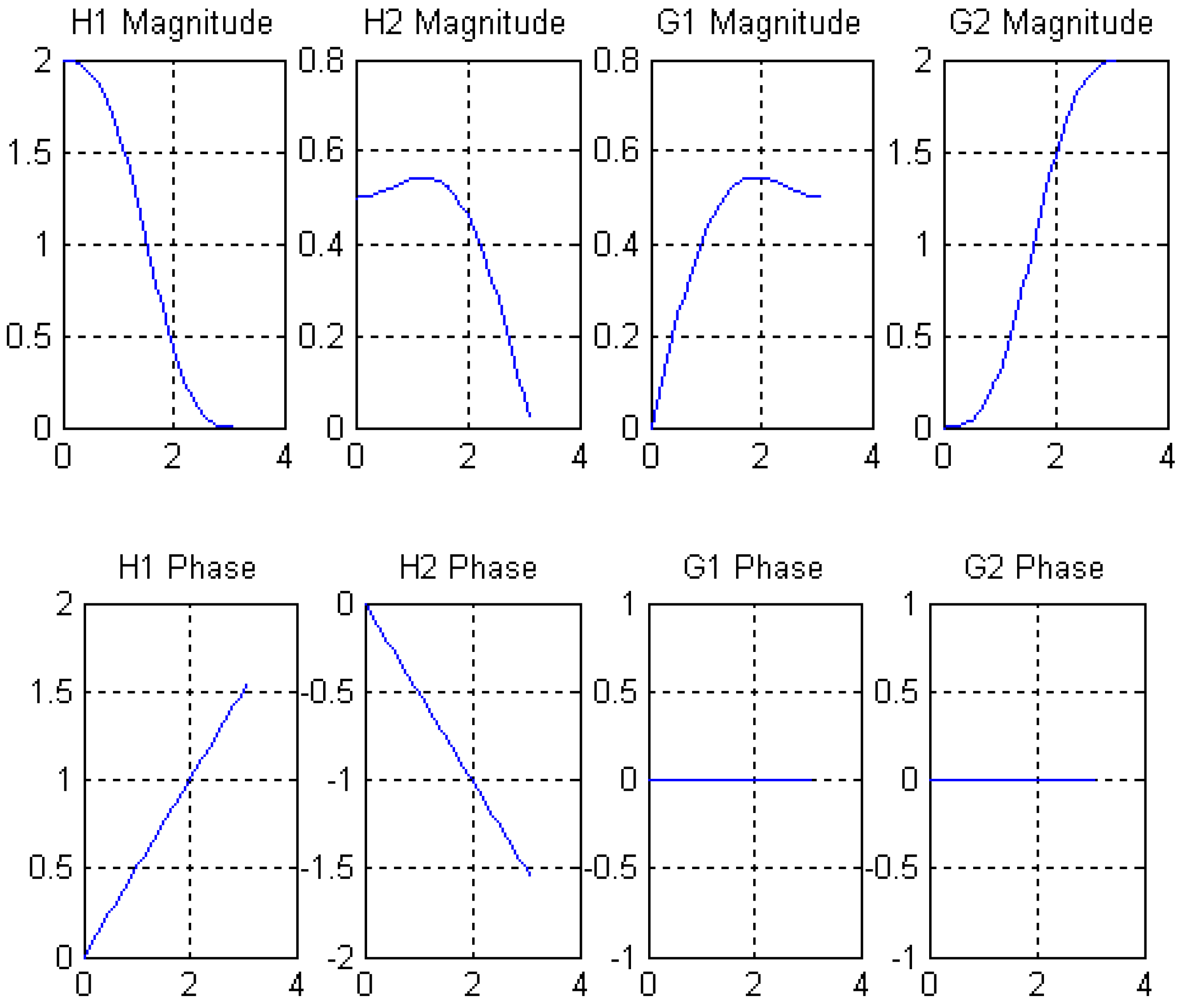
3.1. Construction of Biorthogonal Complete Reconstruction Wavelet Filters
3.2. Construction of Even Length Symmetric Compactly-Supported Biorthogonal Wavelet Filters
3.3. Length 8-4 Rational Coefficients Symmetric Compactly-Supported Biorthogonal Wavelet Filters
4. Experiments
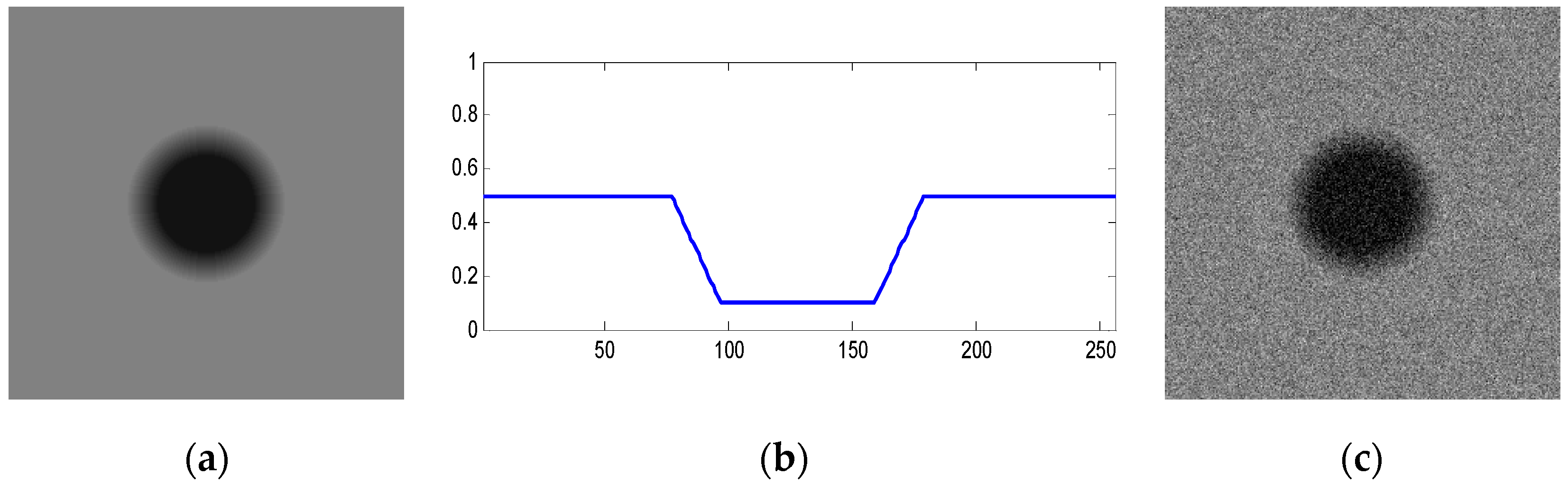
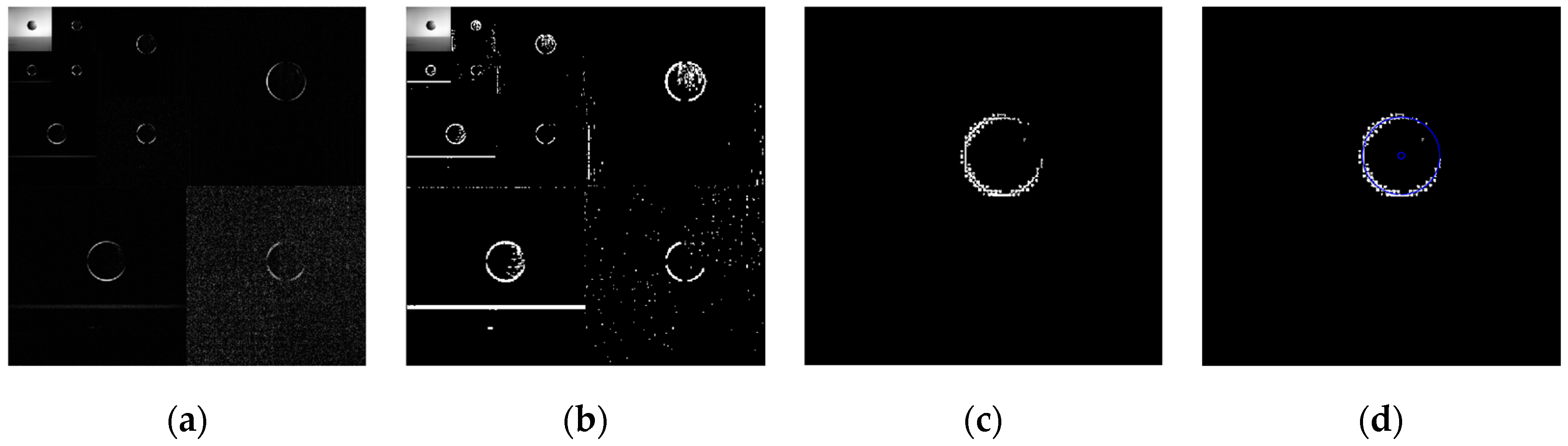
4.1. Edge Detection for Images under Noisy Environments
4.2. Edge Detection for Noisy Image by Different Wavelet Filters
4.3. Edge Detection for Image with Gray-Gradient Edge under Noisy Environment
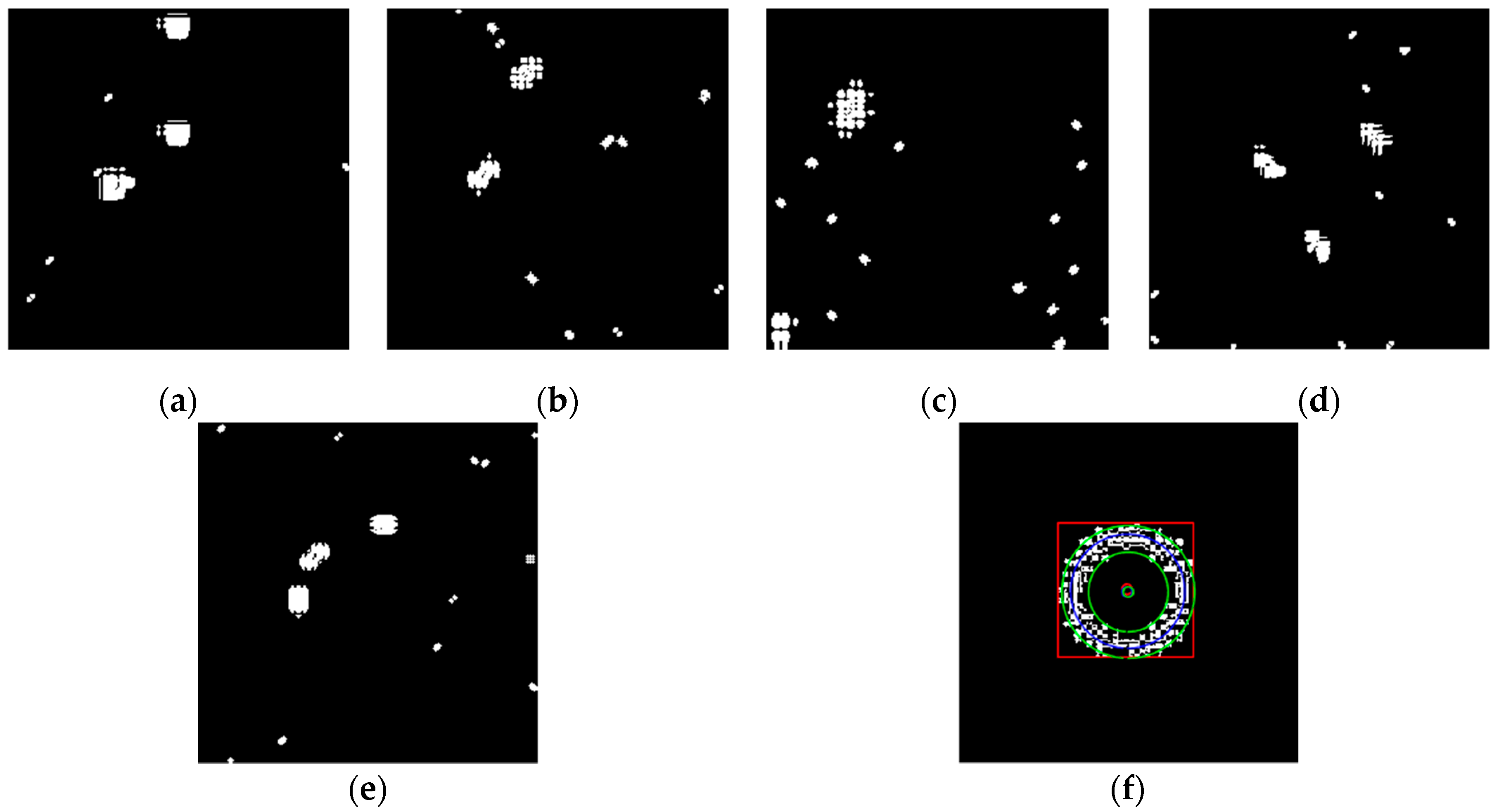
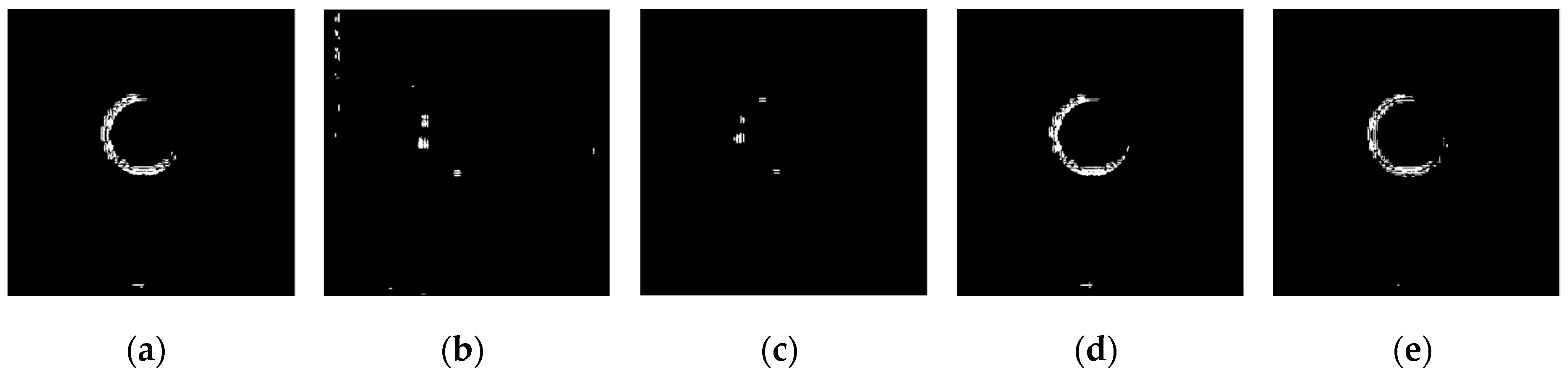
4.4. Edge Detection for High-Speed Moving Target Image under Noisy Environment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, Q.; Shang, Y. Research on the Principle and Application of Photogrammetry; Science Press: Beijing, China, 2014. [Google Scholar]
- Lei, X. Research on Key Technologies and Applications of High Speed Vision System for Dynamic Measurement; University of Science and Technology of China: Hefei, China, 2016. [Google Scholar]
- Zhang, D. Research and Applications on Vision-Based Structural Motion Extraction Algorithms; University of Science and Technology of China: Hefei, China, 2017. [Google Scholar]
- Bringas, F.; Goni, G. Early Dynamics of Deep Blue XBT probes. J. Atmos. Ocean. Technol. 2015, 32, 2253–2263. [Google Scholar] [CrossRef]
- You, D.; Gao, X.; Katayama, S. Monitoring of high-power laser welding using high-speed photographing and image processing. Mech. Syst. Signal Process. 2014, 49, 39–52. [Google Scholar] [CrossRef]
- Duarte-Campos, L.; Wijnberg, K.M.; Oyarte-Gálvez, L.; Hulscher, S.J.M.H. Laser particle counter validation for aeolian sand transport measurements using a high speed camera. Aeolian Res. 2017, 25, 37–44. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J. A non-local algorithm for image denoising. Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. 2005, 2, 60–65. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J. Nonlocal image and movie denoising. Int. J. Comput. Vis. 2008, 76, 123–139. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2272–2279. [Google Scholar]
- Xu, J.; Zhang, L.; Zuo, W.; Zhang, D.; Feng, X. Patch group based nonlocal self-similarity prior learning for image denoising. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 244–252. [Google Scholar]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, L.; Shi, G.; Li, X. Nonlocally centralized sparse representation for image restoration. IEEE Trans. Image Process. 2013, 22, 1620–1630. [Google Scholar] [CrossRef]
- Zha, Z.; Liu, X.; Huang, X.; Shi, H.; Xu, Y.; Wang, Q.; Tang, L.; Zhang, X. Analyzing the Group Sparsity Based on the Rank Minimization Methods. In Proceedings of the 2017 IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Weiss, Y.; Freeman, W.T. What makes a good model of natural images? In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Lan, X.; Roth, S.; Huttenlocher, D.; Black, M.J. Efficient belief propagation with learned higher-order Markov random fields. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 269–282. [Google Scholar]
- Li, S.Z. Markov Random Field Modeling in Image Analysis; Springer: London, UK, 2009. [Google Scholar]
- Roth, S.; Black, M.J. Fields of experts. Int. J. Comput. Vis. 2009, 82, 205–229. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Gu, S.; Xie, Q.; Meng, D.; Zuo, W.; Feng, X.; Zhang, L. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Gu, S. Learning Deep CNN Denoiser Prior for Image Restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2808–2817. [Google Scholar]
- Yin, J.; Chen, B.; Li, Y. Highly Accurate Image Reconstruction for Multimodal Noise Suppression Using Semisupervised Learning on Big Data. IEEE Trans. Multimed. 2018, 20, 3045–3056. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, H.; Luo, Y. Theory and Application of Wavelet; Science Press: Beijing, China, 2004. [Google Scholar]
- Kuang, Z.; Cui, M. Rational filter wavelets. J. Math. Anal. Appl. 1999, 239, 227–244. [Google Scholar]
- Liu, Z.; Zheng, N.; Song, Y. Design of high performance rational coefficient 9/7 biorthogonal wavelet filter. J. Xi’an Jiaotong Univ. 2005, 8, 847–851. [Google Scholar]
- Wang, H.; Cheng, L.; Wu, X. Construction of biorthogonal scale filters with M band rational coefficients. Progress Nat. Sci. 2003, 13, 132–137. [Google Scholar]
- Han, F.; Xu, S.; Zheng, D. Discussion on Wavelet Bases Selection for Digital Image Compression. J. Sens. Technol. 2004, 3, 154–157. [Google Scholar]
- Hu, H.; Ye, H. Adaptive wavelet bases and image denoising. Commun. Appl. Math. Comput. 2016, 30, 156–164. [Google Scholar]
- Li, Q.; Song, W. Tool Wear State Monitoring Using Lipschitz Exponent. Mach. Des. Manuf. 2014, 259–262. [Google Scholar] [CrossRef]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. IEEE Trans. Neural Netw. 1991, 6, 861–867. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, J. A one-layer recurrent neural network with a discontinuous hard-limiting activation function for quadratic programming. IEEE Trans. Neural Netw. 2008, 19, 558–570. [Google Scholar]
- Zeng, Z.; Huang, T.; Zheng, W.X. Multistability of Recurrent Neural Networks with Time-varying Delays and the Piecewise Linear Activation Function. IEEE Trans. Neural Netw. 2010, 21, 1371–1377. [Google Scholar] [CrossRef] [PubMed]
- Özbay, Y.; Tezel, G. A new method for classification of ECG arrhythmias using neural network with adaptive activation function. Digit. Signal Process. 2010, 20, 1040–1049. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; People’s Posts and Telecommunications Press: Beijing, China, 2017. [Google Scholar]
- Zhang, Y. The Beauty of Deep Learning: Data Processing and Best Practices in the AI Era; Electronics Industry Press: Beijing, China, 2018. [Google Scholar]
- Han, F.; Duan, F.; Zhang, B.; Duan, X. Design of Rational Number Wavelet Filter for Vision Sensor. J. Sens. Technol. 2010, 23, 533–537. [Google Scholar]
- Han, F.; Duan, F.; Zhang, B.; Duan, X. Design of even number rational symmetric compactly-supported biorthogonal wavelet filter. Comput. Eng. Appl. 2010, 46, 10–13. [Google Scholar]
- Han, F.; Duan, F.; Duan, X.; Zhang, C. Design of Odd Number Rational Coefficients Symmetric Compactly-Supported Biorthogonal Wavelet Filters. Comput. Sci. Inf. Technol. 2010, 1, 76–80. [Google Scholar]









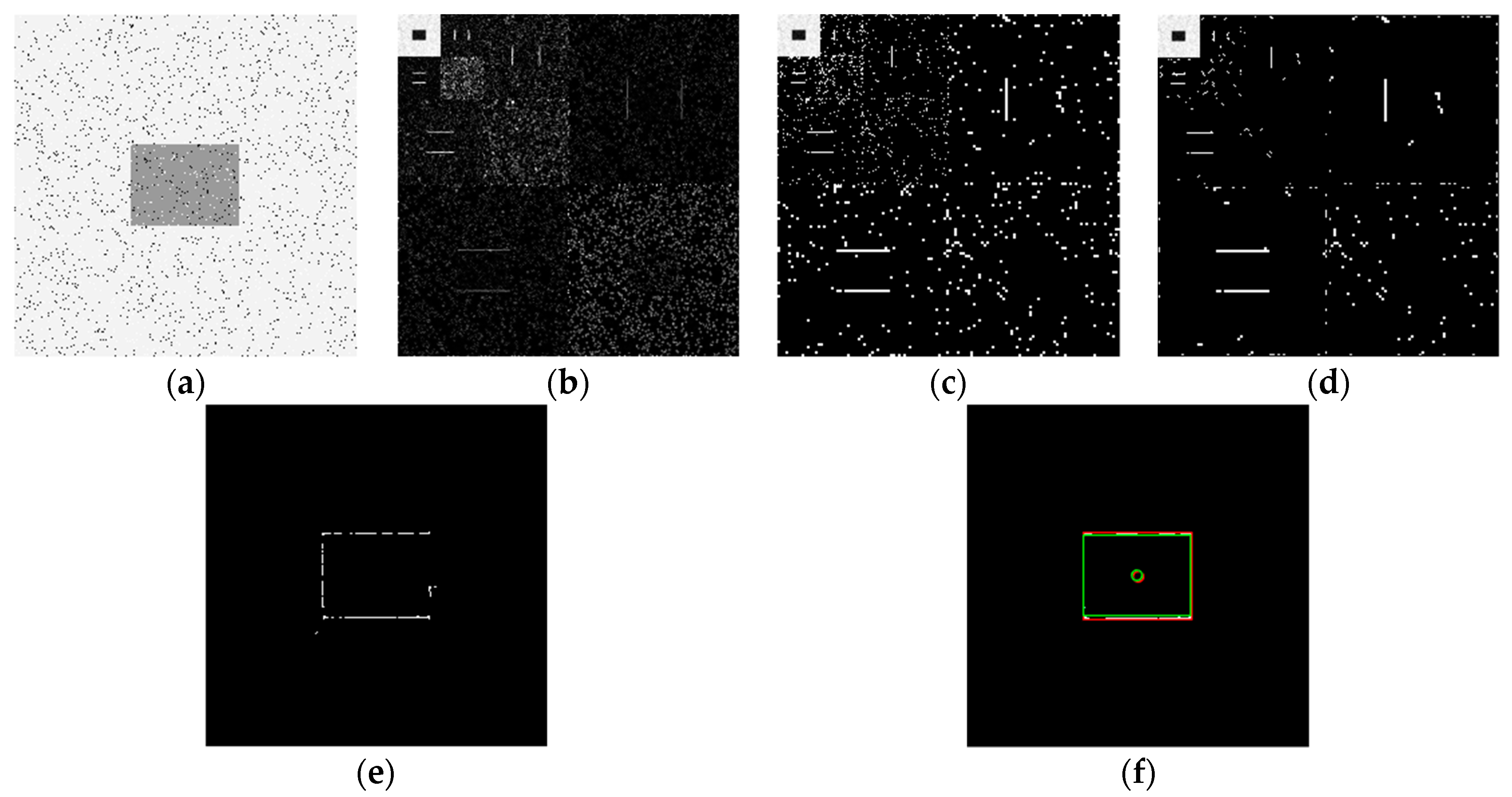
















| Left-Top | Right-Top | Right-Down | Left-Down | Center | MSE | |
|---|---|---|---|---|---|---|
| Original | (98,88) | (98,168) | (158,168) | (158,88) | (128,128) | 0 |
| Gaussian Figure 13f | (95,87) | (95,170) | (162,170) | (162,87) | (128.5,128.5) | 0.0460 |
| Salt and pepper Figure 15f | (96,88) | (96,169) | (161,169) | (161,88) | (128.5,128.5) | 0.0211 |
| Speckle Figure 15f | (96,87) | (96,170) | (162,170 | (162,87) | (129,128.5) | 0.0424 |
| Left-Top | Right-Top | Right-Down | Left-Down | Enclosing Rectangle Center | Fitting Circle Center | Fitting Circle Radius | MSE | |
|---|---|---|---|---|---|---|---|---|
| Original | (78,78) | (78,178) | (178,178) | (178,78) | (128,128) | (128,128) | 40 | 0 |
| Figure 23a | (72,72) | (72,177) | (177,177) | (177,72) | (124.5,124.5) | (125.0,125.0) | 43.88 | 0.2004 |
| Figure 23b | (71,71) | (71,181) | (181,181) | (181,71) | (126,126) | (126.2,126.2) | 43.58 | 0.2441 |
| Figure 23c | (73,73) | (73,184) | (184,184) | (184,73) | (128.5,128.5) | (129.5,129.5) | 44.48 | 0.1639 |
| Figure 23d | (73,73) | (73,177) | (177,177) | (177,73) | (125,125) | (125.6,125.6) | 43.64 | 0.1333 |
| Figure 23e | (72,72) | (72,185) | (185,185) | (185,72) | (128.5,128.5) | (127.2,127.2) | 44.32 | 0.2637 |
| Figure 23f | (79,79) | (79,177) | (177,177) | (177,79) | (128,128) | (128.1,128.1) | 42.20 | 0.0243 |
| Figure 24f | (76,75) | (76,177) | (177,177) | (177,75) | (126.5,126) | (127.5,127.5) | 42.97 | 0.0458 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Liu, B.; Zhu, J.; Zhang, B. Algorithm Design for Edge Detection of High-Speed Moving Target Image under Noisy Environment. Sensors 2019, 19, 343. https://doi.org/10.3390/s19020343
Han F, Liu B, Zhu J, Zhang B. Algorithm Design for Edge Detection of High-Speed Moving Target Image under Noisy Environment. Sensors. 2019; 19(2):343. https://doi.org/10.3390/s19020343
Chicago/Turabian StyleHan, Fangfang, Bin Liu, Junchao Zhu, and Baofeng Zhang. 2019. "Algorithm Design for Edge Detection of High-Speed Moving Target Image under Noisy Environment" Sensors 19, no. 2: 343. https://doi.org/10.3390/s19020343
APA StyleHan, F., Liu, B., Zhu, J., & Zhang, B. (2019). Algorithm Design for Edge Detection of High-Speed Moving Target Image under Noisy Environment. Sensors, 19(2), 343. https://doi.org/10.3390/s19020343




