1. Introduction
A Wireless Sensor Network (WSN) is an ad hoc network whose nodes have four basic units: Sensing, processing, communication, and power (often comprising just a battery). Each node operates as long as it has energy [
1]. In order to increase sensor nodes autonomy, methods leading to energy saving in WSN have appeared [
2]. Transmission bandwidth is tightly associated with energy consumption—the larger the bandwidth the higher the energy consumption [
1].
A signal is said to be sparse if there is a base in which it can be represented with only a few non-zero coefficients. Compressive Sensing (CS) [
3] explores sparsity to reduce the number of coefficients required to represent a given signal within some reconstruction fidelity. In CS, few coefficients are obtained through linear measurements (projections), and the original signal can be inferred from them by means of a linear program or greedy algorithm [
4]. This works if the quantity of measurements is a bit larger than the signal sparsity (which can be much lower than its
Nyquist limit [
3]).
In a WSN, a sink node receives traffic from several sensor nodes, and usually has much more computational power than these other nodes, that must be simple and be low power consuming. Such a scenario fits the CS paradigm: Simple encoding and complex decoding [
5]. In this work, the sparsity of collected signals is explored by means of CS to reduce the quantity of transmissions in WSNs, saving sensor nodes energy.
Notwithstanding CS remarkable signal encoding capability, CS decoding has a phase change behavior: If the quantity of measurements is sufficiently large then a reasonable signal estimative (in terms of mean squared error) is possible; otherwise signal is incorrectly reconstructed. This hampers rate-distortion management by controlling the quantity of coefficients and one must rely mostly on coefficients quantization for rate-distortion control. Therefore, we investigate an incremental quantization scheme for CS coefficients to provide a finner rate-distortion control. In addition, this scheme allows the sensor nodes to first encode signals with a coarse quality and let the sink (the application layer) to ask for extra bits to improve the signal, without requiring significant extra sensor node resources.
In summary, we investigate CS-coded transmissions in order to save sensor nodes energy. Real-life signals are used in simulations and distinct recovery methods are also investigated. The robustness of CS-coded framework against packets loss is verified, and a novel successive approximation scheme for energy conservation of sensor nodes is proposed.
After this introduction,
Section 2 presents a brief literature review on techniques for energy saving in WSN. This allows to better situate our work within the field and discuss our objectives and contributions.
Section 3 brings the Compressive Sensing fundamentals and the reconstruction methods investigated and, within it,
Section 3.2 presents the problem model and employed notation.
Section 4 discusses the experimental methodology and presents results on the rate-distortion performance and energy consumption of quantized CS measurements encoding in WSN.
Section 4.4 presents the impact of packet losses in the rate-distortion performance. The incremental transmissions scheme, using successive approximation, is presented in
Section 5. Then, conclusions are presented in
Section 6.
2. Energy Conservation Schemes in WSN
Several energy conservation/saving schemes have been proposed for WSNs. WSN-based signal acquisition using CS is discussed in [
6]. The correlations among signals detected by different sensors are explored to further reduce the amount of samples required for reconstruction. Environmental data gathered by a WSN located in the Intel Berkeley Research Lab [
7] are considered in [
6]. Spatial correlation of the sensed signal is explored in [
8] in order to propose a compressive-based sleeping WSN, in which a TDMA scheme is employed imposing only a fraction of the sensor nodes to be active in each time slot. Data gathered by the active nodes are transmitted to a base station and data corresponding to the sleeping nodes are estimated from others.
A cluster-based energy-efficient data collection by using the CS framework is proposed in [
9]. The WSN is divided in clusters using two distinct communication models: In the first one, sensor nodes send their measurements to the cluster head that forwards the CS measurements directly to a Base Station; the second method uses intermediate cluster heads to forward CS measurements to the base station. Authors calculate the power consumption for both methods.
A belief propagation algorithm [
10] is considered in [
11] to reconstruct CS measurements sent by sensor nodes, and iterative message passing is used to find the solution. A star topology is considered, in which sensor nodes directly send their CS measurements to the sink.
WSN employ digital communication, consequently coefficients derived from sensor measurements must be quantized before transmission. However, the analyses performed in [
6,
8,
9,
11] disregard this aspect, assuming that coefficients are densely quantized. Some insight on the quantization of compressive sensed measurements is presented in [
12,
13,
14]. In [
12], the 1-bit Compressive Sensing framework is proposed, which preserves only the sign information of each random measurement and the signal is recovered within a scale factor. This 1-bit CS framework is applied to data gathering in WSNs in [
15].
In [
13], an empirical analysis of the rate-distortion performance of CS is presented, in the context of image compression. The average distortion introduced by quantization on CS measurements is studied in [
14] by comparing two reconstruction algorithms, the Basis Pursuit [
16] and the Subspace Pursuit [
17] CS recovery schemes. In [
18], a CS-based coding technique that considers a binned progressive quantization framework in order to overcome the poor performance of CS applied to image compression is presented. The decoder firstly generates an initial reconstructed image, then quantization refinement occurs in order to subsequently improve the reconstructed image. The finer the quantization of the coefficients, the more bits are required for their transmission. In the present work, the amount of energy spent for transmission is considered a critical issue since one desires to consume the less energy while guaranteeing the best representation of the monitored signal; and both aspects will depend upon the CS-coefficients quantization scheme.
Authors in [
19] address the dimensionality reduction problem, applied to hyperspectral images, by using manifold learning methods. They propose the UL-Isomap scheme, in order to solve the main problems of the LIsomap method [
20]: The shortcoming of random landscape and the slow computation speed of LIsomap. A Vector Quantization is considered to improve the landmark selection, and the computational speed of LIsomap scheme is accelerated by using random projections, in order to reduce the bands of HSI data. In [
21], authors consider the nonlinear dimensionality reduction problem, also applied to hyperspectral image classification, and propose an Enhanced-Local Tangent Space Alignment (ENH-LTSA) method. As the work in [
19], this proposed scheme applies random projections to reduce the dimension of HSI data, improving the construction of the local tangent space. It aims to reduce the computational complexity of the LTSA method [
22].
Compressive Sensing scheme also considers a random projection framework, since the signal to be compressed is projected in the sensing matrix to generate
M CS coefficients. However, unlike [
19,
21], we apply the CS scheme to compress environmental data gathered by a WSN. Furthermore, our work aims to investigate some network aspects, such as the energy consumption of sensor nodes and the impact of packets loss in the reconstruction of the monitored signals.
A simple way to mitigate transmission losses (or packet erasures) is by using
acknowledgments (ACK) [
23]. When a transmission is received, the sink may send an ACK, confirming the receipt of the measurement. If the sensor node receives the ACK, then the subsequent data can be sent. Otherwise, a retransmission is required. We consider a WSN without ACKs, since to retransmit packets means greater energy consumption. Authors in [
24] investigate the characteristics of lossy links in WSNs, and apply the CS framework to overcome this problem. Experimental results show that the WSN can transmit with high quality, while reducing energy consumption because of the CS characteristics, i.e., if there is a sufficient number of received packets and if the sink is capable of identifying which coefficients (packets) were lost. The transmission over a noisy channel and the evaluation of the reconstruction error in the presence of packet erasures while saving sensor nodes energy, are considered in [
25]. Two approaches for CS are studied in [
25]: A cluster-based method that considers aggregation to compress data, and a consensus-based scheme in order to estimate the linear projections of sensor nodes; a basis pursuit denoising (BPDN) algorithm [
16] is used for reconstruction by the sink node.
In order to save sensor nodes energy in a surveillance application using a Visual Sensor Network (VSN), a routing framework called PRoFIT is proposed in [
26]. In this VSN application scenario, sensing nodes divide images into bit-planes [
27]. There are two layers that are created for captured images. The first one contains the most significant bit-planes (transmitted with higher priority) and the second layer bares less significant bit-planes (transmitted with lower priority). From the first layer, the image is reconstructed at the sink with a certain degree of detail, so that some immediate action can be taken based on the image content. If a more detailed reconstruction is required, the sink uses the second layer with remaining bit-planes. This strategy can be understood as a successive approximation scheme [
28], in which bit-planes are incrementally transmitted, in order to provide a better reconstruction.
Objectives and Contributions
In this paper we investigate a quantized CS framework, aiming at reducing the amount of transmissions in a WSN. In doing so, one expects that network nodes save energy, thus increasing WSN autonomy. We consider different environmental data: temperature, humidity, and illumination [
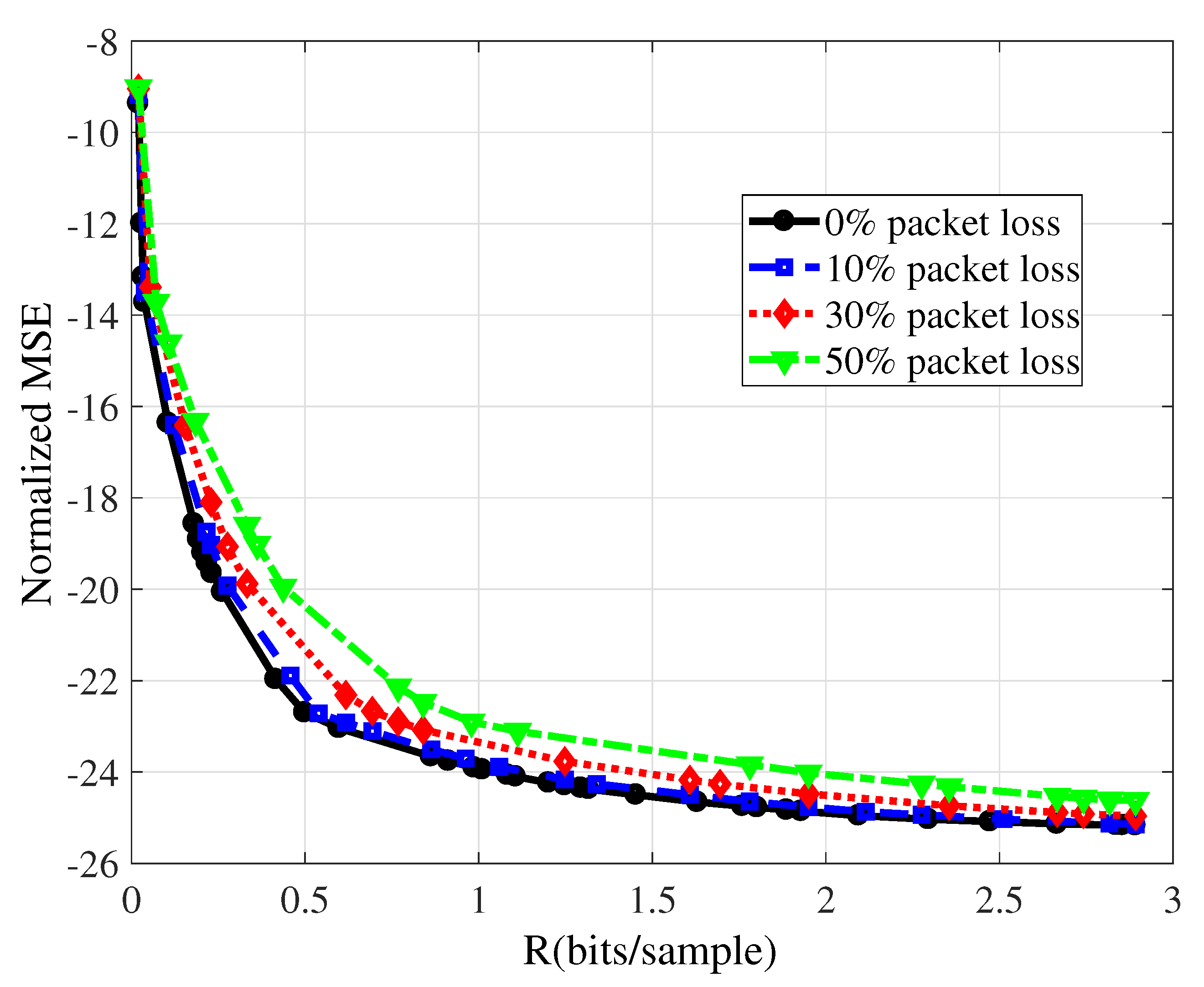
7]. For reconstruction, we investigate the performance of three distinct CS reconstruction schemes. We also evaluate the impact of packet loss in the rate-distortion performance of that encoding scheme.
As the transmitted CS measurements are quantized, the rate-distortion behavior of the reconstruction of monitored signals must be evaluated. This is done considering an exhaustive combination of uniform quantizers with distinct amounts of CS coefficients. The analysis generates an RD operational curve that goes over the best compromises between rate and distortion, allowing to reduce energy consumption in transmissions (bits, packets, and bursts) carried out by each sensor node, while keeping the rate-distortion performance sufficiently close to the optimal.
We propose to employ quantization refinements to incrementally transmit CS measurements, resulting in a successive approximation framework for CS. Consequently, at any operational RD point, an increment in rate is mapped into how many extra coefficients the sensor shall transmit or how many extra bits shall be used to improve previously transmitted CS measurements or both simultaneously. In practice, this scheme allows sensor nodes to first encode signals with a coarse quality and let the sink (the application layer) to ask for refinements without requiring significant extra sensor node resources, thus providing a sink-based control of the RD operational point of sensor nodes. It is worth to mention that while the RD control is coordinated by the sink, each sensor can be at different operational points. To the best of our knowledge, this is the first time that the incremental CS quantized measurements is discussed.
3. Compressive Sensing Framework
Let a signal
(a column vector) be sparse in some domain and
be its sparse representation (that is with
non-null coefficients)
in which
is a transform that provides a sparse
, for example, DCT or Wavelet. Consider that
in which
(
) is the vector that contains the coefficients (linear measurements) and
is called
measurement (or sensing) matrix [
29]. The
m-th coefficient in
is obtained by the inner product between
and the measurement function
(the
m-th row of
sensing matrix). Given
, a reconstruction procedure should aim at finding the solution for
, with the smallest
norm for
(the number of its non-zero entries). (
is the complex conjugate transpose of
.) Unfortunately, this is an ill-posed problem requiring a combinatorial approach [
3].
Alternatively, in order to circumvent the combinatorial problem, one minimizes the
norm of the reconstructed signal [
4]. In this case, the optimization problem is given by
where
is the
norm of the signal
, being
the components of
.
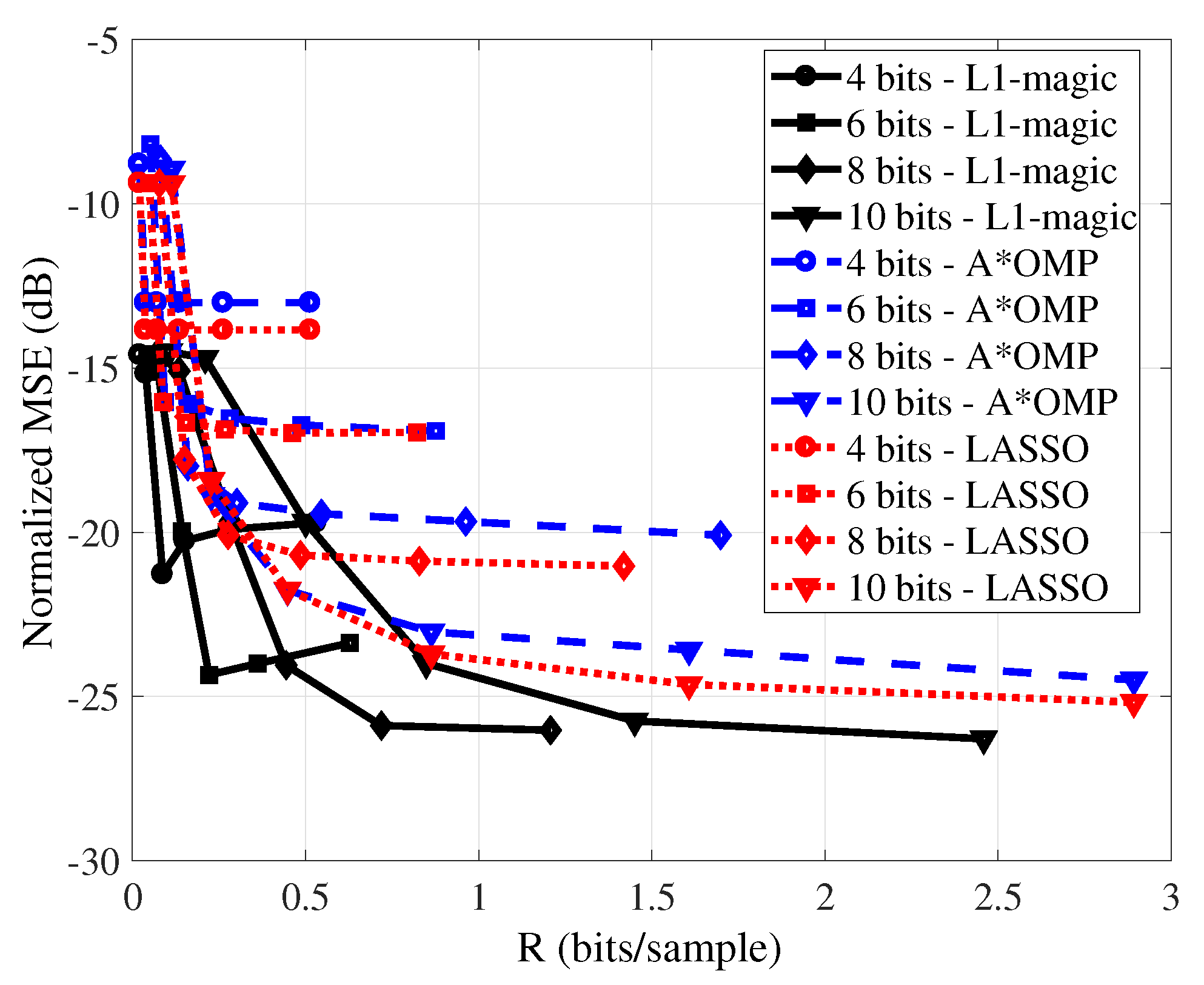
3.1. Reconstruction Methods
There are some convex optimization algorithms that can be used to solve (
3). Following, three distinct recovery methods considered in this work are briefly mentioned: The Newton algorithm with a log-barrier method, used in the L1-magic MatLab toolbox [
30]; the greedy-based algorithm called A*OMP [
31]; and the shrinkage-based algorithm called Least Absolute Shrinkage and Selection Operator (LASSO) [
32].
3.1.1. Newton + Log-barrier
The recovery procedure aims at minimizing the
norm of
with quadratic constraints, i.e.,
in which
is an empirically chosen parameter. This optimization is done by recasting the problem in Equation (
4) as a
Second-Order Cone Program (SOCP) [
30]. Then, a Newton algorithm with a logarithmic barrier (log-barrier) method [
33] is used to solve the optimization problem in Equation (
4). The recovery procedure is implemented in the L1-magic package [
30]. In [
34], authors consider the algorithm in L1-magic to reconstruct CS-coded environmental signal (temperature) in a WSN. The advantage of using the
Newton + log-barrier method is that it directly minimizes the L1-norm of the sparse signal, which is small with respect to their energy.
3.1.2. A* Orthogonal Matching Pursuit
The A*OMP is an algorithm based on the
Orthogonal Matching Pursuit (OMP) algorithm [
35], that uses atoms from a dictionary to expand
. At each iteration, the expansion uses the dictionary atom having the largest inner-product with the residue. After each iteration, the orthogonal projection of the residue onto the selected atoms is computed. At iteration
l, the set of atoms
selected from
for representing
incorporates the dictionary atom that best matches
, doing
in which
and
are dictionary atoms (columns of the dictionary
),
is the vector of the coefficients and
is the residue after the
l-th interaction. At the end,
contains the support of
(the original signal to be coded), and
contains their nonzero entries (that define the sparsity of the signal).
The A*OMP considers the best-first search tree [
36], in which multiple paths can be evaluated during the search to improve reconstruction accuracy. The search is called A* and looks for the sparsest solution [
31]. The
A*Search gives an advantage to the A*OMP against the OMP algorithm, smaller average run-times [
31]. Authors in [
6] considered MP-based algorithms to reconstruct environmental signals, such as temperature, humidity, and illumination.
3.1.3. LASSO
The
Least Absolute Shrinkage and Selection Operator (LASSO) [
32] aims at minimizing the residual sum of squares, subject to the sum of the absolute values of the coefficients being less than a constant. The reconstruction of CS measurements by LASSO can be expressed as
in which
is a nonnegative scalar.
LASSO was used to reconstruct temperature and humidity CS-coded signals in [
37]. Moreover, since LASSO minimizes the sum of square errors, it is a well-suited method to recover noisy data [
38]. In this work, we implemented LASSO using the SPGL1 software packet [
39].
3.2. Using CS in WSNs
We employ CS to encode and decode environmental data monitored by a WSN.
Figure 1 depicts the basics of the coding/decoding process:
Sensing—The WSN node
makes measurements (from the environment), and stores them in a vector
Compression—The compressed sensing vector
(
),
is obtained from
using (
2).
Quantization—For transmission, the compressive sensed coefficients are quantized using a uniform scalar quantizer of bit-depth B (that is, with reconstruction levels), this produces the quantized coefficients vector .
Transmission—Each node forwards its quantized coefficients vector to the sink node.
Reception—Due to possible packet loss, the received coefficients vector at the sink node is
with
.
Reconstruction—The is used at the sink to reconstruct a version of the original signal.
5. Successive Approximation Using CS-WSNs
So far, we have used CS to code the signal captured by WSN nodes allowing to configure the RD operating point—. However, it could be necessary to improve the reconstructed signal at the sink node, even at expenses of more bits. One could retransmit the signal at a higher rate, and this would waste resources. On the other hand, some form of scalability could be pursued. We propose to do that using an incremental transmission framework for CS-Coded WSN-signals. This guarantees good RD performance while economizing resources, and, consequently, saving sensor energy. Extra-bits are transmitted to refine already known quantized CS coefficients or convey unknown coefficients leading to an improve in the signal reconstruction in an incremental fashion. This strategy keeps RD performance as good as possible, since any extra bit transmitted by nodes is used in the reconstruction and not to replace previously known ones. It is straightforward to see that this strategy allows to save energy in sensor nodes.
We employ a successive approximation scheme such that nodes may incrementally transmit CS measurements. Let a given node to code a set of
measurements using
bits and transmit them, spending a total of
bits; this defines the operational point
in the
space. Suppose now that the sink node (decoder) needs more information, in order to generate a better version of the reconstructed signal, subject to an increment of
bits. The increment must improve RD performance while remaining as close as possible to the optimal RD points. In any case,
corresponds to the selection of a new operational point
. The
and
correspondent increase in the quantity of transmitted bits is
where
and
are known.
may be seen as the target increment in rate, demanded by the sink, and Equation (
15) presents the mapping from the target to the increments in the quantities of bits and measurements leading to a new operational point.
It is desirable for the sequence of operational points resulting from extra transmissions to provide a path along the optimal RD curve. Therefore, each
should satisfy
where
is the distortion function while
is the set of new candidates—Equation (
16) means that, from
, one must search for
leading to the smallest distortion among all
candidates.
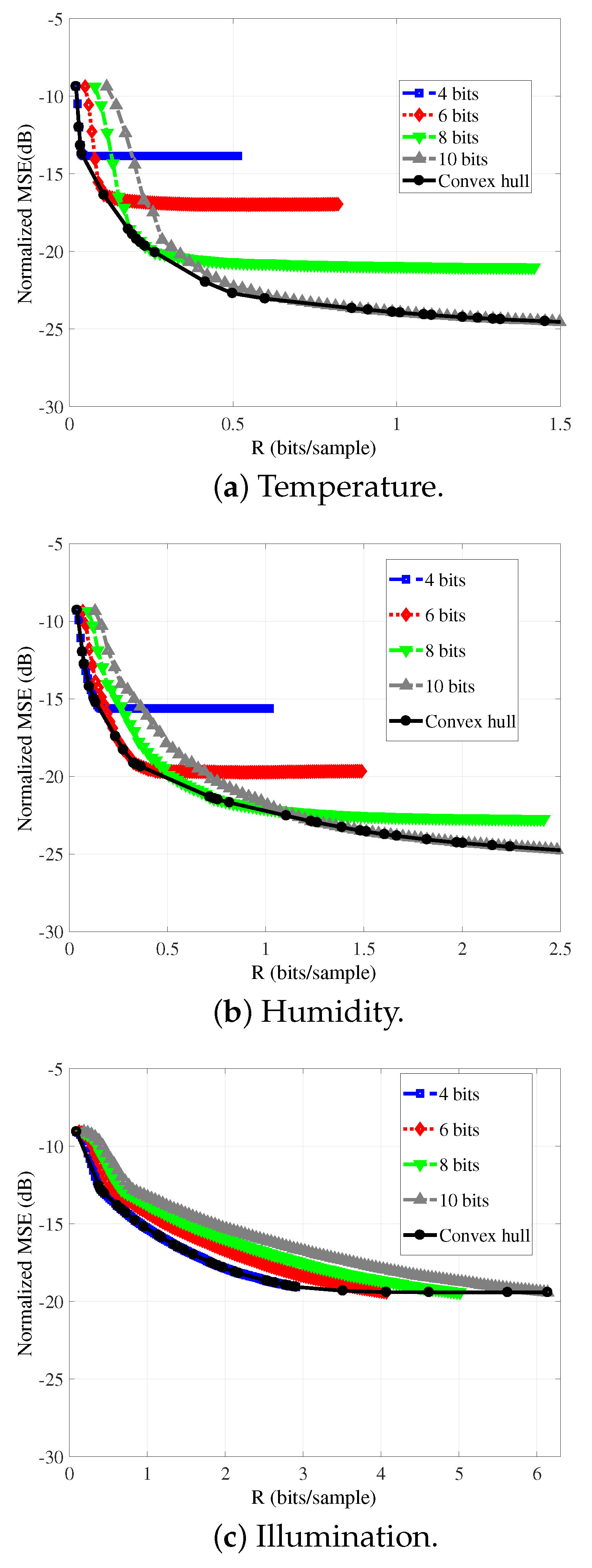
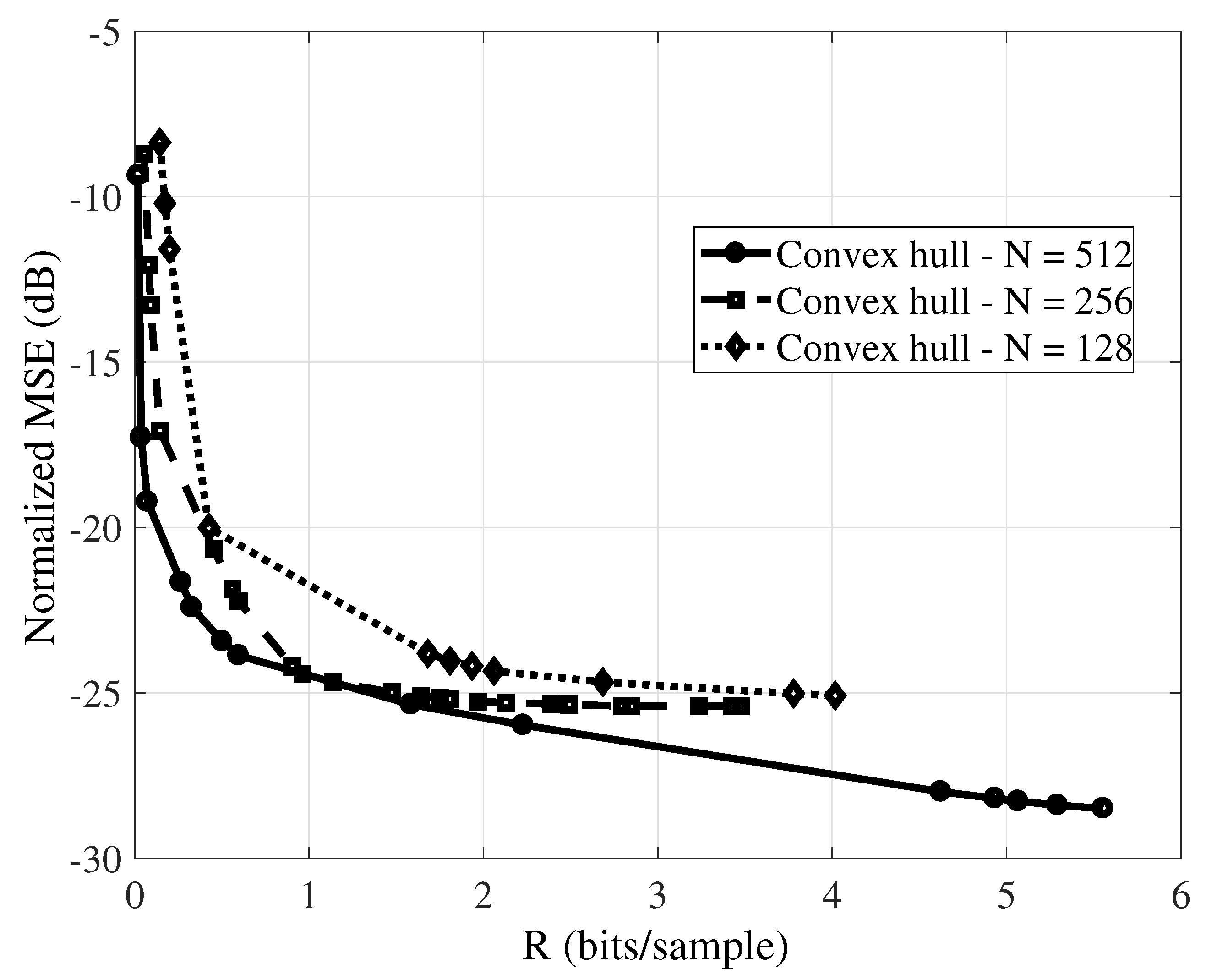
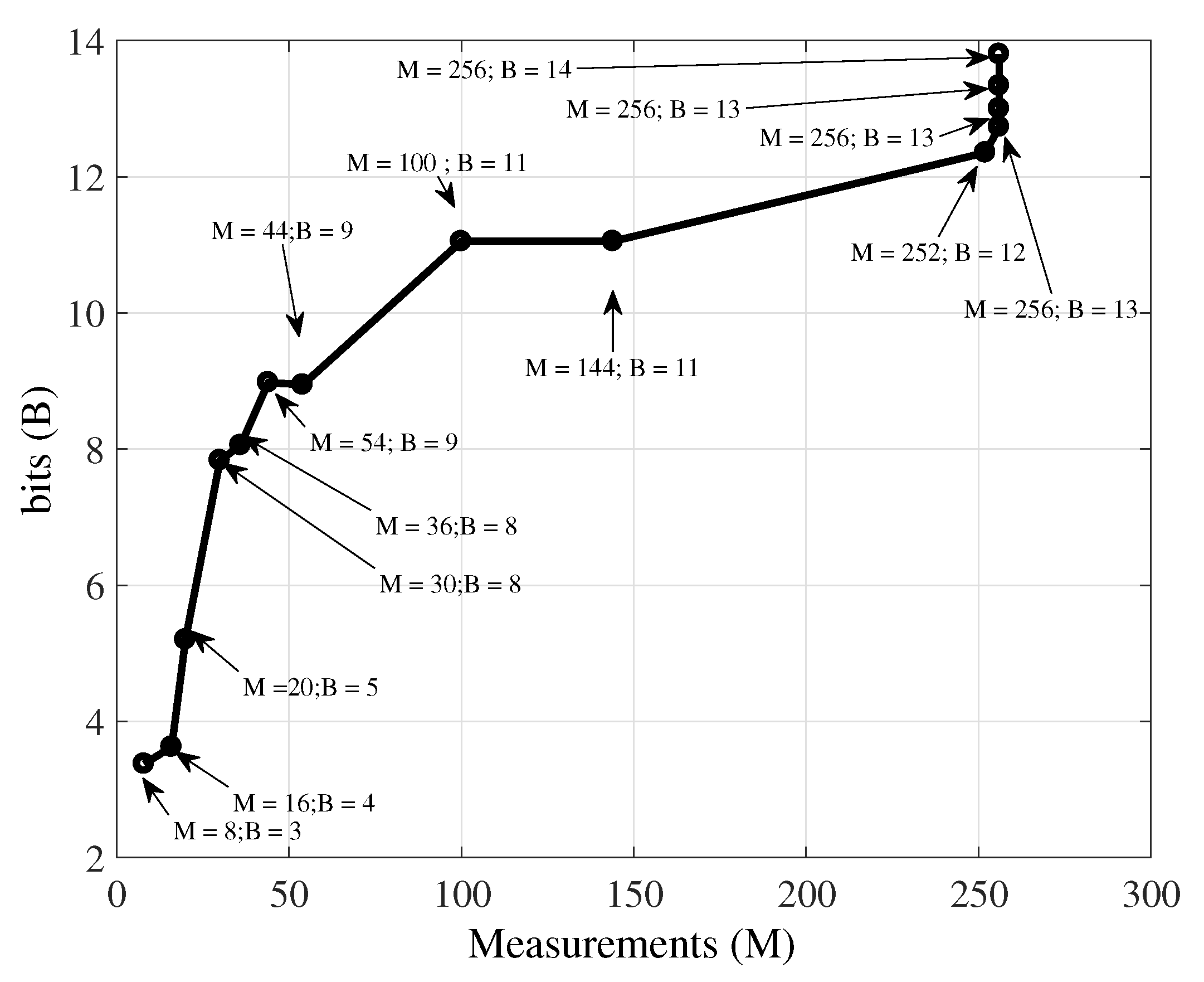
Figure 7 illustrates that idea. It presents an optimal coding path (sequence of encoder setups) on the
plane, the
pairs having the best RD trade-of. It depicts the convex hull of the RD of the temperature signal, with the number of measurements (
M) ranging from 8 to 256, in increments of 2, and quantized bit-depths values (
B) varying within the set {4,5,6,7,8,9,10,11,12,13}, for a signal block of length
, this considers the NMSE as distortion criterion.
5.1. Moving along Pairs
Increments in
M and
B may occur in several ways: the number of measurements increases while bit-depth is unaltered, the coefficients quantization may be refined while number of measurements is unaltered, or both are incremented simultaneously. The first two possibilities correspond to paths along horizontal or vertical directions on the
plane, respectively. In the more general case, instead, both
M and
B could change jointly, moving the coder setup up and to the right in
Figure 7. Therefore, starting from a given
operational RD point, the coder should move to a new
pair leading to the minimal distortion for the resulting increment in the rate.
Each operational point represents a specific CS-quantized coding setup on the plane. The quantizers are designed such that their input-output mappings intersect. The quantization rule using bits refines the quantization rule for B bits. Thus, when moving from the operational point i to the operational point just the refinements of previously transmitted values need to be transmitted, i.e., bits per value.
The initial RD-optimal setup point is defined from the initial rate. The measurements are quantized and transmitted with bits. If there is demand for more bits, then a new RD-optimal point is to be used. The new point may be selected from an operational setup table according to the desired rate increase. That is, for an operational point there may be several possible operational setups to use, the one to be used will depend on the actual increase in the quantity of transmitted bits subject to distortion reduction. Once that is decided, the sensor sends the extra measurements quantized with bits and the extra bits refining the already transmitted measurements.
Nevertheless, one must still compute the operational point to which the sensor node must shift. A sensor node can not do that on-line, as its energy would be exhausted due to the extensive required computations. Alternatively, a training set can be employed to analyze the RD performance and generate a table indicating the best shift at a given operational point and the desired increment in the quantity of transmitted bits. That data can be used in two different fashions: sensor nodes can be aware of the table and fetch the new operational point for a given rate increment; or, alternatively, the sink may inform the sensor node of the new operational point; the later reduces the requirements on sensor node memory size and marginally increases the data sent by the sink to request the relevant bits for signal reconstruction improvement.
5.2. Successive Approximation Table Construction
Given that
coefficients have been already transmitted, one can define the set of new possible quantities of CS coefficients as
,
. From Equation (
15), one can compute the corresponding possible bit-depths
, for a predefined target increment
. Dividing both sides of Equation (
15) by
, one obtains
Consequently, to build the successive approximation encoding table (the one that provides the increments and for moving to the next RD-optimal point subject to the operational point () increment in rate ), one may use Algorithm 1. In this procedure, is the current RD-optimal pair of node ; is the proportional increment in the rate; is the amount of points generated in each operational curve; is a factor that limits the amount of operational curves that are tested. The value of defines the possible increments in , stored in . For each of them, the correspondent bit-depth increase is computed in lines 7–9. The best choice among them (leading to the same increment bits in rate) is evaluated in the eleventh line. This provides an “incremental path” (or successive approximation) for encoding and transmission of CS quantized measurements. If this process is performed off-line, it does not impact the energy consumption of the sensor nodes; however, sensor nodes either need to be aware of the table or be informed about the new operational setup.
Table construction complexity is controlled by and , that limits the quantity of CS reconstructions that are evaluated for the training data. The input factor defines the rate increment that is evaluated while defines the number of possible operational points to be tested at a given () to choose the next operational point . In other words, defines the amount of candidate setups for the given percent increment in rate . Note that the larger is, the more trials are required, i.e., more (, ) are generated and analyzed. Suppose that one starts at a rate and wants to increment it to , as increases, the sensor traverses less operational points to go from a rate to a rate . Therefore, restricts the amount of generated curves that have to be tested. The smaller that is, the more precisely the rate can be adjusted, at expenses of a more complex training process.
| Algorithm 1: Construction of the successive approximation table |
input: N, , ,
output:
![Sensors 19 00266 i001 Sensors 19 00266 i001]() |
To illustrate the procedure, assume that the initial RD-optimal point is
, the next point (the first refinement point) is chosen from at most ten
pairs, i.e.,
, for a fixed rate increment defined by
. Each one of the 10 candidates produces a distortion. After testing, the one leading to the minimal distortion is chosen—Equation (
16). This is the next operational point, for example,
. At this point, the same process applies, resulting in the operational point
, for example. The procedure is iterated until
, restricting the maximum number of measurements as a fraction of the signal block length
N,
.
5.3. Simulation Results
5.3.1. Rate-Distortion Evaluation
We consider temperature, humidity, and illumination signals, gathered by a WSN in the Intel Berkeley Research Lab [
7]. In this setup, we consider a block length of
samples and LASSO for reconstruction. From each
point, we consider rates increments of 10%, i.e.,
. We also impose
(
) and
. The Bjontegaard Delta metric (
) is used to evaluate the RD performance of the successive approximation scheme against the exhaustively generated optimal RD curve. The dataset employed to obtain the table mapping the successive approximation setups is different from the one employed to evaluate the RD performance.
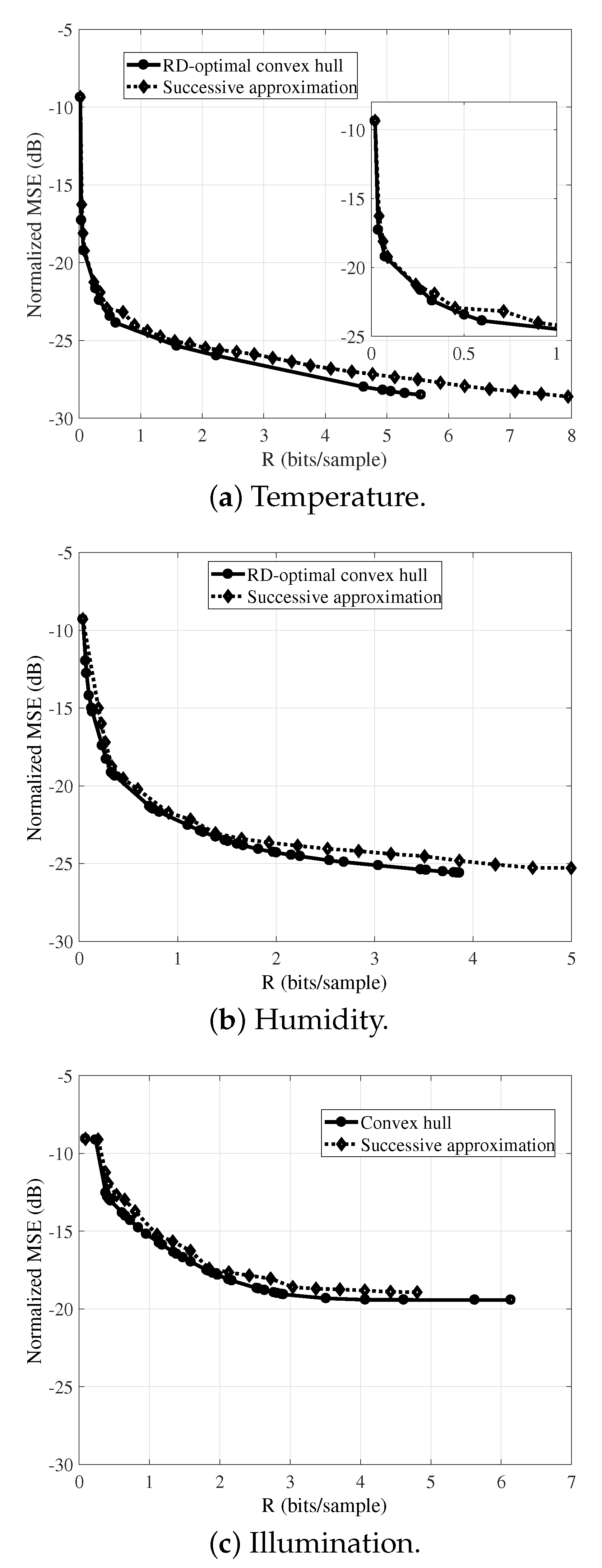
Figure 8 presents the RD-optimal convex hull curve (as in
Section 4.2) and the successive-approximation scheme rate-distortion curve for the reconstruction of the temperature (a), humidity (b), and illumination (c) signals. The Bjontegaard Delta between the exhaustively generated RD-optimal curves and the successive approximation RD performances for temperature, humidity, and illumination signals are
dB,
dB, and
dB. The results indicate that the successive-approximation scheme operational-RD curve closely matches the RD-optimal convex hull for the three monitored signals. Nevertheless, for each one, the incremental-transmission scheme operational curves contain more RD points than the convex hull does, meaning that it allows a finer adjustment of the rate.
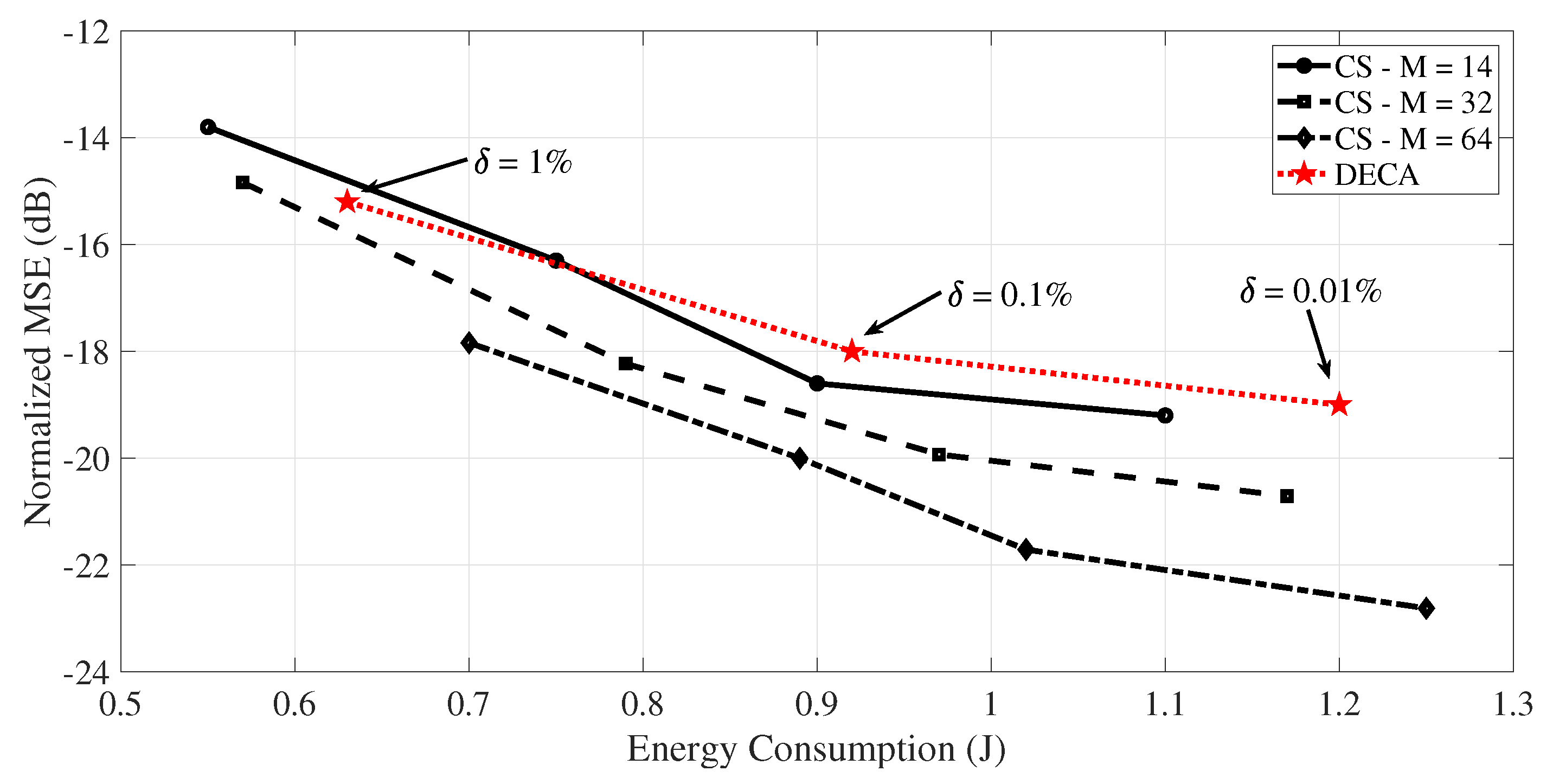
5.3.2. Energy Consumption Evaluation: Case Studies
We now empirically evaluate the possible energy savings derived from the use of the proposed successive approximation scheme at sensor nodes. In the experiment, we evaluate the energy consumed when a sensor node traverses its operational curve, moving on a sequence of operational points . We compare the energy expenditure when the proposed successive approximation mechanism is employed against simply transmitting the whole data using one encoder with the operational set-up leading to the same total.
In this experiment (Scenario 1) we consider the same set-up used in
Section 4.3.
Table 3 presents the results. The first column shows the operational points traveled by the sensor (the first encoder configuration (RD operational point) is
. At each operational point, the following one is obtained considering
and
.). The second column presents the energy required to transmit the
CS measurements using
bits without using the proposed scheme. The third column presents the energy consumed when the successive approximation scheme is employed. The last column in
Table 3 shows the percentage reduction in energy consumption gained by using the proposed scheme. The reduction comes from having to transmit only extra measurements and refinement bits. This energy economy behavior is steadily observed for all operational points.
Now we consider another operational curve to be traversed by sensor nodes. The same fifteen-node WSN used in simulations of the previous scenario are also considered for Scenario 2, but in this case all sensor nodes traverse their operational curve transmitting to the sink
CS coefficients, each one with
bits, using the proposed successive approximation scheme. Results are shown in
Table 4, presenting the average MSEs and the average energy consumptions for all network nodes. One observes the same energy economy behavior as in Scenario 1, for all operational points.
A disadvantage of the proposed successive approximation scheme is the fact that sensor nodes are unable to perform an on-line construction of their operational curves (successive approximation tables). This is so because of the extensive required computations to generate the operational points. Thus, sensor nodes must be aware of the table or the sink must inform the new operational point. However, results presented in
Figure 8, and
Table 3 and
Table 4 show that the proposed scheme provides a rate-distortion performance that closely matches the convex hull, while sensor nodes save their energy.
6. Conclusions
In this work, the quantization of compressive sensed measurements in WSNs was considered. The resulting rate-distortion performance using three distinct reconstruction methods was analyzed for temperature, humidity, and illumination data. RD analyses were presented for a different quantity of CS measurements and quantizer bit-depths (M and B, respectively) using for signal reconstruction the norm minimization, A*OMP, and LASSO algorithms. The best results were obtained with the first one, and LASSO outperformed the A*OMP recovery algorithm. In the tests, other features of CS-based WSN data encoding were evaluated as the capability to save sensor nodes energy and robustness against packet losses.
We proposed an scheme to incrementally transmit CS encoded sensor nodes measurements. The proposed scheme refines the data available at the sink upon its demand in terms of fractional rate increments. The scheme designs superimposed quantization rules for the measurements, allowing to reuse previously transmitted values as the quantization intervals get slender. Using this scheme, sensor nodes need only to transmit quantization refinements of already partially known measurements. This allows to save sensor nodes energy. Experiments show that the proposed scheme has a rate-distortion performance that closely matches the optimal RD curve.
It shall be highlighted that the presented strategy goes beyond choosing a CS-encode-quantize operational points, since we devised a strategy to shift between operational points in order to obtain a scalable bit-stream. In doing so, the proposed scheme allows for reconstructing the sensor data under an RD trade-off that includes the inherent non-linearities of both CS recovering algorithms and quantization.