Airborne Visual Detection and Tracking of Cooperative UAVs Exploiting Deep Learning
Abstract
:1. Introduction
- -
- Sun illumination. Indeed, wide portions of the field-of-view (FOV) may be saturated if the Sun direction is quasi-frontal with respect to the camera. Also, the object appearance (e.g., color and intensity) can change as a function of the Sun direction.
- -
- Local background. Detection and tracking algorithms may suffer from sudden variations of the local background, e.g., caused by continuous passages of the target above/below the horizon.
- -
- Target scale. Depending on the mission scenario, the target distance can vary from tens to hundreds of meters. Consequently, the image processing algorithms must be able to deal with significant variations of the size of FOV region occupied by the target.
2. Related Work
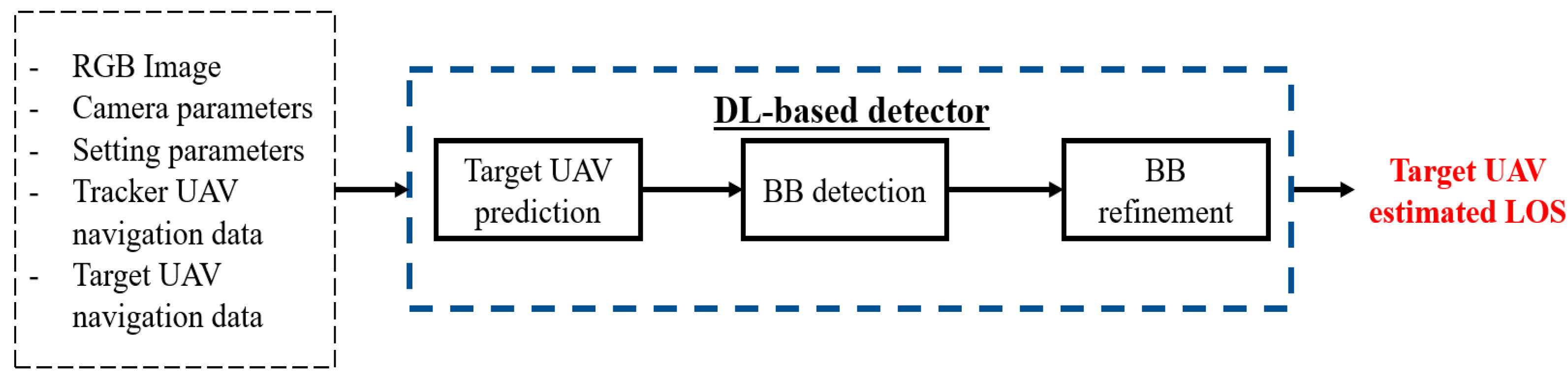
3. Detection and Tracking Architecture
3.1. DL-Based Detector
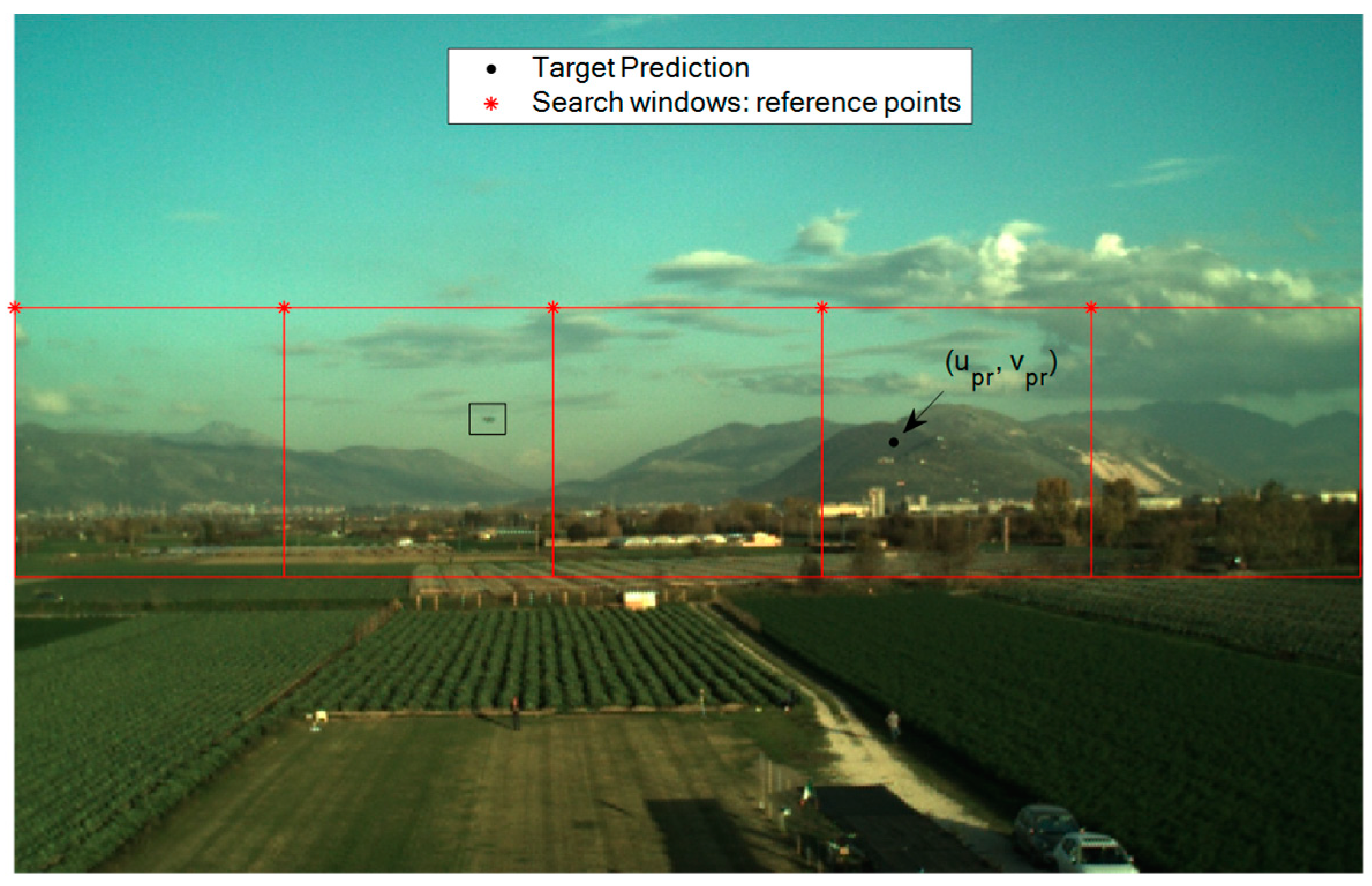
3.1.1. Target UAV Prediction
- -
- Computing the difference between the two position vectors in ECEF (Pe,tracker and Pe,target for the tracker and target, respectively), obtained using either the GNSS position fix or, more in general, the positioning solution available to the onboard autopilot.
- -
- Exploiting Differential GNSS (DGNSS) and Carrier-Phase DGNSS (CDGNSS) algorithms.
3.1.2. Bounding Box Detection
3.1.3. Bounding Box Refinement
3.2. DL-Based Tracker
4. Flight Test Campaign
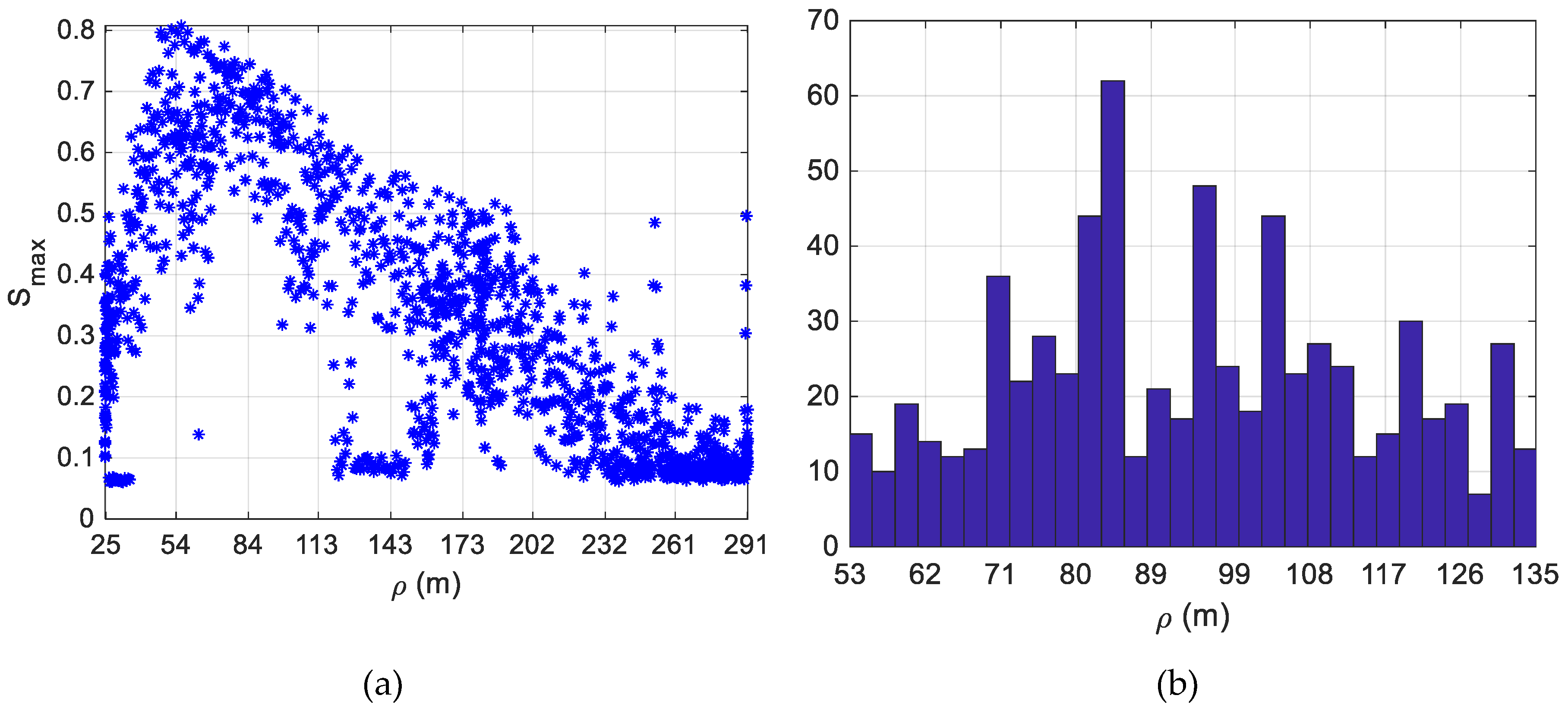
4.1. Database A
4.2. Database B
5. Results
- -
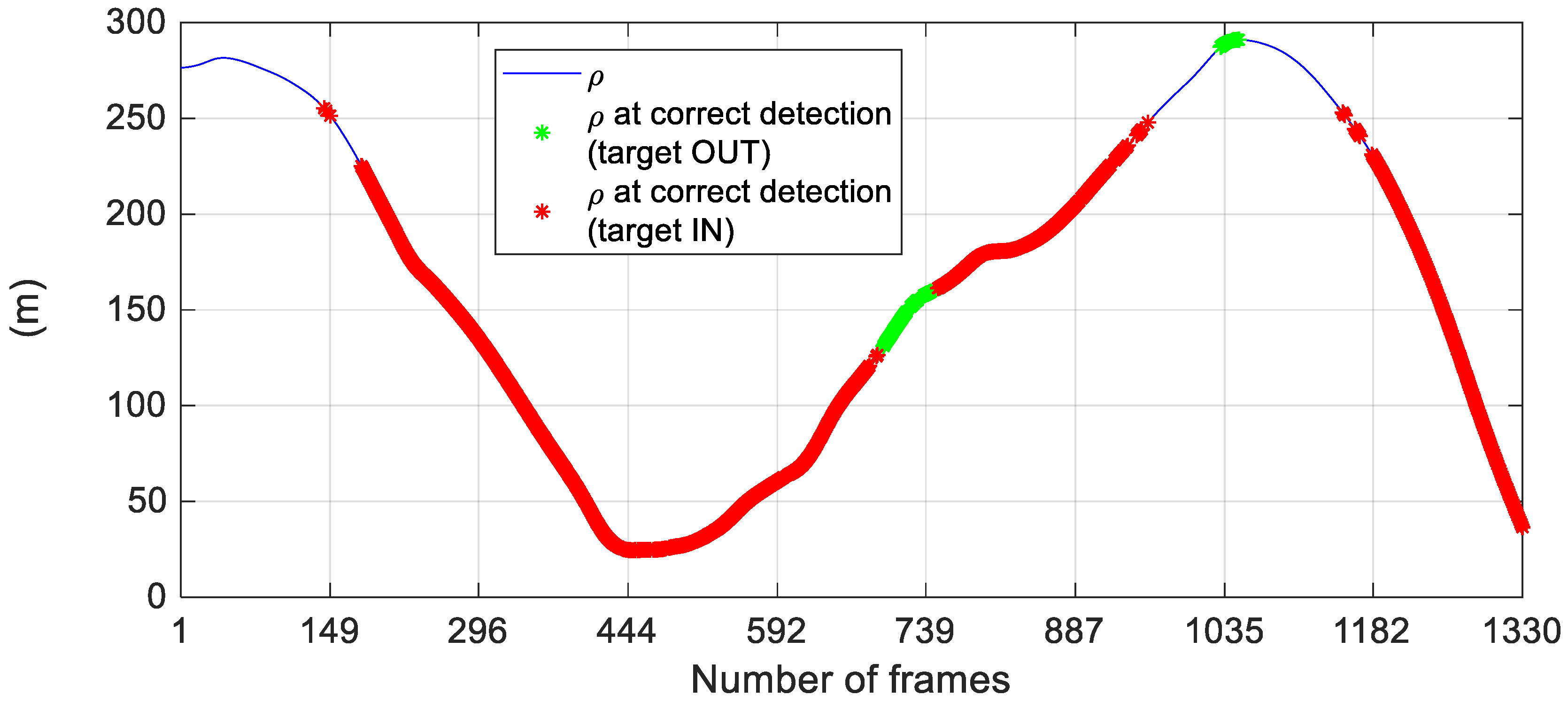
- Percentage of Correct Detections (CD), i.e., the ratio between the number of frames in which the target is correctly declared to be either inside the image plane (less than 10-pixel error both horizontally and vertically) or outside the image plane and the total number of frames.
- -
- Percentage of Wrong Detections (WD), i.e., the ratio between the number of frames in which the target is correctly declared to be inside the image plane but the error is larger than 10 pixels either horizontally or vertically, and the total number of frames.
- -
- Percentage of Missed Detections (MD), i.e., the ratio between the number of frames in which the target is wrongly declared to be outside the image plane (it is not detected even if it is present in the image) and the total number of frames.
- -
- Percentage of False Alarms (FA), i.e., the ratio between the number of frames in which the target is wrongly declared to be inside the image plane (it is detected even if it is not present in the image) and the total number of frames.
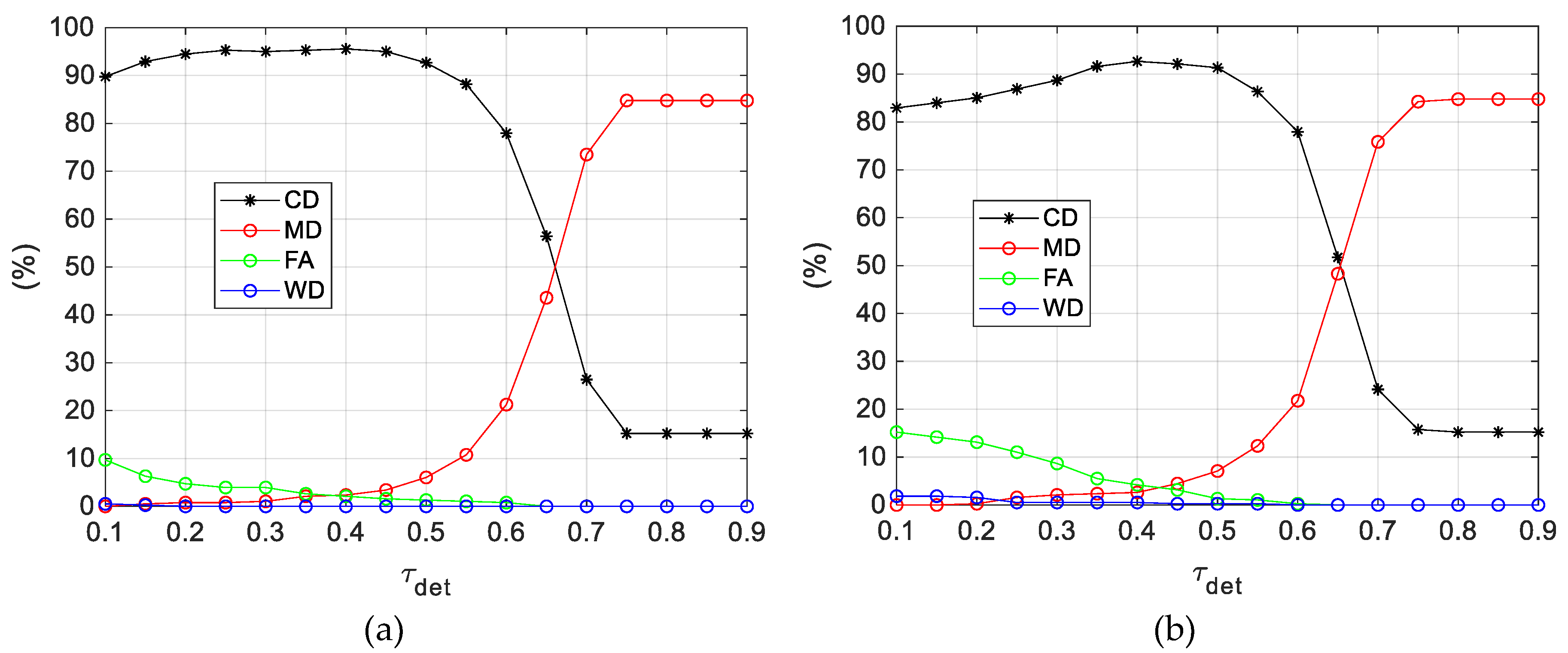
5.1. Detector Performance on FT3-A
- -
- WD is always 0% (except for a couple of wrong detections occurring if τdet is set below 0.20), which implies that, when the target is inside the FOV, it is always detected, and its LOS is estimated with a relatively-high accuracy level.
- -
- CD and MD reach an asymptotic value (15.2% and 84.8%, respectively) when τdet gets larger than 0.70. This occurs since the selection of large values of τdet prevents false alarms for the 58 images (see NOUT in Table 1) where the target is outside the FOV (or is not visible).
- -
- The best performance in term of CD (95.5%) is obtained setting τdet to 0.40. However, this choice leads to a residual FA of 2.1%. As τdet increases, FA goes to 0% but MD also increases to the detriment of the number of correct detections. In general, the trade-off in the choice of τdet, i.e., the problem of finding the best compromise between CD, FA and MD, depends on the mission task. For instance, cooperative UAVs can be used to improve navigation performance in GNSS-challenging areas [13]. In this case it is more important to limit the occurrence of false alarms, thus choosing larger values of τdet.
5.2. Detector and Tracker Performance on FT3-A
5.3. Detector and Tracker Performance on FT1-B and FT2-B
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Se, S.; Firoozfam, P.; Goldstein, N.; Wu, L.; Dutkiewicz, M.; Pace, P.; Pierre Naud, J.L. Automated UAV-based mapping for airborne reconnaissance and video exploitation. In Proceedings of the SPIE 7307, Orlando, FL, USA, 28 April 2009; pp. 73070M-1–73070M-7. [Google Scholar]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Ham, Y.; Han, K.K.; Lin, J.J.; Golparvar-Fard, M. Visual monitoring of civil infrastructure systems via camera-equipped Unmanned Aerial Vehicles (UAVs): A review of related works. Vis. Eng. 2016, 4, 1–8. [Google Scholar] [CrossRef]
- Qi, J.; Song, D.; Shang, H.; Wang, N.; Hua, C.; Wu, C.; Qi, X.; Han, J. Search and rescue rotary-wing uav and its application to the lushan ms 7.0 earthquake. J. Field Rob. 2016, 33, 290–321. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Perspectives for remote sensing with unmanned aerial vehicles in precision agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef]
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [Green Version]
- Bürkle, A.; Segor, F.; Kollmann, M. Towards autonomous micro uav swarms. J. Intell. Rob. Syst. 2011, 61, 339–353. [Google Scholar] [CrossRef]
- Sahingoz, O.K. Networking models in flying ad-hoc networks (FANETs): Concepts and challenges. J. Intell. Rob. Syst. 2014, 74, 513–527. [Google Scholar] [CrossRef]
- Barrientos, A.; Colorado, J.; Cerro, J.D.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area coverage and path planning for fleets of mini aerial robots. J. Field Rob. 2011, 28, 667–689. [Google Scholar] [CrossRef] [Green Version]
- Messous, M.A.; Senouci, S.M.; Sedjelmaci, H. Network connectivity and area coverage for UAV fleet mobility model with energy constraint. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016. [Google Scholar]
- Vetrella, A.R.; Causa, F.; Renga, A.; Fasano, G.; Accardo, D.; Grassi, M. Multi-UAV Carrier Phase Differential GPS and Vision-based Sensing for High Accuracy Attitude Estimation. J. Intell. Rob. Syst. 2019, 93, 245–260. [Google Scholar] [CrossRef]
- Vetrella, A.R.; Fasano, G.; Accardo, D. Attitude estimation for cooperating UAVs based on tight integration of GNSS and vision measurements. Aerosp. Sci. Technol. 2019, 84, 966–979. [Google Scholar] [CrossRef]
- Vetrella, A.R.; Opromolla, R.; Fasano, G.; Accardo, D.; Grassi, M. Autonomous Flight in GPS-Challenging Environments Exploiting Multi-UAV Cooperation and Vision-aided Navigation. AIAA Information Systems-AIAA Infotech@Aerospace 2017, Grapevine, TX, USA, 5 January 2017. [Google Scholar]
- Stoven-Dubois, A.; Jospin, L.; Cucci, D.A. Cooperative Navigation for an UAV Tandem in GNSS Denied Environments. In Proceedings of the 31st International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 2332–2339. [Google Scholar]
- Maza, I.; Ollero, A.; Casado, E.; Scarlatti, D. Classification of multi-UAV Architectures. In Handbook of Unmanned Aerial Vehicles, 1st ed.; Springer: Dordrecht, The Netherlands, 2015; pp. 953–975. [Google Scholar]
- Goel, S.; Kealy, A.; Lohani, B. Development and experimental evaluation of a low-cost cooperative UAV localization network prototype. J. Sens. Actuator Networks 2018, 7, 42. [Google Scholar] [CrossRef]
- Yanmaz, E.; Yahyanejad, S.; Rinner, B.; Hellwagner, H.; Bettstetter, C. Drone networks: Communications, coordination, and sensing. Ad Hoc Networks 2018, 68, 1–15. [Google Scholar] [CrossRef]
- Militaru, G.; Popescu, D.; Ichim, L. UAV-to-UAV Communication Options for Civilian Applications. In Proceedings of the 2018 IEEE 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; pp. 1–4. [Google Scholar]
- Chmaj, G.; Selvaraj, H. Distributed Processing Applications for UAV/drones: A Survey. In Progress in Systems Engineering; Advances in Intelligent Systems and Computing; Springer: Berlin, Germany, 2015; Volume 366, pp. 449–454. [Google Scholar]
- He, L.; Bai, P.; Liang, X.; Zhang, J.; Wang, W. Feedback formation control of UAV swarm with multiple implicit leaders. Aerosp. Sci. Technol. 2018, 72, 327–334. [Google Scholar] [CrossRef]
- Trujillo, J.C.; Munguia, R.; Guerra, E.; Grau, A. Cooperative monocular-based SLAM for multi-UAV systems in GPS-denied environments. Sensors 2018, 18, 1351. [Google Scholar] [CrossRef] [PubMed]
- Basiri, M.; Schill, F.; Lima, P.; Floreano, D. On-board relative bearing estimation for teams of drones using sound. IEEE Rob. Autom Lett. 2016, 1, 820–827. [Google Scholar] [CrossRef]
- Kohlbacher, A.; Eliasson, J.; Acres, K.; Chung, H.; Barca, J.C. A low cost omnidirectional relative localization sensor for swarm applications. In Proceedings of the 2018 IEEE 4th World Forum on Internet of Things (WF-IoT), Singapore, 5–8 February 2018; pp. 694–699. [Google Scholar]
- Pugh, J.; Martinoli, A. Relative localization and communication module for small-scale multi-robot systems. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 188–193. [Google Scholar]
- Walter, V.; Saska, M.; Franchi, A. Fast mutual relative localization of uavs using ultraviolet led markers. In Proceedings of the 2018 IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 1217–1226. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, J.; Shen, Y.; Zhang, X. Autonomous Navigation of UAVs in Large-Scale Complex Environments: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2019, 68, 2124–2136. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the 2016 IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Fasano, G.; Accardo, D.; Moccia, A.; Maroney, D. Sense and avoid for unmanned aircraft systems. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 82–110. [Google Scholar] [CrossRef]
- Lai, J.; Ford, J.J.; Mejias, L.; O’Shea, P. Characterization of Sky-region Morphological-temporal Airborne Collision Detection. J. Field Rob. 2013, 30, 171–193. [Google Scholar] [CrossRef]
- Fasano, G.; Accardo, D.; Tirri, A.E.; Moccia, A.; De Lellis, E. Sky region obstacle detection and tracking for vision-based UAS sense and avoid. J. Intell. Rob. Syst. 2016, 84, 121–144. [Google Scholar] [CrossRef]
- Huh, S.; Cho, S.; Jung, Y.; Shim, D. Vision-based sense-and-avoid framework for unmanned aerial vehicles. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3427–3439. [Google Scholar] [CrossRef]
- James, J.; Ford, J.J.; Molloy, T. Learning to Detect Aircraft for Long-Range Vision-Based Sense-and-Avoid Systems. IEEE Rob. Autom. Lett. 2018, 3, 4383–4390. [Google Scholar] [CrossRef] [Green Version]
- Unlu, E.; Zenou, E.; Riviere, N. Using shape descriptors for UAV detection. Electron. Imaging 2018, 9, 1–5. [Google Scholar] [CrossRef]
- Unlu, E.; Zenou, E.; Riviere, N.; Dupouy, P.E. Deep learning-based strategies for the detection and tracking of drones using several cameras. IPSJ Trans. Comput. Vision Appl. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Martínez, C.; Campoy, P.; Mondragón, I.F.; Sánchez-Lopez, J.L.; Olivares-Méndez, M.A. HMPMR strategy for real-time tracking in aerial images, using direct methods. Mach. Vision Appl. 2014, 25, 1283–1308. [Google Scholar] [CrossRef] [Green Version]
- Gökçe, F.; Üçoluk, G.; Şahin, E.; Kalkan, S. Vision-based detection and distance estimation of micro unmanned aerial vehicles. Sensors 2015, 15, 23805–23846. [Google Scholar]
- Li, P.; Wang, D.; Wang, L.; Lu, H. Deep visual tracking: Review and experimental comparison. Pattern Recognit. 2018, 76, 323–338. [Google Scholar] [CrossRef]
- Li, J.; Ye, D.H.; Chung, T.; Kolsch, M.; Wachs, J.; Bouman, C. Multi-target detection and tracking from a single camera in Unmanned Aerial Vehicles (UAVs). In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4992–4997. [Google Scholar]
- Rozantsev, A.; Lepetit, V.; Fua, P. Detecting flying objects using a single moving camera. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 879–892. [Google Scholar] [CrossRef]
- Wu, Y.; Sui, Y.; Wang, G. Vision-based real-time aerial object localization and tracking for UAV sensing system. IEEE Access 2017, 5, 23969–23978. [Google Scholar] [CrossRef]
- Sun, S.; Yin, Y.; Wang, X.; Xu, D. Robust Visual Detection and Tracking Strategies for Autonomous Aerial Refueling of UAVs. IEEE Transactions on Instrumentation and Measurement 2019, in press. [Google Scholar] [CrossRef]
- Cledat, E.; Cucci, D.A. Mapping Gnss Restricted Environments with a Drone Tandem and Indirect Position Control. ISPRS Annals 2017, 4, 1–7. [Google Scholar] [CrossRef]
- Krajnik, T.; Nitsche, M.; Faigl, J.; Vanek, P.; Saska, M.; Preucil, L.; Duckett, T.; Mejail, M.A. A practical multirobot localization system. J. Intell. Rob. Syst. 2014, 76, 539–562. [Google Scholar] [CrossRef]
- Olivares-Mendez, M.A.; Mondragon, I.; Cervera, P.C.; Mejias, L.; Martinez, C. Aerial object following using visual fuzzy servoing. In Proceedings of the 1st Workshop on Research, Development and Education on Unmanned Aerial Systems (RED-UAS), Sevilla, Spain, 30 November–1 December 2011. [Google Scholar]
- Duan, H.; Xin, L.; Chen, S. Robust Cooperative Target Detection for a Vision-Based UAVs Autonomous Aerial Refueling Platform via the Contrast Sensitivity Mechanism of Eagle’s Eye. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 18–30. [Google Scholar] [CrossRef]
- Opromolla, R.; Vetrella, A.R.; Fasano, G.; Accardo, D. Airborne Visual Tracking for Cooperative UAV Swarms. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech@ Aerospace, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Opromolla, R.; Fasano, G.; Accardo, D. A Vision-Based Approach to UAV Detection and Tracking in Cooperative Applications. Sensors 2018, 18, 3391. [Google Scholar] [CrossRef] [PubMed]
- The Kalibr Visual-Inertial Calibration Toolbox. Available online: https://github.com/ethz-asl/kalibr (accessed on 1 September 2019).
- Yang, Z.; Shen, S. Monocular visual–inertial state estimation with online initialization and camera–imu extrinsic calibration. IEEE Trans. Autom. Sci. Eng. 2017, 14, 39–51. [Google Scholar] [CrossRef]
- Camera Calibration Toolbox for Matlab. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 1 September 2019).
- Guo, Y.; Liu, Y.; Oerlemans, A.; Lao, S.; Wu, S.; Lew, M.S. Deep learning for visual understanding: A review. Neurocomputing 2016, 187, 27–48. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. Computer Vision—ECCV 2016. ECCV 2016. In Lecture Notes in Computer Science; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, October 2016. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Zhang, S.; Wen, L.; Bian, X.; Lei, Z.; Li, S.Z. Single-shot refinement neural network for object detection. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 July 2018; pp. 4203–4212. [Google Scholar]
- Deng, L.; Yang, M.; Li, T.; He, Y.; Wang, C. RFBNet: Deep Multimodal Networks with Residual Fusion Blocks for RGB-D Semantic Segmentation. arXiv preprint, 2019; arXiv:1907.00135. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv preprint, 2018; arXiv:1804.02767. [Google Scholar]
- Liu, L.; Ouyang, W.; Wang, X.; Fieguth, P.; Chen, J.; Liu, X.; Pietikäinen, M. Deep learning for generic object detection: A survey. arXiv preprint, 2018; arXiv:1809.02165. [Google Scholar]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, in press. [Google Scholar] [CrossRef]
- Deep Learning Toolbox. Available online: https://it.mathworks.com/help/deeplearning/index.html (accessed on 1 September 2019).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Brown, A.K. Test results of a GPS/inertial navigation system using a low cost MEMS IMU. In Proceedings of the 11th Annual Saint Petersburg International Conference on Integrated Navigation System, Saint Petersburg, Russia, 24–26 May 2004. [Google Scholar]
- Nuske, S.T.; Dille, M.; Grocholsky, B.; Singh, S. Representing substantial heading uncertainty for accurate geolocation by small UAVs. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Eichler, S. Performance Evaluation of the IEEE 802.11p WAVE Communication Standard. In Proceedings of the 2007 IEEE 66th Vehicular Technology Conference, Baltimore, MD, USA, 30 September–3 October 2007; pp. 2199–2203. [Google Scholar]










| FT | N | NIN | NOUT | ρ (m) | ∆u/∆v (pixel) | ||
|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||||
| 1 | 398 | 376 | 22 | 84.2 | 17.1 | 38/24 | 59/26 |
| 2 | 361 | 319 | 42 | 105.9 | 19.5 | 30/26 | 50/26 |
| 3 | 381 | 323 | 58 | 120.2 | 19.5 | 33/21 | 42/21 |
| FT | N | NIN | NOUT | ρ (m) | ∆u/∆v (pixel) | ||
|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||||
| 1 | 1330 | 1275 | 75 | 168.9 | 86.5 | 4/2 | 9/4 |
| 2 | 735 | 735 | 0 | 20.5 | 1.7 | 4/7 | 6/9 |
| BB Refinement Enabled | BB Refinement Not Enabled | |||
|---|---|---|---|---|
| Az Error (°) | El Error (°) | Az Error (°) | El Error (°) | |
| Mean | −0.046 | 0.057 | −0.049 | 0.063 |
| Std | 0.023 | 0.016 | 0.046 | 0.051 |
| Rms | 0.051 | 0.059 | 0.067 | 0.081 |
| Detector | CD | MD | FA + WD |
|---|---|---|---|
| DL-based | 95.5% | 2.4% | 2.1% |
| [48] | 78% | 18% | 4% |
| τdet | τtr | MD | FA | CD | WD | |
|---|---|---|---|---|---|---|
| DL-based detector | 0.40 | / | 2.4% | 2.1% | 95.5% | 0.0% |
| DL-based detector and tracker | 0.40 | 0.40 | 3.2% | 1.8% | 95.0% | 0.0% |
| 0.40 | 0.30 | 1.8% | 2.1% | 96.1% | 0.0% | |
| 0.40 | 0.20 | 1.3% | 2.4% | 96.3% | 0.0% | |
| 0.40 | 0.10 | 0.5% | 3.7% | 95.5% | 0.3% |
| τdet | τtr | MD | FA | CD | WD | |
|---|---|---|---|---|---|---|
| DL-based detector | 0.65 | / | 43.6% | 0% | 56.4% | 0% |
| DL-based detector and tracker | 0.65 | 0.65 | 40.4% | 0% | 59.6% | 0% |
| 0.65 | 0.40 | 11.0% | 0% | 89.0% | 0% | |
| 0.65 | 0.20 | 7.35% | 0% | 92.65% | 0% |
| τdet | τtr | MD | FA | CD | WD | |
|---|---|---|---|---|---|---|
| DL-based detector and tracker | 0.50 | 0.50 | 71.65% | 0.08% | 28.27% | 0% |
| 0.50 | 0.30 | 61.73% | 0.15% | 38.12% | 0% | |
| 0.50 | 0.15 | 58.2% | 0.15% | 41.65% | 0% | |
| 0.50 | 0.075 | 42.8% | 0.3% | 56% | 0.9% |
| τdet | τtr | MD | FA | CD | WD | |
|---|---|---|---|---|---|---|
| DL-based detector and tracker | 0.20 | 0.20 | 39.62% | 1.05% | 57.59% | 1.73% |
| 0.20 | 0.15 | 36.54% | 1.05% | 60.68% | 1.73% | |
| 0.20 | 0.10 | 31.65% | 1.20% | 65.64% | 1.50% | |
| 0.20 | 0.075 | 29.55% | 1.43% | 67.59% | 1.43% |
| τdet = 0.20 and τtr = 0.075 | τdet = 0.50 and τtr = 0.15 | |||
|---|---|---|---|---|
| Az Error (°) | El Error (°) | Az Error (°) | El Error (°) | |
| Mean | −0.016 | 0.040 | −0.025 | 0.036 |
| Std | 0.062 | 0.034 | 0.035 | 0.023 |
| Rms | 0.064 | 0.053 | 0.043 | 0.043 |
| τdet | MD | CD | WD | |
|---|---|---|---|---|
| DL-based detector and tracker | 0.50 | 23.3% | 75.9% | 0.8% |
| 0.30 | 5.3% | 93.6% | 1.1% | |
| 0.20 | 4.9% | 94% | 1.1% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opromolla, R.; Inchingolo, G.; Fasano, G. Airborne Visual Detection and Tracking of Cooperative UAVs Exploiting Deep Learning. Sensors 2019, 19, 4332. https://doi.org/10.3390/s19194332
Opromolla R, Inchingolo G, Fasano G. Airborne Visual Detection and Tracking of Cooperative UAVs Exploiting Deep Learning. Sensors. 2019; 19(19):4332. https://doi.org/10.3390/s19194332
Chicago/Turabian StyleOpromolla, Roberto, Giuseppe Inchingolo, and Giancarmine Fasano. 2019. "Airborne Visual Detection and Tracking of Cooperative UAVs Exploiting Deep Learning" Sensors 19, no. 19: 4332. https://doi.org/10.3390/s19194332
APA StyleOpromolla, R., Inchingolo, G., & Fasano, G. (2019). Airborne Visual Detection and Tracking of Cooperative UAVs Exploiting Deep Learning. Sensors, 19(19), 4332. https://doi.org/10.3390/s19194332







