Size Dependence of the Magnetoelastic Properties of Metallic Glasses for Actuation Applications
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luborsky, F.E. Chapter 6: Amorphous ferromagnets. In Ferromagnetic Materials; Wohlfart, T.E., Ed.; North-Holland: Amsterdam, The Netherlands, 1980; Volume 1, ISBN 0-444-85311-1. [Google Scholar]
- Squire, P.T. Magnetomechanical measurements of magnetically soft amorphous materials. Meas. Sci. Technol. 1994, 5, 67–81. [Google Scholar] [CrossRef]
- Atkinson, D.; Squire, P.T.; Gibbs, M.R.J.; Hogsdon, S.N. Implications of magnetic and magnetoelastic measurements for the domain structure of FeSiB amorphous wires. J. Phys. D Appl. Phys. 1994, 27, 1354–1362. [Google Scholar] [CrossRef]
- Marín, P.; Marcos, M.; Hernando, A. High magnetomechanical coupling on magnetic microwire for sensors with biological applications. Appl. Phys. Lett. 2010, 96, 262512. [Google Scholar] [CrossRef]
- Stoyanov, P.G.; Grimes, C.A. A remote query magnetostrictive viscosity sensor. Sens. Actuat. A Phys. 2000, 80, 8–14. [Google Scholar] [CrossRef]
- Herrero-Gómez, C.; Marín, P.; Hernando, A. Bias free magnetomechanical coupling on magnetic microwires for sensing applications. Appl. Phys. Lett. 2013, 103, 142414. [Google Scholar] [CrossRef]
- Stoyanov, P.G.; Doherty, S.A.; Grimes, C.A.; Seitz, W.R. A remotely interrogatable sensor for chemical monitoring. IEEE Trans. Mag. 1998, 34, 1315–1317. [Google Scholar] [CrossRef]
- Grimes, C.A.; Mungle, C.S.; Zeng, K.; Jain, M.K.; Dreschel, W.R.; Paulose, M.; Ong, G.K. Wireless magnetoelastic resonance sensors: A critical review. Sensors 2002, 2, 294–313. [Google Scholar] [CrossRef]
- Lopes, A.C.; Sagasti, A.; Lasheras, A.; Muto, V.; Gutiérrez, J.; Kouzoudis, D.; Barandiarán, J.M. Accurate determination of the Q quality factor in magnetoelastic resonant platforms for advanced biological detection. Sensors 2018, 18, 887. [Google Scholar] [CrossRef]
- Menti, C.; Henriques, J.A.P.; Missell, F.P.; Roesch-Ely, M. Antibody based magneto-elastic biosensors: Potential devices for detection of pathogens and associated toxins. Appl. Microbiol. Biotechnol. 2016, 100, 6149–6163. [Google Scholar] [CrossRef]
- Sagasti, A.; Llano, M.; Lasheras, A.; Lopes, A.C.; Feuchtwanger, J.; Gutiérrez, J. Influence of the length-to-width ratio on the ΔE effect of amorphous magnetoelastic ribbons for actuation applications. Key Eng. Mater. 2019, accepted, in press. [Google Scholar]
- Schmidt, A.; Grimes, C. Characterization of nano-dimensional thin-film elastic moduli using magnetoelastic sensors. Sens. Actuat. A Phys. 2001, 94, 189–196. [Google Scholar] [CrossRef]
- Schmidt, S.; Grimes, C.A. Elastic modulus measurement of thin films coated onto magnetoelastic ribbons. IEEE Trans. Mag. 2001, 37, 2731–3733. [Google Scholar] [CrossRef]
- Lasheras, A.; Gutiérrez, J.; Barandiarán, J.M. Quantification of size effects in the magnetoelectric response of metallic glass/PVDF laminates. Appl. Phys. Lett. 2016, 108, 222903. [Google Scholar] [CrossRef]
- Saiz, P.G.; Gandía, D.; Lasheras, A.; Sagasti, A.; Quintana, I.; Fernández-Gubieda, M.L.; Gutiérrez, J.; Arriortua, M.; Lopes, A.C. Enhanced mass sensitivity in novel magnetoelastic resonators for advanced detection systems. Sens. Actuat. B Chem. 2019, 296, 126612. [Google Scholar] [CrossRef]
- Sagasti, A.; Lopes, A.C.; Lasheras, A.; Palomares, V.; Carrizo, J.; Gutiérrez, J.; Barandiarán, J.M. Corrosion resistant metallic glasses for biosensing applications. AIP Adv. 2018, 8, 047702. [Google Scholar] [CrossRef]
- Metglas Inc. Magnetic Materials. Available online: https://metglas.com/magnetic-materials/ (accessed on 10 January 2019).
- Gutiérrez, J.; Lasheras, A.; Martins, P.; Pereira, N.; Barandiarán, J.M.; Lanceros-Méndez, S. Metallic glass/PVDF magnetoelectric laminates for resonant sensors and actuators: A review. Sensors 2017, 17, 1251. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Chapter III. Elastic waves. In Theory of Elasticity; Oxford Pergamon Press: Oxford, UK, 1975; p. 116. [Google Scholar]
- Savage, H.; Abbundi, R. Perpendicular susceptibility, magnetomechanical coupling and shear modulus in Tb_0.27 Dy_0.73 Fe_2. IEEE Trans. Mag. 1978, 14, 545–547. [Google Scholar] [CrossRef]
- Herzer, G. Magnetic materials for electronic article surveillance. J. Magn. Magn. Mater. 2003, 254–255, 598–602. [Google Scholar] [CrossRef]
- Usov, N.A. Magnetization curling in soft type ferromagnetic particles with large aspect ratios. J. Magn. Magn. Mater. 1999, 203, 277–279. [Google Scholar] [CrossRef]
- Zhukova, V.; Usov, N.A.; Zhukov, A.; González, J. Length effect in a Co-rich amorphous wire. Phys. Rev. B 2002, 65, 134407. [Google Scholar] [CrossRef]
- Chen, D.-X.; Pardo, E.; Sanchez, A. Demagnetizing factors of rectangular prisms and ellipsoids. IEEE Trans. Magn. 2002, 38, 1742–1752. [Google Scholar] [CrossRef]
- Chen, D.-X.; Pardo, E.; Sanchez, A. Demagnetizing factors for rectangular prisms. IEEE Trans. Magn. 2005, 41, 2077–2088. [Google Scholar] [CrossRef]
- Bozorth, R.M. Chapter 19: Measurement of magnetic quantities. In Ferromagnetism; IEEE Press: Piscataway, NJ, USA, 1993; p. 847. ISBN 0-7803-1032-2. [Google Scholar]
- Clark, A.E.; Wun-Fogle, M. A new method of magnetostrictivity and magnetostriction measurement. IEEE Trans. Magn. 1989, 25, 3611–3613. [Google Scholar] [CrossRef]

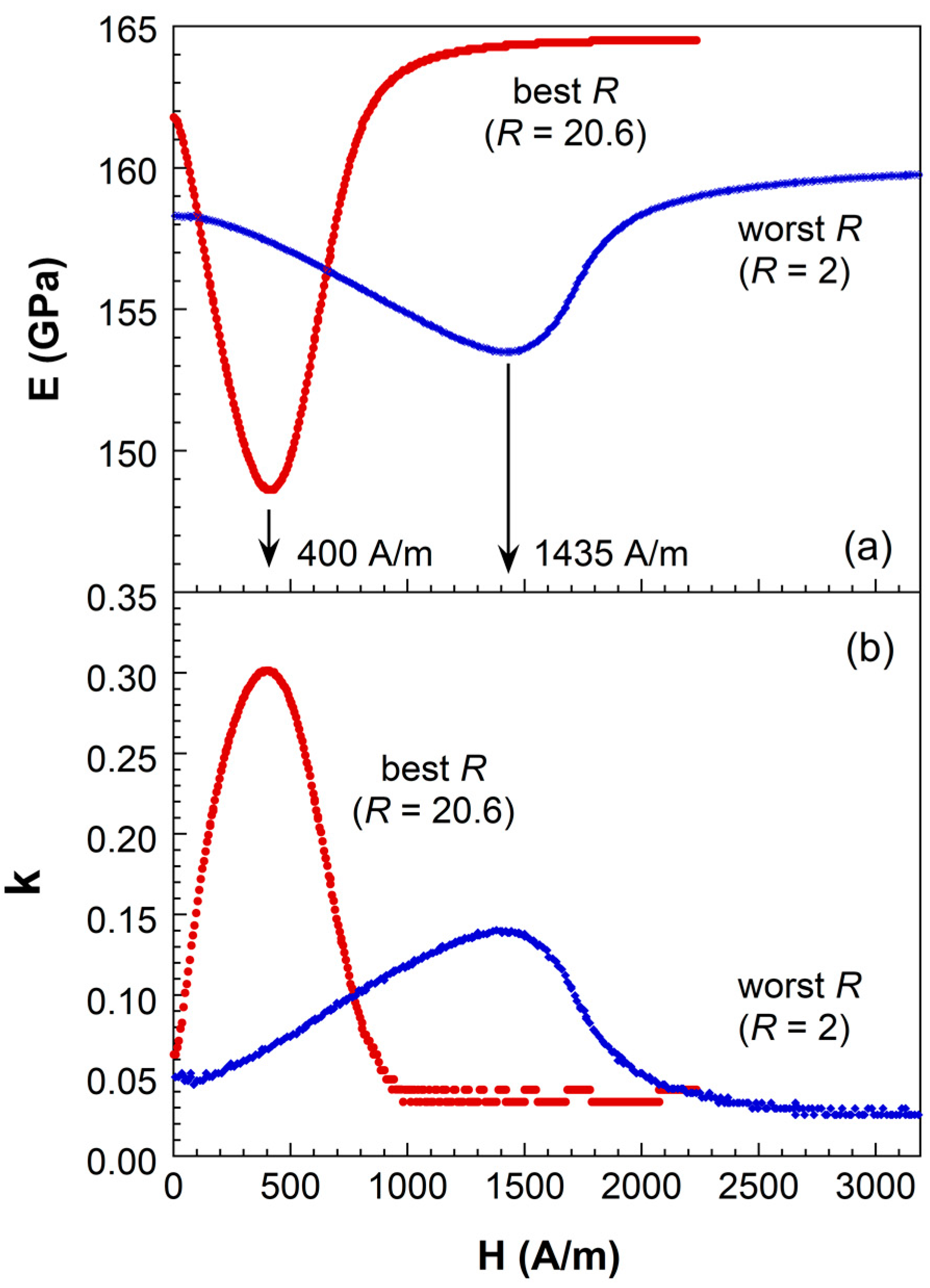

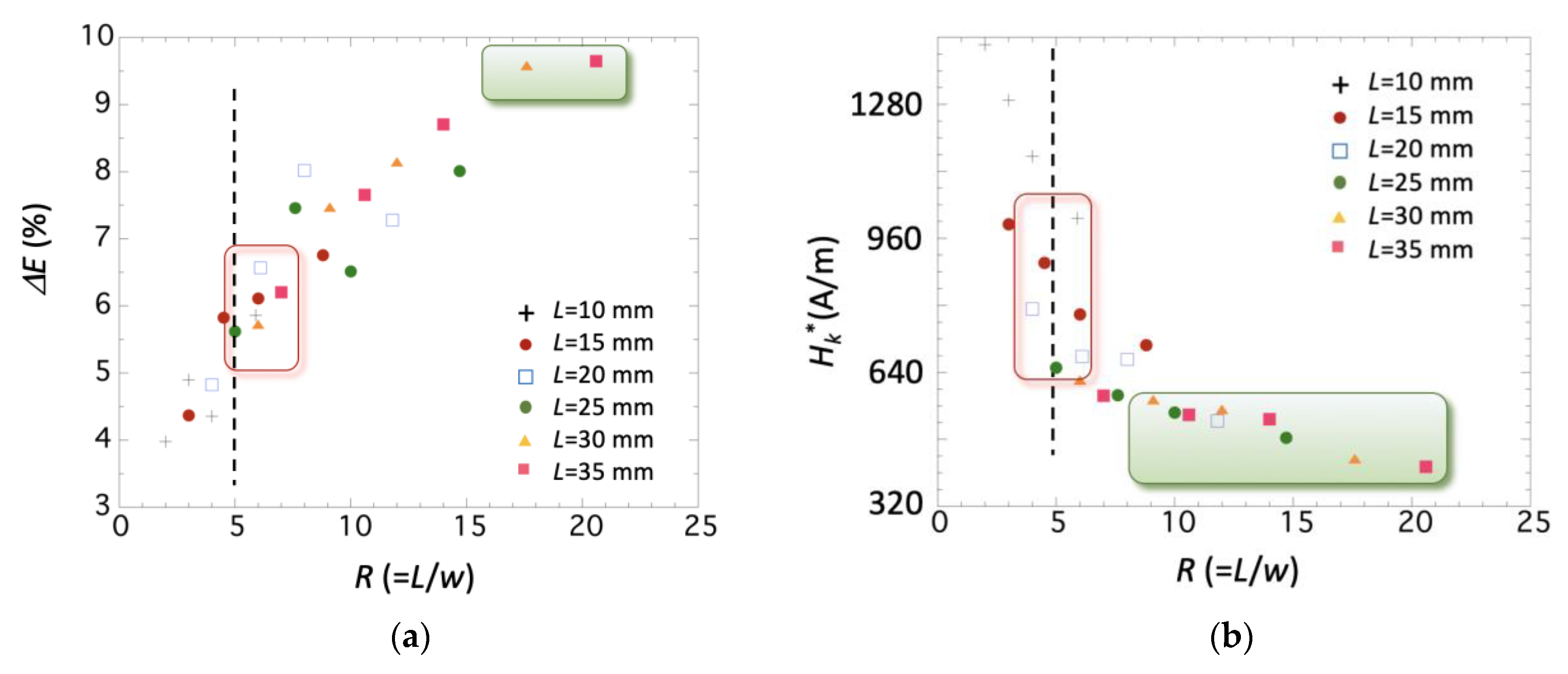
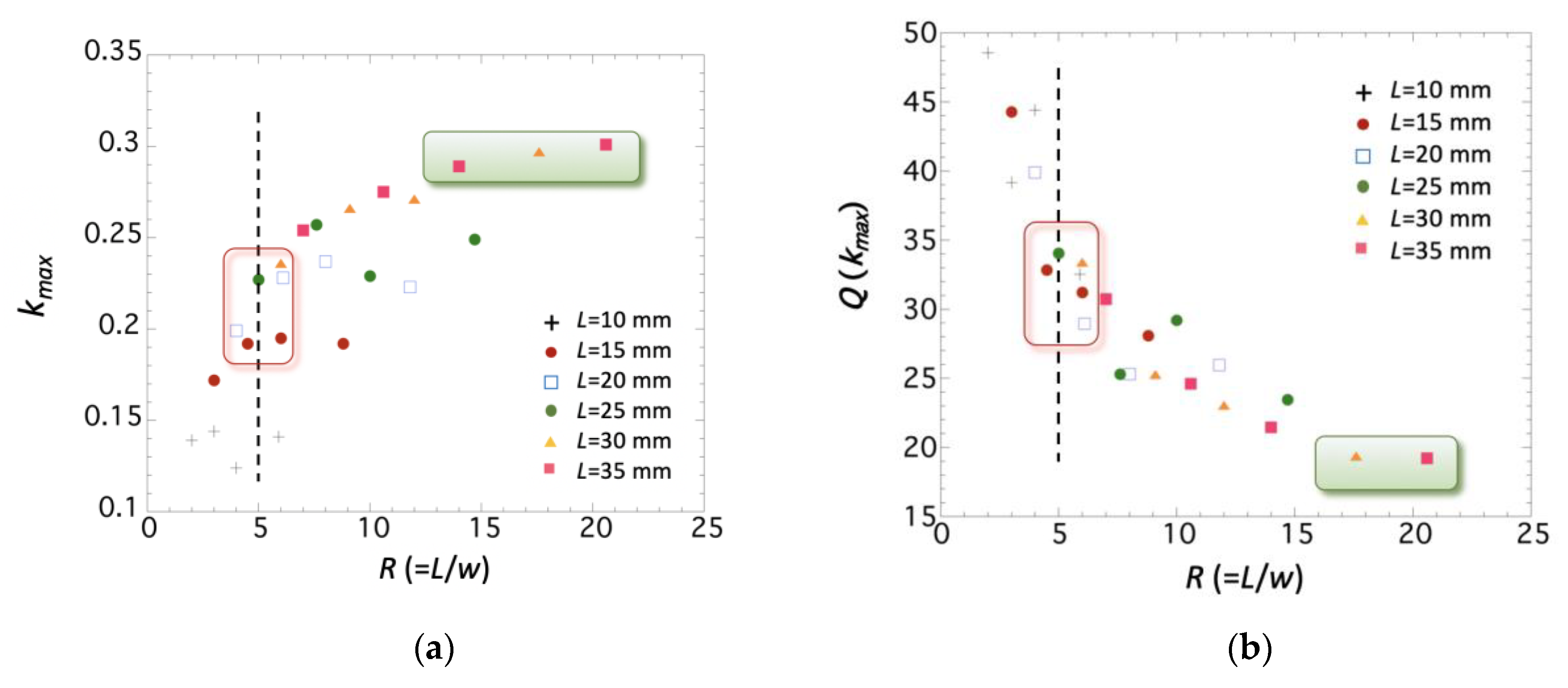
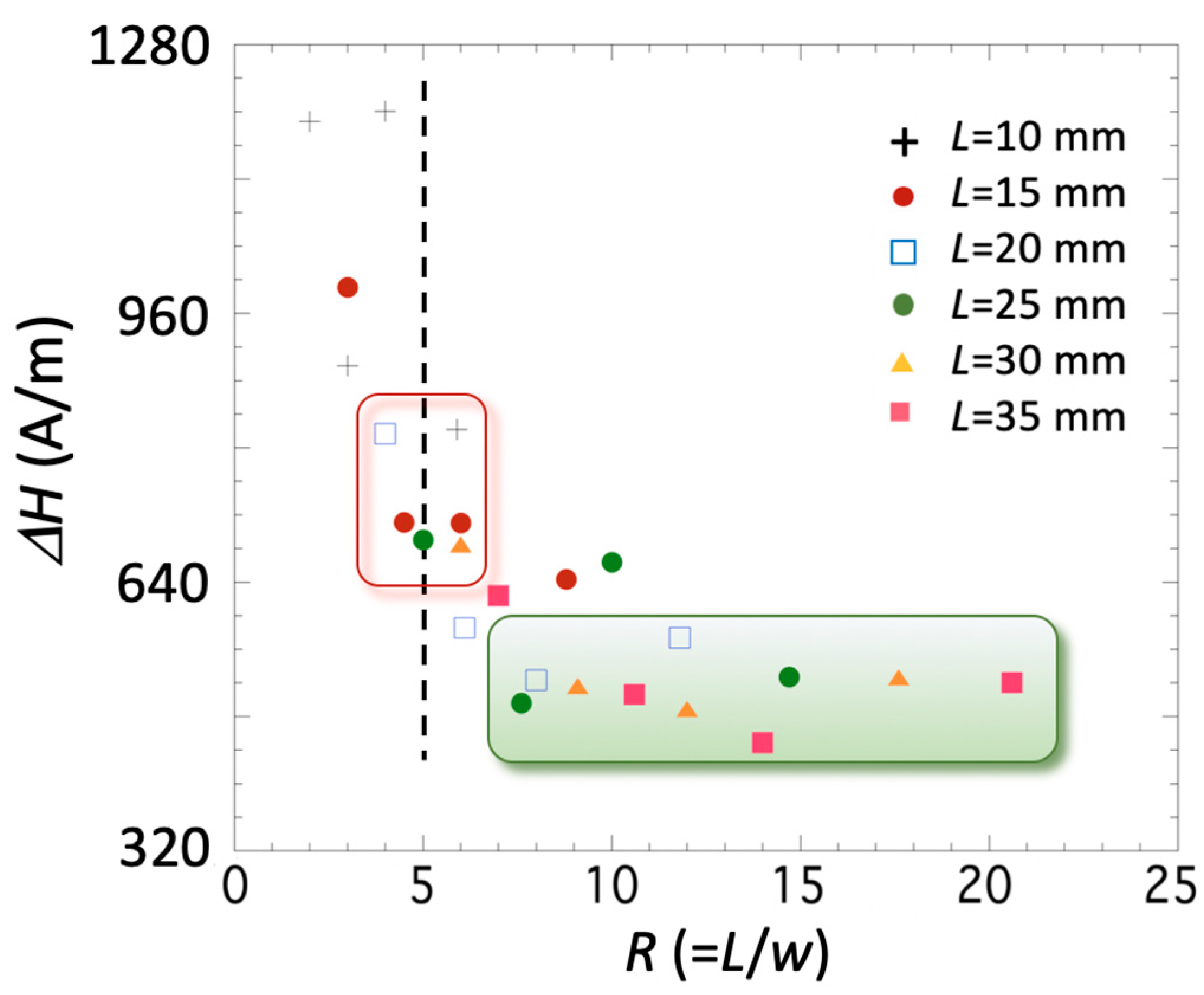
| L (mm) | w (mm) | R = L/w | fr (Hz) | Emin (GPa) | ES (GPa) | ΔE (%) | kmax | Q (kmax) | ΔH (A/m) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 35 | 5 | 7 | 63,145 | 154.3 | 164.5 | 6.2 | 582.4 | 0.25 | 30.7 | 622.2 |
| 35 | 3.33 | 10.6 | 63,100 | 154.1 | 166.9 | 7.7 | 536.9 | 0.27 | 24.6 | 505.0 |
| 35 | 2.5 | 14 | 62,240 | 149.9 | 164.2 | 8.7 | 526.5 | 0.29 | 21.5 | 447.5 |
| 35 | 1.66 | 20.6 | 61,965 | 148.6 | 164.5 | 9.6 | 413.2 | 0.30 | 19.2 | 518.5 |
| 30 | 5 | 6 | 73,655 | 154.3 | 163.6 | 5.7 | 619.8 | 0.23 | 33.4 | 682.9 |
| 30 | 3.33 | 9.1 | 73,160 | 152.2 | 164.5 | 7.5 | 572.8 | 0.26 | 25.3 | 514.5 |
| 30 | 2.5 | 12 | 73,397 | 153.2 | 166.8 | 8.1 | 549.6 | 0.27 | 23 | 487.4 |
| 30 | 1.66 | 17.6 | 72,400 | 149.1 | 164.9 | 9.6 | 432.4 | 0.29 | 19.4 | 524.9 |
| 25 | 5 | 5 | 88,782 | 155.7 | 164.9 | 5.6 | 649.4 | 0.23 | 34 | 688.5 |
| 25 | 3.33 | 7.6 | 87,645 | 151.7 | 163.9 | 7.5 | 583.9 | 0.26 | 25.3 | 494.6 |
| 25 | 2.5 | 10 | 88,180 | 153.6 | 164.3 | 6.5 | 542.5 | 0.23 | 29.2 | 662.1 |
| 25 | 1.66 | 14.7 | 87,700 | 151,9 | 165.1 | 8 | 482.6 | 0.25 | 23.4 | 525.7 |
| 20 | 5 | 4 | 110,993 | 155.7 | 163.6 | 4.8 | 789.0 | 0.2 | 39.9 | 814.5 |
| 20 | 3.33 | 6.1 | 109,942 | 152.8 | 163.5 | 6.6 | 675.7 | 0.23 | 28.9 | 583.9 |
| 20 | 2.5 | 8 | 109,760 | 152.3 | 165.5 | 8 | 669.3 | 0.24 | 25.3 | 521.7 |
| 20 | 1.66 | 11.8 | 110,060 | 153.1 | 165.1 | 7.3 | 522.5 | 0.22 | 25.9 | 572.0 |
| 15 | 5 | 3 | 148,012 | 155.7 | 162.9 | 4.4 | 990.8 | 0.17 | 44.3 | 988.4 |
| 15 | 3.33 | 4.5 | 153,475 | 167.5 | 177.8 | 5.8 | 899.1 | 0.19 | 32.8 | 709.2 |
| 15 | 2.5 | 6 | 147,500 | 154.7 | 164.7 | 6.1 | 776.0 | 0.19 | 31.2 | 708.4 |
| 15 | 1.66 | 8.8 | 153,050 | 166.5 | 178.6 | 6.8 | 702.8 | 0.19 | 28.1 | 641.4 |
| 10 | 5 | 2 | 220,400 | 153.5 | 159.9 | 4 | 1418.4 | 0.14 | 48.5 | 1185.5 |
| 10 | 3.33 | 3 | 221,295 | 154.7 | 162.7 | 4.9 | 1286.0 | 0.14 | 39.2 | 895.1 |
| 10 | 2.5 | 4 | 222,902 | 157 | 164.1 | 4.4 | 1152.7 | 0.12 | 44.4 | 1197.4 |
| 10 | 1.66 | 5.9 | 221,175 | 154.6 | 164.2 | 5.9 | 1005.2 | 0.14 | 32.5 | 819.3 |
| L (mm) | w (mm) | R = L/w | Emin (GPa) | ES (GPa) | ΔE (%) | kmax | Q (kmax) | ΔH (A/m) | |
|---|---|---|---|---|---|---|---|---|---|
| 30 | 5 | 6 | 154.3 | 163.6 | 5.7 | 619.8 | 0.23 | 33.4 | 682.9 |
| 20 | 3.33 | 6.1 | 152.8 | 163.5 | 6.6 | 675.7 | 0.23 | 28.9 | 583.9 |
| 15 | 2.5 | 6 | 154.7 | 164.7 | 6.1 | 776.2 | 0.19 | 31.2 | 708.4 |
| 10 | 1.66 | 5.9 | 154.6 | 164.2 | 5.9 | 1005.2 | 0.14 | 32.5 | 819.3 |
| L = 2c (mm) | w = 2a (mm) | R = c/a | a/b 1 | c/(ab)1/2 | Nf 2 |
|---|---|---|---|---|---|
| 30 | 5 | 6 | 166.7 | 77.5 | 0.00014248 |
| 20 | 3.33 | 6.1 | 111 | 63.3 | 0.00019609 |
| 15 | 2.5 | 6 | 83.3 | 54.8 | 0.00022911 |
| 10 | 1.66 | 5.9 | 55.3 | 44.8 | 0.00101335 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagasti, A.; Gutiérrez, J.; Lasheras, A.; Barandiarán, J.M. Size Dependence of the Magnetoelastic Properties of Metallic Glasses for Actuation Applications. Sensors 2019, 19, 4296. https://doi.org/10.3390/s19194296
Sagasti A, Gutiérrez J, Lasheras A, Barandiarán JM. Size Dependence of the Magnetoelastic Properties of Metallic Glasses for Actuation Applications. Sensors. 2019; 19(19):4296. https://doi.org/10.3390/s19194296
Chicago/Turabian StyleSagasti, Ariane, Jon Gutiérrez, Andoni Lasheras, and José Manuel Barandiarán. 2019. "Size Dependence of the Magnetoelastic Properties of Metallic Glasses for Actuation Applications" Sensors 19, no. 19: 4296. https://doi.org/10.3390/s19194296
APA StyleSagasti, A., Gutiérrez, J., Lasheras, A., & Barandiarán, J. M. (2019). Size Dependence of the Magnetoelastic Properties of Metallic Glasses for Actuation Applications. Sensors, 19(19), 4296. https://doi.org/10.3390/s19194296








