Geometry Optimisation of a Hall-Effect-Based Soft Fingertip for Estimating Orientation of Thin Rectangular Objects
Abstract
1. Introduction
2. Related Works
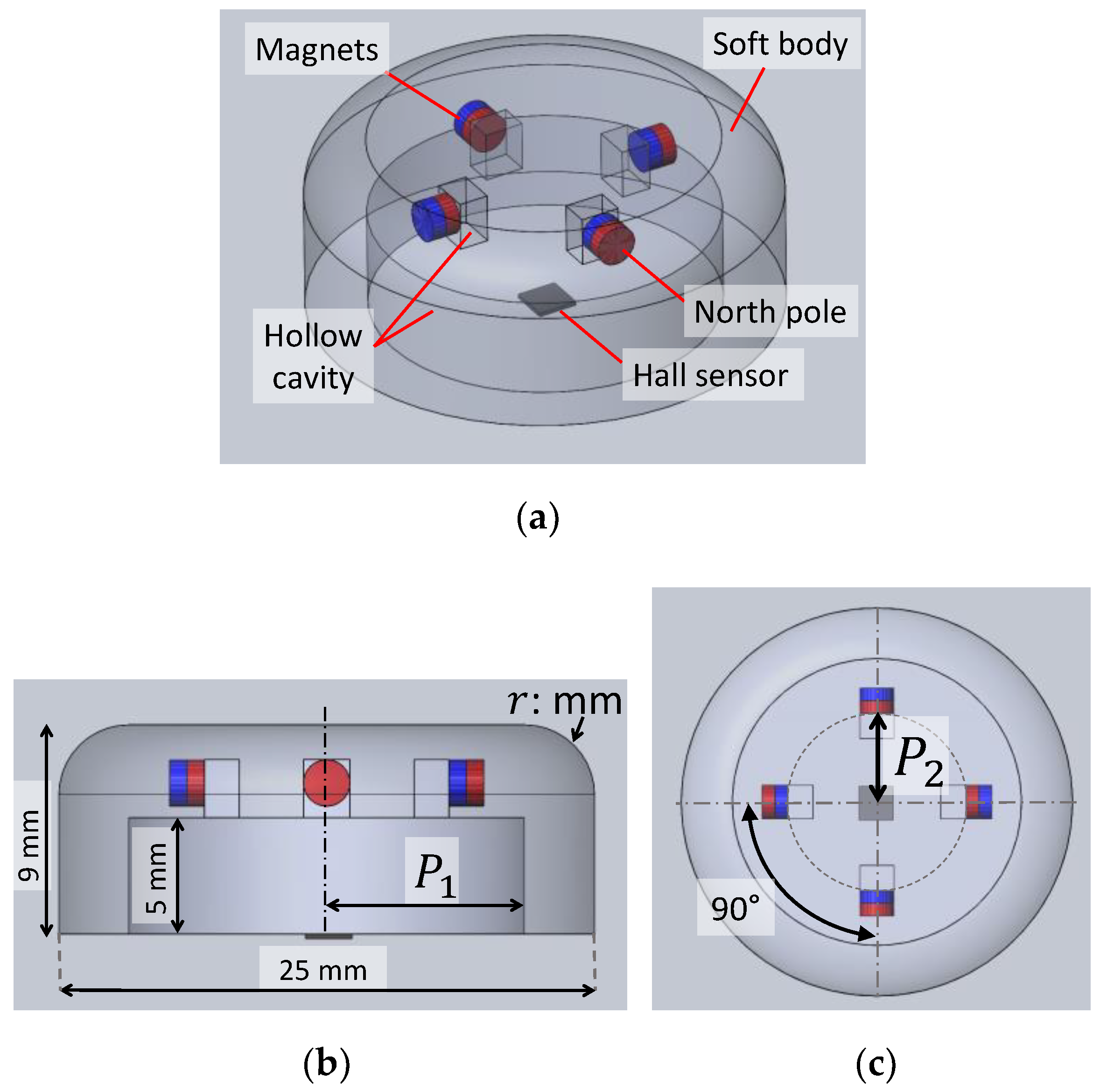
3. Configuration Design of Soft Fingertip
4. Design Optimisation and Fingertip Fabrication
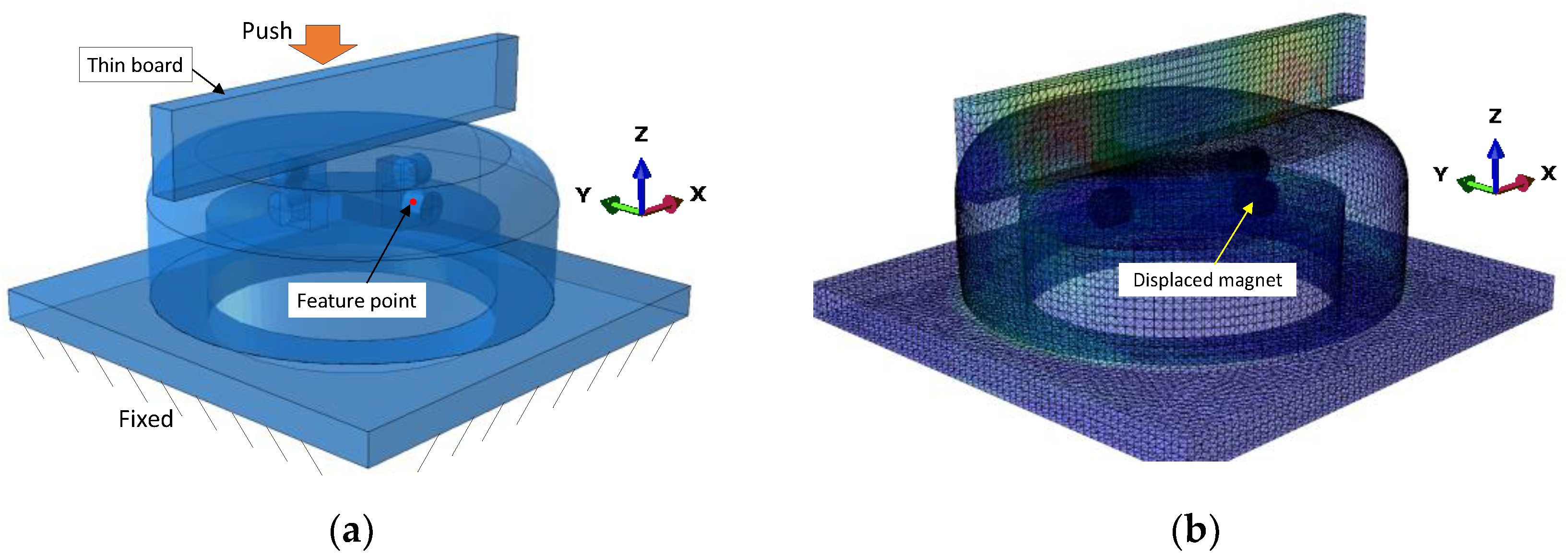
4.1. Finite Element Simulation
4.2. Optimisation Framework
4.3. Optimisation Results
4.4. Fingertip Fabrication
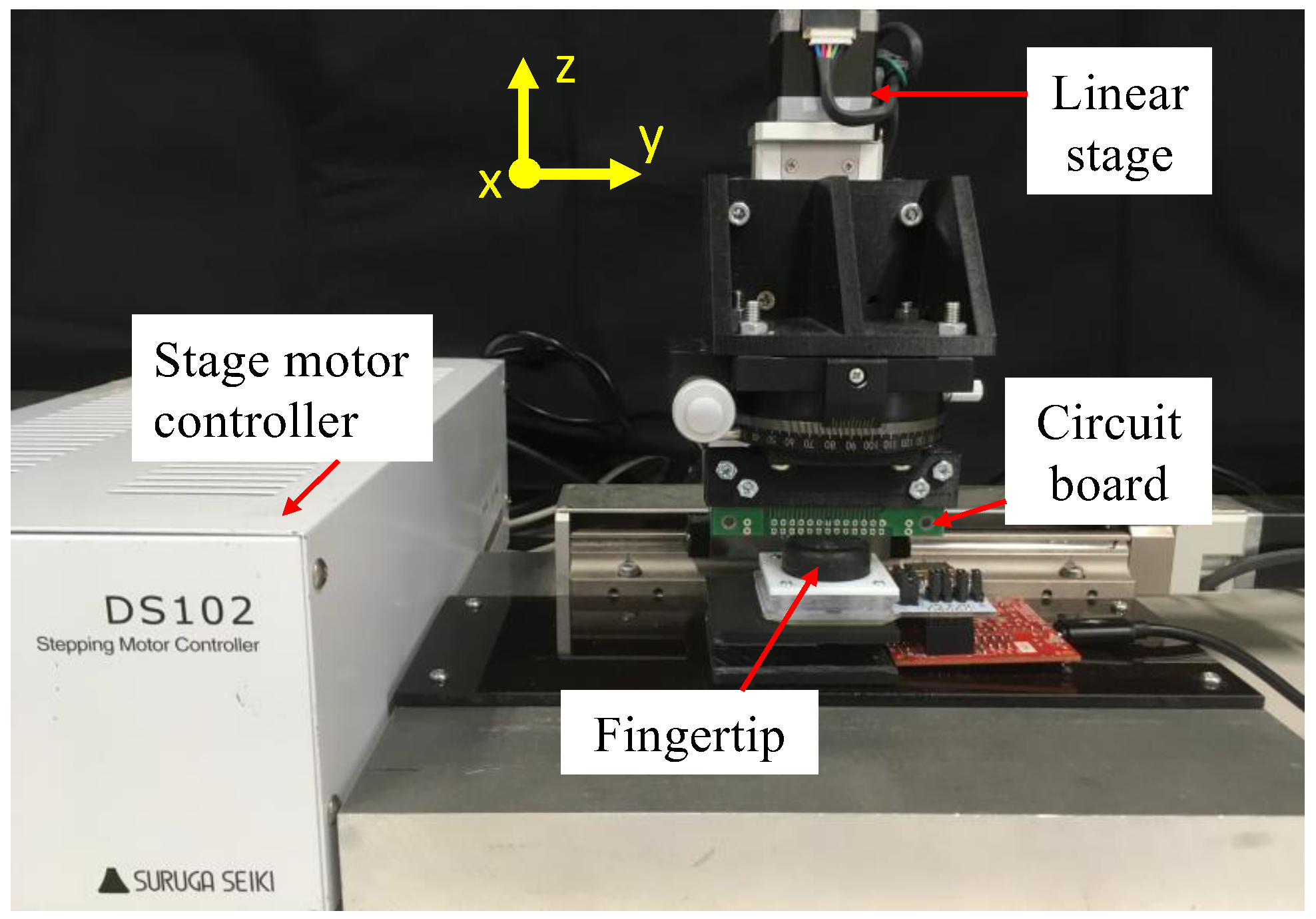
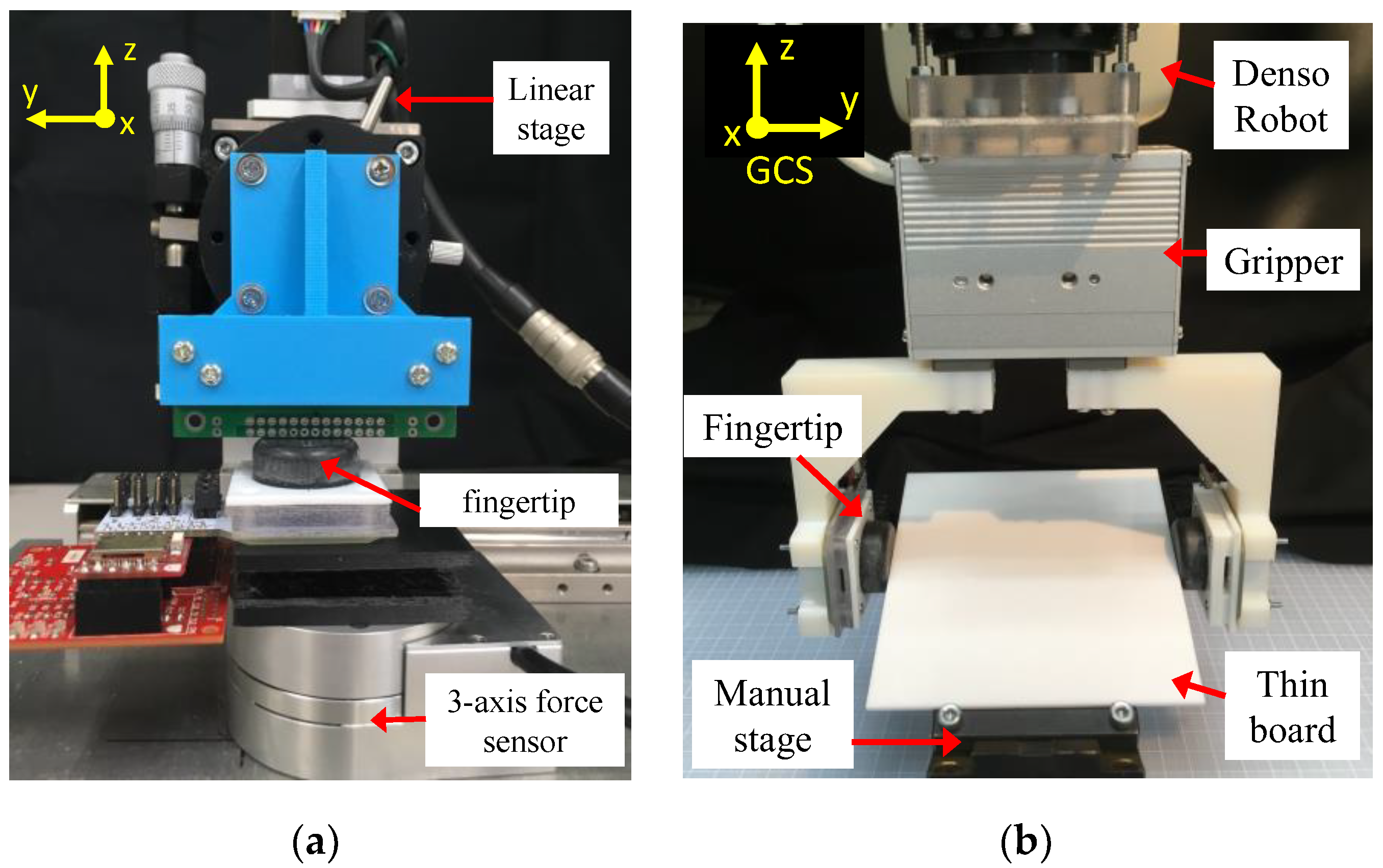
5. Experiments
5.1. Pushing Test with Different Object Orientations
5.1.1. Experimental Process
5.1.2. Calibration Method
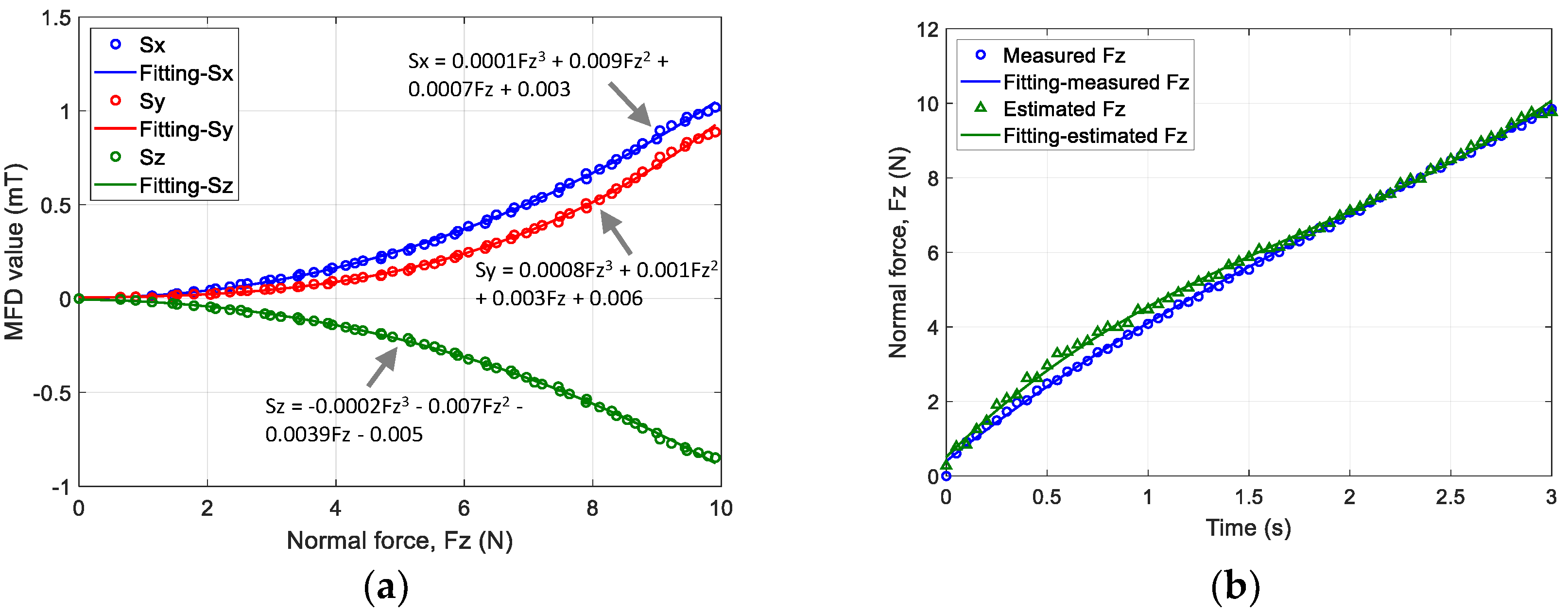
5.2. Three-Axis Force Estimation and Hysteresis
5.2.1. Force Calibration Setup
5.2.2. Hysteresis Tests
5.3. Grasping Tests
6. Results and Discussion
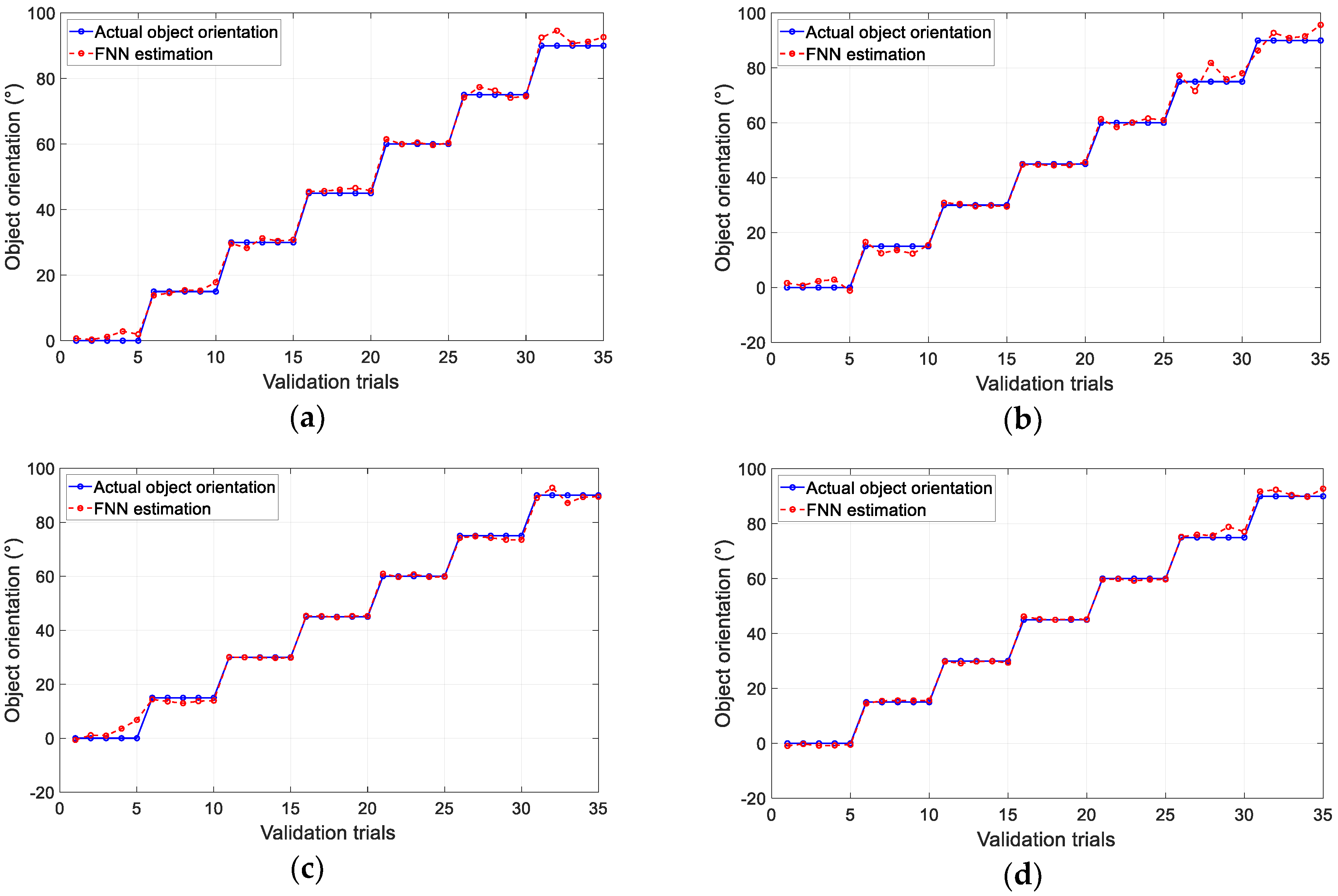
6.1. Pushing Tests with Different Object Orientations
6.2. Three-Axis Force Estimation and Hysteresis
6.3. Grasping Tests
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kawasetsu, T.; Horii, T.; Ishihara, H.; Asada, M. Deformation response of a magnetic type tactile sensor with a two-layered surface made of a non-magnetic and a magnetorheological elastomer. J. Jpn. Soc. Appl. Electromagn. Mech. 2016, 24, 204–209. [Google Scholar] [CrossRef]
- Pirozzi, S.; Natale, C. Tactile-based manipulation of wires for switchgear assembly. IEEE/ASME Trans. Mechatron. 2018, 23, 2650–2661. [Google Scholar] [CrossRef]
- Wang, H.; Kow, J.; Raske, N.; de Boer, G.; Ghajari, M.; Hewson, R.; Alazmani, A.; Culmer, P. Robust and high-performance soft inductive tactile sensors based on the Eddy-current effect. Sens. Actuators A Phys. 2018, 271, 44–52. [Google Scholar] [CrossRef]
- De Maria, G.; Natale, C.; Pirozzi, S. Force/tactile sensor for robotic applications. Sens. Actuators A Phys. 2012, 175, 60–72. [Google Scholar] [CrossRef]
- Tomo, T.P.; Regoli, M.; Schmitz, A.; Natale, L.; Kristanto, H.; Somlor, S.; Jamone, L.; Metta, G.; Sugano, S. A new silicone structure for uSkin—A soft, distributed, digital 3-axis skin sensor and its integration on the humanoid robot iCub. IEEE Rob. Autom. Lett. 2018, 3, 2584–2591. [Google Scholar] [CrossRef]
- Rosle, M.H.B.; Kojima, R.; Wang, Z.; Hirai, S. Soft fingertip with tactile sensation for detecting grasping orientation of thin object. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1304–1309. [Google Scholar]
- Dwivedi, A.; Ramakrishnan, A.; Reddy, A.; Patel, K.; Ozel, S.; Onal, C.D. Design, modeling, and validation of a soft magnetic 3-D force sensor. IEEE Sens. J. 2018, 18, 3852–3863. [Google Scholar] [CrossRef]
- Chathuranga, D.S.; Wang, Z.; Noh, Y.; Nanayakkara, T.; Hirai, S. Magnetic and mechanical modeling of a soft three-axis force sensor. IEEE Sens. J. 2016, 16, 5298–5307. [Google Scholar] [CrossRef]
- Tomo, T.P.; Schmitz, A.; Wong, W.K.; Kristanto, H.; Somlor, S.; Hwang, J.; Jamone, L.; Sugano, S. Covering a robot fingertip with uSkin: A soft electronic skin with distributed 3-axis force sensitive elements for robot hands. IEEE Rob. Autom. Lett. 2018, 3, 124–131. [Google Scholar] [CrossRef]
- Kawasetsu, T.; Horii, T.; Ishihara, H.; Asada, M. Mexican-hat-like response in a flexible tactile sensor using a magnetorheological elastomer. Sensors 2018, 18, 587. [Google Scholar] [CrossRef] [PubMed]
- Mirzanejad, H.; Agheli, M. Soft force sensor made of magnetic powder blended with silicone rubber. Sens. Actuator A Phys. 2019, 293, 108–118. [Google Scholar] [CrossRef]
- Chatzipirpiridis, G.; Erne, P.; Ergeneman, O.; Pane, S.; Nelson, B.J. A magnetic force sensor on a catheter tip for minimally invasive surgery. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Milan, Italy, 25–29 August 2015. [Google Scholar]
- Chathuranga, D.S.; Wang, Z.; Noh, Y.; Nanayakkara, T.; Hirai, S. Robust real time material classification algorithm using soft three axis tactile sensor: Evaluation of the algorithm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015. [Google Scholar]
- Goka, M.; Nakamoto, H.; Takenawa, S. A magnetic type tactile sensor by GMR elements and inductors. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Liu, Y.; Han, H.; Liu, T.; Yi, J.; Li, Q.; Inoue, Y. A novel tactile sensor with electromagnetic induction and its application on stick-slip interaction detection. Sensors 2016, 16, 430. [Google Scholar] [CrossRef] [PubMed]
- Jamone, L.; Metta, G.; Nori, F.; Sandini, G. James: A humanoid robot acting over an unstructured world. In Proceedings of the 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006. [Google Scholar]
- Kappassov, Z.; Baimukashev, D.; Adiyatov, O.; Salakchinov, S.; Massalin, Y.; Varol, H.A. A series elastic tactile sensing array for tactile exploration of deformable and rigid objects. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 520–525. [Google Scholar]
- Silva, A.; Brites, M.; Paulino, T.; Moreno, P. Estimation of lightweight object’s mass by a humanoid robot during a precision grip with soft tactile sensors. In Proceedings of the 3rd IEEE International Conference on Robotic Computing, Naples, Italy, 25–27 February 2019. [Google Scholar]
- Bicchi, A. A criterion for optimal design of multi-axis force sensors. Rob. Auton. Syst. 1992, 10, 269–286. [Google Scholar] [CrossRef][Green Version]
- Ruther, P.; Spinner, S.; Cornils, M.; Paul, O. Cantilever-based tactile sensor with improved sensitivity for dimensional metrology of deep narrow drillings. In Proceedings of the TRANSDUCERS and EUROSENSORS ’07—4th International Conference on Solid-State Sensors, Actuators and Microsystems, Lyon, France, 10–14 June 2007; pp. 1469–1472. [Google Scholar]
- D’Amore, A.; De Maria, G.; Grassia, L.; Natale, C.; Pirozzi, S. Silicone-rubber-based tactile sensors for the measurement of normal and tangential components of the contact force. J. Appl. Polym. Sci. 2011, 122, 3757–3769. [Google Scholar] [CrossRef]
- Kang, M.K.; Lee, S.; Kim, J.H. Shape optimization of a mechanically decoupled six-axis force/torque sensor. Sens. Actuators A Phys. 2014, 209, 41–51. [Google Scholar] [CrossRef]
- Hammond, F.L.; Kramer, R.K.; Wan, Q.; Howe, R.D.; Wood, R.J. Soft tactile sensor arrays for force feedback in micromanipulation. IEEE Sens. J. 2014, 14, 1443–1452. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Chamber dimension optimization of a bellow-type soft actuator for food material handling. In Proceedings of the IEEE International Conference on Soft Robotics, Livorno, Italy, 24–28 April 2018; pp. 382–387. [Google Scholar]
- Wang, Z.; Hirai, S. Geometry and material optimization of a soft pneumatic gripper for handling deformable object. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 612–617. [Google Scholar]
- Winstone, B.; Griffiths, G.; Melhuish, C.; Pipe, T.; Rossiter, J. TACTIP—Tactile fingertip device, challenges in reduction of size to ready for robot hand integration. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics, Guangzhou, China, 11–14 December 2012; pp. 160–166. [Google Scholar]











| No. | Design | P1 (mm) | P2 (mm) | Displacement (mm) |
|---|---|---|---|---|
| 1 | A | 9.0 | 5.5 | 0.562 |
| 2 | B | 10.0 | 6.5 | 0.536 |
| 3 | C | 8.5 | 4.5 | 0.549 |
| 4 | D | 10.0 | 4.5 | 0.770 |
| Design | Average Error Using PFM (°) | Average Error Using FNN (°) |
|---|---|---|
| A | 1.584 | 1.185 |
| B | 2.063 | 1.671 |
| C | 1.908 | 1.044 |
| D | 1.052 | 0.779 |
| Trained Object Orientation | Untrained Object Orientation | |||||||
|---|---|---|---|---|---|---|---|---|
| 0° | 10° | 20° | 30° | 5° | 15° | 25° | ||
| Intuitive design, Design A | Average error (°) | 1.35 | 1.05 | 4.15 | 3.99 | 4.13 | 0.51 | 2.04 |
| Overall average error (°) | 2.64 | 2.23 | ||||||
| Optimal design, Design D | Average error (°) | 1.28 | 2.65 | 1.42 | 1.75 | 1.02 | 2.45 | 1.97 |
| Overall average error (°) | 1.78 | 1.81 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosle, M.H.; Wang, Z.; Hirai, S. Geometry Optimisation of a Hall-Effect-Based Soft Fingertip for Estimating Orientation of Thin Rectangular Objects. Sensors 2019, 19, 4056. https://doi.org/10.3390/s19184056
Rosle MH, Wang Z, Hirai S. Geometry Optimisation of a Hall-Effect-Based Soft Fingertip for Estimating Orientation of Thin Rectangular Objects. Sensors. 2019; 19(18):4056. https://doi.org/10.3390/s19184056
Chicago/Turabian StyleRosle, Muhammad Hisyam, Zhongkui Wang, and Shinichi Hirai. 2019. "Geometry Optimisation of a Hall-Effect-Based Soft Fingertip for Estimating Orientation of Thin Rectangular Objects" Sensors 19, no. 18: 4056. https://doi.org/10.3390/s19184056
APA StyleRosle, M. H., Wang, Z., & Hirai, S. (2019). Geometry Optimisation of a Hall-Effect-Based Soft Fingertip for Estimating Orientation of Thin Rectangular Objects. Sensors, 19(18), 4056. https://doi.org/10.3390/s19184056






