1. Introduction
The LoRa (Low-Power Long-Range) modulation technique is an excellent solution for many internet-of-things (IoT) applications due to its excellent energy consumption, link robustness and long-range capabilities at the expense of low bit rates [
1,
2]. LoRa uses a modified form of chirp spread spectrum (CSS) modulation, wherein the carrier frequency of a sinusoid is linearly varied across a specific bandwidth. This results in a set of signals known as chirps [
3], which are distinguishable by their starting frequencies.
The behavior of a LoRa chirp is controlled by both the spreading factor,
, and the bandwidth parameter,
. The spreading factor is an integer value, typically ranging from 6 to 12, while the specified bandwidth can be chosen from values in the range of
to 500 kHz [
4,
5]. Each chirp (or symbol) is encoded with
bits, which means that there are
possible symbol values, where
M is the modulation order [
6]. The instantaneous frequency of a chirp linearly increases or decreases across the bandwidth specified by
over the symbol duration [
3]. The tradeoff between the range capabilities and the nominal bit rate depends on
and
. For instance, high
and low
allow for higher receiver sensitivity, but at a lower bit rate, whereas low
and high
lead to reduced receiver sensitivity, but a higher bit rate.
As the demand for long-range, low-power IoT devices increases, so does the need to improve the spectral efficiency of these devices’ transmission. One promising solution is to implement a set of pulse shaping and matched square-root raised cosine (SRRC) filters in LoRa transmitters and receivers, respectively. The use of these filters can significantly reduce the bandwidth containing 99% of the total mean signal power while also reducing the out-of-band emissions created by LoRa devices [
6,
7,
8]. The increase in spectral efficiency allows us to accommodate a larger number of IoT devices.
The challenge is that since LoRa devices are characterized by their low complexity, it is more difficult to justify the added resources required for filtering, especially when longer filters are required (which is often the case for LoRa devices with lower bandwidth settings [
8]). Since the cost of implementing multipliers in hardware can prove significant, a preferred solution should eliminate the need for multiplications altogether. As such, the main objective of this paper is to investigate the feasibility of implementing a “multiplier-less” pulse shaping filter in a LoRa transmitter.
Replacing hardware multipliers in a pulse-shaping filter can be done with a look-up table (LUT), provided there is a finite number of input sample values to the filter that are known. Instead of multiplying each incoming sample by a filter coefficient using a hardware multiplier, the result of every possible multiplication can be precalculated and stored in the LUT. Then, the LUT can output the correct product of the required multiplication based on the associated input sample value. The size of the LUT depends on both the number of unique input sample values and the filter length. In such an implementation, the complexity of the filter is measured by the cost of the memory instead of hardware multipliers.
The problem with LoRa is that since discrete-time LoRa chirps are made up of samples, the multiplier-less filter must be able to accommodate the M possible input values for each chirp waveform. Furthermore, implementing multiple settings and ensuring the continuous phase of modulated chirp waveforms exponentially increase the already large number of unique filter inputs. While many of the chirp sample values are repeated among spreading factors and/or symbol values, the memory requirement of the LUT is still significant. The LoRa end-devices are particularly constrained by the additional memory requirements as these devices have a greater need for low energy consumption and few complex operations than the LoRa gateway.
In this paper, two methods of optimizing LoRa transmitters are proposed in order to reduce the complexity of filtering. First, waveform segmentation is used to generate an entire basic LoRa chirp waveform from only a portion of the total number of chirp samples in order to reduce the size of the chirp generation ROM. While this does not directly impact the LUT size, it reduces the overall memory requirement. This method is inspired by the CSS transceiver design presented in [
9] and it has been adapted for LoRa.
The second method involves quantizing the LoRa chirp samples to a significant degree so as to reduce the number of unique input values to the multiplier-less filter, which helps to reduce the LUT size. While chirp segmentation does not add any error, quantization adds some rounding errors to the quantized chirp signals. It is important to ensure that the desired sample reduction can be achieved without significant performance degradation.
The feasibility of implementing a multiplier-less SRRC pulse shaping filter in a LoRa transmitter will be evaluated in terms of the tradeoff between the potential sample reduction and impact of quantization noise on the performance. In order to quantify the effectiveness of the sample reduction, the number of samples required to form LoRa chirp waveforms and subsequent filtered signals shall be compared to that of an unoptimized LoRa device. The degree of sample reduction, therefore, depends on which spreading factors are supported, the length of the pulse shaping filter, if chirp segmentation is used, and the quantization step size (if any).
Finally, the performance of the system will be evaluated for LoRa signals with various degrees of quantization. A LoRa communication system is simulated in Matlab, and the performance is evaluated in terms of the occupied bandwidth (OBW) of transmitted LoRa signals, the output of the fast Fourier transform (FFT) performed for symbol demodulation, and the bit-error-rate (BER). The goal is to find appropriate levels of quantization in order to significantly reduce the overall memory requirement while maintaining excellent performance.
2. Sample Reduction Methods
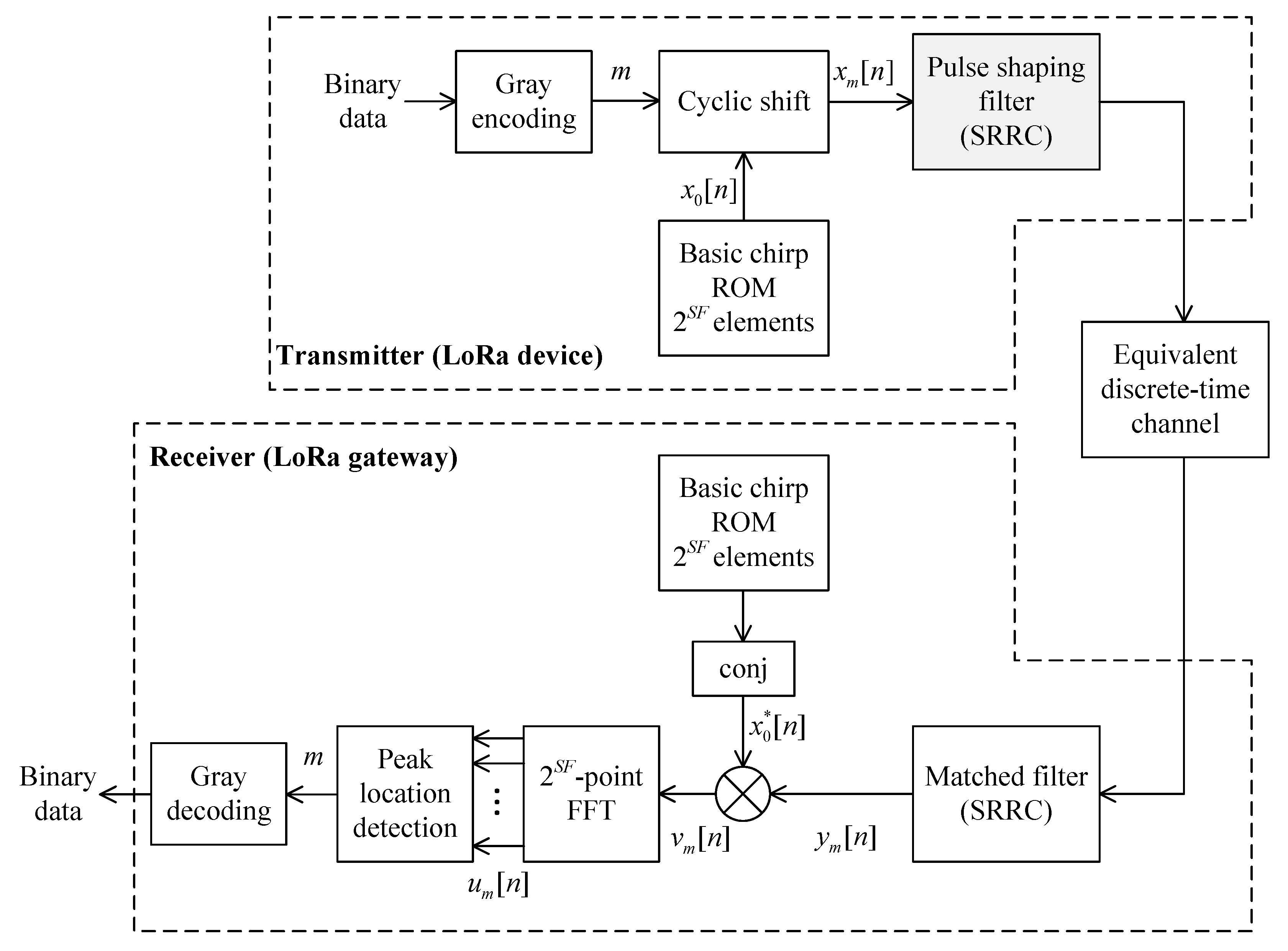
Figure 1 illustrates a block diagram of a LoRa system that implements a pulse shaping filter at the transmitter and a matched filter at the receiver. While the performance benefits brought by implementing these filters are demonstrated in detail in [
6,
8], this paper focuses on reducing the complexity of implementing the pulse shaping filter in a LoRa end device’s transmitter.
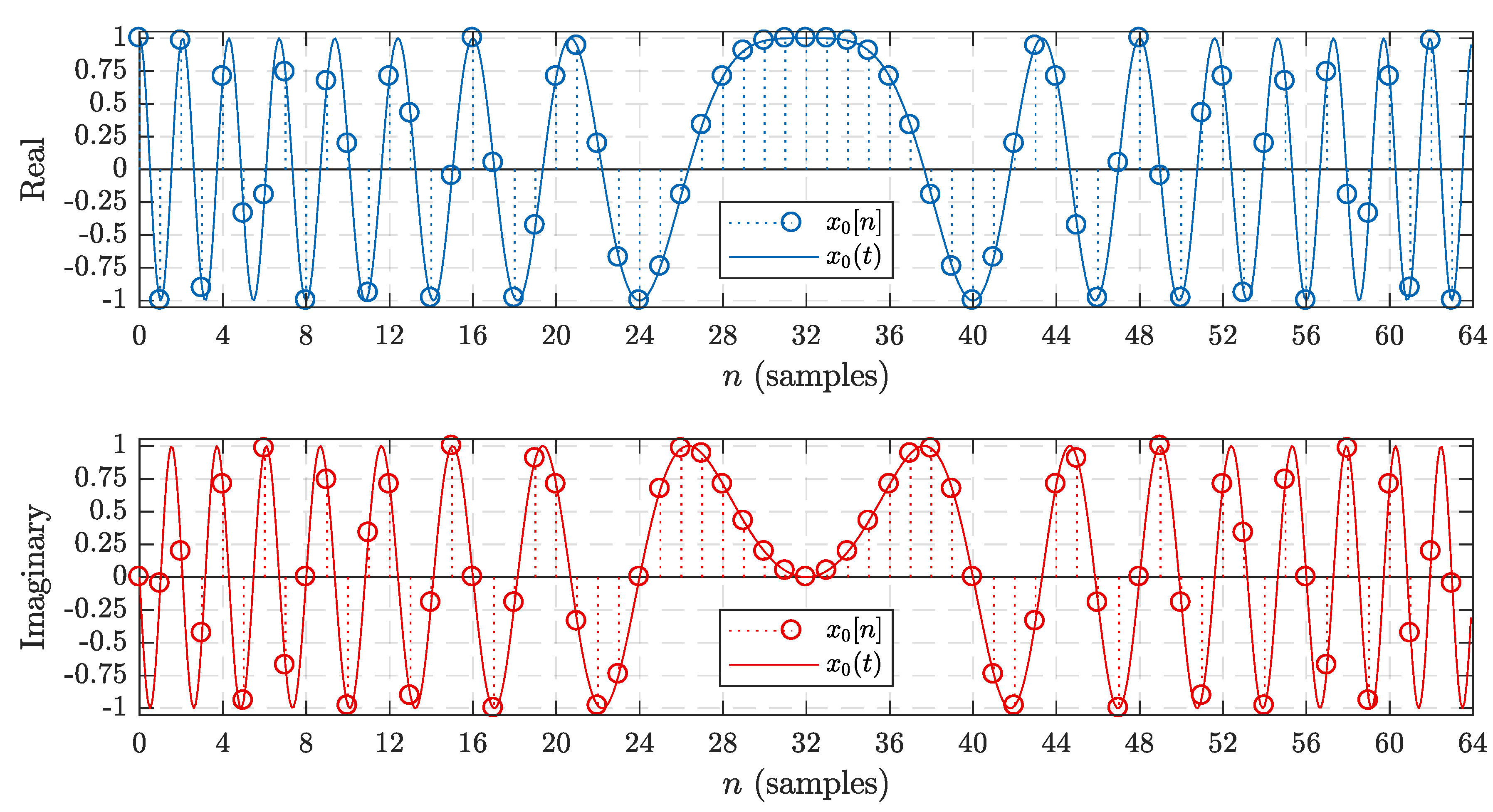
Basic LoRa chirp waveforms are used as the basis for the LoRa modulation technique. They are used in both the preamble and payload of transmitted LoRa packets. The expression for a continuous-time basic LoRa chirp waveform is shown in (
1), where
is the symbol duration in seconds and
is the chirp rate in Hz/second. The continuous-time chirp waveform is then sampled at a rate of
for digital implementation [
6]. The expression for a discrete-time basic LoRa chirp is given below in (2), where
. As an example,
Figure 2 plots the real and imaginary components of both
and
with
and
kHz.
LoRa symbols are modulated by cyclically shifting the basic chirp waveform by the symbol value,
m, as shown in (
3).
Furthermore, in order to maintain the phase continuity between subsequent chirps, each modulated chirp waveform obtained from (
3) is multiplied by the complex conjugate of its first sample,
. This causes the instantaneous phase of the chirp to be zero at both the beginning and end of the symbol duration, rather than causing sharp phase discontinuities between consecutive modulated chirps [
3,
6]. Performing phase correction changes the modulated chirp waveform expression given by (
3) to that of (
4).
While performing the complex multiplication will not affect the number of samples required for chirp generation, it will drastically affect the number of unique filter inputs. However, as in the case of basic chirp samples, it turns out that many phase-corrected sample values are shared among multiple settings, as well as modulated chirp waveforms associated with other symbols.
In terms of implementation, the real and imaginary components are considered separately as they correspond to the I and Q channels in a practical system. However, since the magnitude of at each sample index is always equal to 1, the sequence of sample values for the I and Q channels are subject to the same patterns. Therefore, the properties discussed in this paper that are used to simplify the chirp generation shall apply to both the real and imaginary samples of . Both components also contain the same sample values, albeit the signs and sample indices may differ.
With that in mind, the following subsections detail the proposed methods and the resulting sample reduction compared to a standard LoRa device. It is also important to note that while basic chirp samples obtained from (2) are used for chirp generation, the LUT must account for each possible phase-corrected modulated chirp sample obtained from (
4).
2.1. Chirp Waveform Segmentation
It is perhaps more intuitive to begin by examining the inherent symmetry in the sequence of
basic chirp samples that make up the waveform. For instance, consider the basic chirp waveform shown in
Figure 2 once again. Both components appear to exhibit a symmetry about the midpoint located at
, which is
in this case.
While it may not be obvious from
Figure 2, there are several other patterns present in the sequence of chirp sample values as well. A close inspection reveals that a basic chirp waveform can be divided into four segments, each containing
samples according to (
5) and (6), where
k is an integer representing the segment number. More importantly, each of these segments contains identical sample values, but they differ with predictable patterns of opposing signs and/or sample order.
Using (
5) with (2) gives the exponential form of
shown in (
7). Substituting each value of
k into (
7) gives the individual waveform segment expressions shown in (8).
As an example, consider the basic chirp sample values of
by segments for
shown in
Table 1. It is important to note that while the analysis below refers to this specific set of data, the following relationships between segments hold for all
settings.
The first segment,
, can be manipulated in order to obtain the remaining three segments with relatively simple operations. First, consider segments 1 and 3. It is obvious from
Table 1 that every odd sample of
has the opposite sign of
at the same sample index value,
n. This relationship can be obtained mathematically by comparing the expressions for
and
in (8) as shown below.
Next, consider the relationship between segments 1 and 4. It is simple to see that
is a reverse indexed copy of
. This can be proven by first finding
as shown below, and then comparing the resulting expression to that of
.
Lastly,
is a reverse indexed copy of
with opposing signs at every odd value of
n. This is confirmed by the following comparison between the expressions for
and
.
In summary,
,
, and
can be found from
using (
9)–(11), respectively. These relationships can be used to generate the
M basic chirp waveform samples from only the first
samples in
. As a result, the number of samples stored in the ROM can be reduced from a total of
to
real and imaginary samples without introducing any error.
In order to quantify the impact of chirp segmentation on the complexity of a practical system, the actual number of real and imaginary samples contained in the ROM and LUT must be considered. Let
represent the number of samples required for chirp generation, while
represents the number of unique samples at the input of the pulse shaping filter. The calculated values of
and
are shown in
Table 2 for a LoRa system using the chirp segmentation method. It should be pointed out that “all” means the support of spreading factors ranging from 6 to 12 in the scope of the study. Here,
is calculated as
, while
is found by counting the number of unique sample values given by (
4) for each possible symbol value. Furthermore,
is counted based on the absolute (unsigned) value of each sample value. This is because the sign of the input samples to the filter can be easily detected and the sign of the corresponding LUT output can be corrected accordingly (by taking the two’s complement), if necessary.
The number of samples required in the filter LUT depends on both the number of filter coefficients (
) and
. The output values of the LUT are found by multiplying each filter coefficient by each unsigned filter input value. Since the filter coefficients are symmetric about the midpoint of the filter, the number of stored multiplications can be reduced to just over half the number of filter coefficients instead. As a result, the total number of samples that must be stored in the transmitter for each spreading factor can be found using (
12). It should be noted that the filter input value of zero included in
can be disregarded since the output of the coefficient multiplication(s) will simply be zero as well.
As an example,
Table 3 displays the total numbers of samples required for three different systems calculated with (
12). This example considers a standard LoRa device that does not use chirp segmentation or a multiplier-less filter (
), and two devices using chirp segmentation with length-17 and 81 multiplier-less SRRC filters, respectively. The filter lengths were selected based on their ability to reduce the occupied bandwidth of LoRa signals for different
settings [
8]. When supporting individual spreading factors, the length-17 filter requires almost double the number of stored samples compared to the standard system. However, when supporting multiple spreading factors, the difference is not as substantial. Furthermore, if the standard device implements filtering with hardware multipliers, it will require the use of at least
multipliers for the filter in addition to the samples provided in
Table 3.
In this regard, chirp segmentation improves the feasibility of implementing the length-17 filter without significant resource usage. For accommodating longer filters, the use of chirp segmentation alone does not provide a significant reduction in complexity due to the large number of samples. However, these results were obtained by modelling the system with a very small quantization step size (i.e., Matlab precision) in order to exactly represent the theoretical response. If the quantization step size is increased, it is possible to reduce the number of unique filter input values in order to accommodate the use of longer filters. This is discussed further in the next section.
2.2. Quantization
In order to implement a practical LoRa system, some level of quantization is necessary to represent the LoRa chirp signals. Since the chirp sample values are normally between , two integer bits are needed to represent a signed chirp signal. Thus, only the number of fractional bits can be varied and investigated. Let B represent the number of fraction bits used for the system such that the uniform quantization step size is .
Assuming the use of chirp segmentation, the values of
will be those found in
Table 2 as before. However,
depends on the quantization factor, i.e., the number of fraction bits,
B.
Table 4 contains the values of
found for five different values of
B, namely 2, 4, 6, 8, and 10 bits.
Once again, the total number of samples required to implement the LoRa transmitter for each quantization factor can be found from (
12). The calculated values of
for LoRa devices utilizing chirp segmentation and quantization are shown in
Table 5 and
Table 6 with filter lengths of 17 and 81 taps, respectively. Note that the results for the standard system do not change with quantization.
By comparing the results in
Table 5 and
Table 6 with that of
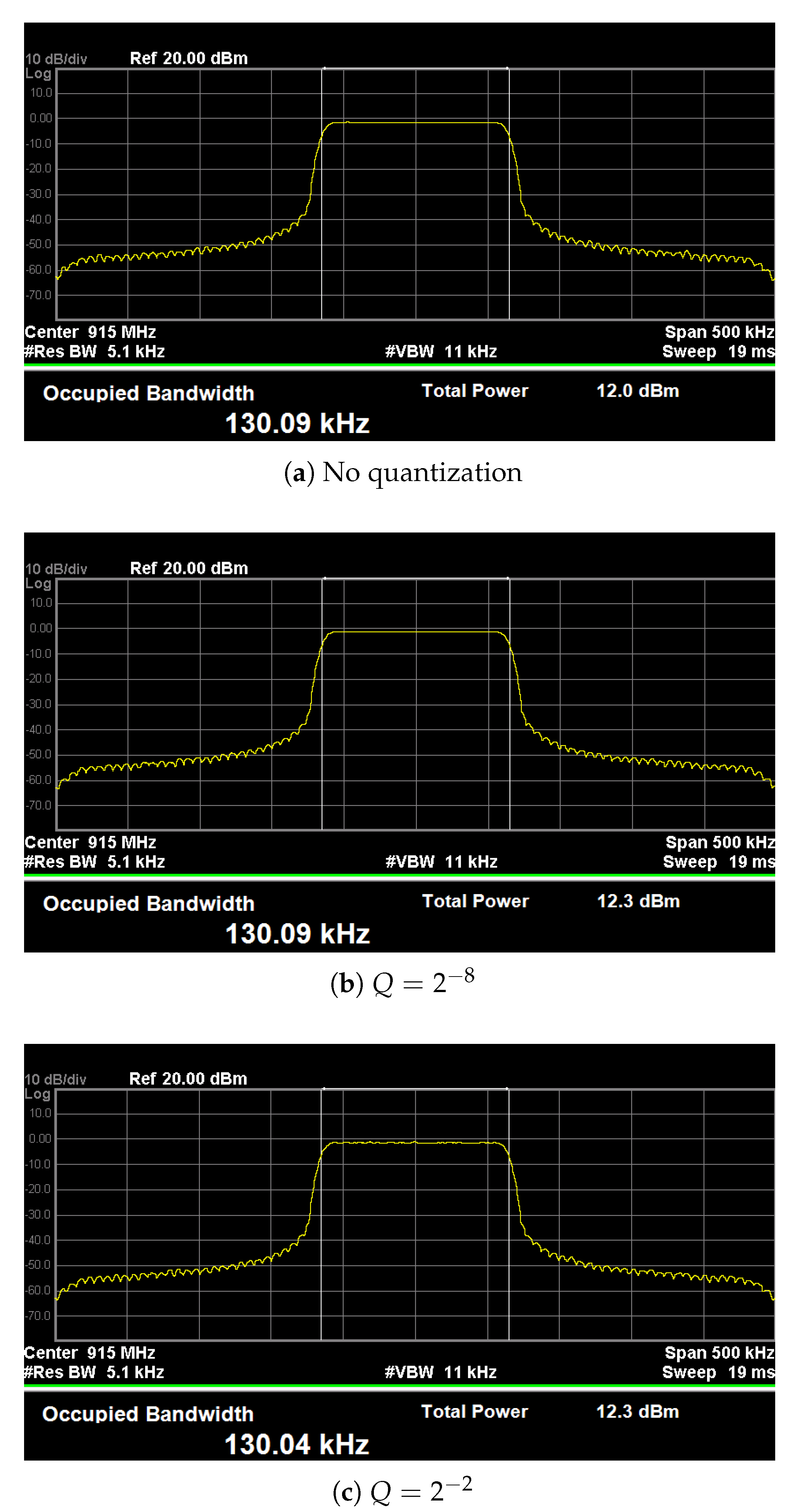
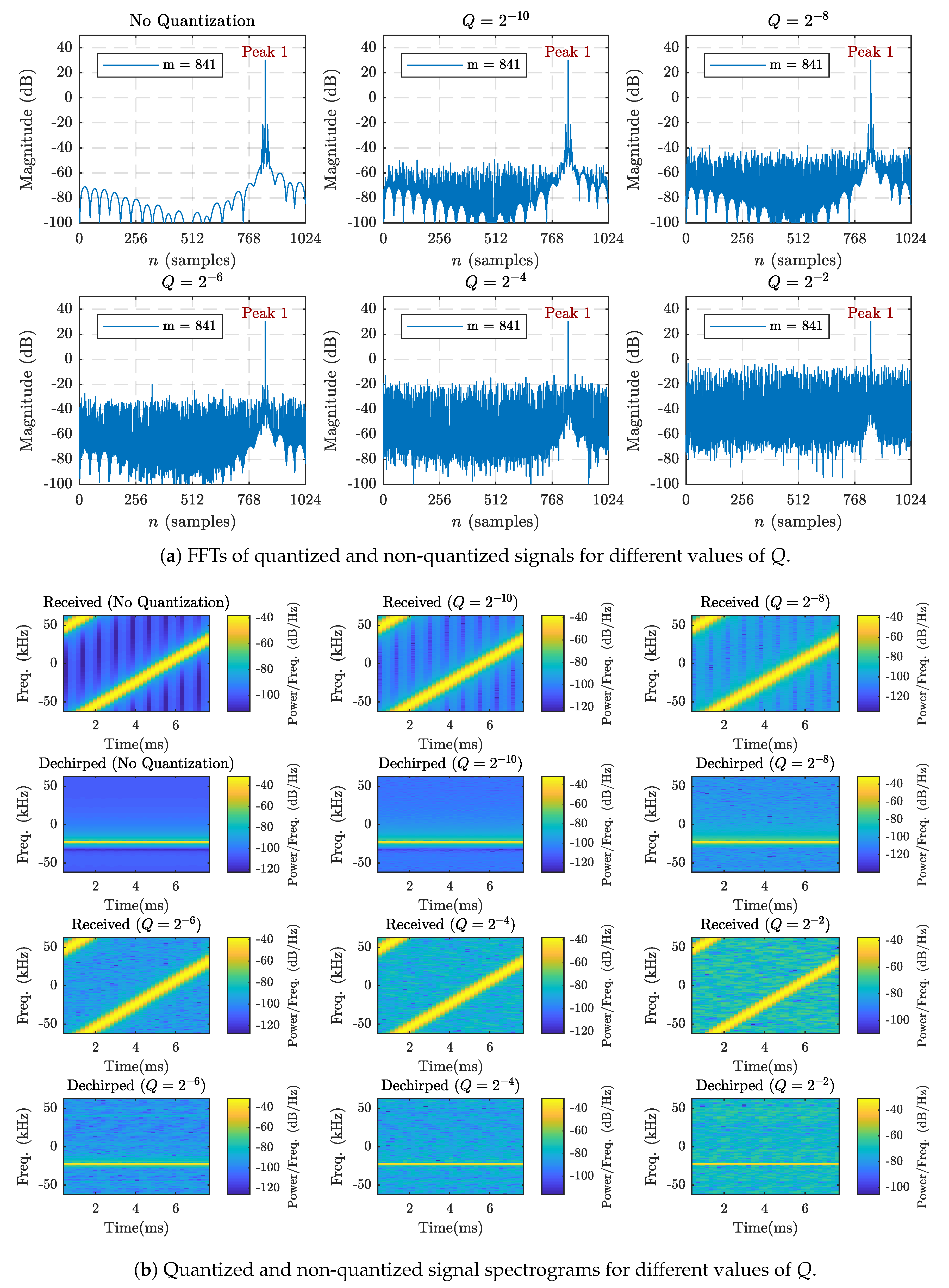
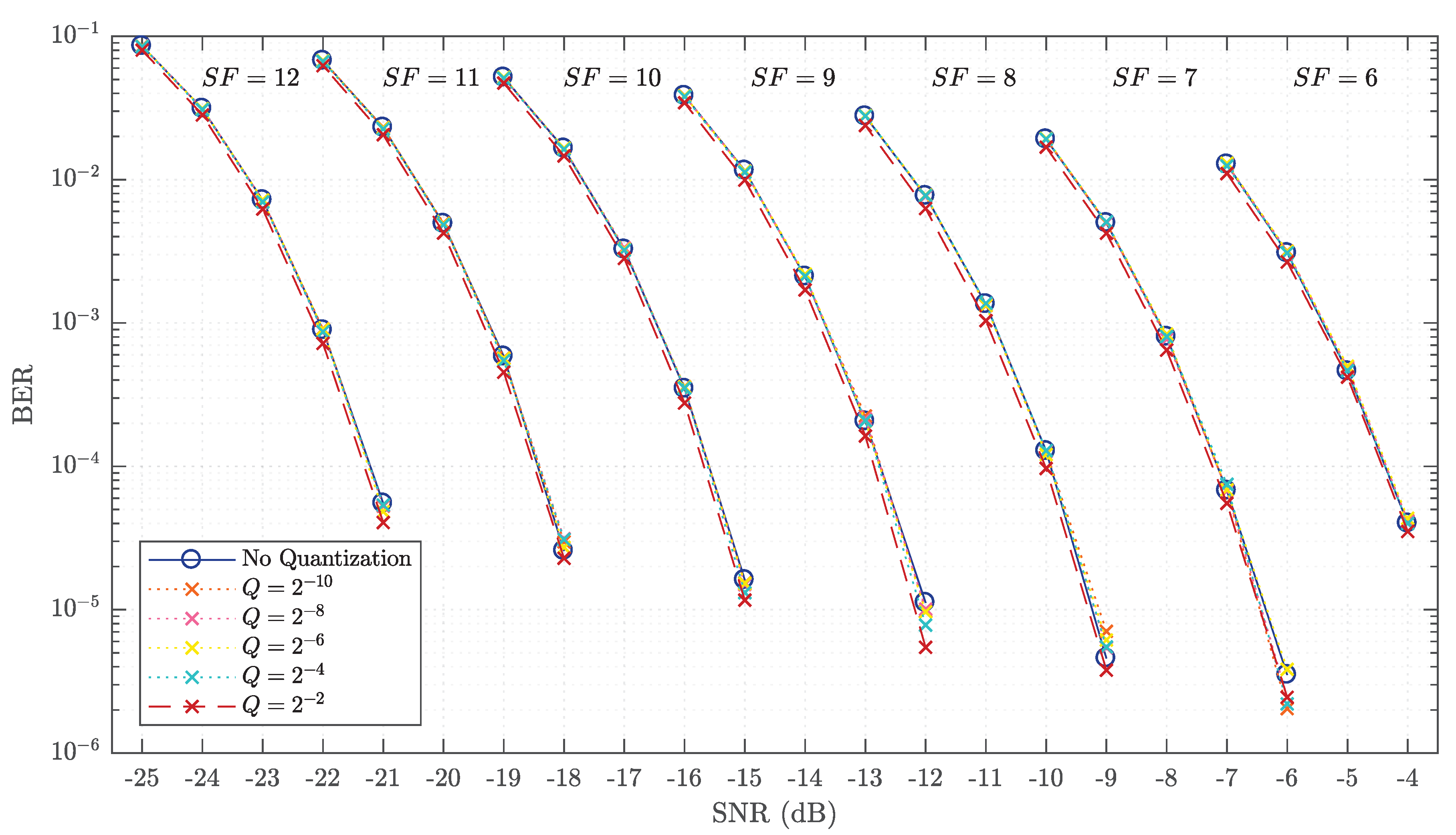
Table 3, it is clear that quantization provides a more significant reduction in stored samples than using chirp segmentation alone. In fact, using chirp segmentation and quantization not only can match, but improve upon the results obtained for a standard system that does not use multiplier-less filtering. Representing the real and imaginary chirp samples with 8-bit fractional precision for both cases of filters would be an appropriate solution in this regard. Not only is there a significant sample reduction from the standard case, but no hardware multipliers would be required. The main concern with quantizing the LoRa chirp signals is the potential impact on the decoding performance. The performance results and comparison presented in the next section shall remove this concern.
4. Conclusions
Two methods were presented to reduce the complexity of implementing multiplier-less SRRC pulse shaping filters in LoRa transmitters. These methods focus on reducing the required number of samples in the ROM used to generate basic chirp signals, as well as those required for the multiplier-less filter LUT. Chirp segmentation can be used to generate the entire basic LoRa chirp waveform from only a quarter of its samples without adding any additional error to the signal. Quantization can also be used to exponentially decrease the number of unique samples at the input to the multiplier-less pulse shaping filter at the cost of introducing small errors to the transmitted signal.
Using both methods allows for a reduction in the number of stored samples so as to not only match, but also improve upon the results obtained from a standard LoRa device that does not contain a multiplier-less filter. For example, a system using 10-bit fractional precision and a length-17 multiplier-less pulse shaping filter requires fewer samples to be stored in memory compared to a standard LoRa system when supporting spreading factors 6 to 12. Even a device with a length-81 filter requires fewer stored samples than a standard device by quantizing the LoRa chirp samples to 8 fractional bits.
Furthermore, it was shown that moderate levels of quantization do not hinder the decoding performance of LoRa devices, even under harsh channel conditions. Therefore, the quantization factor can be chosen based on the complexity requirements of the system. For example, devices intended for long-range communication require larger spreading factors and, as a result, a higher quantization factor to compensate for the added complexity. In conclusion, using the proposed sample reduction methods can aid in further alleviating the complexity concerns associated with implementing SRRC filters in LoRa devices.