A Lightweight Leddar Optical Fusion Scanning System (FSS) for Canopy Foliage Monitoring
Abstract
1. Introduction
2. Materials and Methods
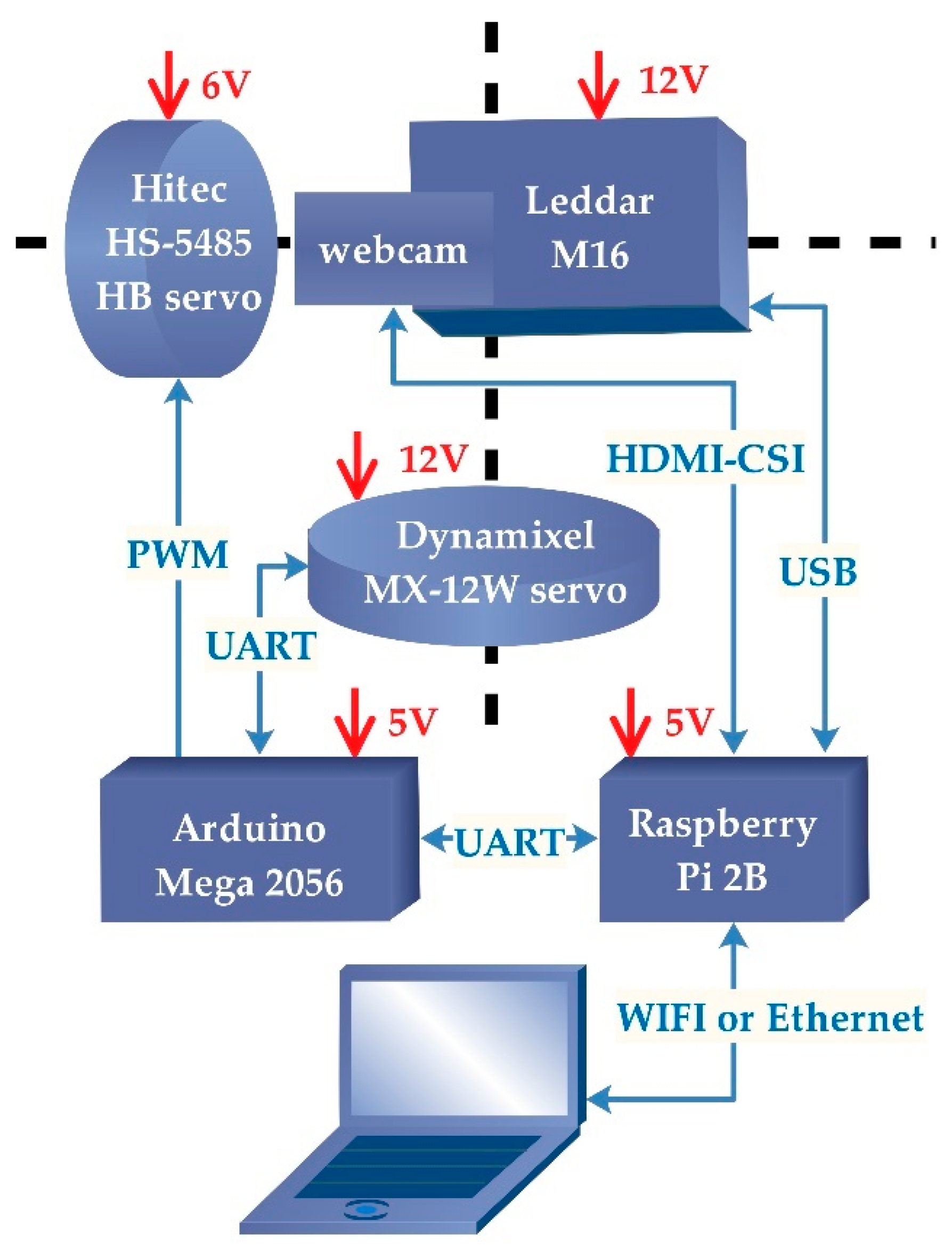
2.1. Hardware Customization and Data Processing Framework
2.2. Coordinate System Conversion for Calibration
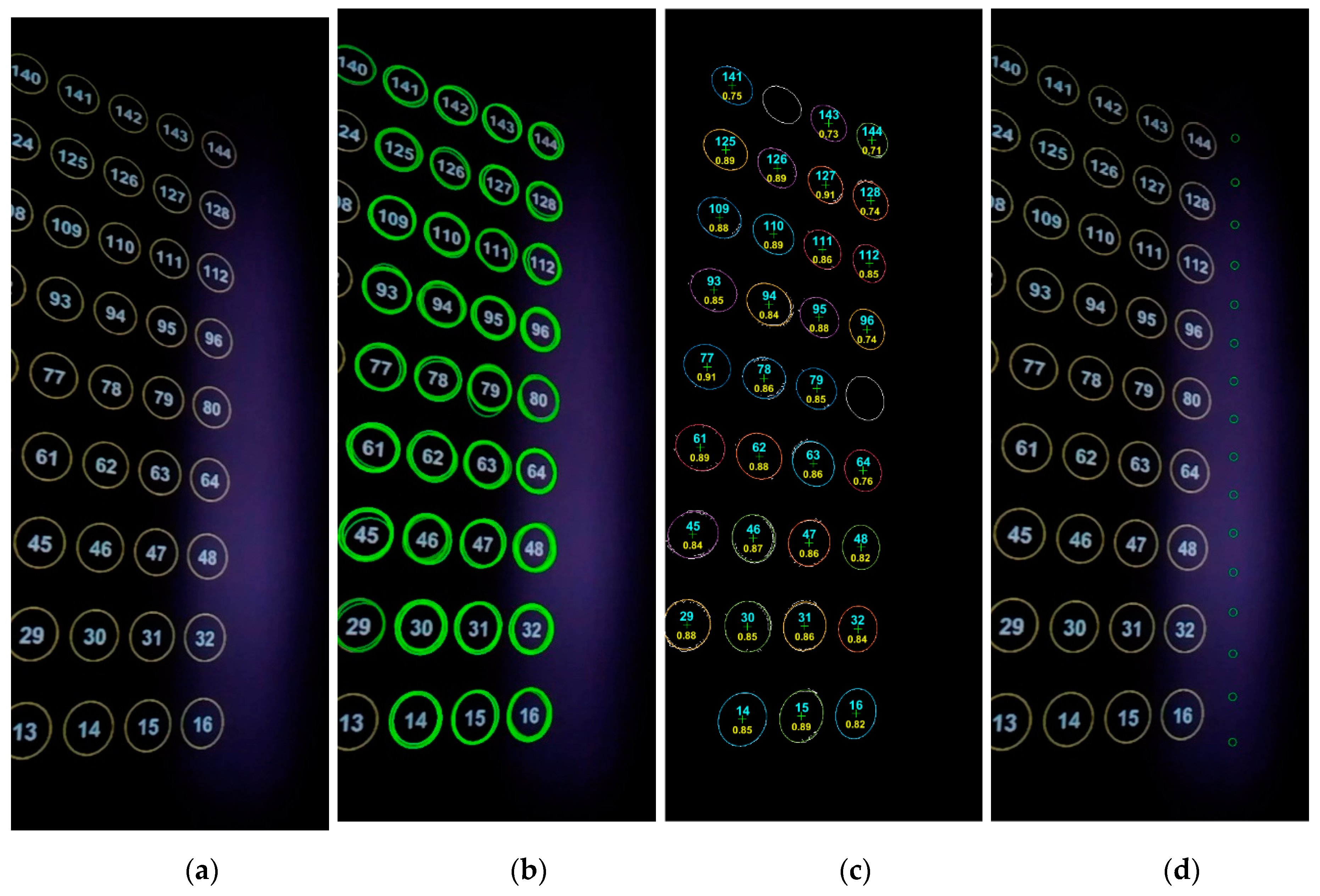
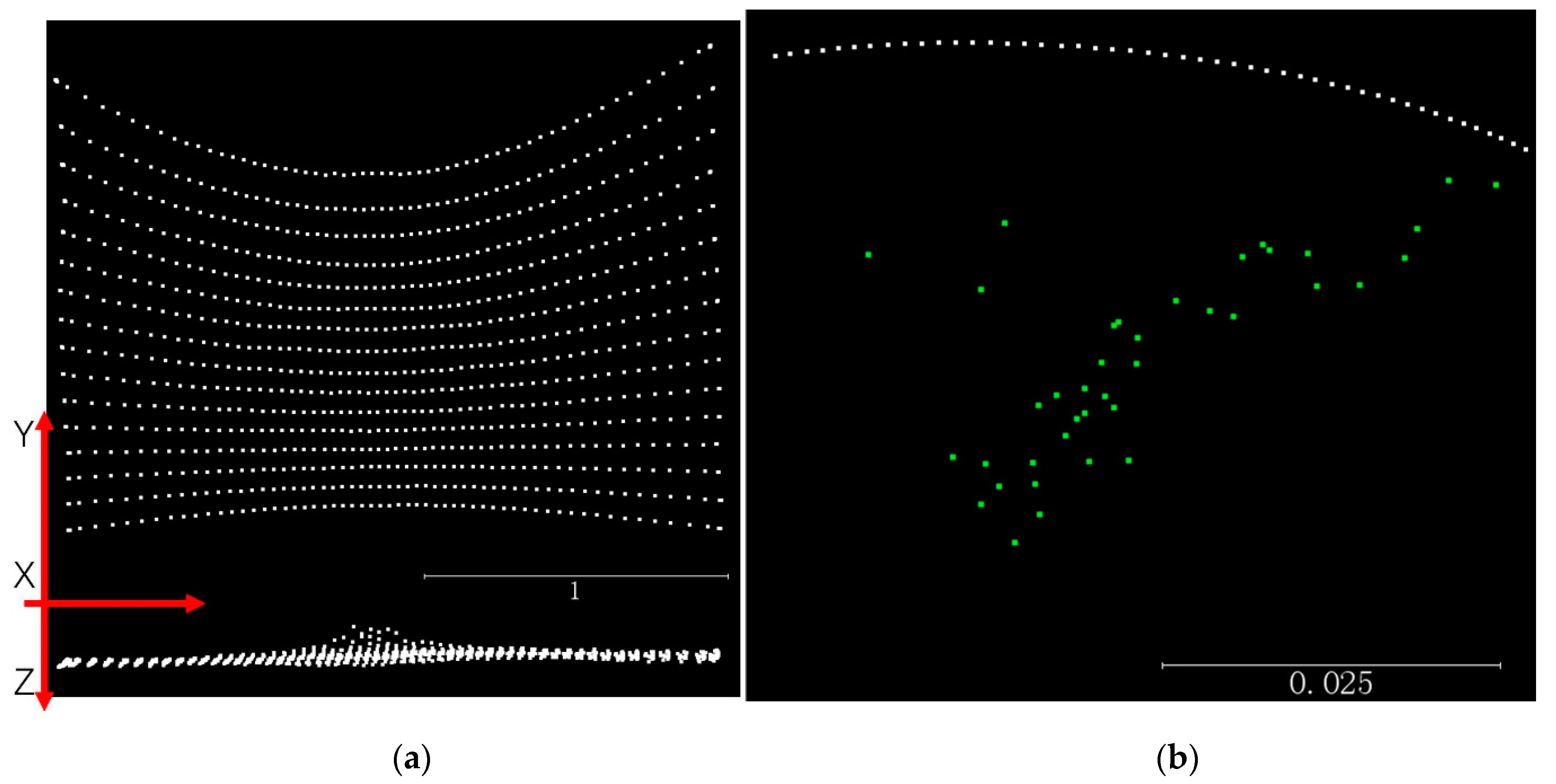
2.3. Calibration Experiment
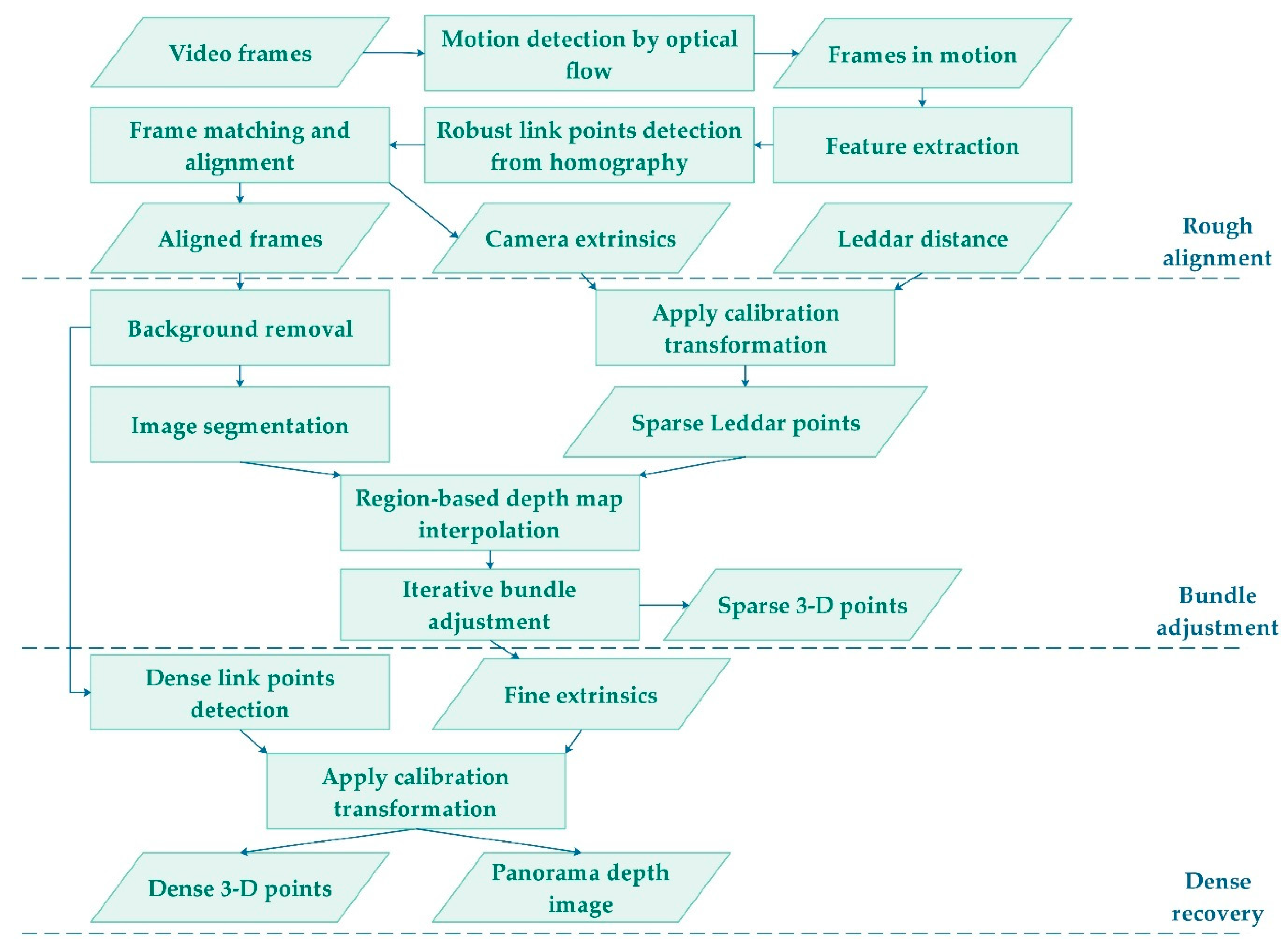
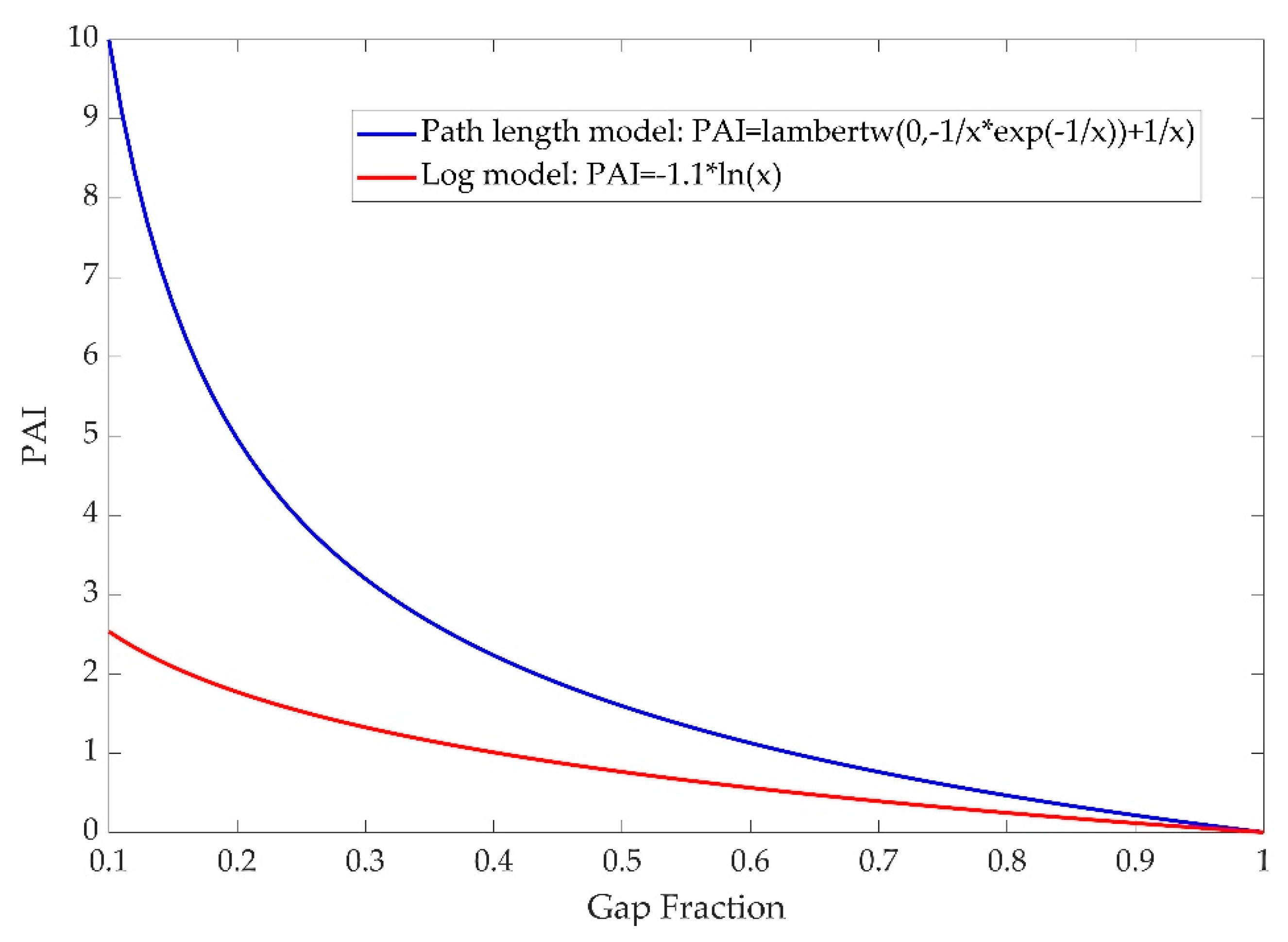
2.4. Fusion-Based Dense Point Cloud Recovery from FSS
2.5. Application: Tracking the Autumn Leaf Drop Processes with the FSS
3. Results and Discussion
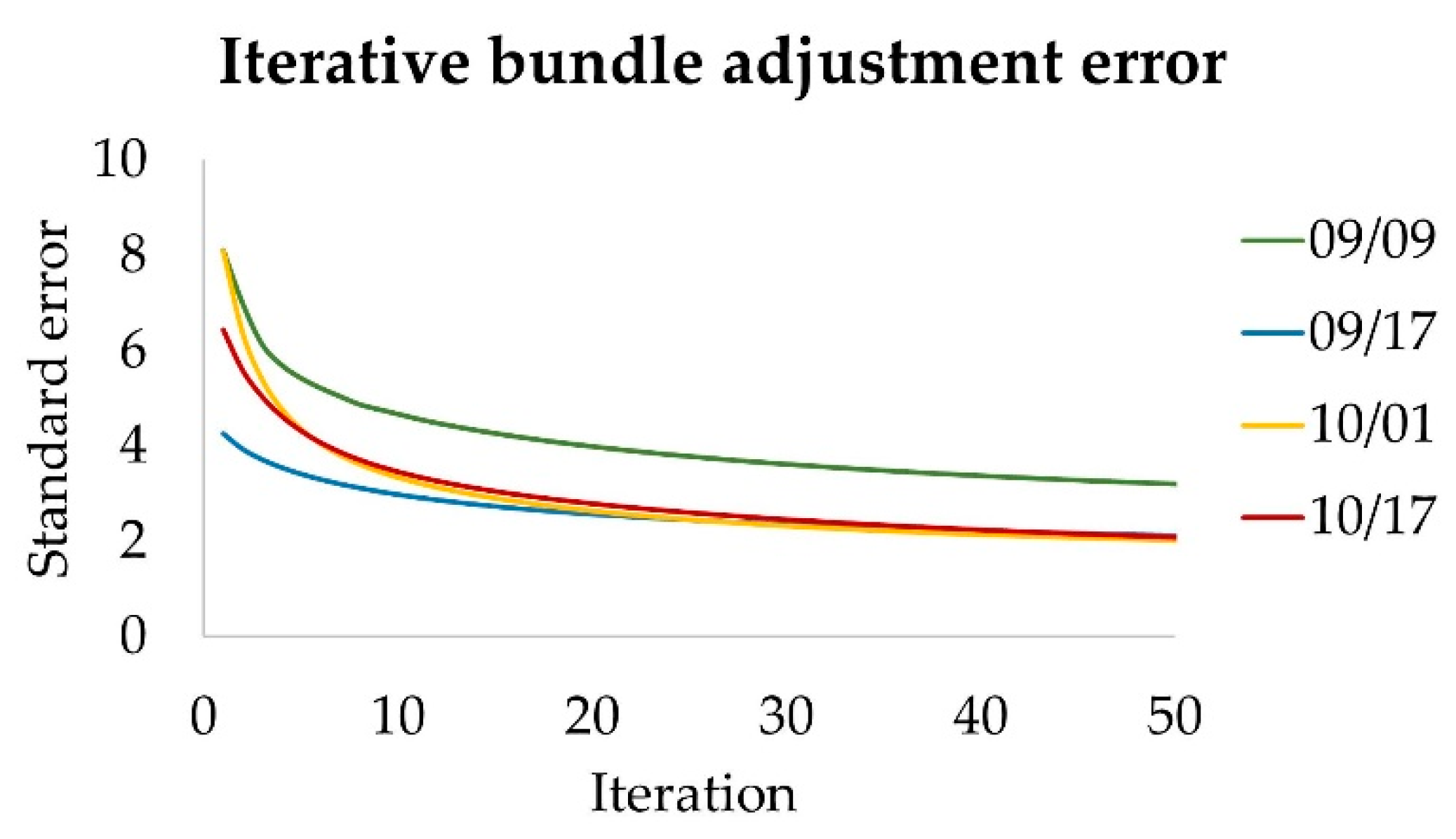
3.1. Calibration
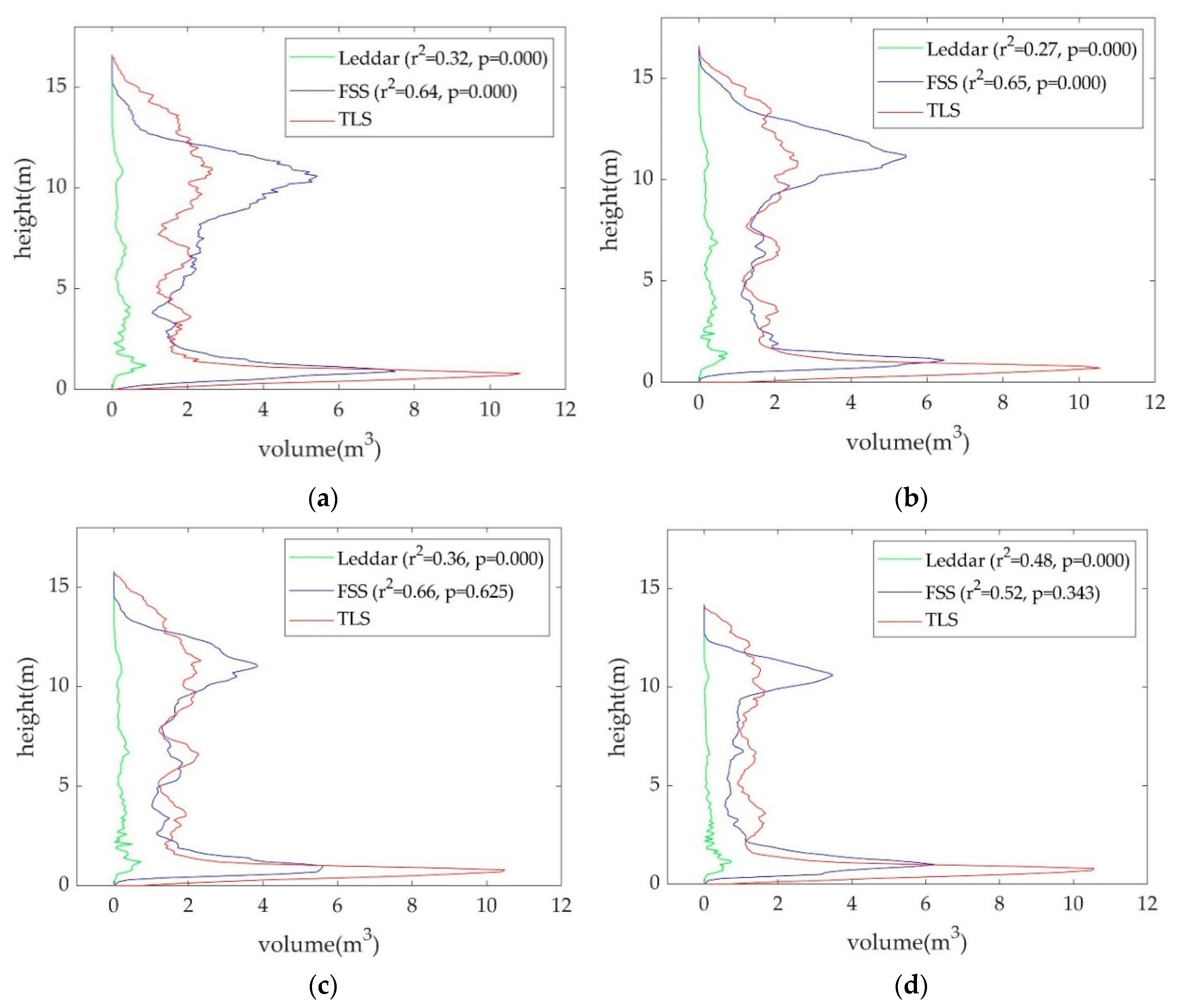
3.2. Fusion-Based Dense 3D Recovery
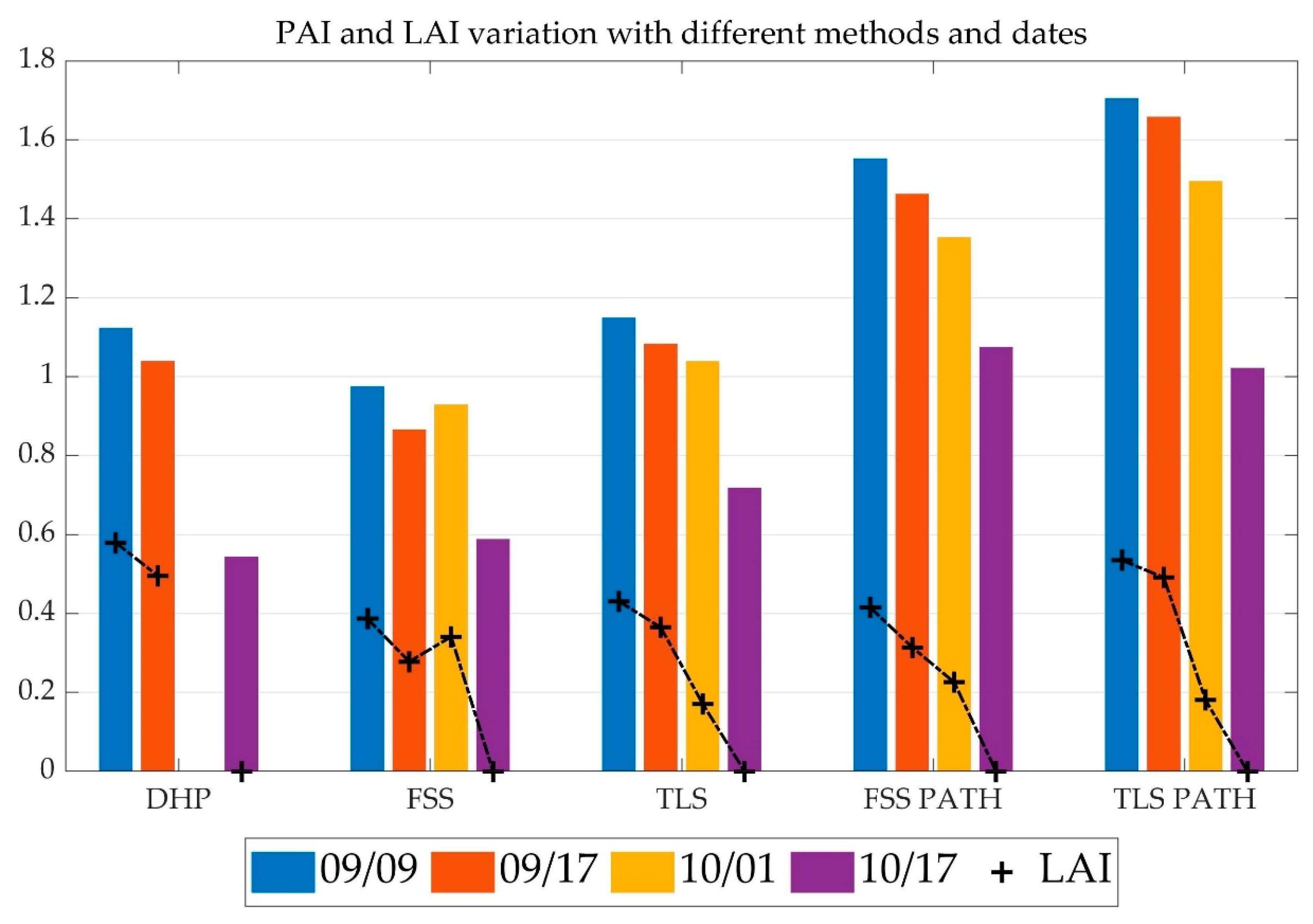
3.3. Tracking Changes of Canopy Vertical Volume Profile, PAI, and LAI
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- van der Sande, M.T.; Zuidema, P.A.; Sterck, F. Explaining biomass growth of tropical canopy trees: The importance of sapwood. Oecologia 2015, 177, 1145–1155. [Google Scholar] [CrossRef] [PubMed]
- Sumida, A.; Watanabe, T.; Miyaura, T. Interannual variability of leaf area index of an evergreen conifer stand was affected by carry-over effects from recent climate conditions. Sci. Rep. 2018, 8, 13590. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Ryu, Y.; Jiang, C.; Hwang, Y. Continuous observation of vegetation canopy dynamics using an integrated low-cost, near-surface remote sensing system. Agric. For. Meteorol. 2019, 264, 164–177. [Google Scholar] [CrossRef]
- de Wit, C.T. Photosynthesis of Leaf Canopies. 1965. Available online: https://library.wur.nl/WebQuery/wurpubs/413358 (accessed on 11 September 2019).
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Springer Netherlands: New York, NY, USA, 1981. [Google Scholar]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Zhao, K.; García, M.; Liu, S.; Guo, Q.; Chen, G.; Zhang, X.; Zhou, Y.; Meng, X. Terrestrial lidar remote sensing of forests: Maximum likelihood estimates of canopy profile, leaf area index, and leaf angle distribution. Agric. For. Meteorol. 2015, 209, 100–113. [Google Scholar] [CrossRef]
- Li, Y.; Su, Y.; Hu, T.; Xu, G.; Guo, Q. Retrieving 2-D leaf angle distributions for deciduous trees from terrestrial laser scanner data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4945–4955. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving leaf area index (LAI) estimation by correcting for clumping and woody effects using terrestrial laser scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Hopkinson, C.; Lovell, J.; Chasmer, L.; Jupp, D.; Kljun, N.; van Gorsel, E. Integrating terrestrial and airborne lidar to calibrate a 3D canopy model of effective leaf area index. Remote Sens. Environ. 2013, 136, 301–314. [Google Scholar] [CrossRef]
- Hancock, S.; Essery, R.; Reid, T.; Carle, J.; Baxter, R.; Rutter, N.; Huntley, B. Characterising forest gap fraction with terrestrial lidar and photography: An examination of relative limitations. Agric. For. Meteorol. 2014, 189, 105–114. [Google Scholar] [CrossRef]
- Calders, K.; Armston, J.; Newnham, G.; Herold, M.; Goodwin, N. Implications of sensor configuration and topography on vertical plant profiles derived from terrestrial LiDAR. Agric. For. Meteorol. 2014, 194, 104–117. [Google Scholar] [CrossRef]
- Jupp, D.L.; Culvenor, D.; Lovell, J.; Newnham, G.; Strahler, A.; Woodcock, C. Estimating forest LAI profiles and structural parameters using a ground-based laser called Echidna®. Tree Physiol. 2009, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Yan, G.; Mu, X.; Luo, J. Indirect measurement of leaf area index on the basis of path length distribution. Remote Sens. Environ. 2014, 155, 239–247. [Google Scholar] [CrossRef]
- Hu, R.; Bournez, E.; Cheng, S.; Jiang, H.; Nerry, F.; Landes, T.; Saudreau, M.; Kastendeuch, P.; Najjar, G.; Colin, J.; et al. Estimating the leaf area of an individual tree in urban areas using terrestrial laser scanner and path length distribution model. ISPRS J. Photogramm. Remote Sens. 2018, 144, 357–368. [Google Scholar] [CrossRef]
- Lovell, J.; Jupp, D.L.; Culvenor, D.; Coops, N. Using airborne and ground–based ranging lidar to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, J. Unsupervised extrinsic parameters calibration for multi-bem LiDARs. In Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering, Los Angeles, CA, USA, 1–2 July 2013; pp. 1110–1113. [Google Scholar]
- Olivier, P. Leddar Optical Time–of–Flight Sensing Technology: A New Approach to Detection and Ranging. 2015. Available online: https://dlwx5us9wukuhO.cloudfront.net/app/uploads/dlm_uploads/2016/02/Leddar-Optical-Time-of-Flight-Sensing-Technology-l.pdf (accessed on 11 September 2019).
- Gangadharan, S.; Burks, T.F.; Schueller, J.K. A comparison of approaches for citrus canopy profile generation using ultrasonic and Leddar® sensors. Comput. Electron. Agric. 2019, 156, 71–83. [Google Scholar] [CrossRef]
- Arnay, R.; Hernández–Aceituno, J.; Toledo, J.; Acosta, L. Laser and Optical Flow Fusion for a Non–Intrusive Obstacle Detection System on an Intelligent Wheelchair. IEEE Sens. J. 2018, 18, 3799–3805. [Google Scholar] [CrossRef]
- Mimeault, Y.; Cantin, D. Lighting system with driver assistance capabilities. U.S. Patent No. 8,600,656, 3 December 2013. [Google Scholar]
- Godejord, B. Characterization of a Commercial LIDAR Module for Use in Camera Triggering System. Master’s Thesis, Norwegian University of Science and Technology NTNU, Taibei, Taiwan, 2018. [Google Scholar]
- Thakur, R. Scanning LIDAR in Advanced Driver Assistance Systems and Beyond: Building a road map for next–generation LIDAR technology. IEEE Consum. Electron. Mag. 2016, 5, 48–54. [Google Scholar] [CrossRef]
- Mimeault, Y. Parking management system and method using lighting system. U.S. Patent No. 8,723,689, 13 May 2014. [Google Scholar]
- Hentschke, M.; Pignaton de Freitas, E.; Hennig, C.; Girardi da Veiga, I. Evaluation of Altitude Sensors for a Crop Spraying Drone. Drones 2018, 2, 25. [Google Scholar] [CrossRef]
- Elaksher, A.F.; Bhandari, S.; Carreon-Limones, C.A.; Lauf, R. Potential of UAV lidar systems for geospatial mapping. In Proceedings of the Lidar Remote Sensing for Environmental Monitoring, San Diego, CA, USA, 6–10 August 2017; p. 104060L. [Google Scholar]
- Bohren, J.; Foote, T.; Keller, J.; Kushleyev, A.; Lee, D.; Stewart, A.; Vernaza, P.; Derenick, J.; Spletzer, J.; Satterfield, B. Little ben: The ben franklin racing team’s entry in the 2007 DARPA urban challenge. J. Field Rob. 2008, 25, 598–614. [Google Scholar] [CrossRef]
- Muhammad, N.; Lacroix, S. Calibration of a rotating multi-beam lidar. In Proceedings of the IROS 2010: IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5648–5653. [Google Scholar]
- Atanacio-Jiménez, G.; González-Barbosa, J.-J.; Hurtado-Ramos, J.B.; Ornelas-Rodríguez, F.J.; Jiménez-Hernández, H.; García–Ramirez, T.; González-Barbosa, R. LIDAR velodyne HDL–64E calibration using pattern planes. Int. J. Adv. Rob. Syst. 2011, 8, 59. [Google Scholar] [CrossRef]
- Levinson, J.; Thrun, S. Unsupervised Calibration for Multi–beam Lasers. In Proceedings of the Experimental Robotics: The 12th International Symposium on Experimental Robotics, Delhi, India, 18–21 December 2010; p. 179. [Google Scholar]
- Sheehan, M.; Harrison, A.; Newman, P. Self-calibration for a 3D laser. Int. J. Rob. Res. 2012, 31, 675–687. [Google Scholar] [CrossRef]
- Li, J.; He, X.; Li, J. 2D LiDAR and camera fusion in 3D modeling of indoor environment. In Proceedings of the 2015 National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 June 2015; pp. 379–383. [Google Scholar]
- Budge, S.E.; Badamikar, N.S.; Xie, X. Automatic registration of fused lidar/digital imagery (texel images) for three–dimensional image creation. Optical Engineering 2014, 54, 031105. [Google Scholar] [CrossRef]
- Bodensteiner, C.; Hübner, W.; Jüngling, K.; Solbrig, P.; Arens, M. Monocular camera trajectory optimization using LiDAR data. In Proceedings of the Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 7 November 2011; pp. 2018–2025. [Google Scholar]
- Park, Y.; Yun, S.; Won, C.S.; Cho, K.; Um, K.; Sim, S. Calibration between color camera and 3D LIDAR instruments with a polygonal planar board. Sensors 2014, 14, 5333–5353. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Deng, Z. Extrinsic calibration of a camera and a lidar based on decoupling the rotation from the translation. In Proceedings of the Intelligent Vehicles Symposium (IV), Alcalá de Henares, Spain, 3–7 June 2012; pp. 642–648. [Google Scholar]
- Fremont, V.; Bonnifait, P. Extrinsic calibration between a multi–layer lidar and a camera. In Proceedings of the 2008 IEEE International Conference on MFI, Heidelberg, Germany, 3–6 September 2006; pp. 214–219. [Google Scholar]
- Debattisti, S.; Mazzei, L.; Panciroli, M. Automated extrinsic laser and camera inter-calibration using triangular targets. In Proceedings of the Intelligent Vehicles Symposium (IV), Gold Coast, Australia, 23–26 June 2013; pp. 696–701. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, England, 2003. [Google Scholar]
- De Silva, V.; Roche, J.; Kondoz, A. Robust fusion of LiDAR and wide-anglse camera data for autonomous mobile robots. Sensors 2018, 18, 2730. [Google Scholar] [CrossRef] [PubMed]
- Jia, Q.; Fan, X.; Luo, Z.; Song, L.; Qiu, T. A fast ellipse detector using projective invariant pruning. IEEE Trans. Image Process. 2017, 26, 3665–3679. [Google Scholar] [CrossRef] [PubMed]
- Fitzgibbon, A.W.; Pilu, M.; Fisher, R.B. Direct least squares fitting of ellipses. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 Aug 1996; pp. 253–257. [Google Scholar]
- Newton, I. De analysi per aequationes numero terminorum infinitas. 1711. [Google Scholar]
- Newton, I.; Colson, J. The Method of Fluxions and Infinite Series; with Its Application to the Geometry of Curve-lines... Translated from the Author’s Latin Original Not Yet Made Publick. To which is Subjoin’d a Perpetual Comment Upon the Whole Work... by J. Colson; Henry Woodfall: London, UK, 1736. [Google Scholar]
- Ypma, T.J. Historical development of the Newton-Raphson method. SIAM Rev. 1995, 37, 531–551. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; Wiley Online Library: New York, NY, USA, 1981; p. ix. 308p, Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9780470434697 (accessed on 11 September 2019).
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the European conference on computer vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Nock, R.; Nielsen, F. Statistical region merging. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1452–1458. [Google Scholar] [CrossRef]
- Pertuz, S.; Kamarainen, J. Region-based depth recovery for highly sparse depth maps. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 2074–2078. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Zanewich, K.P.; Pearce, D.W.; Rood, S.B. Heterosis in poplar involves phenotypic stability: Cottonwood hybrids outperform their parental species at suboptimal temperatures. Tree Physiol. 2018, 38, 789–800. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Hu, R.; Qi, J.; Shao, J.; Li, D.; Wan, P.; Qiao, C.; Shen, A.; Yan, G. Estimation of forest leaf area index using terrestrial laser scanning data and path length distribution model in open–canopy forests. Agric. For. Meteorol. 2018, 263, 323–333. [Google Scholar] [CrossRef]
- Schleppi, P.; Conedera, M.; Sedivy, I.; Thimonier, A. Correcting non-linearity and slope effects in the estimation of the leaf area index of forests from hemispherical photographs. Agric. For. Meteorol 2007, 144, 236–242. [Google Scholar] [CrossRef]
- Thimonier, A.; Sedivy, I.; Schleppi, P. Estimating leaf area index in different types of mature forest stands in Switzerland: A comparison of methods. Eur. J. For. Res. 2010, 129, 543–562. [Google Scholar] [CrossRef]
- Lang, A. Simplified estimate of leaf area index from transmittance of the sun’s beam. Agric. For. Meteorol. 1987, 41, 179–186. [Google Scholar] [CrossRef]
- Lang, A.; Xiang, Y. Estimation of leaf area index from transmission of direct sunlight in discontinuous canopies. Agric. For. Meteorol. 1986, 37, 229–243. [Google Scholar] [CrossRef]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground–based lidar instrument (Echidna®). Can. J. Remote Sens. 2008, 34, S426–S440. [Google Scholar] [CrossRef]
- Pimont, F.; Soma, M.; Dupuy, J.-L. Accounting for Wood, Foliage Properties, and Laser Effective Footprint in Estimations of Leaf Area Density from Multiview–LiDAR Data. Remote Sens. 2019, 11, 1580. [Google Scholar] [CrossRef]







| TLS | DHP | FSS | 2D LiDAR | |
|---|---|---|---|---|
| Spatial resolution | ++ | ++ | + | - |
| Detection range | ++ | + | + | - |
| Equipment affordability | - | - | + | ++ |
| Operative efficiency | + | ++ | + | + |
| 3D measurement accuracy | ++ | - | + | + |
| Portability and scalability | - | - | + | ++ |
| Repeatability and durability | - | - | + | + |
| Camera | Leddar | Tilt Servo | Pan Servo |
|---|---|---|---|
| OmniVision OV5647 | M16 module | Hitec HS-5485HB | Dynamixel MX-12W |
| FOV: 54° × 41° | Distance: 0 to 50 m | Max angle: 118° | Max angle: 360° |
| Lens: f = 3.6 mm, f/2.9 | Frequency: ≤100 s−1 | PWM: 750–2250 μs | Steps: 4096 |
| Calibration: no IR | Wavelength: 940 nm | Deadband: 8 µs | Resolution: 0.088° |
| Application: IR filter | Power: 12/24 V, 4 W | Power: 4.8–6.0 V | Voltage: 12 V |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Z.; Hopkinson, C.; Rood, S.B.; Barnes, C.; Xu, F.; Pearce, D.; Jones, E. A Lightweight Leddar Optical Fusion Scanning System (FSS) for Canopy Foliage Monitoring. Sensors 2019, 19, 3943. https://doi.org/10.3390/s19183943
Xi Z, Hopkinson C, Rood SB, Barnes C, Xu F, Pearce D, Jones E. A Lightweight Leddar Optical Fusion Scanning System (FSS) for Canopy Foliage Monitoring. Sensors. 2019; 19(18):3943. https://doi.org/10.3390/s19183943
Chicago/Turabian StyleXi, Zhouxin, Christopher Hopkinson, Stewart B. Rood, Celeste Barnes, Fang Xu, David Pearce, and Emily Jones. 2019. "A Lightweight Leddar Optical Fusion Scanning System (FSS) for Canopy Foliage Monitoring" Sensors 19, no. 18: 3943. https://doi.org/10.3390/s19183943
APA StyleXi, Z., Hopkinson, C., Rood, S. B., Barnes, C., Xu, F., Pearce, D., & Jones, E. (2019). A Lightweight Leddar Optical Fusion Scanning System (FSS) for Canopy Foliage Monitoring. Sensors, 19(18), 3943. https://doi.org/10.3390/s19183943






