Survey of Deep-Learning Approaches for Remote Sensing Observation Enhancement
Abstract
1. Introduction
- More data available for training DNNs, especially for cases of supervised learning such as classification, where annotations are typically provided by users.
- More processing power, and especially the explosion in availability of Graphical Processing Units (GPUs) which are optimized for high through-processing of parallelizable problems such as training DNNs.
- More advanced algorithms which have allowed DNNs to grow considerably both in terms of depth and output dimensions, leading to superior performance compared to more traditional shallow architectures.
- High dimensionality of observations where Multispectral (MS) and Hyperspectral (HS) are often the input and thus exploiting spatial and spectral correlations is of paramount importance.
- Massive amounts of information encoded in each observation due to the large distance between sensor and scene, e.g., 400–600 km for low Earth orbit satellites, which implies that significantly more content is encoded in each image compared to a typical natural image.
- Sensor specific characteristics, including the radiometric resolution which unlike typical 8-bit imagery, in many cases involves observations of 12-bits per pixel.
- Challenging imaging conditions which are adverse affected by environmental conditions including the impact of the atmospheric effects such as clouds on the acquired imagery.
2. Deep Neural Network Paradigms
2.1. Convolutional Neural Networks (CNNs)
2.1.1. Key Components of CNNs
2.1.2. Training and Optimization of CNNs
2.1.3. Prototypical CNN Architectures
2.2. Autoencoders (AE)
2.2.1. Sparse Autoencoders
2.2.2. Denoising Autoencoders
2.2.3. Variational Autoencoders
2.3. Generative Adversarial Networks
2.4. Performance Evaluation
2.4.1. Evaluation Metrics
- Peak Signal-to-Noise Ratio (PSNR) is a well-established image quality metric, typically employed for 8-bit images, an expresses image quality in decibels (dB), so that higher is better.
- Mean Squared Error (MSE) is a generic signal quality metric where lower values are sought.
- Structural Similarity Index (SSIM) is an image quality metric which considers the characteristics of the human visual signal, such that values 1 indicate better performance.
- Signal-to-Reconstruction Error (SRE) is given in decibels (dB) and the higher values indicate higher quality.
- Spectral Angle Mapper (SAM) is an image metric typically employed for MS and HS imagery and values close to 0 indicate higher quality reconstruction.
2.4.2. Remote Sensing EO Platforms
- Sentinel 2 satellite carrying the 12 band MSI instrument with spatial resolution between 10 and 20 m for most bands in the visible, near and shortwave infrared.
- Landsat 7 and more recently Landsat 8 also acquire HS imagery over 11 bands in the visible to infrared range at 30 and 100 m resolution, respectively.
- SPOT 6 and 7 provide PAN imagery at 2 m spatial resolution and MS at 8 m resolution offering a swatch of 60 km
- Pleiades 1A and 1B acquire PAN imagery at m and MS at 2 m, offering high agility for responsive tasking.
- QuickBird and IKONOS are two decommissioned satellites offering m and 1 m panchromatic (PAN) and and 4 m 4-band MS imaging, respectively.
- Worldview-3 acquiring cm PAN and m eight-band MS imagery, as well as shortwave infrared imagery at m resolution.
- GaoFen-1 is equipped with two instrument sets, 2 cameras offering 2 m PAN, 8 m MS and four wide-field cameras acquiring MS imagery at 16 m resolution.
- Jilin-1 satellite family by Chang Guang Satellite Technology Co. Ltd, Changchun City, Jilin Province, China [48].
- The Airborne visible/infrared imaging spectrometer (AVIRIS) is a 224 band HS airborne instrument for which several annotated acquisitions are available.
- The Hyperion instrument aboard the EO-1 satellite is another well-known HS instrument capturing imagery over 200 bands, which was decommissioned in 2017.
- ROSIS is a 102 band HS airborne instrument which is also associated with annotated acquisitions.
2.4.3. Typical Datasets and Data Sources
- UC Merced contains 100 images of size from 21 different classes at m resolution.
- NWPU-RESIS45 [49] contains 700 images from 45 scene classes (31,500 images in total).
- RSCNN7 contains 2800 images from seven different classes.
- NWPU-RESISC45 is a data set of aerial imagery of scenes from 45 categories, and each category contains 700 images of size of pixels.
- Indian Pines, Salinas, Cuprite and Kennedy Space Center from AVIRIS.
- Pavia Center and University from ROSIS offers 102 spectral bands over an urban area as 1.3 m resolution.
- Botswaba from EO-1 Hyperion offers 145 calibrated bands over different land cover types including seasonal swamps, occasional swamps, and drier woodlands.
- Kaggle Open Source Dataset and more specifically the Draper Satellite Image Chronology contains over 1000 high-resolution aerial photographs taken in southern California.
- Caltech, which is a publicly available aerial database that comprises an aircraft dataset and a vehicle dataset.
3. Super-Resolution
3.1. Super-Resolution of Remote Sensing Observations
3.1.1. Single-Image Super-Resolution
3.1.2. Multispectral and Hyperspectral Image Super-Resolution
3.1.3. Video Super-Resolution
3.2. Discussion
- In terms of single-image, single-band super-resolution, approaches based on the GAN framework appear to achieve the highest quality image estimation. This observation for the case of remote sensing is in-line with results for methods applied in generic natural image.
- For the case of spatial-spectral super-resolution, the best performing approaches pay special attention of simultaneously increasing the spatial resolution without introducing unwanted artifacts in the spectral domain, unlike early approaches which consider each spectral channel independently.
- Exploiting temporal information, which for many remote sensing cases, can be directly translated to access to multi-view imagery given the regular imaging protocols in satellites imaging.
- Super-resolution of video sequences require the exploitation of both spatial and temporal information, such as the approach proposed in [95] which encodes spatio-temporal information using a recurrent residual network and is applied to the restoration of generic video sequences. This methodology however has not been explored in the context of remote sensing, where methods primarily consider single frames.
- Although numerous approaches have been proposed for addressing the combination of two resolution dimensions, methods which can simultaneously enhance remote sensing images along their spatial, spectral and temporal dimensions have not been considered.
4. Pan-Sharpening
4.1. AE-Based Approaches
4.2. CNN-Based Approaches
4.3. Discussion
- The majority of state-of-the-art performing methods rely on some variant of CNNs, typically employing fully convolutional architectures, while AE approaches are significantly less used for this problem.
- The introduction of successful CNN components such as inception modules and residual/skip connections lead to higher quality outputs.
- Among the best performing methods are the ones that employ two-stream architectures in which cases the PAN and MS are first analyzed independently by two separate paths and the extracted features are then jointly processed to produce the output.
- GANs has also been introduced in the problem of pan-sharpening with some promising initial results; however, more detailed analysis is required to justify any potential benefits.
5. Restoration
5.1. Denoising and Deblurring
5.2. Missing Data Recovery
5.3. Discussion
- Highest performing methods for restoration involve CNN architectures with multiscale feature extraction capabilities, while GANs architectures also appear promising.
- While the case of denoising with known noise characteristics has been explored, further research involving unknown or mixed distribution noise is required.
- The use of multiple sources of observations with different quality characteristics targeting restoration is also another topic of great importance.
- Estimating missing observation, especially the cases involving cloud occlusion of optical imagery, using radar observations which are impervious to this problem also warrants further investigation.
6. Fusion
6.1. Fusion of MS and HS Observations
6.2. Fusion of Spectral and Radar Observations
6.3. Discussion
- Almost exclusively, CNN architectures have been used for HS and MS fusion, the majority of which follow the same principles as the case of pan-sharpening.
- Although different approaches have been proposed for addressing pairs of resolution dimensions, i.e., spatial-spectral and spatial-temporal, no approach has been put forward for increasing the resolution along spatial, spectral and temporal resolution.
- There is limited investigation in fusion of observation from different modalities, i.e., optical and radar. We believe this domain to be extremely promising and hence more research needs to be conducted.
7. Challenges and Perspectives
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| (S) AE | (Stacked) Autoencoder |
| CNN | Convolutional Neural Network |
| DNN | Deep Neural Network |
| EO | Earth Observation |
| GAN | Generative Adversarial Network |
| HS | Hyperspectral |
| NDVI | Normalized Difference Vegetation Index |
| MS | Multispectral |
| MSE | Mean Squared Error |
| RGB | Red-Green-Blue color channels |
| PAN | Panchromatic |
| PSNR | Peak Signal-to-Noise Ratio |
| SAE | Stacked Autoencoders |
| SAM | Spectral Angle Mapper |
| SAR | Synthetic Aperture Radar |
| SWIR | Shortwave Infrared |
| SSIM | Structural SIMilarity (Index) |
References
- Nativi, S.; Mazzetti, P.; Santoro, M.; Papeschi, F.; Craglia, M.; Ochiai, O. Big data challenges in building the global earth observation system of systems. Environ. Model. Softw. 2015, 68, 1–26. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Chen, X.W.; Lin, X. Big data deep learning: Challenges and perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef]
- Karalas, K.; Tsagkatakis, G.; Zervakis, M.; Tsakalides, P. Deep learning for multi-label land cover classification. In Proceedings of the Image and Signal Processing for Remote Sensing XXI. International Society for Optics and Photonics, Toulouse, France, 15 October 2015; Volume 9643, p. 96430Q. [Google Scholar]
- Maqueda, A.I.; Loquercio, A.; Gallego, G.; García, N.; Scaramuzza, D. Event-based vision meets deep learning on steering prediction for self-driving cars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5419–5427. [Google Scholar]
- Wang, S.; Su, Z.; Ying, L.; Peng, X.; Zhu, S.; Liang, F.; Feng, D.; Liang, D. Accelerating magnetic resonance imaging via deep learning. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 514–517. [Google Scholar]
- Ribes, A.; Schmitt, F. Linear inverse problems in imaging. IEEE Signal Process. Mag. 2008, 25, 84–99. [Google Scholar] [CrossRef]
- Yu, G.; Sapiro, G.; Mallat, S. Solving inverse problems with piecewise linear estimators: From Gaussian mixture models to structured sparsity. IEEE Trans. Image Process. 2012, 21, 2481–2499. [Google Scholar]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1026–1034. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Wang, T.; Sun, M.; Hu, K. Dilated deep residual network for image denoising. In Proceedings of the 2017 IEEE 29th International Conference on Tools with Artificial Intelligence (ICTAI), Boston, MA, USA, 6–8 November 2017; pp. 1272–1279. [Google Scholar]
- Lin, G.; Wu, Q.; Qiu, L.; Huang, X. Image super-resolution using a dilated convolutional neural network. Neurocomputing 2018, 275, 1219–1230. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Yang, Z.; Ma, X. Learning a dilated residual network for SAR image despeckling. Remote Sens. 2018, 10, 196. [Google Scholar] [CrossRef]
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Stivaktakis, R.; Tsagkatakis, G.; Tsakalides, P. Deep Learning for Multilabel Land Cover Scene Categorization Using Data Augmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1031–1035. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D Deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Fotiadou, K.; Tsagkatakis, G.; Tsakalides, P. Deep convolutional neural networks for the classification of snapshot mosaic hyperspectral imagery. Electron. Imaging 2017, 2017, 185–190. [Google Scholar] [CrossRef]
- Bottou, L. Online learning and stochastic approximations. Online Learn. Neural Netw. 1998, 17, 142. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Bengio, Y. Deep learning of representations for unsupervised and transfer learning. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, Bellevue, WA, USA, 2 July 2011; pp. 17–36. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Springer International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length and Helmholtz free energy. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 28 November–1 December 1994; pp. 3–10. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 153–160. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Shin, H.C.; Orton, M.R.; Collins, D.J.; Doran, S.J.; Leach, M.O. Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1930–1943. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Domain adaptation for large-scale sentiment classification: A deep learning approach. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 513–520. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the ACM 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Doersch, C. Tutorial on variational autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-resolution image synthesis and semantic manipulation with conditional gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8798–8807. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 June 2017; pp. 105–114. [Google Scholar]
- Zeng, Y.; Huang, W.; Liu, M.; Zhang, H.; Zou, B. Fusion of satellite images in urban area: Assessing the quality of resulting images. In Proceedings of the IEEE 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Fan, J. Chinese Earth Observation Program and Policy. In Satellite Earth Observations and Their Impact on Society and Policy; Springer: Berlin, Germany, 2017; pp. 105–110. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21 July 2017; Volume 1, p. 4. [Google Scholar]
- Liebel, L.; Körner, M. Single-Image Super Resolution for Multispectral Remote Sensing Data Using Convolutional Neural Networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 883–890. [Google Scholar] [CrossRef]
- Tuna, C.; Unal, G.; Sertel, E. Single-frame super resolution of remote-sensing images by convolutional neural networks. Int. J. Remote Sens. 2018, 39, 2463–2479. [Google Scholar] [CrossRef]
- Huang, N.; Yang, Y.; Liu, J.; Gu, X.; Cai, H. Single-Image Super-Resolution for Remote Sensing Data Using Deep Residual-Learning Neural Network. In Proceedings of the Springer International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017; pp. 622–630. [Google Scholar]
- Lei, S.; Shi, Z.; Zou, Z. Super-resolution for remote sensing images via local–global combined network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Xu, W.; Guangluan, X.; Wang, Y.; Sun, X.; Lin, D.; Yirong, W. High Quality Remote Sensing Image Super-Resolution Using Deep Memory Connected Network. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8889–8892. [Google Scholar]
- Wang, T.; Sun, W.; Qi, H.; Ren, P. Aerial Image Super Resolution via Wavelet Multiscale Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 769–773. [Google Scholar] [CrossRef]
- Ma, W.; Pan, Z.; Guo, J.; Lei, B. Achieving Super-Resolution Remote Sensing Images via the Wavelet Transform Combined With the Recursive Res-Net. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3512–3527. [Google Scholar] [CrossRef]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar]
- Lu, T.; Wang, J.; Zhang, Y.; Wang, Z.; Jiang, J. Satellite Image Super-Resolution via Multi-Scale Residual Deep Neural Network. Remote Sens. 2019, 11, 1588. [Google Scholar] [CrossRef]
- Pan, Z.; Ma, W.; Guo, J.; Lei, B. Super-Resolution of Single Remote Sensing Image Based on Residual Dense Backprojection Networks. IEEE Trans. Geosci. Remote Sens. 2019, 1–16. [Google Scholar] [CrossRef]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1664–1673. [Google Scholar]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Ma, W.; Pan, Z.; Guo, J.; Lei, B. Super-Resolution of Remote Sensing Images Based on Transferred Generative Adversarial Network. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1148–1151. [Google Scholar]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-Enhanced GAN for Remote Sensing Image Superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, Y.; Peng, Y.; Xia, Y. Accurate Image Super-Resolution Using Cascaded Multi-Column Convolutional Neural Networks. In Proceedings of the 2018 IEEE International Conference on Multimedia and Expo (ICME), San Diego, CA, USA, 23–27 July 2018; pp. 1–6. [Google Scholar]
- Li, Y.; Hu, J.; Zhao, X.; Xie, W.; Li, J. Hyperspectral image super-resolution using deep convolutional neural network. Neurocomputing 2017, 266, 29–41. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Bai, X.; Tang, W.; Lei, P.; Zhou, J. Deep Residual Convolutional Neural Network for Hyperspectral Image Super-Resolution. In Proceedings of the Springer International Conference on Image and Graphics, Shanghai, China, 13–15 September 2017; pp. 370–380. [Google Scholar]
- Yuan, Y.; Zheng, X.; Lu, X. Hyperspectral image superresolution by transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1963–1974. [Google Scholar] [CrossRef]
- Collins, C.B.; Beck, J.M.; Bridges, S.M.; Rushing, J.A.; Graves, S.J. Deep learning for multisensor image resolution enhancement. In Proceedings of the ACM 1st Workshop on Artificial Intelligence and Deep Learning for Geographic Knowledge Discovery, Redondo Beach, CA, USA, 7 November 2016; pp. 37–44. [Google Scholar]
- He, Z.; Liu, L. Hyperspectral Image Super-Resolution Inspired by Deep Laplacian Pyramid Network. Remote Sens. 2018, 10, 1939. [Google Scholar] [CrossRef]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate superresolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Volume 2, p. 5. [Google Scholar]
- Zheng, K.; Gao, L.; Zhang, B.; Cui, X. Multi-Losses Function Based Convolution Neural Network for Single Hyperspectral Image Super-Resolution. In Proceedings of the 2018 IEEE Fifth International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Xi’an, Shaanxi Province, China, 17–20 June 2018; pp. 1–4. [Google Scholar]
- Lanaras, C.; Bioucas-Dias, J.; Galliani, S.; Baltsavias, E.; Schindler, K. Super-resolution of Sentinel-2 images: Learning a globally applicable deep neural network. ISPRS J. Photogramm. Remote Sens. 2018, 146, 305–319. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.; Ulfarsson, M. Sentinel-2 Image Fusion Using a Deep Residual Network. Remote Sens. 2018, 10, 1290. [Google Scholar] [CrossRef]
- Gargiulo, M.; Mazza, A.; Gaetano, R.; Ruello, G.; Scarpa, G. A CNN-Based Fusion Method for Super-Resolution of Sentinel-2 Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4713–4716. [Google Scholar]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Zheng, K.; Gao, L.; Ran, Q.; Cui, X.; Zhang, B.; Liao, W.; Jia, S. Separable-spectral convolution and inception network for hyperspectral image super-resolution. Int. J. Mach. Learn. Cybern. 2019, 1–15. [Google Scholar] [CrossRef]
- Mei, S.; Yuan, X.; Ji, J.; Zhang, Y.; Wan, S.; Du, Q. Hyperspectral Image Spatial Super-Resolution via 3D Full Convolutional Neural Network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef]
- Arun, P.V.; Herrmann, I.; Budhiraju, K.M.; Karnieli, A. Convolutional network architectures for super-resolution/sub-pixel mapping of drone-derived images. Pattern Recognit. 2019, 88, 431–446. [Google Scholar] [CrossRef]
- Ran, Q.; Xu, X.; Zhao, S.; Li, W.; Du, Q. Remote sensing images super-resolution with deep convolution networks. Multimed. Tools Appl. 2019, 1–17. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. Hscnn+: Advanced cnn-based hyperspectral recovery from rgb images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; Volume 3, p. 5. [Google Scholar]
- Han, X.H.; Shi, B.; Zheng, Y. Residual HSRCNN: Residual Hyper-Spectral Reconstruction CNN from an RGB Image. In Proceedings of the 2018 IEEE 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2664–2669. [Google Scholar]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Zha, Z.J.; Wu, F. Deep residual attention network for spectral image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Eldar, Y.C.; Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Golbabaee, M.; Vandergheynst, P. Hyperspectral image compressed sensing via low-rank and joint-sparse matrix recovery. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2741–2744. [Google Scholar]
- Tsagkatakis, G.; Tsakalides, P. Compressed hyperspectral sensing. In Image Sensors and Imaging Systems 2015; International Society for Optics and Photonics: Washington, DC, USA, 2015; Volume 9403, p. 940307. [Google Scholar]
- Yuan, H.; Yan, F.; Chen, X.; Zhu, J. Compressive Hyperspectral Imaging and Super-resolution. In Proceedings of the 2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, June 27–29 2018; pp. 618–623. [Google Scholar]
- Arce, G.R.; Brady, D.J.; Carin, L.; Arguello, H.; Kittle, D.S. Compressive coded aperture spectral imaging: An introduction. IEEE Signal Process. Mag. 2013, 31, 105–115. [Google Scholar] [CrossRef]
- Xiong, Z.; Shi, Z.; Li, H.; Wang, L.; Liu, D.; Wu, F. Hscnn: Cnn-based hyperspectral image recovery from spectrally undersampled projections. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Honolulu, HI, USA, 21–26 July 2017; Volume 2. [Google Scholar]
- Wang, L.; Zhang, T.; Fu, Y.; Huang, H. HyperReconNet: Joint Coded Aperture Optimization and Image Reconstruction for Compressive Hyperspectral Imaging. IEEE Trans. Image Process. 2018, 28, 2257–2270. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Zhou, L.; Wang, S.; Wang, Z. Video Satellite Imagery Super Resolution via Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2398–2402. [Google Scholar] [CrossRef]
- Xiao, A.; Wang, Z.; Wang, L.; Ren, Y. Super-Resolution for “Jilin-1” Satellite Video Imagery via a Convolutional Network. Sensors 2018, 18, 1194. [Google Scholar] [CrossRef] [PubMed]
- Jiang, K.; Wang, Z.; Yi, P.; Jiang, J. A progressively enhanced network for video satellite imagery superresolution. IEEE Signal Process. Lett. 2018, 25, 1630–1634. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Jiang, J.; Xiao, J.; Yao, Y. Deep Distillation Recursive Network for Remote Sensing Imagery Super-Resolution. Remote Sens. 2018, 10, 1700. [Google Scholar] [CrossRef]
- Yang, W.; Feng, J.; Xie, G.; Liu, J.; Guo, Z.; Yan, S. Video super-resolution based on spatial-temporal recurrent residual networks. Comput. Vis. Image Underst. 2018, 168, 79–92. [Google Scholar] [CrossRef]
- Zhang, Y.; Mishra, R.K. A review and comparison of commercially available pan-sharpening techniques for high resolution satellite image fusion. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 182–185. [Google Scholar]
- Huang, W.; Xiao, L.; Wei, Z.; Liu, H.; Tang, S. A new pan-sharpening method with deep neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1037–1041. [Google Scholar] [CrossRef]
- Cai, W.; Xu, Y.; Wu, Z.; Liu, H.; Qian, L.; Wei, Z. Pan-Sharpening Based on Multilevel Coupled Deep Network. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7046–7049. [Google Scholar]
- Wei, Y.; Yuan, Q.; Shen, H.; Zhang, L. Boosting the accuracy of multispectral image pansharpening by learning a deep residual network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1795–1799. [Google Scholar] [CrossRef]
- Azarang, A.; Ghassemian, H. A new pansharpening method using multi resolution analysis framework and deep neural networks. In Proceedings of the 2017 3rd International Conference on IEEE Pattern Recognition and Image Analysis (IPRIA), Shahrekord, Iran, 19–20 April 2017; pp. 1–6. [Google Scholar]
- Azarang, A.; Manoochehri, H.E.; Kehtarnavaz, N. Convolutional Autoencoder-Based Multispectral Image Fusion. IEEE Access 2019, 7, 35673–35683. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, B.; Huang, G.; Zhong, F.; Chen, Z. Remote sensing image fusion with convolutional neural network. Sens. Imaging 2016, 17, 10. [Google Scholar] [CrossRef]
- Li, N.; Huang, N.; Xiao, L. Pan-sharpening via residual deep learning. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5133–5136. [Google Scholar]
- Wei, Y.; Yuan, Q. Deep residual learning for remote sensed imagery pansharpening. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017; pp. 1–4. [Google Scholar]
- Rao, Y.; He, L.; Zhu, J. A residual convolutional neural network for pan-shaprening. In Proceedings of the 2017 International Workshop on IEEE Remote Sensing with Intelligent Processing (RSIP), Shanghai, China, 18–21 May 2017; pp. 1–4. [Google Scholar]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1753–1761. [Google Scholar]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Wei, Y.; Yuan, Q.; Meng, X.; Shen, H.; Zhang, L.; Ng, M. Multi-scale-and-depth convolutional neural network for remote sensed imagery pan-sharpening. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3413–3416. [Google Scholar]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. CNN-based pansharpening of multi-resolution remote-sensing images. In Proceedings of the 2017 IEEE Joint Urban Remote Sensing Event (JURSE), Dubai, United Arab Emirates, 6–8 March 2017; pp. 1–4. [Google Scholar]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-adaptive CNN-based pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote Sensing Image Fusion With Deep Convolutional Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Sun, M.; Ou, Y. Pan-Sharpening Using an Efficient Bidirectional Pyramid Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5549–5563. [Google Scholar] [CrossRef]
- Yao, W.; Zeng, Z.; Lian, C.; Tang, H. Pixel-wise Regression using U-Net and its Application on Pansharpening. Neurocomputing 2018, 312, 364–371. [Google Scholar] [CrossRef]
- Eghbalian, S.; Ghassemian, H. Multi spectral image fusion by deep convolutional neural network and new spectral loss function. Int. J. Remote Sens. 2018, 39, 3983–4002. [Google Scholar] [CrossRef]
- Guo, Y.; Ye, F.; Gong, H. Learning an efficient convolution neural network for pansharpening. Algorithms 2019, 12, 16. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Liu, Q. PSGAN: A Generative Adversarial Network for Remote Sensing Image Pan-Sharpening. arXiv 2018, arXiv:1805.03371. [Google Scholar]
- Zhang, Y.; Li, X.; Zhou, J. SFTGAN: A generative adversarial network for pan-sharpening equipped with spatial feature transform layers. J. Appl. Remote Sens. 2019, 13, 026507. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y. Hyperspectral imagery denoising by deep learning with trainable nonlinearity function. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1963–1967. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y.; Jia, X. Deep convolutional networks with residual learning for accurate spectral-spatial denoising. Neurocomputing 2018, 312, 372–381. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y.; Hu, J.; Chen, D.Y. Trainable spectral difference learning with spatial starting for hyperspectral image denoising. Neural Netw. 2018, 108, 272–286. [Google Scholar] [CrossRef]
- Chen, C.; Xu, Z. Aerial-Image Denoising Based on Convolutional Neural Network with Multi-Scale Residual Learning Approach. Information 2018, 9, 169. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral image denoising employing a spatial-spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1205–1218. [Google Scholar] [CrossRef]
- Liu, W.; Lee, J. A 3-D Atrous Convolution Neural Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5701–5715. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Liu, X.; Shen, H.; Zhang, L. Hybrid Noise Removal in Hyperspectral Imagery With a Spatial-Spectral Gradient Network. arXiv 2018, arXiv:1810.00495. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 667–682. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, Y.; Bai, L. Generative Adversarial Network for Deblurring of Remote Sensing Image. In Proceedings of the 2018 IEEE 26th International Conference on Geoinformatics, Kunming, China, 28–30 June 2018; pp. 1–4. [Google Scholar]
- Xu, W.; Xu, G.; Wang, Y.; Sun, X.; Lin, D.; Wu, Y. Deep Memory Connected Neural Network for Optical Remote Sensing Image Restoration. Remote Sens. 2018, 10, 1893. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing Data Reconstruction in Remote Sensing image with a Unified Spatial-Temporal-Spectral Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Das, M.; Ghosh, S.K. A deep-learning-based forecasting ensemble to predict missing data for remote sensing analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5228–5236. [Google Scholar] [CrossRef]
- Das, M.; Ghosh, S.K. Deep-STEP: A deep learning approach for spatiotemporal prediction of remote sensing data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1984–1988. [Google Scholar] [CrossRef]
- Dong, J.; Yin, R.; Sun, X.; Li, Q.; Yang, Y.; Qin, X. Inpainting of Remote Sensing SST Images With Deep Convolutional Generative Adversarial Network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 173–177. [Google Scholar] [CrossRef]
- Yu, Y.; Gong, Z.; Zhong, P.; Shan, J. Unsupervised Representation Learning with Deep Convolutional Neural Network for Remote Sensing Images. In Proceedings of the Springer International Conference on Image and Graphics, Shanghai, China, 13–15 September 2017; pp. 97–108. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE cOnference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2536–2544. [Google Scholar]
- Bermudez, J.D.; Happ, P.N.; Feitosa, R.Q.; Oliveira, D.A. Synthesis of Multispectral Optical Images from SAR/Optical Multitemporal Data Using Conditional Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1220–1224. [Google Scholar] [CrossRef]
- Grohnfeldi, C.; Schmitt, M.; Zhu, X. A Conditional Generative Adversarial Network to Fuse SAR And Multispectral Optical Data For Cloud Removal From Sentinel-2 Images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1726–1729. [Google Scholar]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2012, 22, 119–133. [Google Scholar] [CrossRef]
- Simone, G.; Farina, A.; Morabito, F.C.; Serpico, S.B.; Bruzzone, L. Image fusion techniques for remote sensing applications. Inf. Fusion 2002, 3, 3–15. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Wang, Z.; Wang, Z.J.; Ward, R.K.; Wang, X. Deep learning for pixel-level image fusion: Recent advances and future prospects. Inf. Fusion 2018, 42, 158–173. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and hyperspectral image fusion using a 3-D-convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and Multispectral Image Fusion via Deep Two-Branches Convolutional Neural Network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Zhou, F.; Hang, R.; Liu, Q.; Yuan, X. Pyramid Fully Convolutional Network for Hyperspectral and Multispectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1549–1558. [Google Scholar] [CrossRef]
- Tan, Z.; Yue, P.; Di, L.; Tang, J. Deriving high spatiotemporal remote sensing images using deep convolutional network. Remote Sens. 2018, 10, 1066. [Google Scholar] [CrossRef]
- Kwan, C.; Budavari, B.; Bovik, A.C.; Marchisio, G. Blind quality assessment of fused worldview-3 images by using the combinations of pansharpening and hypersharpening paradigms. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1835–1839. [Google Scholar] [CrossRef]
- Scarpa, G.; Gargiulo, M.; Mazza, A.; Gaetano, R. A CNN-Based Fusion Method for Feature Extraction from Sentinel Data. Remote Sens. 2018, 10, 236. [Google Scholar] [CrossRef]
- Hughes, L.H.; Schmitt, M.; Mou, L.; Wang, Y.; Zhu, X.X. Identifying corresponding patches in sar and optical images with a pseudo-siamese cnn. IEEE Geosci. Remote Sens. Lett. 2018, 15, 784–788. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.X.; Zeisl, B.; Pollefeys, M. Fusing meter-resolution 4-D InSAR point clouds and optical images for semantic urban infrastructure monitoring. IEEE Trans. Geosci. Remote Sens. 2017, 55, 14–26. [Google Scholar] [CrossRef]
- Quan, D.; Wang, S.; Liang, X.; Wang, R.; Fang, S.; Hou, B.; Jiao, L. Deep Generative Matching Network for Optical and SAR Image Registration. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6215–6218. [Google Scholar]
- Hughes, L.; Schmitt, M.; Zhu, X. Mining Hard Negative Samples for SAR-Optical Image Matching Using Generative Adversarial Networks. Remote Sens. 2018, 10, 1552. [Google Scholar] [CrossRef]
- Merkle, N.; Auer, S.; Müller, R.; Reinartz, P. Exploring the potential of conditional adversarial networks for optical and SAR image matching. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1811–1820. [Google Scholar] [CrossRef]
- DeFries, R.; Chan, J.C.W. Multiple criteria for evaluating machine learning algorithms for land cover classification from satellite data. Remote Sens. Environ. 2000, 74, 503–515. [Google Scholar] [CrossRef]
- Kubat, M.; Holte, R.C.; Matwin, S. Machine learning for the detection of oil spills in satellite radar images. Mach. Learn. 1998, 30, 195–215. [Google Scholar] [CrossRef]
- Lu, Y.; Inamura, M. Spatial resolution improvement of remote sensing images by fusion of subpixel-shifted multi-observation images. Int. J. Remote Sens. 2003, 24, 4647–4660. [Google Scholar] [CrossRef]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine learning for the geosciences: Challenges and opportunities. IEEE Trans. Knowl. Data Eng. 2018, 8, 1544–1554. [Google Scholar] [CrossRef]
- Rick Chang, J.; Li, C.L.; Poczos, B.; Vijaya Kumar, B.; Sankaranarayanan, A.C. One Network to Solve Them All–Solving Linear Inverse Problems Using Deep Projection Models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5888–5897. [Google Scholar]
- Liu, H.; Fu, Z.; Han, J.; Shao, L.; Liu, H. Single satellite imagery simultaneous super-resolution and colorization using multi-task deep neural networks. J. Vis. Commun. Image Represent. 2018, 53, 20–30. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. Deepsd: Generating high resolution climate change projections through single image super-resolution. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, VA, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar]
- Lin, D.Y.; Wang, Y.; Xu, G.L.; Fu, K. Synthesizing remote sensing images by conditional adversarial networks. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 48–50. [Google Scholar]
- Deng, X.; Zhu, Y.; Newsam, S. What Is It Like Down There? Generating Dense Ground-Level Views and Image Features From Overhead Imagery Using Conditional Generative Adversarial Networks. arXiv 2018, arXiv:1806.05129. [Google Scholar]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195. [Google Scholar] [CrossRef]
- Karpatne, A.; Watkins, W.; Read, J.; Kumar, V. Physics-guided neural networks (pgnn): An application in lake temperature modeling. arXiv 2017, arXiv:1710.11431. [Google Scholar]
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.; Zwart, J.; Steinbach, M.; Kumar, V. Physics guided RNNs for modeling dynamical systems: A case study in simulating lake temperature profiles. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019; pp. 558–566. [Google Scholar]
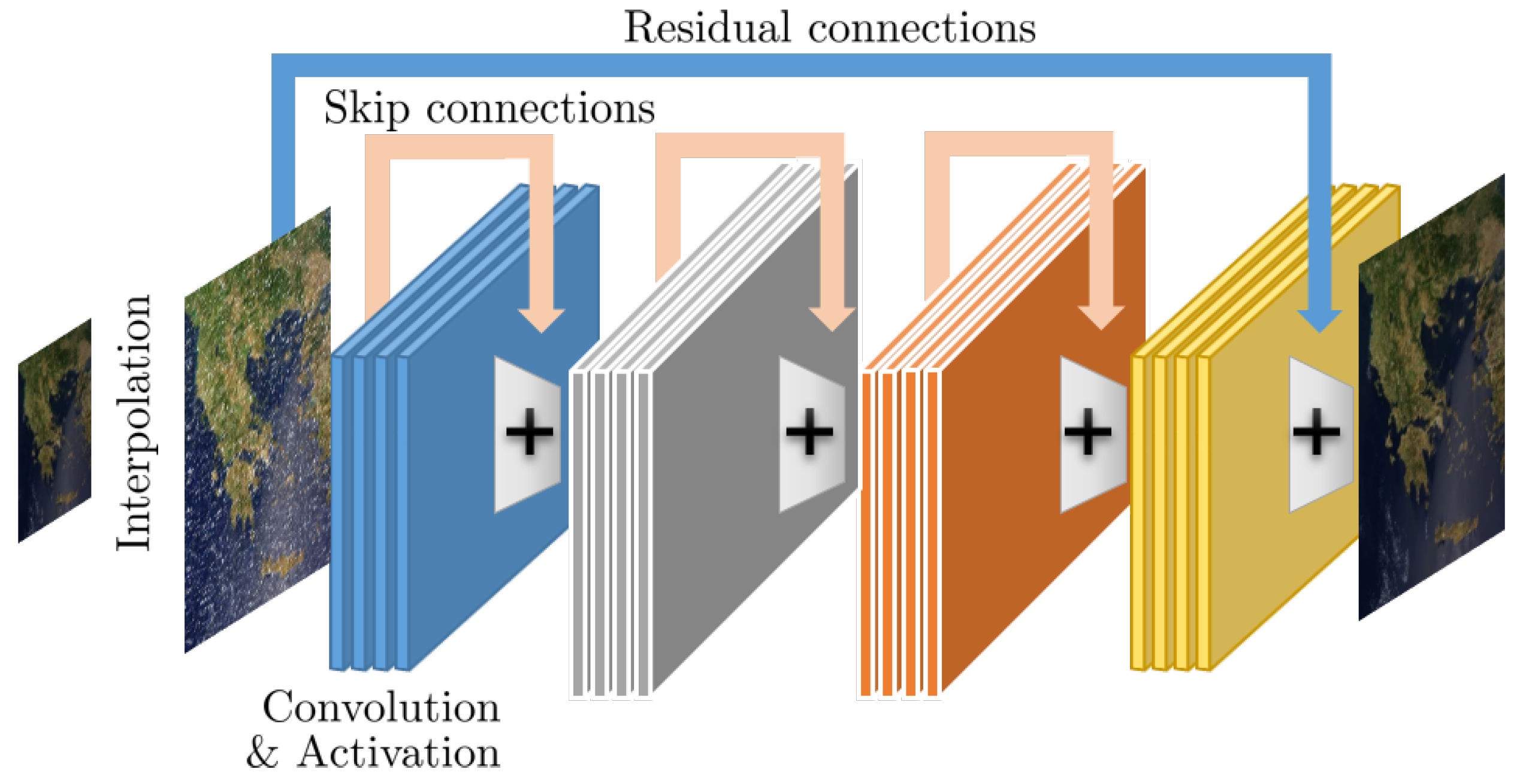
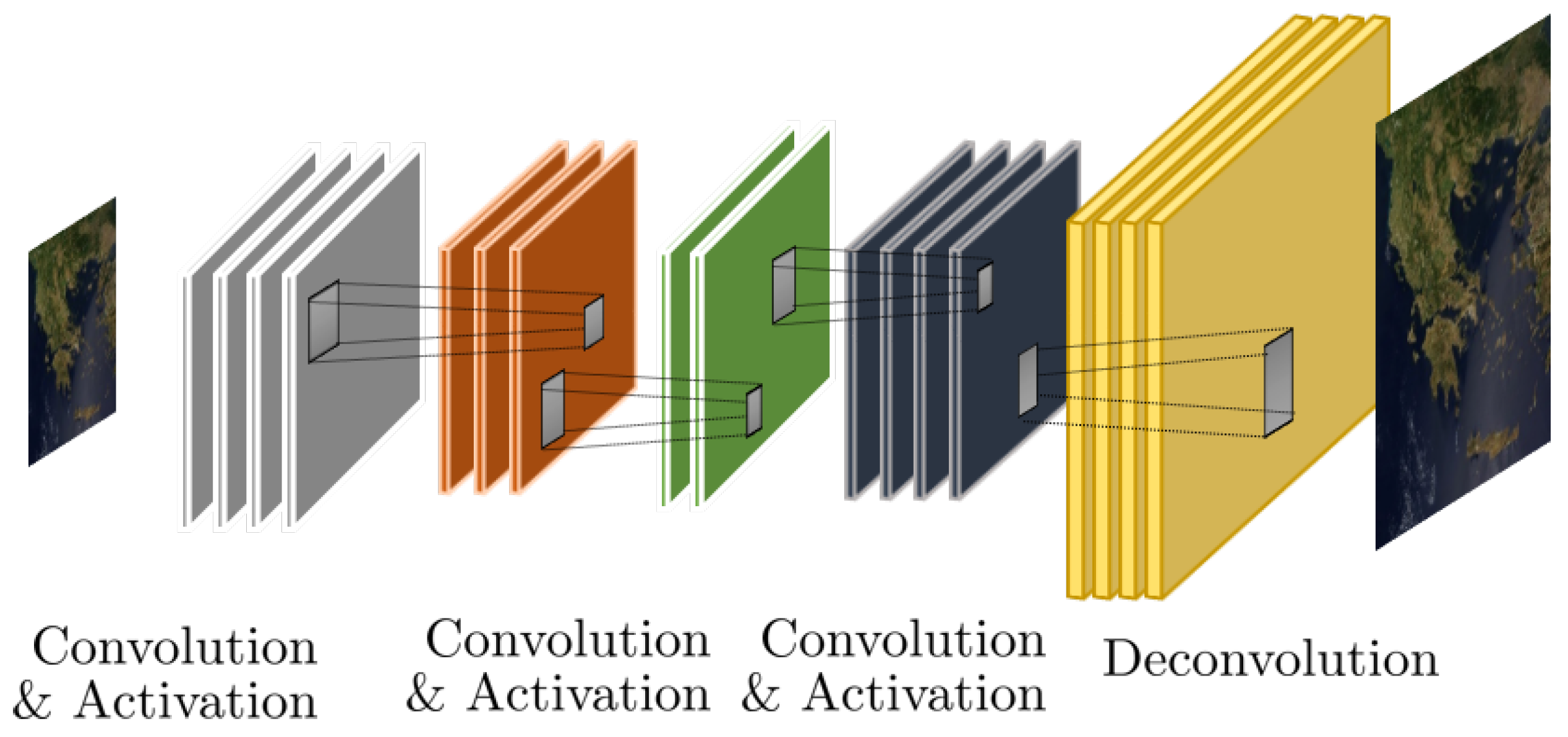
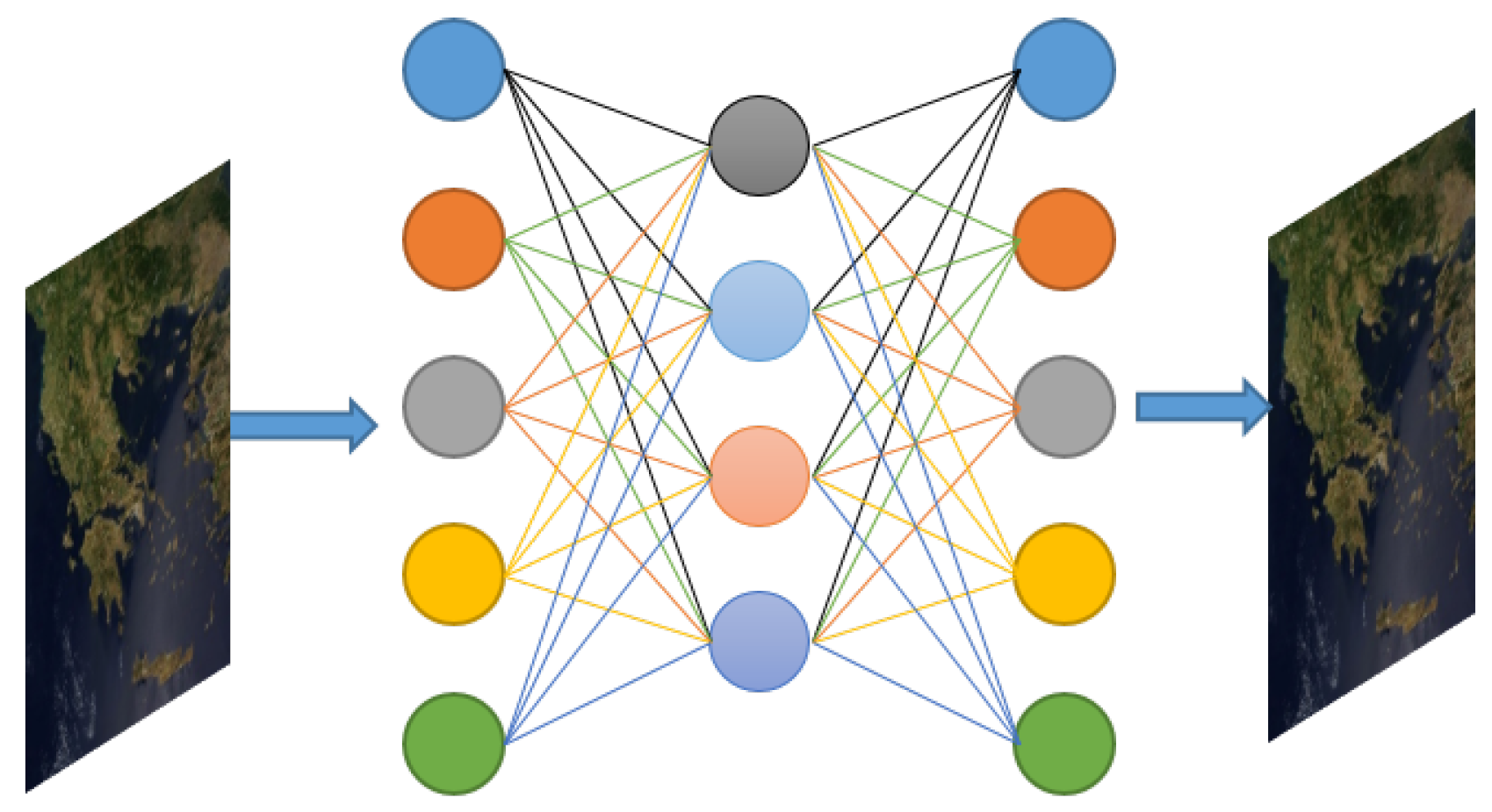
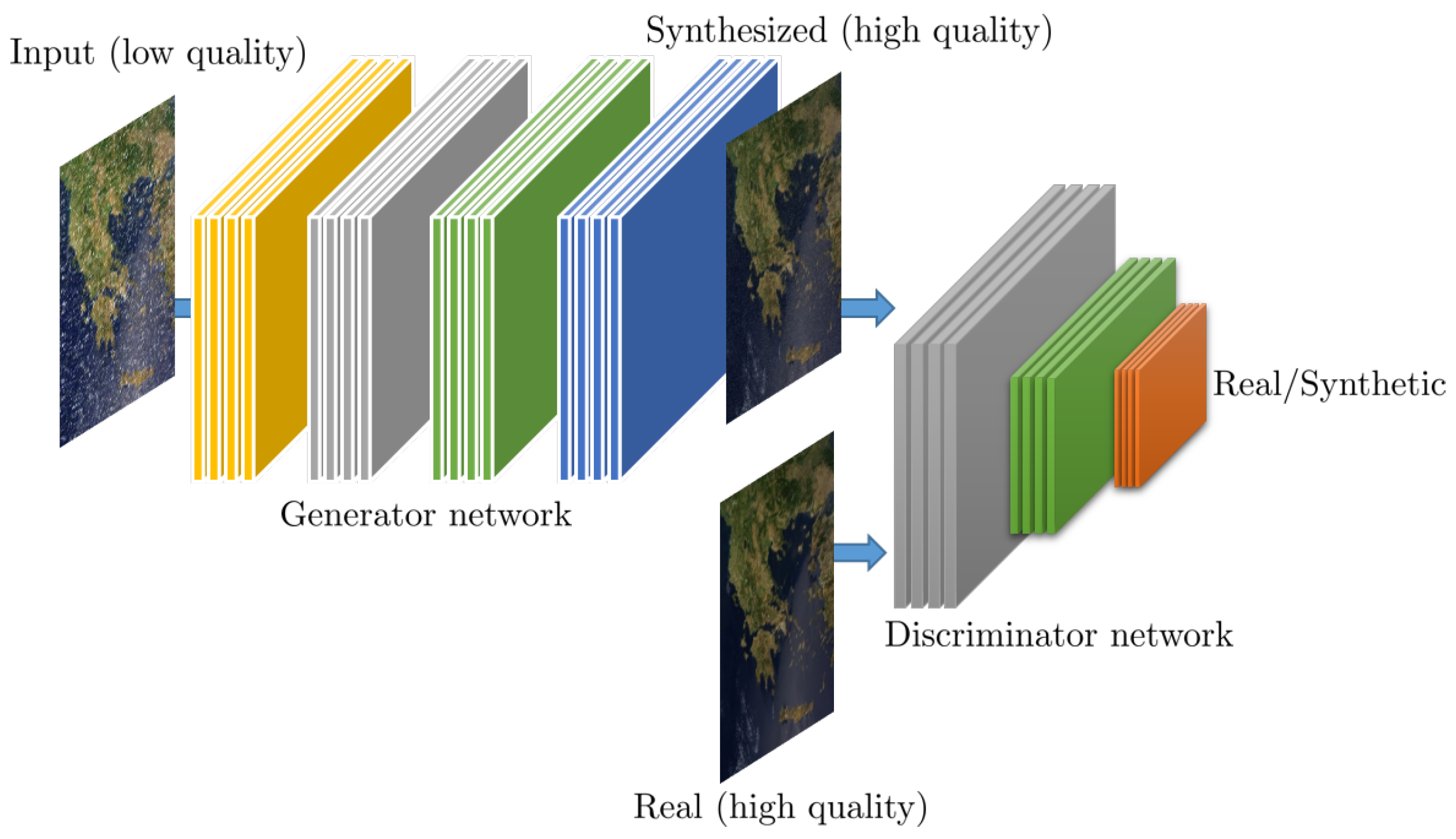
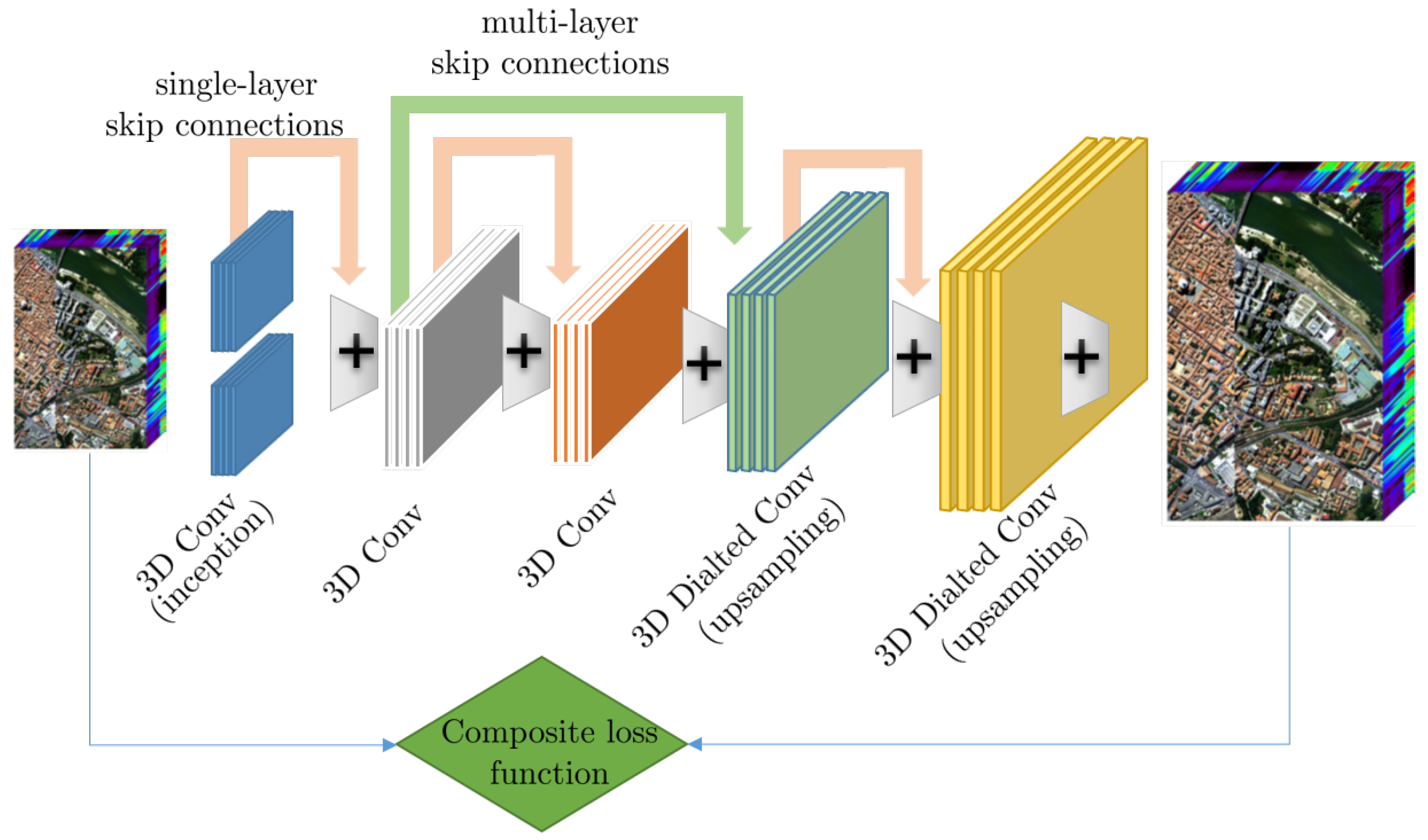
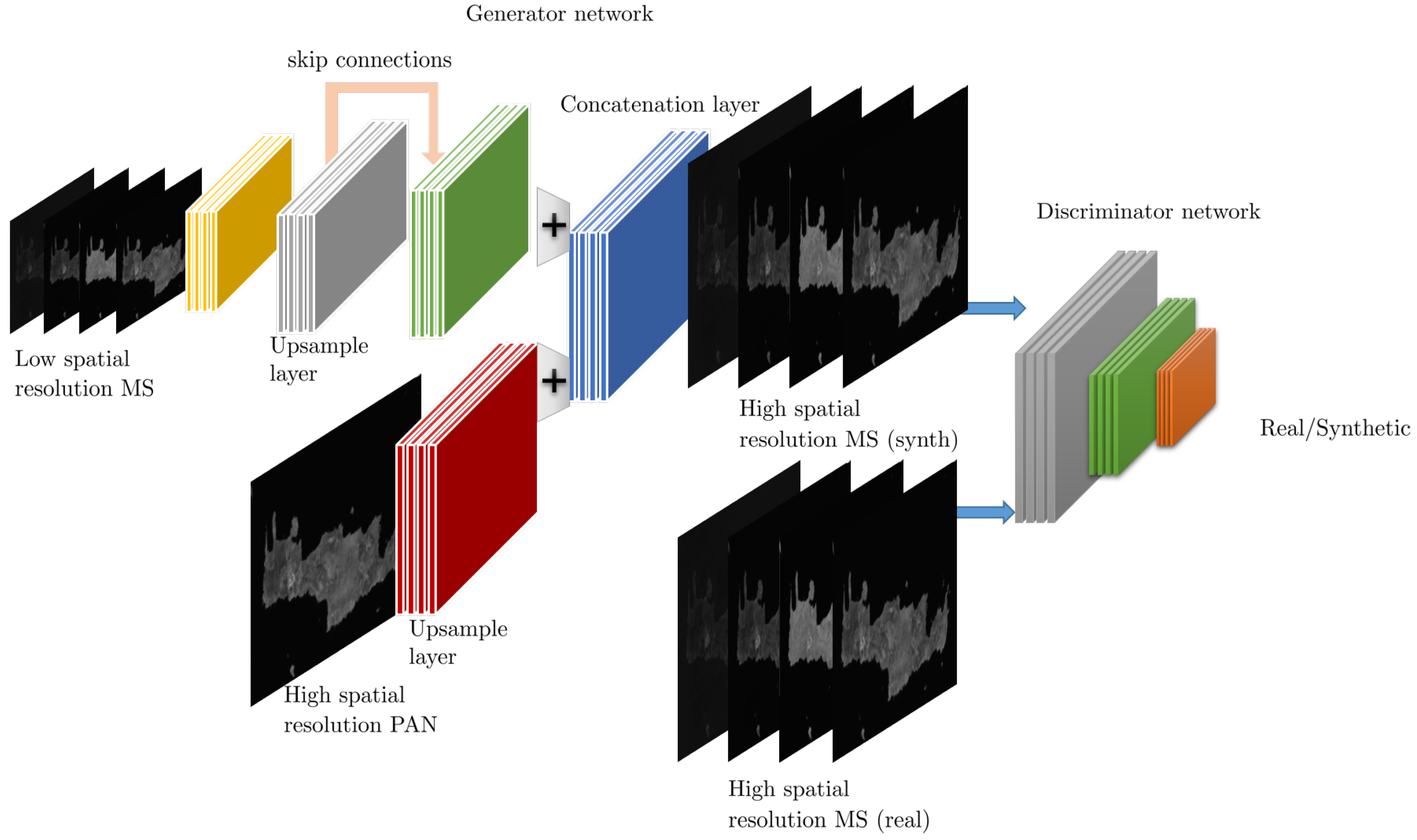
| Methods | Observation Type | Approach |
|---|---|---|
| [51,52,53] | Single-Image/band | single-scale CNN |
| [54,55,56,57,59] | Single-Image/band | multiscale CNN |
| [62,63,64] | Single Image | GAN |
| [68] | HS/MS | multiscale CNN (LPN) |
| [72] | HS/MS | multiple loss CNN |
| [77] | HS/MS | band-specific CNN |
| [78] | HS/MS | 3D-CNN |
| [91,92,93] | Video frames | CNN variants |
| Method | Dataset | Performance Gain | ||
|---|---|---|---|---|
| LGCNet [54] | UC Merced | +9% | +7% | +5% |
| WMCNN [56] | RSSCN7 | +8% | +3% | |
| [62] | UCMERCED/RSSCN7/NWPU-RESIS45 | +9% | +7% | |
| TGAN [63] | UC Merced (airplanes) pre-trained on the DIV2K | +16% | ||
| DMCN [55] | UC Merced | +10% | +8% | +7% |
| MRNN [59] | NWPU-RESISC45 | +13% | ||
| FRDBPN [60] | UC Merced | +5% | ||
| EEGAN [64] | Kaggle | +14% | 4% | +13% |
| Method | Dataset | Performance Gain | ||
|---|---|---|---|---|
| [68] | UC Merced | +2% | ||
| MLFN [72] | UC Merced | +11% | ||
| SSIN [77] | UC Merced | +8% | +6% | +4% |
| 3D-FCNN [78] | UC Merced | +9% | +5% | +3% |
| Method | Approach |
|---|---|
| [97,98,100,101] | AE variants |
| [76,102] | CNN based on SRCNN architecture |
| [99,103,104,105,106] | CNN with residual connections |
| [107,108] | Inception-like CNN for multiscale feature extraction |
| [110] | Target-adapted CNN |
| [111,112] | Two-stream CNN architecture |
| [113] | CNN-based pixel-level regression over multiple scales |
| [114] | Two CNNs associated with spectral and spectral dimension |
| [116] | Two-stream GAN-CNN architecture |
| Method | Dataset | Baseline Approaches | |
|---|---|---|---|
| MTF-GLP | PNN | ||
| PUNET [110,113] | Ikonos/WorldView-2 | - | +15%/+16% |
| DRPNN [99] | QuickBird/WorldView-2 | +35%/+25% | +8%/+5% |
| MSDCNN [107] | QuickBird/WorldView-2 | +35%/+26% | +7%/+5% |
| RSIFNN [111] | Gaofen-1/QuickBird | - | +11%/+8% |
| L1-RL-FT [110] | WorldView-2/WorldView-3 | +38%/+29% | +14%/+37% |
| BDPN [112] | QuickBird/WorldView-3 | - | +25%/+ 11% |
| [115] | WorldView-2 | - | +33% |
| [114] | Pleiades/WorldView-2 | +50%/+26% | +46%/+20% |
| PNN [76] | WorldView-2/Ikonos | +25%/+21% | - |
| PanNet [106] | WorldView-3 | - | +15% |
| PSGAN [116] | QuickBird/GF-1 | - | +18%/+35% |
| Method | Observation Type | Approach |
|---|---|---|
| [120] | HSI + Gaussian noise | CNN with trainable activation function |
| [121,122] | HSI + Gaussian noise | Residual CNN with key band selection |
| [123] | Aerial RGB + Gaussian noise | Multiscale CNN for learning residual noise component |
| [124] | HSI + Gaussian noise | Multiscale 3D CNN using neighboring bands |
| [125] | HSI + Gaussian/Poisson noise | Multiscale 3D CNN w/atrous layers |
| [127] | HSI + mixed noise | 2D CNN with residual connection |
| [127,128] | Noise & Blur | GAN architecture |
| [131] | Missing spatial measurements | CNN-based fusion using auxiliary observations |
| [132,133] | Missing temporal measurements | CNN for recovery via temporal prediction |
| [134] | Cloud occlusions | GAN |
| [137] | Missing MS observations | cGAN using multitemporal MS and SAR observation |
| Method | Dataset | Comparison to BM4D [139] |
|---|---|---|
| HDnTSDL [122] | Washington DC Mall (HYDICE) | +12%/+10%/+13% (Gaussian w/ = 15/25/50) |
| SSDRN [121] | PAVIA (ROSIS) | +2%/+3%/+4% (Gaussian w/ = 15/25/50) |
| SSGN [126] | Pavia (ROSIS), Washington DC Mall (HYDICE), Indian Pines (AVIRIS) | +20%/+17% (Gaussian, Gaussian+stripe) |
| [124] | Washington DC Mall (HYDICE) | +6%/+8%/+11% (Gaussian w/ = 25/50/100) |
| [125] | Pavia University (ROSIS), Indian Pines (AVIRIS) | +1%/+4% (Gaussian w/ = 10) |
| Method | Inputs | Objective | Approach |
|---|---|---|---|
| [142] | MS and HS | spatial/spectral resolution | 3D-CNN using concatenated observations |
| [143,144] | MS and HS | spatial/spectral resolution | Fusion using two-stream CNNs |
| [145] | MS and HS | spatial/temporal resolution | CNN sub-networks fusion |
| [147] | MS and SAR | NDVI estimation | CNN using concatenated observations |
| [148,150] | RGB and SAR | registration | GAN-based framework |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsagkatakis, G.; Aidini, A.; Fotiadou, K.; Giannopoulos, M.; Pentari, A.; Tsakalides, P. Survey of Deep-Learning Approaches for Remote Sensing Observation Enhancement. Sensors 2019, 19, 3929. https://doi.org/10.3390/s19183929
Tsagkatakis G, Aidini A, Fotiadou K, Giannopoulos M, Pentari A, Tsakalides P. Survey of Deep-Learning Approaches for Remote Sensing Observation Enhancement. Sensors. 2019; 19(18):3929. https://doi.org/10.3390/s19183929
Chicago/Turabian StyleTsagkatakis, Grigorios, Anastasia Aidini, Konstantina Fotiadou, Michalis Giannopoulos, Anastasia Pentari, and Panagiotis Tsakalides. 2019. "Survey of Deep-Learning Approaches for Remote Sensing Observation Enhancement" Sensors 19, no. 18: 3929. https://doi.org/10.3390/s19183929
APA StyleTsagkatakis, G., Aidini, A., Fotiadou, K., Giannopoulos, M., Pentari, A., & Tsakalides, P. (2019). Survey of Deep-Learning Approaches for Remote Sensing Observation Enhancement. Sensors, 19(18), 3929. https://doi.org/10.3390/s19183929





