Analysis of Scattering by Plasmonic Gratings of Circular Nanorods Using Lattice Sums Technique
Abstract
:1. Introduction
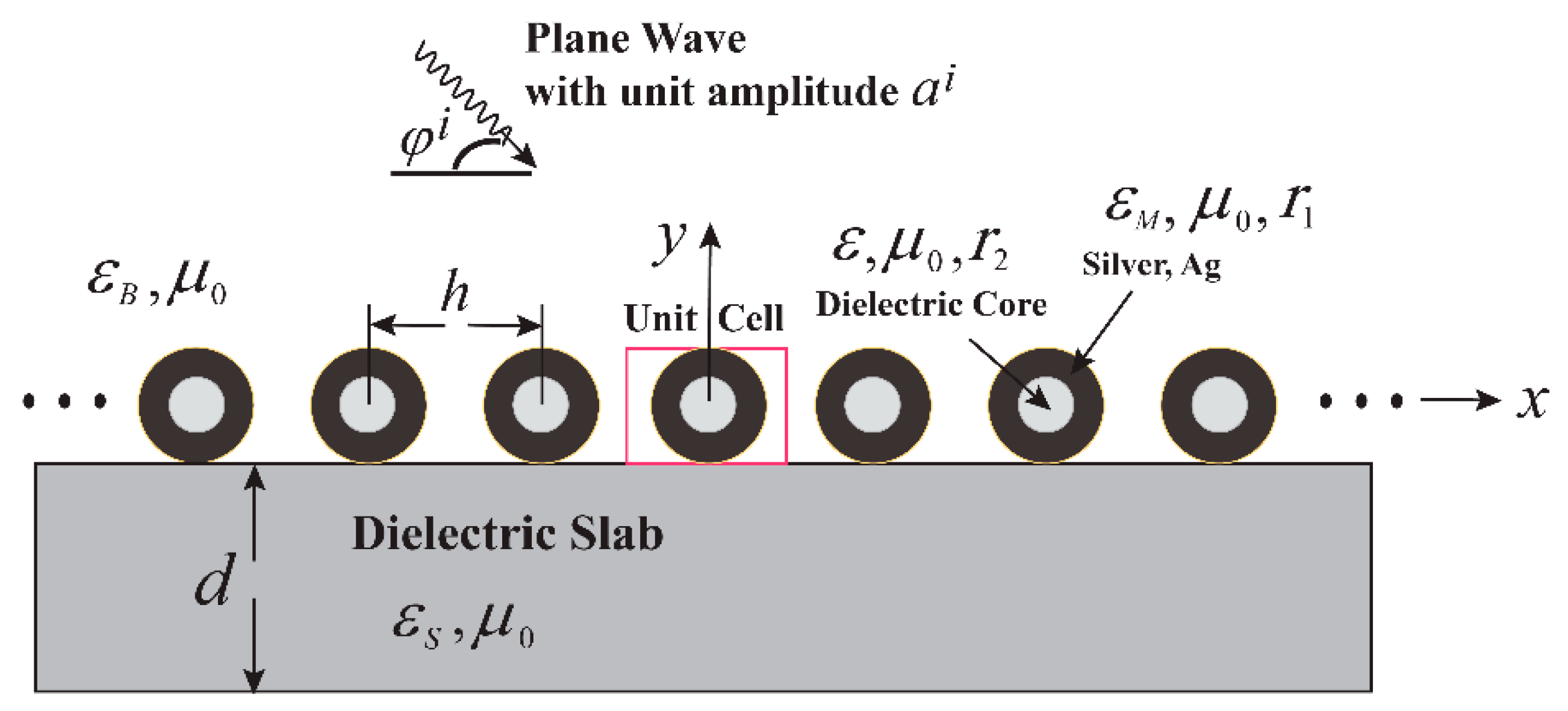
2. Formulation of the Problem
3. Numerical Results and Discussions
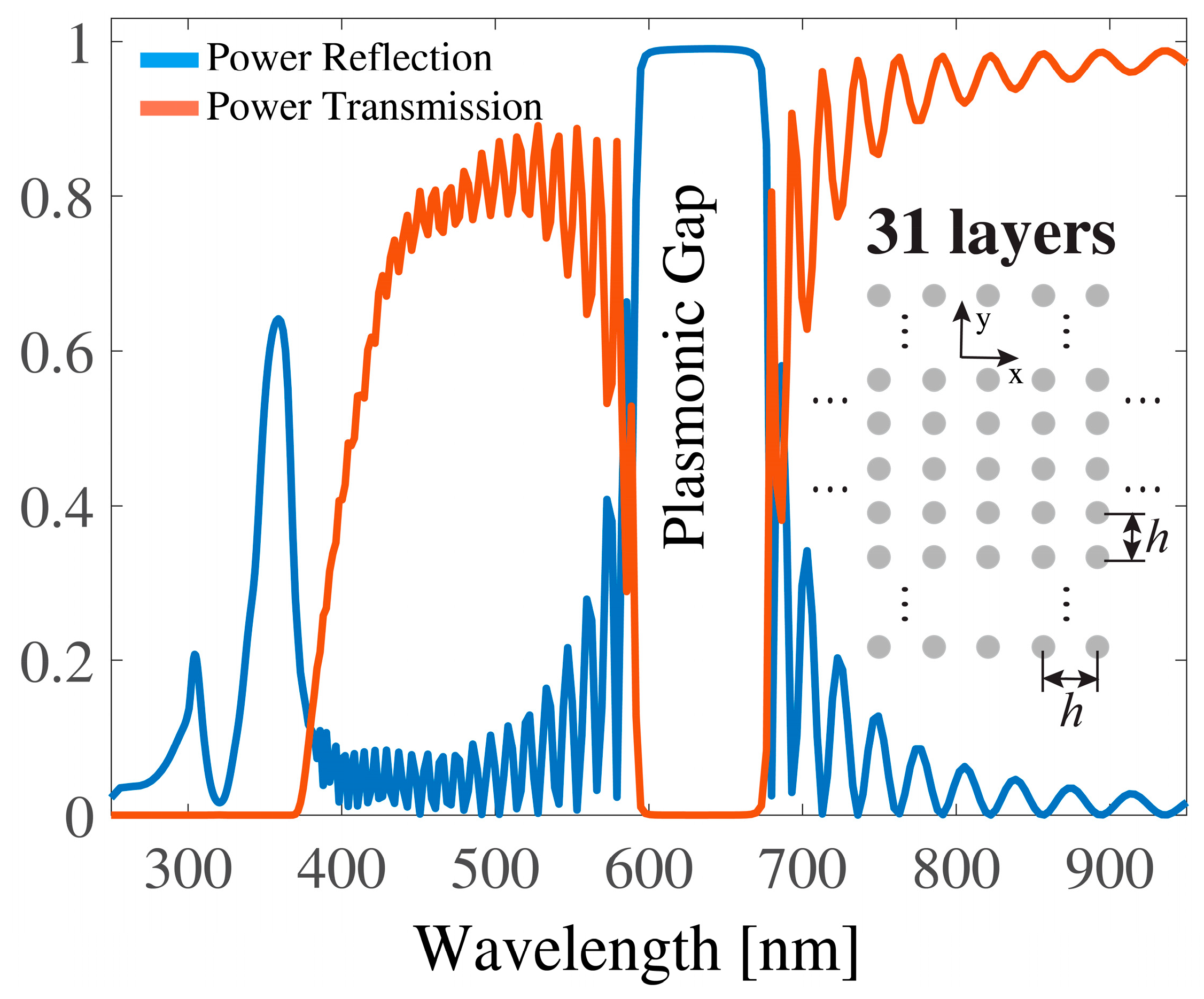
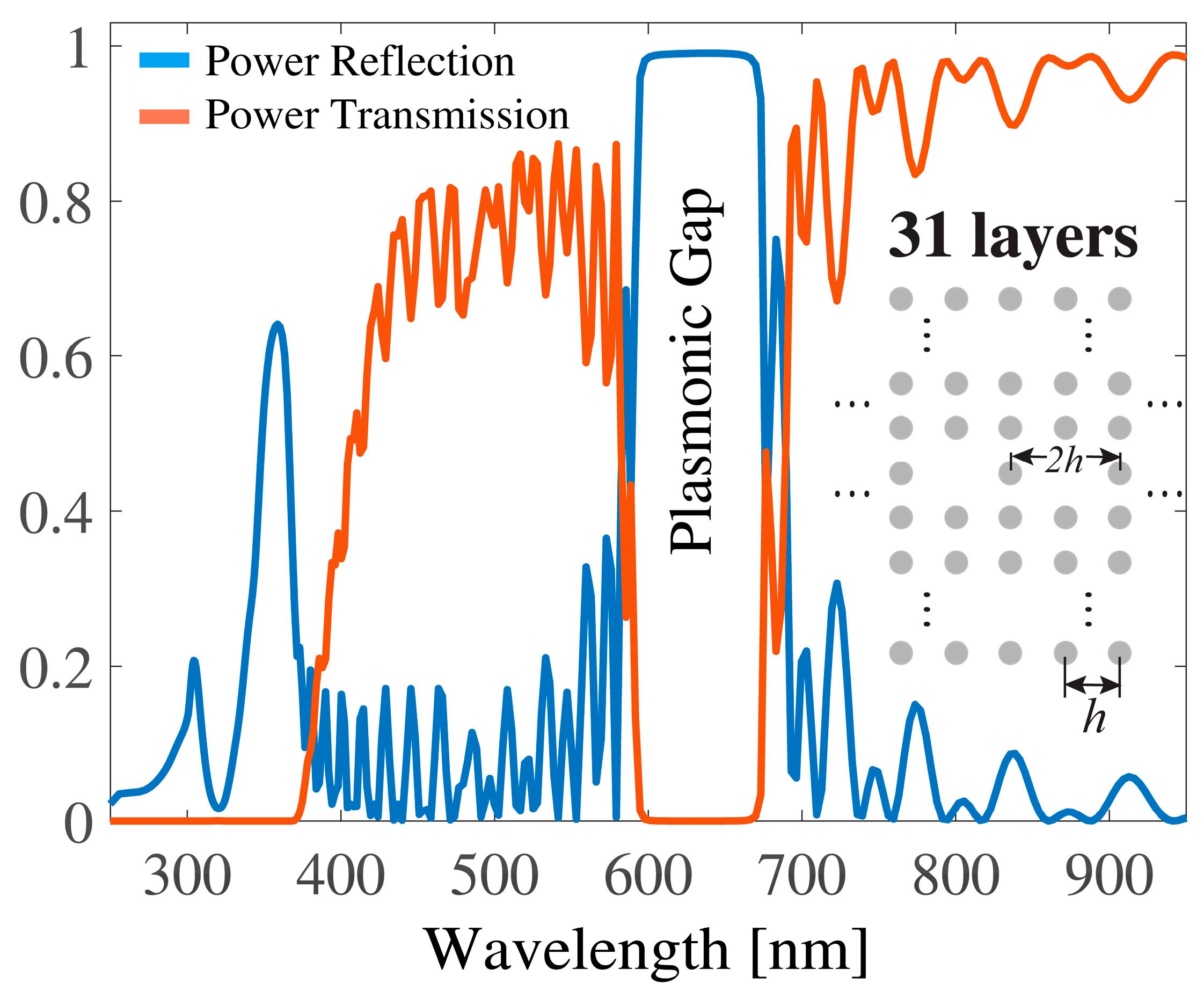
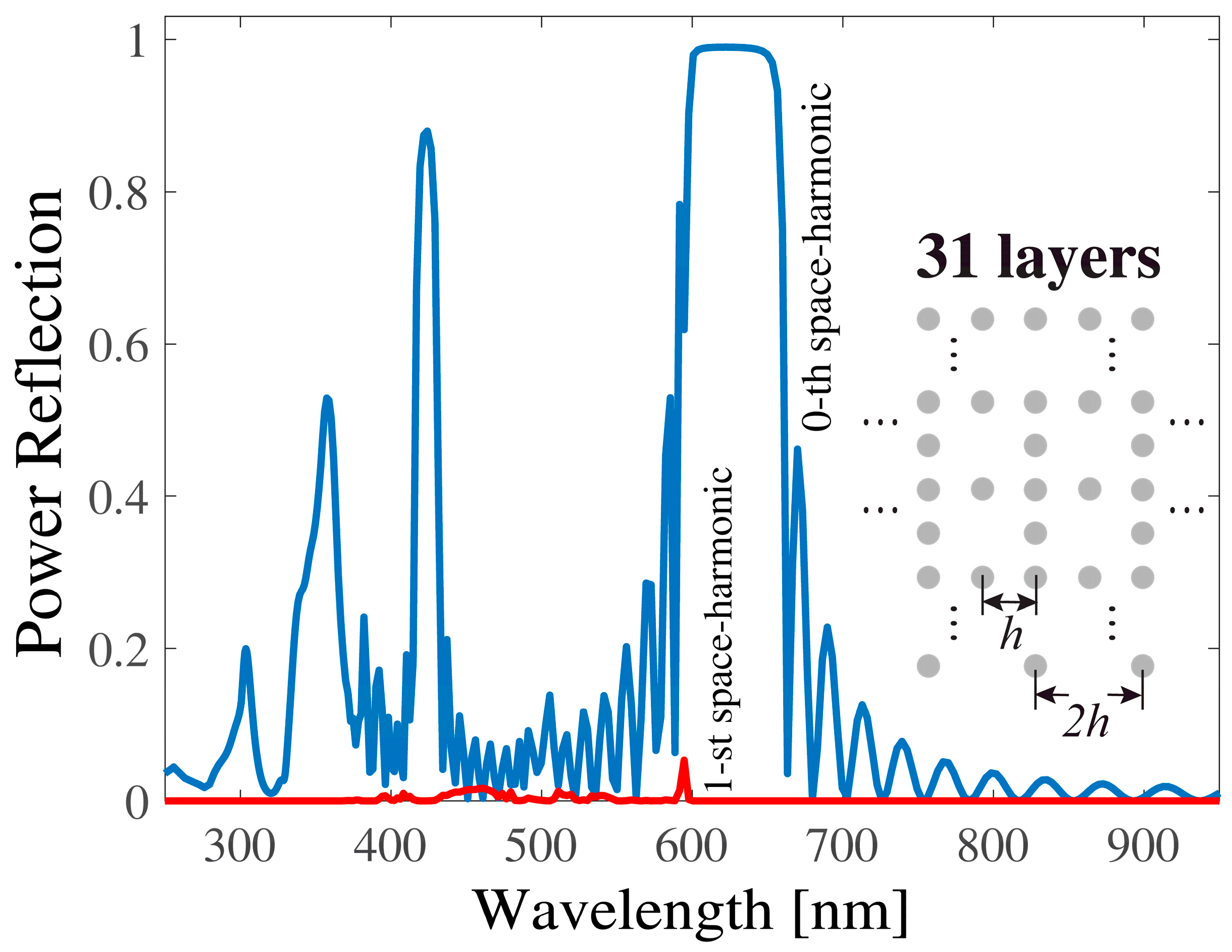
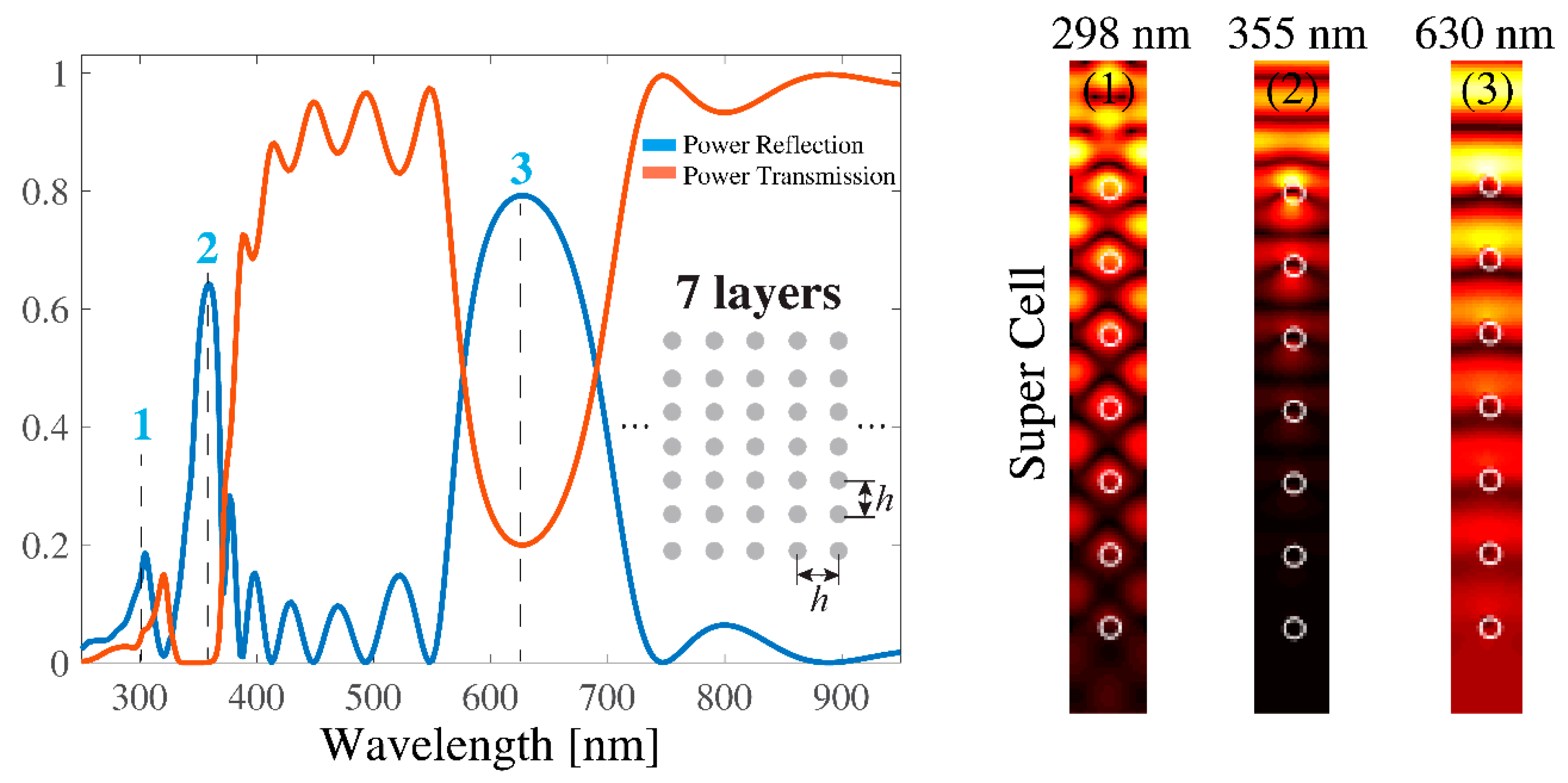
3.1. Light Scattering by Multlayered Structures of Plasmonic Nanocylinders with and without Defects
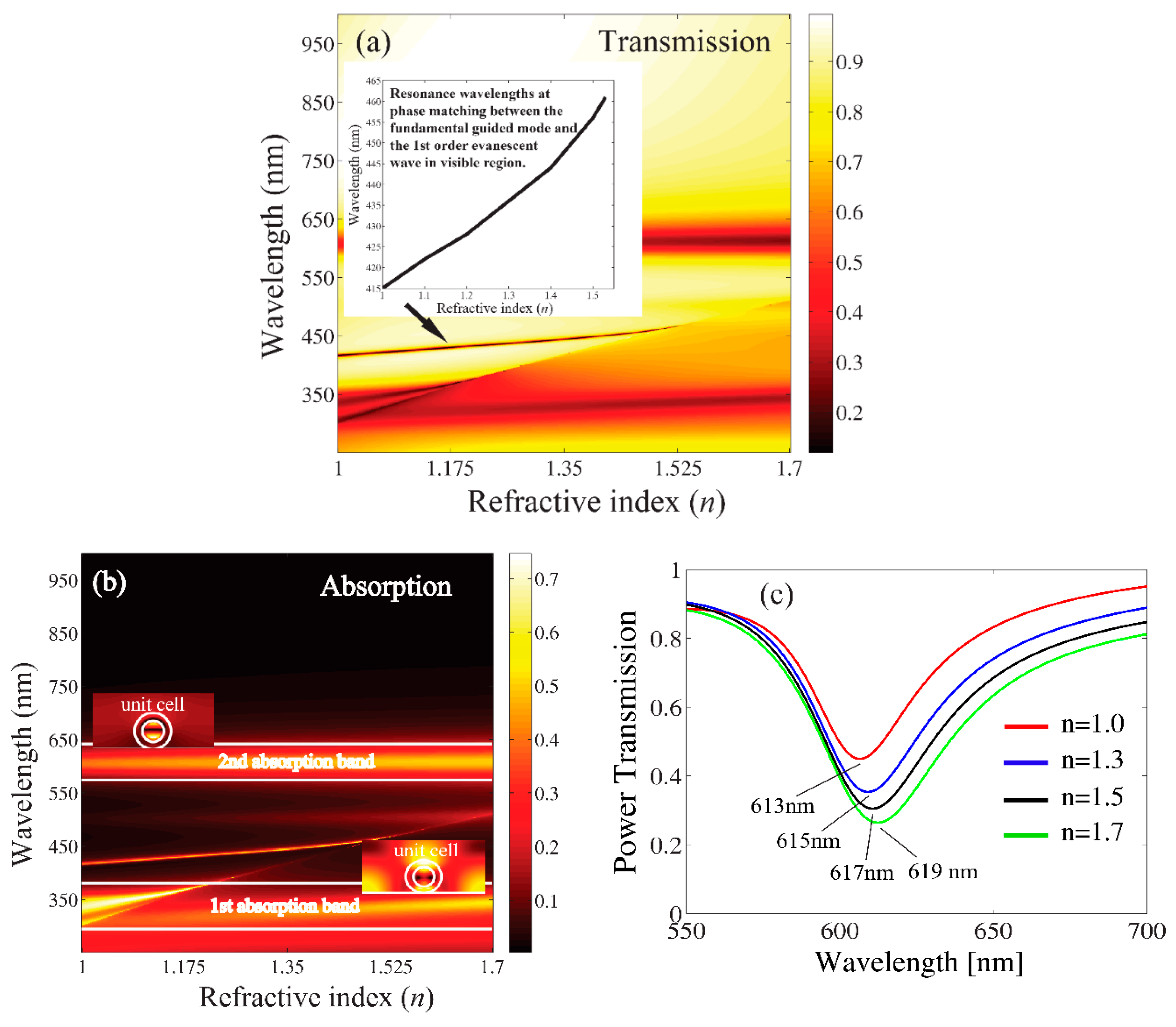
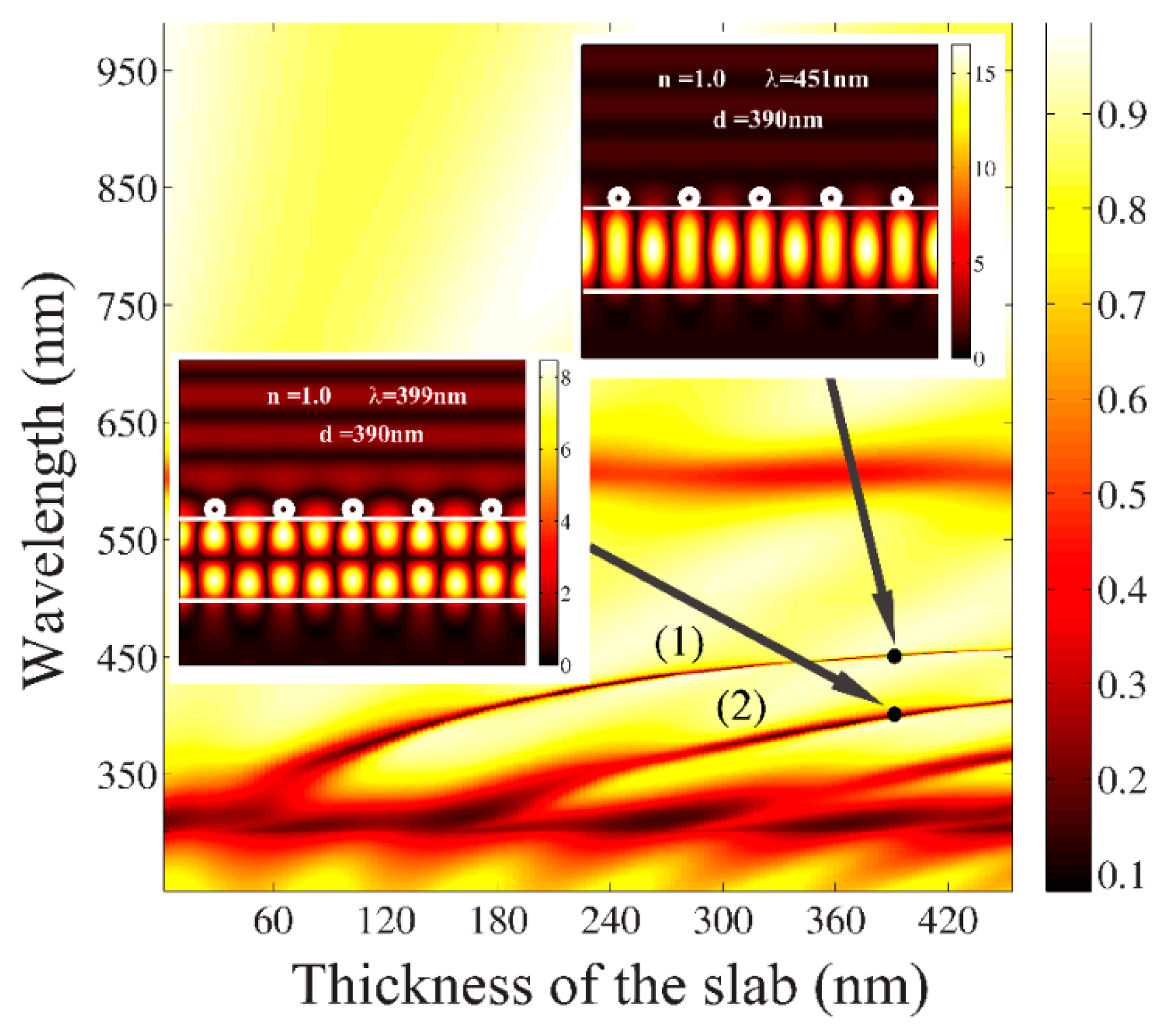
3.2. Coupling between Plasmonic Grating and a Dielectric Slab for Application as a Refractive Index Sensor
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Kravets, V.; Schedin, F.; Grigorenko, A. Extremely narrow plasmon resonances based on diffraction coupling of localized plasmons in arrays of metallic nanoparticles. Phys. Rev. Lett. 2008, 101, 087403. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Ternovsky, V. Light scattering by a thin wire with a surface-plasmon resonance: Bifurcations of the Poynting vector field. Phys. Rev. B 2006, 73, 235432. [Google Scholar] [CrossRef]
- Nguyen-Huu, N.; Cada, M.; Pistora, J. Imperfectly geometric shapes of nanograting structures as solar absorbers with superior performance for solar cells. Opt. Express 2014, 22, A282–A294. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Fan, S. Superscattering of light from subwavelength nanostructures. Phys. Rev. Lett. 2010, 105, 013901. [Google Scholar] [CrossRef] [PubMed]
- Mirzaei, A.; Shadrivov, I.V.; Miroshnichenko, A.E.; Kivshar, Y.S. Cloaking and enhanced scattering of core-shell plasmonic nanowires. Opt. Express 2013, 21, 10454–10459. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen-Huu, N.; Cada, M.; Pistora, J.; Yasumoto, K. Tunable optical filter based on gold and silver double-sided gratings and its application as plasmonic sensor. J. Lightwave Technol. 2014, 32, 3477–3484. [Google Scholar] [CrossRef]
- Natarov, D.; Sauleau, R.; Nosich, A. Periodicity-enhanced plasmon resonances in the scattering of light by sparse finite gratings of circular silver nanowires. IEEE Photonics Technol. Lett. 2012, 24, 43–45. [Google Scholar]
- Mayer, K.; Hafner, J. Localized surface plasmon resonance sensors. Chem. Rev. 2011, 111, 3828–3857. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Wei, H.; Zhang, S.; Xu, H. Recent advances in plasmonic sensors. Sensors 2014, 14, 7959–7973. [Google Scholar] [CrossRef] [PubMed]
- Yasumoto, K.; Toyama, H.; Kushta, T. Accurate analysis of two-dimensional electromagnetic scattering from multilayered periodic arrays of circular cylinders using lattice sums technique. IEEE Trans. Antennas Propag. 2004, 52, 2603–2611. [Google Scholar] [CrossRef]
- Yasumoto, K. Electromagnetic Theory and Applications for Photonic Crystals; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Jandieri, V.; Baccarelli, P.; Valerio, G.; Schettini, G. 1-D periodic lattice sums for complex and leaky waves in 2-D structures using higher-order Ewald formulation. IEEE Trans. Antennas Propag. 2019, 67, 2364–2378. [Google Scholar] [CrossRef]
- Jandieri, V.; Yasumoto, K. Electromagnetic scattering by layered cylindrical arrays of circular rods. IEEE Trans. Antennas Propag. 2011, 59, 2437–2441. [Google Scholar] [CrossRef]
- Felbacq, D.; Tayeb, G.; Maystre, D. Scattering by a random set of parallel cylinders. J. Opt. Soc. Am. A 1994, 11, 2526–2538. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Jandieri, V.; Yasumoto, K.; Jia, H. Effect of Periodic Defects on Electromagnetic Scattering by Two-Dimensional Photonic Crystals. J. Infrared Millim. Waves 2006, 27, 301–317. [Google Scholar] [CrossRef]
- Jandieri, V.; Okropiridze, L.; Yasumoto, K.; Erni, D.; Pistora, J. Efficient Analysis Method of Light Scattering by a Grating of Plasmonic Nanorods. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 1436–1448. [Google Scholar] [CrossRef]
- Jandieri, V.; Yasumoto, K.; Pistora, J. Rigorous analysis of electromagnetic scattering by grating of plasmonic nanorods coupled to magneto-optical slab. IEEE Trans. Magn. 2017, 53, 1000306. [Google Scholar] [CrossRef]
- Jia, H.; Yasumoto, K.; Toyama, H. Reflection and transmission properties of layered periodic arrays of circular cylinders embedded in magnetized ferrite slab. IEEE Trans. Antennas Propag. 2005, 53, 1145–1153. [Google Scholar]
- Luk’yanchuk, B.; Zheludev, N.; Maier, S.; Halas, N.; Nordlander, P.; Giessen, H.; Chong, C. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jandieri, V.; Yasumoto, K.; Pistora, J.; Erni, D. Analysis of Scattering by Plasmonic Gratings of Circular Nanorods Using Lattice Sums Technique. Sensors 2019, 19, 3923. https://doi.org/10.3390/s19183923
Jandieri V, Yasumoto K, Pistora J, Erni D. Analysis of Scattering by Plasmonic Gratings of Circular Nanorods Using Lattice Sums Technique. Sensors. 2019; 19(18):3923. https://doi.org/10.3390/s19183923
Chicago/Turabian StyleJandieri, Vakhtang, Kiyotoshi Yasumoto, Jaromir Pistora, and Daniel Erni. 2019. "Analysis of Scattering by Plasmonic Gratings of Circular Nanorods Using Lattice Sums Technique" Sensors 19, no. 18: 3923. https://doi.org/10.3390/s19183923
APA StyleJandieri, V., Yasumoto, K., Pistora, J., & Erni, D. (2019). Analysis of Scattering by Plasmonic Gratings of Circular Nanorods Using Lattice Sums Technique. Sensors, 19(18), 3923. https://doi.org/10.3390/s19183923




