WHSP-Net: A Weakly-Supervised Approach for 3D Hand Shape and Pose Recovery from a Single Depth Image
Abstract
1. Introduction
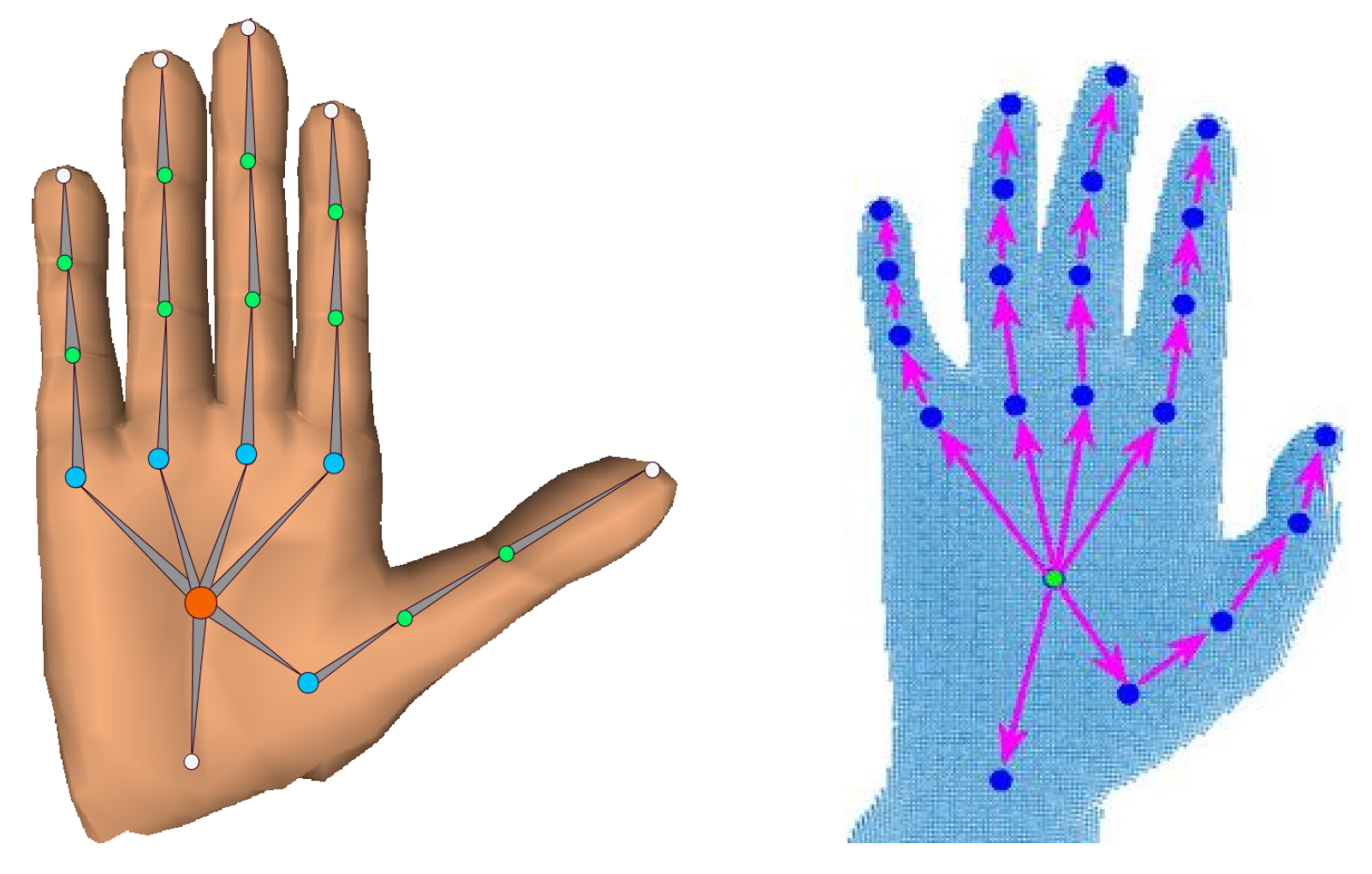
- A new deep network for structured 3D hand pose estimation embeds a simple bone-to-joint layer to respect hand structure in the learning (see Section 4.1).
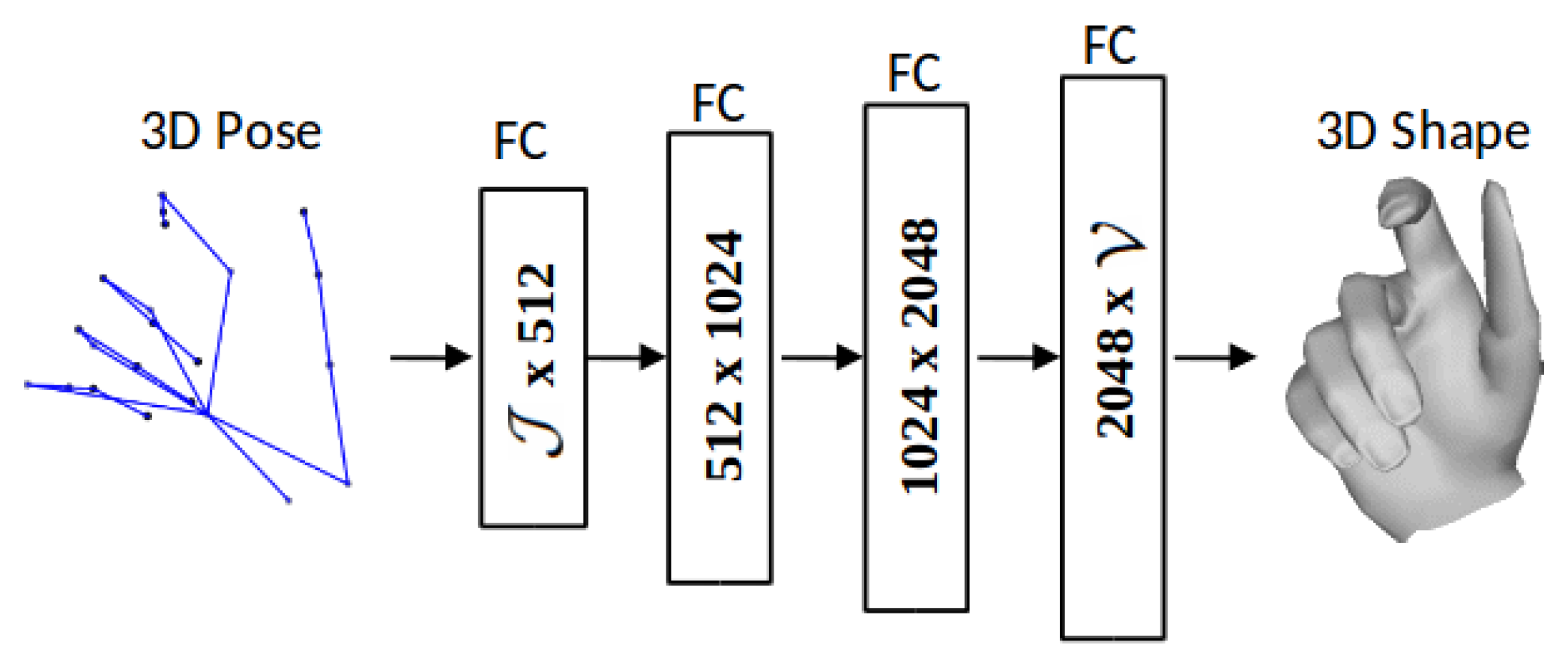
- A novel 3D hand shape decoder generates dense hand mesh vertices given sparse joint positions by mixed training with labeled synthetic data and unlabeled real data (see Section 4.2).
- A new depth image synthesizer reconstructs 2D depth image from dense 3D hand mesh. It acts as a weak-supervision in training, thereby partly compensating the deficiency of missing hand shape ground truth in real benchmarks (see Section 4.3).
- A novel weakly-supervised end-to-end pipeline for 3D hand pose and shape recovery, which we call WHSP-Net, is trained by learning from unlabeled real data to a fully-labeled synthetic data (see Section 4).
2. Related Work
2.1. Depth Based Hand Pose Estimation
2.2. 3D Hand Shape and Pose Estimation
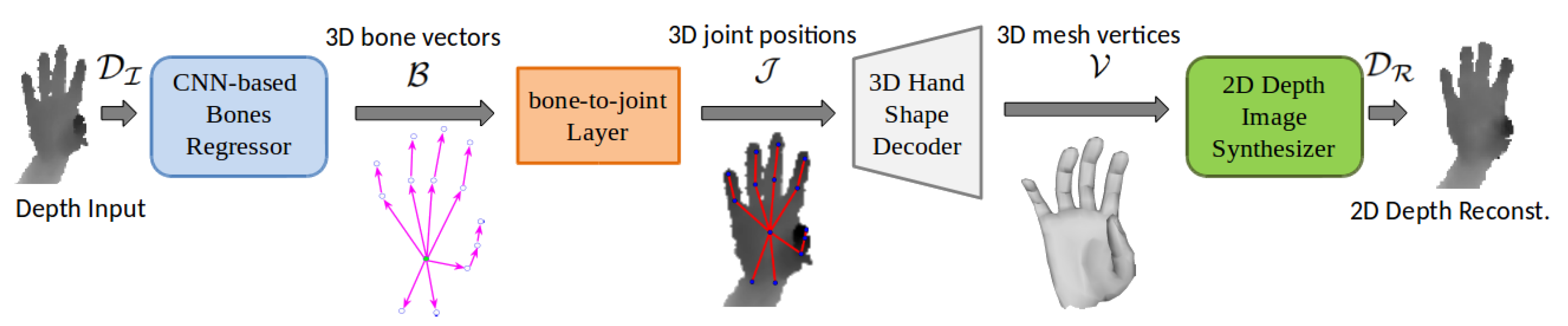
3. Method Overview
4. The Proposed WHSP Approach
4.1. Structured Hand Pose Estimation
4.2. Hand Shape Decoding
4.3. Depth Image Synthesis
5. Network Training
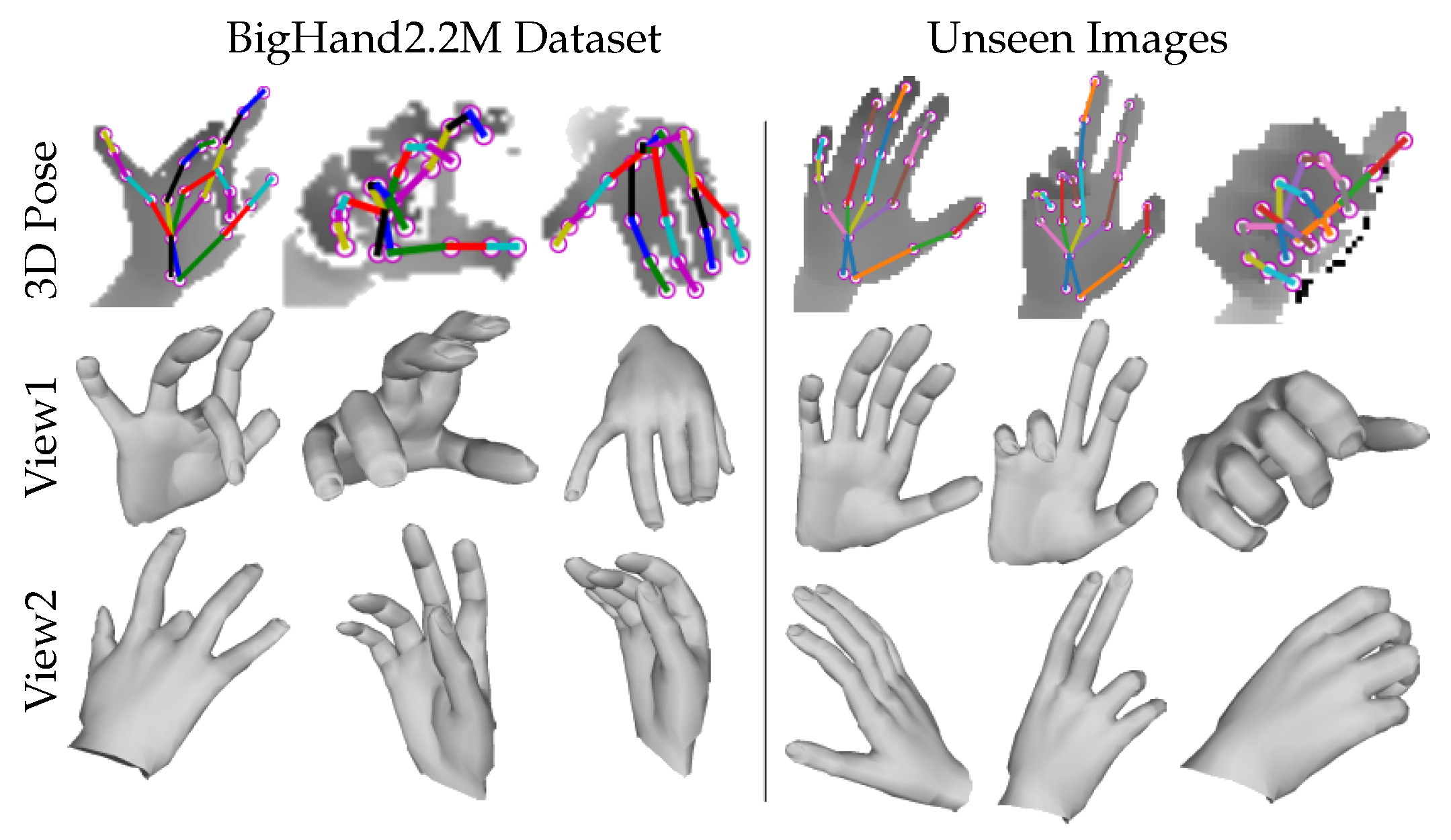
6. Experiments and Results
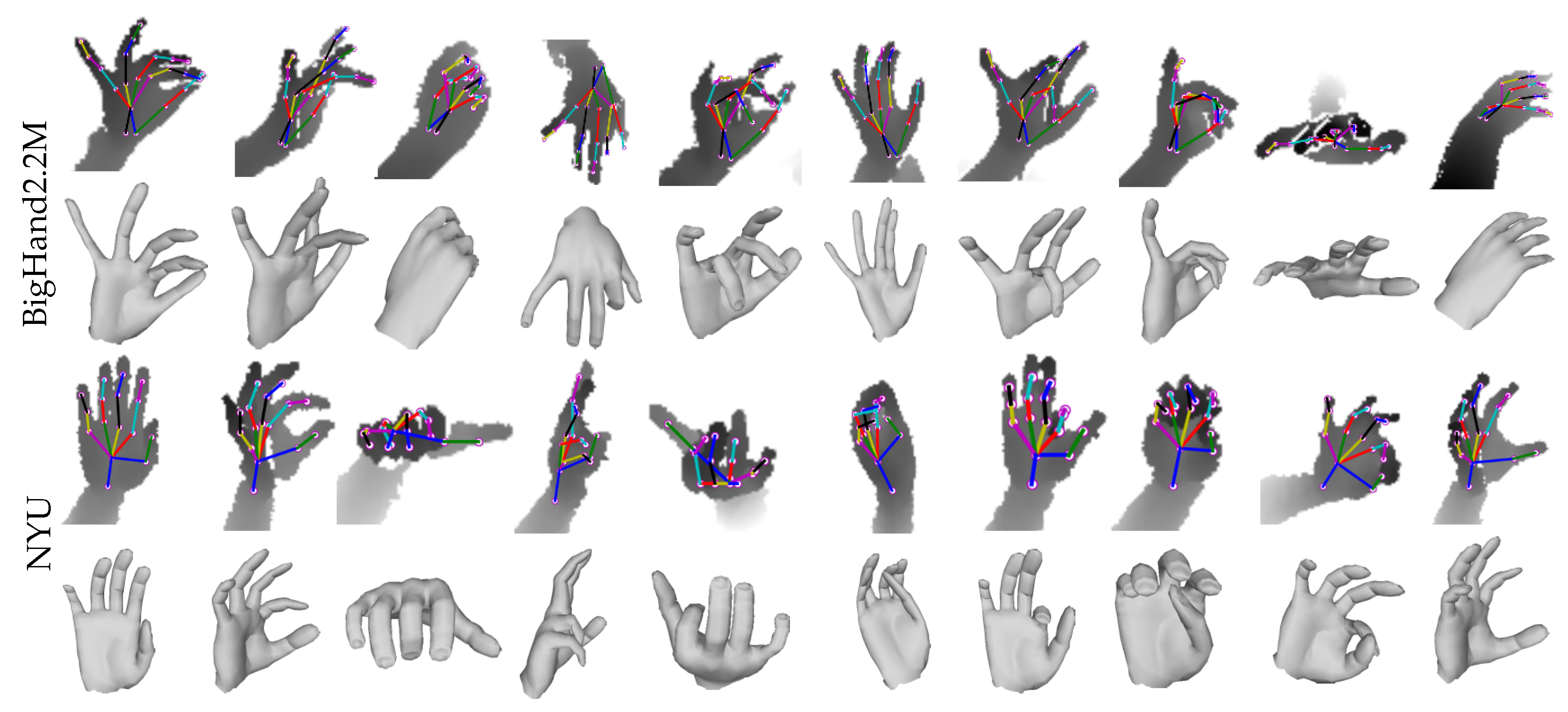
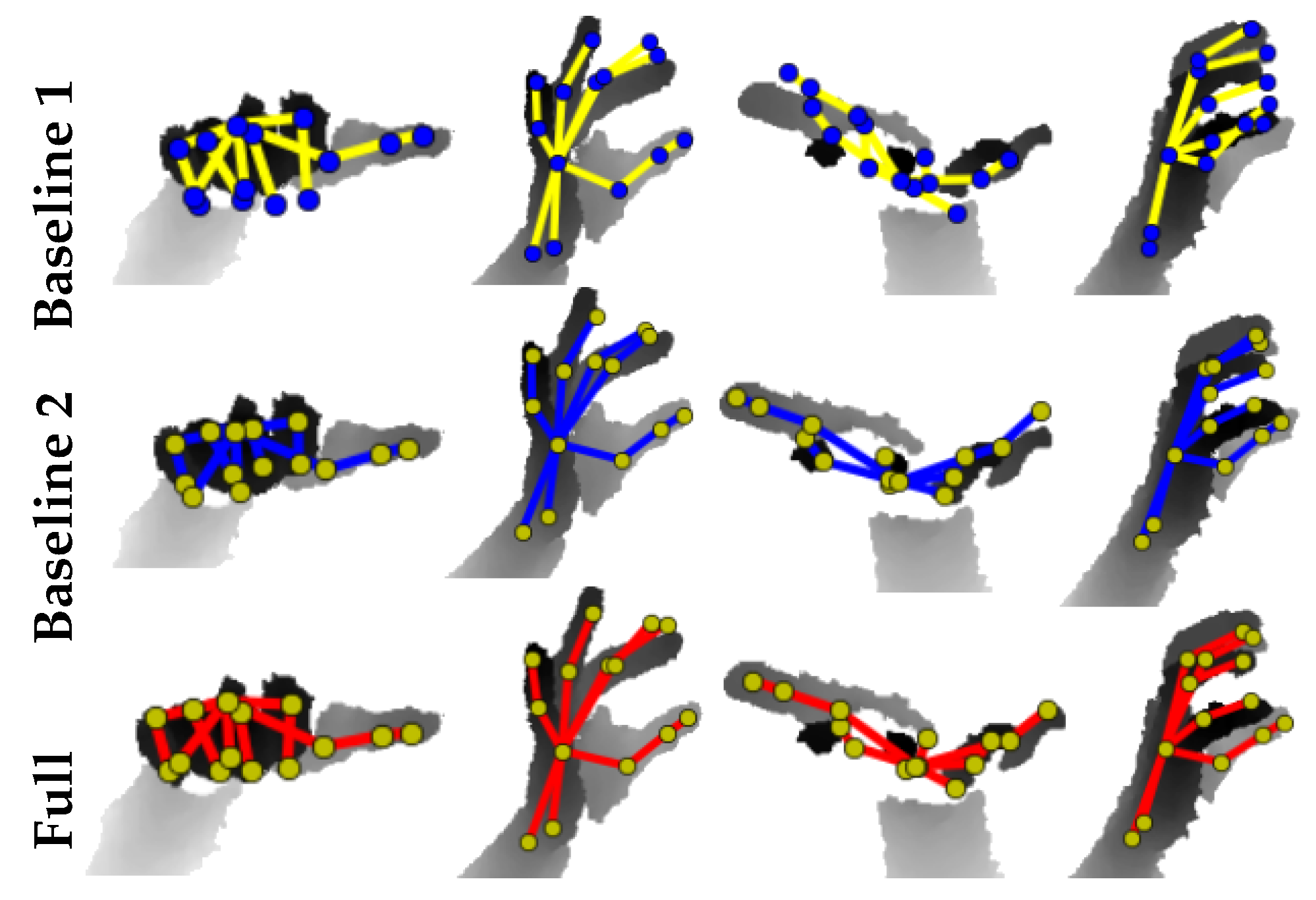
6.1. Datasets, Baselines and Evaluation Metrics
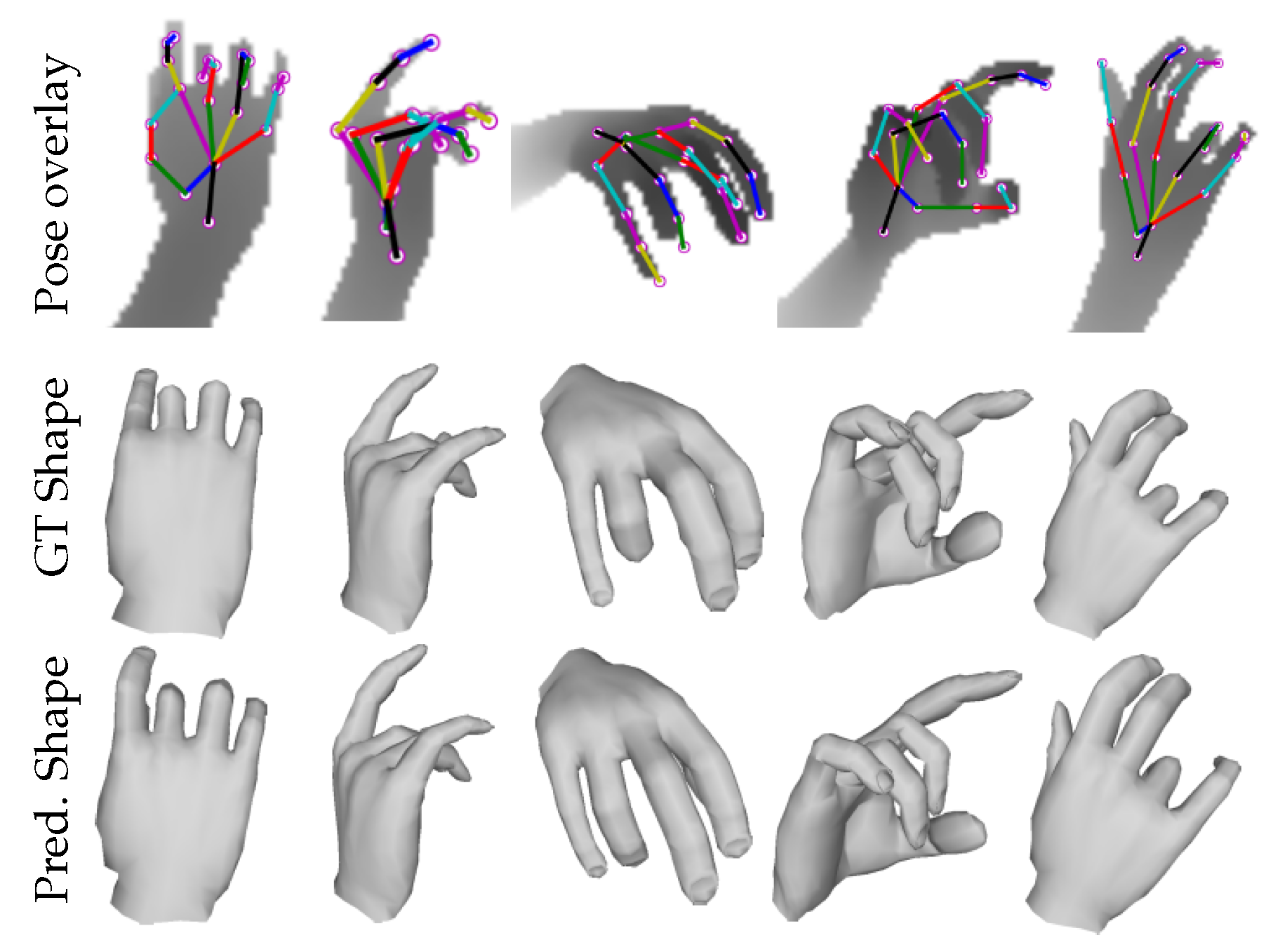
6.2. Evaluation of 3D Hand Shape Estimation
6.3. Evaluation of 3D Hand Pose Estimation
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mueller, F.; Bernard, F.; Sotnychenko, O.; Mehta, D.; Sridhar, S.; Casas, D.; Theobalt, C. GANerated hands for real-time 3D hand tracking from monocular RGB. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 49–59. [Google Scholar]
- Malik, J.; Elhayek, A.; Ahmed, S.; Shafait, F.; Malik, M.; Stricker, D. 3DAirSig: A Framework for Enabling In-Air Signatures Using a Multi-Modal Depth Sensor. Sensors 2018, 18, 3872. [Google Scholar] [CrossRef] [PubMed]
- Rad, M.; Oberweger, M.; Lepetit, V. Feature Mapping for Learning Fast and Accurate 3D Pose Inference from Synthetic Images. arXiv 2017, arXiv:1712.03904. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. V2V-PoseNet: Voxel-to-Voxel Prediction Network for Accurate 3D Hand and Human Pose Estimation from a Single Depth Map. arXiv 2017, arXiv:1711.07399. [Google Scholar]
- Poier, G.; Opitz, M.; Schinagl, D.; Bischof, H. MURAUER: Mapping Unlabeled Real Data for Label AUstERity. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Hilton Waikoloa Village, HI, USA, 8–10 January 2019; pp. 1393–1402. [Google Scholar]
- Yuan, S.; Garcia-Hernando, G.; Stenger, B.; Moon, G.; Chang, J.Y.; Lee, K.M.; Molchanov, P.; Kautz, J.; Honari, S.; Ge, L.; et al. Depth-Based 3D Hand Pose Estimation: From Current Achievements to Future Goals. In Proceedings of the IEEE CVPR, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Ge, L.; Ren, Z.; Yuan, J. Point-to-point regression pointnet for 3d hand pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 475–491. [Google Scholar]
- Oberweger, M.; Lepetit, V. Deepprior++: Improving fast and accurate 3d hand pose estimation. In Proceedings of the ICCV Workshop, Venice, Italy, October 22–29 2017; Volume 840, p. 2. [Google Scholar]
- Wan, C.; Probst, T.; Van Gool, L.; Yao, A. Dense 3d regression for hand pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 5147–5156. [Google Scholar]
- Zhou, X.; Wan, Q.; Zhang, W.; Xue, X.; Wei, Y. Model-based deep hand pose estimation. arXiv 2016, arXiv:1606.06854. [Google Scholar]
- Malik, J.; Elhayek, A.; Stricker, D. Simultaneous Hand Pose and Skeleton Bone-Lengths Estimation from a Single Depth Image. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Dibra, E.; Wolf, T.; Oztireli, C.; Gross, M. How to Refine 3D Hand Pose Estimation from Unlabelled Depth Data? In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Sun, X.; Shang, J.; Liang, S.; Wei, Y. Compositional human pose regression. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, October 22–29 2017; Volume 2, p. 7. [Google Scholar]
- Taylor, J.; Stebbing, R.; Ramakrishna, V.; Keskin, C.; Shotton, J.; Izadi, S.; Hertzmann, A.; Fitzgibbon, A. User-specific hand modeling from monocular depth sequences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 644–651. [Google Scholar]
- Khamis, S.; Taylor, J.; Shotton, J.; Keskin, C.; Izadi, S.; Fitzgibbon, A. Learning an efficient model of hand shape variation from depth images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 2540–2548. [Google Scholar]
- Joseph Tan, D.; Cashman, T.; Taylor, J.; Fitzgibbon, A.; Tarlow, D.; Khamis, S.; Izadi, S.; Shotton, J. Fits like a glove: Rapid and reliable hand shape personalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 5610–5619. [Google Scholar]
- Tagliasacchi, A.; Schröder, M.; Tkach, A.; Bouaziz, S.; Botsch, M.; Pauly, M. Robust Articulated-ICP for Real-Time Hand Tracking. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2015; Volume 34, pp. 101–114. [Google Scholar]
- Tkach, A.; Tagliasacchi, A.; Remelli, E.; Pauly, M.; Fitzgibbon, A. Online generative model personalization for hand tracking. ACM Trans. Graph. (TOG) 2017, 36, 243. [Google Scholar] [CrossRef]
- Remelli, E.; Tkach, A.; Tagliasacchi, A.; Pauly, M. Low-dimensionality calibration through local anisotropic scaling for robust hand model personalization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2535–2543. [Google Scholar]
- Sanchez-Riera, J.; Srinivasan, K.; Hua, K.L.; Cheng, W.H.; Hossain, M.A.; Alhamid, M.F. Robust rgb-d hand tracking using deep learning priors. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2289–2301. [Google Scholar] [CrossRef]
- Malik, J.; Elhayek, A.; Nunnari, F.; Varanasi, K.; Tamaddon, K.; Heloir, A.; Stricker, D. DeepHPS: End-to-end Estimation of 3D Hand Pose and Shape by Learning from Synthetic Depth. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–10 September 2018; pp. 110–119. [Google Scholar]
- Boukhayma, A.; de Bem, R.; Torr, P.H.S. 3D Hand Shape and Pose from Images in the Wild. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Romero, J.; Tzionas, D.; Black, M.J. Embodied hands: Modeling and capturing hands and bodies together. ACM Trans. Graph. (TOG) 2017, 36, 245. [Google Scholar] [CrossRef]
- Ge, L.; Ren, Z.; Li, Y.; Xue, Z.; Wang, Y.; Cai, J.; Yuan, J. 3D Hand Shape and Pose Estimation from a Single RGB Image. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Supancic, J.S.; Rogez, G.; Yang, Y.; Shotton, J.; Ramanan, D. Depth-based hand pose estimation: Data, methods, and challenges. In Proceedings of the IEEE International Conference on Computer Vision, Las Condes, Chile, 11–18 December 2015; pp. 1868–1876. [Google Scholar]
- Chen, X.; Wang, G.; Guo, H.; Zhang, C. Pose Guided Structured Region Ensemble Network for Cascaded Hand Pose Estimation. arXiv 2017, arXiv:1708.03416. [Google Scholar] [CrossRef]
- Madadi, M.; Escalera, S.; Baro, X.; Gonzalez, J. End-to-end Global to Local CNN Learning for Hand Pose Recovery in Depth data. arXiv 2017, arXiv:1705.09606. [Google Scholar]
- Ye, Q.; Kim, T.K. Occlusion-aware Hand Pose Estimation Using Hierarchical Mixture Density Network. arXiv 2017, arXiv:1711.10872. [Google Scholar]
- Ge, L.; Liang, H.; Yuan, J.; Thalmann, D. Robust 3D hand pose estimation in single depth images: From single-view CNN to multi-view CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3593–3601. [Google Scholar]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Training a feedback loop for hand pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, Las Condes, Chile, 11–18 December 2015; pp. 3316–3324. [Google Scholar]
- Wang, G.; Chen, X.; Guo, H.; Zhang, C. Region Ensemble Network: Towards Good Practices for Deep 3D Hand Pose Estimation. J. Vis. Commun. Image Represent. 2018, 55, 404–414. [Google Scholar] [CrossRef]
- Wu, Y.; Ji, W.; Li, X.; Wang, G.; Yin, J.; Wu, F. Context-Aware Deep Spatiotemporal Network for Hand Pose Estimation From Depth Images. IEEE Trans. Cybern. 2018. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Wang, G.; Chen, X.; Zhang, C.; Qiao, F.; Yang, H. Region Ensemble Network: Improving Convolutional Network for Hand Pose Estimation. In Proceedings of the ICIP, Beijing, China, 17–20 September 2017. [Google Scholar]
- Tompson, J.; Stein, M.; Lecun, Y.; Perlin, K. Real-time continuous pose recovery of human hands using convolutional networks. ACM Trans. Graph. (ToG) 2014, 33, 169. [Google Scholar] [CrossRef]
- Sinha, A.; Choi, C.; Ramani, K. Deephand: Robust hand pose estimation by completing a matrix imputed with deep features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 4150–4158. [Google Scholar]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Hands deep in deep learning for hand pose estimation. In Proceedings of the CVWW, Styria, Austria, 9–11 February 2015. [Google Scholar]
- Malik, J.; Elhayek, A.; Stricker, D. Structure-Aware 3D Hand Pose Regression from a Single Depth Image. In Proceedings of the EuroVR, London, UK, 22–23 October 2018. [Google Scholar]
- Ye, Q.; Yuan, S.; Kim, T.K. Spatial Attention Deep Net with Partial PSO for Hierarchical Hybrid Hand Pose Estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Wan, C.; Yao, A.; Van Gool, L. Hand Pose Estimation from Local Surface Normals. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Wan, C.; Probst, T.; Van Gool, L.; Yao, A. Crossing nets: Combining gans and vaes with a shared latent space for hand pose estimation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xu, C.; Govindarajan, L.N.; Zhang, Y.; Cheng, L. Lie-X: Depth image based articulated object pose estimation, tracking, and action recognition on lie groups. Int. J. Comput. Vis. 2017, 123, 454–478. [Google Scholar] [CrossRef]
- Wu, X.; Finnegan, D.; O’Neill, E.; Yang, Y.L. HandMap: Robust hand pose estimation via intermediate dense guidance map supervision. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 237–253. [Google Scholar]
- Hu, T.; Wang, W.; Lu, T. Hand Pose Estimation with Attention-and-Sequence Network. In Proceedings of the Pacific Rim Conference on Multimedia, Hefei, China, 21–22 September 2018; pp. 556–566. [Google Scholar]
- Wan, C.; Probst, T.; Van Gool, L.; Yao, A. Dense 3D Regression for Hand Pose Estimation. arXiv 2017, arXiv:1711.08996. [Google Scholar]
- Cai, Y.; Ge, L.; Cai, J.; Yuan, J. Weakly-supervised 3d hand pose estimation from monocular rgb images. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 666–682. [Google Scholar]
- Yuan, S.; Ye, Q.; Stenger, B.; Jain, S.; Kim, T.K. Bighand2. 2m benchmark: Hand pose dataset and state of the art analysis. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2605–2613. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 37–49. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014. [Google Scholar]
- Tang, D.; Jin Chang, H.; Tejani, A.; Kim, T.K. Latent regression forest: Structured estimation of 3d articulated hand posture. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 3786–3793. [Google Scholar]
- Sun, X.; Wei, Y.; Liang, S.; Tang, X.; Sun, J. Cascaded hand pose regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 824–832. [Google Scholar]
- Chen, X.; Wang, G.; Zhang, C.; Kim, T.K.; Ji, X. SHPR-Net: Deep Semantic Hand Pose Regression From Point Clouds. IEEE Access 2018, 6, 43425–43439. [Google Scholar] [CrossRef]


| Method | 3D Err. | 3D Err. | 3D Err. |
|---|---|---|---|
| DeepModel [10] | – | 11.36 | – |
| HandScales [11] | 6.5 | 9.67 | – |
| DeepHPS [21] | 5.2 | 6.3 | 11.8 |
| Baseline 3 [ours] | 4.37 | 5.24 | 6.37 |
| Full [ours] | 3.71 | 4.32 | 5.12 |
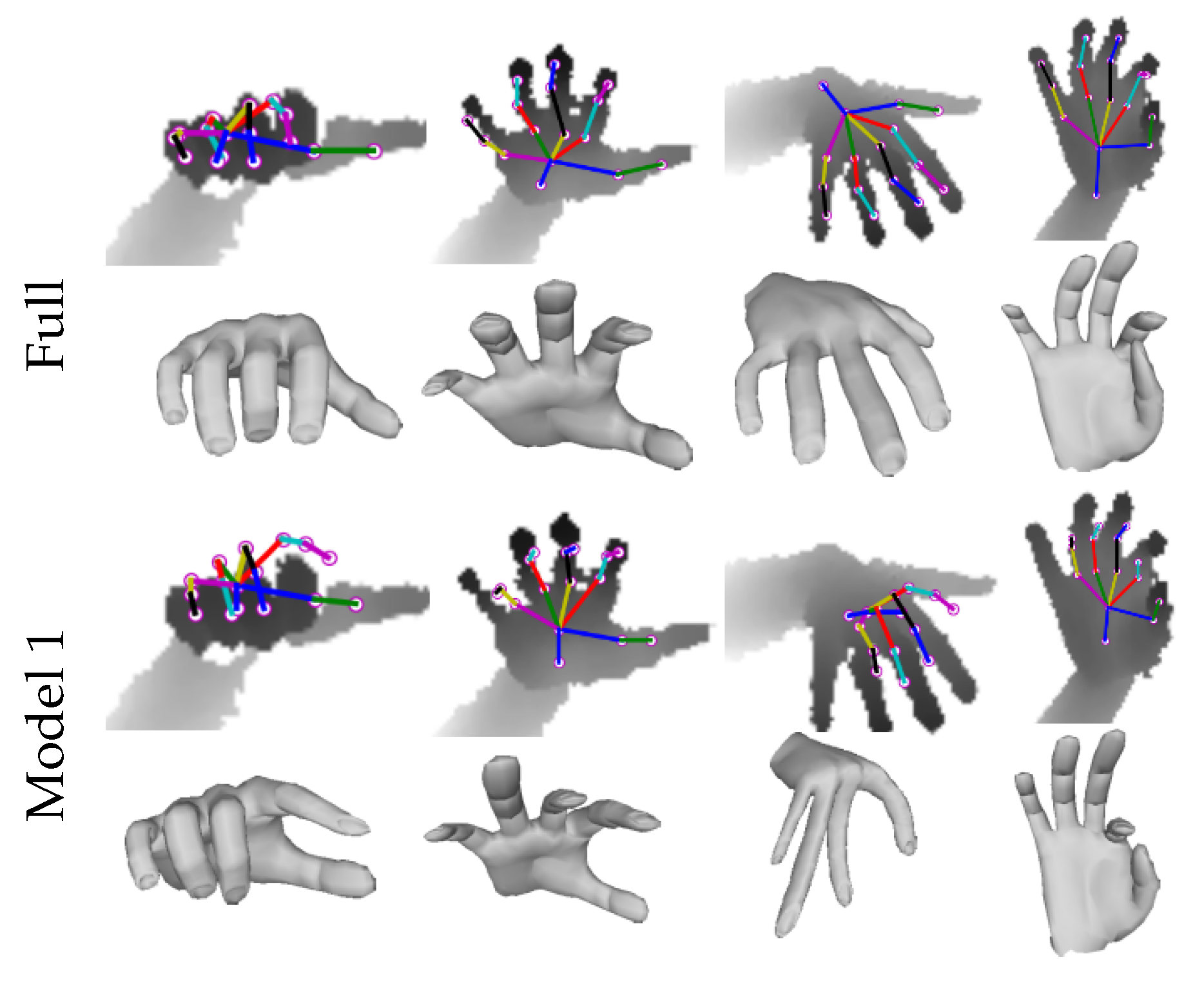
| Method | Pipeline | 3D Err. |
|---|---|---|
| Full | →→→ | 10.39 |
| Model 1 | →→→ | 23.63 |
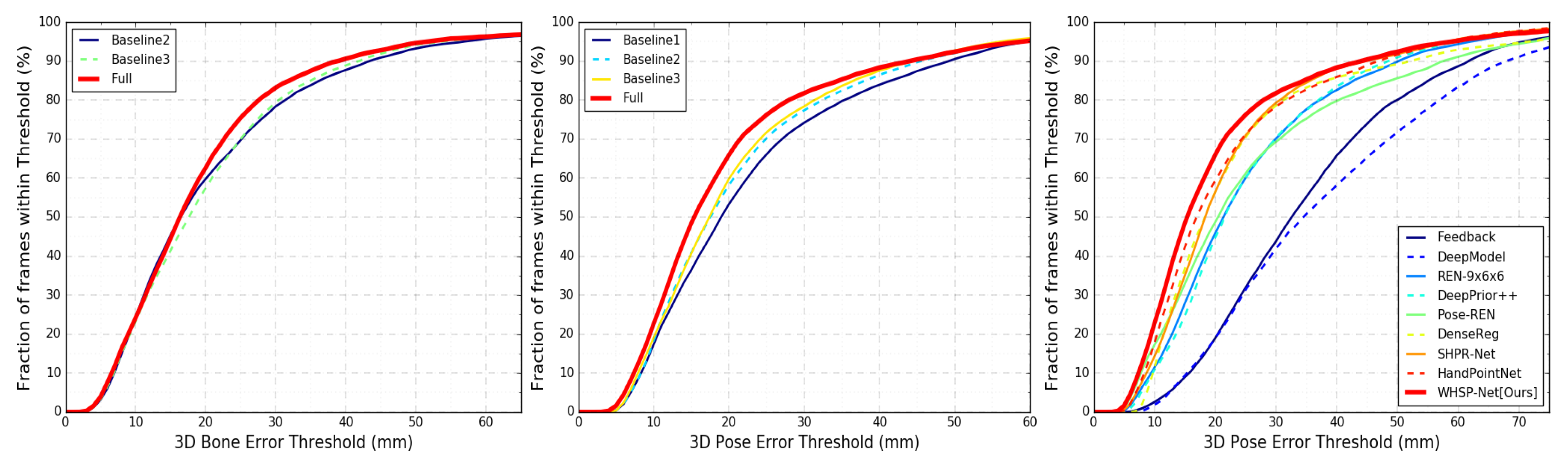
| Method | 3D Err. | 3D Err. |
|---|---|---|
| Baseline 1 | – | 11.83 |
| Baseline 2 | 8.40 | 10.70 |
| Baseline 3 | 8.24 | 10.39 |
| Full | 7.80 | 9.24 |
| Method | 3D Err. (mm) |
|---|---|
| Feedback [30] | 15.9 |
| HandPointNet [7] | 10.54 |
| DenseReg [9] | 10.214 |
| SHPR-Net [52] | 10.77 |
| MURAUER [5] | 9.45 |
| V2V-PoseNet [4] | 8.41 |
| FeatureMapping [3] | 7.44 |
| DeepModel [10] | 17.0 |
| HandScales [11] | 16.0 |
| DeepHPS [21] | 14.20 |
| WHSP-Net (Ours) | 9.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, J.; Elhayek, A.; Stricker, D. WHSP-Net: A Weakly-Supervised Approach for 3D Hand Shape and Pose Recovery from a Single Depth Image. Sensors 2019, 19, 3784. https://doi.org/10.3390/s19173784
Malik J, Elhayek A, Stricker D. WHSP-Net: A Weakly-Supervised Approach for 3D Hand Shape and Pose Recovery from a Single Depth Image. Sensors. 2019; 19(17):3784. https://doi.org/10.3390/s19173784
Chicago/Turabian StyleMalik, Jameel, Ahmed Elhayek, and Didier Stricker. 2019. "WHSP-Net: A Weakly-Supervised Approach for 3D Hand Shape and Pose Recovery from a Single Depth Image" Sensors 19, no. 17: 3784. https://doi.org/10.3390/s19173784
APA StyleMalik, J., Elhayek, A., & Stricker, D. (2019). WHSP-Net: A Weakly-Supervised Approach for 3D Hand Shape and Pose Recovery from a Single Depth Image. Sensors, 19(17), 3784. https://doi.org/10.3390/s19173784





