Laser Safety Calculations for Imaging Sensors
Abstract
1. Introduction
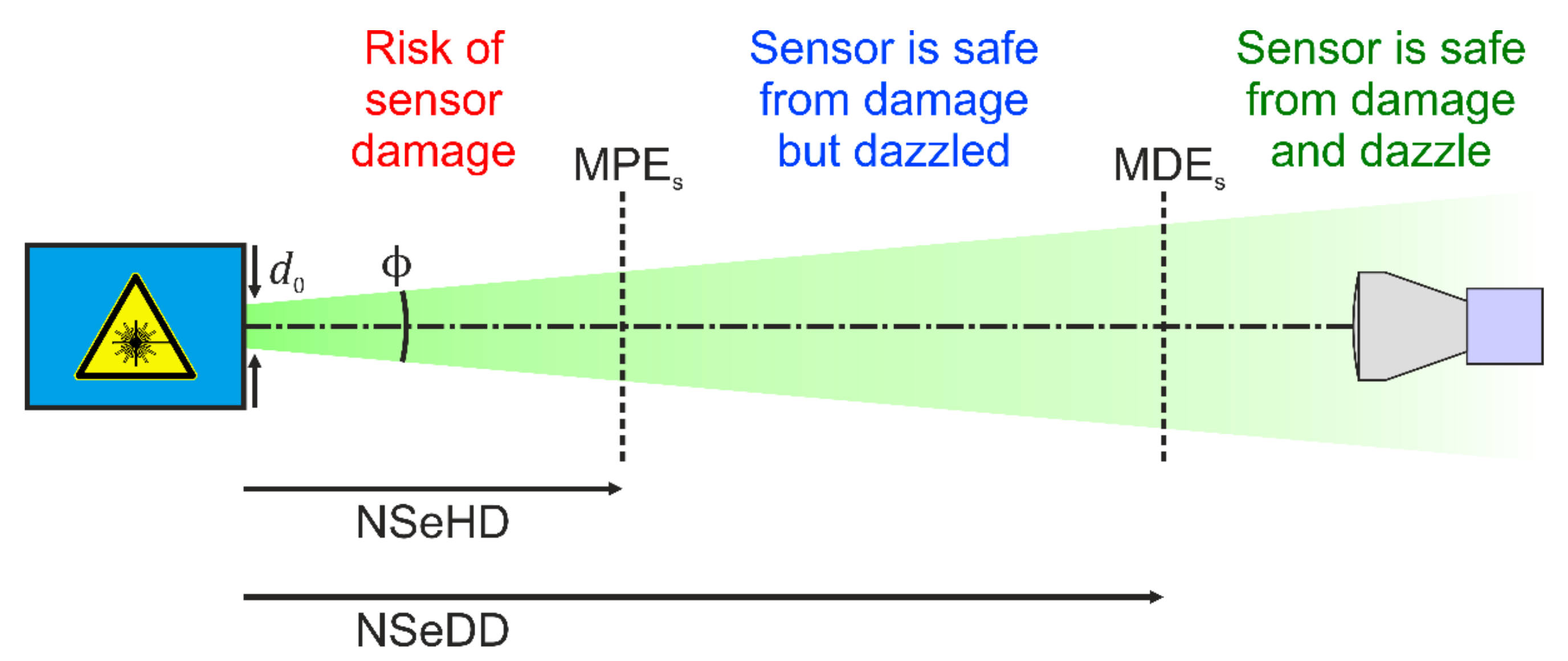
- The statement of a maximum laser irradiance to prevent sensor damage:Maximum Permissible Exposure for a Sensor, MPES
- Statement of a hazard distance corresponding to the MPES:Nominal Sensor Hazard Distance, NSeHD
- Statement of a laser irradiance that corresponds to a certain dazzle level:Maximum Dazzle Exposure for a Sensor, MDES
- Statement of a hazard distance corresponding to the MDES:Nominal Sensor Dazzle Distance, NSeDD
- The possibility to calculate the size of a dazzle spot at the imaging sensor depending on the parameters of laser source, camera lens and imaging sensor.
- Equivalent to laser safety calculations for the human eye, the values of MPES and MDES shall be stated for the position of the entrance aperture of the camera lens. In this case, a user can position a power meter at a well-accessible place to compare calculated exposure values with the laser irradiance.
- Since users, who are not experts in the field, should also be able to be perform such calculations, closed-form expressions shall be derived containing only well-known operations and functions. The equations should be as simple as possible but still sufficiently accurate. In any case, the necessity of performing calculations using a computer should be avoided because of equations that can only be solved numerically.
- As far as possible, the equations shall include only standard parameters that are usually specified by the manufacturer of laser source, camera lens or imaging sensor.
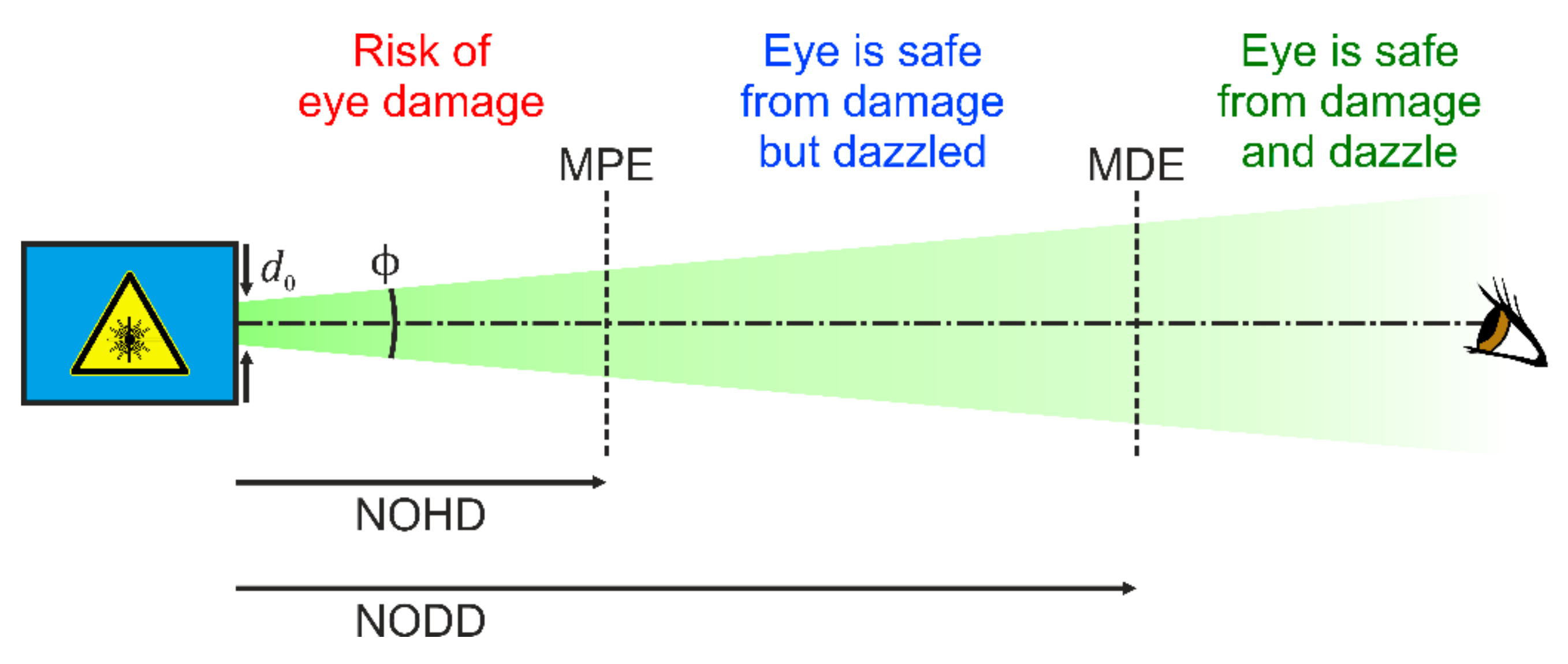
2. Dazzle Scenario
3. Estimation of the Focal Plane Irradiance
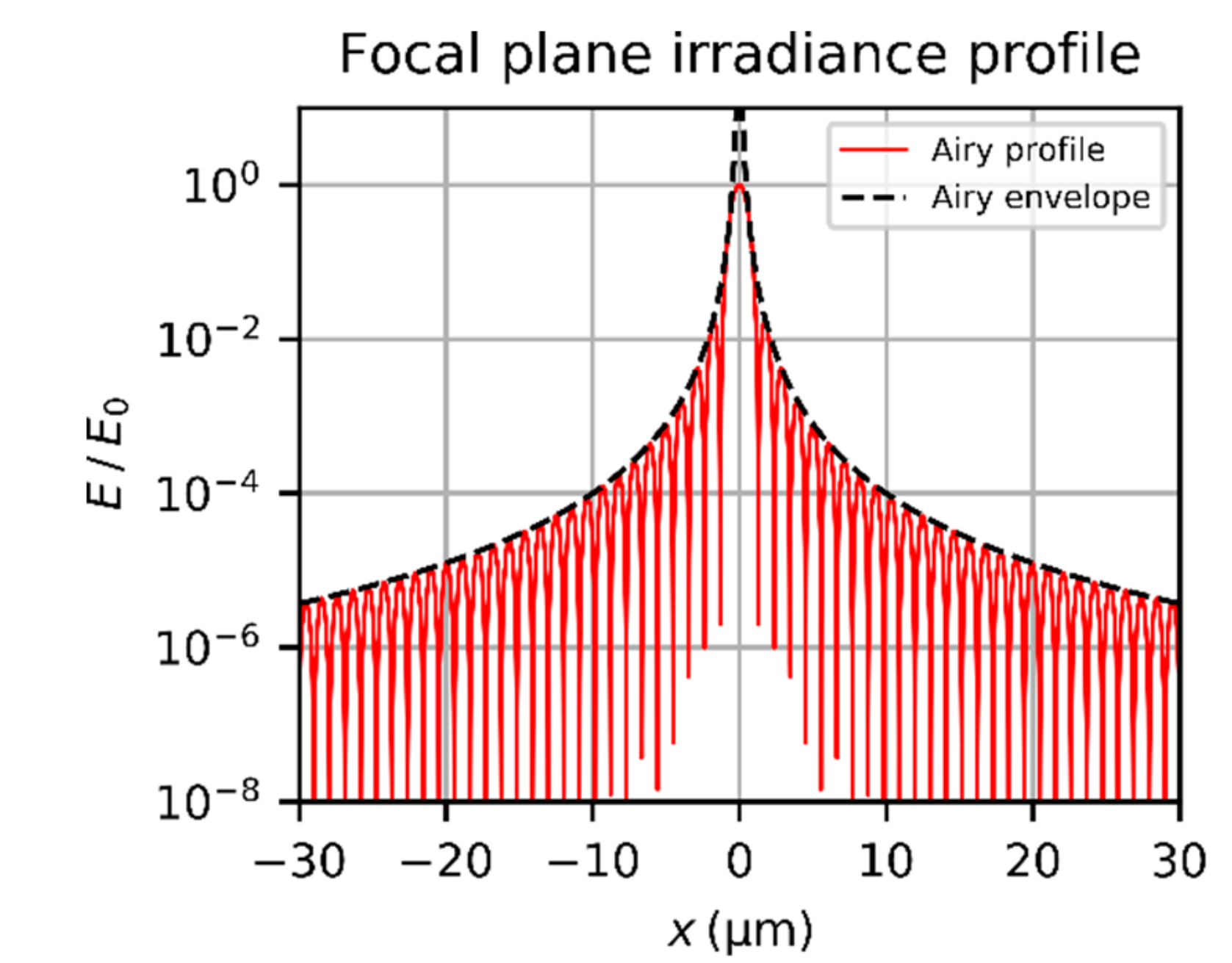
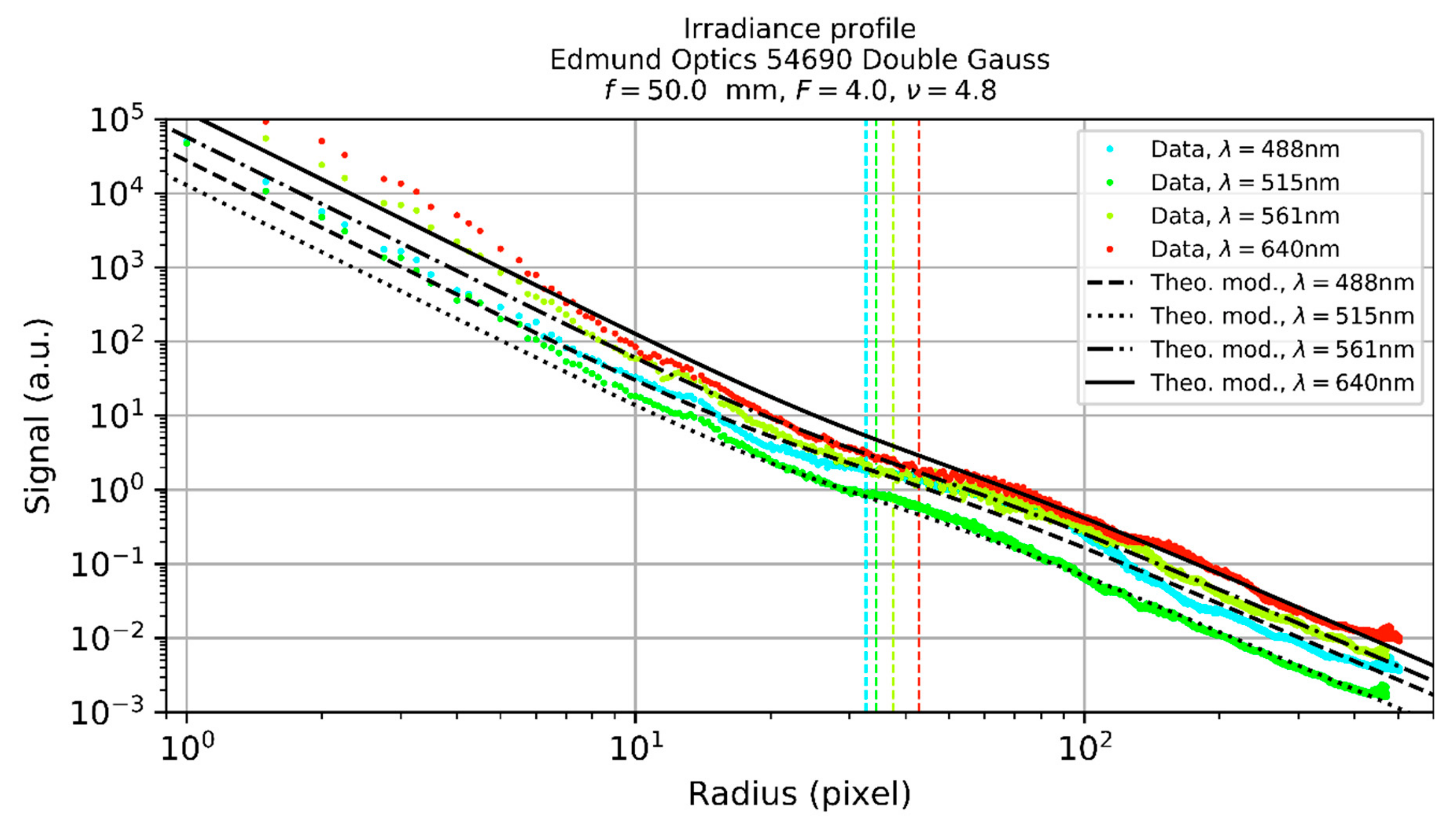
3.1. Airy Diffraction Pattern
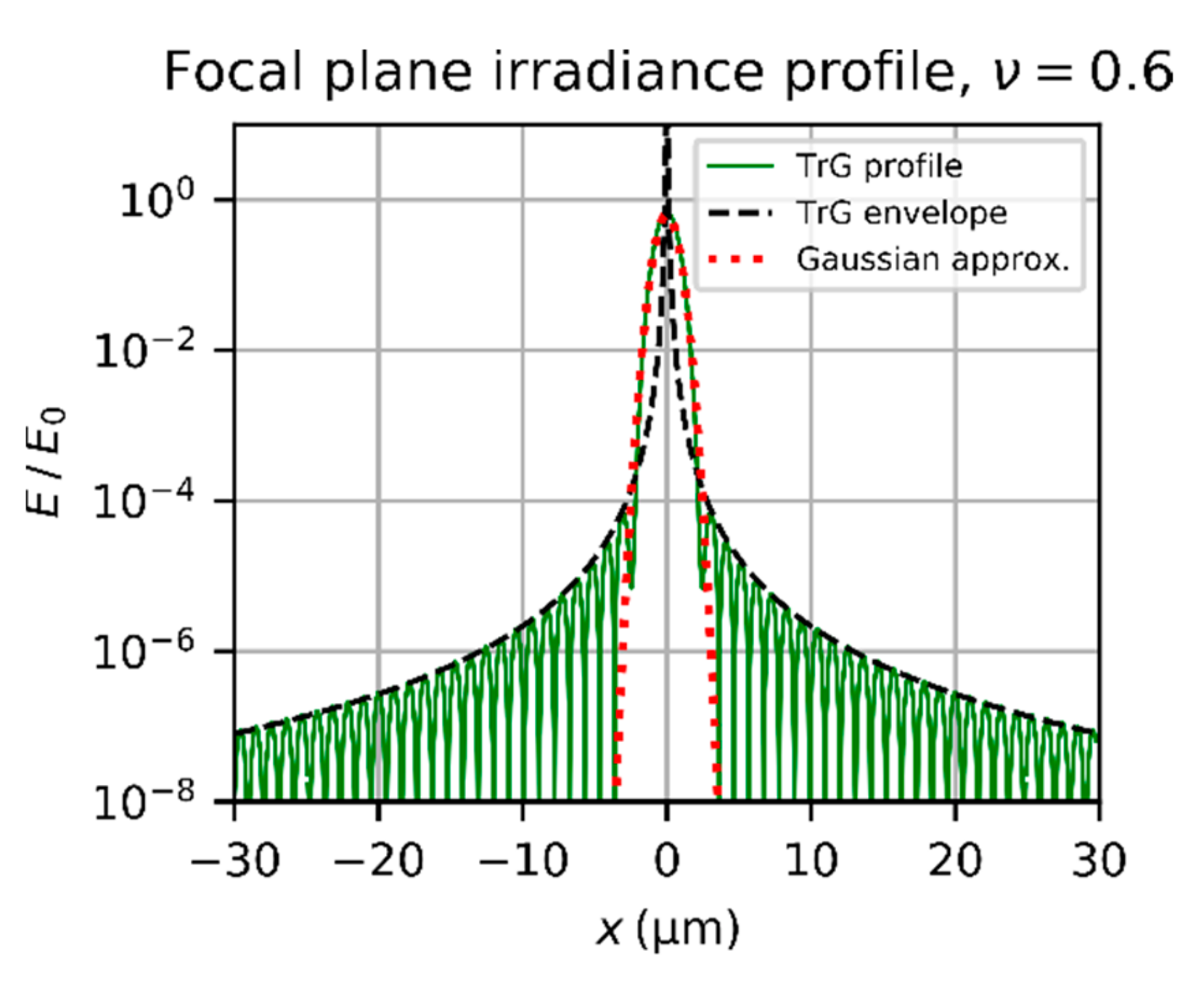
- As shown in Figure 3, the period of the oscillations of the irradiance profile is in the order of some micrometers (the radius of the first dark ring is ). The pixel size of most imaging sensors is typically larger than 3 µm. Thus, the camera image will show an averaged irradiance pattern.
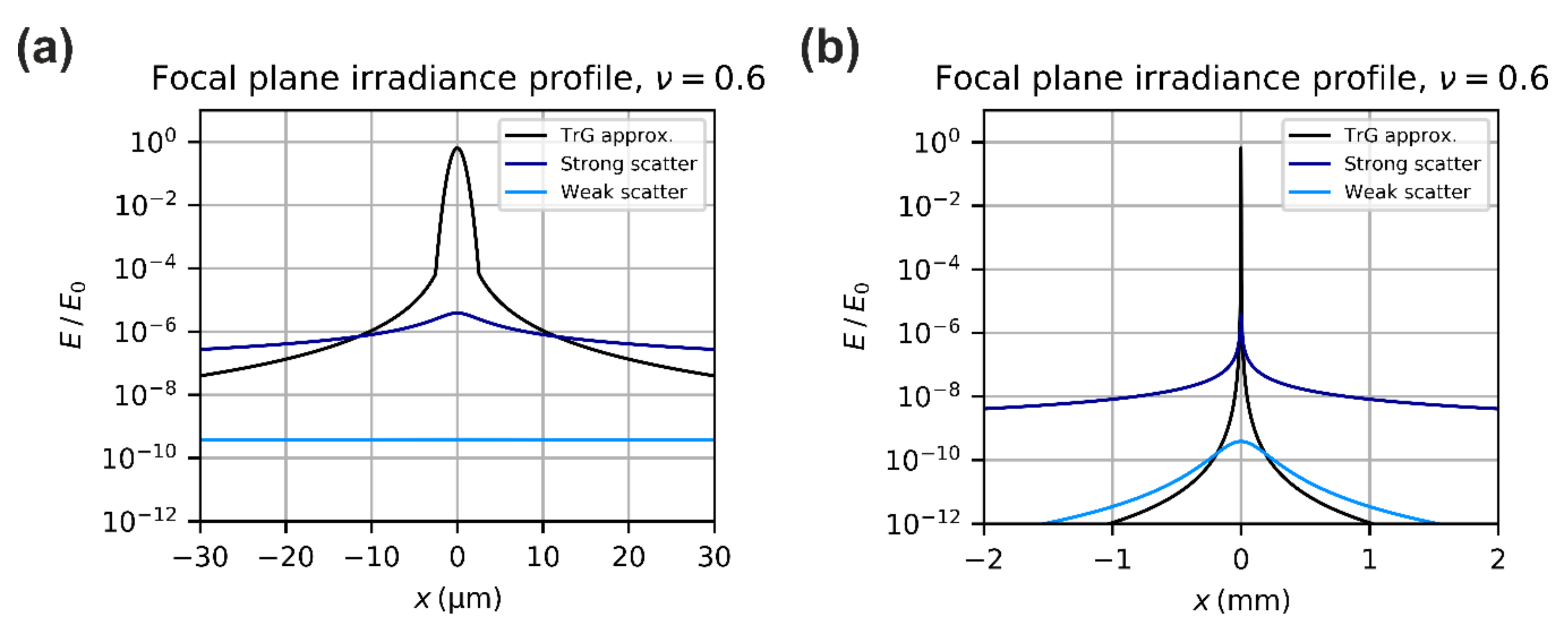
- As mentioned in the introduction, scattering of light at the optical elements of the camera lens has major influence on the size of the dazzle spot for high laser power. Especially in the wings of the dazzle spot, the scattered component dominates the irradiance distribution.
- Aberrations reduce the contrast of the irradiance oscillations.
- Laser systems may show fluctuations of laser power and have jitter in laser beam pointing, which additionally blurs the Airy diffraction pattern in the camera image.
- In real situations, the laser system and/or the sensor system may move, for example, due to vibrations.
- On long distances between laser and camera sensor, the atmospheric turbulence will cause an additional blur to the laser dazzle spot.
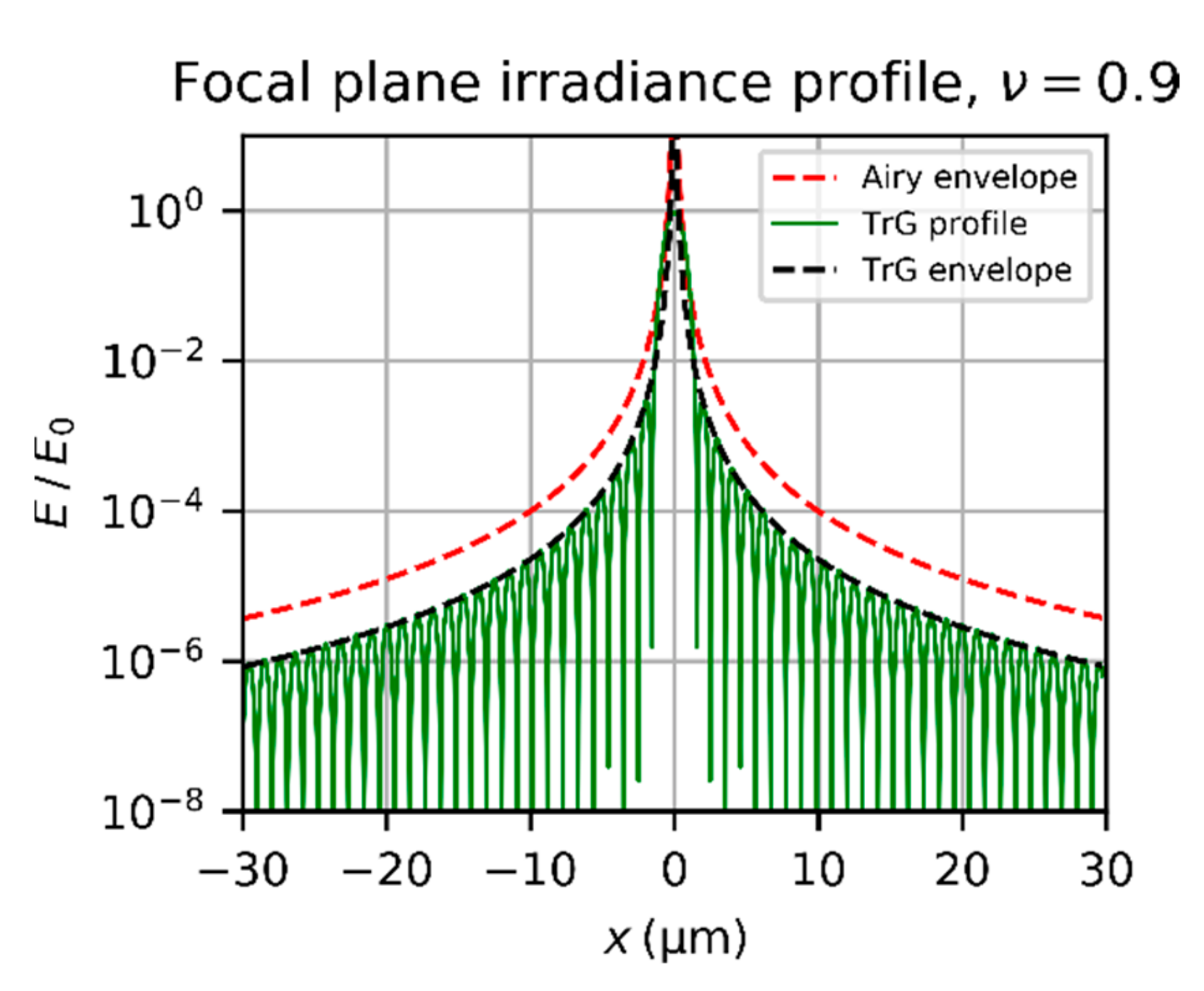
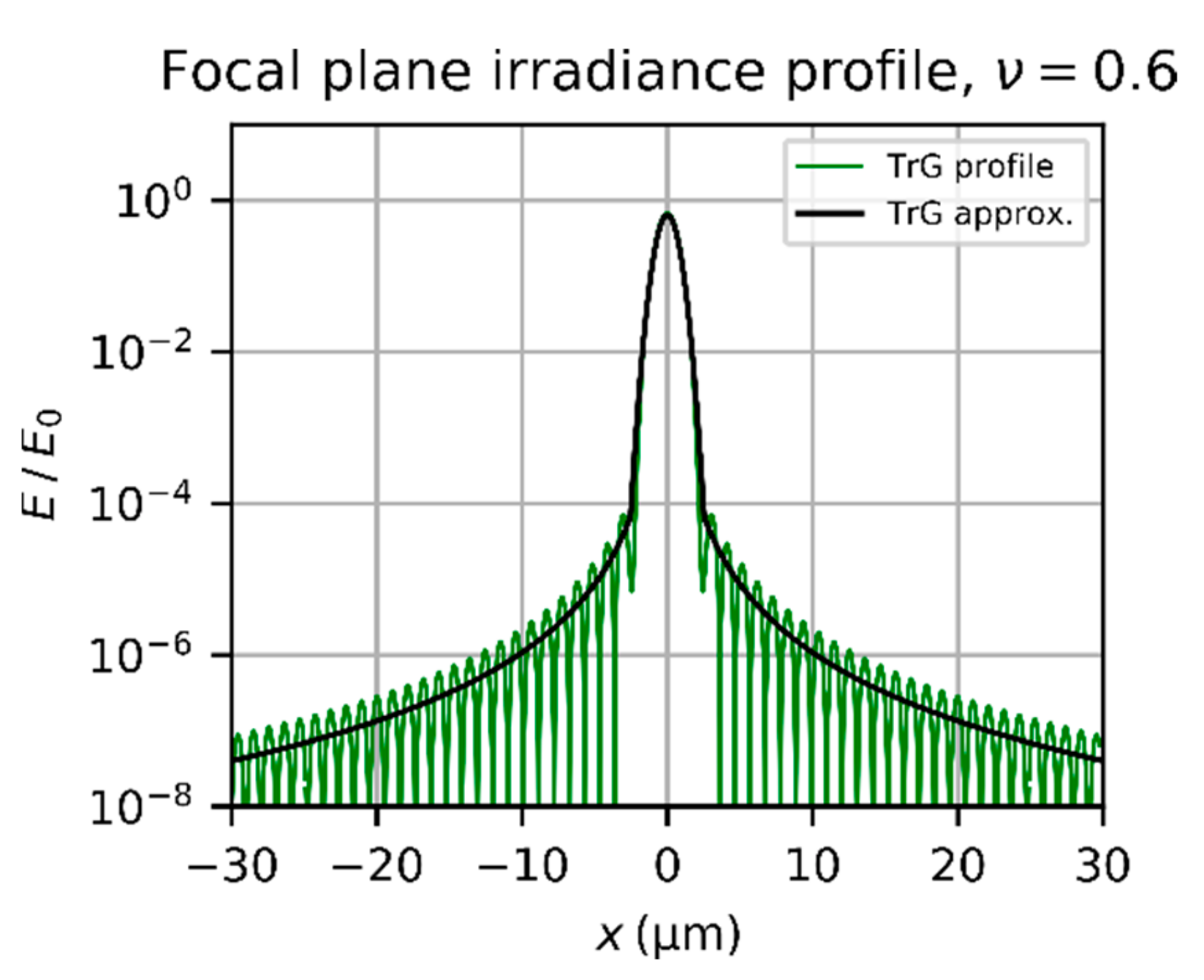
3.2. Diffraction Pattern of a Truncated Gaussian Beam
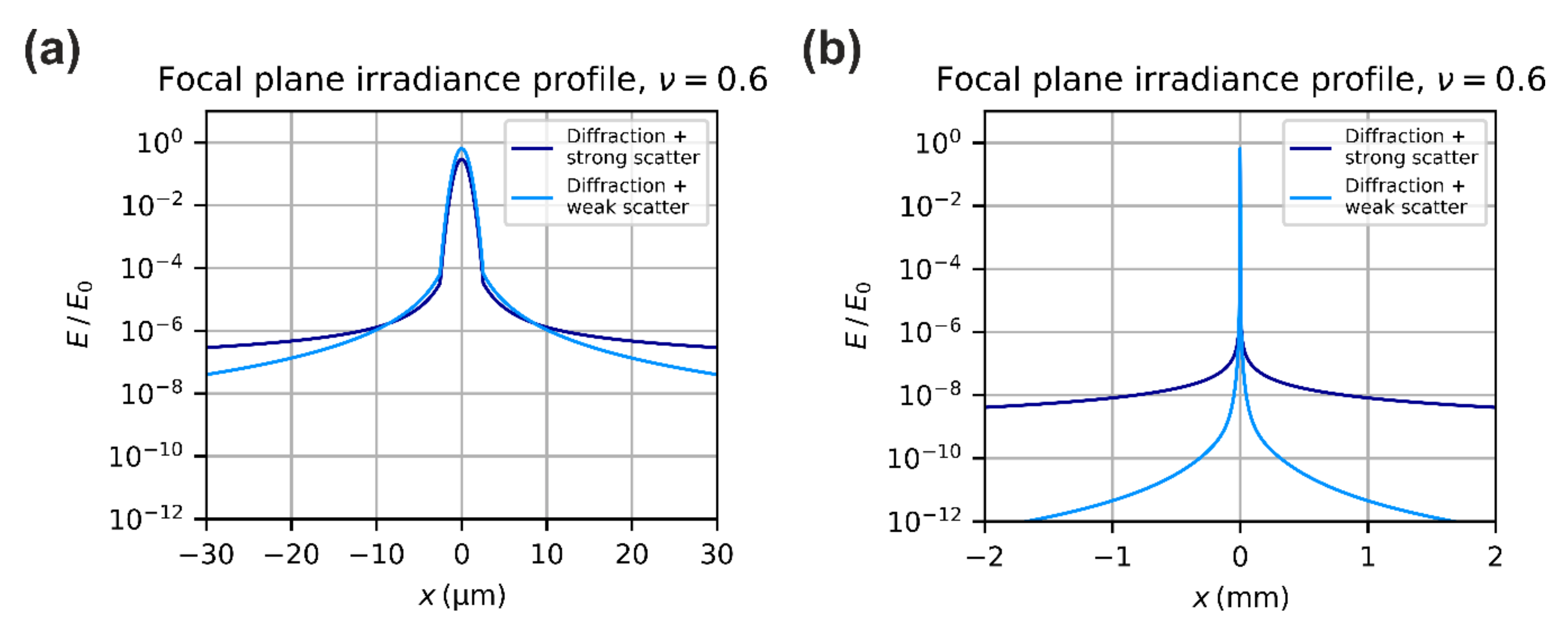
3.3. Stray Light Irradiance
3.4. Aberrations
- One goal of the laser safety calculations is to estimate the onset of laser damage. By neglecting the aberrations, a higher peak irradiance is estimated, which leads to a lower value of the calculated MPES. This can be interpreted as a safety factor, equivalent to the MPE for the human eye. The MPE for the human eye is derived from experimentally estimated ED50-values for eye damage, and is defined as a value that is usually a factor of 10 below these ED50 threshold values.
- Regarding laser dazzle of sensors, the other aim of the laser safety calculation is to estimate the dazzle spot size. In this case, the aberrations have a minor influence, since the size of the dazzle spot at larger dazzle levels is mainly caused by the stray light. Only for very low laser powers, slightly above the onset of laser dazzle, this assumption will cause some error in the dazzle spot size by neglecting aberrations.
- For commercial camera lenses, information on aberrations is typically provided, if at all, in form of diagrams. To transfer this information to values is complex.
- The treatment of aberrations using analytical expressions would increase the complexity of the equations for laser safety calculations a lot.
3.5. Total Focal Plane Irradiance
4. Laser safety Calculations for Sensors
4.1. Maximum Permissible Exposure for a Sensor
4.2. Maximum Dazzle Exposure for a Sensor
4.3. Hazard Distances
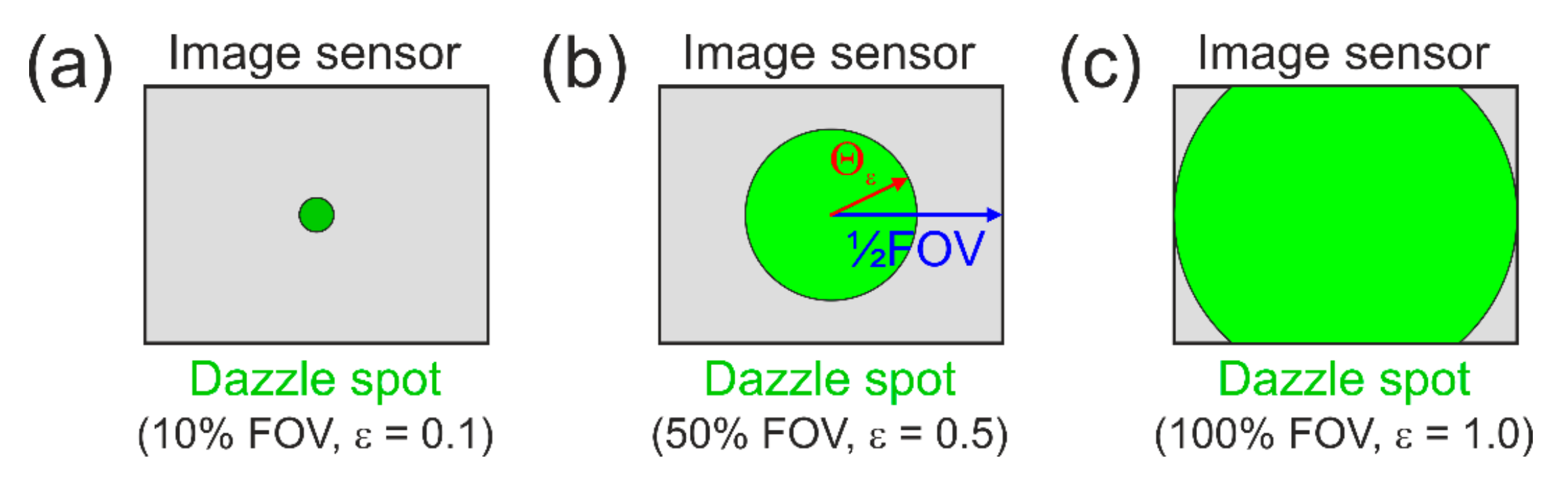
4.4. Size of the Dazzle Spot
5. Parameters for Laser Safety Calculations
- the scatter parameters of the camera lens,
- the damage threshold of the imaging sensor and
- the saturation threshold of the imaging sensor.
5.1. Scatter Parameters
5.2. Laser Damage Threshold
5.3. Laser Saturation Threshold
6. Calculation Examples
6.1. Example 1: Calculation of MPES and NSeHD for a Monochrome CMOS Sensor
- Laser: Laser Quantum Ventus 532 (continuous-wave)
- (1)
- Maximum laser output power:
- (2)
- Wavelength:
- (3)
- Beam diameter at the camera lens: (1/e2)
- Camera lens: Qioptiq Apo-Rodagon-N 4.0/80
- (1)
- Focal length:
- (2)
- f-number:
- (3)
- No. of optical elements: (the specification states up to 8 lenses for the lenses of the Apo-Rodagon series, depending on the focal length)
- (4)
- Focal spot diameter (1/e2):
- Results for 1 s exposure:
- (1)
- Occurrence of damage observed at a focal peak irradiance of 85 kW/cm2
- (2)
- Estimated LIDT (for 1 s exposure):
6.1.1. MPES
6.1.2. NSeHD
- Divergence (1/e2):
- Beam diameter at the laser exit port (1/e2):
6.2. Example 2: Calculation of Dazzle Spot Size and MDES
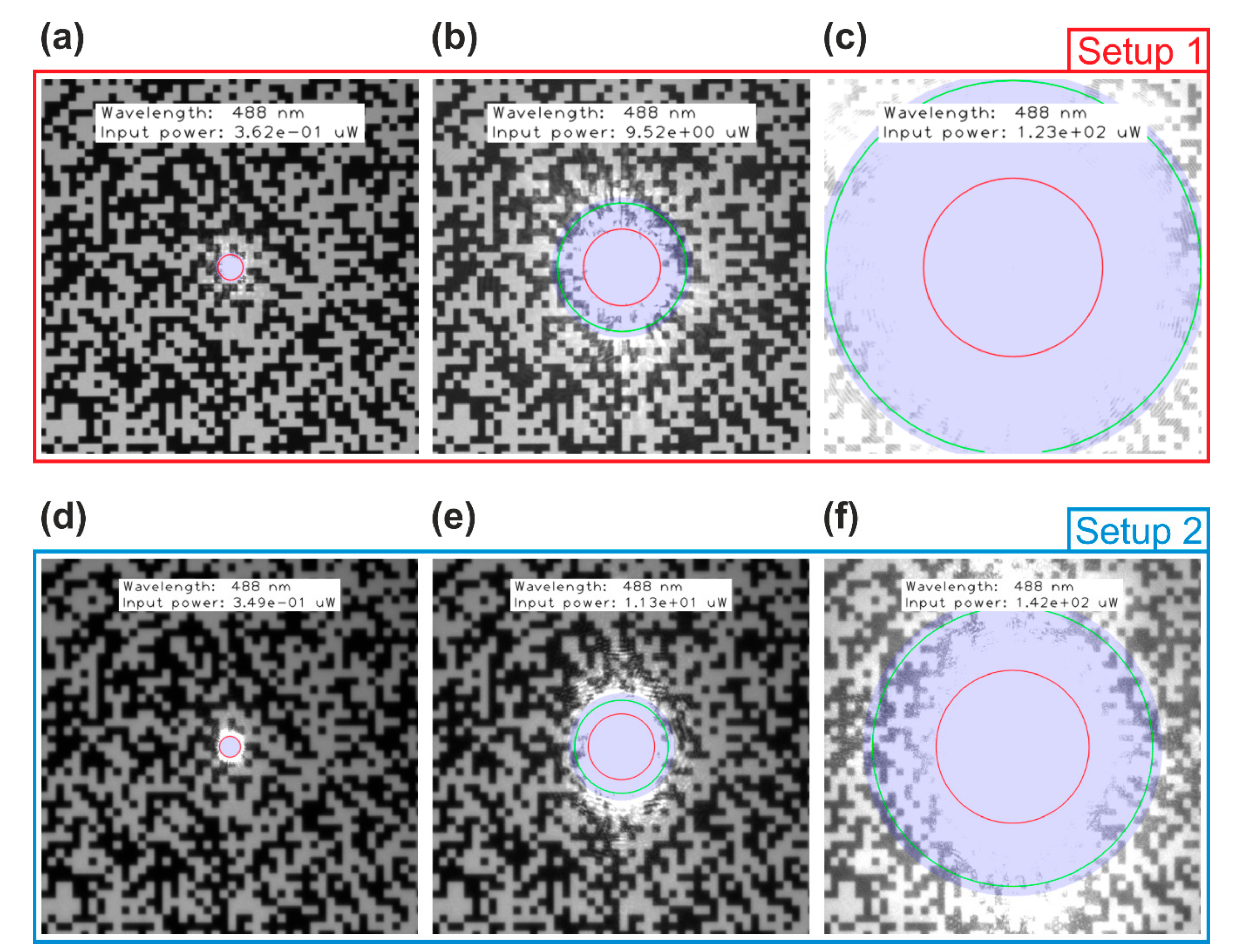
6.2.1. Dazzle Spot Size
- For large dazzle spots (Figure 12c,f), the dazzle spot size cannot be estimated assuming diffraction only. As stated in Section 3.4, the main contribution to the dazzle spot is scattered light. The green circle coincides roughly with the edge of the blue disk.
- When the diffraction and the scatter contribution are nearly equal (Figure 13e), there is some difference of the spot sizes for diffraction and scatter only to the numerically calculated dazzle spot size, but it keeps within limits.
6.2.2. MDES
6.3. Comparison of MPES and MDES
7. Conclusions
Funding
Conflicts of Interest
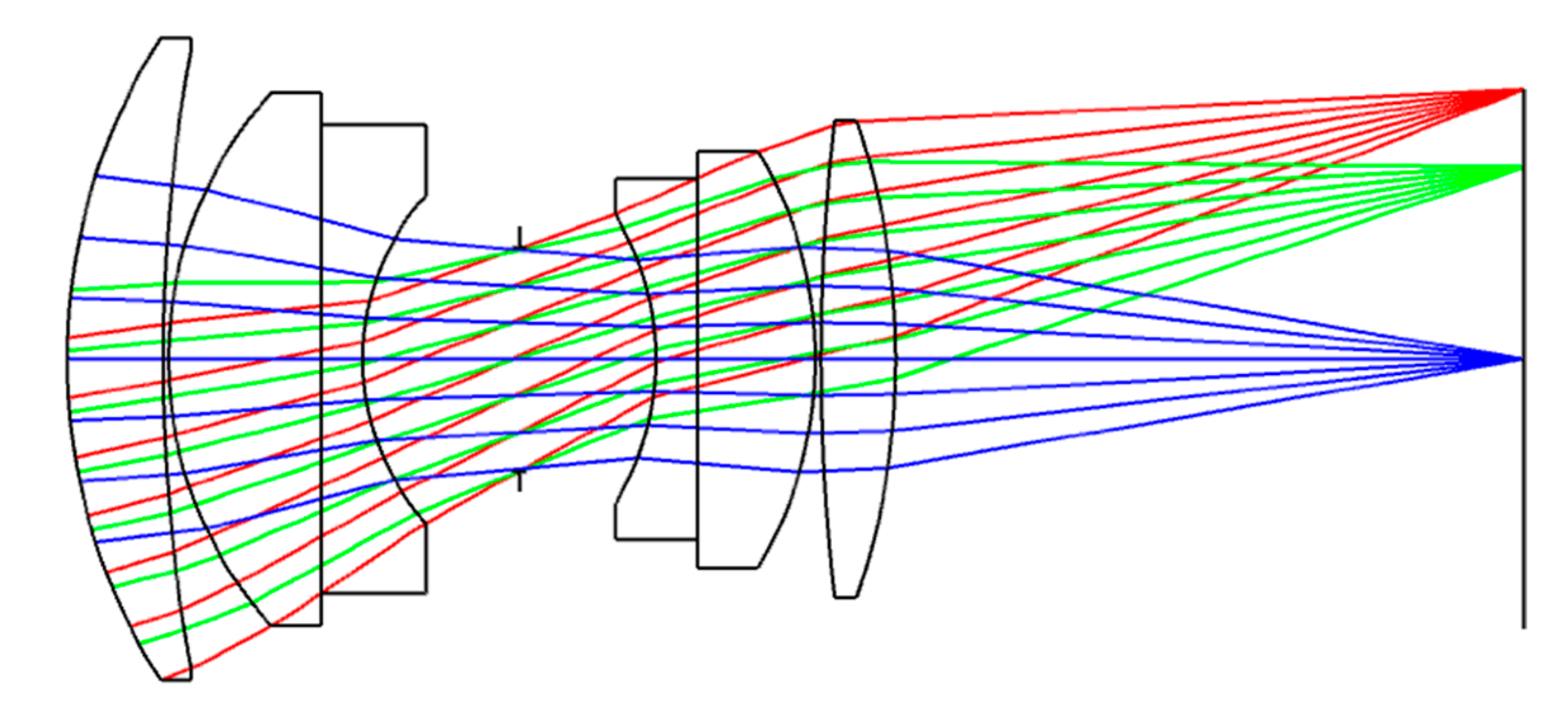
Appendix A. Comment on Camera Lenses
Approximation 2 used in Equation (30) Includes Two Simplifications
- The size of the beam at the different scattering surfaces of the camera lens is equal to the size of the entering beam.
- The size of the beam at the different scattering surfaces of the camera lens is constant.
Appendix B. Limits of Applicability
Appendix B.1. Applicability of Simplification S1 and Simplification S2

| Parameter | Values |
|---|---|
| 400 nm, 550 nm, 700 nm, 1000 nm | |
| 10 mm, 50 mm, 100 mm | |
| 1.0, 8.0, 22.0 | |
| −1, −2, −3 | |
| 0.01, 0.1, 1.0, 10.0 | |
| 10-2, 10-3, 10-4 | |
| 2, 10, 20 |
Appendix B.2. Applicability of Simplification S3
Appendix C. Spot Size Calculations
| Calculated Dazzle Spot Radius (pixel) | Measured Dazzle Spot Radius (pixel) | MDES (µW/cm2) | |||||
|---|---|---|---|---|---|---|---|
| 2.94 × 10−04 | 7.06 × 10−04 | 2 | 0 | 2 | 2 | 0.004 | 1.40 × 10−04 |
| 3.38 × 10−03 | 8.11 × 10−03 | 5 | 0 | 5 | 3 | 0.009 | 1.33 × 10−03 |
| 4.99 × 10−02 | 0.120 | 11 | 0 | 12 | 8 | 0.02 | 1.60 × 10−02 |
| 0.151 | 0.362 | 16 | 0 | 19 | 17 | 0.04 | 0.109 |
| 0.245 | 0.587 | 19 | 7 | 25 | 18 | 0.05 | 0.122 |
| 0.705 | 1.69 | 27 | 34 | 41 | 32 | 0.08 | 0.410 |
| 1.77 | 4.25 | 37 | 56 | 63 | 46 | 0.12 | 0.882 |
| 3.97 | 9.52 | 49 | 82 | 89 | 72 | 0.19 | 2.41 |
| 7.91 | 19.0 | 61 | 111 | 118 | 103 | 0.27 | 5.68 |
| 9.96 | 23.9 | 66 | 122 | 130 | 115 | 0.31 | 7.44 |
| 12.5 | 30.1 | 71 | 135 | 142 | 131 | 0.35 | 10.3 |
| 15.8 | 37.9 | 77 | 148 | 156 | 152 | 0.40 | 14.8 |
| 25.0 | 60.1 | 90 | 179 | 188 | 204 | 0.54 | 31.0 |
| 31.5 | 75.7 | 97 | 197 | 206 | 232 | 0.62 | 42.8 |
| 39.7 | 95.2 | 105 | 216 | 225 | n.m. | n.m. | - |
| 51.1 | 123 | 114 | 239 | 249 | n.m. | n.m. | - |
| 60.0 | 144 | 120 | 256 | 266 | n.m. | n.m. | - |
| 70.5 | 169 | 127 | 273 | 283 | n.m. | n.m. | - |
| 99.6 | 239 | 143 | 314 | 325 | n.m. | n.m. | - |
| 125 | 301 | 154 | 344 | 356 | n.m. | n.m. | - |
| 158 | 379 | 166 | 377 | 390 | n.m. | n.m. | - |
| 379 | 910 | 223 | 536 | 551 | n.m. | n.m. | - |
| 488 | 1170 | 242 | 594 | 609 | n.m. | n.m. | - |
| 674 | 1620 | 270 | 675 | 692 | n.m. | n.m. | - |
| Calculated Dazzle Spot Radius (pixel) | Measured Dazzle Spot Radius (pixel) | MDES (µW/cm2) | |||||
|---|---|---|---|---|---|---|---|
| 5.45 × 10−04 | 1.31 × 10−03 | 3 | 0 | 3 | 3 | 0.008 | 4.44 × 10−04 |
| 5.20 × 10−03 | 1.25 × 10−02 | 7 | 0 | 7 | 5 | 0.01 | 1.96 × 10−03 |
| 5.97 × 10−02 | 0.143 | 15 | 0 | 15 | 13 | 0.03 | 3.53 × 10−02 |
| 0.161 | 0.386 | 21 | 0 | 22 | 20 | 0.05 | 0.119 |
| 0.255 | 0.611 | 24 | 0 | 27 | 22 | 0.06 | 0.149 |
| 0.611 | 1.47 | 32 | 17 | 40 | 36 | 0.09 | 0.479 |
| 1.47 | 3.52 | 43 | 44 | 59 | 53 | 0.14 | 1.16 |
| 2.67 | 6.40 | 52 | 62 | 76 | 73 | 0.19 | 2.40 |
| 5.32 | 12.8 | 66 | 88 | 102 | 104 | 0.28 | 5.64 |
| 6.40 | 15.4 | 70 | 96 | 110 | 113 | 0.30 | 6.85 |
| 8.06 | 19.3 | 76 | 106 | 120 | 126 | 0.33 | 8.96 |
| 10.1 | 24.3 | 82 | 118 | 132 | 151 | 0.40 | 14.1 |
| 16.1 | 38.6 | 95 | 143 | 159 | 196 | 0.52 | 27.4 |
| 20.2 | 48.6 | 103 | 158 | 174 | 223 | 0.59 | 37.91 |
| 24.9 | 59.7 | 110 | 172 | 189 | n.m. | n.m. | - |
| 31.3 | 75.2 | 119 | 190 | 207 | n.m. | n.m. | - |
| 39.5 | 94.7 | 129 | 209 | 227 | n.m. | n.m. | - |
| 46.4 | 111 | 136 | 223 | 241 | n.m. | n.m. | - |
| 59.7 | 143 | 148 | 247 | 267 | n.m. | n.m. | - |
| 75.2 | 180 | 159 | 272 | 292 | n.m. | n.m. | - |
| 94.6 | 227 | 172 | 298 | 320 | n.m. | n.m. | - |
| 227 | 545 | 230 | 425 | 450 | n.m. | n.m. | - |
| 286 | 686 | 249 | 466 | 493 | n.m. | n.m. | - |
| 423 | 1010 | 283 | 546 | 574 | n.m. | n.m. | - |
| Calculated Dazzle Spot Radius (pixel) | Measured Dazzle Spot Radius (pixel) | MDES (µW/cm2) | |||||
|---|---|---|---|---|---|---|---|
| 5.18 × 10−04 | 7.82 × 10−04 | 2 | 0 | 2 | 5 | 0.007 | 4.42 × 10−03 |
| 4.94 × 10−03 | 7.47 × 10−03 | 5 | 0 | 5 | 8 | 0.01 | 2.17 × 10−02 |
| 5.67 × 10−02 | 8.58 × 10−02 | 11 | 0 | 11 | 14 | 0.02 | 9.80 × 10−02 |
| 0.153 | 0.231 | 16 | 0 | 16 | 17 | 0.02 | 0.188 |
| 0.242 | 0.366 | 18 | 0 | 19 | 19 | 0.03 | 0.257 |
| 0.581 | 0.878 | 25 | 0 | 26 | 26 | 0.04 | 0.603 |
| 1.39 | 2.11 | 33 | 0 | 37 | 43 | 0.06 | 1.97 |
| 2.54 | 3.83 | 40 | 9 | 48 | 57 | 0.08 | 3.89 |
| 5.06 | 7.65 | 50 | 40 | 64 | 75 | 0.10 | 7.21 |
| 6.08 | 9.19 | 54 | 47 | 70 | 80 | 0.11 | 8.45 |
| 7.65 | 11.6 | 58 | 55 | 77 | 87 | 0.12 | 10.4 |
| 9.64 | 14.6 | 63 | 64 | 85 | 94 | 0.13 | 12.4 |
| 15.3 | 23.1 | 73 | 82 | 103 | 111 | 0.15 | 18.4 |
| 19.2 | 29.1 | 79 | 92 | 113 | 122 | 0.17 | 23.5 |
| 23.7 | 35.8 | 84 | 102 | 123 | 130 | 0.18 | 27.3 |
| 29.8 | 45.0 | 91 | 114 | 135 | 149 | 0.20 | 38.6 |
| 37.5 | 56.7 | 98 | 126 | 148 | 165 | 0.23 | 49.8 |
| 44.1 | 66.6 | 104 | 136 | 157 | 181 | 0.25 | 63.2 |
| 56.7 | 85.8 | 113 | 152 | 174 | 204 | 0.28 | 85.0 |
| 71.4 | 108 | 122 | 168 | 191 | 236 | 0.32 | 124 |
| 89.9 | 136 | 132 | 185 | 209 | 276 | 0.38 | 185 |
| 216 | 326 | 176 | 266 | 294 | 459 | 0.63 | 680 |
| 272 | 411 | 191 | 293 | 322 | n.m. | n.m. | - |
| 402 | 607 | 217 | 343 | 375 | n.m. | n.m. | - |
References
- Laser Incidents. Available online: https://www.faa.gov/about/initiatives/lasers/laws/ (accessed on 22 August 2019).
- Laser/aircraft incident statistics. Available online: https://www.laserpointersafety.com/latest-stats/latest-stats.html (accessed on 22 August 2019).
- Shannon, D.C. Non-lethal laser dazzling as a personnel countermeasure. Proc. SPIE 2013, 8898, 88980G. [Google Scholar] [CrossRef]
- Hauck, J.P.; Hamadani, S.; Fine, K.; Edrich, D.A.; Eagan, J. ColorDazl/Daylight Dazzler and eye protection. Proc. SPIE 2009, 7323, 732313. [Google Scholar] [CrossRef]
- Jull, E.I.L.; Gleeson, H.F. Tuneable and switchable liquid crystal laser protection system. Appl. Opt. 2017, 56, 8061–8066. [Google Scholar] [CrossRef] [PubMed]
- Quercioli, F. Beyond laser safety glasses: augmented reality in optics laboratories. Appl. Opt. 2017, 56, 1148–1150. [Google Scholar] [CrossRef] [PubMed]
- Wirth, J.H.; Watnik, A.T.; Swartzlander, G.A. Experimental observations of a laser suppression imaging system using pupil-plane phase elements. Appl. Opt. 2017, 56, 9205–9211. [Google Scholar] [CrossRef] [PubMed]
- Ruane, G.J.; Watnik, A.T.; Swartzlander, G.A. Reducing the risk of laser damage in a focal plane array using linear pupil-plane phase elements. Appl. Opt. 2015, 54, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Ritt, G.; Eberle, B. Automatic Laser Glare Suppression in Electro-Optical Sensors. Sensors 2015, 15, 792–802. [Google Scholar] [CrossRef] [PubMed]
- Ritt, G.; Eberle, B. Automatic Suppression of Intense Monochromatic Light in Electro-Optical Sensors. Sensors 2012, 12, 14113–14128. [Google Scholar] [CrossRef]
- Ritt, G.; Schwarz, B.; Eberle, B. Preventing image information loss of imaging sensors in case of laser dazzle. Opt. Eng. 2019, 58, 013109. [Google Scholar] [CrossRef]
- Schleijpen, (H.)M.A.; van den Heuvel, J.C.; Mieremet, A.L.; Mellier, B.; van Putten, F.J.M. Laser dazzling of focal plane array cameras. Proc. SPIE 2007, 6543, 65431B. [Google Scholar] [CrossRef]
- Schleijpen, (H.)M.A.; Dimmeler, A.; Eberle, B.; van den Heuvel, J.C.; Mieremet, A.L.; Bekman, H.; Mellier, B. Laser dazzling of focal plane array cameras. Proc. SPIE 2007, 6738, 67380O. [Google Scholar] [CrossRef]
- Benoist, K.W.; Schleijpen, (H.)M.A. Modelling of the over-exposed pixel area of CCD cameras caused by laser dazzling. Proc. SPIE 2014, 9251, 92510H. [Google Scholar] [CrossRef]
- Durécu, A.; Vasseur, O.; Bourdon, P.; Eberle, B.; Bürsing, H.; Dellinger, J.; Duchateau, N. Assessment of laser-dazzling effects on TV-cameras by means of pattern recognition algorithms. Proc. SPIE 2007, 6738, 67380J. [Google Scholar] [CrossRef]
- Durécu, A.; Bourdon, P.; Vasseur, O. Laser-dazzling effects on TV-cameras: analysis of dazzling effects and experimental parameters weight assessment. Proc. SPIE 2007, 6738, 67380L. [Google Scholar] [CrossRef]
- Durécu, A.; Vasseur, O.; Bourdon, P. Quantitative assessment of laser-dazzling effects on a CCD-camera through pattern-recognition algorithms performance measurements. Proc. SPIE 2009, 7483, 74830N. [Google Scholar] [CrossRef]
- Santos, C.N.; Chrétien, S.; Merella, L.; Vandewal, M. Visible and near-infrared laser dazzling of CCD and CMOS cameras. Proc. SPIE 2018, 10797, 107970S. [Google Scholar] [CrossRef]
- Ritt, G.; Eberle, B. Evaluation of protection measures against laser dazzling for imaging sensors. Opt. Eng. 2017, 56, 033108. [Google Scholar] [CrossRef]
- Ritt, G.; Koerber, M.; Forster, D.; Eberle, B. Protection performance evaluation regarding imaging sensors hardened against laser dazzling. Opt. Eng. 2015, 54, 053106. [Google Scholar] [CrossRef]
- Williamson, C.A. Simple computer visualization of laser eye dazzle. J. Laser Appl. 2016, 28, 012003. [Google Scholar] [CrossRef]
- Coelho, J.M.P.; Freitas, J.; Williamson, C.A. Optical eye simulator for laser dazzle events. Appl. Opt. 2016, 55, 2240–2251. [Google Scholar] [CrossRef] [PubMed]
- Steinvall, O.; Sandberg, S.; Hörberg, U.; Persson, R.; Berglund, F.; Karslsson, K.; Öhgren, J.; Yu, Z.; Söderberg, P. Laser dazzling impacts on car driver performance. Proc. SPIE 2013, 8898, 88980H. [Google Scholar] [CrossRef]
- Vandewal, M.; Eeckhout, M.; Budin, D.; Pétriaux, A.; Perneel, C.; Williamson, C.A.; Santos, C.N. Evaluation of laser dazzling induced task performance degradation. Proc. SPIE 2018, 10797, 10797E. [Google Scholar] [CrossRef]
- Williamson, C.A.; McLin, L.N. Nominal ocular dazzle distance (NODD). Appl. Opt. 2015, 54, 1564. [Google Scholar] [CrossRef]
- Williamson, C.A.; McLin, L.N. Determination of a laser eye dazzle safety framework. J. Laser Appl. 2018, 30, 032010. [Google Scholar] [CrossRef]
- McLin, L.N.; Smith, P.A.; Barnes, L.E.; Dykes, J.R.; Kuyk, T.; Novar, B.J.; Garcia, P.V.; Williamson, C.A. Scaling laser disability glare functions with ’K’ factors to predict dazzle. J. Laser Appl. 2013, 278–287. [Google Scholar] [CrossRef]
- Schwarz, B.; Ritt, G.; Koerber, M.; Eberle, B. Laser-induced damage threshold of camera sensors and micro-optoelectromechanical systems. Opt. Eng. 2017, 56, 034108. [Google Scholar] [CrossRef]
- Özbilgin, T.; Yeniay, A. Laser dazzling analysis of camera sensors. Proc. SPIE 2018, 10797, 107970Q. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Urey, H. Spot size, depth-of-focus, and diffraction ring intensity formulas for truncated Gaussian beams. Appl. Opt. 2004, 43, 620–625. [Google Scholar] [CrossRef]
- Haskal, H.M. Laser recording with truncated Gaussian beams. Appl. Opt. 1979, 18, 2143–2146. [Google Scholar] [CrossRef]
- Coleman, H.S. Stray Light in Optical Systems. J. Opt. Soc. Am. 1947, 37, 434–451. [Google Scholar] [CrossRef]
- Kuwabara, G. On the Flare of Lenses. J. Opt. Soc. Am. 1953, 43, 53–57. [Google Scholar] [CrossRef]
- Blazey, R. Light Scattering by Laser Mirrors. Appl. Opt. 1967, 6, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Harvey, J.E. Light-scattering characteristics of optical surfaces. PhD Thesis, The University of Arizona, Tucson, AZ, USA, 1976. [Google Scholar]
- Peterson, G.L. Analytic expressions for in-field scattered light distributions. Proc. SPIE 2004, 5178, 184–193. [Google Scholar] [CrossRef]
- Pfisterer, R.N. Approximated Scatter Models for Stray Light Analysis. Optics&Photonics News 2011, 22, 16–17. [Google Scholar]
- Scattering in ASAP. Available online: http://www.breault.com/knowledge-base/scattering-asap (accessed on 29 July 2019).
- Wein, S.J. Small-angle scatter measurement. PhD Thesis, The University of Arizona, Tucson, AZ, USA, 1989. [Google Scholar]
- Greynolds, A.W. Formulas For Estimating Stray-Radiation Levels in Well-Baffled Optical Systems. Proc. SPIE 1981, 257, 39–49. [Google Scholar] [CrossRef]
- Harvey, J.E.; Schröder, S.; Choi, N.; Duparré, A. Total integrated scatter from surfaces with arbitrary roughness, correlation widths, and incident angles. Opt. Eng. 2012, 51, 013402. [Google Scholar] [CrossRef]
- American National Standard for Safe Use of Lasers Outdoors; ANSI Z136.6-2015; Laser Institute of America: Orlando, FL, USA, 2015.
- TROS Laserstrahlung Teil 2: Messungen und Berechnungen von Expositionen Gegenüber Laserstrahlung; Bundesanstalt für Arbeitsschutz und Arbeitsmedizin (BAuA): Dortmund, Germany, 20 July 2018; p. 38.
- Bartoli, F.; Esterowitz, L.; Kruer, M.; Allen, R. Irreversible laser damage in IR detector materials. Appl. Opt. 1977, 16, 2934–2937. [Google Scholar] [CrossRef] [PubMed]
- EMVA Standard 1288, Standard for Characterization of Image Sensors and Cameras; Release 3.1; European Machine Vision Association: Barcelona, Spain, 2016; p. 7.
- Holst, G.C.; Lomheim, T.S. Array parameters. In CMOS/CCD Sensors and Camera Systems, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2007; p. 110. [Google Scholar]
- Landeau, S. Evaluation of super-resolution imager with binary fractal test target. Proc. SPIE 2014, 9249, 924909. [Google Scholar] [CrossRef]
- Betensky, E.; Kreitzer, M.; Moskovich, J. Camera lenses. In Handbook of Optics, Volume II, Devices, Measurements, and Properties, 2nd ed.; Bass, M., Van Stryland, E.W., Williams, D.R., Wolfe, W.L., Eds.; McGraw-Hill, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Smith, W.J. The Biotar or Double-Gauss Lens. In Modern Lens Design, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 2005; pp. 319–340. [Google Scholar]


| 445 | 2.8 | 0.3 | 9.7 | 2.6 |
| 1.0 | 1.8 | 1.1 | ||
| 2.0 | 1.4 | 1.0 | ||
| 11.0 | 0.3 | 37.9 | 10.4 | |
| 1.0 | 7.1 | 4.3 | ||
| 2.0 | 5.5 | 4.0 | ||
| 532 | 2.8 | 0.3 | 11.5 | 3.2 |
| 1.0 | 2.2 | 1.3 | ||
| 2.0 | 1.7 | 1.2 | ||
| 11.0 | 0.3 | 45.3 | 12.4 | |
| 1.0 | 8.5 | 5.2 | ||
| 2.0 | 6.6 | 4.8 | ||
| 635 | 2.8 | 0.3 | 13.8 | 3.8 |
| 1.0 | 2.6 | 1.6 | ||
| 2.0 | 2.0 | 1.4 | ||
| 11.0 | 0.3 | 54.1 | 14.8 | |
| 1.0 | 10.1 | 6.2 | ||
| 2.0 | 7.8 | 5.7 |
| Camera Lens. | Focal Length | f-Number | No. of Lenses | Coating | Price (approx.) |
|---|---|---|---|---|---|
| LINOS MeVis-C 1.8/50 | 50.6 | 1.8 | 7 | unk. | 700 € |
| Edmund Optics 54690 (Double Gauss) | 50 | 4.0 | 6 | MgF2 | 500 € |
| Edmund Optics 67715 | 25 | 1.4 | 7 | BBAR | 500 € |
| Edmund Optics 86410 | 100 | 2.8 | 7 | BBAR | 500 € |
| Schneider-Kreuznach Xenoplan 2.8/50 | 50.2 | 2.8 | 6 | unk. | 630 € |
| Navitar NMV-75 | 75 | 2.5 | 5 | unk. | 185 € |
| Navitar NMV-100 | 100 | 2.8 | 5 | unk. | 170 € |
| Camera Lens | Scatter Parameters | ||
|---|---|---|---|
| (rad) | |||
| LINOS MeVis-C 1.8/50 | −2.50 | 1.18 | 5.29 × 10−03 |
| Edmund Optics 54690 (Double Gauss) | −2.54 | 5.83 | 3.81 × 10−03 |
| Edmund Optics 67715 | −2.14 | 0.92 | 7.43 × 10−03 |
| Edmund Optics 86410 | −2.64 | 10.81 | 4.09 × 10−03 |
| Schneider-Kreuznach Xenoplan 2.8/50 | −2.29 | 3.36 | 5.15 × 10−03 |
| Navitar NMV-75 | −2.39 | 0.49 | 5.46 × 10−03 |
| Navitar NMV-100 | −2.45 | 0.12 | 5.56 × 10−03 |
| Mean | −2.42 | 3.24 | 5.25 × 10−03 |
| Median | −2.45 | 1.18 | 5.29 × 10−03 |
| Standard deviation | 0.17 | 3.89 | 1.18 × 10−03 |
| Coefficient of variation | 0.07 | 1.20 | 0.22 |
| 1-on-1 LIDT (kW/cm2) | ||||
|---|---|---|---|---|
| Imaging Sensor | Exposure Time (s) | |||
| 0.25 | 1 | 5 | 10 | |
| CMOS, monochrome | 75 ± 7 | 73 ± 15 | 56 ± 4 | 48 ± 3 |
| CMOS, color | 56.7 ± 1.8 | |||
| CCD, monochrome | 146 ± 9 | 118 ± 9 | 93 ± 19 | 95 ± 21 |
| CCD, color | 14 ± 2 | 13 ± 2 | 11 ± 1 | 8.1 ± 0.8 |
| Parameter | Setup 1 | Setup 2 |
|---|---|---|
| Camera | VRmagic VRmC-12/BW-Pro | Allied Vision Mako G-158B |
| Imaging sensor | Aptina MT9V024 | Sony IMX273 |
| No. of pixels | 754 × 480 | 1456 × 1088 |
| Quantum efficiency | 0.48 (all wavelengths) | 0.63 (488, 515, 561 nm) 0.56 (640 nm) |
| Pixel size (µm) | 6 | 3.45 |
| Fill factor | ||
| Exposure time (ms) | 8.3 | 8.3 |
| Maximum pixel value | 255 | 255 |
| Saturation capacity (e-) | 6000 | 10500 |
| Camera lens | Schneider-Kreuznach Apo-Xenoplan 2.0/35-2001 | Kowa LM25NC3 |
| Focal length (mm) | 35.1 | 25 |
| f-number | 2 | 1.8 |
| No. of optical elements | 7 | 7 |
| Laser | Toptica iChrome MLE-L | |
| Wavelength (nm) | 488 / 515 / 561 / 640 | |
| Maximum laser power (mW) | 1.6 / 0.7 / 1.6 / 1.0 | 0.96 / 0.42 / 0.89 / 0.61 |
| Beam diameter (cm) | 16.8 / 16.6 / 15.9 / 16.0 | |
| Test chart | Fractal test chart [48] | |
| Mean pixel value | 93 | 63 |
| Sensor | ||||
|---|---|---|---|---|
| 488 nm | 515 nm | 561 nm | 640 nm | |
| VRmagic VRmC-12/BW-Pro | 1.11 | 1.03 | 0.96 | 0.79 |
| Allied Vision Mako G-158B | 5.24 | 4.81 | 4.42 | 4.43 |
| Calculated Dazzle Spot Radius (pixel) | Measured Dazzle Spot Radius (pixel) | MDES (µW/cm2) | |||||
|---|---|---|---|---|---|---|---|
| 2.78 × 10−04 | 4.20 × 10−04 | 2 | 0 | 2 | 3 | 0.004 | 1.94 × 10−03 |
| 3.19 × 10−03 | 4.82 × 10−03 | 4 | 0 | 4 | 13 | 0.02 | 0.107 |
| 4.72 × 10−02 | 7.13 × 10−02 | 9 | 0 | 10 | 18 | 0.02 | 0.263 |
| 0.143 | 0.215 | 14 | 0 | 14 | 21 | 0.03 | 0.377 |
| 0.231 | 0.349 | 16 | 0 | 17 | 23 | 0.03 | 0.451 |
| 0.667 | 1.01 | 23 | 0 | 27 | 29 | 0.04 | 0.771 |
| 1.67 | 2.53 | 31 | 27 | 42 | 44 | 0.06 | 1.92 |
| 3.75 | 5.66 | 40 | 50 | 60 | 64 | 0.09 | 4.22 |
| 7.48 | 11.3 | 51 | 72 | 82 | 80 | 0.11 | 7.12 |
| 9.42 | 14.2 | 55 | 80 | 90 | 85 | 0.12 | 8.15 |
| 11.9 | 17.9 | 59 | 89 | 99 | 91 | 0.13 | 9.67 |
| 14.9 | 22.5 | 64 | 99 | 109 | 97 | 0.13 | 11.3 |
| 23.7 | 35.7 | 75 | 121 | 132 | 111 | 0.15 | 15.6 |
| 29.8 | 45.0 | 81 | 134 | 145 | 121 | 0.17 | 19.3 |
| 37.5 | 56.6 | 87 | 148 | 159 | 131 | 0.18 | 23.0 |
| 48.3 | 72.9 | 95 | 164 | 176 | 153 | 0.21 | 34.0 |
| 56.7 | 85.7 | 100 | 176 | 188 | 169 | 0.23 | 43.6 |
| 66.7 | 101 | 105 | 188 | 200 | 186 | 0.26 | 55.5 |
| 94.2 | 142 | 118 | 216 | 230 | 222 | 0.31 | 87.1 |
| 119 | 179 | 128 | 238 | 252 | 260 | 0.36 | 129 |
| 149 | 225 | 138 | 261 | 276 | 298 | 0.41 | 182 |
| 358 | 541 | 185 | 372 | 389 | 475 | 0.65 | 596 |
| 461 | 696 | 201 | 412 | 430 | n.m. | n.m. | - |
| 637 | 961 | 224 | 469 | 488 | n.m. | n.m. | - |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ritt, G. Laser Safety Calculations for Imaging Sensors. Sensors 2019, 19, 3765. https://doi.org/10.3390/s19173765
Ritt G. Laser Safety Calculations for Imaging Sensors. Sensors. 2019; 19(17):3765. https://doi.org/10.3390/s19173765
Chicago/Turabian StyleRitt, Gunnar. 2019. "Laser Safety Calculations for Imaging Sensors" Sensors 19, no. 17: 3765. https://doi.org/10.3390/s19173765
APA StyleRitt, G. (2019). Laser Safety Calculations for Imaging Sensors. Sensors, 19(17), 3765. https://doi.org/10.3390/s19173765




