NLOS Identification and Mitigation Using Low-Cost UWB Devices
Abstract
1. Introduction
2. Measurement Campaign
2.1. Hardware
- The CIR must be extracted from the chip sequentially in chunks of data through the serial port, which requires to download 4064 bytes per CIR estimate [19]. That is, the latency introduced to obtain this parameter is about 300 ms for each CIR estimate.
- CIR measurements correspond to the wireless channel between the the emitter and the receiver at a given time instant. However, these two devices could be different from the ones involved in the ranging process depending on the mode of operation considered. For example, Pozyx devices allow for a so-called remote mode in which a node A (typically connected to a computer to receive the measurements) can command a remote node B to perform a ranging operation between the node B itself and a third node C. In this case, the CIR available at A corresponds to the channel between A and B, instead of the channel between the two nodes involved in the ranging process, i.e., B and C. Thus, NLOS detection would be possible only between nodes A and B, rather than between nodes B and C, which are the ones that really participate in the ranging process.
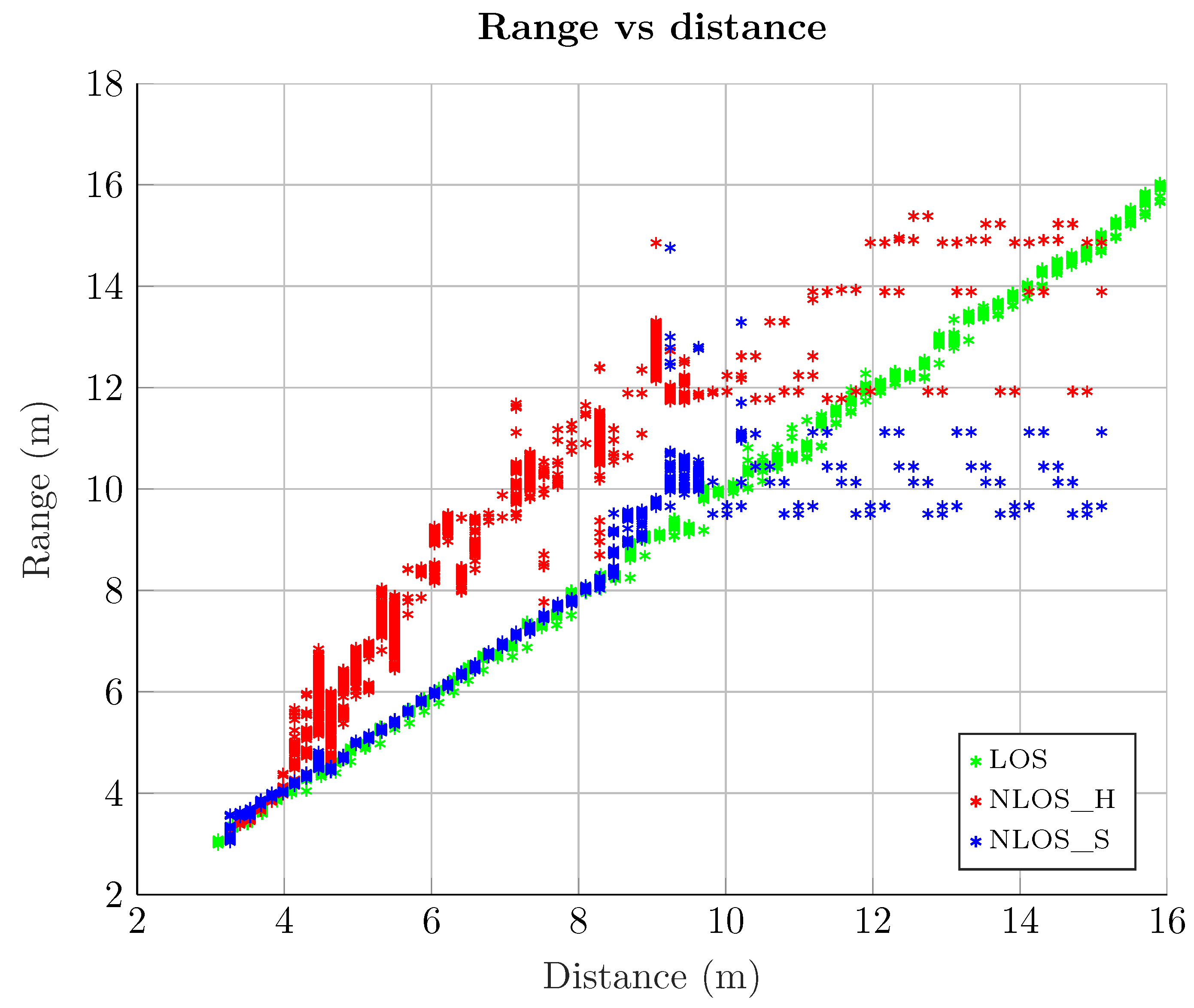
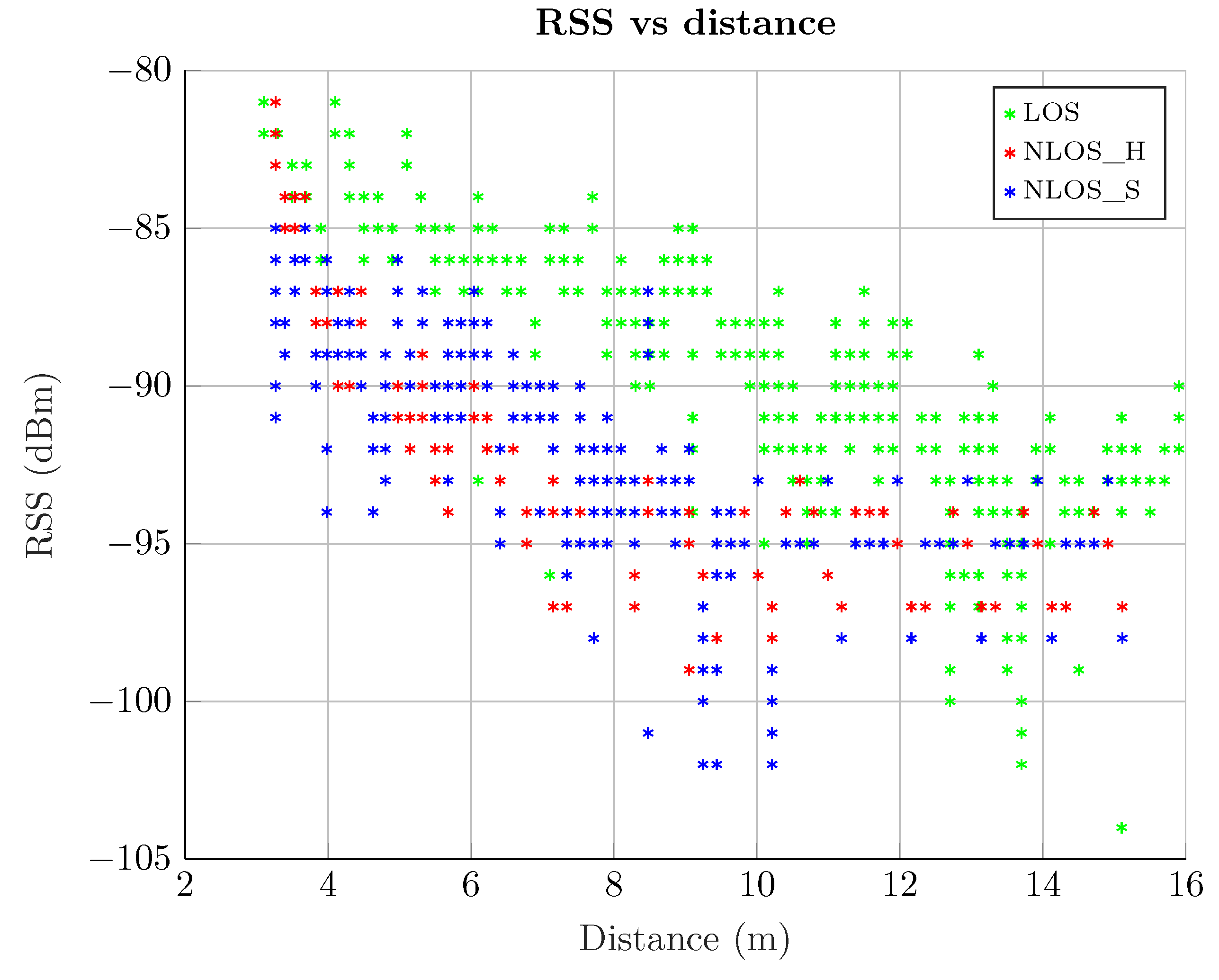
2.2. LOS Versus NLOS
- LOS scenario. In this case, both emitter and receiver have no obstacles between them and their separation distance is enough to ensure good communication between them.
- NLOS Soft scenario. Here there is an obstacle that obstructs a possible LOS, so that the main signal path has to go through it (e.g., a wall). In this case, the main and secondary paths reach the receiver attenuated by this obstacle, causing that the RSS do not correspond to the distance, as in the LOS case.
- NLOS Hard scenario. In this case, the emitter and the receiver are physically located in such a way that the secondary paths are received with more RSS than the main one. Basically, the obstacles ensure that the main path is considerably attenuated, or even completely blocked, whereas the reflected paths easily reach the receiver. Thus, in this NLOS Hard scenario, the receiver will always intercept a secondary path, which is a delayed version of the main path.
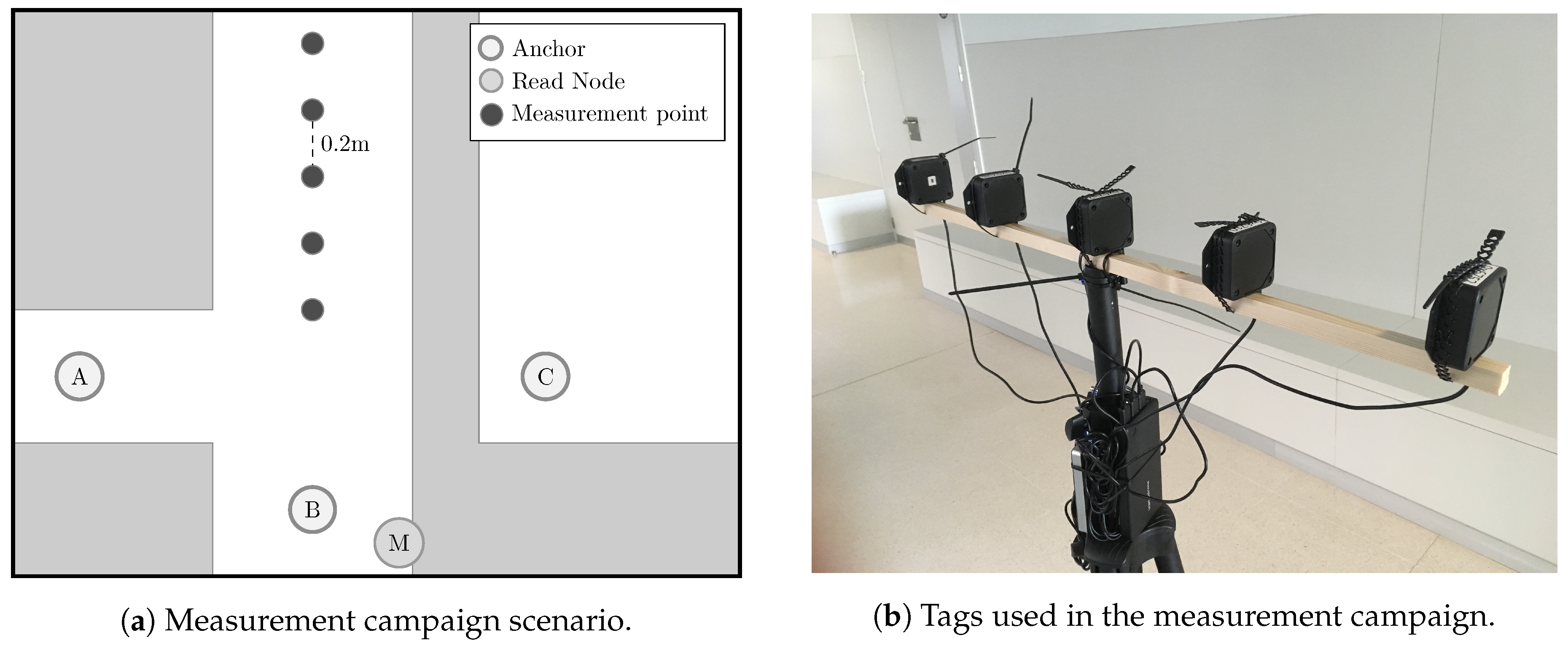
2.3. Environment
2.4. Hardware Setup
2.5. Measurements Analysis
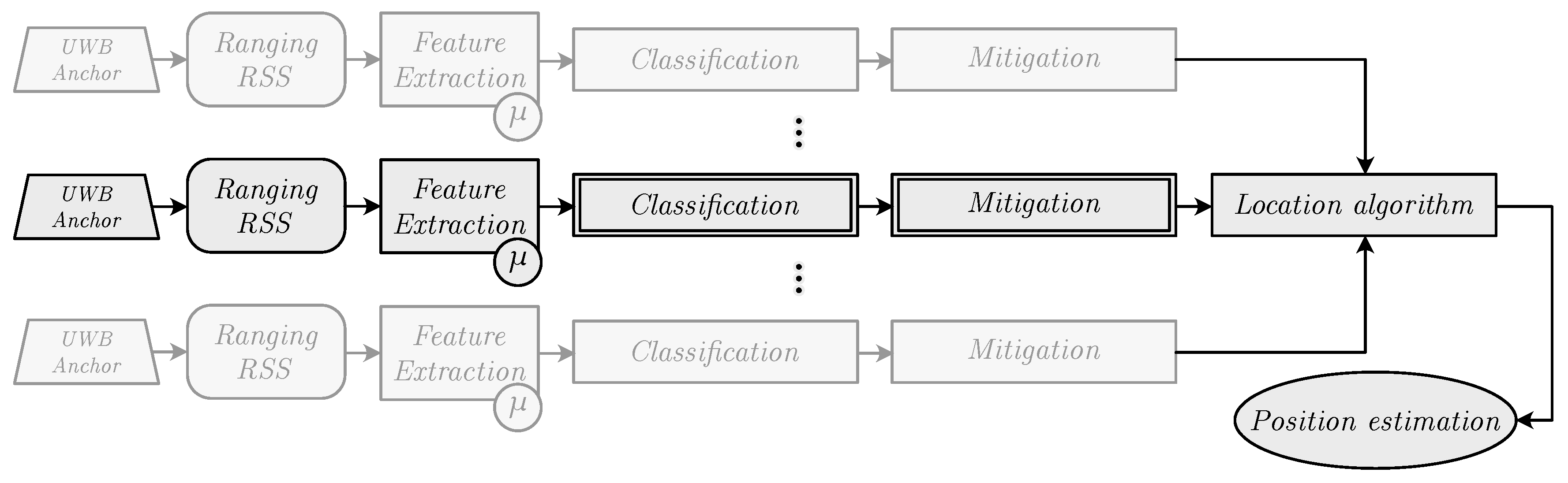
3. Machine Learning
3.1. Algorithms
3.1.1. Binary Decision Tree
3.1.2. Support Vector Machine
3.1.3. k-Nearest Neighbors
3.1.4. Gaussian Process Regression and Classification Models
3.1.5. Generalized Linear Models
3.2. Input Features
3.3. Bayesian Optimization
3.4. Discrete Measurement Points
4. Results
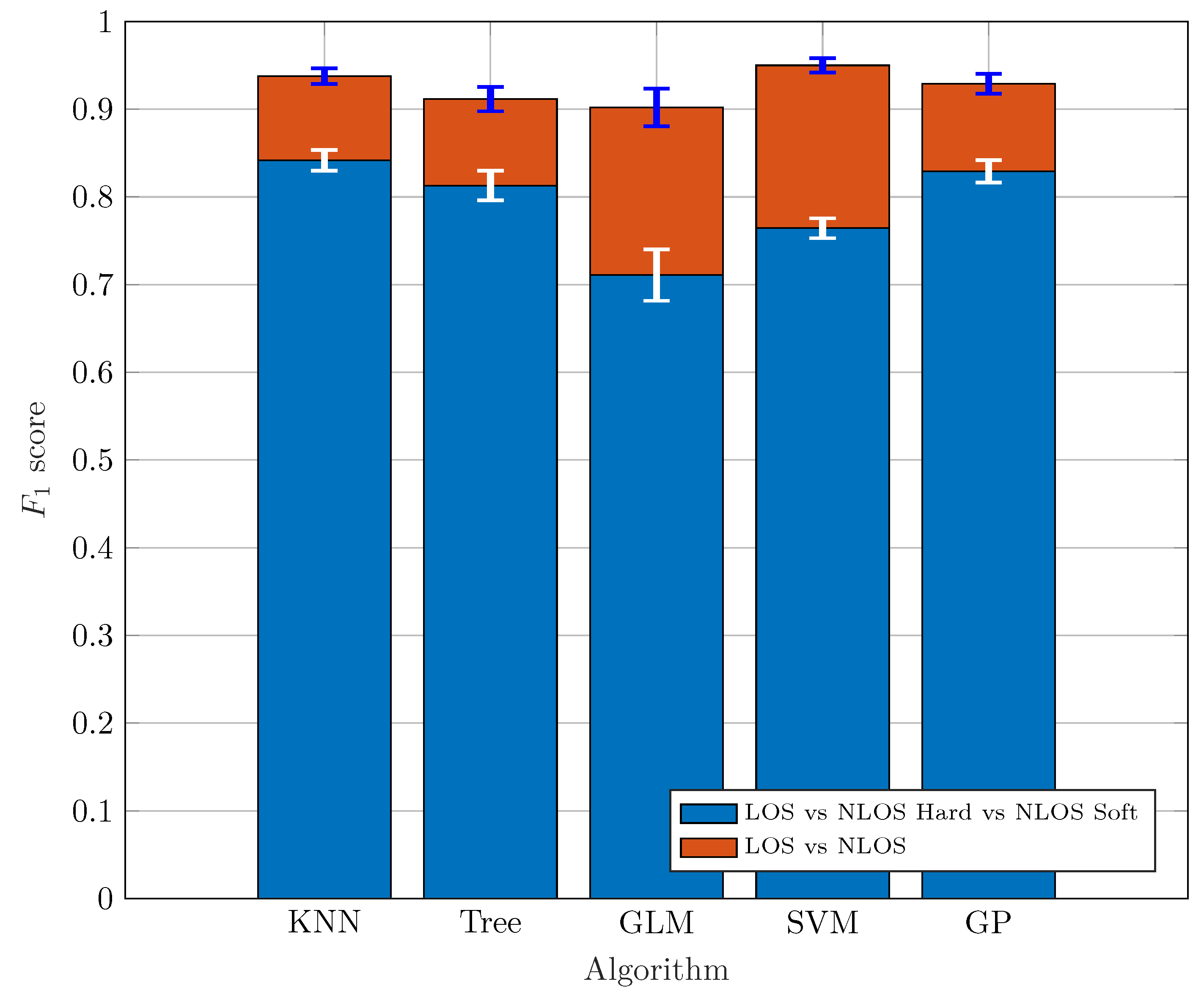
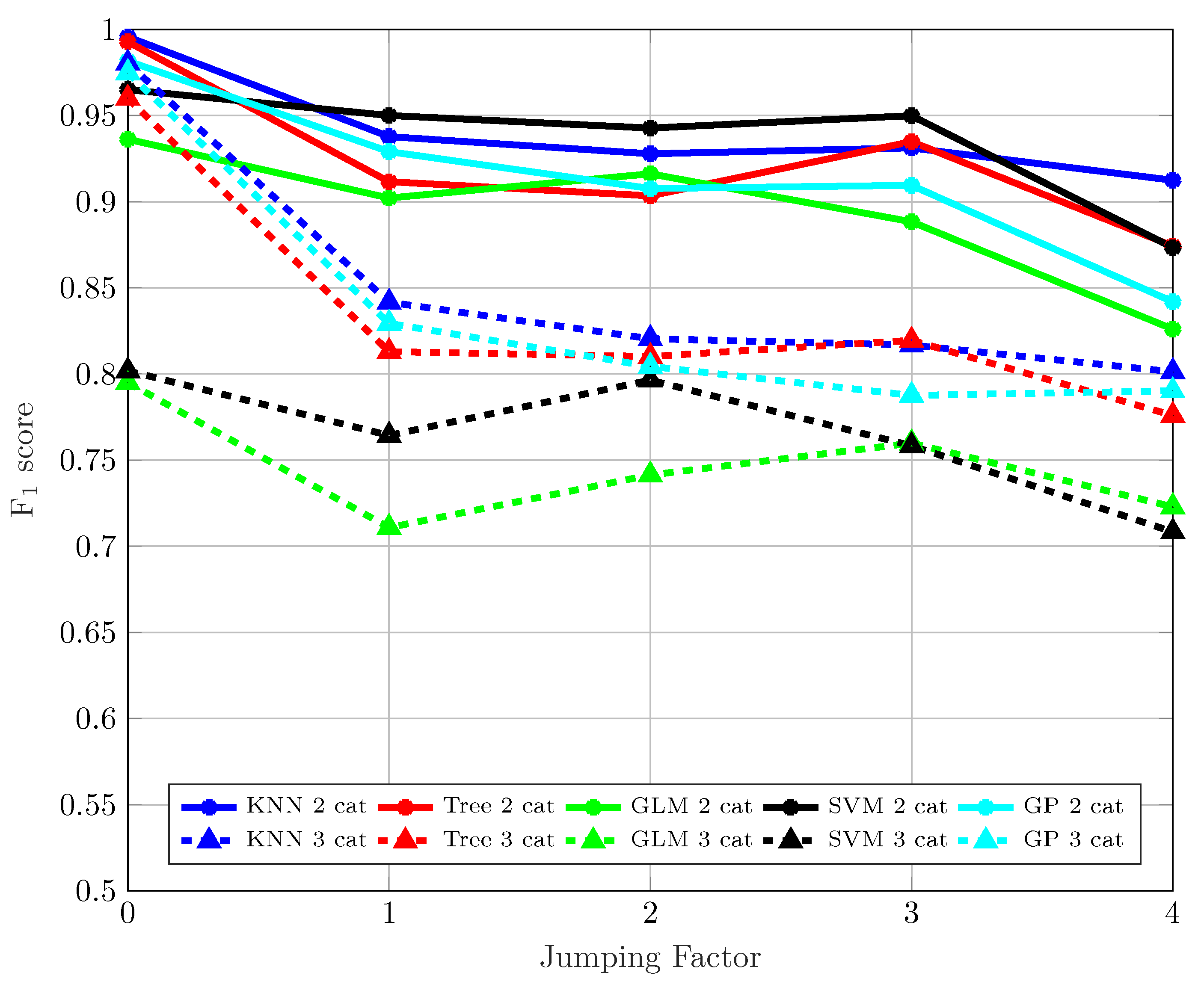
4.1. Classification
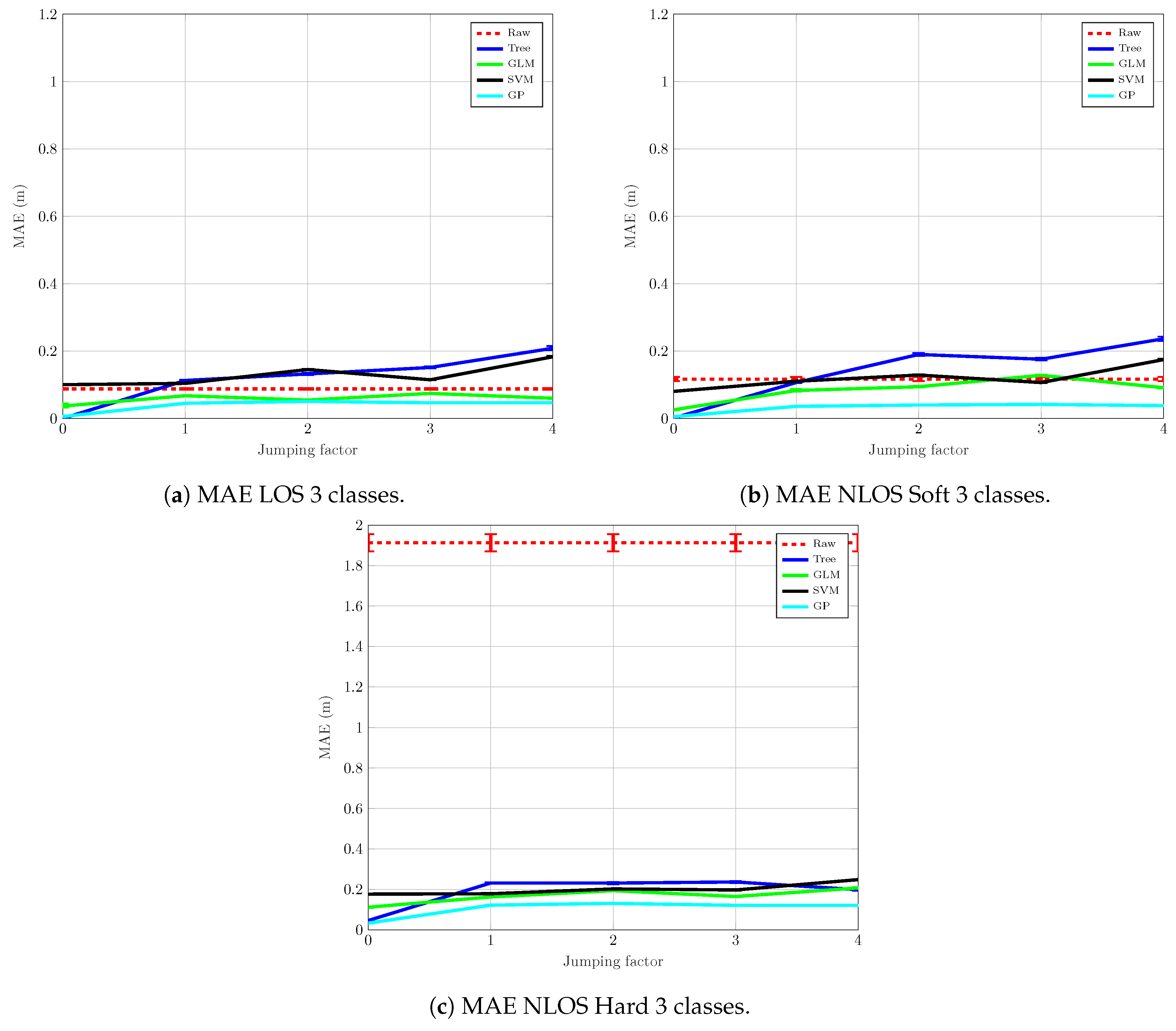
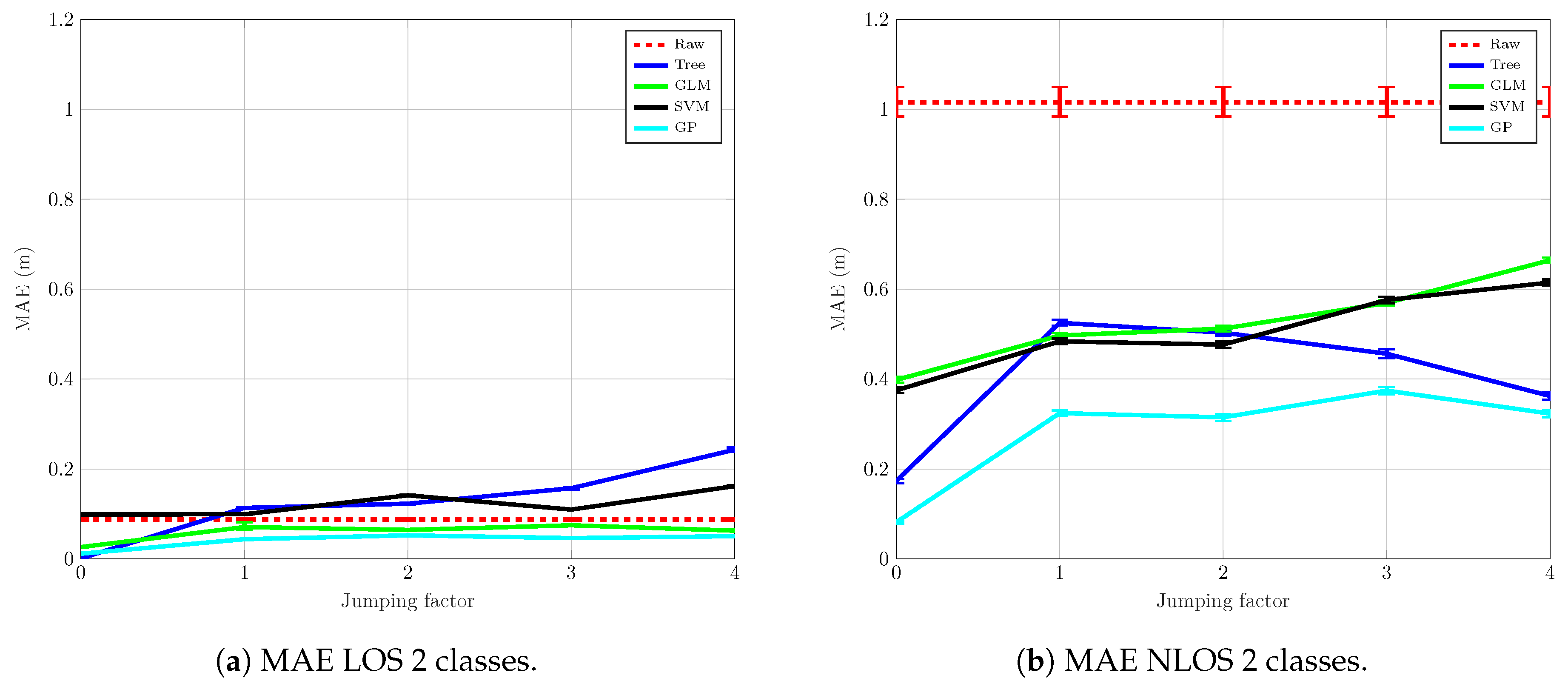
4.2. Mitigation
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Acronyms
| API | application programming interface |
| CIR | channel impulse response |
| GLM | generalized linear model |
| GP | Gaussian process |
| k-NN | k-nearest neighbors |
| LED | leading edge detection |
| LOS | line-of-sight |
| MAE | mean absolute error |
| ML | machine learning |
| NLOS | non-line-of-sight |
| PRF | pulse repetition frequency |
| RFID | radio-frequency identification |
| ROS | Robot Operating System |
| RSS | received signal strength |
| SVM | support vector machine |
| TDOA | time difference of arrival |
| TOA | time of arrival |
| TOF | time of flight |
| TWR | two-way ranging |
| UWB | ultra-wideband |
References
- Laaraiedh, M.; Yu, L.; Avrillon, S.; Uguen, B. Comparison of hybrid localization schemes using RSSI, TOA, and TDOA. In Proceedings of the 17th European Wireless 2011-Sustainable Wireless Technologies, Vienna, Austria, 27–29 April 2011; pp. 1–5. [Google Scholar]
- Dardari, D.; Conti, A.; Ferner, U.; Giorgetti, A.; Win, M.Z. Ranging with ultrawide bandwidth signals in multipath environments. Proc. IEEE 2009, 97, 404–426. [Google Scholar] [CrossRef]
- Decarli, N.; Dardari, D.; Gezici, S.; D’Amico, A.A. LOS/NLOS detection for UWB signals: A comparative study using experimental data. In Proceedings of the IEEE 5th International Symposium on Wireless Pervasive Computing 2010, Modena, Italy, 5–7 May 2010; pp. 169–173. [Google Scholar]
- Jourdan, D.B.; Dardari, D.; Win, M.Z. Position error bound for UWB localization in dense cluttered environments. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 613–628. [Google Scholar] [CrossRef]
- Borras, J.; Hatrack, P.; Mandayam, N.B. Decision theoretic framework for NLOS identification. In Proceedings of the 48th IEEE Vehicular Technology Conference (VTC), Ottawa, ON, Canada, 21 May 1998; Volume 2, pp. 1583–1587. [Google Scholar]
- Venkatesh, S.; Buehrer, R.M. Non-line-of-sight identification in ultra-wideband systems based on received signal statistics. IET Microw. Antennas Propag. 2007, 1, 1120–1130. [Google Scholar] [CrossRef]
- Maali, A.; Mimoun, H.; Baudoin, G.; Ouldali, A. A new low complexity NLOS identification approach based on UWB energy detection. In Proceedings of the IEEE Radio and Wireless Symposium, San Diego, CA, USA, 18–22 January 2009; pp. 675–678. [Google Scholar] [CrossRef]
- Al-Jazzar, S.; Caffery, J., Jr. New algorithms for NLOS identification. In Proceedings of the 14th IST Mobile and Wireless Communications Summit, Dresden, Germany, 19–23 June 2005. [Google Scholar]
- Güvenç, İ.; Chong, C.C.; Watanabe, F.; Inamura, H. NLOS Identification and Weighted Least-Squares Localization for UWB Systems Using Multipath Channel Statistics. EURASIP J. Adv. Signal Process. 2007, 2008, 271984. [Google Scholar] [CrossRef]
- Marano, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS identification and mitigation for localization based on UWB experimental data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Wann, C.D.; Hsueh, C.S. NLOS mitigation with biased Kalman filters for range estimation in UWB systems. In Proceedings of the IEEE Region 10 Conference (TENCON), Taipei, Taiwan, 30 October–2 November 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.J.; García-Naya, J.A. NLOS Classification based on RSS and Ranging Statistics Obtained from Low-Cost UWB Devices. 2019. Available online: http://dx.doi.org/10.21227/swz9-y281 (accessed on 7 August 2019).
- UDC. Area Científica. Available online: https://goo.gl/maps/59pCfNgZ75Siy6gf7 (accessed on 3 June 2019).
- Pozyx. Pozyx Site. Available online: http://www.pozyx.com/ (accessed on 22 May 2019).
- DecaWave. Decawave Site. Available online: http://www.decawave.com/ (accessed on 22 May 2019).
- Decuir, J. Two Way Time Transfer Based Ranging. Contrib. IEEE 2004, 802, 15. [Google Scholar]
- Dashti, M.; Ghoraishi, M.; Haneda, K.; Takada, J.I. High-precision time-of-arrival estimation for UWB localizers in indoor multipath channels. In Novel Applications of the UWB Technologies; IntechOpen: London, UK, 2011. [Google Scholar]
- Barral, V.; Suárez-Casal, P.; Escudero, C.; García-Naya, J.A. Assessment of UWB ranging bias in multipath environments. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016. [Google Scholar]
- Pozyx. Pozyx Register Overview. Available online: https://www.pozyx.io/product-info/developer-tag/datasheet-register-overview (accessed on 3 June 2019).
- Yang, W.; Peipei, C.; Xinwei, Z.; Qinyu, Z.; Naitong, Z. Characterization of indoor ultra-wide band NLOS channel. In Proceedings of the IEEE Annual Wireless and Microwave Technology Conference, Clearwater Beach, FL, USA, 4–5 December 2006; pp. 1–5. [Google Scholar]
- Rasmussen, C.E.; Nickisch, H. Gaussian processes for machine learning (GPML) toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- CESGA. Centro Tecnolóxico de Supercomputación de Galicia. Available online: https://www.cesga.es/en/cesga (accessed on 22 May 2019).
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin, Germany, 1995. [Google Scholar]
- Platt, J.C.; Cristianini, N.; Shawe-Taylor, J. Large margin DAGs for multiclass classification. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2000; pp. 547–553. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 1997; pp. 155–161. [Google Scholar]
- Mullin, M.D.; Sukthankar, R. Complete Cross-Validation for Nearest Neighbor Classifiers. In Proceedings of the Seventeenth International Conference on Machine Learning (ICML 2000), Stanford, CA, USA, 29 June–2 July 2000; pp. 639–646. [Google Scholar]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin, Germany, 2003; pp. 63–71. [Google Scholar]
- Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Soc. Ser. A Gen. 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.; García-Naya, J.A. NLOS Classification Based on RSS and Ranging Statistics Obtained from Low-Cost UWB Devices. In Proceedings of the 27th European Signal Processing Conference, EUSIPCO, A Coruña, Spain, 2–6 September 2019. [Google Scholar]
- Betrò, B. Bayesian methods in global optimization. J. Glob. Optim. 1991, 1, 1–14. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Musa, A.; Nugraha, G.D.; Han, H.; Choi, D.; Seo, S.; Kim, J. A decision tree-based NLOS detection method for the UWB indoor location tracking accuracy improvement. Int. J. Commun. Syst. 2019. [Google Scholar] [CrossRef]
- Bregar, K.; Hrovat, A.; Mohorcic, M. NLOS Channel Detection with Multilayer Perceptron in Low-Rate Personal Area Networks for Indoor Localization Accuracy Improvement. In Proceedings of the 8th Jožef Stefan International Postgraduate School Students’ Conference, Ljubljana, Slovenia, 31 May–1 June 2016. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barral, V.; Escudero, C.J.; García-Naya, J.A.; Maneiro-Catoira, R. NLOS Identification and Mitigation Using Low-Cost UWB Devices. Sensors 2019, 19, 3464. https://doi.org/10.3390/s19163464
Barral V, Escudero CJ, García-Naya JA, Maneiro-Catoira R. NLOS Identification and Mitigation Using Low-Cost UWB Devices. Sensors. 2019; 19(16):3464. https://doi.org/10.3390/s19163464
Chicago/Turabian StyleBarral, Valentín, Carlos J. Escudero, José A. García-Naya, and Roberto Maneiro-Catoira. 2019. "NLOS Identification and Mitigation Using Low-Cost UWB Devices" Sensors 19, no. 16: 3464. https://doi.org/10.3390/s19163464
APA StyleBarral, V., Escudero, C. J., García-Naya, J. A., & Maneiro-Catoira, R. (2019). NLOS Identification and Mitigation Using Low-Cost UWB Devices. Sensors, 19(16), 3464. https://doi.org/10.3390/s19163464




