Two Degree-of-Freedom Fiber-Coupled Heterodyne Grating Interferometer with Milli-Radian Operating Range of Rotation
Abstract
:1. Introduction
2. Materials and Methods
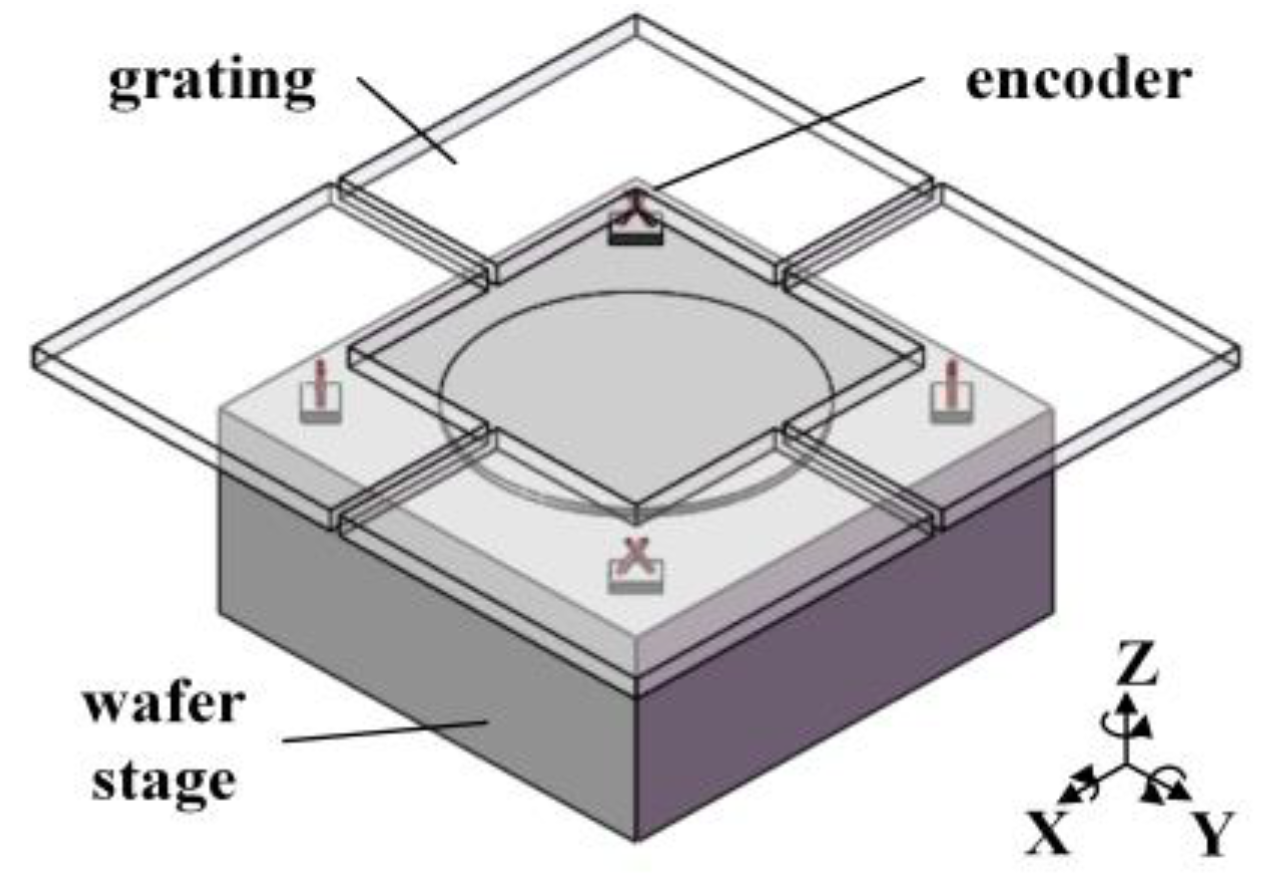
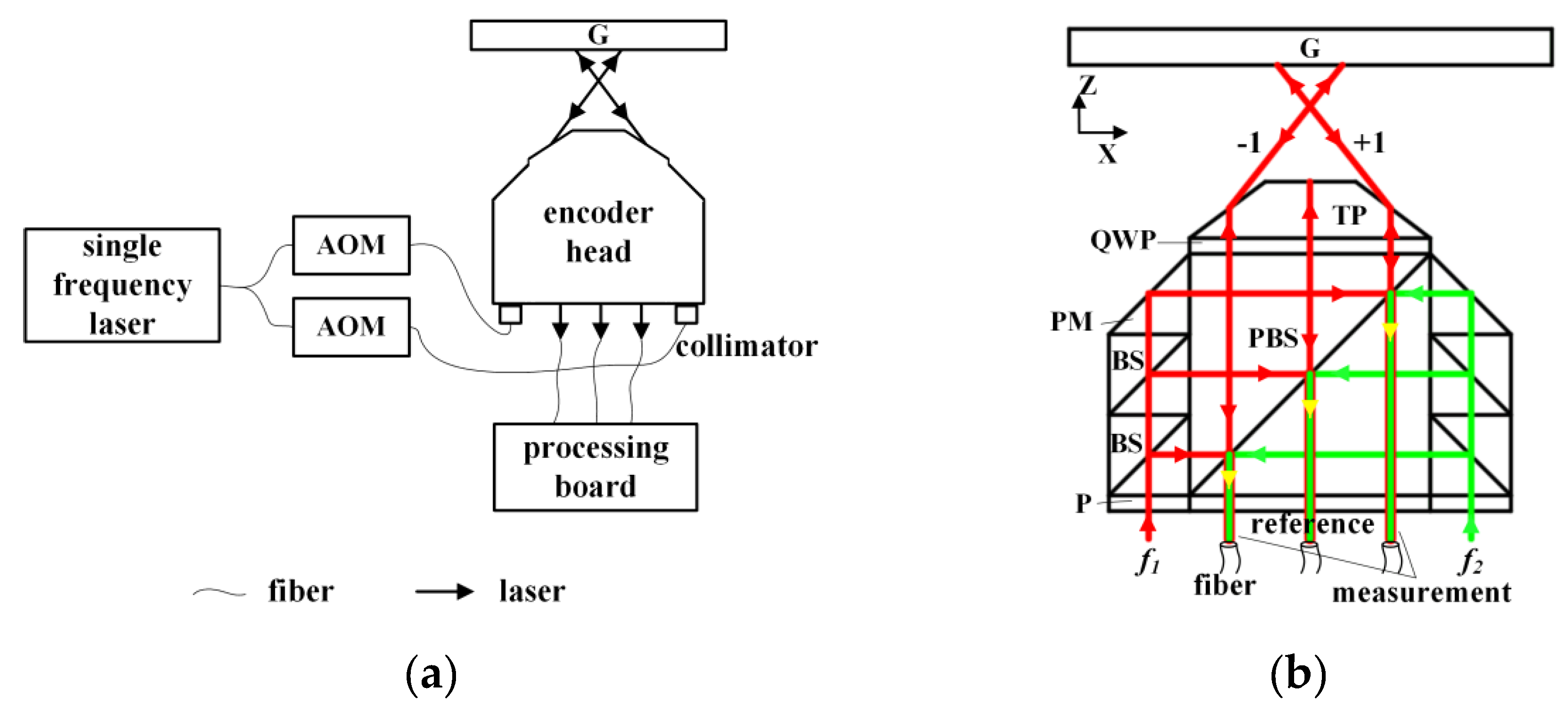
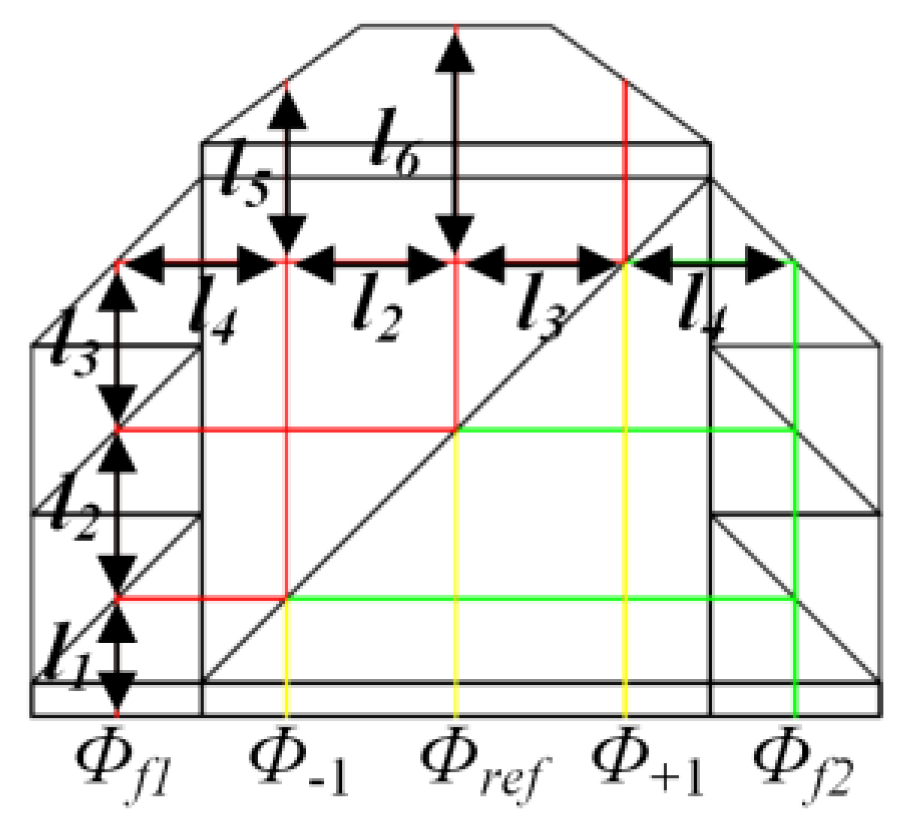
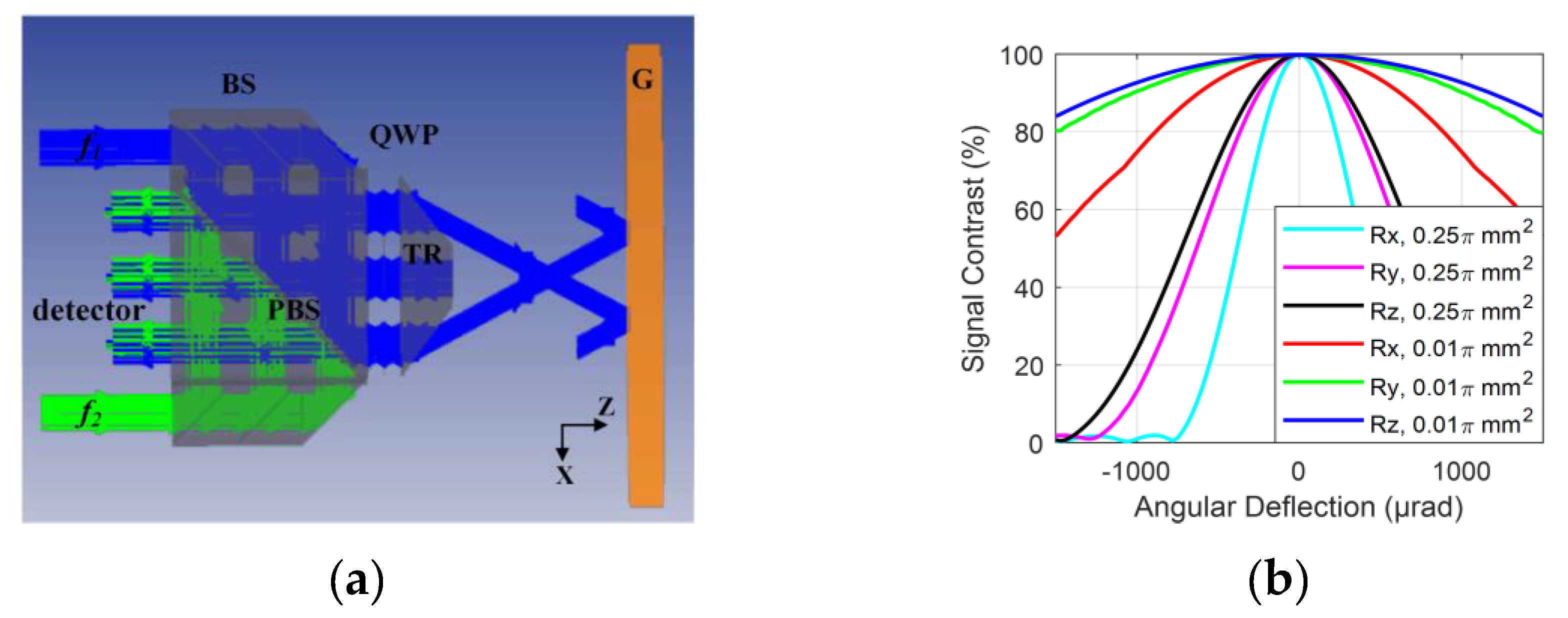
2.1. Optical Configuration and Principle
2.2. Simulation
3. Results and Discussion
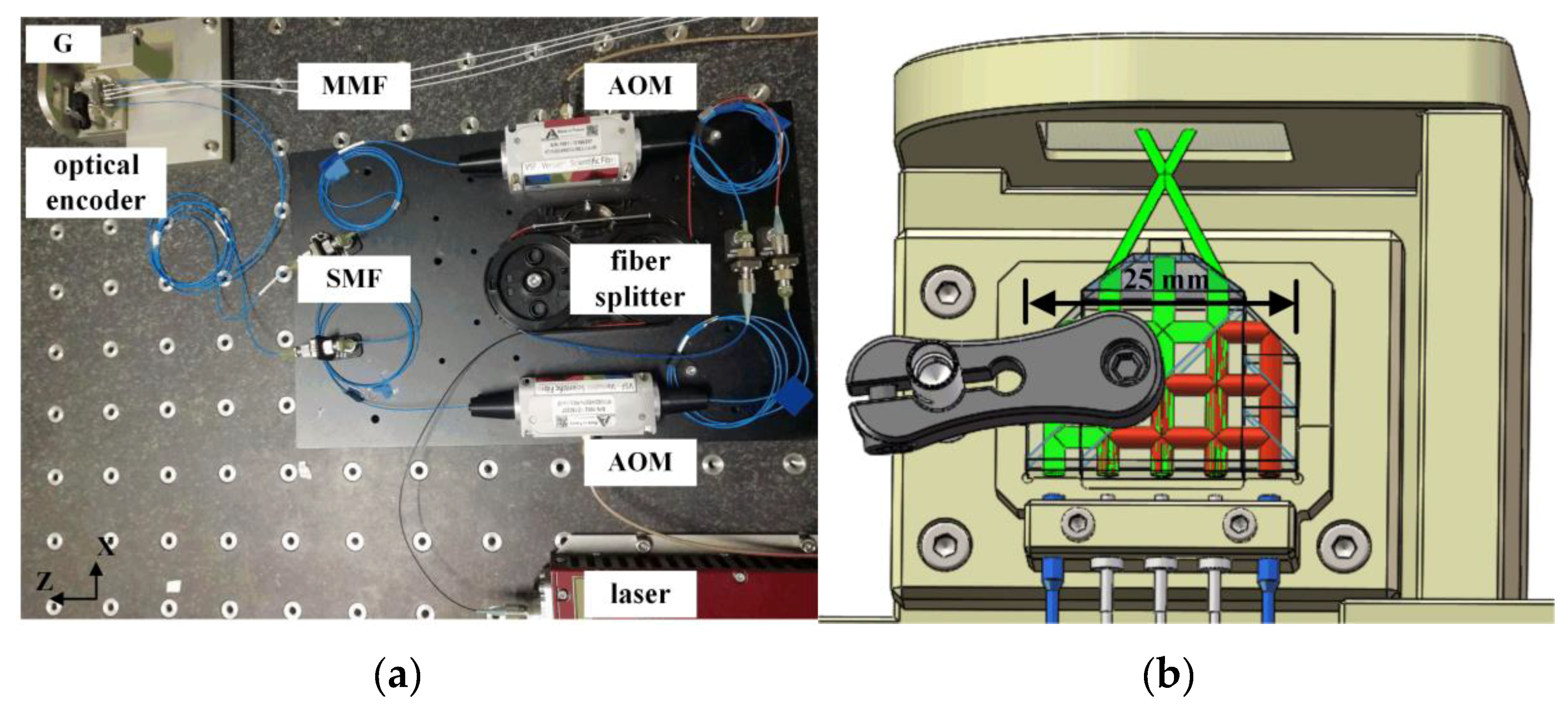
3.1. Experimental Setup
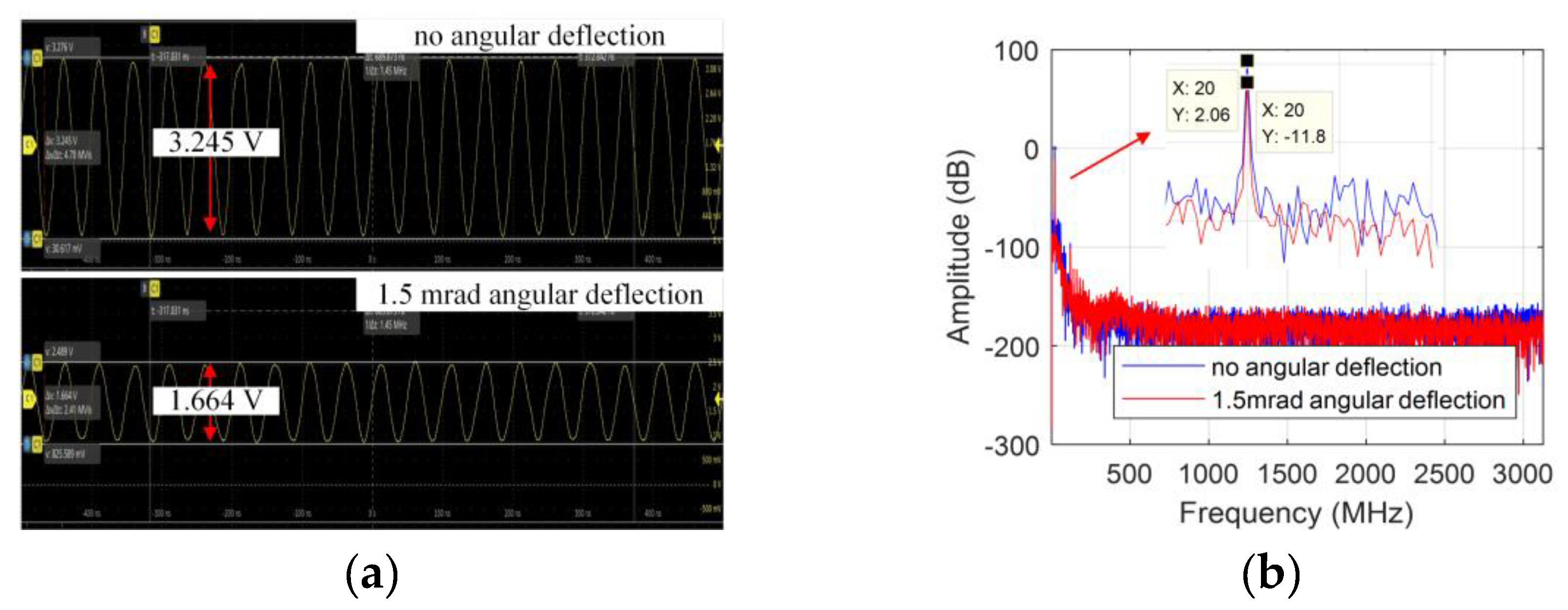
3.2. Large Operating Range of Rotation
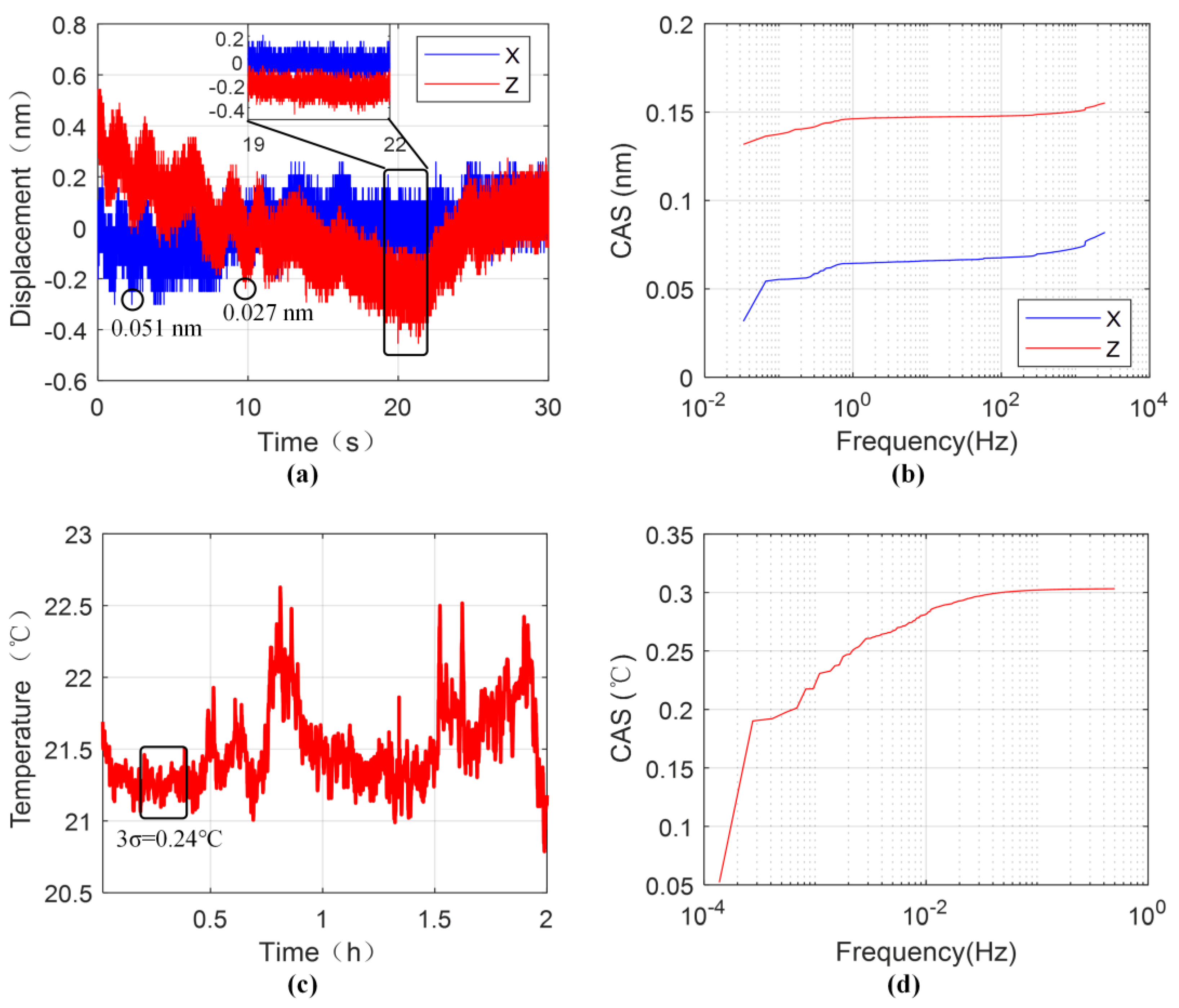
3.3. Measurement Stability
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bosse, H.; Wilkening, U. Developments at PTB in nanometrology for support of the semiconductor industry. Meas. Sci. Technol. 2005, 16, 2155–2166. [Google Scholar] [CrossRef]
- De Jong, F.; van der Pasch, B.; Castenmiller, T.; Vleeming, B.; Droste, R.; van de Mast, F. Enabling the lithography roadmap: An immersion tool based on a novel stage positioning system. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 22–27 February 2009; p. 72741S. [Google Scholar]
- Castenmiller, T.; van de Mast, F.; de Kort, T.; van de Vin, C.; de Wit, M.; Stegen, R.; van Cleef, S. Towards ultimate optical lithography with NXT: 1950i dual stage immersion platform. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 21–25 February 2010; p. 76401N. [Google Scholar]
- Birch, K.; Downs, M. An updated Edlén equation for the refractive index of air. Metrologia 1993, 30, 155. [Google Scholar] [CrossRef]
- Teimel, A. Technology and applications of grating interferometers in high-precision measurement. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Kunzmann, H.; Pfeifer, T.; Flügge, J. Scales vs. laser interferometers performance and comparison of two measuring systems. CIRP Ann. 1993, 42, 753–767. [Google Scholar] [CrossRef]
- Heilmann, R.K.; Chen, C.G.; Konkola, P.T.; Schattenburg, M.L. Dimensional metrology for nanometre-scale science and engineering: Towards sub-nanometre accurate encoders. Nanotechnology 2004, 15, S504. [Google Scholar] [CrossRef]
- Cheng, F.; Fan, K.-C. Linear diffraction grating interferometer with high alignment tolerance and high accuracy. Appl. Opt. 2011, 50, 4550–4556. [Google Scholar] [CrossRef] [PubMed]
- Guan, J.; Köchert, P.; Weichert, C.; Tutsch, R. A high performance one-dimensional homodyne encoder and the proof of principle of a novel two-dimensional homodyne encoder. Precis. Eng. 2013, 37, 865–870. [Google Scholar] [CrossRef]
- De Groot, P.J.; Badami, V.G.; Liesener, J. Concepts and geometries for the next generation of precision heterodyne optical encoders. In Proceedings of the Annual Meeting of the American Society for Precision Engineering (ASPE 2016), Portland, OR, USA, 23–28 October 2016; pp. 146–149. [Google Scholar]
- Guan, J.; Köchert, P.; Weichert, C.; Köning, R.; Siaudinyte, L.; Flügge, J. A differential interferometric heterodyne encoder with 30 picometer periodic nonlinearity and sub-nanometer stability. Precis. Eng. 2017, 50, 114–118. [Google Scholar] [CrossRef]
- Xing, X.; Chang, D.; Hu, P.; Tan, J. Spatially separated heterodyne grating interferometer for eliminating periodic nonlinear errors. Opt. Express 2017, 25, 31384–31393. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wei, C.; Jia, W.; Li, S.; Yu, J.; Li, M.; Xiang, C.; Xiang, X.; Wang, J.; Ma, J. Two-degree-freedom displacement measurement based on a short period grating in symmetric Littrow configuration. Opt. Commun. 2016, 380, 382–386. [Google Scholar] [CrossRef]
- Hsieh, H.-L.; Chen, J.-C.; Lerondel, G.; Lee, J.-Y. Two-dimensional displacement measurement by quasi-common-optical-path heterodyne grating interferometer. Opt. Express 2011, 19, 9770–9782. [Google Scholar] [CrossRef]
- Köchert, P.; Flügge, J.; Weichert, C.; Köning, R.; Manske, E. Phase measurement of various commercial heterodyne He–Ne-laser interferometers with stability in the picometer regime. Meas. Sci. Technol. 2012, 23, 074005. [Google Scholar] [CrossRef]
- Wu, C.-C.; Hsu, C.-C.; Lee, J.-Y.; Chen, Y.-Z.; Yang, J.-S. Littrow-type self-aligned laser encoder with high tolerance using double diffractions. Opt. Commun. 2013, 297, 89–97. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Translational displacement computational algorithm of the grating interferometer without geometric error for the wafer stage in a photolithography scanner. Opt. Express 2018, 26, 34734–34752. [Google Scholar] [CrossRef] [PubMed]
- Holmes, M.; Evans, C. Displacement Measuring Interferometry Measurement Uncertainty. Available online: http://www.aspe.net/publications/Summer_2004/04SU%20Extended%20Abstracts/Holmes-Evans-1645.PDF (accessed on 20 July 2019).
- Kao, C.-F.; Lu, S.-H.; Shen, H.-M.; Fan, K.-C. Diffractive laser encoder with a grating in Littrow configuration. Jpn. J. Appl. Phys. 2008, 47, 1833. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Zhang, M.; Zhu, Y.; Ye, W.; Wang, L.; Xia, Y. Two Degree-of-Freedom Fiber-Coupled Heterodyne Grating Interferometer with Milli-Radian Operating Range of Rotation. Sensors 2019, 19, 3219. https://doi.org/10.3390/s19143219
Yang F, Zhang M, Zhu Y, Ye W, Wang L, Xia Y. Two Degree-of-Freedom Fiber-Coupled Heterodyne Grating Interferometer with Milli-Radian Operating Range of Rotation. Sensors. 2019; 19(14):3219. https://doi.org/10.3390/s19143219
Chicago/Turabian StyleYang, Fuzhong, Ming Zhang, Yu Zhu, Weinan Ye, Leijie Wang, and Yizhou Xia. 2019. "Two Degree-of-Freedom Fiber-Coupled Heterodyne Grating Interferometer with Milli-Radian Operating Range of Rotation" Sensors 19, no. 14: 3219. https://doi.org/10.3390/s19143219
APA StyleYang, F., Zhang, M., Zhu, Y., Ye, W., Wang, L., & Xia, Y. (2019). Two Degree-of-Freedom Fiber-Coupled Heterodyne Grating Interferometer with Milli-Radian Operating Range of Rotation. Sensors, 19(14), 3219. https://doi.org/10.3390/s19143219