Simultaneous Floating-Base Estimation of Human Kinematics and Joint Torques
Abstract
1. Introduction
2. Background
2.1. Notation
- Let and be the set of real and natural numbers, respectively.
- Let denote a n-dimensional column vector, while x denotes a scalar quantity. We advise the reader to pay attention to the notation style: we define vectors, matrices with bold small and capital letters, respectively, and scalars with non-bold style.
- Let be the norm of the vector .
- Let and be the zero and identity matrices , respectively. The notation represents the zero matrix .
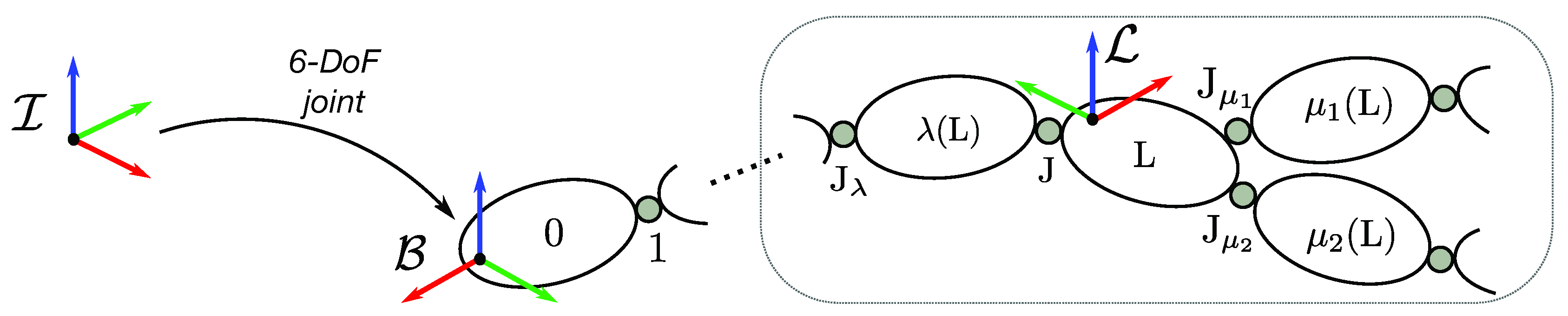
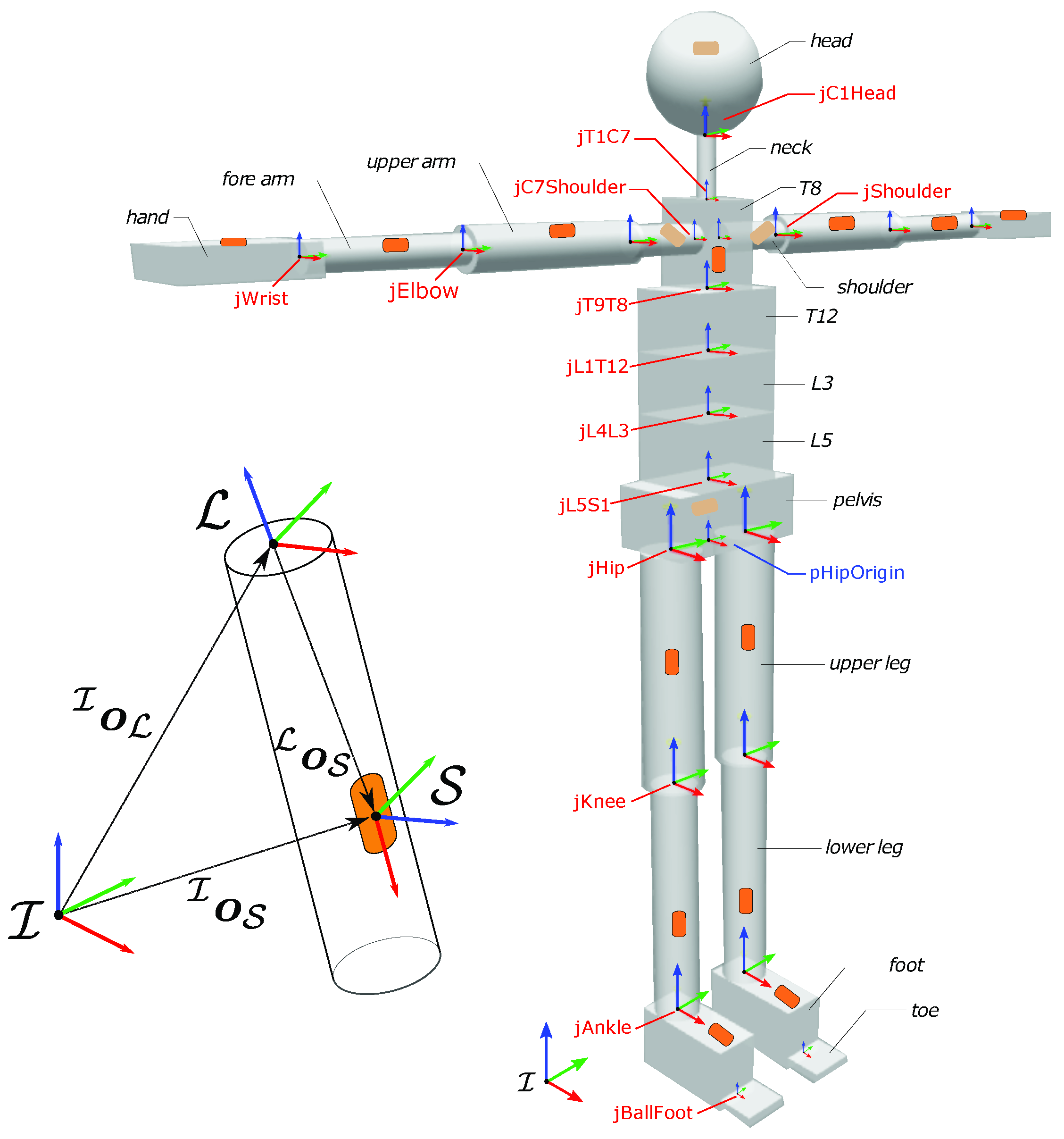
- Let be an inertial frame with z-axis pointing against the gravity (g denotes the norm of the gravitational acceleration). Let denote the base frame, i.e., a frame attached to the base link. Let be the generic frame attached to a link, and the frame of a joint.
- Let each frame be identified by an origin and an orientation, e.g., or .
- Let be the coordinate vector connecting with , pointing towards , expressed with respect to (w.r.t.) frame .
- Let be a rotation matrix such that .
- Let denote the skew-symmetric matrix such that , being × the cross product operator in .
- Let and denote the first-order and second-order time derivatives of , respectively.
- Given a stochastic variable , let denote its probability density and the conditional probability of given the assumption that another stochastic variable has occurred.
- If is the expected value of a stochastic variable , let and be the mean and covariance of , respectively. Let be the expression for the normal distribution of .
2.2. Human Kinematics and Dynamics Modeling
2.3. Case-Study Human Model
3. Simultaneous Floating-Base Estimation of Human Whole-Body Kinematics and Dynamics
3.1. Offline Estimation of Sensor Position
3.2. Estimation of Human Kinematics
3.3. Offline Contact Classification
| Algorithm 1 Offline Feet Contact Cassification. | |
| Require: FT sensor forces (z component) for right foot and left foot | |
| 1: | procedure |
| 2: | N ← number of samples |
| 3: | ← threshold on fz = mean() |
| 4: | main loop: |
| 5: | for do |
| 6: | if then |
| 7: | Classify j as double support sample |
| 8: | else |
| 9: | if then |
| 10: | Classify j as right single support sample |
| 11: | else |
| 12: | Classify j as left single support sample |
| 13: | end if |
| 14: | end if |
| 15: | end for |
| 16: | end procedure |
3.4. Maximum-A-Posteriori Algorithm for Floating-Base Dynamics Estimation
- Since we broke the univocal relation between each link and its parent joint, we redefine the serialization of all the kinematics and dynamics quantities in the vector w.r.t. the fixed-base serialization of the same vector in Section 4 of [7], thusbeingIn the new serialization, is the proper sensor acceleration of Equation (12) and is the external wrench acting on each link. Similarly for the joint quantities, is the internal wrench (or joint wrench) exchanged from to through the joint , while is the joint acceleration.
- The variable was removed from . The joint torque can be obtained as a projection of the joint wrench on the motion freedom subspace, such that , for each joint of the model.
- The first set of equations accounts for the sensor measurements. The number of equations depends on how many sensors are conveyed into the vector and it does not depend on the number of links in the model (more than one sensor could be associated to the same link, e.g., the combination of an IMU + a FT sensor). In general, the sensor matrices are not changed within the new floating-base formalism. The only difference is that the accelerometer has a different relation with the acceleration of the body. In particular, if the frame of a link and the frame associated to the IMU located on the same link are rigidly connected, thenSimilarly, for the FT sensor frames rigidly connected to the feet frames, the measurement equation is
- The second set of equations represents the compact matrix form for Equations (16) and (17) given the new serialization of in Equation (14). The matrix is a matrix with rows and d columns, i.e., the number of rows of in Equation (14). The matrix blocks in for the acceleration of Equation (16) are recursively the following:The blocks in for Newton–Euler equations related to Equation (17) are instead:All the other blocks in are equal to 0. Unlike , the term is affected by the new representation of the acceleration w.r.t. the one in [7]. Each subterm is such that
4. Experiments and Analysis
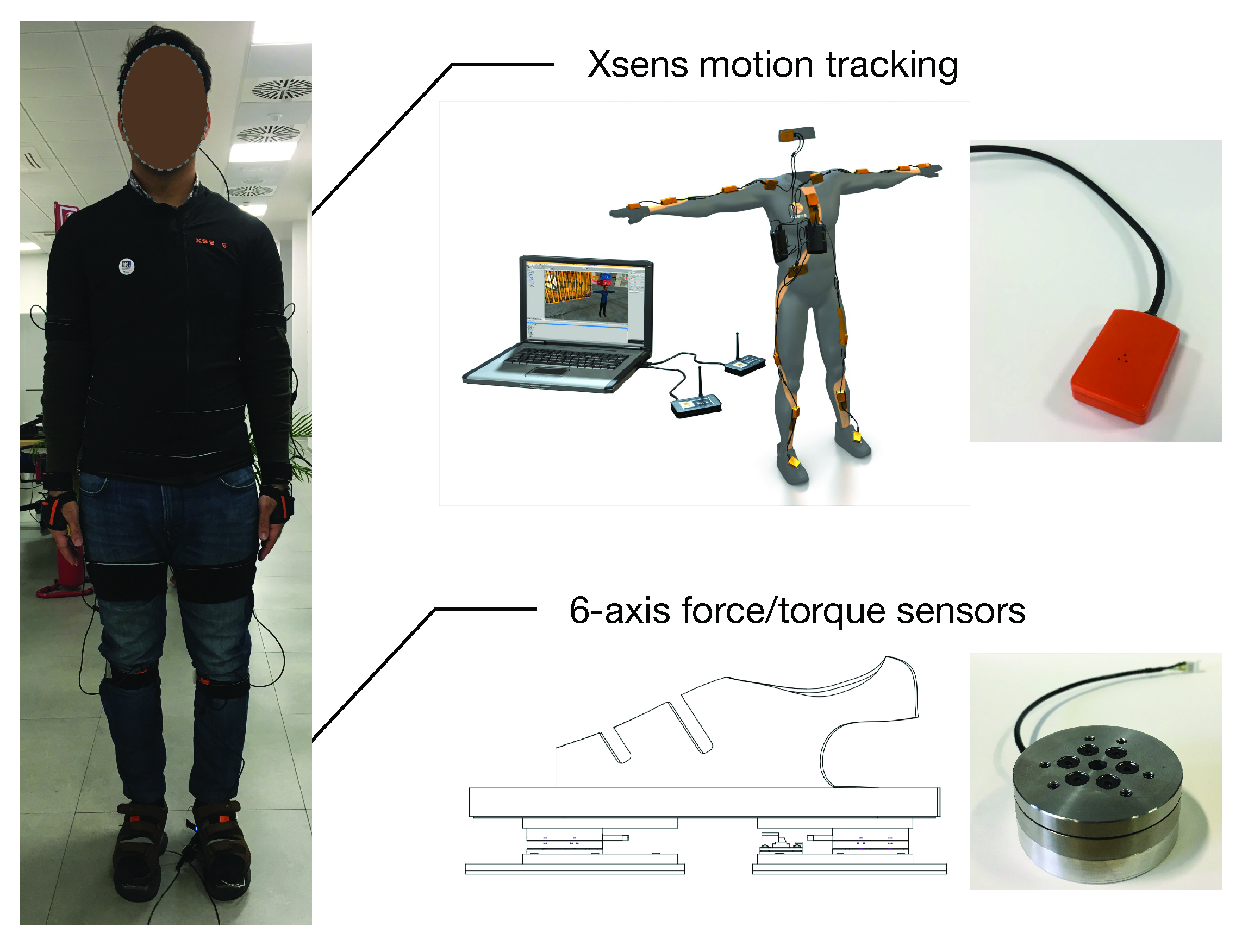
4.1. Experimental Setup
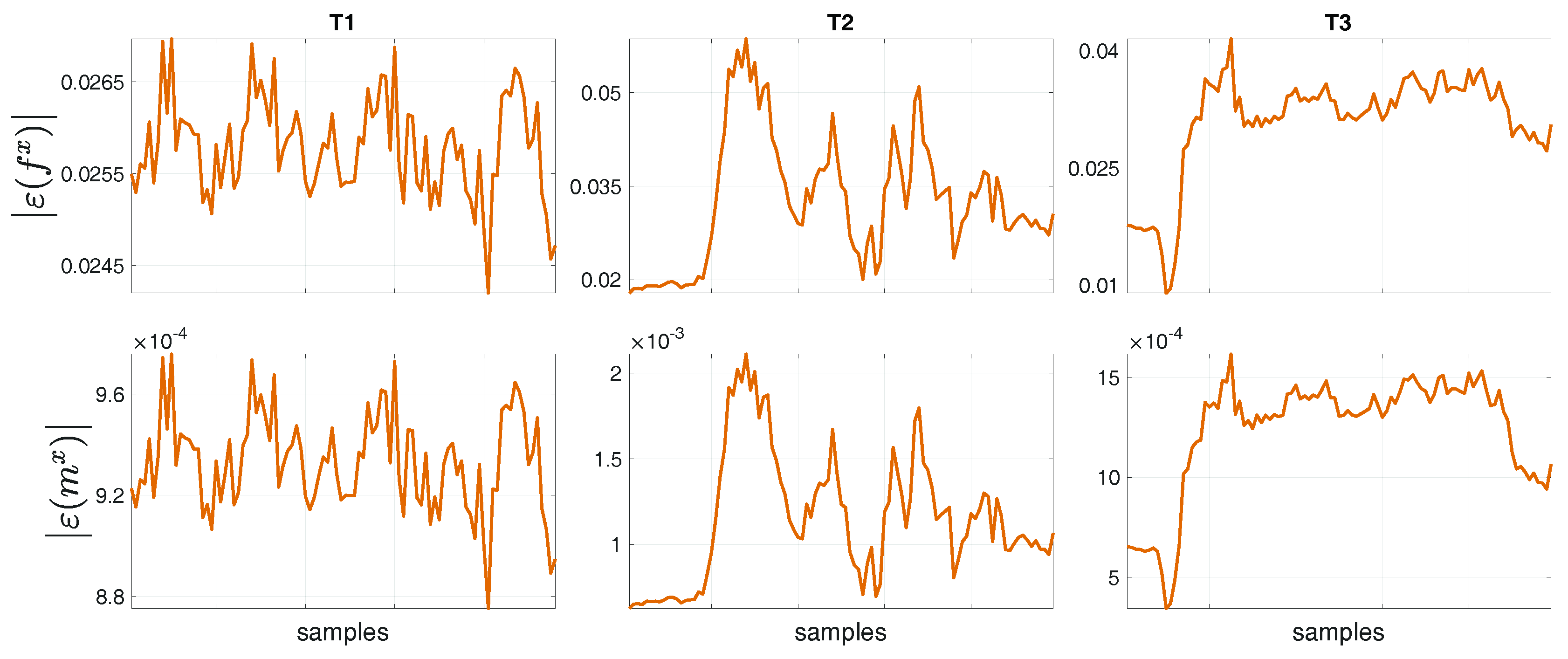
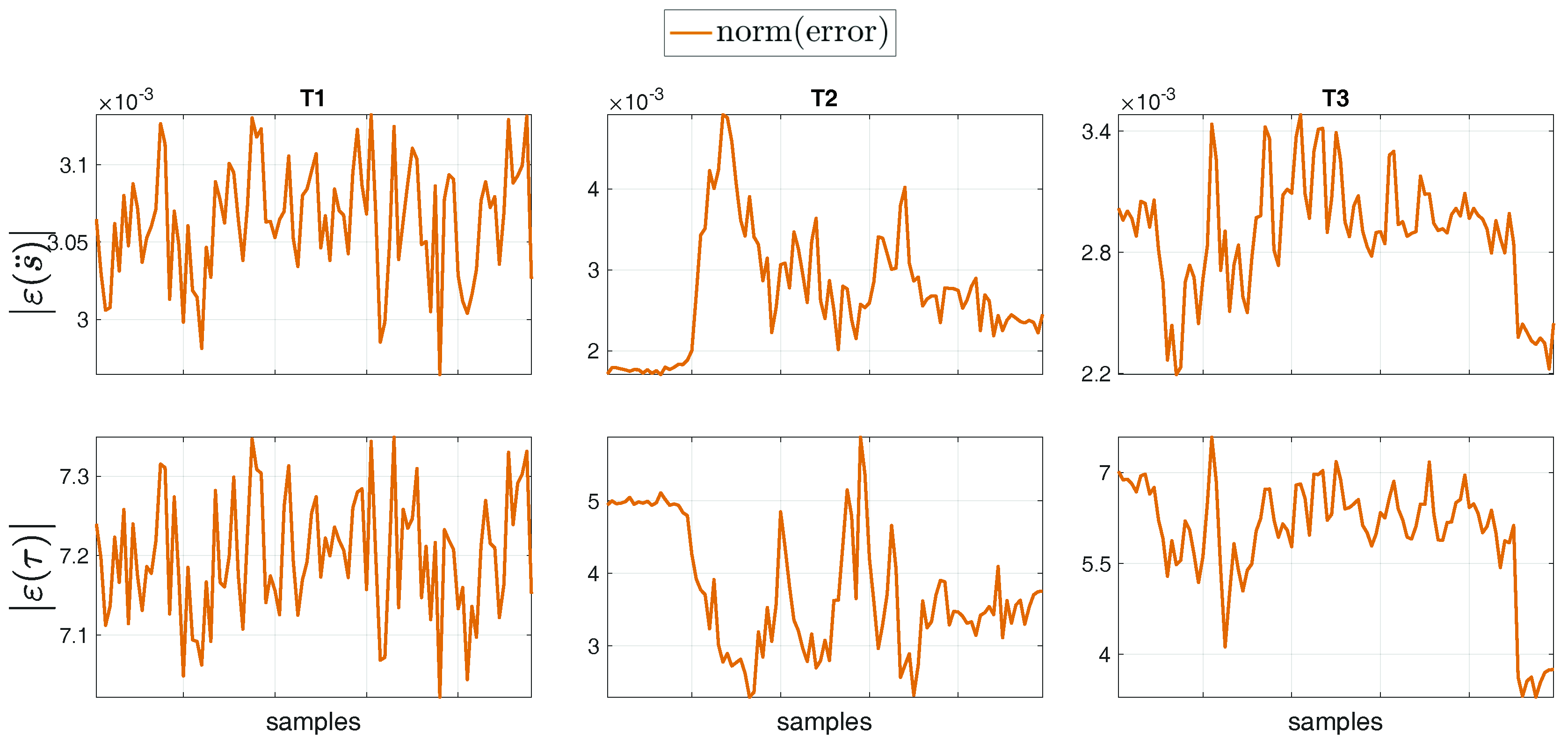
4.2. Comparison between Measurement and Estimation
4.3. Human Joint Torques Estimation during Gait
4.4. Comparison between Fixed-Base and Floating-Base Algorithms
4.5. A Word of Caution on the Covariances Choice
- low values for the covariance if trusting in the sensor measurements;
- low values for the model covariance for trusting the dynamic model; and
- high values for the covariance , which means that the end-user does not know any a priori information on the estimation.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- The conditional probability is:which implicitly makes the assumption that the set of measurements equations is affected by a Gaussian noise with zero mean and covariance .
- Let the normal distribution of d. The probability density p(d)where the covariance and the mean are, respectively,In particular, covariances and account for the reliability of the model constraints and on the estimation prior, respectively, in the equation .
- To compute , it suffices to combine Equations (A3) and (A4),with covariance matrix and mean as follows:In the Gaussian domain, the MAP solution coincides with the mean in Equation (A7b) yielding to:
References
- Tirupachuri, Y.; Nava, G.; Latella, C.; Ferigo, D.; Rapetti, L.; Tagliapietra, L.; Nori, F.; Pucci, D. Towards Partner-Aware Humanoid Robot Control Under Physical Interactions. arXiv 2019, arXiv:1809.06165. [Google Scholar]
- Flash, T.; Hogan, N. The coordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.; Hara, T.; Arai, T. Human-robot cooperative manipulation with motion estimation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 4, pp. 2240–2245. [Google Scholar] [CrossRef]
- Schaal, S.; Ijspeert, A.; Billard, A. Computational approaches to motor learning by imitation. Philosoph. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2003, 358, 537–547. [Google Scholar] [CrossRef] [PubMed]
- Amor, H.B.; Neumann, G.; Kamthe, S.; Kroemer, O.; Peters, J. Interaction primitives for human-robot cooperation tasks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2831–2837. [Google Scholar] [CrossRef]
- Penco, L.; Brice, C.; Modugno, V.; Mingo Hoffmann, E.; Nava, G.; Pucci, D.; Tsagarakis, N.; Mouret, J.B.; Ivaldi, S. Robust Real-time Whole-Body Motion Retargeting from Human to Humanoid. In Proceedings of the IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018. [Google Scholar]
- Latella, C.; Lorenzini, M.; Lazzaroni, M.; Romano, F.; Traversaro, S.; Akhras, M.A.; Pucci, D.; Nori, F. Towards real-time whole-body human dynamics estimation through probabilistic sensor fusion algorithms. Auton. Robots 2018. [Google Scholar] [CrossRef]
- Mistry, M.; Buchli, J.; Schaal, S. Inverse dynamics control of floating base systems using orthogonal decomposition. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3406–3412. [Google Scholar] [CrossRef]
- Nava, G.; Pucci, D.; Guedelha, N.; Traversaro, S.; Romano, F.; Dafarra, S.; Nori, F. Modeling and Control of Humanoid Robots in Dynamic Environments: iCub Balancing on a Seesaw. In Proceedings of the IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017. [Google Scholar]
- Ayusawa, K.; Venture, G.; Nakamura, Y. Identification of humanoid robots dynamics using floating-base motion dynamics. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2854–2859. [Google Scholar] [CrossRef]
- Mistry, M.; Schaal, S.; Yamane, K. Inertial parameter estimation of floating base humanoid systems using partial force sensing. In Proceedings of the 2009 9th IEEE-RAS International Conference on Humanoid Robots, Paris, France, 7–10 December 2009; pp. 492–497. [Google Scholar] [CrossRef]
- Dasgupta, A.; Nakamura, Y. Making feasible walking motion of humanoid robots from human motion capture data. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 2, pp. 1044–1049. [Google Scholar] [CrossRef]
- Zheng, Y.; Yamane, K. Human motion tracking control with strict contact force constraints for floating-base humanoid robots. In Proceedings of the 2013 13th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Atlanta, GA, USA, 15–17 October 2013; pp. 34–41. [Google Scholar] [CrossRef]
- Li, M.; Deng, J.; Zha, F.; Qiu, S.; Wang, X.; Chen, F. Towards Online Estimation of Human Joint Muscular Torque with a Lower Limb Exoskeleton Robot. Appl. Sci. 2018, 8, 1610. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, 2nd ed.; Texts in Applied Mathematics; Springer-Verlag: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Winter, D. Biomechanics and Motor Control of Human Movement, 4th ed.; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Herman, I. Physics of the Human Body | Irving P. Herman |; Springer: Basel, Switzerland, 2016. [Google Scholar] [CrossRef]
- Hanavan, E.P. A Mathematical Model of the Human Body. Available online: https://apps.dtic.mil/docs/citations/AD0608463 (accessed on 19 June 2019).
- Yeadon, M.R. The simulation of aerial movement—II. A mathematical inertia model of the human body. J. Biomech. 1990, 23, 67–74. [Google Scholar] [CrossRef]
- Rotella, N.; Mason, S.; Schaal, S.; Righetti, L. Inertial sensor-based humanoid joint state estimation. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1825–1831. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and Differentiation of Data by Simplified Least Squares Procedures (ACS Publications). Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer US: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Latella, C.; Kuppuswamy, N.; Romano, F.; Traversaro, S.; Nori, F. Whole-Body Human Inverse Dynamics with Distributed Micro-Accelerometers, Gyros and Force Sensing. Sensors 2016, 16, 727. [Google Scholar] [CrossRef]
- Metta, G.; Fitzpatrick, P.; Natale, L. YARP: Yet Another Robot Platform. Int. J. Adv. Robot. Syst. 2006, 3, 8. [Google Scholar] [CrossRef]
- Nori, F.; Traversaro, S.; Eljaik, J.; Romano, F.; Del Prete, A.; Pucci, D. iCub Whole-Body Control through Force Regulation on Rigid Non-Coplanar Contacts. Front. Robot. AI 2015, 2. [Google Scholar] [CrossRef]


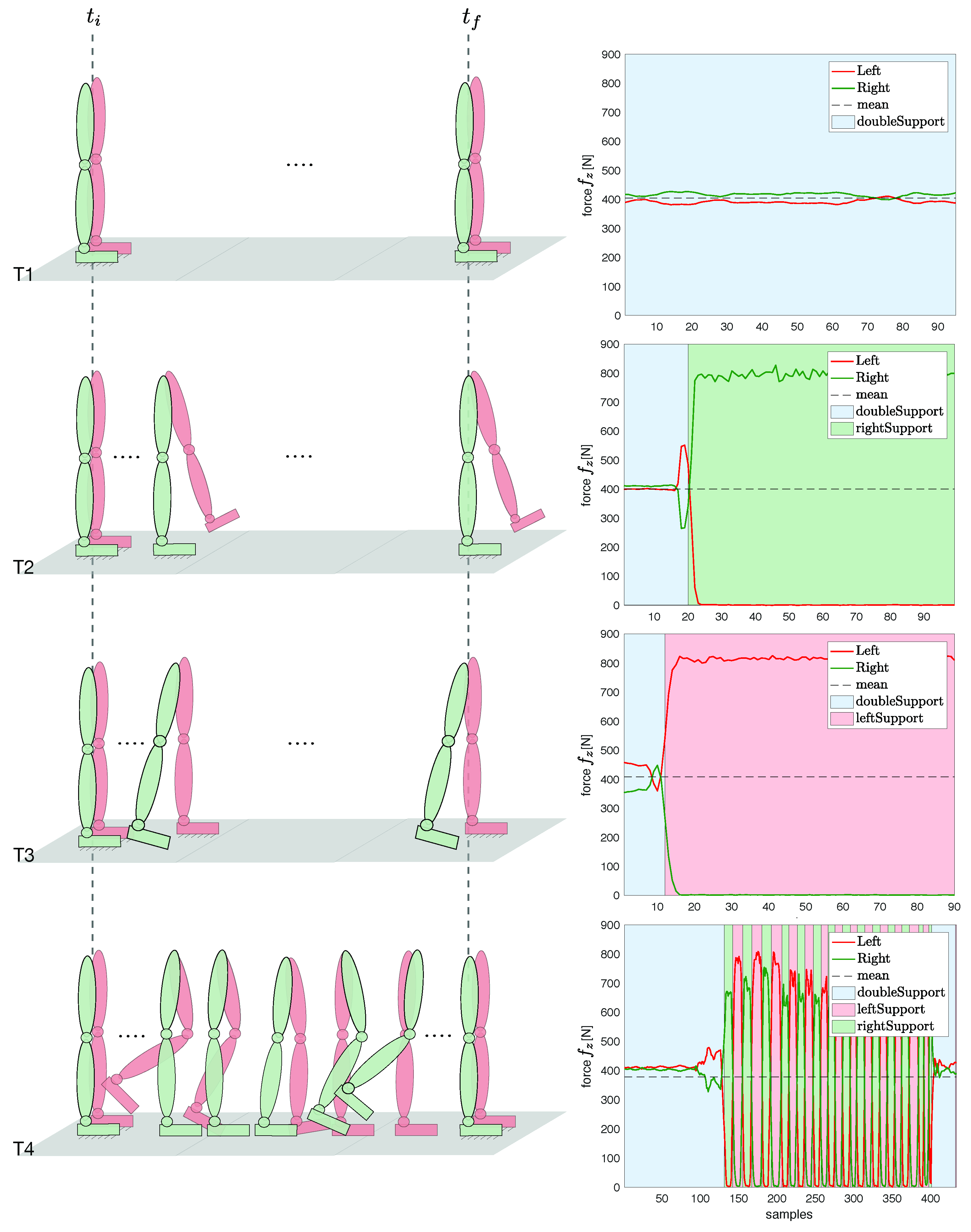
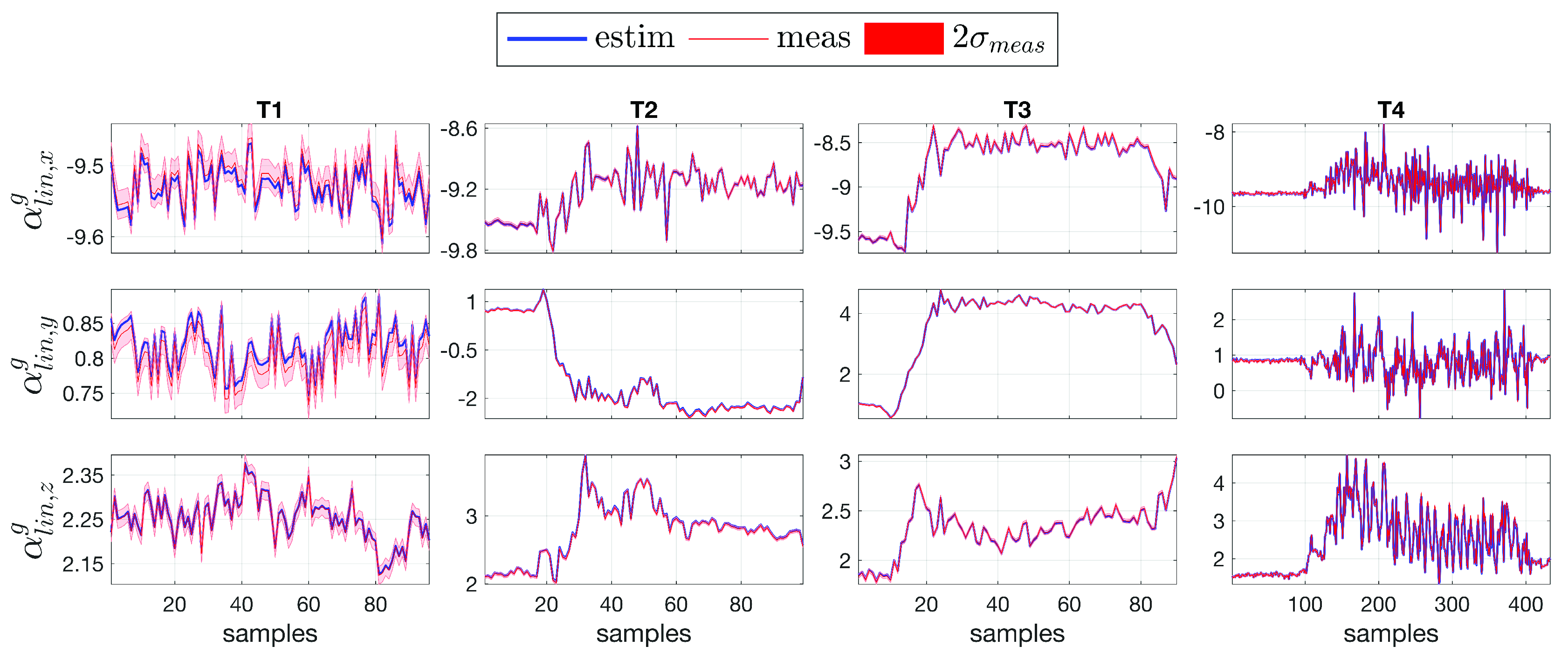
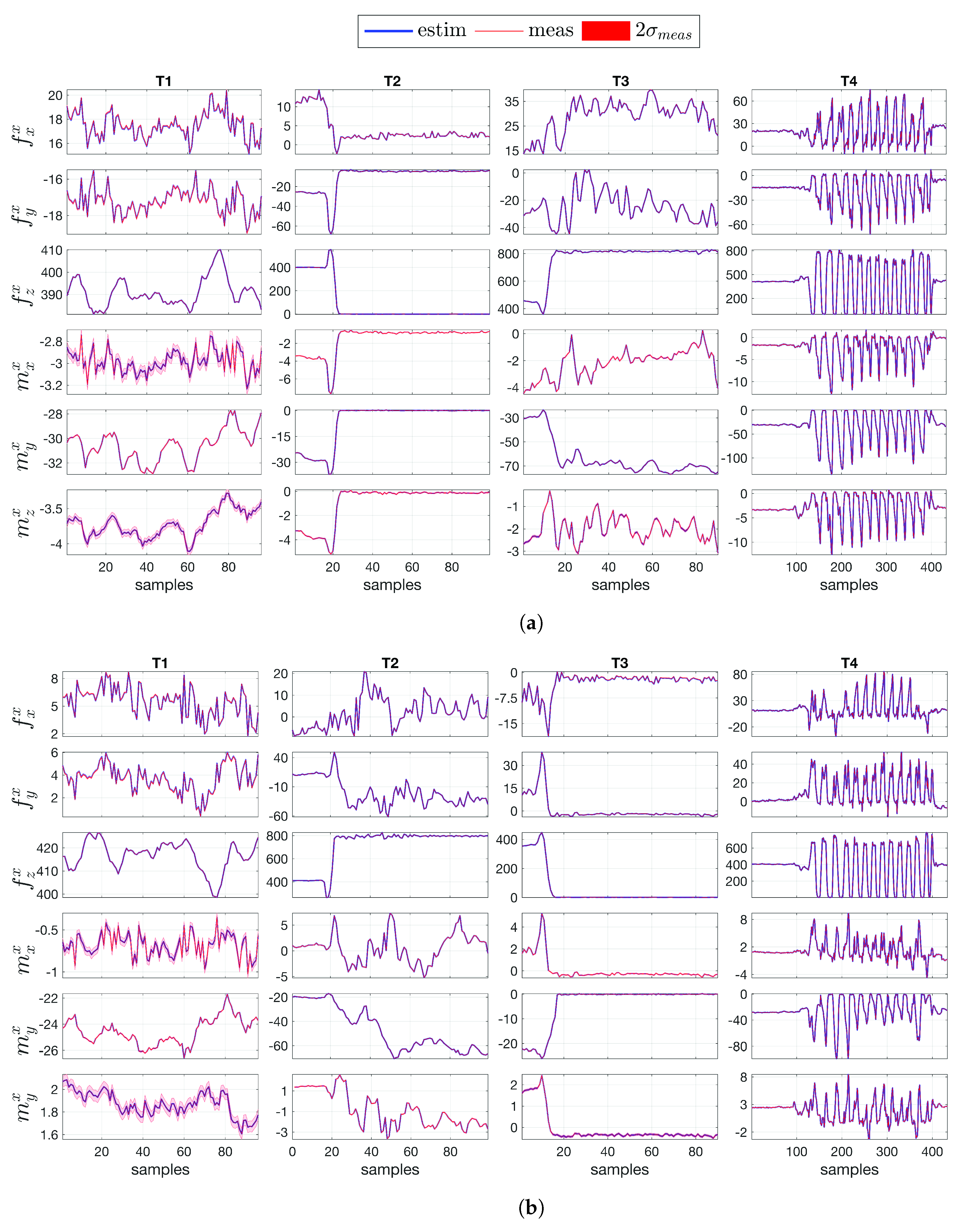
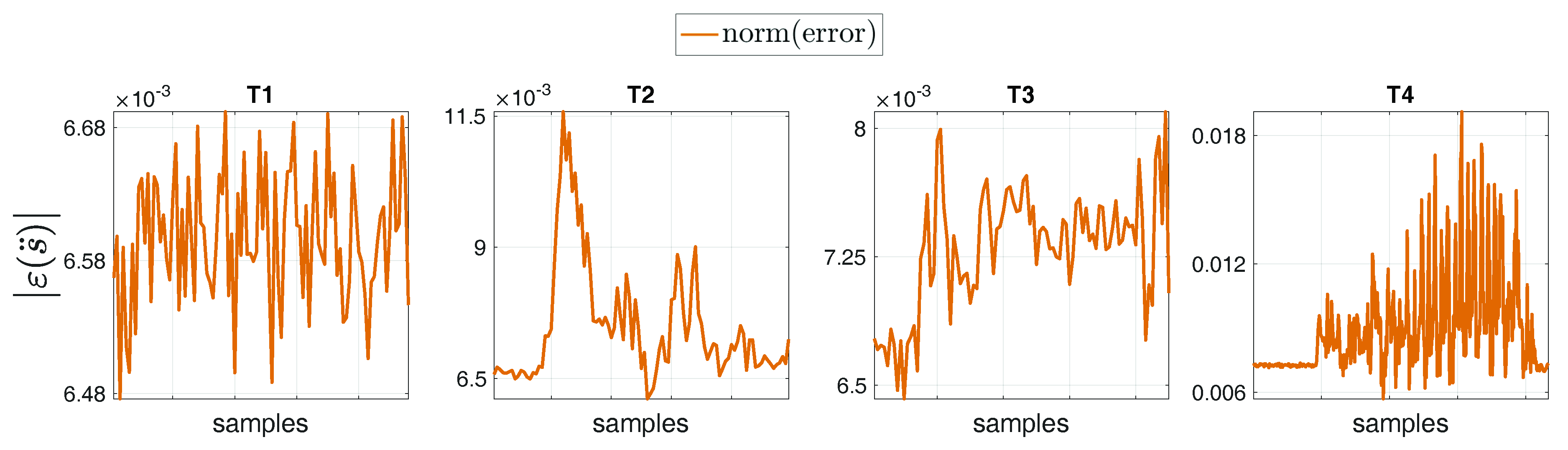
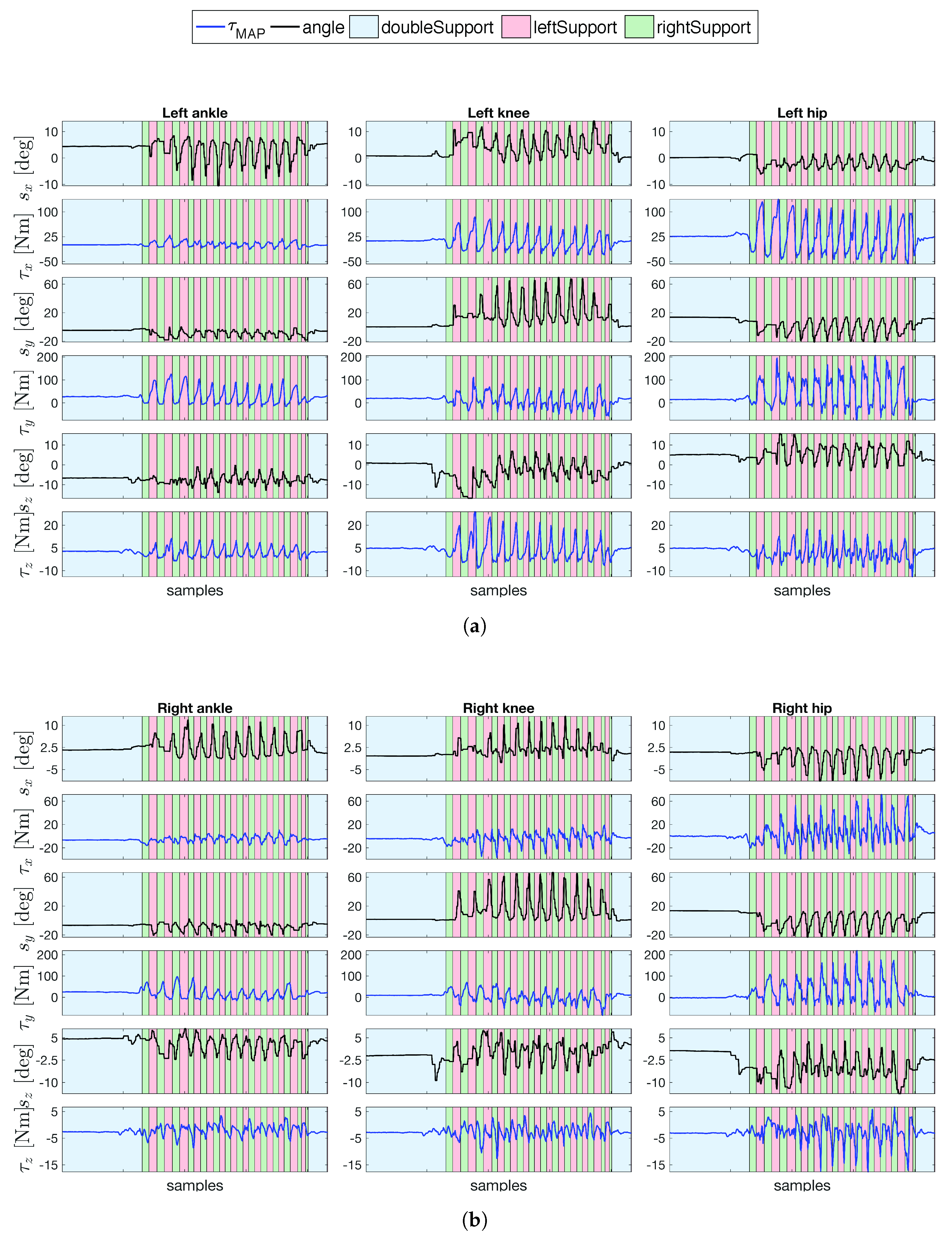

| Task | Type | Description |
|---|---|---|
| T1 | Static double support | Neutral pose, standing still |
| T2 | Static right single support | Sequence 1: static double support |
| Sequence 2: weight balancing on the right foot | ||
| T3 | Static left single support | Sequence 1: static double support |
| Sequence 2: weight balancing on the left foot | ||
| T4 | Static-walking-static | Sequence 1: static double support |
| Sequence 2: walking on a treadmill (Figure 4) | ||
| Sequence 3: static double support |
| Task | Link | [m/s2] | [m/s2] | [m/s2] | [N] | [N] | [N] | [Nm] | [Nm] | [Nm] |
|---|---|---|---|---|---|---|---|---|---|---|
| Base (Pelvis) | - | - | - | - | - | - | ||||
| T1 | Left foot | - | - | - | ||||||
| Right foot | - | - | - | 0.0015 | 0.001 | |||||
| Base (Pelvis) | - | - | - | - | - | - | ||||
| T2 | Left foot | - | - | - | ||||||
| Right foot | - | - | - | |||||||
| Base (Pelvis) | - | - | - | - | - | - | ||||
| T3 | Left foot | - | - | - | ||||||
| Right foot | - | - | - | |||||||
| Base (Pelvis) | - | - | - | - | - | - | ||||
| T4 | Left foot | - | - | - | ||||||
| Right foot | - | - | - |
| Variables | T1 | T2 | T3 | T4 | ||||
|---|---|---|---|---|---|---|---|---|
| min | max | min | max | min | max | min | max | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latella, C.; Traversaro, S.; Ferigo, D.; Tirupachuri, Y.; Rapetti, L.; Andrade Chavez, F.J.; Nori, F.; Pucci, D. Simultaneous Floating-Base Estimation of Human Kinematics and Joint Torques. Sensors 2019, 19, 2794. https://doi.org/10.3390/s19122794
Latella C, Traversaro S, Ferigo D, Tirupachuri Y, Rapetti L, Andrade Chavez FJ, Nori F, Pucci D. Simultaneous Floating-Base Estimation of Human Kinematics and Joint Torques. Sensors. 2019; 19(12):2794. https://doi.org/10.3390/s19122794
Chicago/Turabian StyleLatella, Claudia, Silvio Traversaro, Diego Ferigo, Yeshasvi Tirupachuri, Lorenzo Rapetti, Francisco Javier Andrade Chavez, Francesco Nori, and Daniele Pucci. 2019. "Simultaneous Floating-Base Estimation of Human Kinematics and Joint Torques" Sensors 19, no. 12: 2794. https://doi.org/10.3390/s19122794
APA StyleLatella, C., Traversaro, S., Ferigo, D., Tirupachuri, Y., Rapetti, L., Andrade Chavez, F. J., Nori, F., & Pucci, D. (2019). Simultaneous Floating-Base Estimation of Human Kinematics and Joint Torques. Sensors, 19(12), 2794. https://doi.org/10.3390/s19122794









