An Approach to Frequency Selectivity in an Urban Environment by Means of Multi-Path Acoustic Channel Analysis
Abstract
1. Introduction
2. Overview of Methodology
2.1. Outdoor Acoustic Propagation Modelling Basics
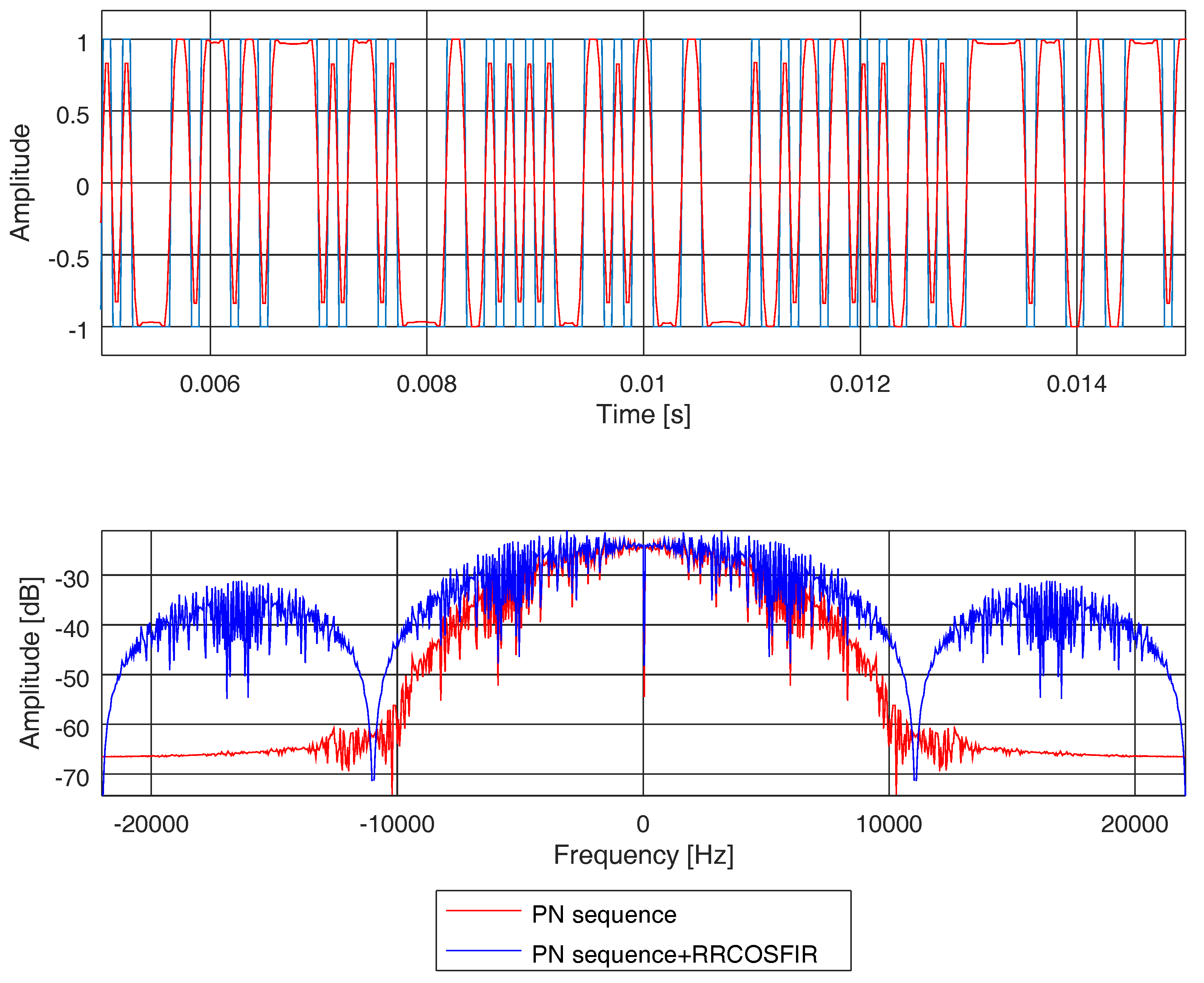
2.2. Wide-Band Channel Sounding with PN-Sequences
2.2.1. PN-Sequence Wide-Band Analysis Proposal
2.2.2. Underwater Acoustic Channel Sounding
3. Real-Operation Acoustic Data Recordings in the DYNAMAP Project
3.1. The DYNAMAP Project
3.2. Description of the Recording Campaign
3.3. Acoustic Environment of the Nodes of the WASN
4. Channel Model Design
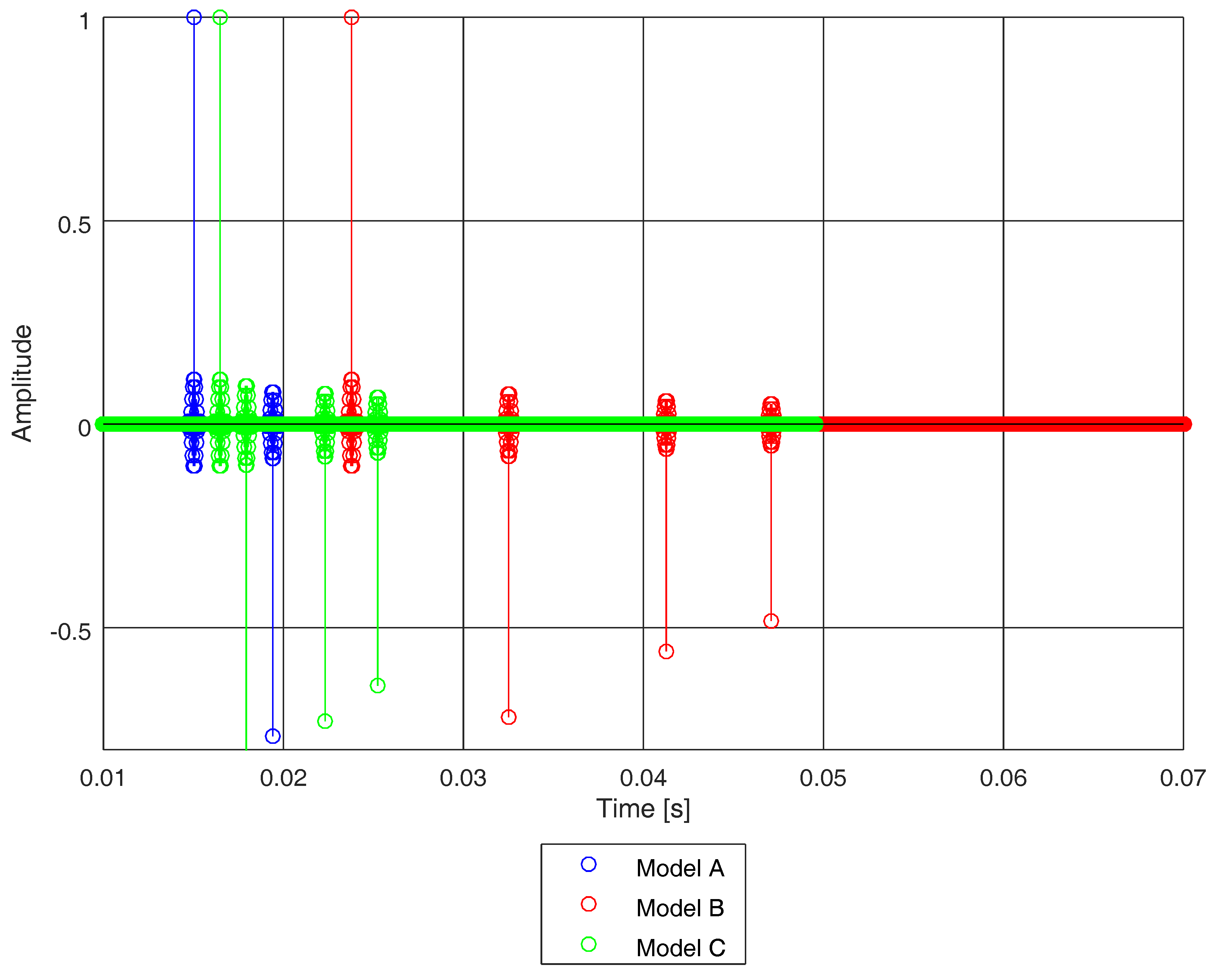
4.1. Outdoor Propagation Models
- Atmospheric density and pressure are assumed constant.
- The density of the air at ground level is 1.205 kg/m3, the temperature is 20°, and the atmospheric pressure is 1 atm.
- The relative humidity is 70%.
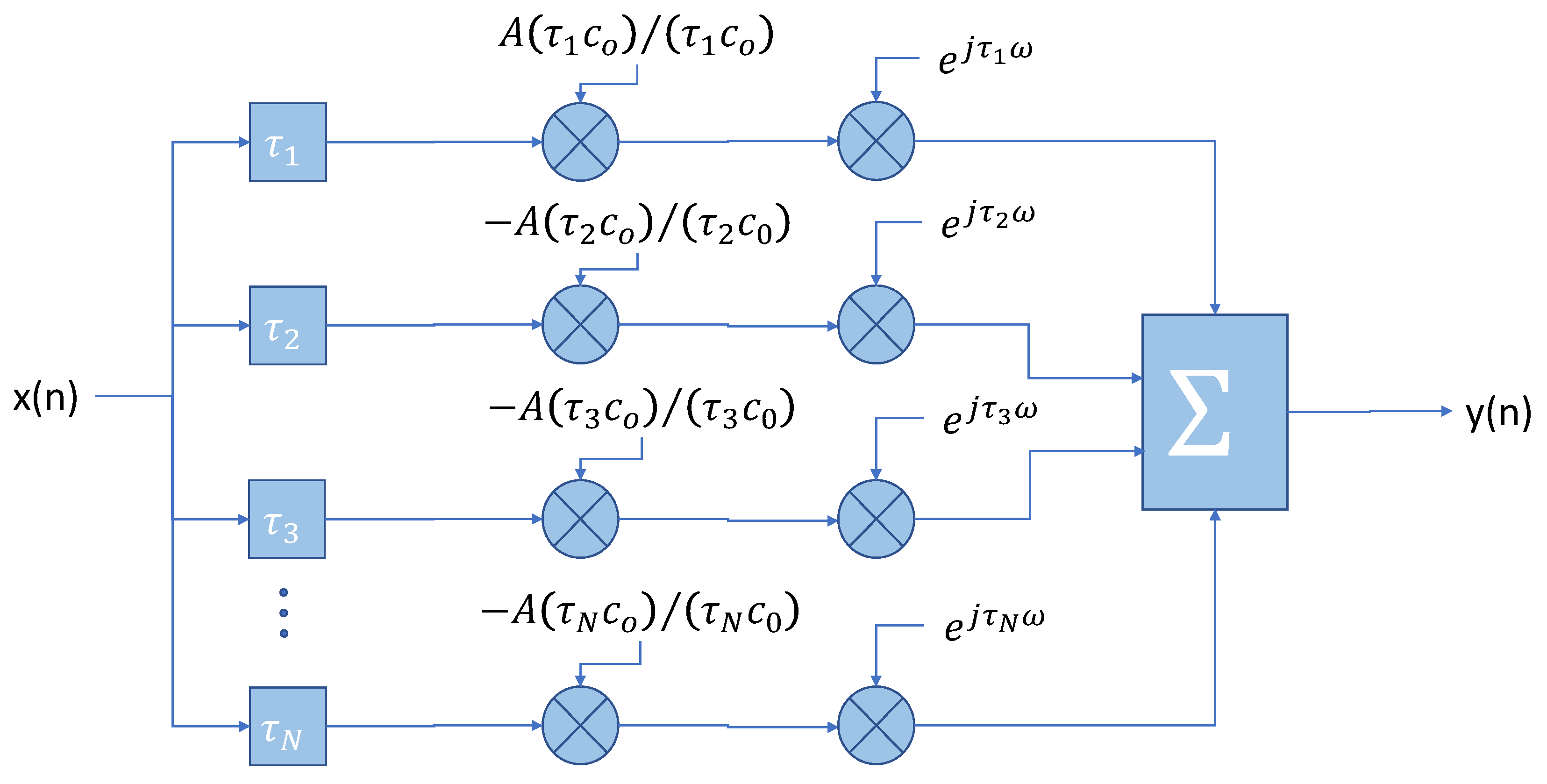
4.2. Impulse Response for the Defined Acoustic Channels
4.3. PN Sequence Channel Estimation
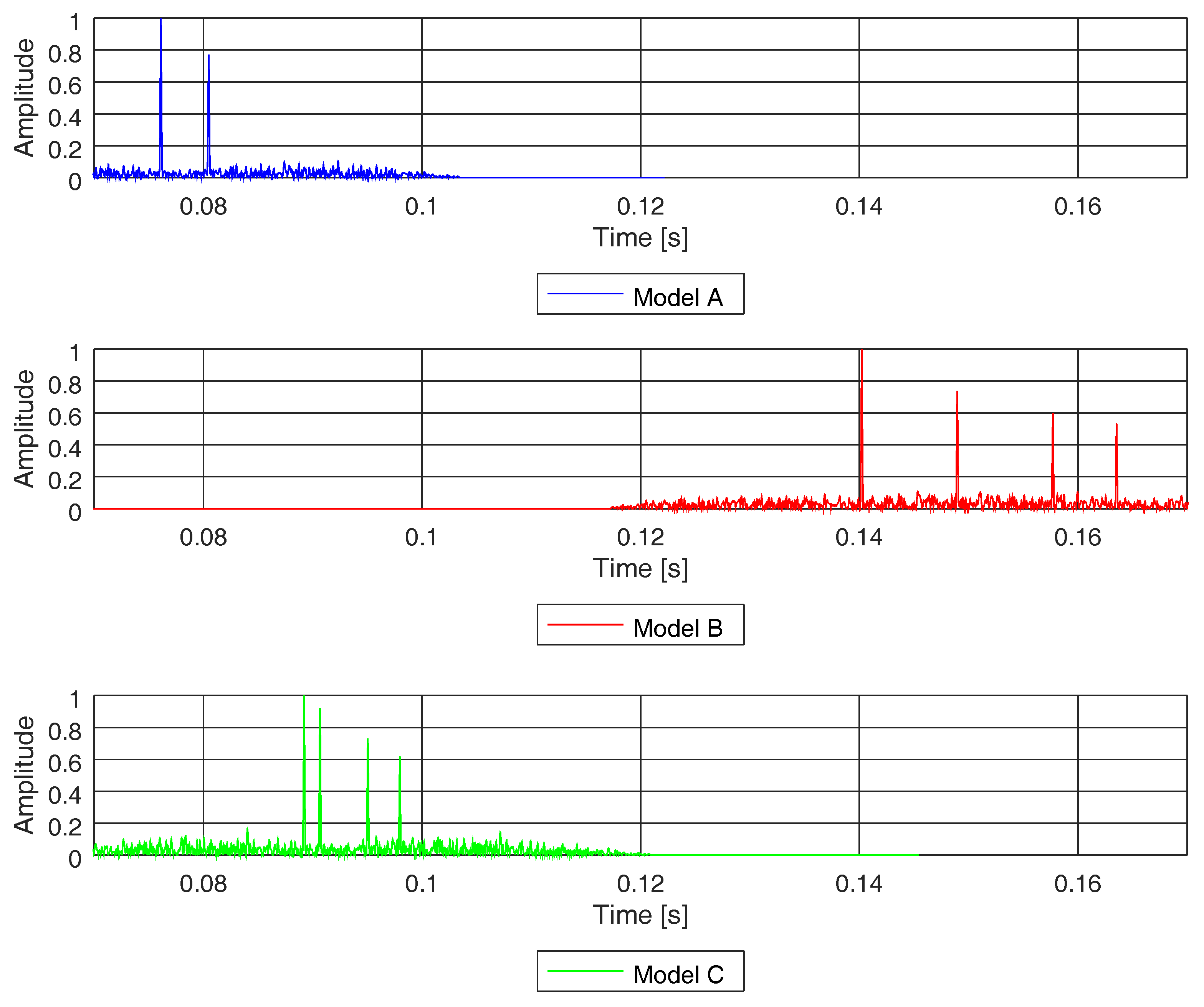
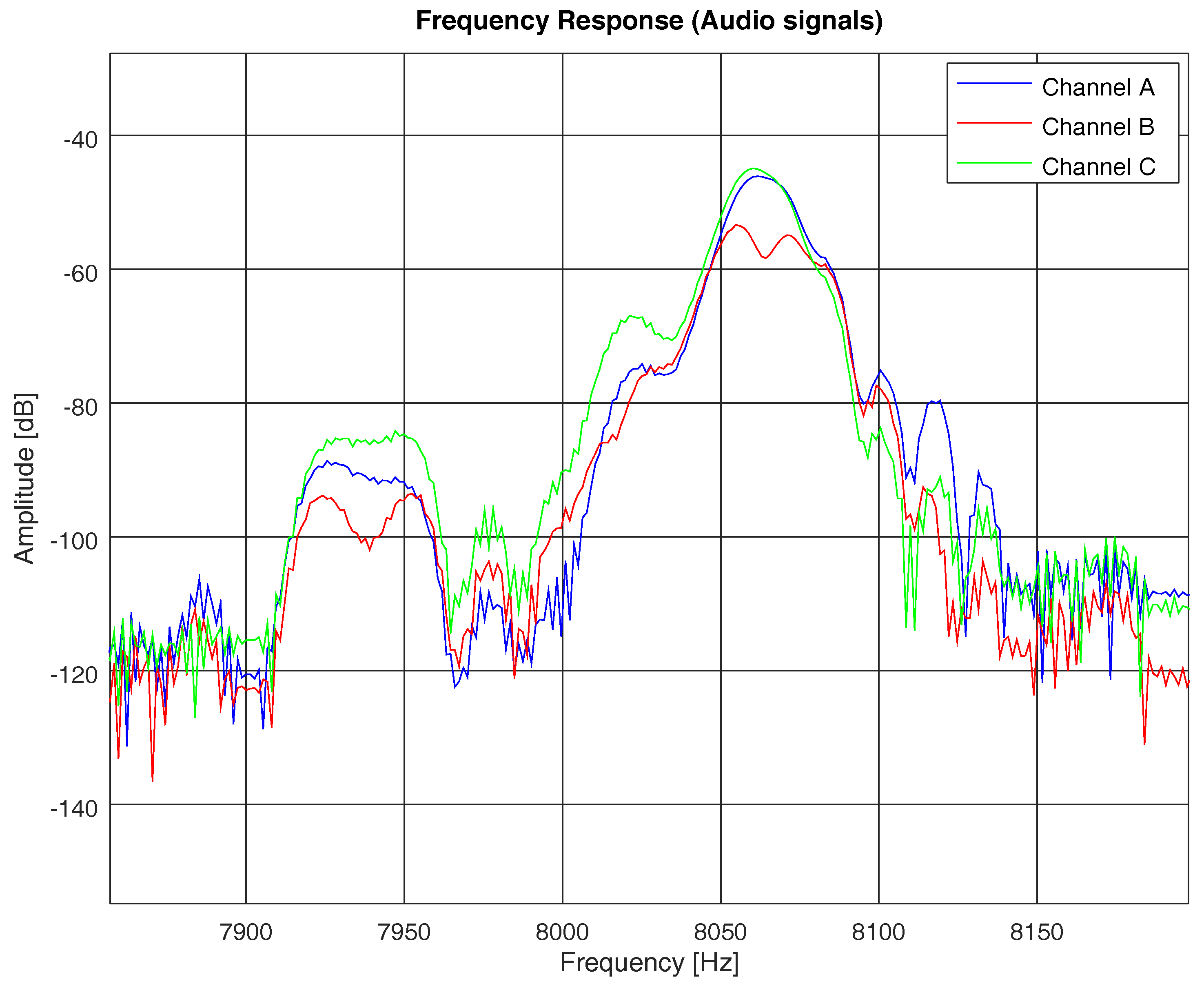
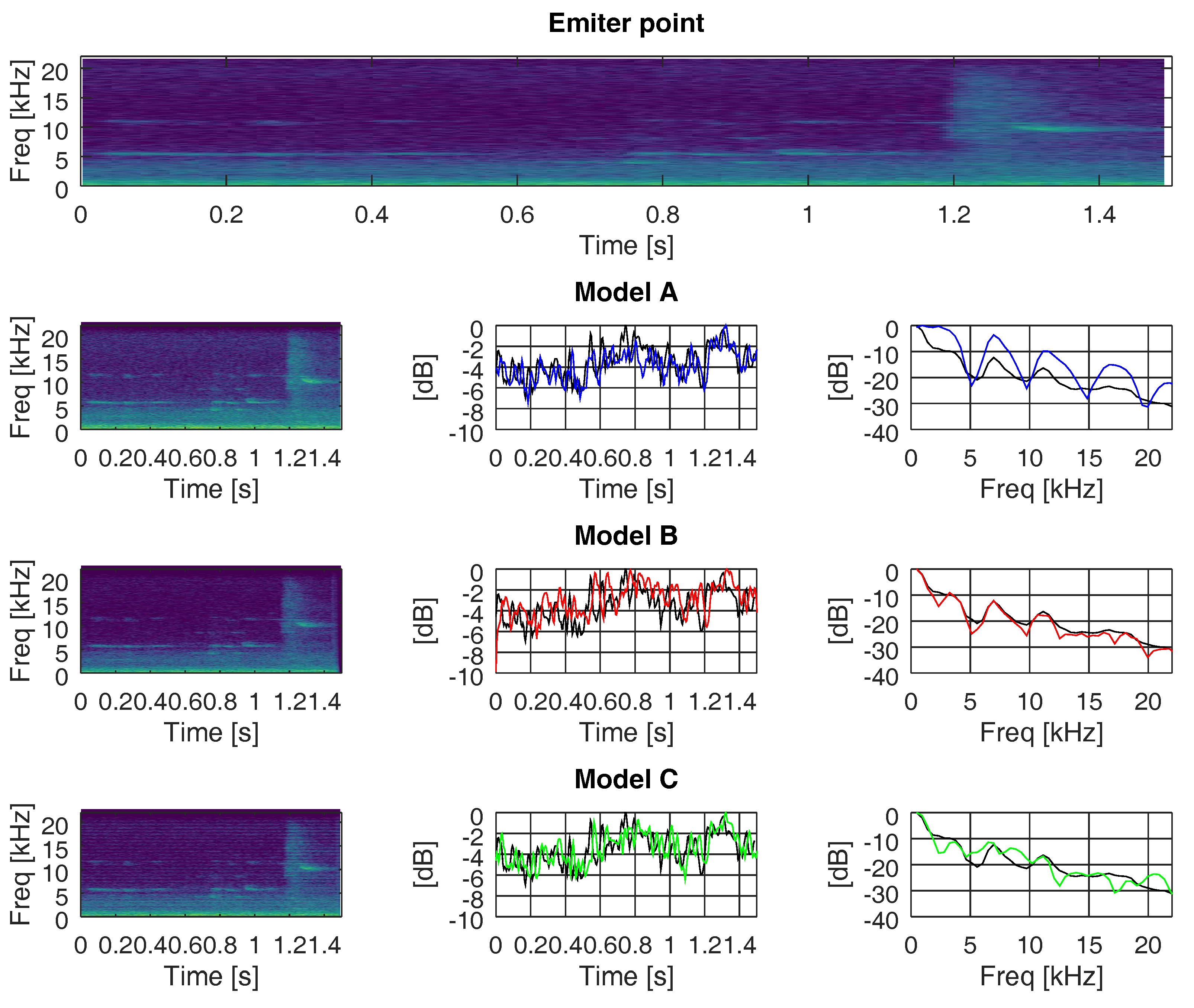
5. Real-Life Acoustic Recording Analysis
5.1. Propagation on Real-Life Acoustic Recordings
5.2. Spectral Distributions over Propagation Channels
6. Conclusions
7. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANE | Anomalous Noise Event |
| ANED | Anomalous Noise Event Detection |
| DYNAMAP | Dynamic Noise Mapping |
| END | European Noise Directive |
| FIR | Finite Impulse Response |
| MIMO | Multiple Input Multiple Output |
| PN | Pseudo-Noise |
| RRCOSFIR | Root Raised Cosine FIR |
| RTN | Road Traffic Noise |
| SNR | Signal-to-Noise Ratio |
| WASN | Wireless Acoustic Sensor Network |
References
- European Commission. Report from the Commission to the European Parliament and the Council On the Implementation of the Environmental Noise Directive in accordance with Article 11 of Directive 2002/49/EC; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Recio, A.; Linares, C.; Banegas, J.R.; Díaz, J. Road traffic noise effects on cardiovascular, respiratory, and metabolic health: An integrative model of biological mechanisms. Environ. Res. 2016, 146, 359–370. [Google Scholar] [CrossRef] [PubMed]
- Miedema, H.; Oudshoorn, C. Annoyance from transportation noise: Relationships with exposure metrics DNL and DENL and their confidence intervals. Environ. Health Perspect. 2001, 109, 409. [Google Scholar] [CrossRef] [PubMed]
- Muzet, A. Environmental noise, sleep and health. Sleep Med. Rev. 2007, 11, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Hygge, S.; Evans, G.W.; Bullinger, M. A prospective study of some effects of aircraft noise on cognitive performance in schoolchildren. Psychol. Sci. 2002, 13, 469–474. [Google Scholar] [CrossRef] [PubMed]
- Dratva, J.; Phuleria, H.C.; Foraster, M.; Gaspoz, J.M.; Keidel, D.; Künzli, N.; Liu, L.J.S.; Pons, M.; Zemp, E.; Gerbase, M.W.; et al. Transportation noise and blood pressure in a population-based sample of adults. Environ. Health Perspect. 2012, 120, 50. [Google Scholar] [CrossRef] [PubMed]
- Hänninen, O.; Knol, A.B.; Jantunen, M.; Lim, T.A.; Conrad, A.; Rappolder, M.; Carrer, P.; Fanetti, A.C.; Kim, R.; Buekers, J.; et al. Environmental burden of disease in Europe: Assessing nine risk factors in six countries. Environ. Health Perspect. 2014, 122, 439. [Google Scholar] [CrossRef]
- Bello, J.P.; Silva, C.; Nov, O.; DuBois, R.L.; Arora, A.; Salamon, J.; Mydlarz, C.; Doraiswamy, H. SONYC: A System for Monitoring, Analyzing, and Mitigating Urban Noise Pollution. Commun. ACM 2019, 62, 68–77. [Google Scholar] [CrossRef]
- Europoean Union, Directive 2002/49/EC of the European Parliament and the Council of 25 June 2002 Relating to the Assessment and Management of Environmental Noise; Official Journal of the European Communities: Brussels, Belgium, 2002; Volume L 189/12.
- Kephalopoulos, S.; Paviotti, M.; Anfosso-Lédée, F. Common Noise Assessment Methods in Europe (CNOSSOS-EU); Report EUR 25379 EN; Publications Office of the European Union: Brussels, Belgium, 2002; pp. 1–180. [Google Scholar]
- World Health Organization, Regional Office Europe. Environmental Noise Guidelines for the European Region; Technical report; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Socoró, J.C.; Alías, F.; Alsina-Pagès, R.M. An Anomalous Noise Events Detector for Dynamic Road Traffic Noise Mapping in Real-Life Urban and Suburban Environments. Sensors 2017, 17, 2323. [Google Scholar] [CrossRef] [PubMed]
- Alías, F.; Alsina-Pagčs, R.M.; Orga, F.; Socoró, J.C. Detection of Anomalous Noise Events for Real-Time Road-Traffic Noise Mapping: The Dynamap’s project case study. Noise Mapp. 2018, 5, 71–85. [Google Scholar] [CrossRef]
- Nilsson, M.; Forssén, J.; Lundén, P.; Peplow, A.; Hellström, B. LISTEN Auralization of Urban Soundscapes; Technical Report, Final Report to the Knowledge Foundation; Stockholm University: Stockholm, Sweden, 2011. [Google Scholar]
- Orga, F.; Alías, F.; Alsina-Pagès, R.M. On the Impact of Anomalous Noise Events on Road Traffic Noise Mapping in Urban and Suburban Environments. Int. J. Environ. Res. Public Health 2017, 15, 13. [Google Scholar] [CrossRef] [PubMed]
- Labairu-Trenchs, A.; Alsina-Pagès, R.M.; Orga, F.; Foraster, M. Noise Annoyance in Urban Life: The Citizen as a Key Point of the Directives. Proceedings 2019, 6, 1. [Google Scholar] [CrossRef]
- Hornikx, M. Acoustic Modelling for Indoor and Outdoor Spaces; Taylor & Francis: Abingdon, UK, 2015. [Google Scholar]
- Luigi, M.; Massimiliano, M.; Aniello, P.; Gennaro, R.; Virginia, P.R. On the validity of immersive virtual reality as tool for multisensory evaluation of urban spaces. Energy Procedia 2015, 78, 471–476. [Google Scholar] [CrossRef]
- Georgiou, F. Modeling for auralization of urban environments. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2018. [Google Scholar]
- Proakis, J. Digital Communications 5th Edition; McGraw Hill: New York, NY, USA, 2007. [Google Scholar]
- Alsina-Pagès, R.; Hervás, M.; Orga, F.; Pijoan, J.; Badia, D.; Altadill, D. Physical layer definition for a long-haul HF Antarctica to Spain radio link. Remote Sens. 2016, 8, 380. [Google Scholar] [CrossRef]
- Hervás, M.; Alsina-Pagès, R.; Orga, F.; Altadill, D.; Pijoan, J.; Badia, D. Narrowband and wideband channel sounding of an Antarctica to Spain ionospheric radio link. Remote Sens. 2015, 7, 11712–11730. [Google Scholar] [CrossRef]
- Stojanovic, M. Underwater acoustic communication. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley: New York, NY, USA, 1999; pp. 1–12. [Google Scholar]
- Sozer, E.M.; Stojanovic, M.; Proakis, J.G. Underwater acoustic networks. IEEE J. Ocean. Eng. 2000, 25, 72–83. [Google Scholar] [CrossRef]
- Borowski, B. Characterization of a very shallow water acoustic communication channel. In Proceedings of the OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009; pp. 1–10. [Google Scholar]
- Kim, J.; Park, K.C.; Park, J.; Yoon, J.R. Coherence bandwidth effects on underwater image transmission in multipath channel. Jpn. J. Appl. Phys. 2011, 50, 07HG05. [Google Scholar] [CrossRef]
- Alsina-Pagès, R.M.; Bergadà, P. The Citizen as a Key Point of the Policies: A First Approach to Auralization for the Acoustic Perception of Noise in an Urban Environment. Multidiscip. Digit. Publ. Inst. Proc. 2018, 4, 11. [Google Scholar] [CrossRef]
- Attenborough, K.; Li, K.M.; Horoshenkov, K. Predicting Outdoor Sound; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Sevillano, X.; Socoró, J.C.; Alías, F.; Bellucci, P.; Peruzzi, L.; Radaelli, S.; Coppi, P.; Nencini, L.; Cerniglia, A.; Bisceglie, A.; et al. DYNAMAP – Development of low cost sensors networks for real time noise mapping. Noise Mapp. 2016, 3, 172–189. [Google Scholar] [CrossRef]
- Hewett, D.P. Sound Propagation in an Urban Environment. Ph.D. Thesis, Oxford University, Oxford, UK, 2010. [Google Scholar]
- Sanchez, G.M.E.; Van Renterghem, T.; Thomas, P.; Botteldooren, D. The effect of street canyon design on traffic noise exposure along roads. Build. Environ. 2016, 97, 96–110. [Google Scholar] [CrossRef]
- Hornikx, M.; Forssén, J. A scale model study of parallel urban canyons. Acta Acust. United Acust. 2008, 94, 265–281. [Google Scholar] [CrossRef]
- Lyon, R.H. Role of multiple reflections and reverberation in urban noise propagation. J. Acoust. Soc. Am. 1974, 55, 493–503. [Google Scholar] [CrossRef]
- Van Renterghem, T.; Botteldooren, D. The importance of roof shape for road traffic noise shielding in the urban environment. J. Sound Vib. 2010, 329, 1422–1434. [Google Scholar] [CrossRef]
- Salomons, E.M. Computational Atmospheric Acoustics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Leon-Garcia, A. Probability and Random Processes for Electrical Engineering: Student Solutions Manual; Pearson Education India: London, UK, 1994. [Google Scholar]
- Golomb, S. Shift Register Sequences; Holden-Day: San Francisco, CA, USA, 1967. [Google Scholar]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Goodney, A.; Cho, Y.H. Acoustic tomography with an underwater sensor network. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–10. [Google Scholar]
- Kaddouri, S.; Beaujean, P.P.J.; Bouvet, P.J.; Real, G. Least square and trended Doppler estimation in fading channel for high-frequency underwater acoustic communications. IEEE J. Ocean. Eng. 2014, 39, 179–188. [Google Scholar] [CrossRef]
- Van Walree, P.A. Propagation and scattering effects in underwater acoustic communication channels. IEEE J. Ocean. Eng. 2013, 38, 614–631. [Google Scholar] [CrossRef]
- Nencini, L. DYNAMAP monitoring network hardware development. In Proceedings of the 22nd International Congress on Sound and Vibration (ICSV22), Florence, Italy, 12–16 July 2015; The International Institute of Acoustics and Vibration (IIAV): Florence, Italy, 2015; pp. 1–4. [Google Scholar]
- Nencini, L. Progetto e realizzazione del sistema di monitoraggio nell’ambito del progetto Dynamap. In Proceedings of the AIA 2017; AIA: Pavia, Italy, 2017. [Google Scholar]
- Zambon, G.; Benocci, R.; Brambilla, G. Statistical road classification applied to stratified spatial sampling of road traffic noise in urban areas. Int. J. Environ. Res. 2016, 10, 411–420. [Google Scholar]
- Zambon, G.; Benocci, R.; Bisceglie, A.; Roman, H.E.; Bellucci, P. The LIFE DYNAMAP project: Towards a procedure for dynamic noise mapping in urban areas. Appl. Acoust. 2017, 124, 52–60. [Google Scholar] [CrossRef]
- Zambon, G.; Benocci, R.; Brambilla, G. Cluster categorization of urban roads to optimize their noise monitoring. Environ. Monit. Assess. 2016, 188, 26. [Google Scholar] [CrossRef]
- Cerniglia, A. Development of a GIS based software for real time noise maps update. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: Hong Kong, China, 2016; Volume 253, pp. 6291–6297. [Google Scholar]
- Socoró, J.C.; Alsina-Pagès, R.M.; Alías, F.; Orga, F. Adapting an Anomalous Noise Events Detector for Real-Life Operation in the Rome Suburban Pilot Area of the DYNAMAP’s Project. In Proceedings of EuroNoise 2018; EAA—HELINA: Heraklion, Crete-Greece, 2018; pp. 693–698. [Google Scholar]
- Foggia, P.; Petkov, N.; Saggese, A.; Strisciuglio, N.; Vento, M. Audio Surveillance of Roads: A System for Detecting Anomalous Sounds. IEEE Trans. Intell. Transp. Syst. 2016, 17, 279–288. [Google Scholar] [CrossRef]
- Memoli, G.; Paviotti, M.; Kephalopoulos, S.; Licitra, G. Testing the acoustical corrections for reflections on a façade. Appl. Acoust. 2008, 69, 479–495. [Google Scholar] [CrossRef]
- Lamancusa, J. Noise Control, Outdoor Noise Propagation; Penn State University: Centre County, PA, USA, 2000. [Google Scholar]
- Attenborough, K.; Taherzadeh, S.; Bass, H.; Di, X.; Raspet, R.; Becker, G.; Gudesen, A.; Chrestman, A.; Daigle, G.; L’Esperance, A.; et al. Benchmark cases for outdoor sound propagation models. J. Acoust. Soc. Am. 1994, 97, 173–191. [Google Scholar] [CrossRef]
- Standards Secretariat, Acoustical Society of America. Method for Calculation of the Absorption of Sound by the Atmosphere; Standards Secretariat, Acoustical Society of America: Melville, NY, USA, 1995. [Google Scholar]












| Sensor ID | Street | GPS Coordinates |
|---|---|---|
| hb106 | Via Litta Modignani | (45.5227587,9.1596847) |
| hb108 | Via Piero e Alberto Pirelli | (45.5144707,9.2107111) |
| hb109 | Viale Stelvio | (45.4929125,9.1919035) |
| hb114 | Via Melchiorre Gioia | (45.4815058,9.1913241) |
| hb115 | Via Fara | (45.4855843,9.1991161) |
| hb116 | Via Moncalieri | (45.5098883,9.1968012) |
| hb117 | Viale Fermi | (45.5089072,9.1802412) |
| hb120 | Via Baldinucci | (45.5032677,9.1686595) |
| hb121 | Via Piero e Alberto Pirelli | (45.5185641,9.2129266) |
| hb123 | Via Galvani | (45.4857107,9.2005241) |
| hb124 | Via Grivola | (45.5179185,9.1943259) |
| hb125 | Via Abba | (45.5028072,9.179285) |
| hb127 | Via Quadrio | (45.4839506,9.1845167) |
| hb129 | Via Crespi | (45.4989476,9.1860456) |
| hb133 | Via Maffucci | (45.4992223,9.1717236) |
| hb135 | via Lambruschini | (45.5024486,9.1548883) |
| hb136 | Via Comasina | (45.5247882,9.1655266) |
| hb137 | via Maestri del Lavoro | (45.518893,9.1997167) |
| hb138 | Via Novaro | (45.5187445,9.1678656) |
| hb139 | Via Bruni | (45.5015796,9.1745067) |
| hb140 | Viale Jenner | (45.4970863,9.1777414) |
| hb144 | Via D’Intignano | (45.5082648,9.2027579) |
| hb145 | Via Fratelli Grimm | (45.5184213,9.2062962) |
| hb151 | Via Veglia | (45.4970074,9.1934109) |
| Model A | Model B | Model C | ||||
|---|---|---|---|---|---|---|
| Length [m] | Delay [ms] | Length [m] | Delay [ms] | Length [m] | Delay [ms] | |
| Path 1 | 5.0 | 14.57 | 8.0 | 23.32 | 5.5 | 16.03 |
| Path 2 | 6.5 | 18.95 | 11.0 | 32.07 | 6.0 | 17.49 |
| Path 3 | - | - | 14.0 | 40.81 | 7.5 | 21.86 |
| Path 4 | - | - | 16 | 46.64 | 8.5 | 24.78 |
| 17.97 ms | 34.50 ms | 19.74 ms | ||||
| 11.30 Hz | 5.79 Hz | 10.13 Hz | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergadà, P.; Alsina-Pagès, R.M. An Approach to Frequency Selectivity in an Urban Environment by Means of Multi-Path Acoustic Channel Analysis. Sensors 2019, 19, 2793. https://doi.org/10.3390/s19122793
Bergadà P, Alsina-Pagès RM. An Approach to Frequency Selectivity in an Urban Environment by Means of Multi-Path Acoustic Channel Analysis. Sensors. 2019; 19(12):2793. https://doi.org/10.3390/s19122793
Chicago/Turabian StyleBergadà, Pau, and Rosa Ma Alsina-Pagès. 2019. "An Approach to Frequency Selectivity in an Urban Environment by Means of Multi-Path Acoustic Channel Analysis" Sensors 19, no. 12: 2793. https://doi.org/10.3390/s19122793
APA StyleBergadà, P., & Alsina-Pagès, R. M. (2019). An Approach to Frequency Selectivity in an Urban Environment by Means of Multi-Path Acoustic Channel Analysis. Sensors, 19(12), 2793. https://doi.org/10.3390/s19122793






