A Novel Rule-Based Approach in Mapping Landslide Susceptibility
Abstract
1. Introduction
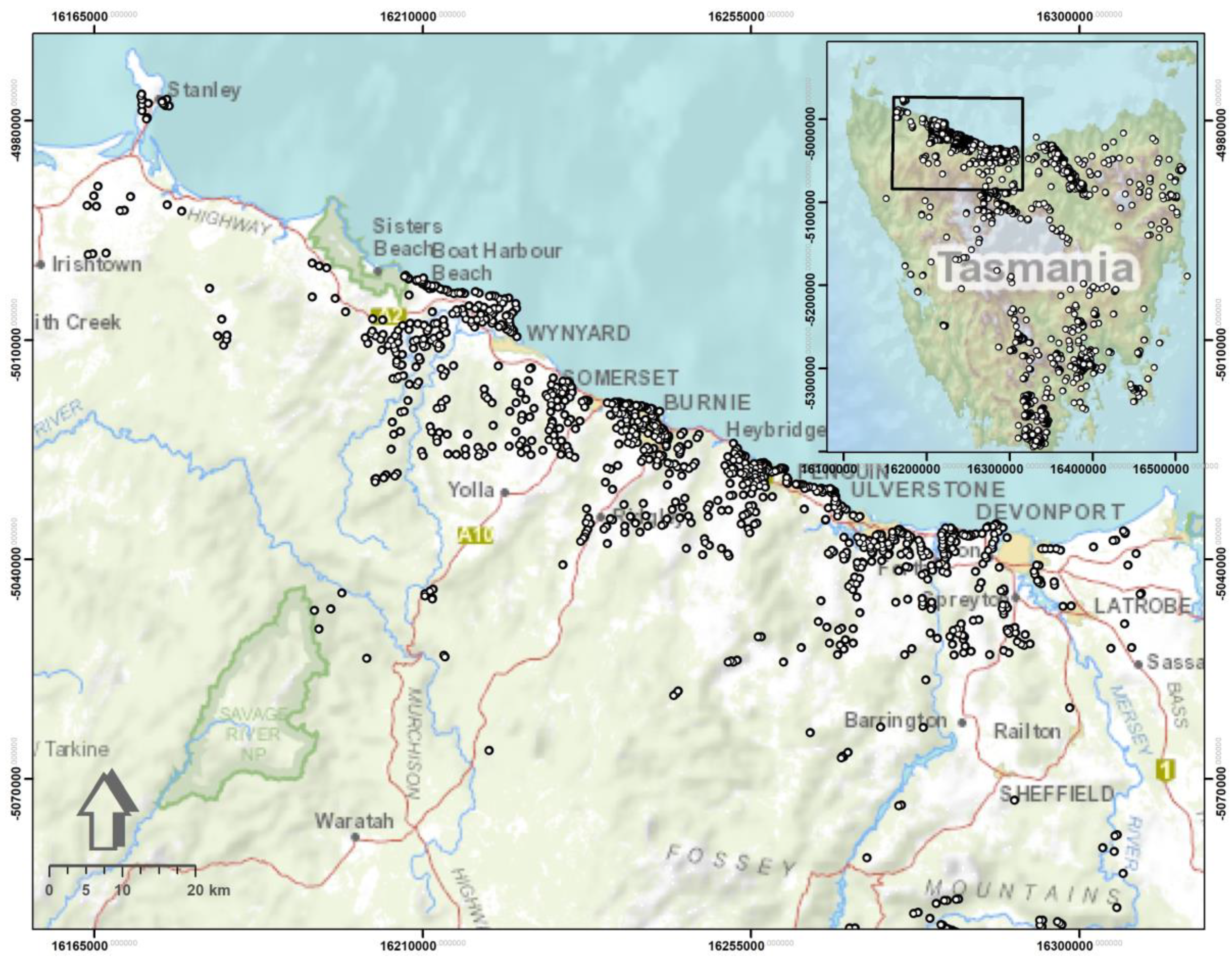
2. Description of the Study Region
3. Materials and Methods
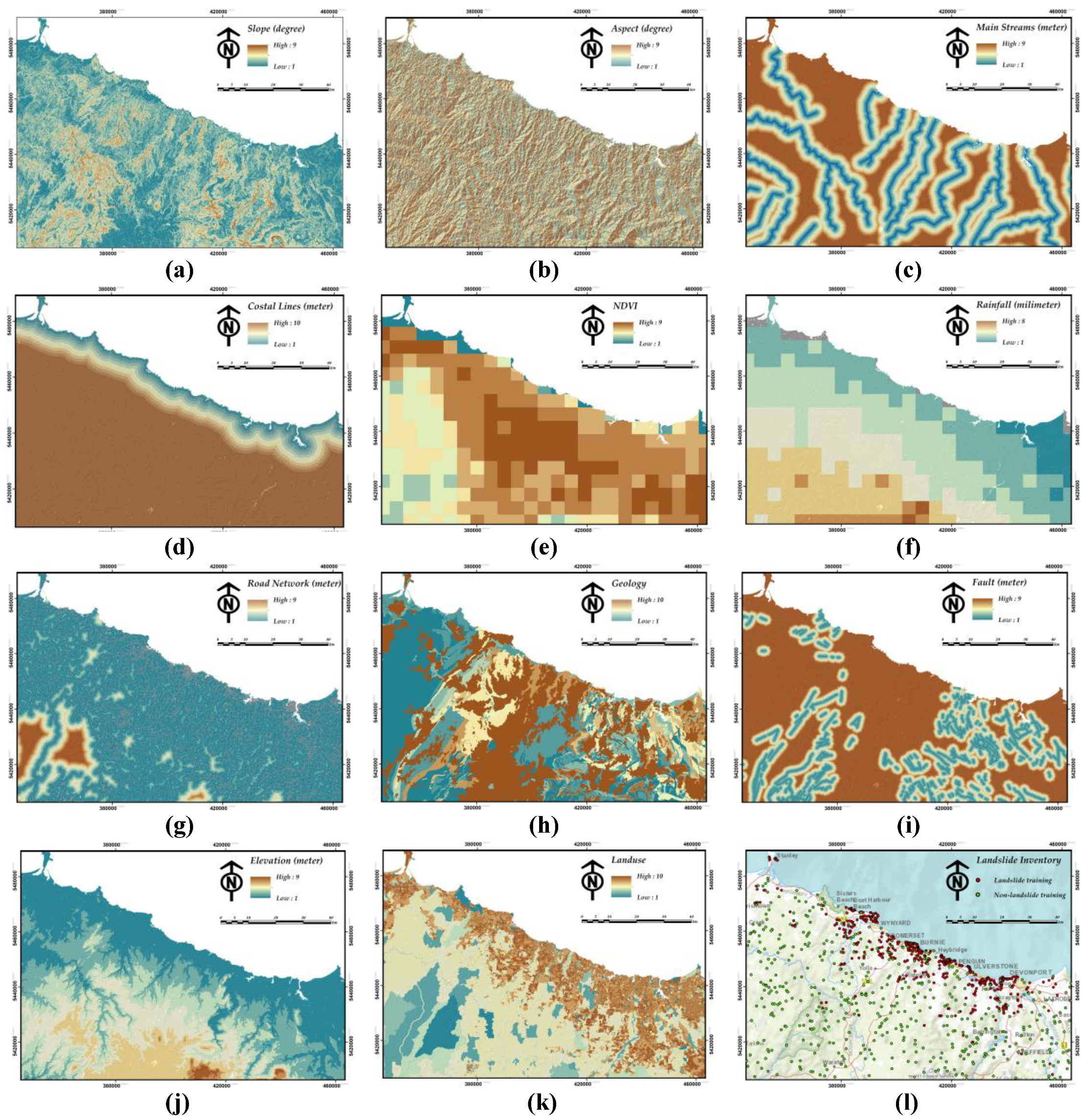
3.1. Landslide-conditioning Factors
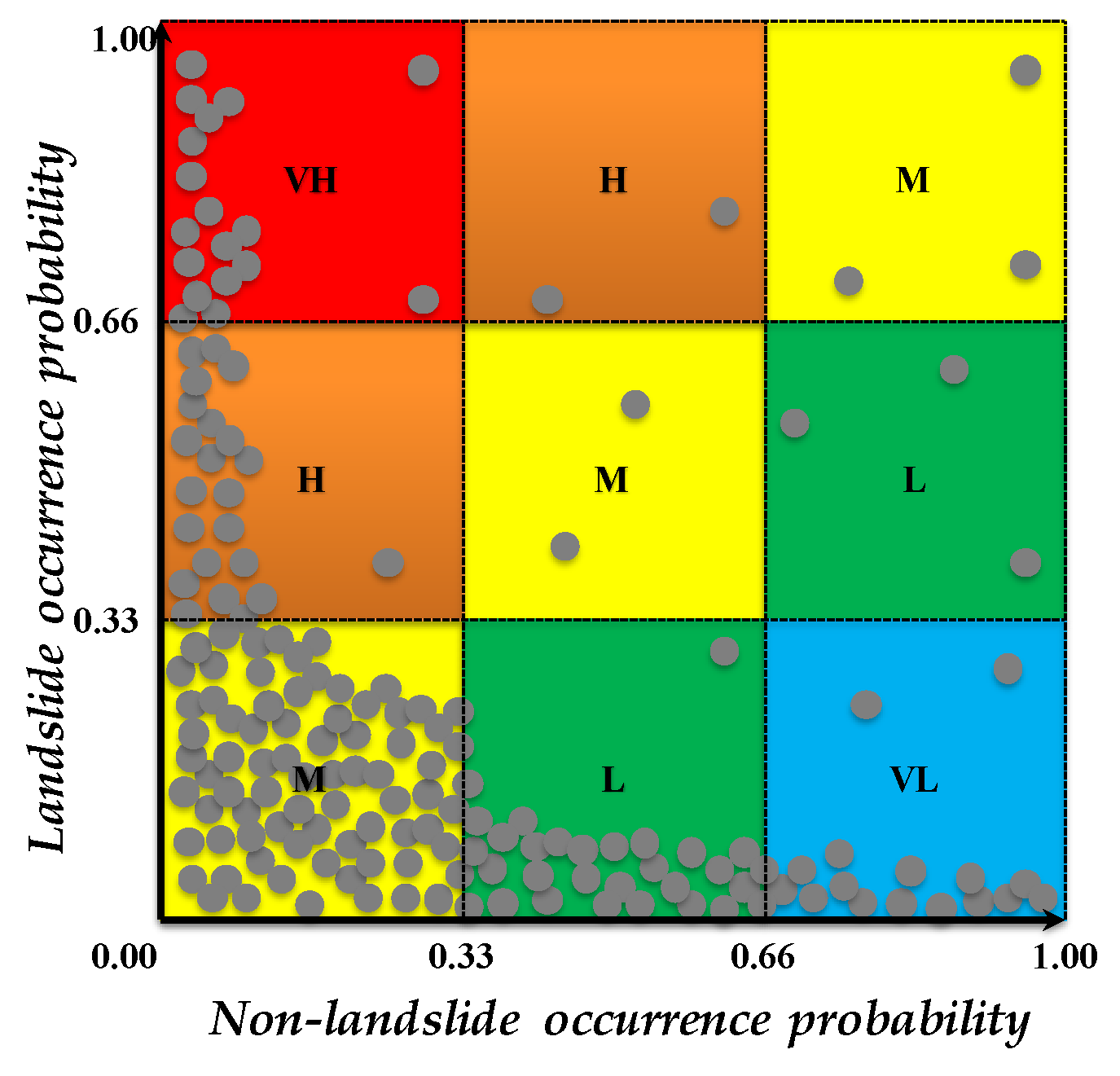
3.2. Description of DoTRules with Modifications for LSM
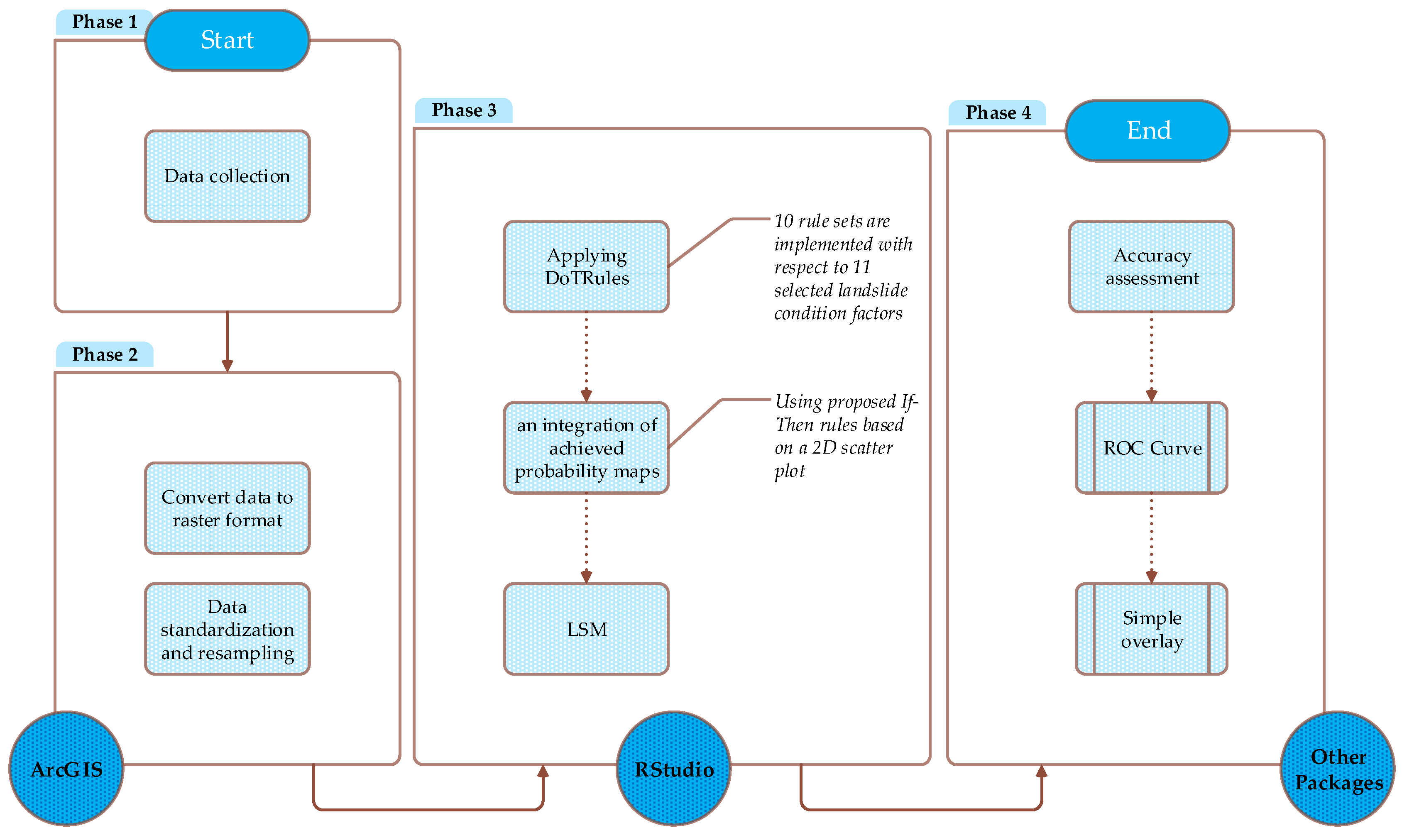
3.3. Methodology Implementation
4. Results
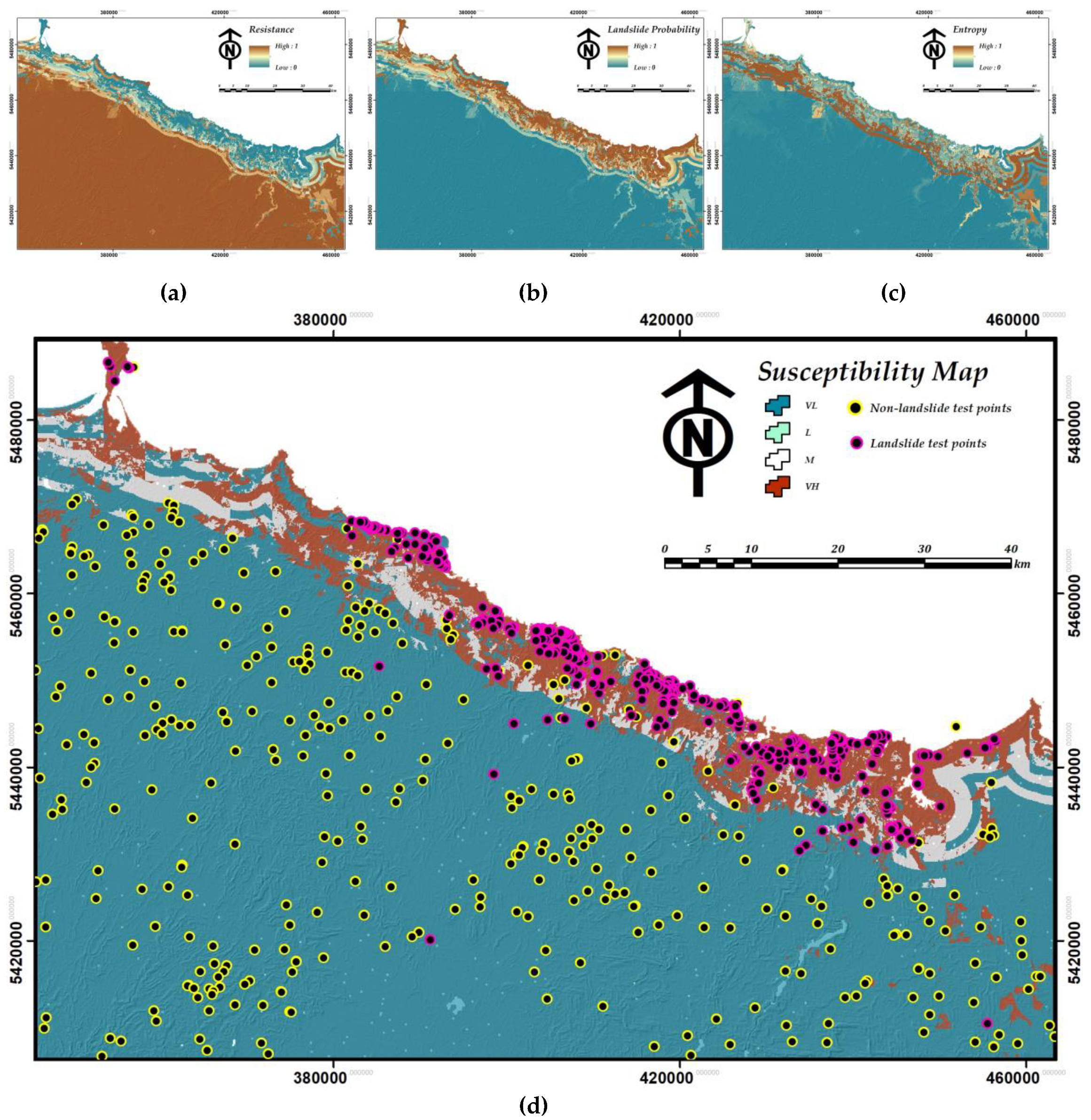
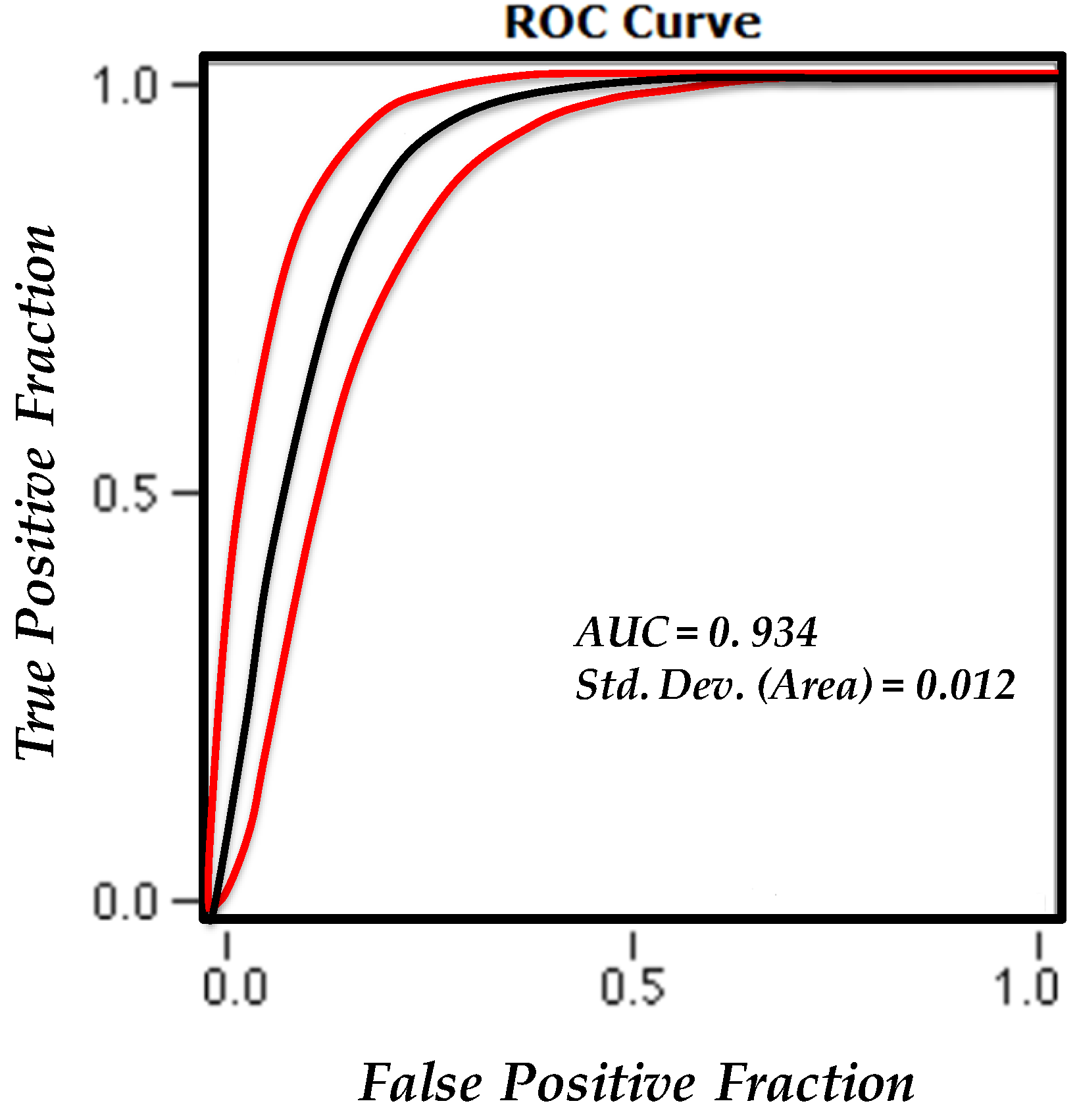
4.1. Validation of the Susceptibility Map Using AUC Estimate
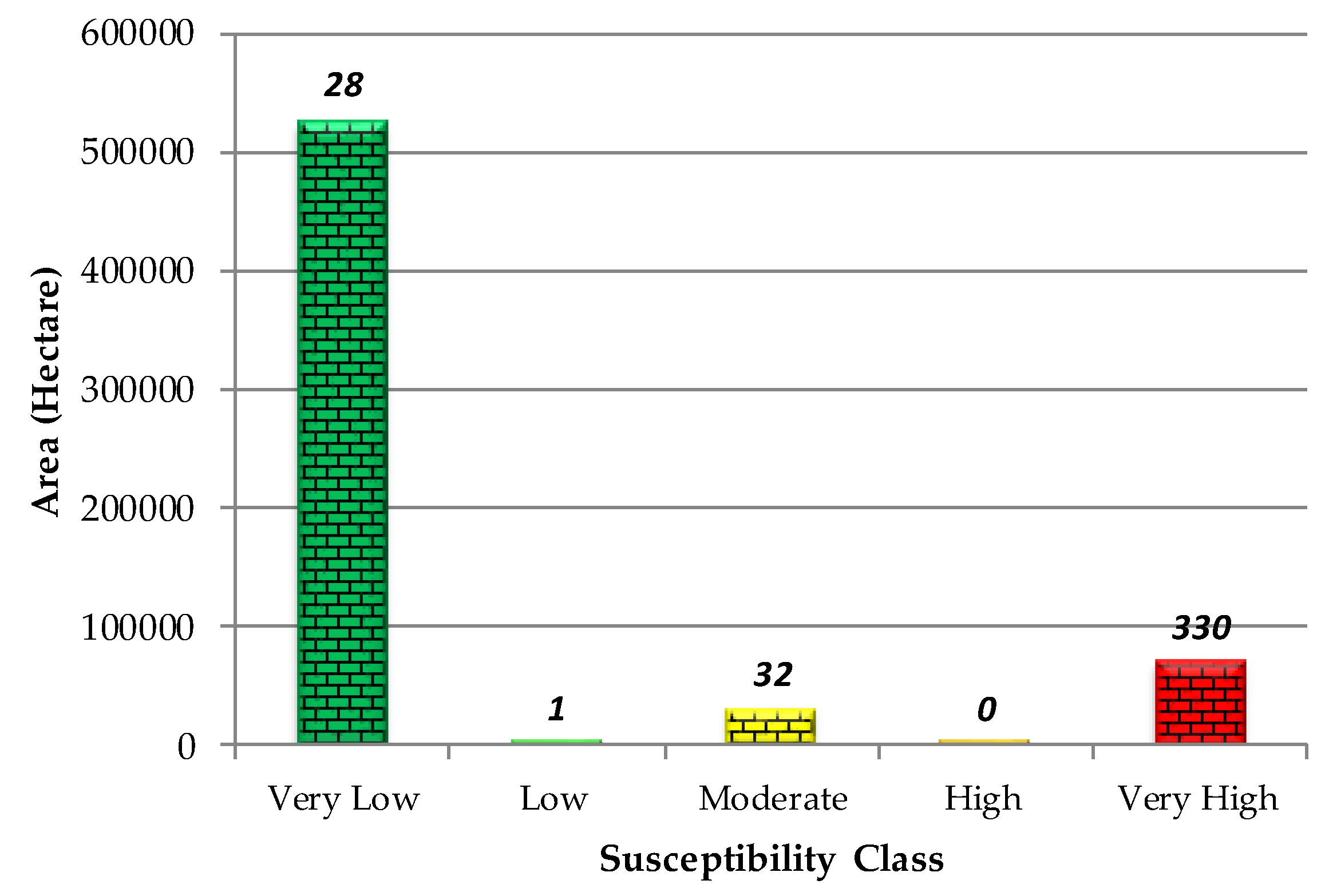
4.2. Validation of the LSM by Overlaying Technique
5. Discussion
5.1. Model Transparency and Spatial Information Extraction
5.2. Reducing Subjectivity of Final LSM
5.3. Decision Aiding and Planning
5.4. Limitation of the Proposed Methodology in LSM
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Pradhan, B.; Sezer, E.A.; Gokceoglu, C.; Buchroithner, M.F. Landslide Susceptibility Mapping by Neuro-Fuzzy Approach in a Landslide-Prone Area (Cameron Highlands, Malaysia). IEEE Trans. Geosci. Remote Sens. 2010, 48, 4164–4177. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Aryal, J.; Gholaminia, K. A new GIS-based technique using an adaptive neuro-fuzzy inference system for land subsidence susceptibility mapping. J. Spat. Sci. 2018, 1–17. [Google Scholar] [CrossRef]
- Carrara, A.; Guzzetti, F.; Cardinali, M.; Reichenbach, P. Use of GIS technology in the prediction and monitoring of landslide hazard. Nat. Hazards 1999, 20, 117–135. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Ohlmacher, G.C.; Davis, J.C. Using multiple logistic regression and GIS technology to predict landslide hazard in northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Caccavale, M.; Matano, F.; Sacchi, M.J.G. An integrated approach to earthquake-induced landslide hazard zoning based on probabilistic seismic scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 2017, 295, 235–259. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Teimoori Yansari, Z.; Panagos, P.; Pradhan, B. Analysis and evaluation of landslide susceptibility: A review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arab. J. Geosci. 2018, 11, 193. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Rahimi, S.; Beglou, M.J. PROMETHEE II and fuzzy AHP: an enhanced GIS-based landslide susceptibility mapping. Nat. Hazards 2014, 73, 77–95. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Shadman Roodposhti, M.; Jankowski, P.; Blaschke, T. A GIS-based extended fuzzy multi-criteria evaluation for landslide susceptibility mapping. Comput. Geosci. 2014, 73, 208–221. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Roodposhti, M.S. Integrating GIS Based Fuzzy Set Theory in Multicriteria Evaluation Methods for Landslide Susceptibility Mapping. Int. J. Geoinform. 2013, 9, 49–57. [Google Scholar]
- Zhou, G.; Esaki, T.; Mitani, Y.; Xie, M.; Mori, J. Spatial probabilistic modeling of slope failure using an integrated GIS Monte Carlo simulation approach. Eng. Geol. 2003, 68, 373–386. [Google Scholar] [CrossRef]
- Westen, C.V.; Terlien, M. An approach towards deterministic landslide hazard analysis in GIS. A case study from Manizales (Colombia). Earth Surf. Process. Landf. 1996, 21, 853–868. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Barredo, J.; Benavides, A.; Hervás, J.; van Westen, C.J. Comparing heuristic landslide hazard assessment techniques using GIS in the Tirajana basin, Gran Canaria Island, Spain. Int. J. Appl. Earth Obs. Geoinf. 2000, 2, 9–23. [Google Scholar] [CrossRef]
- Ruff, M.; Czurda, K. Landslide susceptibility analysis with a heuristic approach in the Eastern Alps (Vorarlberg, Austria). Geomorphology 2008, 94, 314–324. [Google Scholar] [CrossRef]
- Armaş, I.; Vartolomei, F.; Stroia, F.; Braşoveanu, L. Landslide susceptibility deterministic approach using geographic information systems: application to Breaza town, Romania. Nat. Hazards 2014, 70, 995–1017. [Google Scholar] [CrossRef]
- Sabokbar, H.F.; Roodposhti, M.S.; Tazik, E. Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 2014, 226, 15–24. [Google Scholar] [CrossRef]
- Alcantara-Ayala, I. Geomorphology, natural hazards, vulnerability and prevention of natural disasters in developing countries. Geomorphology 2002, 47, 107–124. [Google Scholar] [CrossRef]
- Gokceoglu, C.; Sezer, E. A statistical assessment on international landslide literature (1945–2008). Landslides 2009, 6, 345–351. [Google Scholar] [CrossRef]
- Kadavi, P.; Lee, C.-W.; Lee, S. Application of Ensemble-Based Machine Learning Models to Landslide Susceptibility Mapping. Remote Sens. 2018, 10, 1252. [Google Scholar] [CrossRef]
- Park, S.-J.; Lee, C.-W.; Lee, S.; Lee, M.-J. Landslide Susceptibility Mapping and Comparison Using Decision Tree Models: A Case Study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef]
- Hjort, J.; Luoto, M. Statistical methods for geomorphic distribution modeling. In Treatise on Geomorphology; Academic Press: Cambridge, MA, USA, 2013; pp. 59–73. [Google Scholar]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.-J.; Lee, J.H. A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. CATENA 2014, 114, 21–36. [Google Scholar] [CrossRef]
- Yan, F.; Zhang, Q.; Ye, S.; Ren, B. A novel hybrid approach for landslide susceptibility mapping integrating analytical hierarchy process and normalized frequency ratio methods with the cloud model. Geomorphology 2019, 327, 170–187. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Aryal, J.; Bryan, B.A. A novel algorithm for calculating transition potential in cellular automata models of land-use/cover change. Environ. Model. Softw. 2019, 112, 70–81. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Roodposhti, M.S.; Blaschke, T.; Aryal, J. Comparing GIS-based support vector machine kernel functions for landslide susceptibility mapping. Arab. J. Geosci. 2017, 10, 122. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Middlemann, M.H.; Middelmann, M. Natural Hazards in Australia: Identifying Risk Analysis Requirements; Geoscience Australia: Symonston, Australia, 2007.
- MRT. Mineral Resources Tasmania. Landslides. Available online: http://www.mrt.tas.gov.au/portal/landslides (accessed on 12 July 2018).
- Kiernan, K. Geomorphology Manual; Forestry Commission: Tasmania, Australia, 1990.
- Mazengarb, C.; Stevenson, M. Tasmanian Landslide Map Series: User Guide and Technical Methodology; Tasmanian Geological Survey: Rosny Park, Australia, 2010.
- Stevenson, P.C. Grasping the nettle: The Tasmanian geological survey’s work on landslides, 1971–1988. Pap. Proc. R. Soc. Tasman. 2011, 145, 39–49. [Google Scholar] [CrossRef]
- Shadman Roodposhti, M.; Aryal, J.; Shahabi, H.; Safarrad, T. Fuzzy shannon entropy: a hybrid GIS-based landslide susceptibility mapping method. Entropy 2016, 18, 343. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Wu, Y.; Pei, Y.; Xing, M.; Yang, D. A comparative study on the landslide susceptibility mapping using evidential belief function and weights of evidence models. J. Earth Syst. Sci. 2016, 125, 645–662. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef] [PubMed]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at Hoa Binh province (Vietnam) using an adaptive neuro-fuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Santacana, N.; Baeza, B.; Corominas, J.; De Paz, A.; Marturiá, J. A GIS-Based Multivariate Statistical Analysis for Shallow Landslide Susceptibility Mapping in La Pobla de Lillet Area (Eastern Pyrenees, Spain). Nat. Hazards 2003, 30, 281–295. [Google Scholar] [CrossRef]
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Environ. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. CATENA 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Tralli, D.M.; Blom, R.G.; Zlotnicki, V.; Donnellan, A.; Evans, D.L. Satellite remote sensing of earthquake, volcano, flood, landslide and coastal inundation hazards. ISPRS J. Photogramm. Remote Sens. 2005, 59, 185–198. [Google Scholar] [CrossRef]
- Kanungo, D.; Arora, M.; Sarkar, S.; Gupta, R.J. A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas. Eng. Geol. 2006, 85, 347–366. [Google Scholar] [CrossRef]
- Lee, S.; Talib, J.A. Probabilistic landslide susceptibility and factor effect analysis. Environ. Geol. 2005, 47, 982–990. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Gokceoglu, C. Assessment of landslide susceptibility for a landslide-prone area (north of Yenice, NW Turkey) by fuzzy approach. Environ. Geol. 2002, 41, 720–730. [Google Scholar]
- Shadman, M.; Aryal, J.; Bryan, B. DoTRules: A novel method for calibrating land-use/cover change models using a Dictionary of Trusted Rules. In Proceedings of the MODSIM2017: 22nd International Congress on Modelling and Simulation, Hobart, Australia, 3–8 December 2017; Syme, G., Hatton MacDonald, D., Fulton, B., Piantadosi, J., Eds.; p. 508. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Shadman Roodposhti, M.; Aryal, J.; Lucieer, A.; Bryan, B.A. Uncertainty Assessment of Hyperspectral Image Classification: Deep Learning vs. Random Forest. Entropy 2019, 21, 78. [Google Scholar] [CrossRef]
- Akgun, A.; Türk, N. Landslide susceptibility mapping for Ayvalik (Western Turkey) and its vicinity by multicriteria decision analysis. Environ. Earth. Sci 2010, 61, 595–611. [Google Scholar] [CrossRef]
- Rojas-Mora, J.; Josselin, D.; Aryal, J.; Mangiavillano, A.; Ellerkamp, P. The weighted fuzzy barycenter: Definition and application to forest fire control in the PACA region. Int. J. Agric. Environ. Inform. Syst. 2013, 4, 48–67. [Google Scholar] [CrossRef]
- Lotfi, F.H.; Fallahnejad, R. Imprecise Shannon’s entropy and multi attribute decision making. Entropy 2010, 12, 53–62. [Google Scholar] [CrossRef]
- Nandi, A.; Shakoor, A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng. Geol. 2010, 110, 11–20. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Clague, J.J.; Stead, D. Landslides: Types, Mechanisms and Modeling; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Süzen, M.L.; Doyuran, V. A comparison of the GIS based landslide susceptibility assessment methods: multivariate versus bivariate. Environ. Geol. 2004, 45, 665–679. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. GIS-multicriteria decision analysis for landslide susceptibility mapping: comparing three methods for the Urmia lake basin, Iran. Nat. Hazards 2013, 65, 2105–2128. [Google Scholar] [CrossRef]
- Hayati, E.; Majnounian, B.; Abdi, E.; Sessions, J.; Makhdoum, M. An expert-based approach to forest road network planning by combining Delphi and spatial multi-criteria evaluation. Environ. Monit. Assess. 2013, 185, 1767–1776. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Kayastha, P.; Dhital, M.R.; De Smedt, F. Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping: A case study from the Tinau watershed, west Nepal. Comput. Geosci. 2013, 52, 398–408. [Google Scholar] [CrossRef]
| Criteria | Data Source | Description | H |
|---|---|---|---|
| 1. Slope | Mineral Resources Tasmania (MRT) | This is the slope angle derived from a digital elevation model (DEM) of the 10 metre Lidar DEM. | 9 |
| 2. Aspect | Mineral Resources Tasmania (MRT) | The compass direction that a slope faces derived from the same source as slope. | 9 |
| 3. Mainstreams | Land Information System Tasmania (LIST) | The relative Euclidian distance of each desired pixel from the closet mainstream. | 9 |
| 4. Coastal lines | Land Information System Tasmania (LIST) | The relative Euclidian distance of each desired pixel from coastal lines. | 10 |
| 5. NDVI | Australian Bureau of Meteorology | The normalized difference vegetation index (NDVI) representing vegetation density and condition from Jun 2017 to Jun 2018. | 9 |
| 6. Rainfall | Australian Bureau of Meteorology | A monthly average of a 30 years rainfall (base climatological datasets) from 1961–1990. | 8 |
| 7. Road | Land Information System Tasmania (LIST) | The relative Euclidian distance of each desired pixel from the closet road. | 9 |
| 8. Geology | Mineral Resources Tasmania (MRT) | This Tasmania Geology map is derived from the 1:250,000 scale digital geology of Tasmania. | 10 |
| 9. Faults | Mineral Resources Tasmania (MRT) | The relative Euclidian distance of each desired pixel from the closet geological fault. | 9 |
| 10. Elevation | Mineral Resources Tasmania (MRT) | The representation of the land surface elevation from 10 metre Lidar source. | 9 |
| 11. Land use | the Australian Land Use and Management (ALUM) | The Tasmanian land use map containing 116 land-use sub-classes for the current study area. | 10 |
| 12. Landslides | Mineral Resources Tasmania (MRT) | A number of 641 records containing both active and inactive landslides. | - |
| Rank | Variable Name | Entropy Score |
|---|---|---|
| 1 | Coastal lines | 0.272 |
| 2 | Elevation | 0.378 |
| 3 | Rainfall | 0.437 |
| 4 | Land use | 0.488 |
| 5 | Geology | 0.540 |
| 6 | NDVI | 0.557 |
| 7 | Road | 0.579 |
| 8 | Slope | 0.659 |
| 9 | Faults | 0.659 |
| 10 | Aspect | 0.664 |
| 11 | Mainstreams | 0.671 |
| Rule-set ID | Rule (Composed of Discrete H Values) | Frequency | Matching Landslides | Entropy |
|---|---|---|---|---|
| 1 | 1_1 | 130 | 125 | 0.163 |
| 2 | 1_1_3 | 79 | 75 | 0.200 |
| 3 | 1_1_3_9 | 35 | 34 | 0.129 |
| 4 | 1_1_3_9_10 | 25 | 25 | 0 |
| 5 | 1_1_3_9_10_7 | 10 | 10 | 0 |
| 6 | 1_1_3_9_10_7_1 | 7 | 7 | 0 |
| 7 | 1_1_3_9_10_7_1_2 | 1 | 1 | 0 |
| 8 | 1_1_3_9_10_7_1_2_9 | 1 | 1 | 0 |
| 9 | 1_1_3_9_10_7_1_2_9_5 | 1 | 1 | 0 |
| 10 | 1_1_3_9_10_7_1_2_9_5_2 | 1 | 1 | 0 |
| Summary Statistics | Achieved Values |
|---|---|
| Number of Cases | 782 |
| Number Correct | 677 (86.5% of total) |
| AUC | 0.934 |
| Std. Dev. (Area) | 0.012 |
| Accuracy | 86.6% |
| Sensitivity | 92.6% |
| Specificity | 80.6% |
| Pos Cases Missed | 29 |
| Neg Cases Missed | 76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roodposhti, M.S.; Aryal, J.; Pradhan, B. A Novel Rule-Based Approach in Mapping Landslide Susceptibility. Sensors 2019, 19, 2274. https://doi.org/10.3390/s19102274
Roodposhti MS, Aryal J, Pradhan B. A Novel Rule-Based Approach in Mapping Landslide Susceptibility. Sensors. 2019; 19(10):2274. https://doi.org/10.3390/s19102274
Chicago/Turabian StyleRoodposhti, Majid Shadman, Jagannath Aryal, and Biswajeet Pradhan. 2019. "A Novel Rule-Based Approach in Mapping Landslide Susceptibility" Sensors 19, no. 10: 2274. https://doi.org/10.3390/s19102274
APA StyleRoodposhti, M. S., Aryal, J., & Pradhan, B. (2019). A Novel Rule-Based Approach in Mapping Landslide Susceptibility. Sensors, 19(10), 2274. https://doi.org/10.3390/s19102274







