1. Introduction
A task in robot navigation is to obtain the position immediately, whenever we want to know it. Suppose that a robot navigating in a sensor network is able to automatically obtain the distances to a collection of landmarks, then we can find a subset of nodes in the network such that the robot’s position in the network is uniquely identified. In order to achieve this, the concept of “landmarks in a graph” was developed [
1], and later was extended to the “metric dimension”, in which one considers networks in the graph-structure framework.
Let be a k-dimensional Euclidean space and be the integer set. Assume . Every graph we consider is simple and connected and contains neither multiple edges nor loops. For two vertices of a graph , we denote by (or simply by ) the distance between and , i.e., the number of edges in the shortest path from to . For a positive integer , we call u a t-neighbor of v if . We call the set the t-neighbourhood of v, and let and . In particular, is called the open neighborhood of v and simply denoted by , and is the closed neighborhood of v. The degree of a vertex v is the cardinality of and denoted by .
Given a positive integer k and an ordered set , for a vertex , we regard the k-vector as the metric representation of v with respect to S. If any two distinct vertices of G do not have the identical representation with respect to S, then we call S a resolving set (RS) of G. The metric basis of G is the RS of G with the smallest cardinality. A metric basis of cardinality k is also called a k-metric basis. The metric dimension of G, denoted by , is defined as the cardinality of a metric basis.
For convenience, we summarize the symbols we use in
Table 1.
Due to their important applications and theoretical studies, various versions of metric generators have been proposed, which contribute deep insights into the mathematical properties of the metric dimension involving distances in graphs. Many authors have introduced different variations of metric generators—such as independent resolving sets [
2], local metric sets [
3], resolving dominating sets [
4], strong resolving sets [
5],
k-metric generators [
6], and a mixed metric dimension [
7]—and their properties have been studied.
The subject of determining
of a graph
G was initially studied by Harary, et al. [
8], and Slater [
9] independently proved that determining
of a graph
G is an NP-complete problem [
10]. The metric dimension has been extensively studied not merely for the computational intractability, but also for its applications in many fields, such as robot navigation [
1], telecommunication, chemistry [
2,
11], and combinatorial optimization [
4,
12,
13,
14,
15,
16,
17], among many others.
Honeycomb networks are a variant of meshes and tori that play an essential role in the areas of image processing, cellular phone base stations, computer graphics, and mathematical chemistry [
18,
19,
20], because they have more attractive structural properties with respect to their diameter, degree, the total number of edges, the bisection width, and cost. Stojmenovic [
20] and Parhami [
21] analyzed the topological descriptors of honeycomb networks and presented an united formulation for the honeycomb. In Reference [
18], based on honeycomb and hexagonal meshes, Manuel et al. introduced two new hexagonal networks, which have more interesting properties and features over certain honeycomb networks and meshes. Manuel et al. [
18] posed an interesting open question to determine whether the metric dimensions of these kinds of hex-derived networks (HDNs) are between three and five. Xu and Fan [
22] gave a proof and showed that the metric dimensions of the hex-derived networks
and
are either three or four. However until now, the exact metric dimension of these networks is still unknown. In this paper, we solve this problem for
networks by showing that
for
.
The main contributions of this paper are listed as follows:
We propose a vector coloring scheme to study properties of some networks with metric dimension three. By applying this approach we succeed to process hex-derived networks. Therefore, the proposed approach is a promising approach to determine if a network has metric dimension three.
The hexagonal networks are popular mesh-derived parallel architectures, which are also a kind of sensor network and widely used in computer graphics and cellular phone base stations. Inspired by the important applications of hex-derived network, Manuel et al. started to study the metric dimension of hex-derived networks. They proposed an open problem to determine whether the metric dimension of a kind of hex-derived networks lies between three and five. Xu and Fan showed that it is less than five. In this paper, we apply our approach to completely solve this problem.
2. HDN1 Networks
In this section, we describe the definition of
networks. We follow the presentation in Reference [
22]. The concept of a hexagonal mesh was introduced by Chen et al. [
19]. Recall that a
planar graph is a graph that can be drawn such that no edges cross each other. An
n-dimensional hexagonal mesh for
, denoted by HX(
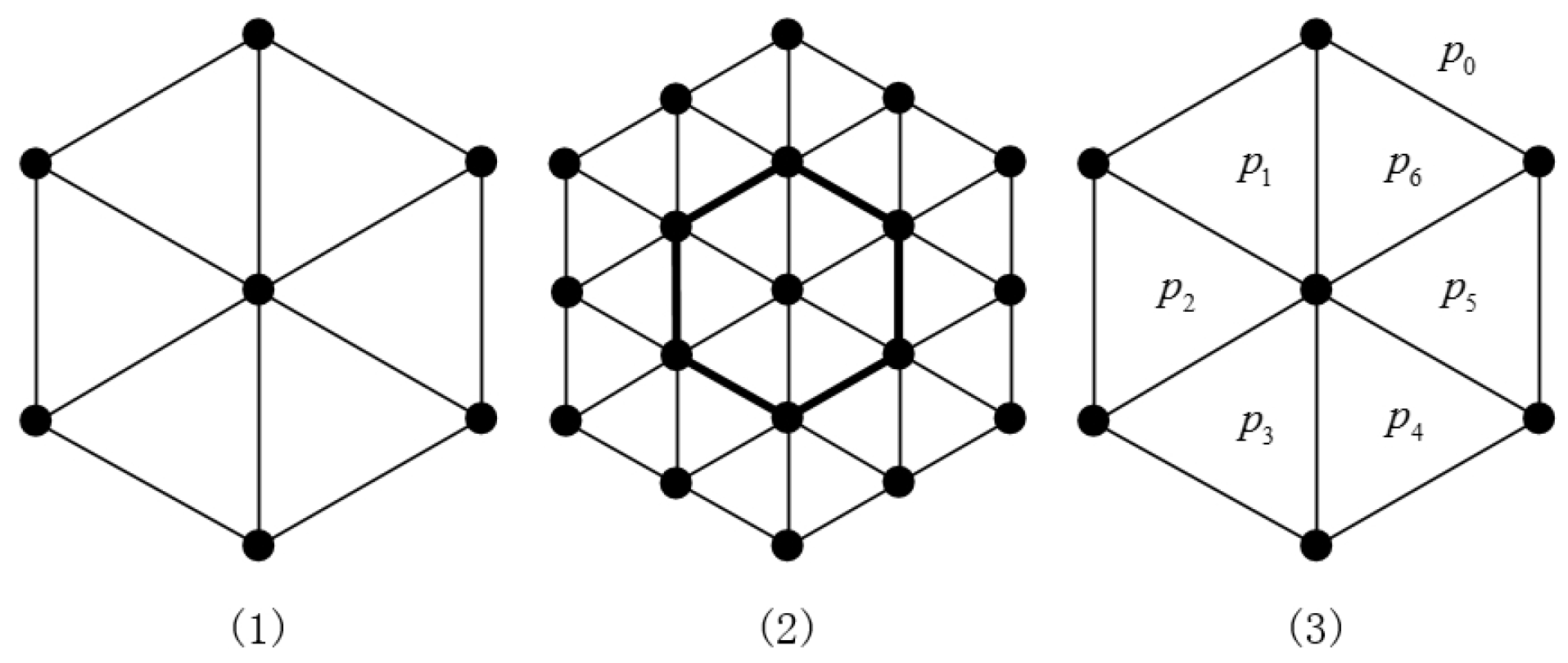
n), is a planar graph which consists of a collection of triangles as shown in
Figure 1. The 2D hexagonal mesh HX(2) is made up of 6 triangles (see
Figure 1(1)). The 3D hexagonal mesh HX(3) is constructed from HX(2) by including additional triangles around the boundary of HX(2) (see
Figure 1(2)). Similarly, HX(
n) is established by including additional triangles around the boundary of HX(
1).
In a planar graph, there are many faces of
G. If two faces
p and
q share at least one edge, they are said to be adjacent, or
p is a neighbor of
q. If a planar graph contains exactly one unbounded face, it is called the
outer face of the graph. For example
Figure 1(3) shows that
has seven faces
, for which
is adjacent to
and
; and
is an outer face. These definitions can be found in Reference [
22].
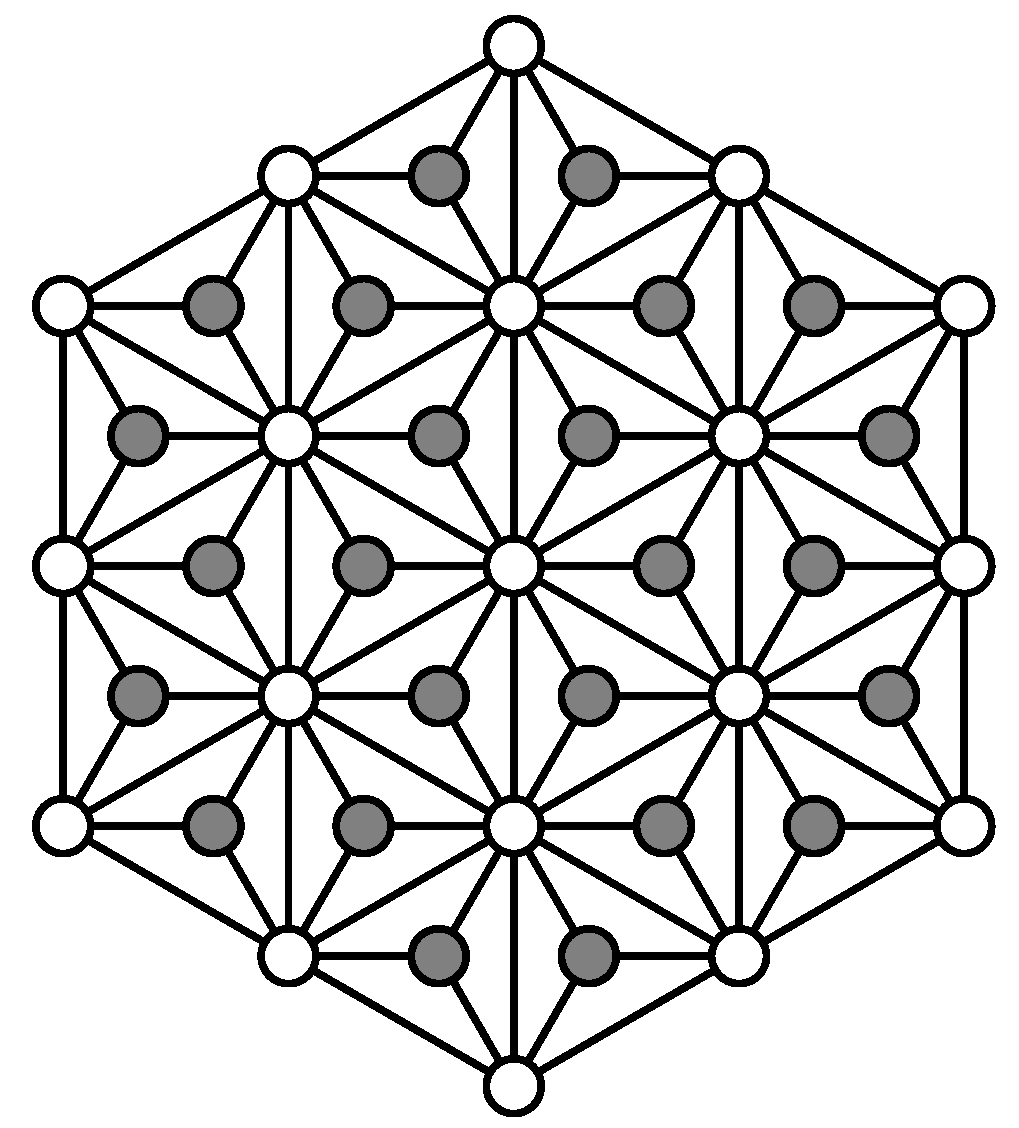
Given a graph HX(
n), we use
to denote the set of non-outer faces of HX
. Now, for each
, we add a new vertex
which is located in the face
p and connects
with the three vertices of
p. The resulting graph is
. As an example,
can be found in
Figure 2, where the gray vertices are the additional vertices based on HX(3).
Suppose that is a neighbor of p for each and have a one-to-one mapping to , respectively. If the vertices of p and are joined with , then we obtain . It is clear that contains as a subgraph. For , we also view and collectively as .
The central vertex of
is denoted by
. For an integer
i, we adopt the following notations:
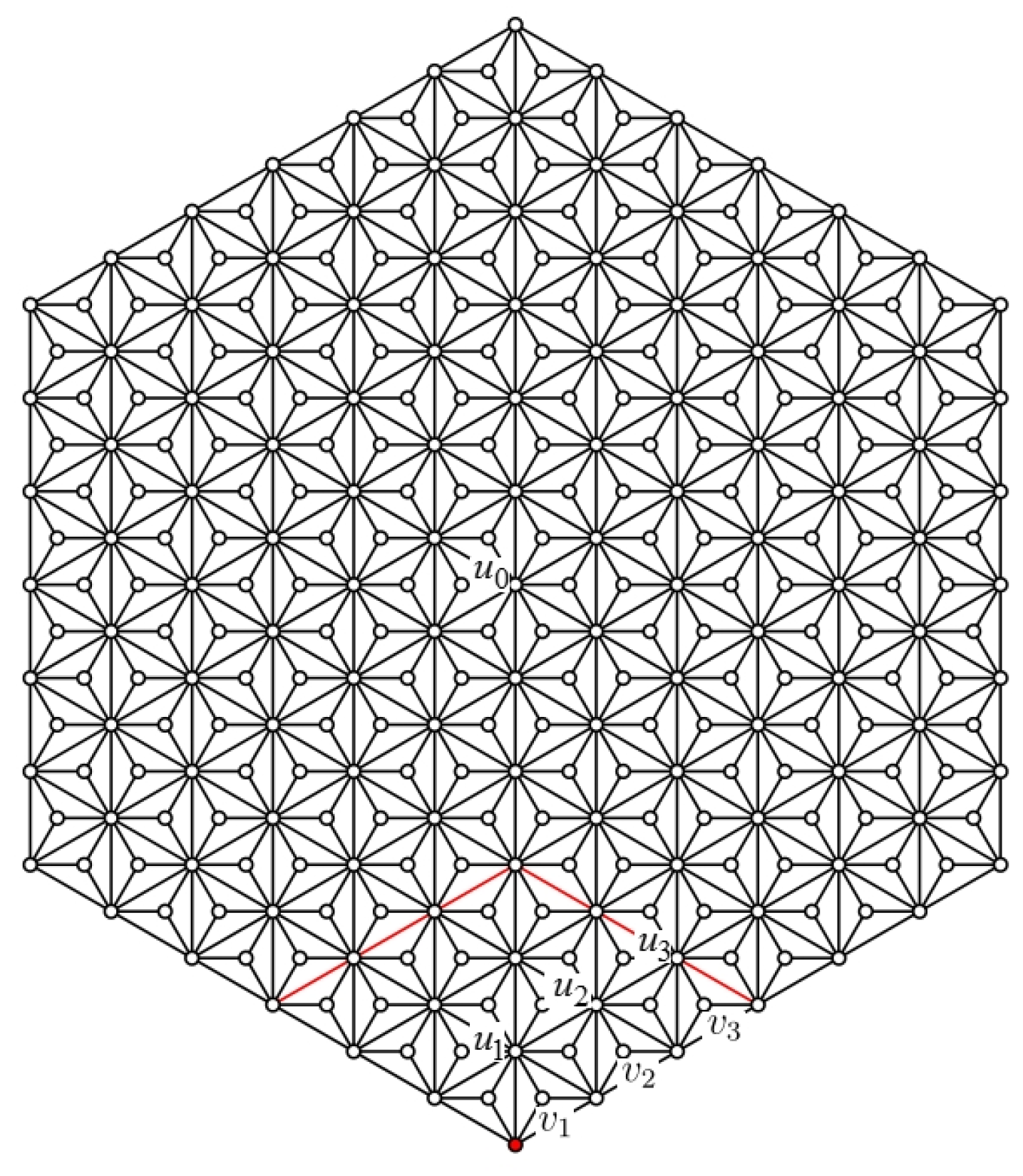
In order to understand the idea clearly, we take the network described in
Figure 3a as an example, which has the nodes
. Assume we use
as landmarks, then a robot, which knows the distances from each element in
S, can obtain its own location in this network at any time. For instance, if the distance vector from
is
, then it is located at the position
C because the distance vectors from
are pairwise distinct.
3. Navigation in Certain Hex-Derived Sensor Networks
P. Manuel et al. [
18] studied the navigation of certain hex-derived networks and proposed an open problem as follows.
Open Problem. Let G be or , then is it true that ?
D. Xu [
22] et al. have provide a proof to show that
is either 3 or 4, as shown in Theorems 1 and 2.
Theorem 1. [22] If , then we have . Theorem 2. [22] If , then we have . Note that the least number of nodes needed for locating any other node in such a network is unknown, we will solve this problem in this paper.
Let G be a graph and W be an ordered subset of with . Assume and for any .
Lemma 1. For any , we have
Proof. Since
and
, we have
☐
Lemma 2. Let t be a positive integer and . If and W is an RS of G, then .
Definition 1. Let and . A function is said to be a -vector coloring scheme on G with respect to v, if the following conditions are fulfilled:
- (i)
For with and , we have .
- (ii)
Let . If , we have .
- (iii)
.
Lemma 3. If there exists a subgraph of G and such that for any , and there exists no -vector coloring scheme on with respect to vertex v, then v is not in any k-metric basis of G.
Proof. Suppose that W is a k-metric basis of G with . Let be an ordered set. For any , . Let . By Lemmas 1 and 2, we have that h satisfies the three conditions of Definition 1, which yields a contradiction. ☐
Corollary 1. Let W be a k-metric basis of G. If is a subgraph of G and such that for any , then there must exist a -vector coloring scheme on with respect to vertex v.
Now, we will present the basic properties of hex-derived networks.
Lemma 4. Let . Suppose that and is an RS of , then we have , for any .
Proof. Suppose that there exists a for some i, then the following two cases are studied. ☐
Let and . By Corollary 1, there exists a 2-vector coloring scheme h on with respect to vertex . Let . For any , by Definition 1, we have and . That is to say, . Consequently, must be one of nine possible vectors for any . Since , then there must exist two vertices with , which is a contradiction with the definition of k-vector coloring scheme (Definition 1).
Case 2. (See
Figure 3b).
Let and . Let . For any , similarly, it can be proved that must be one of nine possible vectors. We have Claim 1 as follows.
Claim 1. There exists no three vertices with .
Proof of Claim 1: Suppose the statement does not hold. Since , then . Consequently, there must exist two vertices, say or , which is a contradiction with Definition 1.
Since and there are nine possibilities for h, then there must exist three pairs of vertices whose h values are equivalent. Note that . From Definition 1, we know that the h values in are distinct for positive integer . Therefore it can be assumed that the three pairs of vertices are , , and with and that for .
Similarly, there are three pairs of vertices , and with and with for .
From for , we have . However, , which yields a contradiction. ☐
In the following, we discuss the vertices in
of
: Let
and
Analogous to the proof of Case 2 in Lemma 4, we have:
Lemma 5. Let . Suppose that and is a resolving set of , then we have .
Lemma 6. Let . Suppose that , is a resolving set of and , then .
Proof. Assume and . Let be a function. Let and for . We list seven properties Qj, as follows (If Qj holds, we say that satisfies Qj):
- (Q1)
If for , then and .
- (Q2)
, for .
- (Q3)
, for .
- (Q4)
There are at most two vertices such that neither nor satisfy .
- (Q5)
If does not satisfy Q1, then v satisfies either Q2 or Q3.
- (Q6)
For any , it is impossible for v to satisfy both Q2 and Q3.
- (Q7)
Given any , then v satisfies Q1.
☐
We have Claim 2 as follows:
Claim 2. Let . For any subgraph of with , we assume without loss of generality that . If for any , then there exists a two-vector coloring scheme on with respect to vertex such that satisfies Q4–Q7.
Proof of Claim 2: Assume for any vertex u in . Define a function with for any vertex u in . By the proof of Corollary 1, we know that satisfies properties (i)–(iii) with in Definition 1. Therefore the function h is a two-vector coloring scheme on . Now we will show that satisfies Q4–Q7 in the following.
It can be seen that a vertex such that does not satisfy Q1 if and only if . Since and , then there are at most two vertices such that neither nor satisfy . Therefore, we have satisfies Q4.
Assume and v does not satisfy Q1, i.e., . It is clear that . Note that for any vertex u in . If , then and for . Therefore we have , for , i.e., satisfies Q2. If , then and for . Therefore we have , , i.e., satisfies Q3. Consequently, we have satisfies Q5.
Suppose does not satisfy Q6. Then there exists for which satisfies Q2 and Q3. Since for , we have . By for , we have . Therefore, we have , a contradiction.
By Lemma 4, we have that satisfies Q7 and the proof of Claim 2 is complete.
If
, as shown in
Figure 4b–e, it can be seen that there are only four distinct cases of
for
in
. By means of computer search, we have that there exists no two-vector coloring scheme
h on subgraph
in
, for which
satisfies Q4–Q7. By Claim 2, we have Lemma 6 holds. ☐
Lemma 7. Let . Suppose that and is an RS of , then we have .
Proof. The proof is by induction on
n. The statement holds for
, which can be confirmed by computer search. Let
and let the statement hold for all
with
1. Suppose the statement does not hold for
. By Lemmas 4–6, all vertices of any basis
W are in
B. On the other hand, for any ordered set
and any vertex
v in
, let
be a metric representation of
v with respect to
W. For any
, since
, we assume
. (See
Figure 5).
Then for , without loss of generality we have and is in for . Therefore we can obtain a vertex with respect to each vertex for . If are distinct, for any , we have for with . Consequently, S is also a basis of − , which yields a contradiction. If are not distinct, then − , which yields a contradiction with . ☐
Now, we have
Theorem 3. If , then .
Proof. For the case
, the results can be verified by solving the instances constructed from an integer linear program introduced in Reference [
2]. Suppose the statement does not hold for
, and we assume that
is a base of
. By Lemmas 4–7, we have
, a contradiction. This completes the proof. ☐