Performance Evaluation Strategies for Eye Gaze Estimation Systems with Quantitative Metrics and Visualizations
Abstract
1. Introduction
1.1. Problem Statement
1.2. Purpose, Scope and Structure of the Paper
2. Related Works: Accuracy Estimates and Visualizations in Gaze Research
2.1. Previous Work on Evaluation of Gaze Estimation Systems
2.2. Data Visualizations in Gaze Research
2.3. Requirement of Well-Defined Accuracy Metrics and Performance Visualization Tools in Eye Gaze Research: Contributions in This Work
3. Experimental Methodology
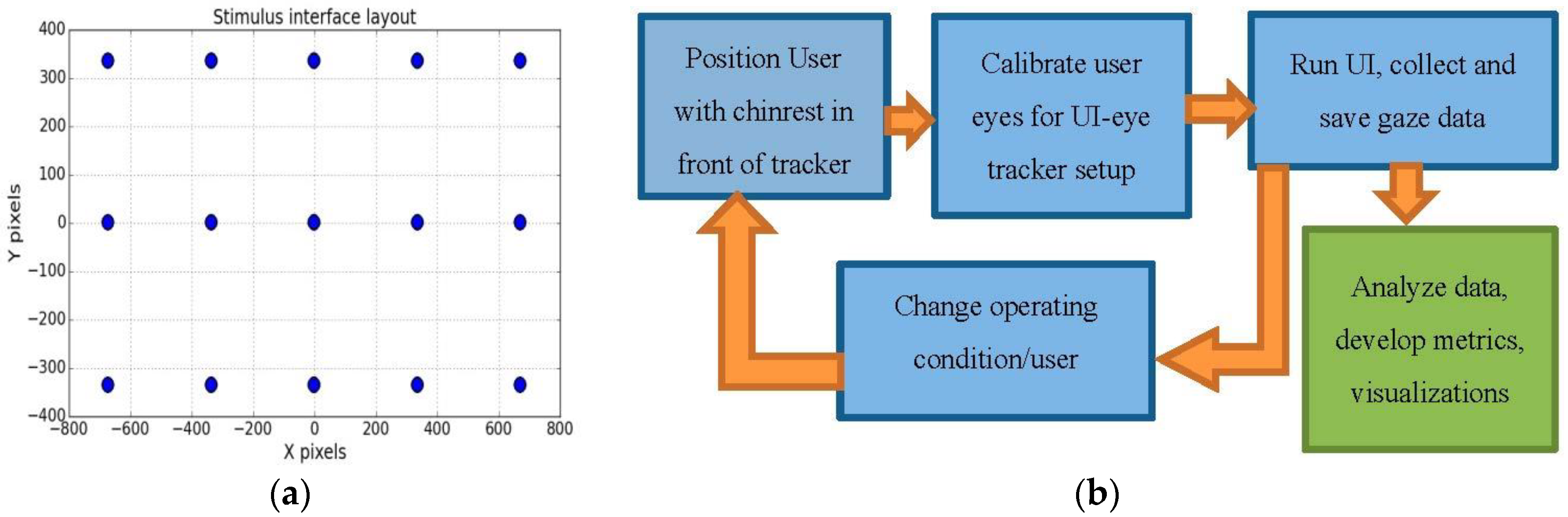
3.1. Experimental Setup and Workflow
3.2. Setup Coordinate System and Eye Movements
3.3. Eye Tracking Experiments Conducted for the Development of Gaze Accuracy Metrics and Visual Tools
4. Deriving Evaluation Metrics for Eye Tracking Devices and Algorithms
4.1. Angular Accuracy Metrics
4.1.1. Gaze Angular Accuracy
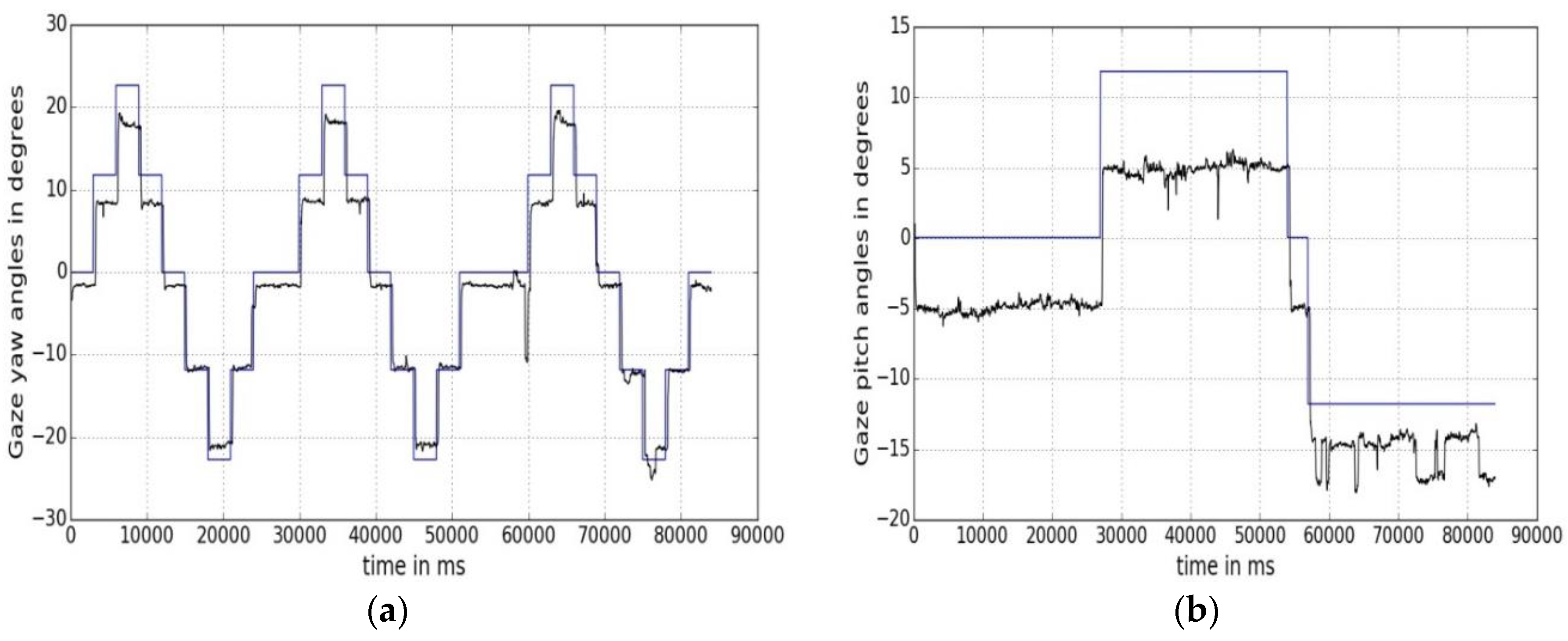
4.1.2. Gaze Yaw and Pitch Angular Accuracies
4.2. Statistical Metrics
4.2.1. Statistical Measures of Eye Tracking Performance
4.2.2. Histogram Based Metrics
4.3. Sensitivity Metrics
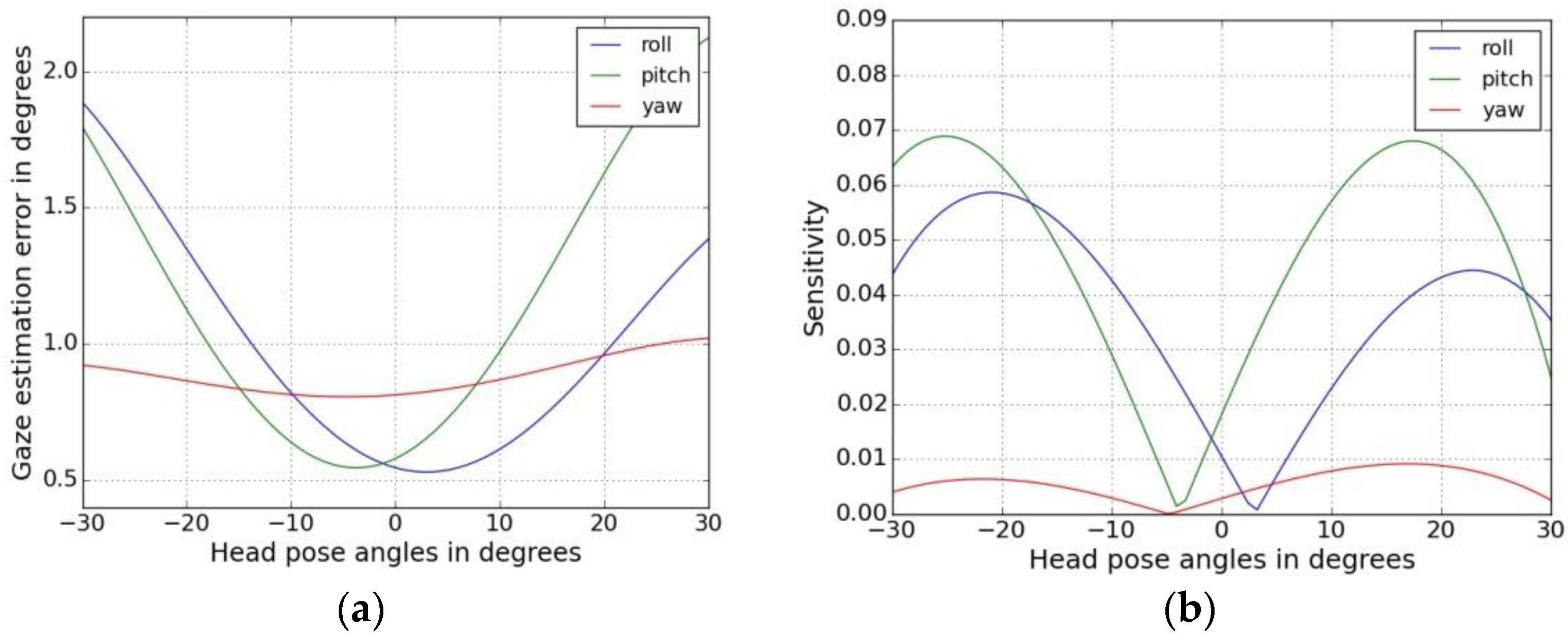
4.3.1. Head Pose Sensitivity
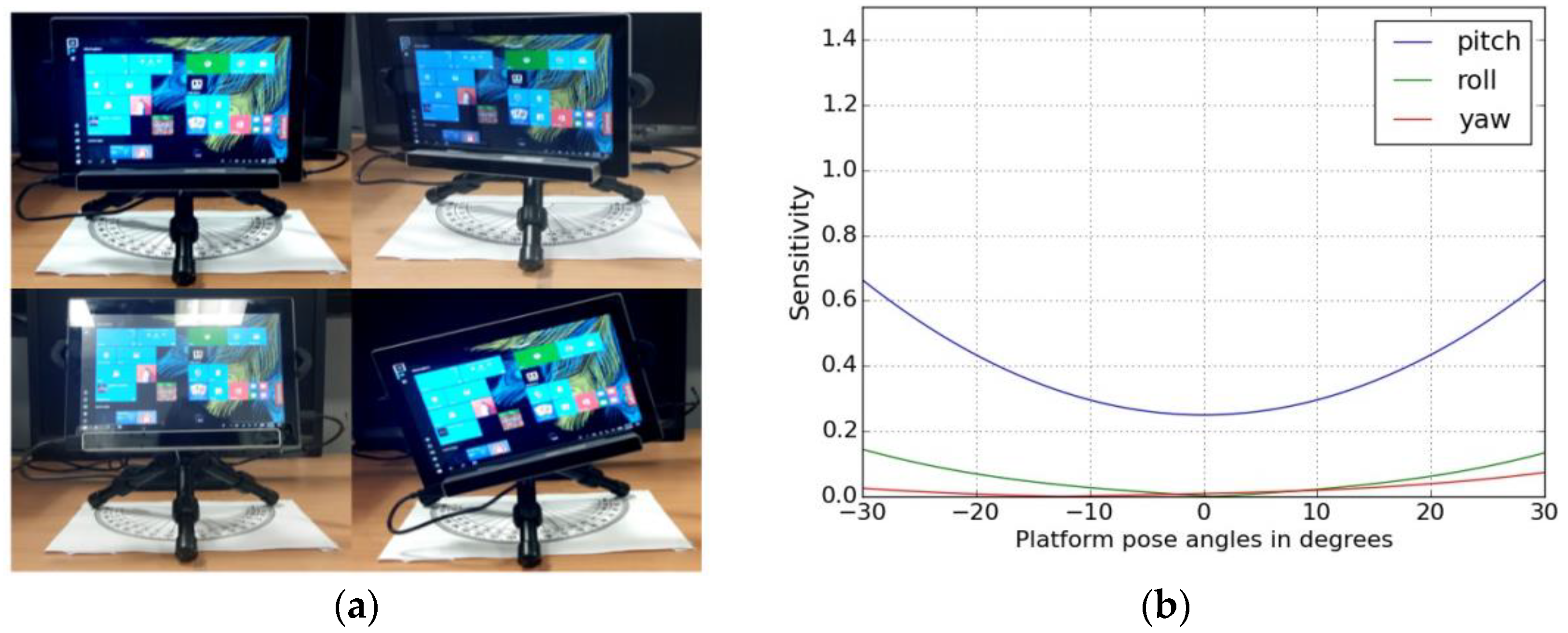
4.3.2. Platform Orientation Sensitivity
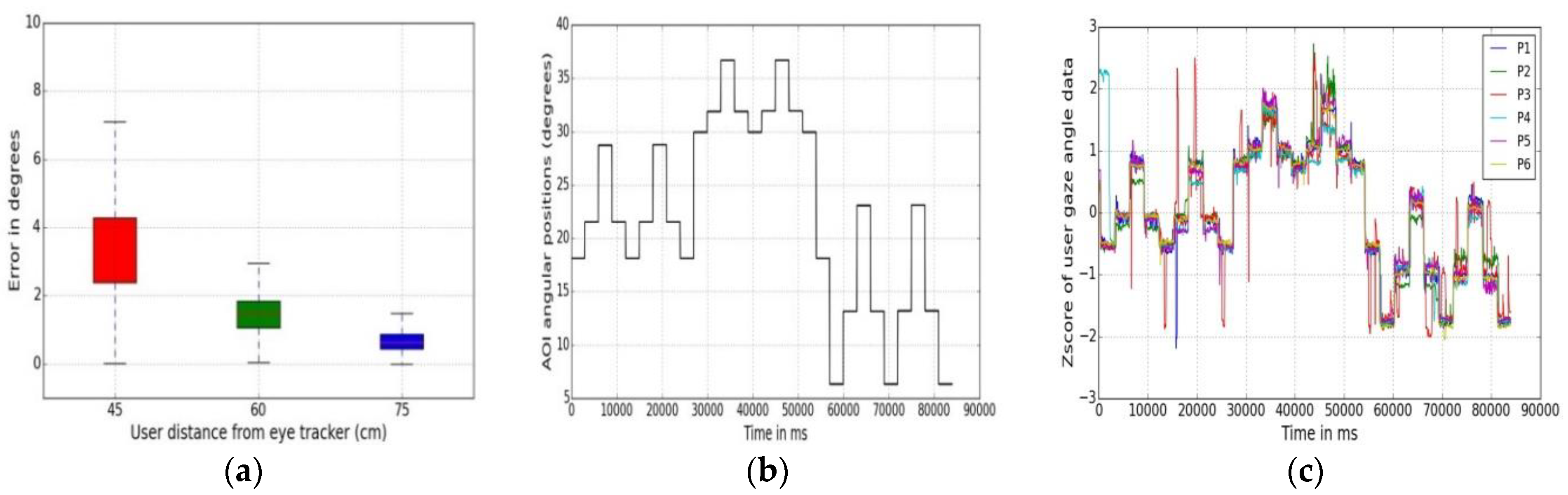
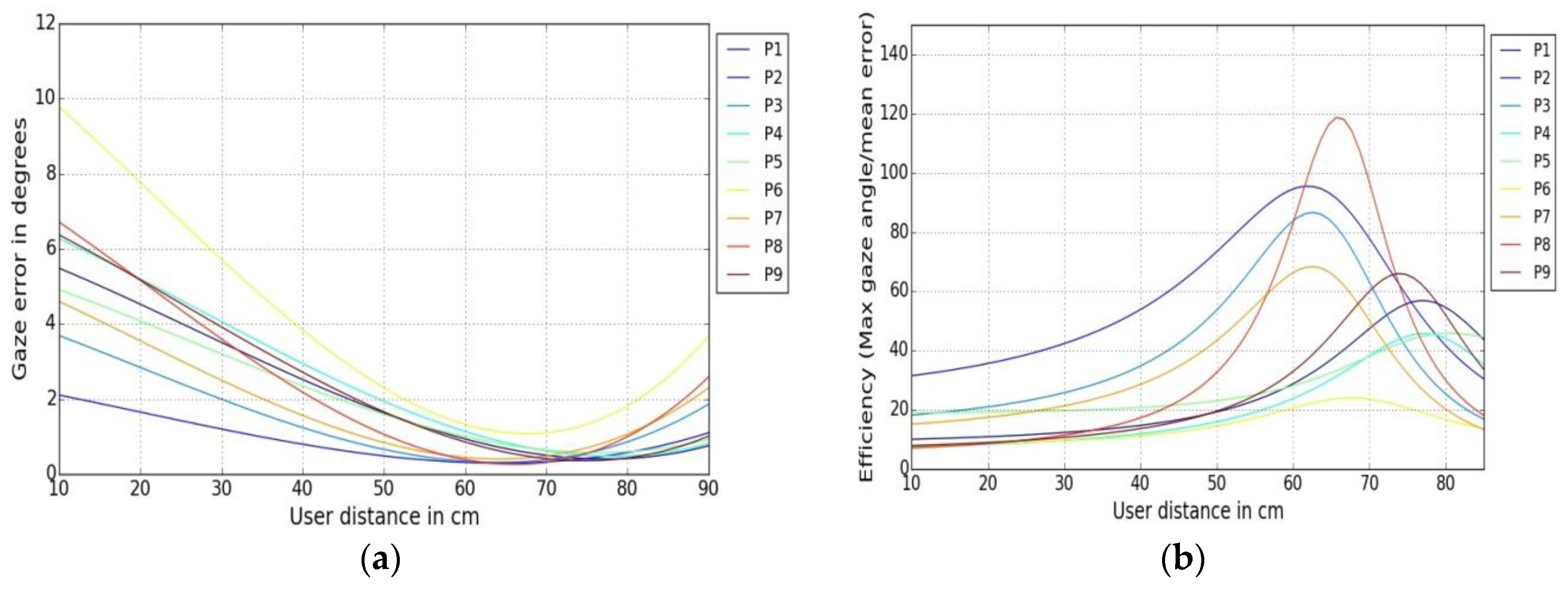
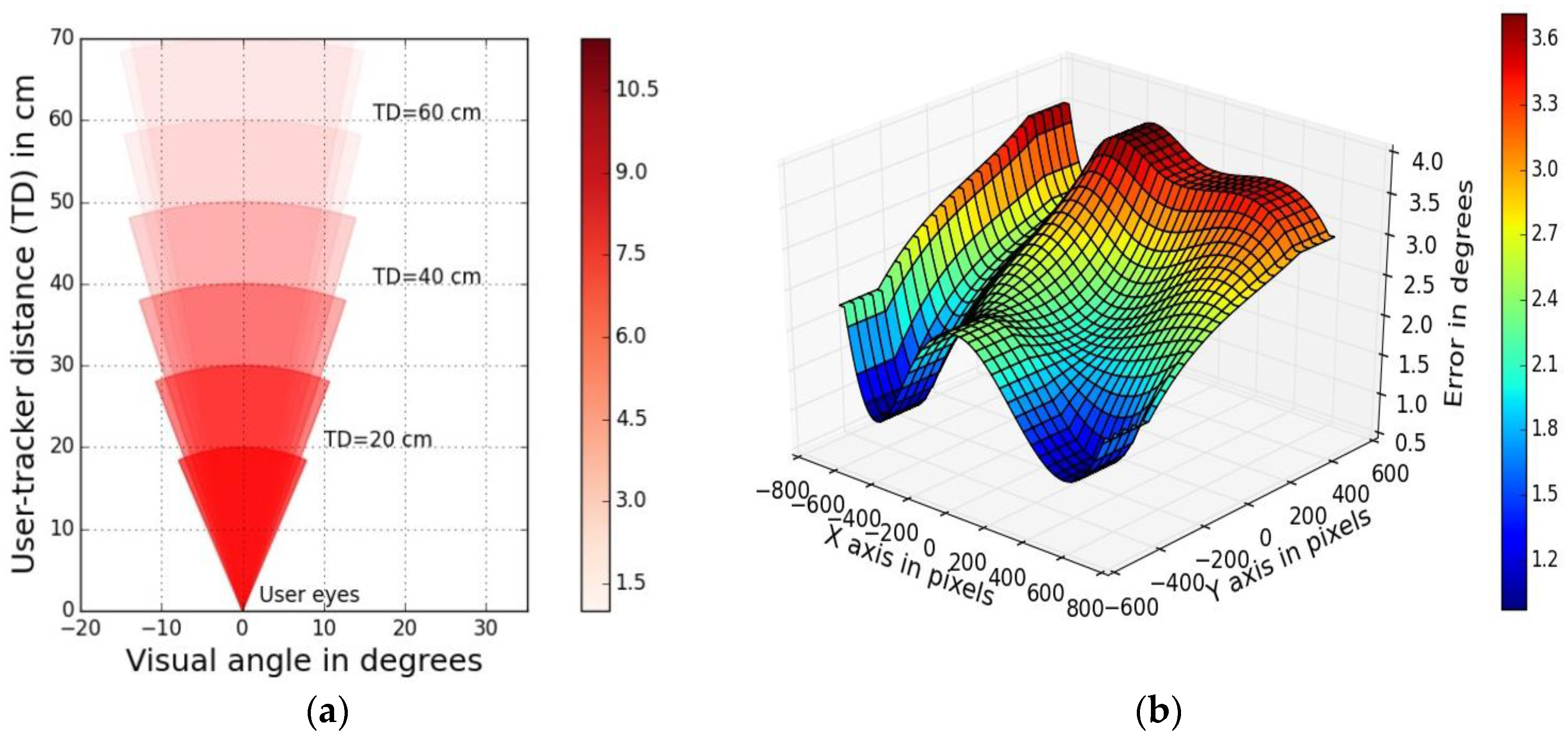
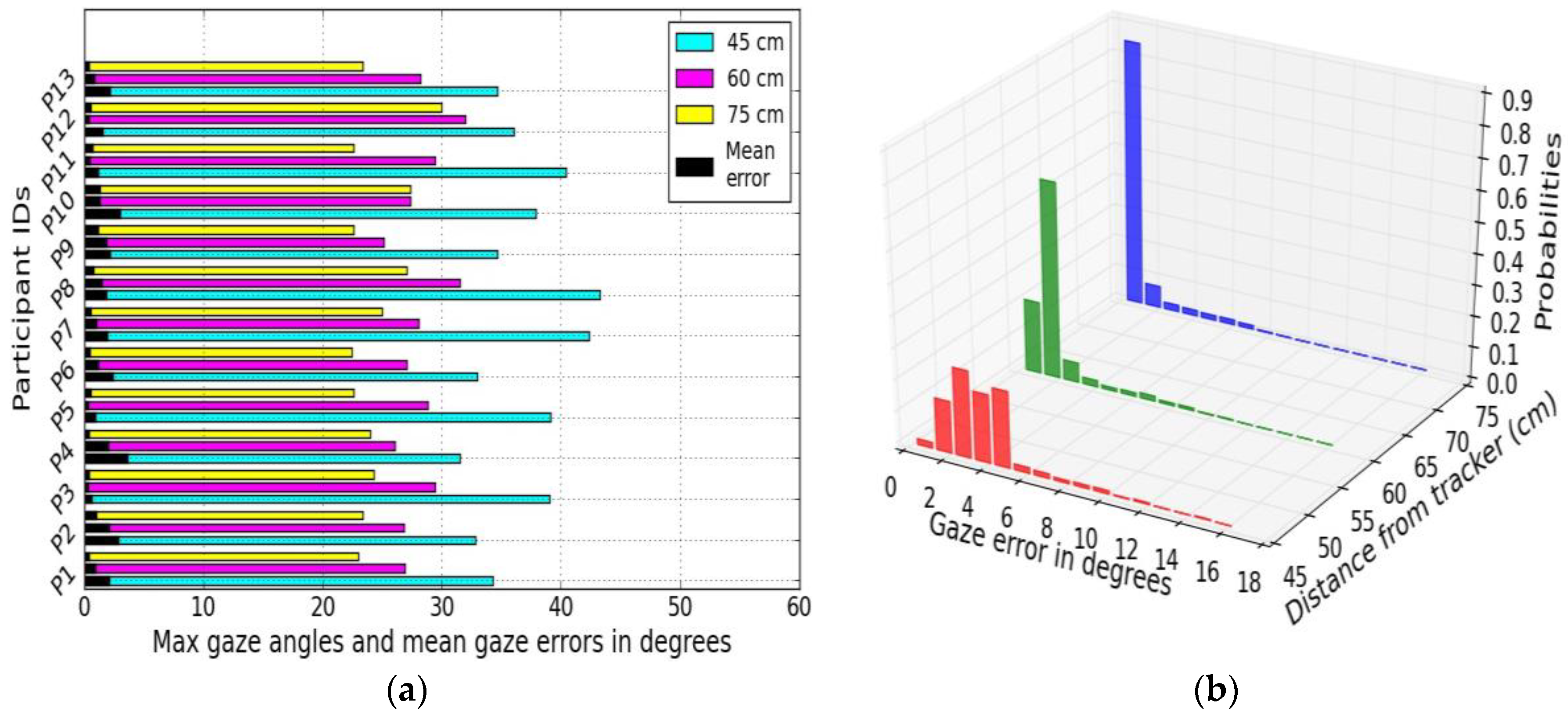
4.3.3. Gaze Tracking Efficiency (Gaze Error Sensitivity to User Distance and Gaze Angle)
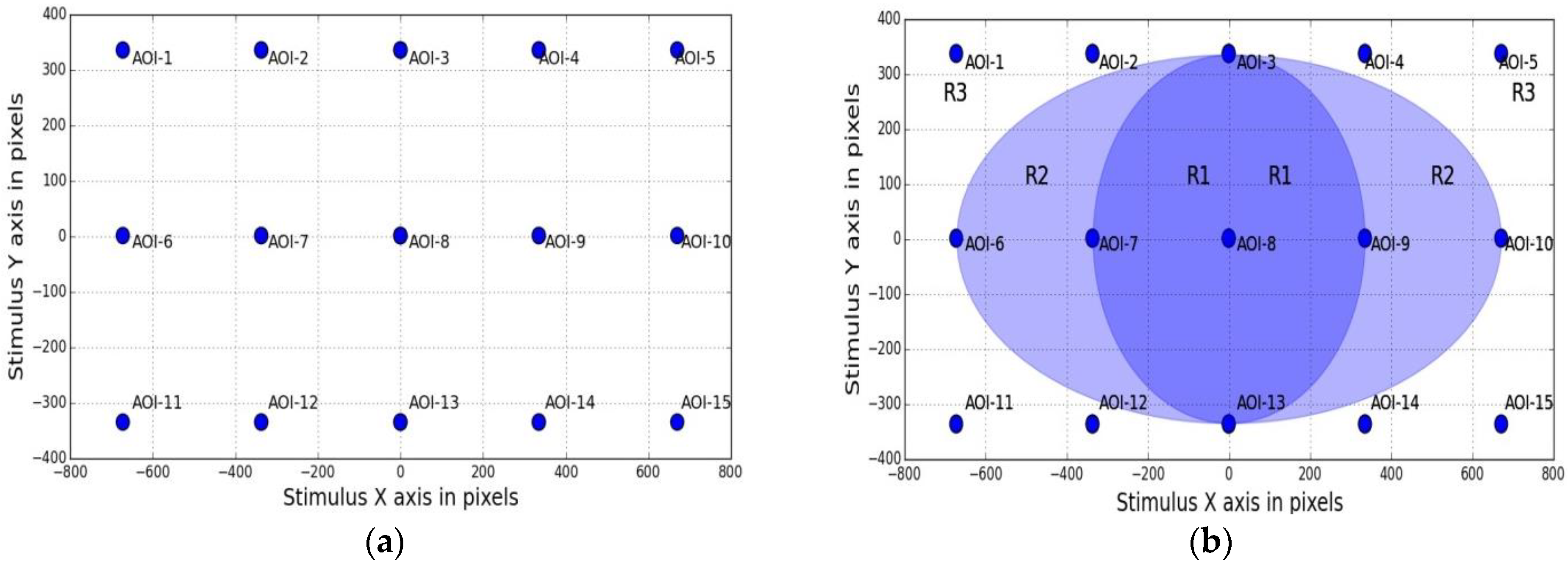
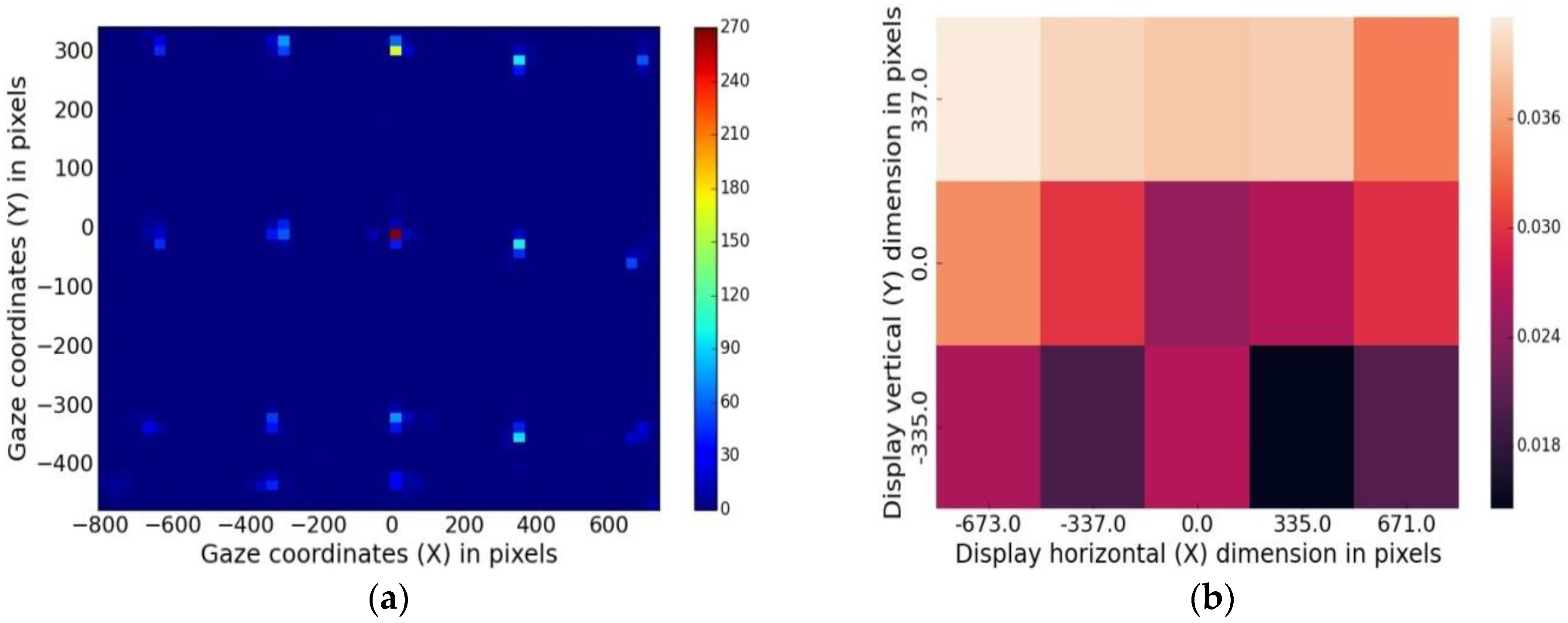
4.3.4. Error Spatial Density (Sensitivity to Spatial Locations of Targets on the Display)
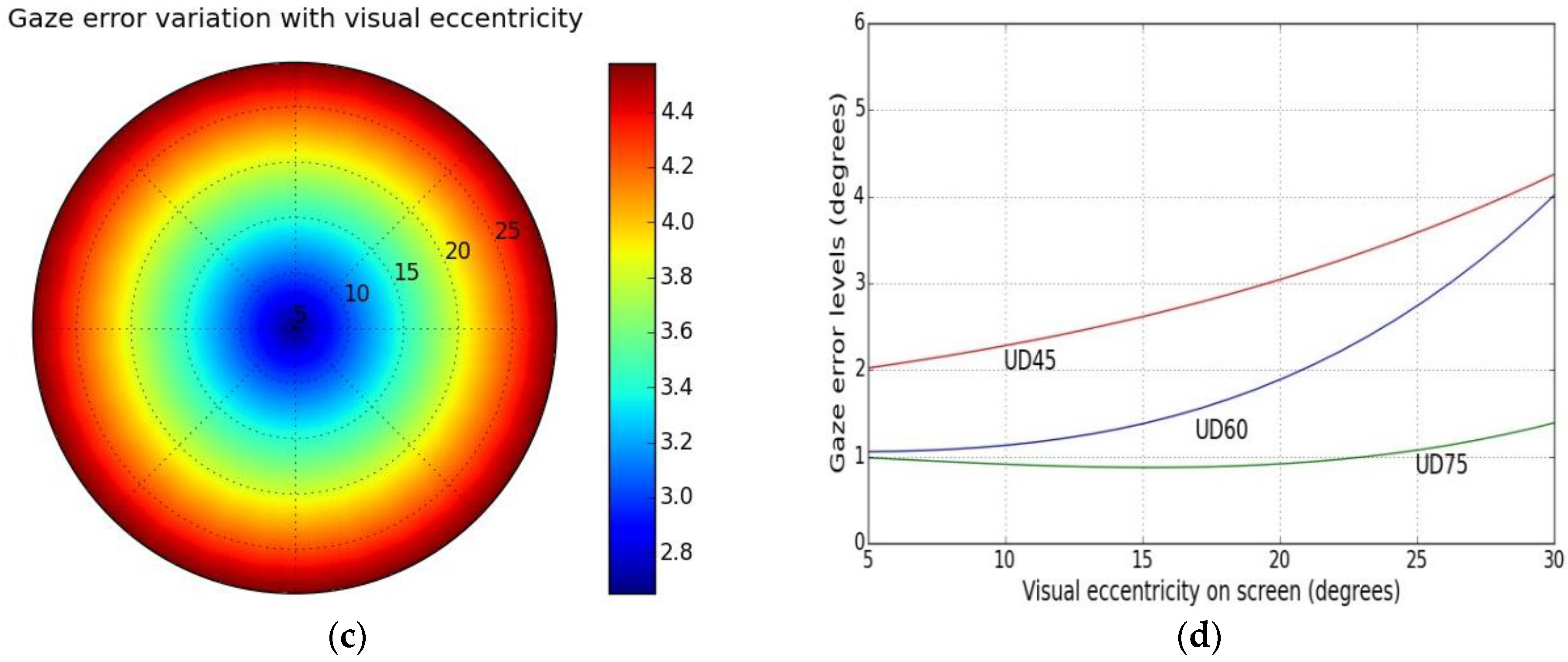
4.4. Gaze Error Analysis with Respect to Visual Eccentricity
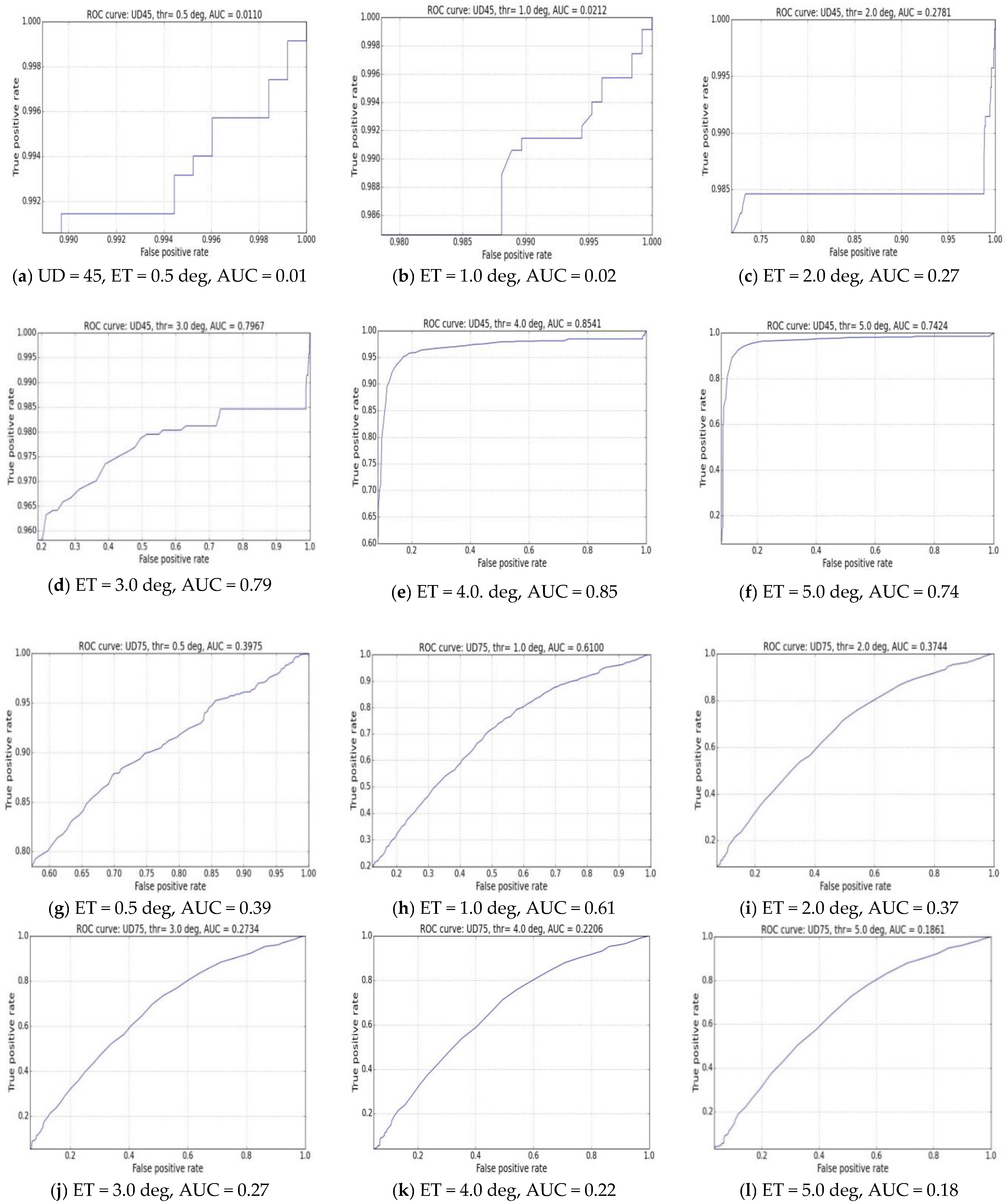
4.5. The ROC Metric: Diagnostic or Subjective Performance Evaluation of Eye Tracking Systems
- The predicted value for a data point is positive if gaze error for that point > ET
- The actual value for a data point is positive if gaze error for that point < M
- The predicted value for a data point is negative if gaze error for that point < ET
- The actual value for a data point is negative if gaze error for that point > M
4.6. Discussion
5. Visualizations for Evaluating Gaze Estimation Systems
5.1. Plots for Data Visualization from Single Eye Tracking Experiments
5.1.1. Data Density Maps
5.1.2. Spatial Error Heat Maps
5.1.3. Gaze Error vs. Visual Field
5.1.4. 3D Gaze Error Distribution Plot
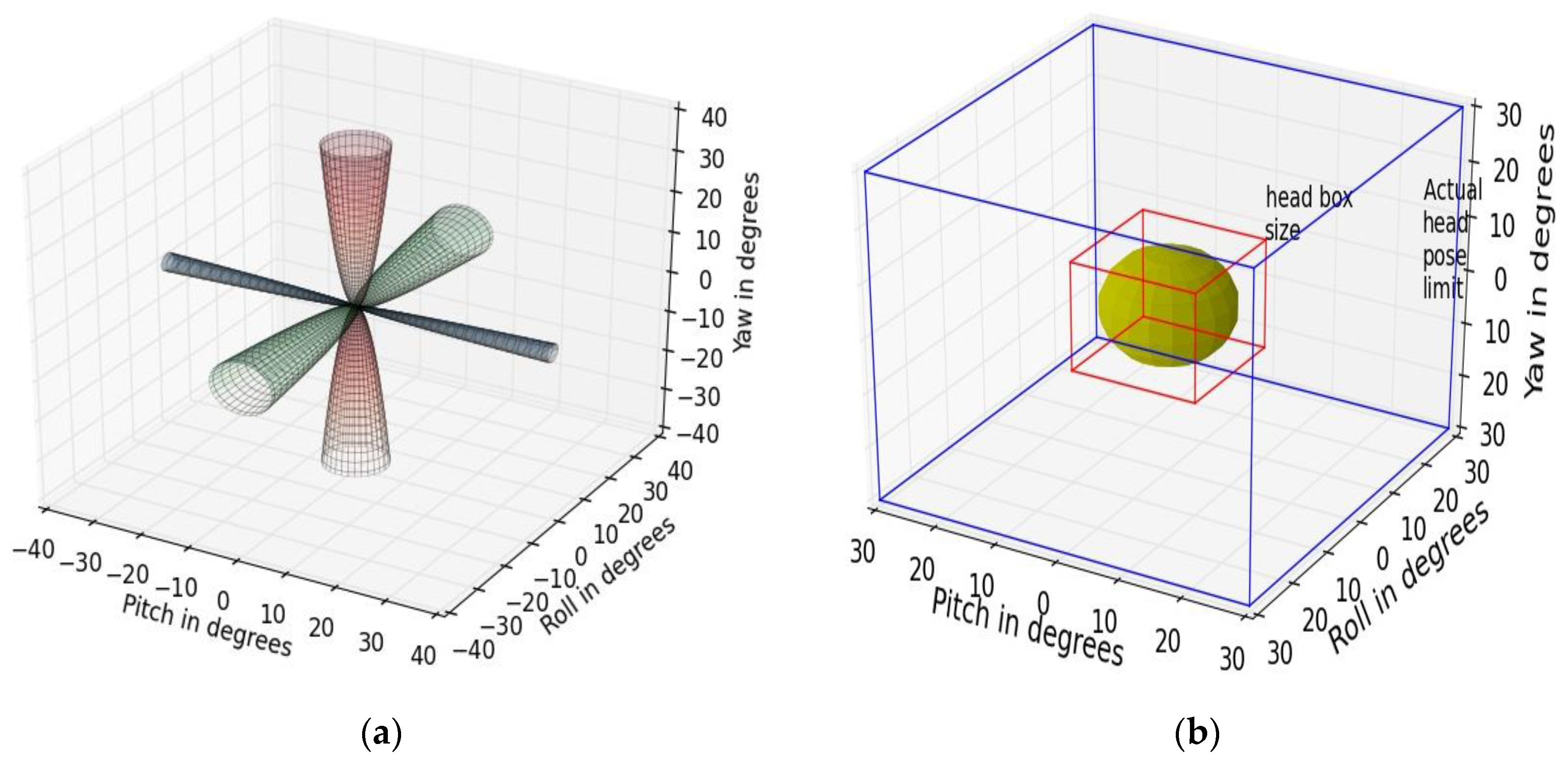
5.1.5. Platform Movement Tolerance Conics
5.1.6. Head-Pose Tolerance Box
5.2. Plots for Data Aggregation from Multiple Eye Tracking Experiments
5.2.1. Stacked Multi-Graphs
5.2.2. Stacked Distributions
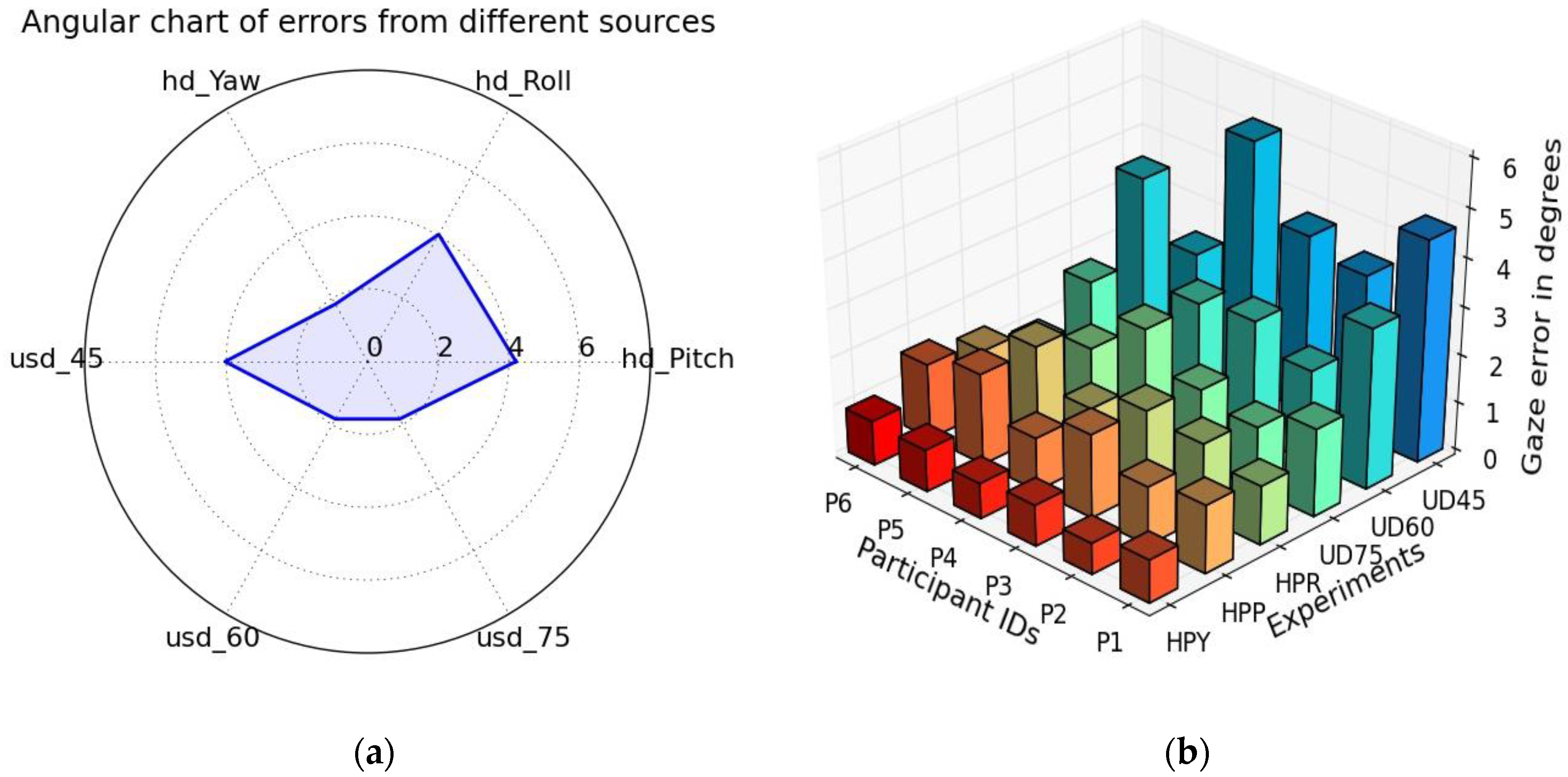
5.2.3. Angular Error Charts for Multiple Experimental Variables
5.2.4. 3D Bar Clusters
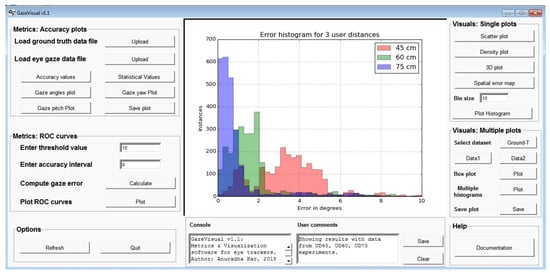
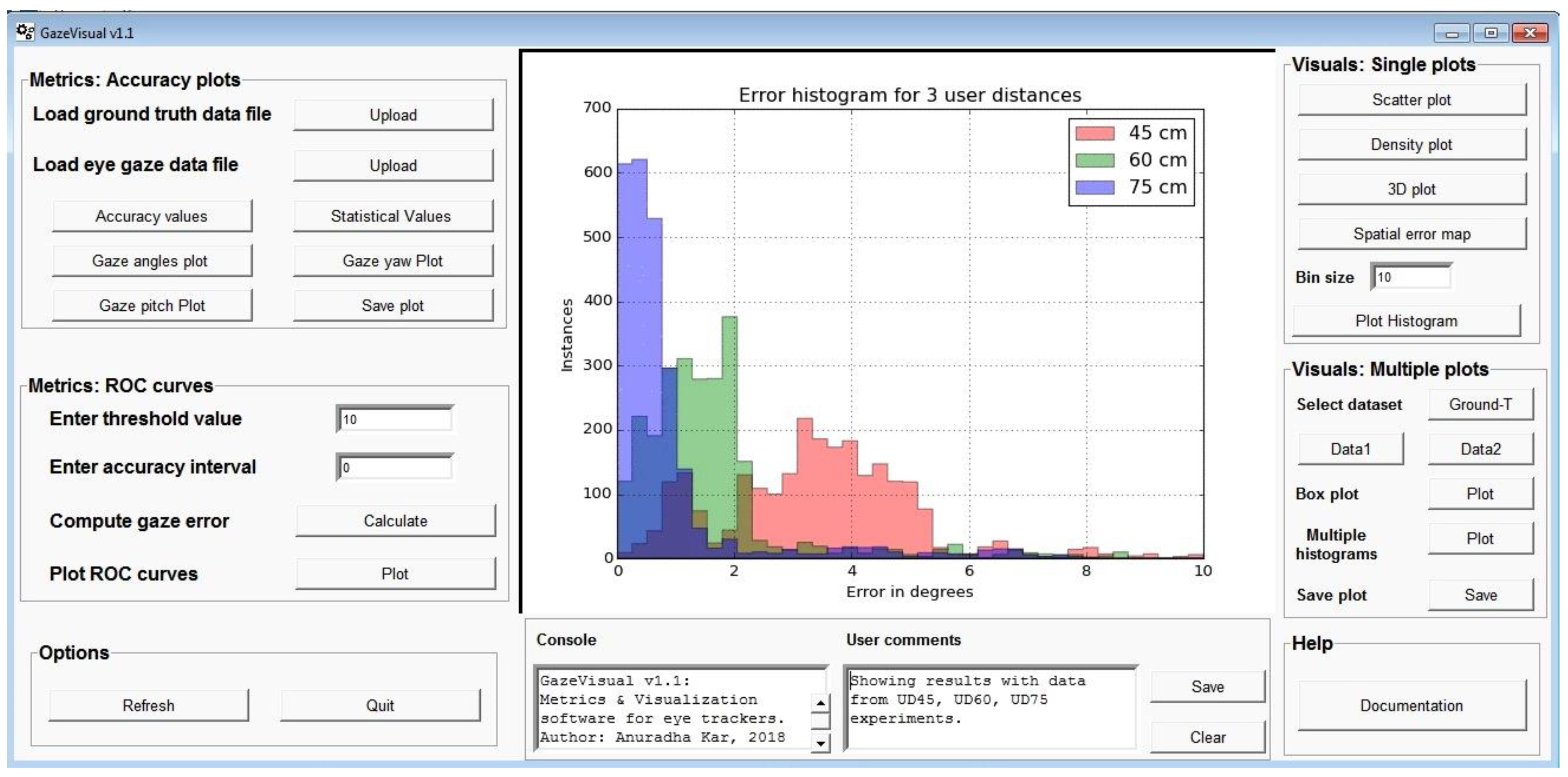
5.3. GazeVisual v1.1: Concept of a Performance Evaluation Tool for Eye Trackers
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kar, A.; Corcoran, P. A Review and Analysis of Eye-Gaze Estimation Systems, Algorithms and Performance Evaluation Methods in Consumer Platforms. IEEE Access 2017, 5, 16495–16519. [Google Scholar] [CrossRef]
- Bulling, A.; Alt, F.; Schmidt, A. Increasing the security of gaze-based cued-recall graphical passwords using saliency masks. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI ‘12), Austin, TX, USA, 5–10 May 2012; ACM: New York, NY, USA, 2012; pp. 3011–3020. [Google Scholar]
- Wood, E.; Bulling, A. EyeTab: Model-based gaze estimation on unmodified tablet computers. In Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA ‘14), Safety Harbor, FL, USA, 26–28 March 2014; ACM: New York, NY, USA, 2014; pp. 207–210. [Google Scholar] [CrossRef]
- Kern, D.; Mahr, A.; Castronovo, S.; Schmidt, A.; Müller, C. Making use of drivers’ glances onto the screen for explicit gaze-based interaction. In Proceedings of the 2nd International Conference on Automotive User Interfaces and Interactive Vehicular Applications (AutomotiveUI ‘10), Pittsburgh, PA, USA, 11–12 November 2010; ACM: New York, NY, USA, 2010; pp. 110–116. [Google Scholar]
- Meissner, M.; Pfeiffer, J.; Pfeiffer, T.; Oppewal, H. Combining Virtual Reality and Mobile Eye Tracking to Provide a Naturalistic Experimental Environment for Shopper Research. J. Bus. Res. 2018. [Google Scholar] [CrossRef]
- Corcoran, P.M.; Nanu, F.; Petrescu, S.; Bigioi, P. Real-time eye gaze tracking for gaming design and consumer electronics systems. IEEE Trans. Consum. Electron. 2012, 58, 347–355. [Google Scholar] [CrossRef]
- Morimoto, C.H.; Mimica, M.R.M. Eye gaze tracking techniques for interactive applications. Comput. Vis. Image Underst. 2005, 98, 4–24. [Google Scholar] [CrossRef]
- Lee, H.C.; Luong, D.T.; Cho, C.W.; Lee, E.C.; Park, K.R. Gaze tracking system at a distance for controlling IPTV. IEEE Trans. Consum. Electron. 2010, 56, 2577–2583. [Google Scholar] [CrossRef]
- Pfeiffer, J.; Pfeiffer, T.; Greif-Winzrieth, A.; Meissner, M.; Renner, P.; Weinhardt, C. Adapting Human-Computer-Interaction of Attentive Smart Glasses to the Trade-Off Conflict in Purchase Decisions: An Experiment in a Virtual Supermarket. In Proceedings of the International Conference on Augmented Cognition: Neurocognition and Machine Learning, Vancouver, BC, Canada, 9–14 July 2017; pp. 219–235. [Google Scholar]
- Pfeiffer, J.; Meißner, M.; Prosiegel, J.; Pfeiffer, T. Classification of goal-directed search and exploratory search using mobile eye-tracking. In Proceedings of the International Conference on Information Systems (ICIS 2014), Auckland, New Zealand, 14–17 December 2014. [Google Scholar]
- Hansen, D.W.; Ji, Q. In the Eye of the Beholder: A Survey of Models for Eyes and Gaze. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 478–500. [Google Scholar] [CrossRef] [PubMed]
- Ruhland, K.; Peters, C.E.; Andrist, S.; Badler, J.B.; Badler, N.I.; Gleicher, M.; Mutlu, B.; McDonnell, R. A review of eye gaze in virtual agents social robotics and HCI: Behaviour generation user interaction and perception. Comput. Gr. Forum 2015. [Google Scholar] [CrossRef]
- Holmqvist, K.; Nyström, M.; Mulvey, F. Eye tracker data quality: What it is and how to measure it. In Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA ‘12), Santa Barbara, CA, USA, 28–30 March 2012; ACM: New York, NY, USA, 2012; pp. 45–52. [Google Scholar]
- Reingold, E.M. Eye Tracking Research and Technology: Towards Objective Measurement of Data Quality. Vis. Cognit. 2014, 22, 635–652. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.M.; Jacobs, R.A.; Tarduno, J.A.; Pelz, J.B. Collecting and Analyzing Eye-Tracking Data in Outdoor Environments. J. Eye Mov. Res. 2012, 5, 1–19. [Google Scholar]
- Špakov, O. Defining Standard Gaze Tracking API. In Proceedings of the CHI 2013 Workshop on “Gaze Interaction in the Post-WIMP World”, Paris, France, 27 April–2 May 2013; pp. 1–4. [Google Scholar]
- Kar, A.; Corcoran, P. Towards the development of a standardized performance evaluation framework for eye gaze estimation systems in consumer platforms. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 2061–2066. [Google Scholar]
- Mora, K.A.F.; Monay, F.; Odobez, J. Eyediap: A Database for the Development and Evaluation of Gaze Estimation Algorithms from RGB and RGB-D Cameras. In Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA ‘14), Safety Harbor, FL, USA, 26–28 March 2014; ACM: New York, NY, USA, 2014; pp. 255–258. [Google Scholar]
- Pfeiffer, T. Towards Gaze Interaction in Immersive Virtual Reality: Evaluation of a Monocular Eye Tracking Set-Up. In Virtuelle und Erweiterte RealitatFunfter Work. der Gifachgr; Shaker Verlag GmbH: Aachen, Germany, 2008; pp. 81–92. [Google Scholar]
- Ooms, K.; Lapon, L.; Dupont, L.; Popelka, S. Accuracy and precision of fixation locations recorded with the low-cost Eye Tribe tracker in different experimental set-ups. J. Eye Mov. Res. 2015, 8, 1–24. [Google Scholar]
- Popelka, S.; Stachoň, Z.; Šašinka, Č.; Doležalová, J. EyeTribe tracker data accuracy evaluation and its interconnection with hypothesis software for cartographic purposes. Comput. Intell. Neurosci. 2016, 2016. [Google Scholar] [CrossRef] [PubMed]
- Funke, G.; Greenlee, E.; Carter, M.; Dukes, A.; Brown, R.; Menke, L. Which eye tracker is right for your research? Performance evaluation of several cost variant eye trackers. In Proceedings of the Human Factors and Ergonomics Society 2016 Annual Meeting, Washington, DC, USA, 19–23 September 2016; pp. 1239–1243. [Google Scholar]
- Mannaru, P.; Balasingam, B.; Pattipati, K.; Sibley, C.; Coyne, J.T. Performance Evaluation of the Gazepoint GP3 Eye Tracking Device Based on Pupil Dilation. In Augmented Cognition: Neurocognition and Machine Learning; Schmorrow, D., Fidopiastis, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10284, pp. 166–175. [Google Scholar]
- Gibaldi, A.; Vanegas, M.; Bex, P.J.; Maiello, G. Evaluation of the Tobii EyeX Eye tracking controller and Matlab toolkit for research. Behav. Res. Methods 2017, 49, 923–946. [Google Scholar] [CrossRef] [PubMed]
- Blascheck, T.; Kurzhals, K.; Raschke, M.; Burch, M.; Weiskopf, D.; Ertl, T. State-of-the-art of visualization for eye tracking data. Proceedings of Eurographics Conference on Visualization (EuroVis), Swansea, UK, 9–13 June 2014; pp. 63–82. [Google Scholar]
- Špakov, O.; Miniotas, D. Visualization of eye gaze data using heat maps. Electron. Electr. Eng. 2007, 2, 55–58. [Google Scholar]
- Maurus, M.; Hammer, J.H.; Beyerer, J. Realistic heatmap visualization for interactive analysis of 3D gaze data. In Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA ‘14), 14–18 March 2014; ACM: New York, NY, USA, 2014; pp. 295–298. [Google Scholar]
- Duchowski, A.T.; Price, M.M.; Meyer, M.; Orero, P. Aggregate gaze visualization with real-time heatmaps. In Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA ‘12), Santa Barbara, CA, USA, 28–30 March 2012; ACM: New York, NY, USA, 2012; pp. 13–20. [Google Scholar]
- Tula, A.D.; Kurauchi, A.; Coutinho, F.; Morimoto, C. Heatmap explorer: An interactive gaze data visualization tool for the evaluation of computer interfaces. In Proceedings of the 15th Brazilian Symposium on Human Factors in Computer Systems, IHC’16, 4–7 October 2016; ACM: New York, NY, USA, 2016; Volume 24, pp. 1–9. [Google Scholar]
- Kurzhals, K.; Hlawatsch, M.; Heimerl, F.; Burch, M.; Ertl, T.; Weiskopf, D. Gaze Stripes: Image-Based Visualization of Eye Tracking Data. IEEE Trans. Vis. Comput. Gr. 2016, 22, 1005–1014. [Google Scholar] [CrossRef] [PubMed]
- Burch, M.; Kumar, A.; Mueller, K.; Weiskopf, D. Color bands: Visualizing dynamic eye movement patterns. In Proceedings of the 2016 IEEE Second Workshop on Eye Tracking and Visualization (ETVIS), Baltimore, MD, USA, 23 October 2016; pp. 40–44. [Google Scholar]
- Kurzhals, K.; Hlawatsch, M.; Seeger, C.; Weiskopf, D. Visual Analytics for Mobile Eye Tracking. IEEE Trans. Vis. Comput. Gr. 2017, 23, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Anderson, N.C.; Anderson, F.; Kingstone, A.; Bischof, W.F. A comparison of scanpath comparison methods. Behav. Res. Methods 2014, 47, 1377–1392. [Google Scholar] [CrossRef] [PubMed]
- Raschke, M.; Chen, X.; Ertl, T. Parallel scan-path visualization. In Proceedings of the Symposium on Eye Tracking Research and Applications (ETRA ‘12), Santa Barbara, CA, USA, 28–30 March 2012; ACM: New York, NY, USA, 2012; pp. 165–168. [Google Scholar]
- Pfeiffer, T.; Memili, C. Model-based real-time visualization of realistic three-dimensional heat maps for mobile eye tracking and eye tracking in virtual reality. In Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research & Applications (ETRA ‘16), Charleston, SC, USA, 14–17 March 2016; ACM: New York, NY, USA, 2016; pp. 95–102. [Google Scholar]
- Voßkühler, A.; Nordmeier, V.; Kuchinke, L. OGAMA (Open Gaze and Mouse Analyzer): Open-source software designed to analyze eye and mouse movements in slideshow study designs. Behav. Res. Methods 2008, 40, 1150. [Google Scholar] [CrossRef] [PubMed]
- Netzel, R.; Weiskopf, D. Hilbert attention maps for visualizing spatiotemporal gaze data. In Proceedings of the 2016 IEEE Second Workshop on Eye Tracking and Visualization (ETVIS), Baltimore, MD, USA, 23 October 2016; pp. 21–25. [Google Scholar]
- Drusch, G.; Bastien, J.C.; Paris, S. Analysing eye-tracking data: From scanpaths and heatmaps to the dynamic visualisation of areas of interest. Adv. Sci. Technol. Higher Educ. Soc. Concept. Age 2014, 20, 205. [Google Scholar]
- Choi, J.; Oh, T.; Kweon, I.S. Human attention estimation for natural images: An automatic gaze refinement approach. arXiv, 2016; arXiv:1601.02852. [Google Scholar]
- Quaia, C.; Optican, L.M. Three-dimensional rotations of the eye. In Adler’s Physiology of the Eye: Clinical Application, 10th ed.; Kaufman, P.L., Alm, A., Eds.; Mosby: New York, NY, USA, 2002; pp. 818–829. [Google Scholar]
- Schor, C.M.; Maxwell, J.S.; Stevenson, S.B. Isovergence surfaces: The conjugacy of vertical eye movements in tertiary positions of gaze. Ophthalmic Physiol. Opt. 1994, 14, 279–286. [Google Scholar] [CrossRef] [PubMed]
- Haslwanter, T. Mathematics of three-dimensional eye rotations. Vision Res. 1995, 35, 1727–1739. [Google Scholar] [CrossRef]
- Tobii, Accuracy and Precision, Test Report, Tobii T60 XL Eye Tracker. 2011. Available online: http://www.tobii.com/ (accessed on 8 August 2018).
- Sheldon, M.R. Introductory Statistics, 4th ed.; Elsevier: Cambridge, MA, USA, 2017. [Google Scholar]
- Imamura, K.; Kuroda, H.; Fujimura, M. Criterial image preparation for a search method for digital watermarking image using correlation coefficient between pixel value histograms. In Proceedings of the 2013 9th International Conference on Information, Communications & Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar]
- Jiang, Q.-r.; Gao, Y. Face recognition based on Detail Histogram Intersection kernel. In Proceedings of the IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; pp. 71–74. [Google Scholar]
- Mahalingam, T.; Mahalakshmi, M. Vision based moving object tracking through enhanced color image segmentation using Haar classifiers. In Proceedings of the Trendz in Information Sciences & Computing (TISC2010), Chennai, India, 17–19 December 2010; pp. 253–260. [Google Scholar]
- Hansen, D.W.; San Agustin, J.; Villanueva, A. Homography normalization for robust gaze estimation in uncalibrated setups. In Proceedings of the 2010 Symposium on Eye-Tracking Research & Applications (ETRA ‘10), Austin, TX, USA, 22–24 March 2010; ACM: New York, NY, USA, 2010; pp. 13–20. [Google Scholar]
- Mantiuk, R.; Kowalik, M.; Nowosielski, A.; Bazyluk, B. Do-It-Yourself Eye Tracker: Low-Cost Pupil-Based Eye Tracker for Computer Graphics Applications. Adv. Multimed. Model. 2012, 7131, 115–125. [Google Scholar]
- Narcizo, F.B.; Hansen, D.W. Depth Compensation Model for Gaze Estimation in Sport Analysis. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 13–16 December 2015; pp. 788–795. [Google Scholar]
- Metz, C.E. Basic principles of ROC analysis. In Seminars in Nuclear Medicine; WB Saunders: Philadelphia, PA, USA, 1978; Volume 8, pp. 283–298. [Google Scholar]
- Turner, D.A. An intuitive approach to receiver operating chararcteristic curve analysis. J. Nucl Med. 1978, 19, 213–220. [Google Scholar] [PubMed]
- Park, S.H.; Goo, J.M.; Jo, C.-H. Receiver Operating Characteristic (ROC) Curve: Practical Review for Radiologists. Korean J. Radiol. 2004, 5, 11–18. [Google Scholar] [CrossRef] [PubMed]
- T Lasko, T.A.; Bhagwat, J.G.; Zou, K.H.; Ohno-Machado, L. The use of receiver operating characteristic curves in biomedical informatics. J. Biomed. Inform. 2005, 38, 404–415. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z. ROC analysis for predictions made by probabilistic classifiers. In Proceedings of the International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 5, pp. 3119–3124. [Google Scholar]
- Blascheck, T.; Burch, M.; Meisel, T.; Schneider, T.; Mumin, S. Exploring Eye Movements with Node-Link Graph Layouts. In Proceedings of the Workshop on Eye Movements for Spatial Research (ET4S), Zurich, Switzerland, 14 January 2018. [Google Scholar]
- Poole, A.; Ball, L.J. Eye Tracking in Human Computer Interaction and Usability Research: Current Status and Future Prospects. In Encyclopedia of Human Computer Interaction; Ghaoui, C., Ed.; Idea Group Reference: Hershey, PA, USA, 2005; pp. 211–219. [Google Scholar]
- Liu, J.; Tang, T.; Wang, W.; Xu, B.; Kong, X.; Xia, F. A Survey of Scholarly Data Visualization. IEEE Access 2018, 6, 19205–19221. [Google Scholar] [CrossRef]
- Qin, X.; Luo, Y.; Tang, N.; Li, G. DeepEye: An automatic big data visualization framework. Big Data Min. Anal. 2018, 1, 75–82. [Google Scholar] [CrossRef]
- Butcher, P.W.S.; Ritsos, P.D. Building Immersive Data Visualizations for the Web. In Proceedings of the 2017 International Conference on Cyberworlds (CW), Chester, UK, 20–22 September 2017; pp. 142–145. [Google Scholar]
- Barz, M.; Daiber, F.; Bulling, A. Prediction of gaze estimation error for error-aware gaze-based interfaces. In Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research & Applications, Charleston, SC, USA, 14–17 March 2016; pp. 275–278. [Google Scholar]
- Milovanović, I. Python Data Visualization Cookbook; Packt Publishing: Birmingham, UK, November 2013; 280p. [Google Scholar]
- Keister, D.M.; Larson, D.; Dostal, J.; Baglia, J. The Radar Graph: The Development of an Educational Tool to Demonstrate Resident Competency. J. Grad. Med. Educ. 2012, 4, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Adams, C.R. Learning Python Data Visualization; Packt Publishing: Birmingham, UK, 2014. [Google Scholar]
- Meier, B. Python GUI Programming Cookbook; Packt Publishing: Birmingham, UK, 2017. [Google Scholar]


| Eye Tracking Platform | No. of Surveyed Papers | No of Papers with Metric: Degree | No. of Papers with Metric: Percentage | No. of Papers with Metric: Others (e.g., pixels, mm) |
|---|---|---|---|---|
| Desktop | 69 | 44 | 16 | 9 |
| Handheld | 21 | 3 | 9 | 9 |
| Automotive | 35 | 11 | 14 | 10 |
| Head-mounted | 57 | 37 | 2 | 18 |
| Eye Tracker and UI setup | Details | Display and Hardware Characteristics | Details | Experimental Variables |
|---|---|---|---|---|
| Tracker type | Desktop based, NIR LEDs + 1 Camera, 3 ps | Screen Size | Desktop: 22 inch Tablet: 10.1 inch | Single user, multiple user |
| Calibration | 6 point | Screen Resolution | Desktop: 1680 × 1050 Tablet: 1920 × 1200 | Fixed and variable user distance |
| Tolerance | Maximum user distance: 80 cm, spectacles allowed, chin-rest used | Screen properties | Desktop: 21.5 inch diagonal, width × height = 18.5” × 11.5” Tablet: 10.1 inch diagonal, width × height = 8.5” × 5.5” | Fixed and variable head pose |
| User interface | 15 AOI locations, AOI radius: 10 pixels | Pixel sizes of desktop and tablet screens | Desktop: 0.275 mm Tablet: 0.113 mm | Screen resolution and pixel size |
| Eye data type | Fixation, AOI duration: 3 s, blinks allowed between AOIs | Hardware details for desktop and tablet | Desktop: Core i7, 3.6 GHz, 16 GB ram Tablet: Intel Atom X5, 1.44 GHz,4 GB ram | Platform orientation |
| User Distance = 45 cm | Max Gaze Angle (degree) | Mean Error (degree) | 95% Confidence Interval |
|---|---|---|---|
| User 1 | 34.24 | 3.63 | 3.54–3.71 |
| User 2 | 32.83 | 3.96 | 3.88–4.04 |
| User 3 | 39.04 | 3.42 | 3.35–3.49 |
| User 4 | 32.99 | 4.61 | 4.51–4.70 |
| User 5 | 34.69 | 3.52 | 3.44–3.59 |
| User Distance = 75 cm | Max Gaze Angle (degree) | Mean Error (degree) | 95% Confidence Interval |
| User 1 | 22.97 | 0.91 | 0.85–0.96 |
| User 2 | 23.36 | 0.98 | 0.93–1.02 |
| User 3 | 24.28 | 0.94 | 0.89–0.99 |
| User 4 | 22.47 | 1.84 | 1.79–1.89 |
| User 5 | 23.36 | 2.08 | 2.02–2.12 |
| Similarity Metric | Datasets Taken at User Distances 45, 60, 75 cm | |||||
|---|---|---|---|---|---|---|
| 45–45 | 45–60 | 45–75 | 60–60 | 60–75 | 75–75 | |
| Correlation | 1.0 | 0.31327 | 0.18693 | 1.0 | 0.61210 | 1.0 |
| Intersection | 2457.07 | 1131.38 | 970.69 | 2502.46 | 1565.38 | 2514.01 |
| Bhattacharyya | 0.0 | 0.47526 | 0.52651 | 8.10 × 10−10 | 0.34091 | 8.10 × 10−10 |
| Eccentricity Region | User. Number | Visual Angles at 45 cm | Mean Error for 45 cm (degrees) | Visual Angles at 60 cm | Mean Error for 60 cm (degrees) | Visual Angles at 75 cm | Mean Error for 75 cm (degrees) |
|---|---|---|---|---|---|---|---|
| R1 | |||||||
| User1 | 15.47 | 2.65 | 12.5 | 1.28 | 10.04 | 1.06 | |
| User2 | 20.32 | 2.19 | 12.99 | 0.8 | 9.98 | 1.12 | |
| User3 | 15.95 | 2.16 | 13.31 | 1.27 | 10.14 | 0.96 | |
| User4 | 15.8 | 2.32 | 12.75 | 1.04 | 10.19 | 0.91 | |
| R2 | |||||||
| User1 | 25.15 | 3.6 | 20.55 | 1.54 | 16.91 | 0.96 | |
| User2 | 26.39 | 2.37 | 21.01 | 1.08 | 16.90 | 0.90 | |
| User3 | 24.83 | 3.9 | 20.18 | 1.91 | 17.16 | 0.71 | |
| User4 | 25.19 | 3.57 | 20.13 | 1.96 | 16.99 | 0.88 | |
| R3 | |||||||
| User1 | 32.10 | 4.58 | 26.08 | 2.14 | 21.70 | 1.15 | |
| User2 | 32.72 | 3.96 | 29.46 | 1.24 | 21.94 | 0.91 | |
| User3 | 32.27 | 4.41 | 25.40 | 2.82 | 21.69 | 1.16 | |
| User4 | 32.02 | 4.66 | 25.34 | 2.88 | 21.90 | 0.96 |
| Variables | Logic for Estimation |
|---|---|
| TP | Logical AND (Gaze error > ET, gaze error ≤ M) |
| FP | Logical AND (Gaze error > ET, gaze error > M) |
| TN | Logical AND (Gaze error < ET, gaze error > M) |
| FN | Logical AND (Gaze error < ET, gaze error ≤ M) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kar, A.; Corcoran, P. Performance Evaluation Strategies for Eye Gaze Estimation Systems with Quantitative Metrics and Visualizations. Sensors 2018, 18, 3151. https://doi.org/10.3390/s18093151
Kar A, Corcoran P. Performance Evaluation Strategies for Eye Gaze Estimation Systems with Quantitative Metrics and Visualizations. Sensors. 2018; 18(9):3151. https://doi.org/10.3390/s18093151
Chicago/Turabian StyleKar, Anuradha, and Peter Corcoran. 2018. "Performance Evaluation Strategies for Eye Gaze Estimation Systems with Quantitative Metrics and Visualizations" Sensors 18, no. 9: 3151. https://doi.org/10.3390/s18093151
APA StyleKar, A., & Corcoran, P. (2018). Performance Evaluation Strategies for Eye Gaze Estimation Systems with Quantitative Metrics and Visualizations. Sensors, 18(9), 3151. https://doi.org/10.3390/s18093151