Supervised PolSAR Image Classification with Multiple Features and Locally Linear Embedding
Abstract
1. Introduction
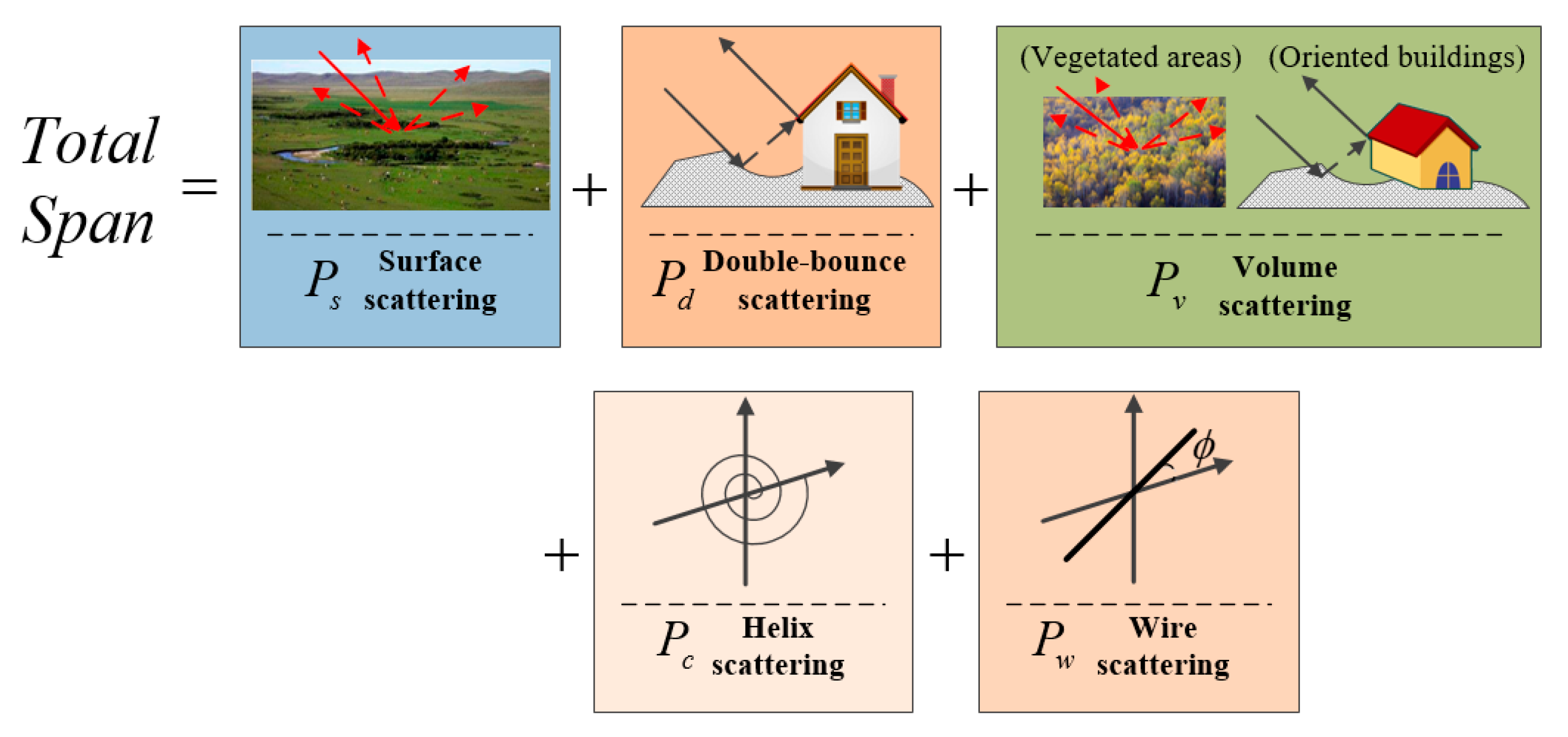
2. Decomposition Scattering Powers
2.1. Deorientation Processing of the Coherence Matrix
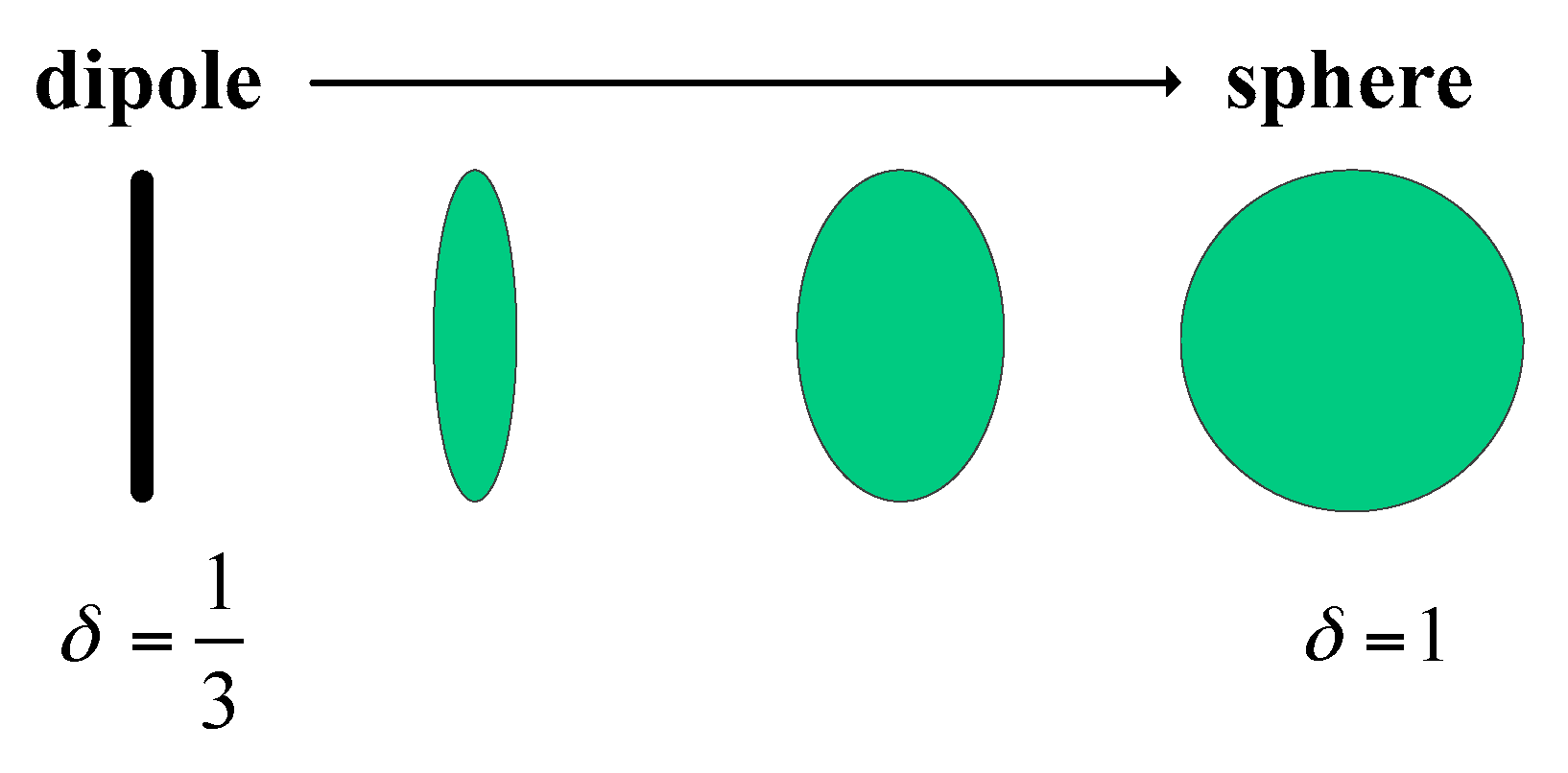
2.2. Two Different Volume Scattering Matrices
2.3. Branch Condition
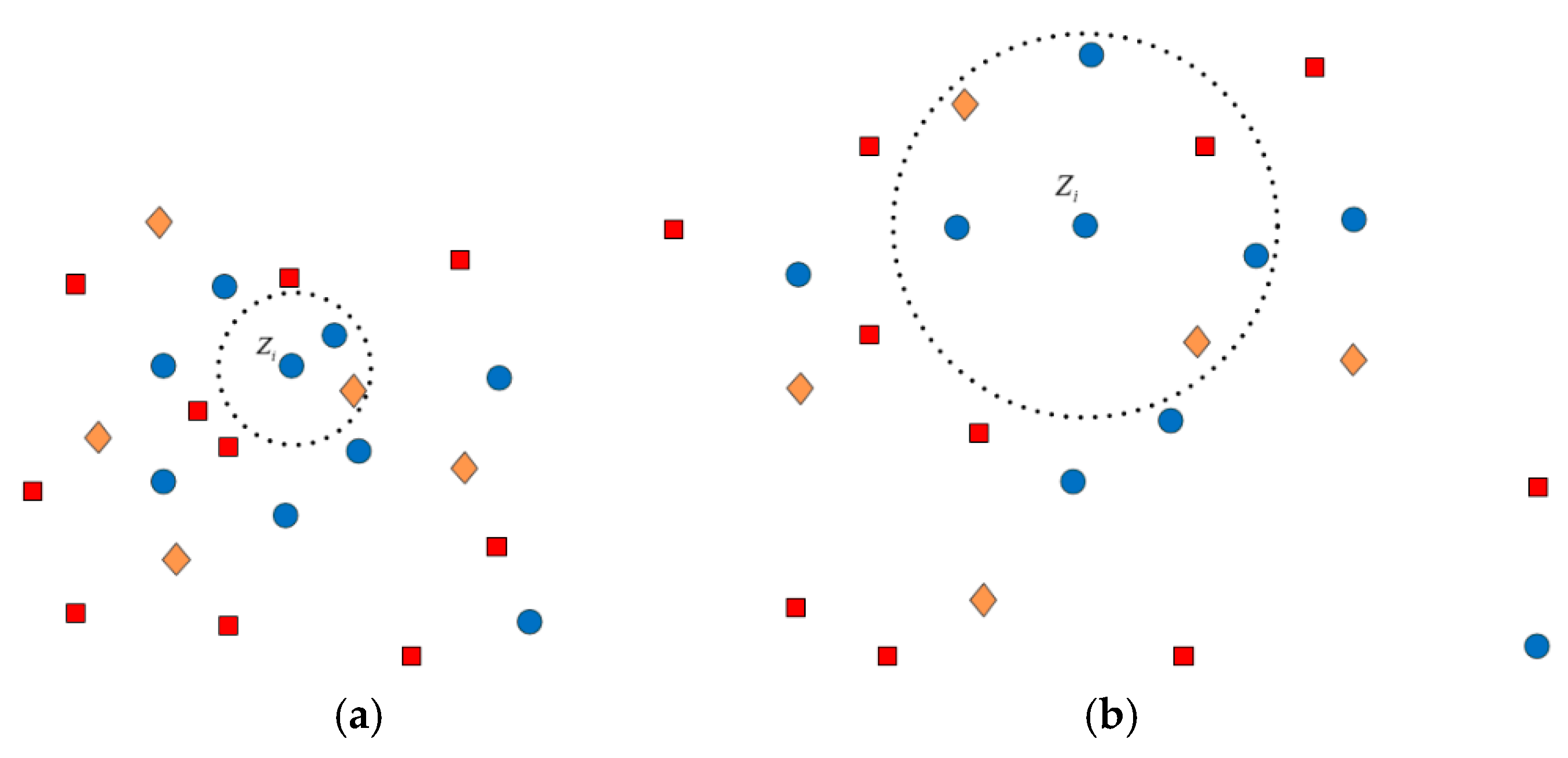
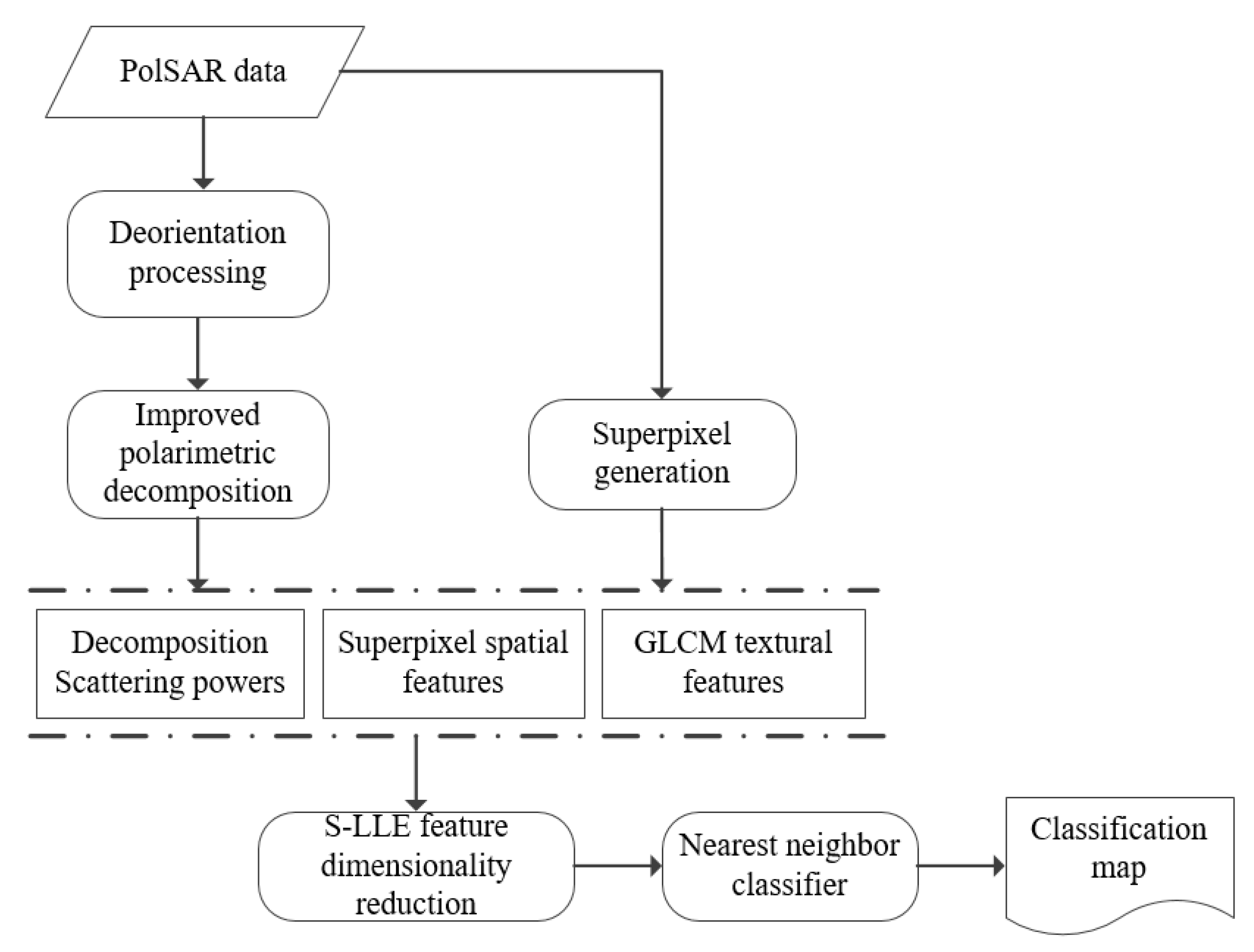
3. Superpixel Generation and Feature Extraction
4. Dimensional Reduction of the Features for PolSAR Image Classification
4.1. Estimation of the Adjacency Graph
4.2. Computation of the Weights for Neighbors
4.3. Solution of the Mapping Projections
5. Experimental Results and Discussions
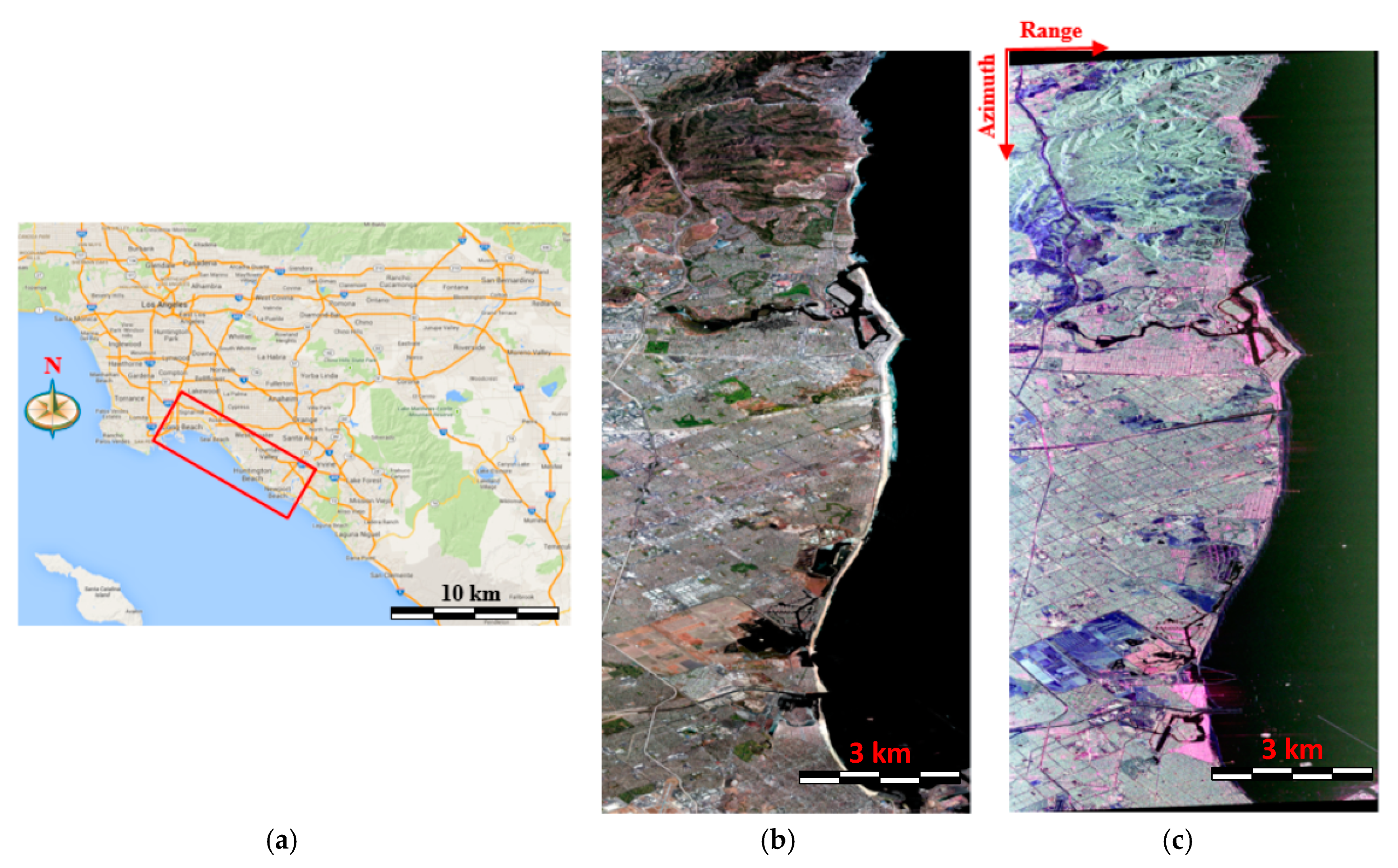
5.1. Study Area Description of AIRSAR Data with the C-Band
5.2. Illustration of the Decomposition Results
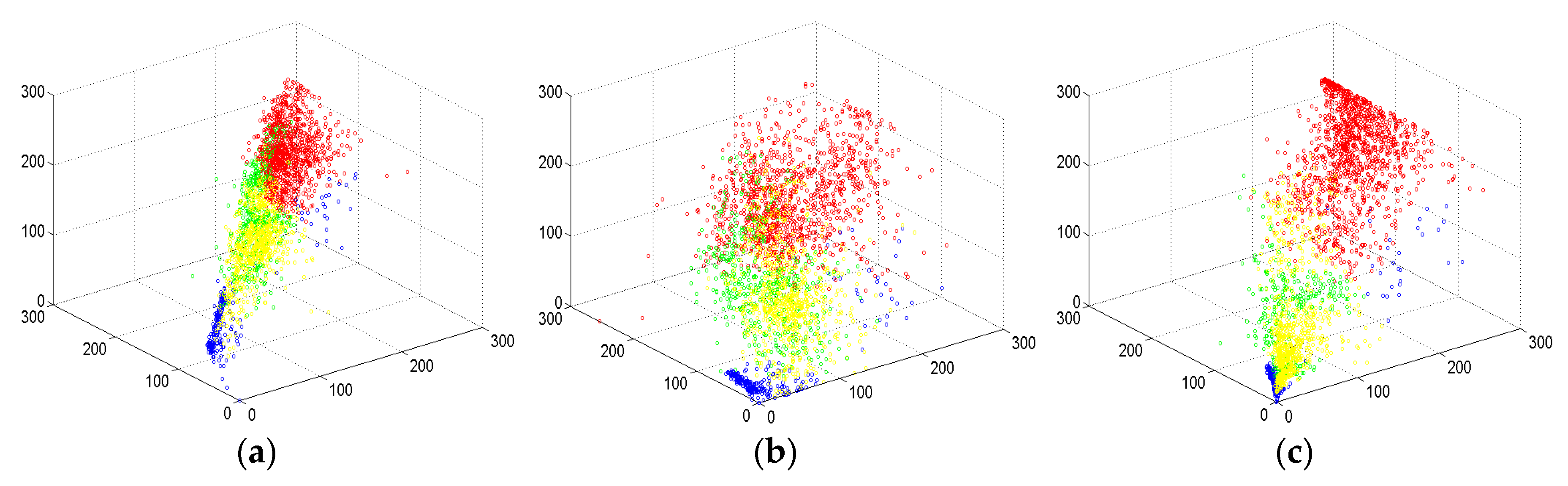
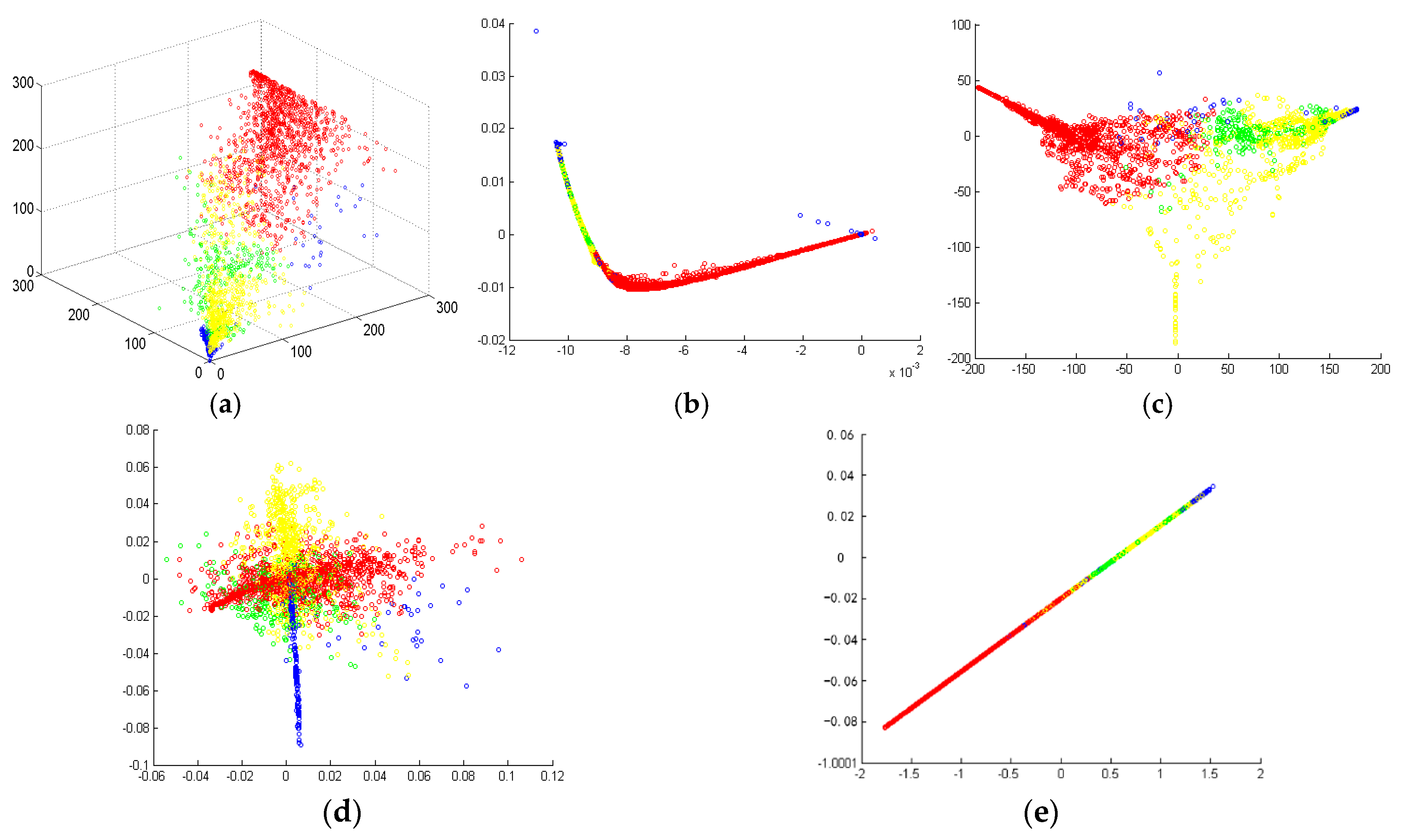
5.3. Demonstration of the Supervised S-LLE Dimensional Reduction Method
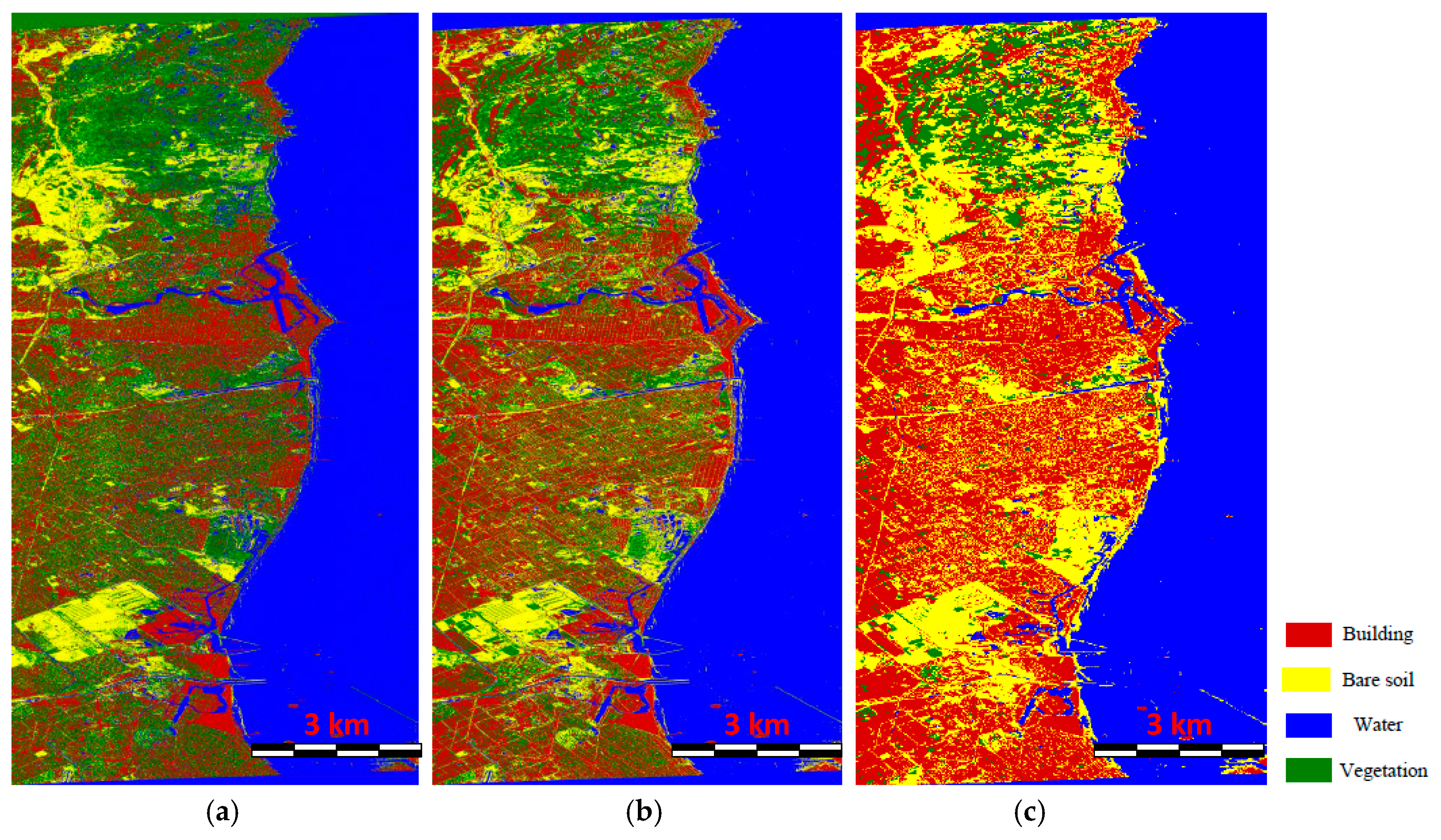
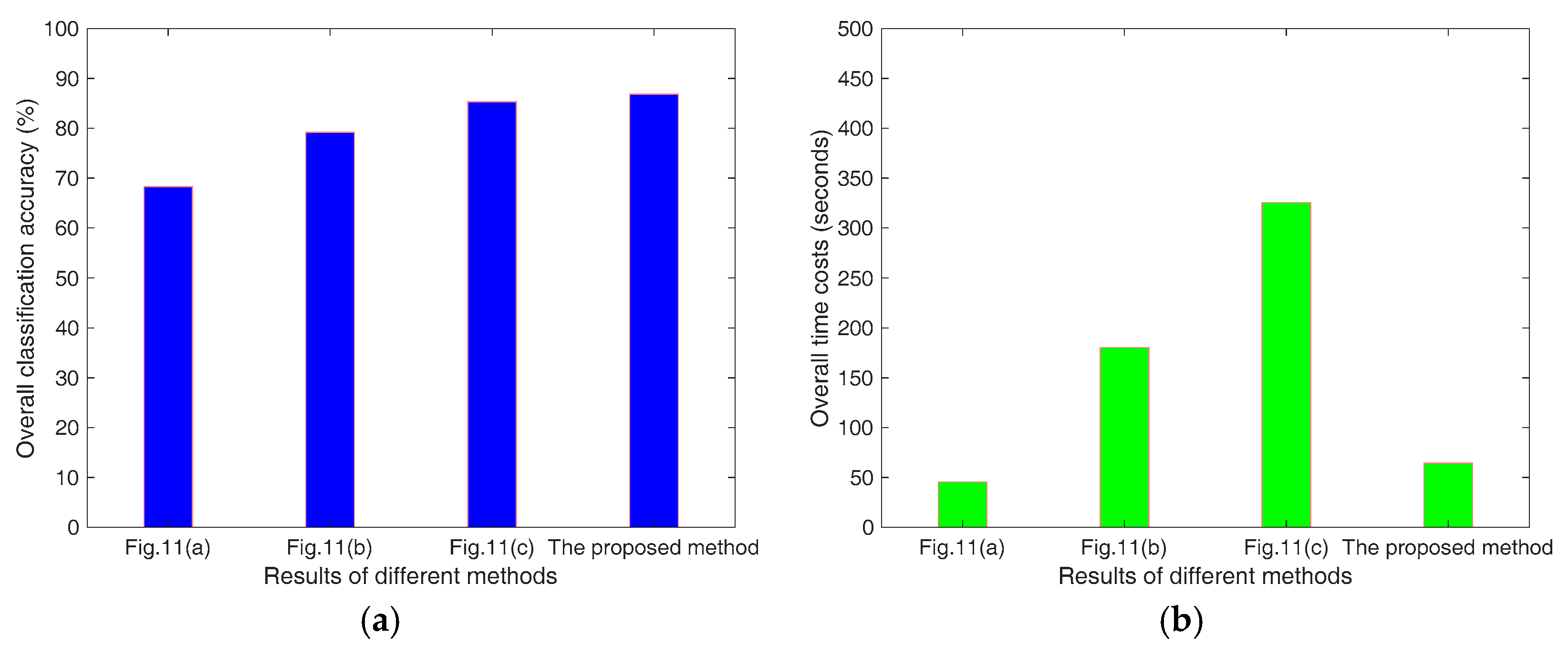
5.4. Comparison of the Classification Results Using Different Methods
5.5. Contribution Analysis of Three Components to the LULC Classification
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Niu, X.; Ban, Y. Multitemporal radarsat-2 polarimetric SAR data for urban land cover classification using an object-based support vector machine and a rule-based approach. Int. J. Remote Sens. 2013, 34, 1–26. [Google Scholar] [CrossRef]
- Kajimoto, M.; Susaki, J. Urban-area extraction from polarimetric SAR images using polarization orientation angle. IEEE Geosci. Remote Sens. Lett. 2013, 10, 337–341. [Google Scholar] [CrossRef]
- Gamba, P.; Benediktsson, J.A.; Wilkinson, G. Foreword to the special issue on urban remote sensing by satellite. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1903–1906. [Google Scholar] [CrossRef]
- Dabboor, M.; Collins, M.J.; Karathanassi, V.; Braun, A. An unsupervised classification approach for polarimetric SAR data based on the chernoff distance for complex wishart distribution. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4200–4213. [Google Scholar] [CrossRef]
- Park, S.-E.; Moon, W.M. Unsupervised classification of scattering mechanisms in polarimetric SAR data using fuzzy logic in entropy and alpha plane. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2652–2664. [Google Scholar] [CrossRef]
- Kersten, P.R.; Lee, J.-S.; Ainsworth, T.L. Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and em clustering. IEEE Trans. Geosci. Remote Sens. 2005, 43, 519–527. [Google Scholar] [CrossRef]
- Lee, J.; Grunes, M.R.; Ainsworth, T.L.; Du, L.; Schuler, D.L.; Cloude, S.R. Unsupervised classification using polarimetric decomposition and the complex wishart classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Tu, S.T.; Chen, J.Y.; Yang, W.; Sun, H. Laplacian eigenmaps-based polarimetric dimensionality reduction for SAR image classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 170–179. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.-M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, B.; Cai, H.; Zhang, Y. Multiple-component scattering model for polarimetric SAT image decomposition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 603–607. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Yajima, Y.; Yamada, H. A four-component decomposition of PolSAR images based on the coherency matrix. IEEE Geosci. Remote Sens. Lett. 2005, 3, 292–296. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Wang, S.; Liu, K.; Pei, J.; Gong, M.; Liu, Y. Unsupervised classification of fully polarimetric SAR images based on scattering power entropy and copolarized ratio. IEEE Geosci. Remote Sens. Lett. 2013, 10, 622–626. [Google Scholar] [CrossRef]
- Cao, F.; Hong, W.; Wu, Y.; Pottier, E. An unsupervised segmentation with an adaptive number of clusters using the span/h/α/a space and the complex wishart clustering for fully polarimetric SAR data analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3454–3467. [Google Scholar] [CrossRef]
- Deng, L.; Wang, C. Improved building extraction with integrated decomposition of time-frequency and entropy-alpha using polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. (JSTARS) 2014, 7, 4058–4068. [Google Scholar] [CrossRef]
- Wu, W.; Guo, H.; Li, X. Man-made target detection in urban areas based on a new azimuth stationarity extraction method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. (JSTARS) 2013, 6, 1138–1146. [Google Scholar] [CrossRef]
- Fukuda, S.; Hitosawa, H. A wavelet-based texture feature set applied to classification of multi-frequency polarimetric SAR images. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2282–2286. [Google Scholar] [CrossRef]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Lin, Z. A novel algorithm for land use and land cover classification using radarsat-2 polarimetric SAR data. Remote Sens. Environ. 2012, 118, 21–39. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, B.; Zhang, J.; Zhang, Y. Classification of polarimetric SAR image based on support vector machine using multiple-component scattering model and texture features. EURASIP J. Adv. Signal Process. 2010, 2010. [Google Scholar] [CrossRef]
- Salehi, M.; Sahebi, M.R.; Maghsoudi, Y. Improving the accuracy of urban land cover classification using radarsat-2 PolSAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1394–1401. [Google Scholar]
- Shi, L.; Zhang, L.; Yang, J.; Zhang, L.; Li, P. Supervised graph embedding for polarimetric SAR image classification. IEEE Geosci. Remote Sens. Lett. 2013, 10, 216–220. [Google Scholar] [CrossRef]
- Xiang, D.; Tang, T.; Zhao, L.; Su, Y. Superpixel generating algorithm based on pixel intensity and location similarity for SAR image classification. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1414–1418. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Wang, W.; Su, Y. Adaptive superpixel generation for polarimetric SAR images with local iterative clustering and SIRV model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3115–3131. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer Verlag: New York, NY, USA, 2002. [Google Scholar]
- Mika, S.; Ratsch, G.; Weston, J.; Scholkopf, B.; Muller, K.-R. Fisher discriminant analysis with kernels. In Proceedings of the 1999 IEEE Signal Processing Society Workshop, Madison, WI, USA, 25 August 1999; pp. 41–48. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, M.; Schwartz, E.L. The isomap algorithm and topological stability. Science 2002, 295, 7. [Google Scholar] [CrossRef] [PubMed]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Raducanu, B.; Dornaika, F. A supervised non-linear dimensionality reduction approach for manifold learning. Pattern Recognit. 2012, 45, 2432–2444. [Google Scholar] [CrossRef]
- Lee, J.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; Raton, B., Ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ainsworth, T.L.; Schuler, D.L.; Lee, J.S. Polarimetric SAR characterization of man-made structures in urban areas using normalized circular-pol correlation coefficients. Remote Sens. Environ. 2008, 112, 2876–2885. [Google Scholar] [CrossRef]
- Xiang, D.; Wang, W.; Tang, T.; Su, Y. Multiple-component polarimetric decomposition with new volume scattering models for polsar urban areas. IET Radar Sonar Navig. 2016, 11, 410–419. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Su, Y. The cross-scattering component of polarimetric SAR in urban areas and its application to model-based scattering decomposition. Int. J. Remote Sens. 2016, 37, 3729–3752. [Google Scholar] [CrossRef]
- Chen, S.-W.; Ohki, M.; Shimada, M.; Sato, M. Deorientation effect investigation for model-based decomposition over oriented built-up areas. IEEE Geosci. Remote Sens. Lett. 2013, 10, 273–277. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J. On complete model-based decomposition of polarimetric SAR coherency matrix data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1991–2001. [Google Scholar] [CrossRef]
- Shan, Z.; Zhang, H.; Wang, C. Four-component model-based decomposition of polarimetric SAR data for special ground objects. IEEE Geosci. Remote Sens. Lett. 2012, 9, 989–993. [Google Scholar] [CrossRef]
- Shan, Z.; Wang, C.; Zhang, H.; An, W. Improved four-component model-based target decomposition for polarimetric SAR data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 75–79. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-component model-based decomposition for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar]
- Antropov, O.; Rauste, Y.; Häme, T. Volume scattering modeling in PolSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T. Potential of estimating soil moisture under vegetation cover by means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Su, Y. Model-based decomposition with cross scattering for polarimetric SAR urban areas. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2496–2500. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y. Four-component scattering power decomposition with extended volume scattering model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Zhang, Z.; Zha, H. Principal manifolds and nonlinear dimensionality reduction via local tangent space alignment. J. Shanghai Univ. 2004, 8, 406–424. [Google Scholar] [CrossRef]


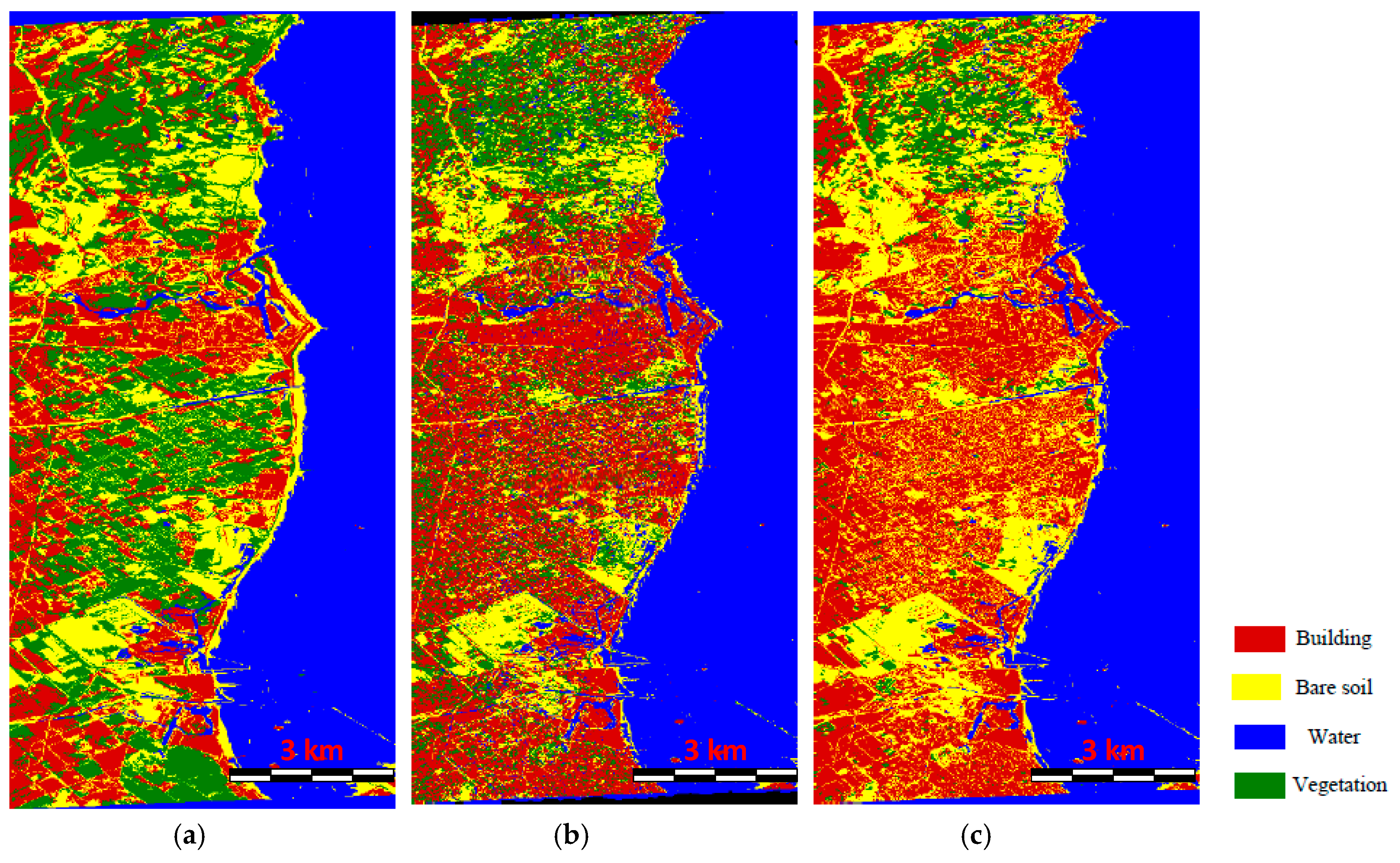
| Class | Building | Bare Soil | Water | Vegetation | Prod. Acc. |
|---|---|---|---|---|---|
| Building | 47.33% | 1.24% | 0.00% | 51.43% | 47.33% |
| Bare soil | 2.17% | 67.55% | 10.41% | 19.87% | 67.55% |
| Water | 0.00% | 10.77% | 89.12% | 0.11% | 89.12% |
| Vegetation | 0.28% | 2.33% | 0.12% | 97.27% | 97.27% |
| User. Acc. | 95.08% | 82.49% | 89.43% | 57.66% | |
| Overall accuracy = 75.32%, Kappa coefficient = 0.6709 | |||||
| Class | Building | Bare Soil | Water | Vegetation | Prod. Acc. |
|---|---|---|---|---|---|
| Building | 70.51% | 0.77% | 0.00% | 28.72% | 70.51% |
| Bare soil | 1.25% | 73.24% | 11.78% | 13.73% | 73.24% |
| Water | 0.00% | 9.84% | 90.08% | 0.08% | 90.08% |
| Vegetation | 5.23% | 1.01% | 0.04% | 93.72% | 93.72% |
| User. Acc. | 91.58% | 86.30% | 88.40% | 68.78% | |
| Overall accuracy = 81.88%, Kappa coefficient = 0.7585 | |||||
| Class | Building | Bare Soil | Water | Vegetation | Prod. Acc. |
|---|---|---|---|---|---|
| Building | 88.67% | 1.15% | 0.00% | 10.18% | 88.67% |
| Bare soil | 2.55% | 89.32% | 1.67% | 6.46% | 89.32% |
| Water | 0.00% | 13.25% | 86.57% | 0.18% | 86.57% |
| Vegetation | 7.32% | 1.68% | 0.17% | 90.83% | 90.83% |
| User. Acc. | 89.98% | 84.74% | 97.91% | 84.37% | |
| Overall accuracy = 88.85%, Kappa coefficient = 0.8513 | |||||
| Without Decomposition | Without SuperPixel Processing | Without Feature Dimensional Reduction | |
|---|---|---|---|
| Building | 32.32% | 65.85% | 84.66% |
| Bare soil | 80.41% | 75.38% | 90.01% |
| Water | 82.25% | 83.31% | 83.25% |
| Vegetation | 82.62% | 84.58% | 88.07% |
| Overall | 69.40% | 77.28% | 86.49% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wei, X.; Xiang, D.; Sun, M. Supervised PolSAR Image Classification with Multiple Features and Locally Linear Embedding. Sensors 2018, 18, 3054. https://doi.org/10.3390/s18093054
Zhang Q, Wei X, Xiang D, Sun M. Supervised PolSAR Image Classification with Multiple Features and Locally Linear Embedding. Sensors. 2018; 18(9):3054. https://doi.org/10.3390/s18093054
Chicago/Turabian StyleZhang, Qiang, Xinli Wei, Deliang Xiang, and Mengqing Sun. 2018. "Supervised PolSAR Image Classification with Multiple Features and Locally Linear Embedding" Sensors 18, no. 9: 3054. https://doi.org/10.3390/s18093054
APA StyleZhang, Q., Wei, X., Xiang, D., & Sun, M. (2018). Supervised PolSAR Image Classification with Multiple Features and Locally Linear Embedding. Sensors, 18(9), 3054. https://doi.org/10.3390/s18093054





