New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV)
Abstract
1. Introduction
2. General Approach to the Data Fusion Model of UAV Navigation
2.1. UAV Motion Model
2.2. New Possibilities Related to the Usage of On-Board Opto-Electronic Cameras
- Usage of the terrain maps and comparing the images of observed specific objects with its position on a preloaded terrain map. This seemingly most obvious method requires the presence of huge collection of observable objects on the board for reliable operation of the recognition system. These images must be recorded under different observation conditions, including aspect, scale, lighting, and so on. Of course, for some characteristic objects these problems are completely surmountable, but on the whole this creates serious difficulties.
- To solve this problem, special techniques have been invented that can be attributed to the allocation of some characteristic small regions (singular points) that are distinguished by a special behavior of the illumination distribution that can be encoded by some set of features that are invariant to the scale and change of the aspect angles [23,24,25,26]. The application of this approach is described in the work [16,27], where it is demonstrated on model images using a 3D map of the local area. In these work we used a computer simulation of a UAV flight and simulated on board video camera imaging. The simulating program is written in MATLAB. Type of the feature points are: ASIFT realized in OpenCV (Python) [26]. Feature points in this model work as in a real flight because the images for the camera model and for the template images were transformed by projective mapping and created by observations from different satellites. However, the use of this method is limited by the need to ensure the closeness of registration conditions. Moreover, significant difference in the resolution level of the reference image and the recorded images in flight also leads to significant errors.
- In tasks of the UAV navigating with the use of a preloaded map of the ground, the matching of reference and observable images plays a fundamental role. In recent years, the methodology based on the images matching with the use of singular points has been further developed. For example ORB methodology versus SIFT and SURF, use a very economical set of binary features of singular points, which allows to significantly reduce the execution time of the registration operation and demonstrate very high resistance to images noise and rotations [28]. In a series of detailed surveys [29,30,31] various alignment methods are examined either on the Oxford dataset test set and on others, while the ORB performance is high in terms of time consuming and the rate of erroneous pixel matching. Meanwhile, from the viewpoint of solving the problems of video navigation, it is more important the accuracy of matching, and more importantly, for specific images such as aerial photographs. In this connection, the results obtained with photogrammetric surveys using ORB-SLAM2 [32,33,34] which show the high potentialities of the ORB methodology, are of great interest in applications related to video navigation.
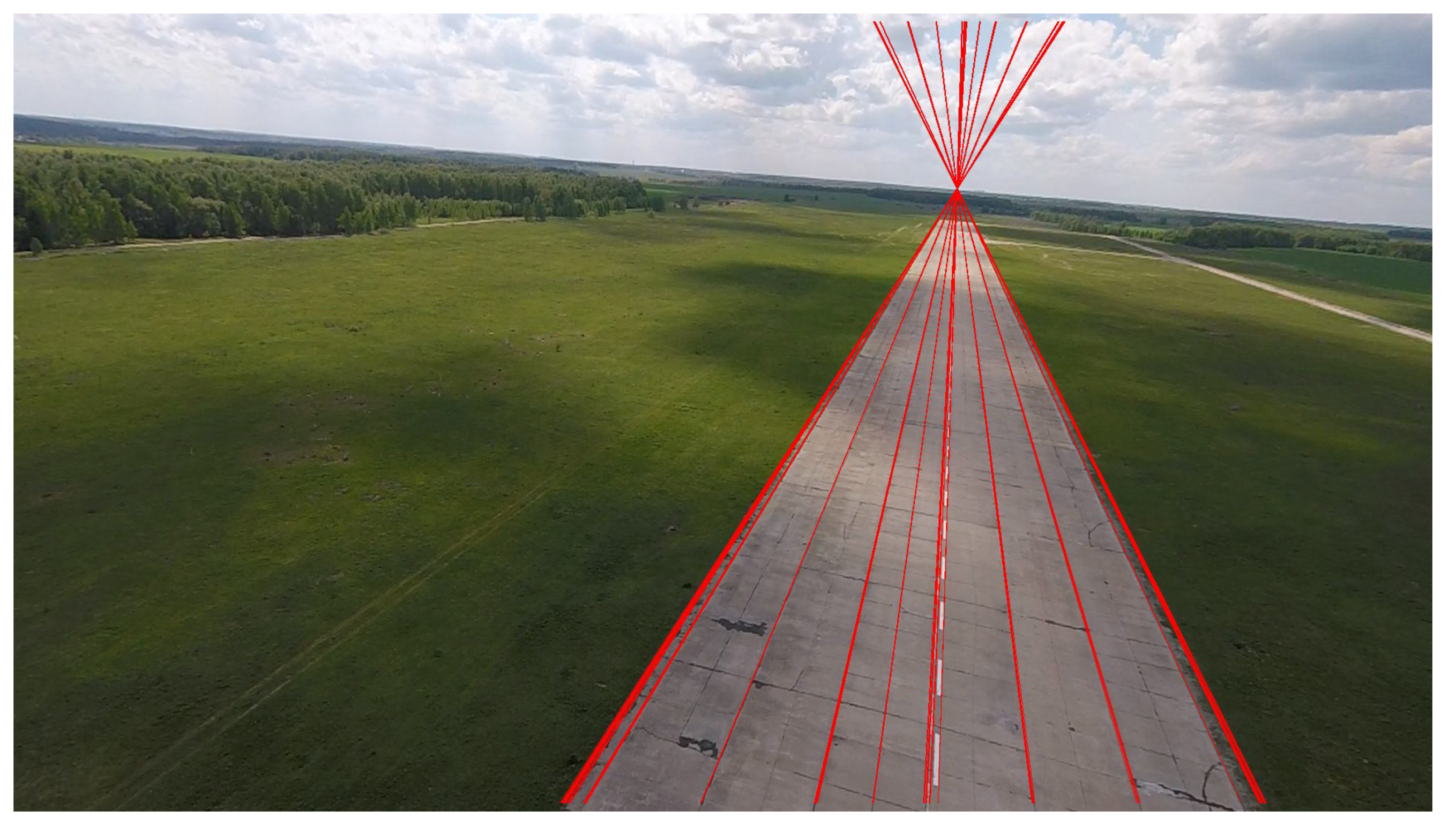
- Similarly to linear objects, it is possible to use curvilinear shape preserving their forms for successful alignment, at least for various season, namely: the boundaries of forest, lands, banks of rivers and water bodies basing on the form [37] and color-texture domains [38,39]. An example is given in (see Figure 3) below.
- It should be noted that the use of the above-mentioned approaches for navigation requires, on the one hand, the solution of the camera calibration problems and the elimination of all kinds of registration nonlinearities, such as distortion [40,41,42], motion blurring [43,44], but the most important peculiarity is the registration of images on 2D photodetector array, that is, the transformation of the 3D coordinates of the object into 2D, which gives only the angular coordinates of objects, known in the literature as bearing-only observations [45]. This is special area of nonlinear filtering problem, which may be solved more or less successfully with the aid of linearized or extended Kalman filtering and also with particle and unscented Kalman filtering. Meanwhile the comparison of various filtering solution shows [46,47] either the presence of uncontrolled bias [48] or the urgent necessity of the filter dimension extension like for particle and unscented filtering. Meanwhile comparison of the filtering accuracy shows almost identical accuracy [49], that is why one should prefer most simple pseudomeasurement Kalman filter without bias, developed on the basis of Pugachev’s conditionally optimal filtering [50,51,52,53]. To obtain 3D coordinates, it is also possible to measure the range, which is possible using stereo systems [54,55,56] or using active radio or laser range finders [6]. The latter can be limited in use because they need essential power and disclose the UAV position, and the stereo systems require very accurate calibration and need the creation of a significant triangulation base which is rather difficult to maintain on small-sized UAV in flight.
- The problem of observing bearings only has long been in the focus of the interests of nonlinear filtering specialists, since it leads to the problem of estimating the position from nonlinear measurements. In the paper [16], we described a new filtering approach using the pseudo-measurement method, which allows expanding the observation system, up to unbiased estimations of the UAV’s own position, on the basis of the determination of bearings of terrestrial objects with known coordinates. However, the filtering is not the only problem which arises in bearing-only observations. Another issue is the association of observed objects with their images on template. Here the various approaches based on RANSAC solutions are necessary [57], such as [58,59], but the most important is the fusion of the current position estimation with the procedure of outliers rejection [60], for details see [16].
- In addition, bearing monitoring requires knowledge of the position of the line of sight of the surveillance system, which is not determined by the orientation angles of the apparatus coming from the INS. That is why it is of interest to estimate the line of sight position from the evolution of the optical flow (OF) or projective matrices describing the transformation of images of terrain sections over two consecutive frames. In the case of visual navigation one needs also the set of angles, determining the orientation of the camera optical axis. The general model, developed for OF observation and describing the geometry of the observation is given in [61], and the corresponding filtering equations for the UAV attitude parameters have been obtained in [62]. These equations and models were tested with the aid of special software package [63] and the possibility of the estimate of coordinates and angular velocities of the UAV were successfully demonstrated in [64,65,66]. However, neither OF nor evolution of projective matrices give the exact values of angles determining the position of the line of sight but define rather the angular velocities, so the problem of the angles estimation remains and must be solved with aid of filtering.
2.3. The UAV Position and the Coordinates Velocities Estimation
2.4. The UAV Angles and Angular Velocities Estimation
Estimation of the Angular Position
3. Joint Estimation of the UAV Attitude with the Aid of Filtering
3.1. Visual-Based Navigation Approaches
3.2. Kalman Filter
3.3. Optical Absolute Positioning
4. Projection Matrices Techniques for Videonavigation
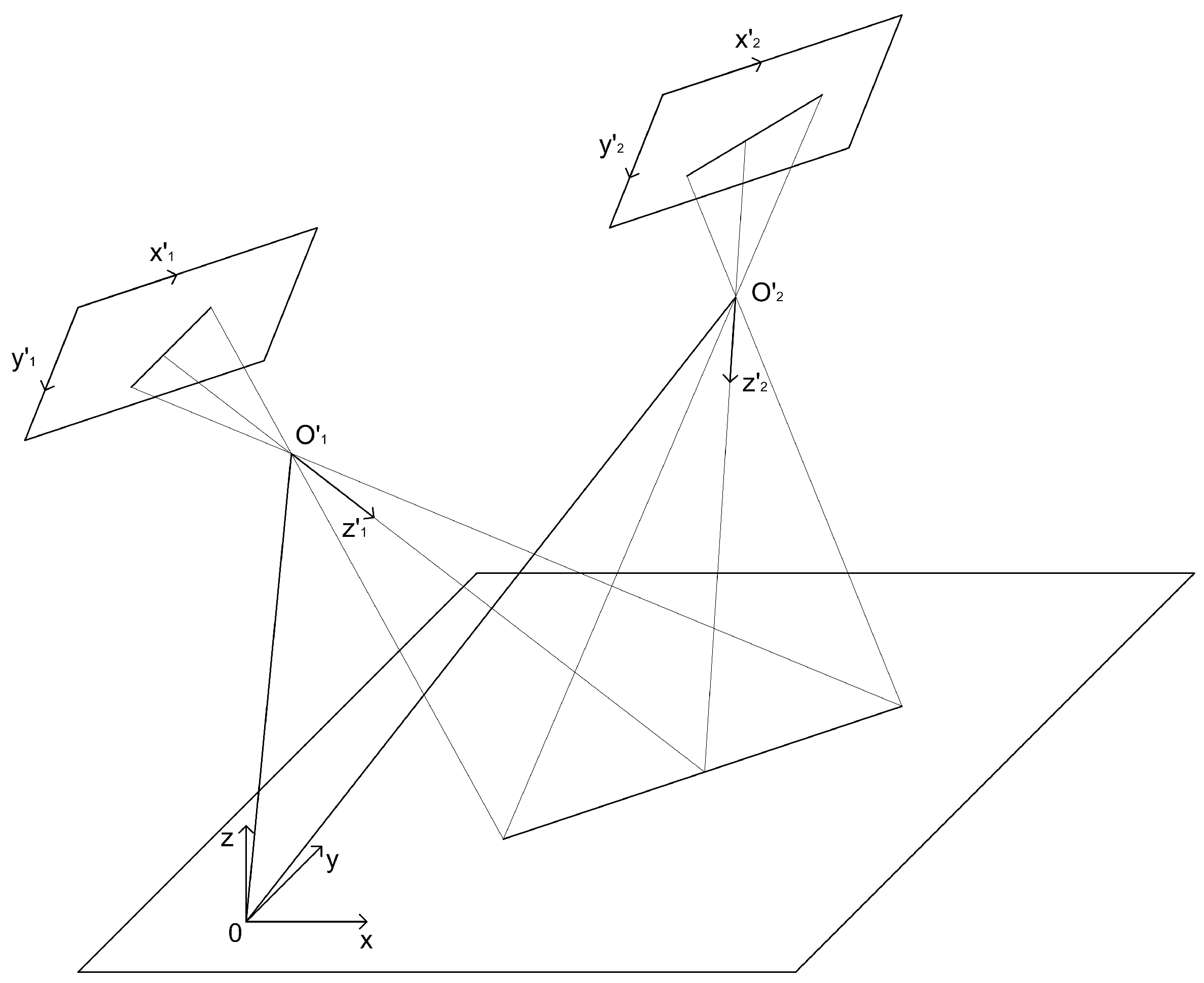
4.1. Coordinate Systems
4.1.1. Earth Coordinate System
- The origin O belongs to the earth surface.
- Axis is directed to the east.
- Axis is directed to the north.
- Axis is directed to the zenith.
4.1.2. The Camera Coordinate System
- is the principal point;
- axis is directed right of the image;
- axis is directed to the top of the image;
- and axis is directed strightforwardly along the optical axis of the camera,
4.1.3. Position of the Camera
4.1.4. Representation of the Camera Rotation with the Aid of Roll, Pitch, Yaw Angles
- Yaw that is rotation about the axis so that positive angle corresponds the anticlockwise rotation.
- Pitch that is rotation about the axis so that for positive angle image moves downward.
- Roll that is rotation about the axis so that positive angle image moves right.
4.2. Projective Representation of the Frame-to-Frame Transformation
4.3. Determining of the Camera Position
- the first one is known , .
- the second one to be determined , .
- .
- .
4.4. Solution of Minimization Problem
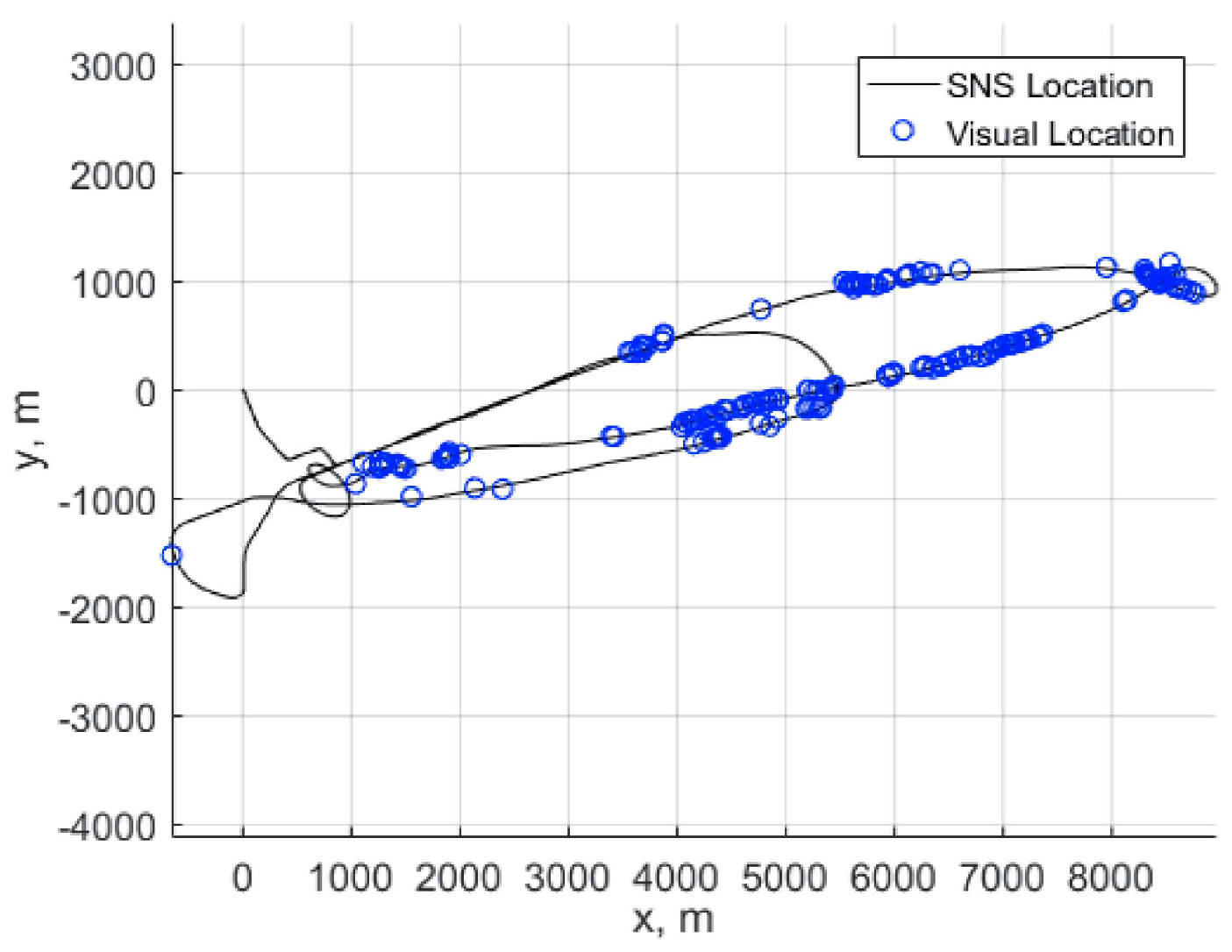
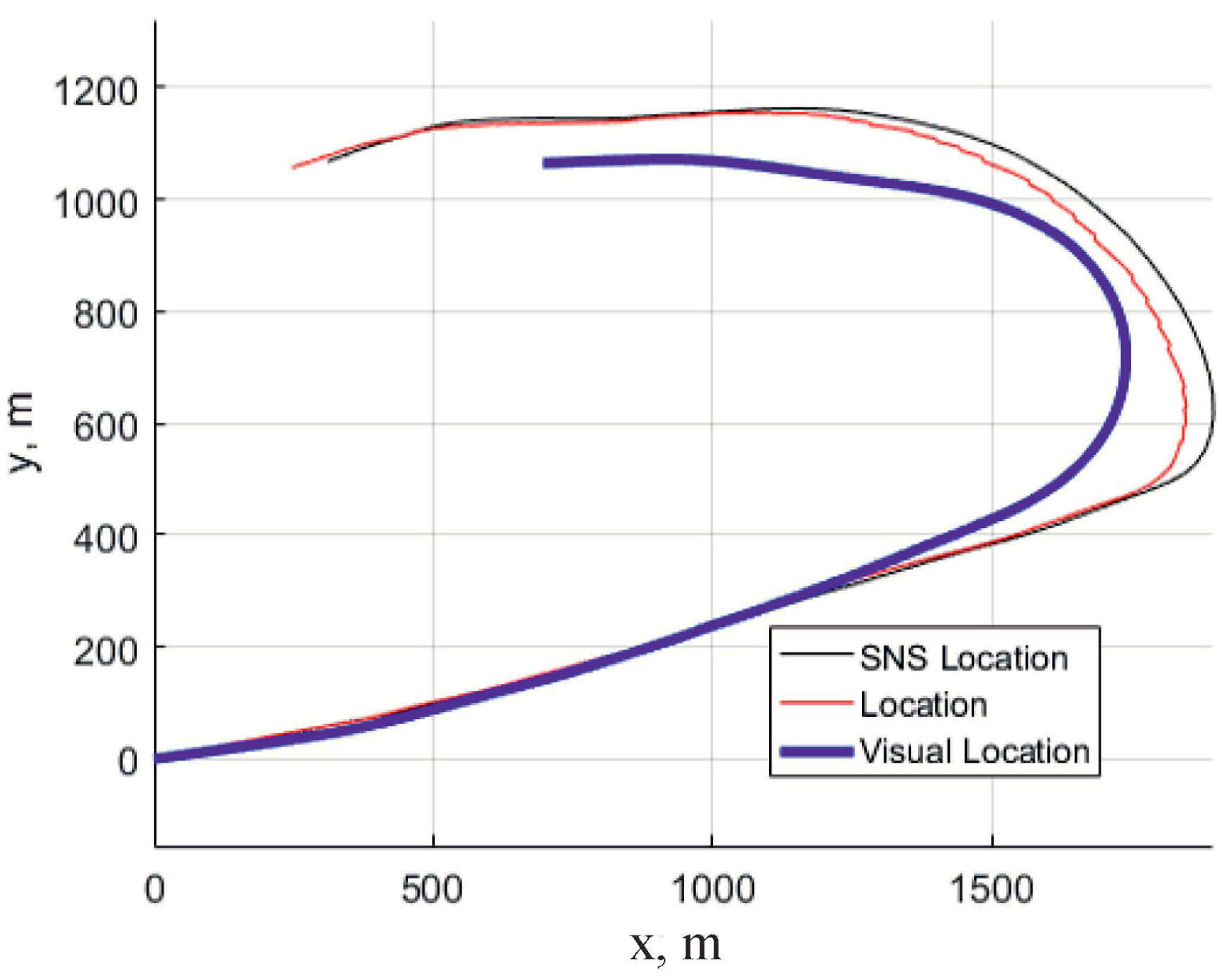
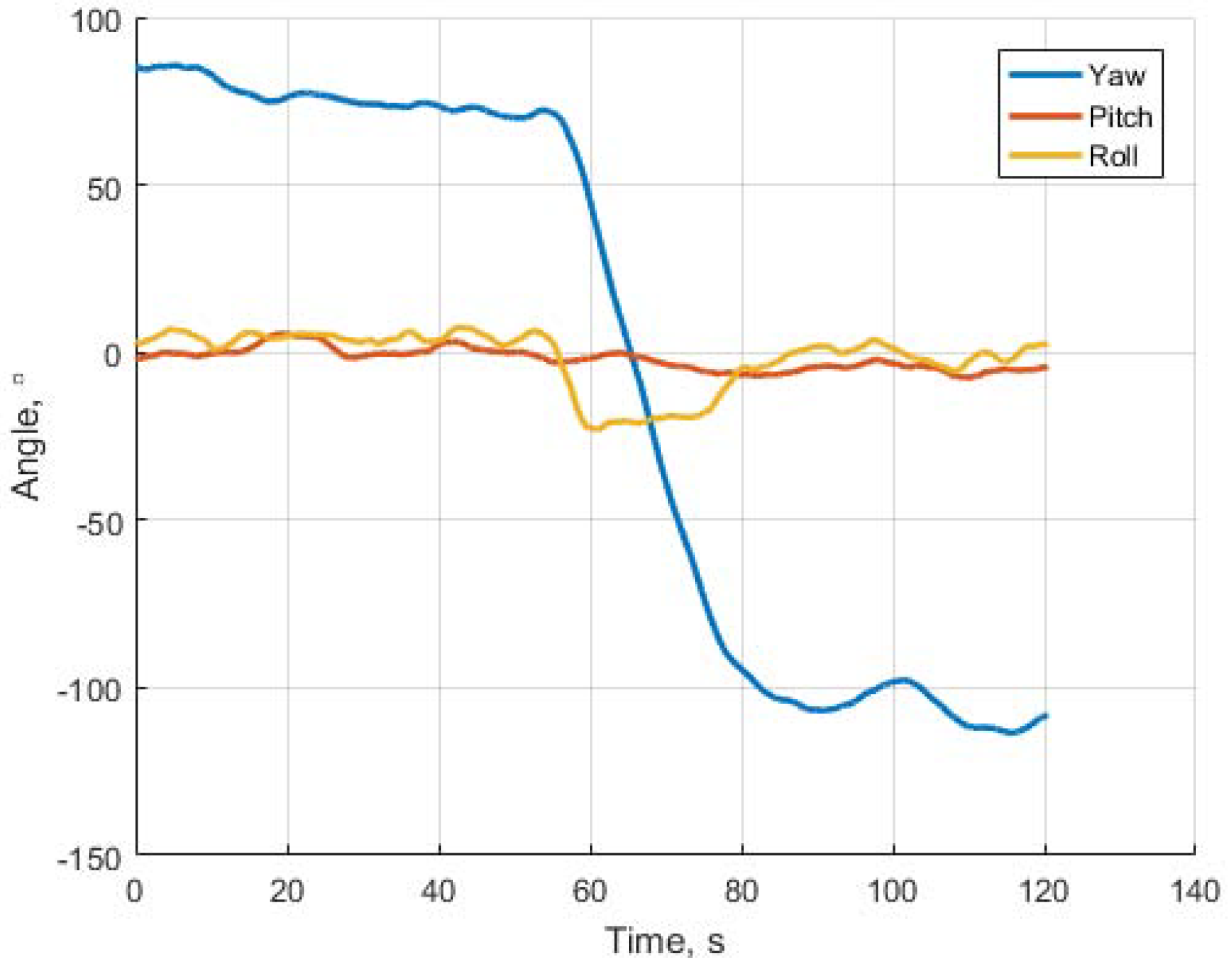
4.5. Testing of the Algorithm
- Choose the map and find the connection with the earth coordinates by determining Q.
- Choose C.
- Choose , .
- Calculate .
- Forget for a moment , .
- Obtain two frames in accordance with from the map.
- Visually test that they correspond to , .
- Calculate the matrix .
- Model is a noise.
- Find .
- Recall , .
- Compare with , and with .
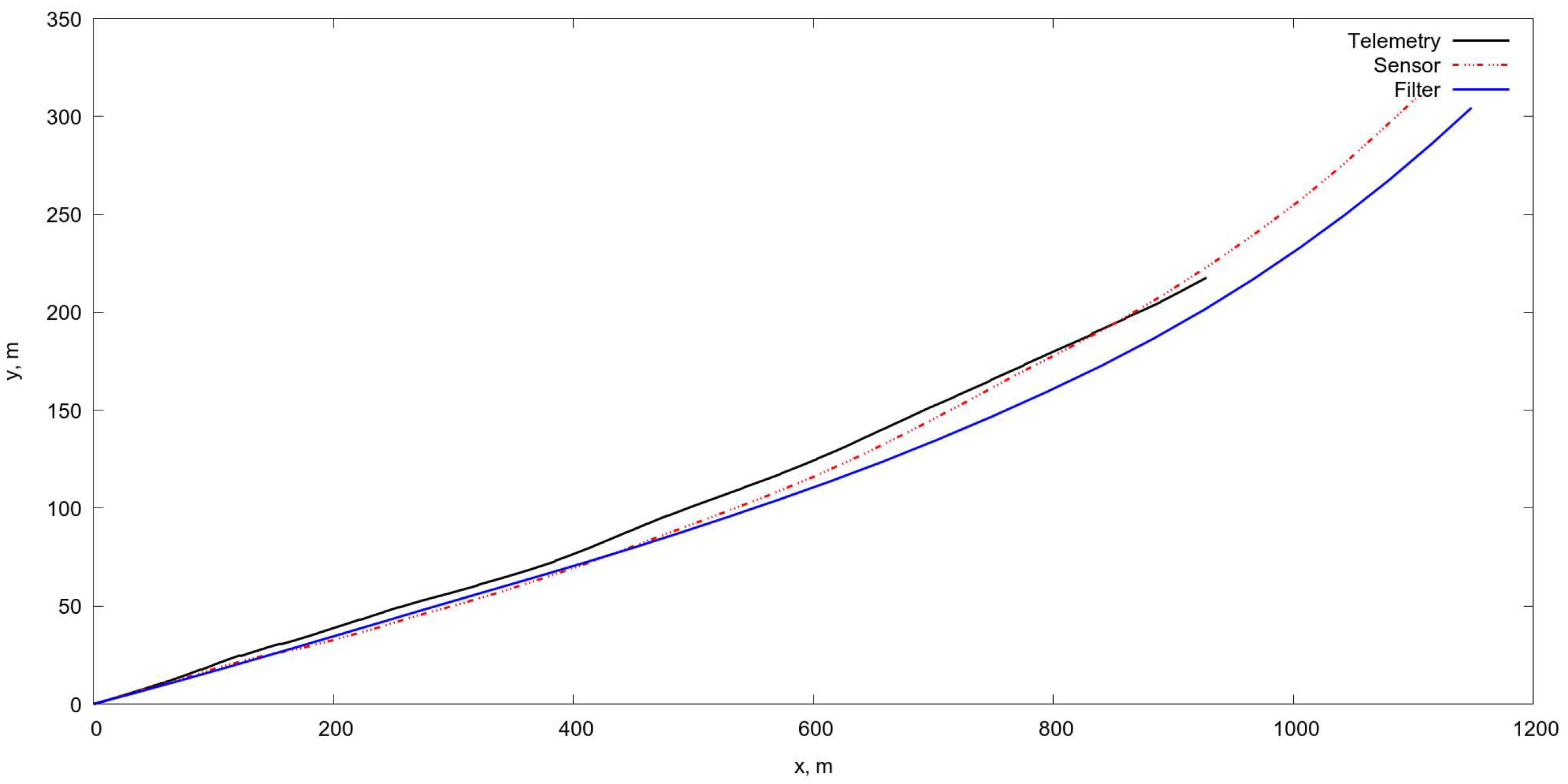
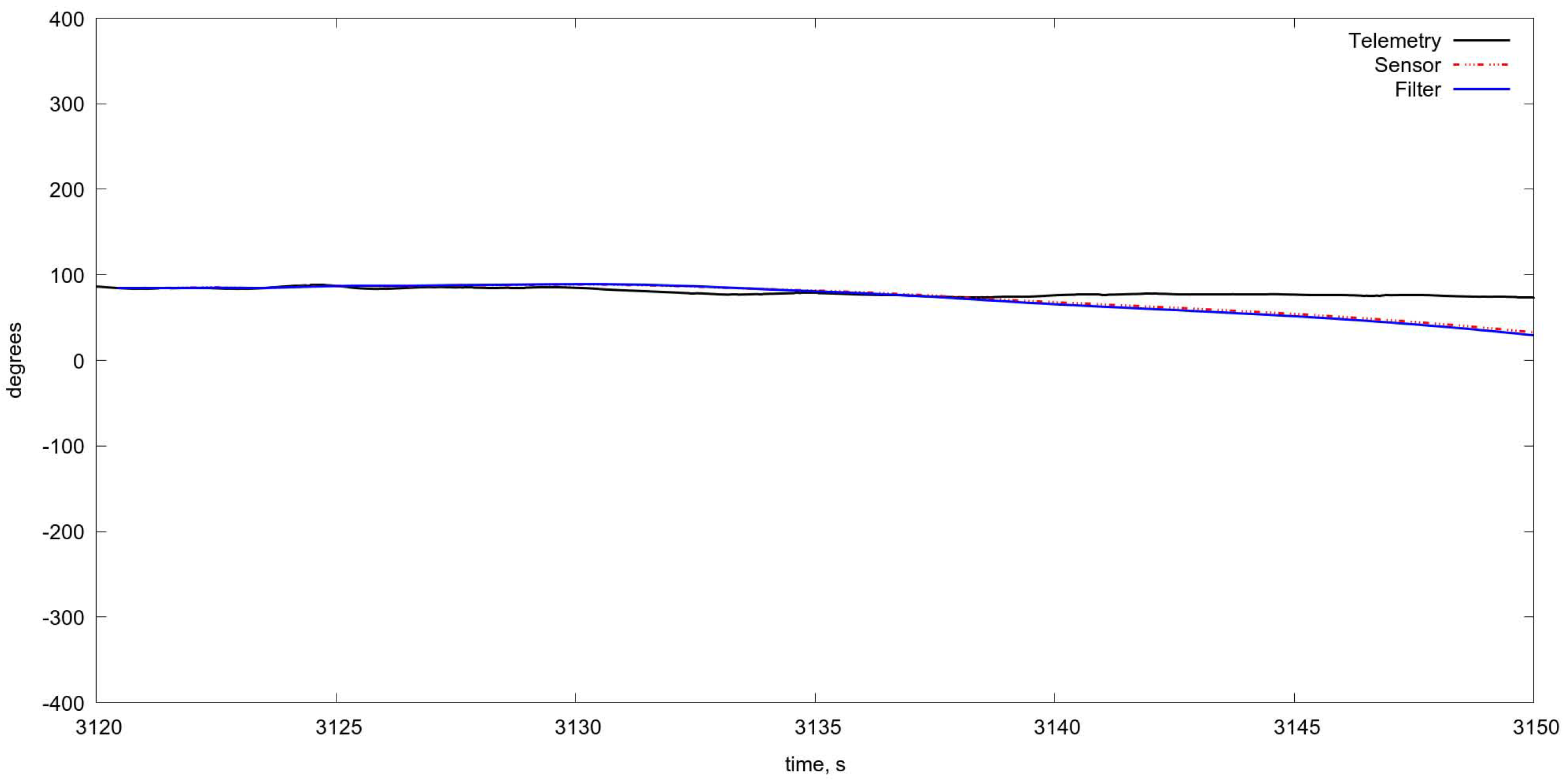
4.5.1. Testing Results
- in the case of the noise absence in the matrix the method gives exact values of rotation and shift , ,
- an increasing of the noise level evidently produce the increasing of errors in estimation, though the exact estimations needs further research with additional flight experiments.
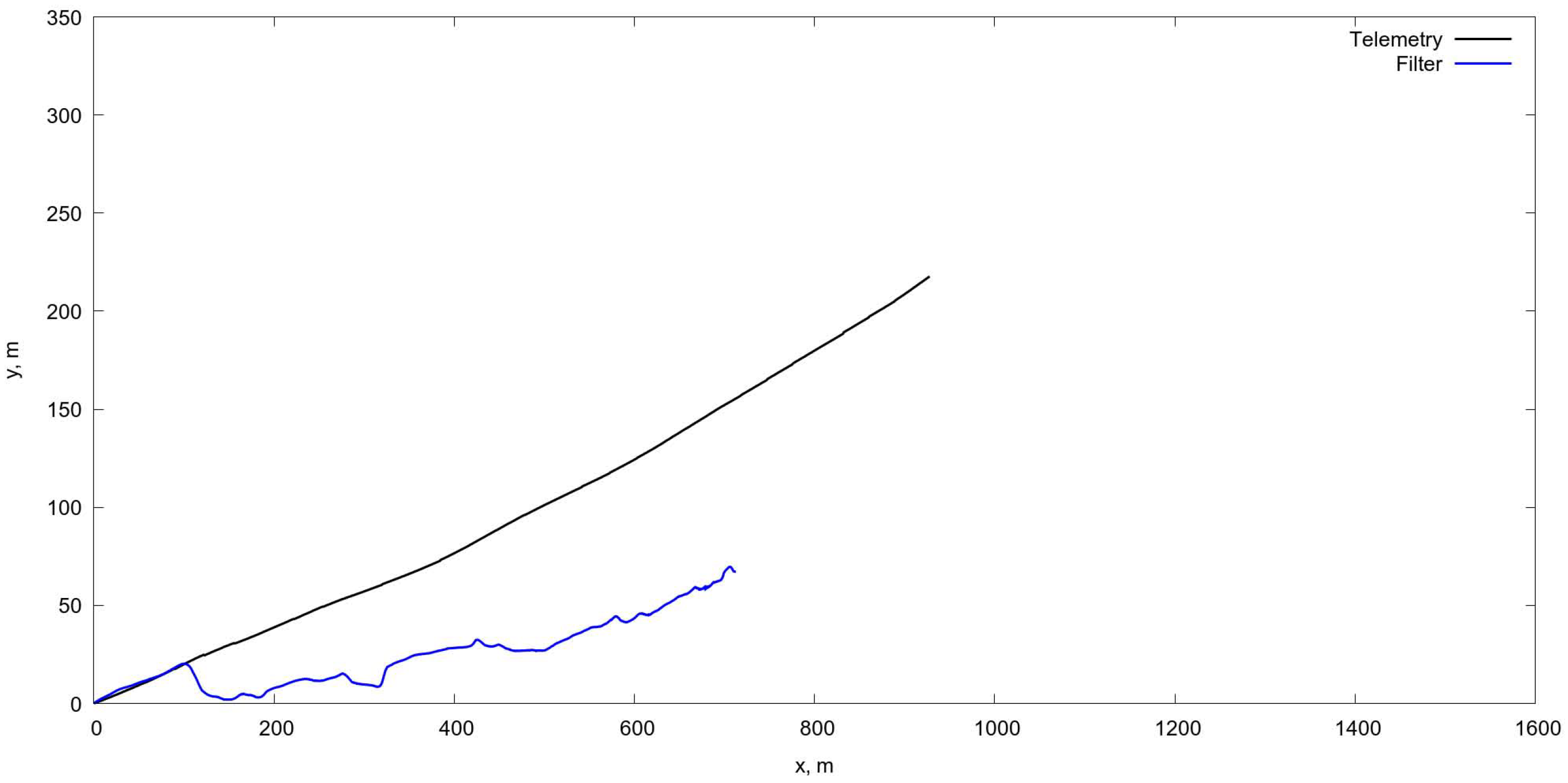
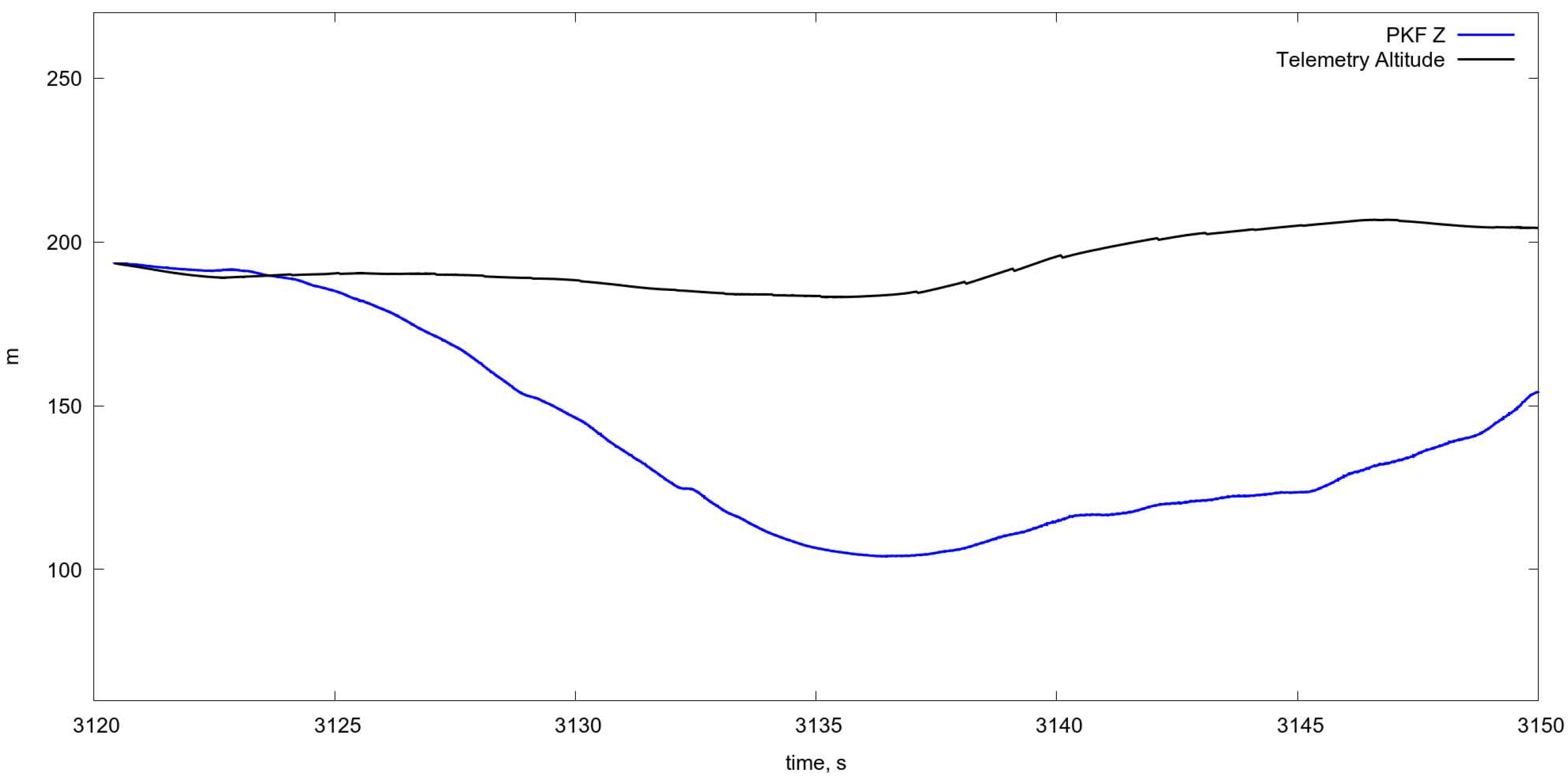
4.5.2. Statistical Analysis of Projective Matrices Algorithm
4.5.3. Comparison of Projective Matrices Algorithm with OF Estimation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miller, B.M. Optimal control of observations in the filtering of diffusion processes I,II. Autom. Remote Control 1985, 46, 207–214, 745–754. [Google Scholar]
- Miller, B.M.; Runggaldier, W.J. Optimization of observations: A stochastic control approach. SIAM J. Control Optim. 1997, 35, 1030–1052. [Google Scholar] [CrossRef]
- Miller, B.M.; Rubinovich, E.Y. Impusive Control in Continuous and Discrete-Continuous Systems; Kluwer Academic/Plenum Publishres: New York, NY, USA, 2003. [Google Scholar]
- Kolosov, K.S. Robust complex processing of UAV navigation measurements. Inf. Process. 2017, 17, 245–257. [Google Scholar]
- Andreev, K.; Rubinovich, E. UAV Guidance When Tracking a Ground Moving Target with Bearing-Only Measurements and Digital Elevation Map Support; Southern Federal University, Engineering Sciences: Rostov Oblast, Russia, 2015; pp. 185–195. (In Russian) [Google Scholar]
- Sidorchuk, D.S.; Volkov, V.V. Fusion of radar, visible and thermal imagery with account for differences in brightness and chromaticity perception. Sens. Syst. 2018, 32, 14–18. (In Russian) [Google Scholar]
- Andreev, K.V. Optimal Trajectories for Unmanned Aerial Vehicle Tracking the Moving Targets Using Linear Antenna Array. Control Sci. 2015, 5, 76–84. (In Russian) [Google Scholar]
- Abulkhanov, D.; Konovalenko, I.; Nikolaev, D.; Savchik, A.; Shvets, E.; Sidorchuk, D. Neural Network-based Feature Point Descriptors for Registration of Optical and SAR Images. In Proceedings of the 10th International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13–15 November 2017; Voulme 10696. [Google Scholar]
- Kanellakis, C.; Nikolakopoulos, G. Survey on Computer Vision for UAVs: Current Developments and Trends. J. Intell. Robot. Syst. 2017, 87, 141–168. [Google Scholar] [CrossRef]
- Konovalenko, I.; Miller, A.; Miller, B.; Nikolaev, D. UAV navigation on the basis of the feature points detection on underlying surface. In Proceedings of the 29th European Conference on Modelling and Simulation (ECMS 2015), Albena, Bulgaria, 26–29 May 2015; pp. 499–505. [Google Scholar]
- Karpenko, S.; Konovalenko, I.; Miller, A.; Miller, B.; Nikolaev, D. Visual navigation of the UAVs on the basis of 3D natural landmarks. In Proceedings of the Eighth International Conference on Machine Vision ICMV 2015, Barcelona, Spain, 19–20 November 2015; Volume 9875, pp. 1–10. [Google Scholar] [CrossRef]
- Cesetti, A.; Frontoni, E.; Mancini, A.; Zingaretti, P.; Longhi, S. A Vision-Based Guidance System for UAV Navigation and Safe Landing using Natural Landmarks. J. Intell. Robot. Syst. 2010, 57, 233–257. [Google Scholar] [CrossRef]
- Miller, B.; Miller, G.; Semenikhin, K. Optimization of the Data Transmission Flow from Moving Object to Nonhomogeneous Network of Base Stations. IFAC PapersOnLine 2017, 50, 6160–6165. [Google Scholar] [CrossRef]
- Miller, B.M.; Miller, G.B.; Semenikhin, V.K. Optimal Channel Choice for Lossy Data Flow Transmission. Autom. Remote Control 2018, 79, 66–77. [Google Scholar] [CrossRef]
- Miller, A.B.; Miller, B.M. Stochastic control of light UAV at landing with the aid of bearing-only observations. In Proceedings of the 8th International Conference on Machine Vision (ICMV), Barcelona, Spain, 19–21 November 2015; Volume 9875. [Google Scholar] [CrossRef]
- Konovalenko, I.; Miller, A.; Miller, B.; Popov, A.; Stepanyan, K. UAV Control on the Basis of 3D Landmark Bearing-Only Observations. Sensors 2015, 15, 29802–29820. [Google Scholar]
- Karpenko, S.; Konovalenko, I.; Miller, A.; Miller, B.; Nikolaev, D. Stochastic control of UAV on the basis of robust filtering of 3D natural landmarks observations. In Proceedings of the Conference on Information Technology and Systems, Olympic Village, Sochi, Russia, 7–11 September 2015; pp. 442–455. [Google Scholar]
- Kunina, I.; Terekhin, A.; Khanipov, T.; Kuznetsova, E.; Nikolaev, D. Aerial image geolocalization by matching its line structure with route map. Proc. SPIE 2017, 10341. [Google Scholar] [CrossRef]
- Pestana, J.; Sanchez-Lopez, J.L.; Saripalli, S.; Campoy, P. Vision based GPS-denied Object Tracking and following for unmanned aerial vehicles. In Proceedings of the 2013 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Linkoping, Sweden, 21–26 October 2013. [Google Scholar] [CrossRef]
- Pestana, J.; Sanchez-Lopez, J.L.; Saripalli, S.; Campoy, P. Computer Vision Based General Object Following for GPS-denied Multirotor Unmanned Vehicles. In Proceedings of the 2014 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 1886–1891. [Google Scholar]
- Pestana, J.; Sanchez-Lopez, J.L.; Saripalli, S.; Campoy, P. A Vision-based Quadrotor Swarm for the participation in the 2013 International Micro Air Vehicle Competition. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 617–622. [Google Scholar]
- Pestana, J.; Sanchez-Lopez, J.L.; de la Puente, P.; Carrio, A.; Campoy, P. A Vision-based Quadrotor Multi-robot Solution for the Indoor Autonomy Challenge of the 2013 International Micro Air Vehicle Competition. J. Intell. Robot. Syst. 2016, 84, 601–620. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Voulme 2, pp. 1150–1157. [Google Scholar]
- Lowe, D. Distinctive image features from scale-invariant key points. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Morel, J.; Yu, G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- 2012 opencv/opencv Wiki GitHub. Available online: https://github.com/Itseez/opencv/blob/master/samples/python2/asift.ru (accessed on 24 September 2014).
- Bishop, A.N.; Fidan, B.; Anderson, B.D.O.; Dogancay, K.; Pathirana, P.N. Optimality analysis of sensor-target localization geometries. Automatica 2010, 46, 479–492. [Google Scholar] [CrossRef]
- Ethan, R.; Vincent, R.; Kurt, K.; Gary, B. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Işik, Ş.; Özkan, K. A Comparative Evaluation of Well-known Feature Detectors and Descriptors. Int. J. Appl. Math. Electron. Comput. 2015, 3, 1–6. [Google Scholar] [CrossRef]
- Adel, E.; Elmogy, M.; Elbakry, H. Image Stitching System Based on ORB Feature-Based Technique and Compensation Blending. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 55–62. [Google Scholar] [CrossRef]
- Karami, E.; Prasad, S.; Shehata, M. Image Matching Using SIFT, SURF, BRIEF and ORB: Performance Comparison for Distorted Images. arXiv, 2017; arXiv:1710.02726. [Google Scholar]
- Burdziakowski, P. Low Cost Hexacopter Autonomous Platform for Testing and Developing Photogrammetry Technologies and Intelligent Navigation Systems. In Proceedings of the 10th International Conference on “Environmental Engineering”, Vilnius, Lithuania, 27–28 April 2017; pp. 1–6. [Google Scholar]
- Burdziakowski, P.; Janowski, A.; Przyborski, M.; Szulwic, J. A Modern Approach to an Unmanned Vehicle Navigation. In Proceedings of the 16th International Multidisciplinary Scientific GeoConference (SGEM 2016), Albena, Bulgaria, 28 June–6 July 2016; pp. 747–758. [Google Scholar]
- Burdziakowski, P. Towards Precise Visual Navigation and Direct Georeferencing for MAV Using ORB-SLAM2. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 394–398. [Google Scholar]
- Ershov, E.; Terekhin, A.; Nikolaev, D.; Postnikov, V.; Karpenko, S. Fast Hough transform analysis: Pattern deviation from line segment. In Proceedings of the 8th International Conference on Machine Vision (ICMV 2015), Barcelona, Spain, 19–21 November 2015; Volume 9875, p. 987509. [Google Scholar]
- Ershov, E.; Terekhin, A.; Karpenko, S.; Nikolaev, D.; Postnikov, V. Fast 3D Hough Transform computation. In Proceedings of the 30th European Conference on Modelling and Simulation (ECMS 2016), Regensburg, Germany, 31 May–3 June 2016; pp. 227–230. [Google Scholar]
- Savchik, A.V.; Sablina, V.A. Finding the correspondence between closed curves under projective distortions. Sens. Syst. 2018, 32, 60–66. (In Russian) [Google Scholar]
- Kunina, I.; Teplyakov, L.M.; Gladkov, A.P.; Khanipov, T.; Nikolaev, D.P. Aerial images visual localization on a vector map using color-texture segmentation. In Proceedings of the International Conference on Machine Vision, Vienna, Austria, 13–15 November 2017; Volume 10696, p. 106961. [Google Scholar] [CrossRef]
- Teplyakov, L.M.; Kunina, I.A.; Gladkov, A.P. Visual localisation of aerial images on vector map using colour-texture segmentation. Sens. Syst. 2018, 32, 19–25. (In Russian) [Google Scholar]
- Kunina, I.; Gladilin, S.; Nikolaev, D. Blind radial distortion compensation in a single image using a fast Hough transform. Comput. Opt. 2016, 40, 395–403. [Google Scholar] [CrossRef]
- Kunina, I.; Terekhin, A.; Gladilin, S.; Nikolaev, D. Blind radial distortion compensation from video using fast Hough transform. In Proceedings of the 2016 International Conference on Robotics and Machine Vision, ICRMV 2016, Moscow, Russia, 14–16 September 2016; Volume 10253, pp. 1–7. [Google Scholar]
- Kunina, I.; Volkov, A.; Gladilin, S.; Nikolaev, D. Demosaicing as the problem of regularization. In Proceedings of the Eighth International Conference on Machine Vision (ICMV 2015), Barcelona, Spain, 19–20 November 2015; Volume 9875, pp. 1–5. [Google Scholar]
- Karnaukhov, V.; Mozerov, M. Motion blur estimation based on multitarget matching model. Opt. Eng. 2016, 55, 100502. [Google Scholar] [CrossRef]
- Bolshakov, A.; Gracheva, M.; Sidorchuk, D. How many observers do you need to create a reliable saliency map in VR attention study? In Proceedings of the ECVP 2017, Berlin, Germany, 27–31 August 2017; Voulme 46. [Google Scholar]
- Aidala, V.J.; Nardone, S.C. Biased Estimation Properties of the Pseudolinear Tracking Filter. IEEE Trans. Aerosp. Electron. Syst. 1982, 18, 432–441. [Google Scholar] [CrossRef]
- Osborn, R.W., III; Bar-Shalom, Y. Statistical Efficiency of Composite Position Measurements from Passive Sensors. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2799–2806. [Google Scholar] [CrossRef]
- Wang, C.-L.; Wang, T.-M.; Liang, J.-H.; Zhang, Y.-C.; Zhou, Y. Bearing-only Visual SLAM for Small Unmanned Aerial Vehicles in GPS-denied Environments. Int. J. Autom. Comput. 2013, 10, 387–396. [Google Scholar] [CrossRef]
- Belfadel, D.; Osborne, R.W., III; Bar-Shalom, Y. Bias Estimation for Optical Sensor Measurements with Targets of Opportunity. In Proceedings of the 16th International Conference on Information, Fusion Istanbul, Turkey, 9–12 July2013; pp. 1805–1812. [Google Scholar]
- Lin, X.; Kirubarajan, T.; Bar-Shalom, Y.; Maskell, S. Comparison of EKF, Pseudomeasurement and Particle Filters for a Bearing-only Target Tracking Problem. Proc. SPIE 2002, 4728, 240–250. [Google Scholar]
- Pugachev, V.S.; Sinitsyn, I.N. Stochastic Differential Systems. Analysis and Filtering; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Miller, B.M.; Pankov, A.R. Theory of Random Processes; Phizmatlit: Moscow, Russian, 2007. (In Russian) [Google Scholar]
- Amelin, K.S.; Miller, A.B. An Algorithm for Refinement of the Position of a Light UAV on the Basis of Kalman Filtering of Bearing Measurements. J. Commun. Technol. Electron. 2014, 59, 622–631. [Google Scholar] [CrossRef]
- Miller, A.B. Development of the motion control on the basis of Kalman filtering of bearing-only measurements. Autom. Remote Control 2015, 76, 1018–1035. [Google Scholar] [CrossRef]
- Volkov, A.; Ershov, E.; Gladilin, S.; Nikolaev, D. Stereo-based visual localization without triangulation for unmanned robotics platform. In Proceedings of the 2016 International Conference on Robotics and Machine Vision, Moscow, Russian, 14–16 September 2016; Voulme 10253. [Google Scholar] [CrossRef]
- Ershov, E.; Karnaukhov, V.; Mozerov, M. Stereovision Algorithms Applicability Investigation for Motion Parallax of Monocular Camera Case. Inf. Process. 2016, 61, 695–704. [Google Scholar] [CrossRef]
- Ershov, E.; Karnaukhov, V.; Mozerov, M. Probabilistic choice between symmetric disparities in motion stereo for lateral navigation system. Opt. Eng. 2016, 55, 023101. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Zuliani, M.; Kenney, C.S.; Manjunath, B.S. The MultiRANSAC Algorithm and its Application to Detect Planar Homographies. Proceedings of 12th the IEEE International Conference on Image Processing (ICIP 2005), Genova, Italy, 11–14 September 2005; Volume 3, pp. 2969–2972. [Google Scholar]
- Civera, J.; Grasa, O.G.; Davison, A.J.; Montiel, J.M.M. 1-Point RANSAC for EKF-Based Structure from Motion. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 3498–3504. [Google Scholar]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Application of the Optical Flow as a Navigation Sensor for UAV. In Proceedings of the 39th IITP RAS Interdisciplinary Conference & School, Olympic Village, Sochi, Russia, 7–11 September 2015; pp. 390–398, ISBN 978-5-901158-28-9. [Google Scholar]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K.; Konovalenko, I.; Sidorchuk, D.; Koptelov, I. UAV navigation on the basis of video sequences registered by on-board camera. In Proceedings of the 40th Interdisciplinary Conference & School Information Technology and Systems 2016, Repino, St. Petersburg, Russia, 25–30 September 2016; pp. 370–376. [Google Scholar]
- Popov, A.; Stepanyan, K.; Miller, B.; Miller, A. Software package IMODEL for analysis of algorithms for control and navigations of UAV with the aid of observation of underlying surface. In Proceedings of the Abstracts of XX Anniversary International Conference on Computational Mechanics and Modern Applied Software Packages (CMMASS2017), Alushta, Crimea, 24–31 May 2017; pp. 607–611. (In Russian). [Google Scholar]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Optical Flow as a Navigation Means for UAVs with Opto-electronic Cameras. In Proceedings of the 56th Israel Annual Conference on Aerospace Sciences, Tel-Aviv and Haifa, Israel, 9–10 March 2016. [Google Scholar]
- Miller, B.M.; Stepanyan, K.V.; Popov, A.K.; Miller, A.B. UAV Navigation Based on Videosequences Captured by the Onboard Video Camera. Autom. Remote Control 2017, 78, 2211–2221. [Google Scholar] [CrossRef]
- Popov, A.K.; Miller, A.B.; Stepanyan, K.V.; Miller, B.M. Modelling of the unmanned aerial vehicle navigation on the basis of two height-shifted onboard cameras. Sens. Syst. 2018, 32, 26–34. (In Russian) [Google Scholar]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Estimation of velocities via Optical Flow. In Proceedings of the International Conference on Robotics and Machine Vision (ICRMV), Moscow, Russia, 14 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B. Pseudomeasurement Kalman filter in underwater target motion analisys & Integration of bearing-only and active-range measurement. IFAC PapersOnLine 2017, 50, 3817–3822. [Google Scholar]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Optical Flow and Inertial Navigation System Fusion in UAV Navigation. In Proceedings of the Conference on Unmanned/Unattended Sensors and Sensor Networks XII, Edinburgh, UK, 26 September 2016; pp. 1–16. [Google Scholar] [CrossRef]
- Caballero, F.; Merino, L.; Ferruz, J.; Ollero, A. Vision-based Odometry and SLAM for Medium and High Altitude Flying UAVs. J. Intell. Robot. Syst. 2009, 54, 137–161. [Google Scholar] [CrossRef]
- Konovalenko, I.; Kuznetsova, E. Experimental Comparison of Methods for Estimation of the Observed Velocity of the Vehicle in Video Stream. Proc. SPIE 2015, 9445. [Google Scholar] [CrossRef]
- Guan, X.; Bai, H. A GPU accelerated real-time self-contained visual navigation system for UAVs. Proceeding of the IEEE International Conference on Information and Automation, Shenyang, China, 6–8 June 2012; pp. 578–581. [Google Scholar]
- Jauffet, C.; Pillon, D.; Pignoll, A.C. Leg-by-leg Bearings-Only Target Motion Analysis Without Observer Maneuver. J. Adv. Inf. Fusion 2011, 6, 24–38. [Google Scholar]
- Miller, B.M.; Stepanyan, K.V.; Miller, A.B.; Andreev, K.V.; Khoroshenkikh, S.N. Optimal filter selection for UAV trajectory control problems. In Proceedings of the 37th Conference on Information Technology and Systems, Kaliningrad, Russia, 1–6 September 2013; pp. 327–333. [Google Scholar]
- Ovchinkin, A.A.; Ershov, E.I. The algorithm of epipole position estimation under pure camera translation. Sens. Syst. 2018, 32, 42–49. (In Russian) [Google Scholar]
- Le Coat, F.; Pissaloux, E.E. Modelling the Optical-flow with Projective-transform Approximation for Lerge Camera Movements. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 199–203. [Google Scholar]
- Longuet-Higgins, H.C. The Visual Ambiguity of a Moving Plane. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1984, 223, 165–175. [Google Scholar] [CrossRef]
- Raudies, F.; Neumann, H. A review and evaluation of methods estimating ego-motion. Comput. Vis. Image Underst. 2012, 116, 606–633. [Google Scholar] [CrossRef]
- Yuan, D.; Liu, M.; Yin, J.; Hu, J. Camera motion estimation through monocular normal flow vectors. Pattern Recognit. Lett. 2015, 52, 59–64. [Google Scholar] [CrossRef]
- Babinec, A.; Apeltauer, J. On accuracy of position estimation from aerial imagery captured by low-flying UAVs. Int. J. Transp. Sci. Technol. 2016, 5, 152–166. [Google Scholar] [CrossRef]
- Martínez, C.; Mondragón, I.F.; Olivares-Médez, M.A.; Campoy, P. On-board and Ground Visual Pose Estimation Techniques for UAV Control. J. Intell. Robot. Syst. 2011, 61, 301–320. [Google Scholar] [CrossRef]
- Pachauri, A.; More, V.; Gaidhani, P.; Gupta, N. Autonomous Ingress of a UAV through a window using Monocular Vision. arXiv, 2016; arXiv:1607.07006v1. [Google Scholar]




| Number of Frame s | Norm of Real Shift from INS | Norm of the Error from INS and Projective Matrices |
|---|---|---|
| 1 | 17.9950 | 0.5238 |
| 2 | 16.6470 | 2.2434 |
| 3 | 17.4132 | 0.9915 |
| 4 | 16.4036 | 3.2009 |
| 5 | 17.2792 | 5.2980 |
| 6 | 16.2951 | 3.7480 |
| 7 | 17.7030 | 6.7479 |
| 8 | 16.4029 | 4.8240 |
| 9 | 17.8309 | 0.1152 |
| 10 | 16.1718 | 3.8627 |
| 11 | 17.2313 | 2.6757 |
| 12 | 15.8342 | 6.7456 |
| 13 | 17.2652 | 2.1774 |
| 14 | 15.7978 | 1.5271 |
| 15 | 17.4473 | 2.2599 |
| 16 | 15.9407 | 3.8367 |
| 17 | 17.4862 | 5.3902 |
| 18 | 16.0020 | 1.9714 |
| 19 | 17.2286 | 2.1162 |
| 20 | 15.9406 | 3.4193 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalenko, I.; Kuznetsova, E.; Miller, A.; Miller, B.; Popov, A.; Shepelev, D.; Stepanyan, K. New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV). Sensors 2018, 18, 3010. https://doi.org/10.3390/s18093010
Konovalenko I, Kuznetsova E, Miller A, Miller B, Popov A, Shepelev D, Stepanyan K. New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV). Sensors. 2018; 18(9):3010. https://doi.org/10.3390/s18093010
Chicago/Turabian StyleKonovalenko, Ivan, Elena Kuznetsova, Alexander Miller, Boris Miller, Alexey Popov, Denis Shepelev, and Karen Stepanyan. 2018. "New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV)" Sensors 18, no. 9: 3010. https://doi.org/10.3390/s18093010
APA StyleKonovalenko, I., Kuznetsova, E., Miller, A., Miller, B., Popov, A., Shepelev, D., & Stepanyan, K. (2018). New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV). Sensors, 18(9), 3010. https://doi.org/10.3390/s18093010






