Kinematic Calibration of a Cable-Driven Parallel Robot for 3D Printing
Abstract
:1. Introduction
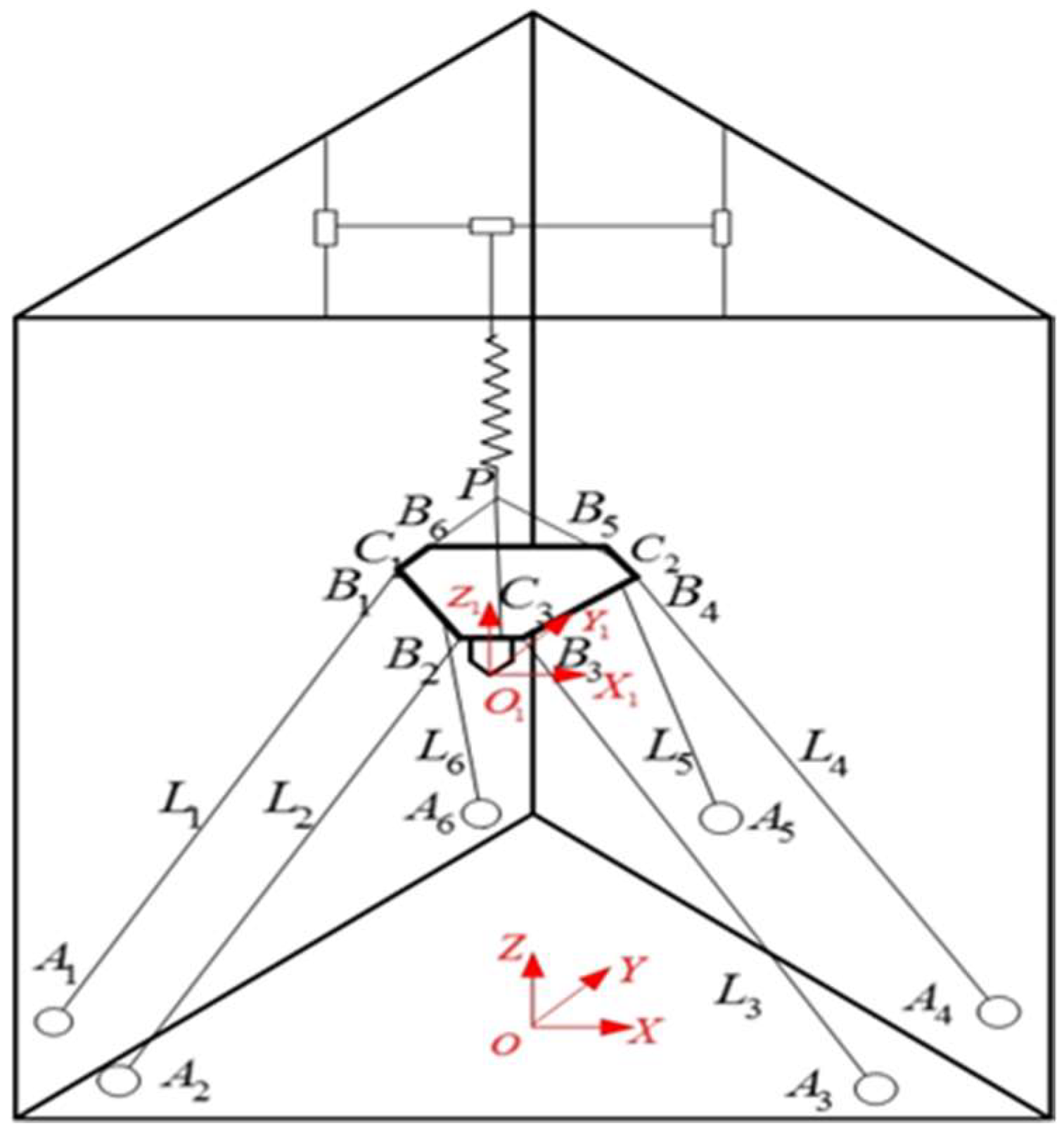
2. Description of Experimental Prototype
3. Kinematic Error Modeling
3.1. Equivalent of Analytical Structure
3.2. Kinematic Error Modeling
4. Optimal Selection
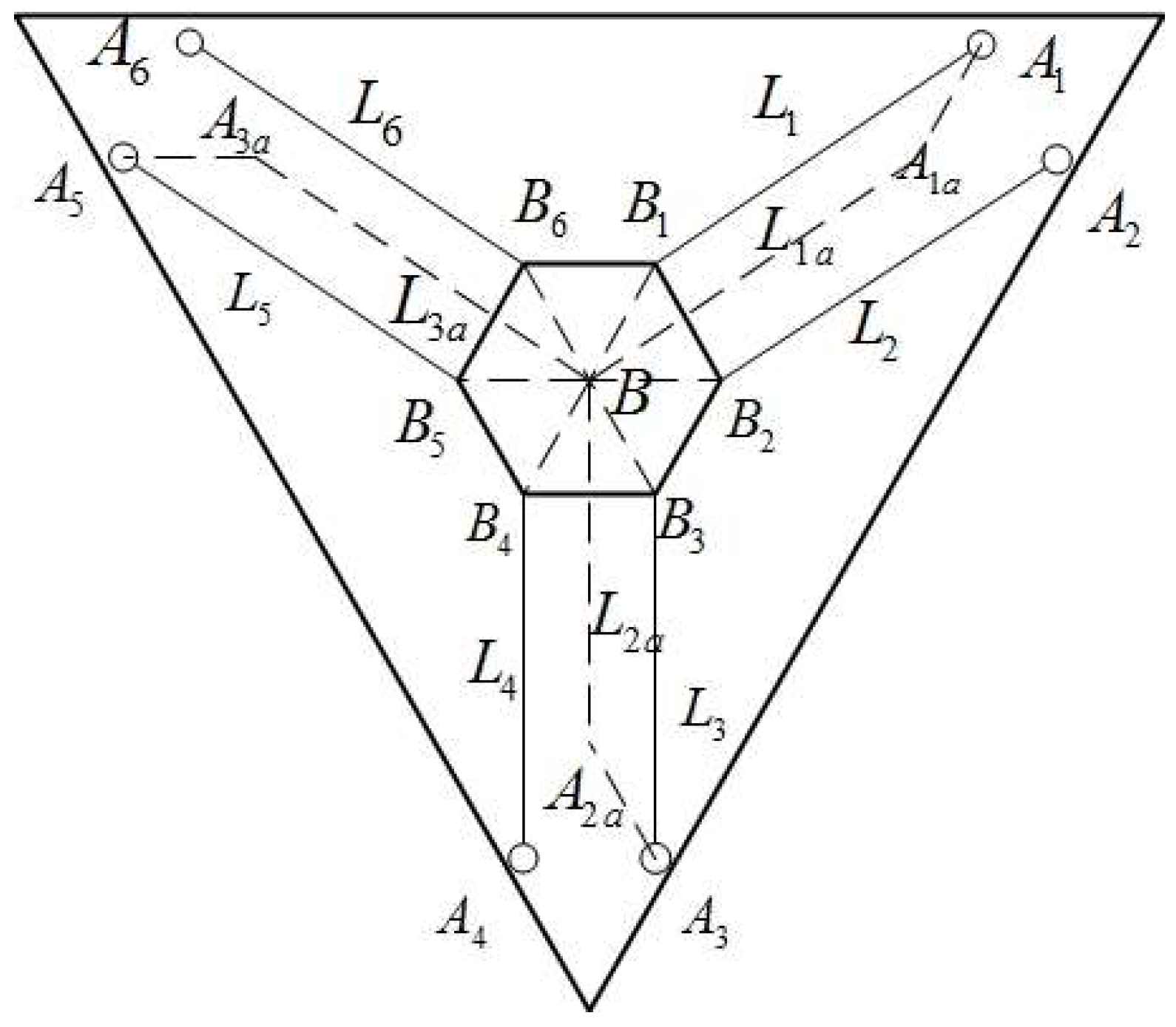
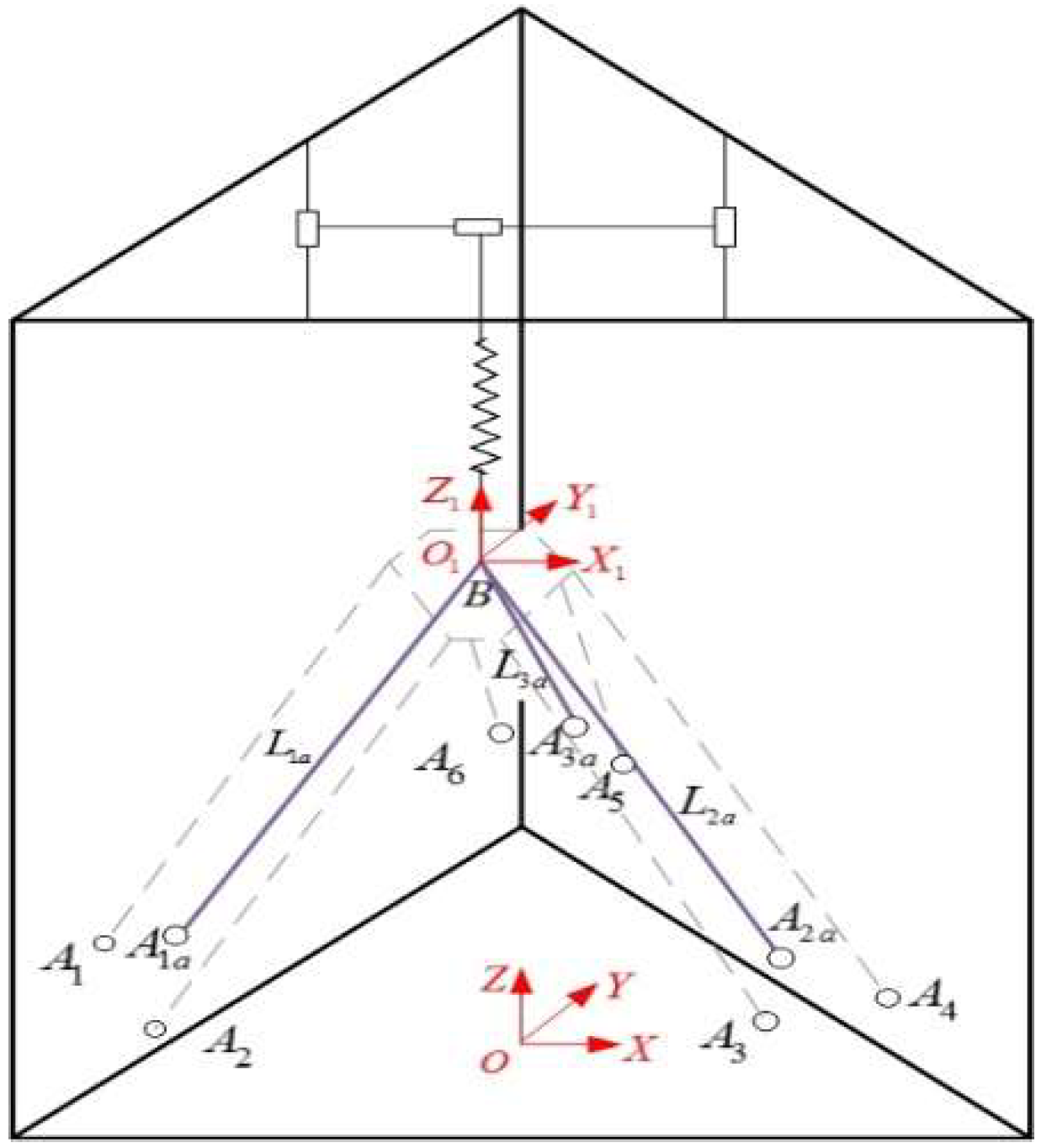
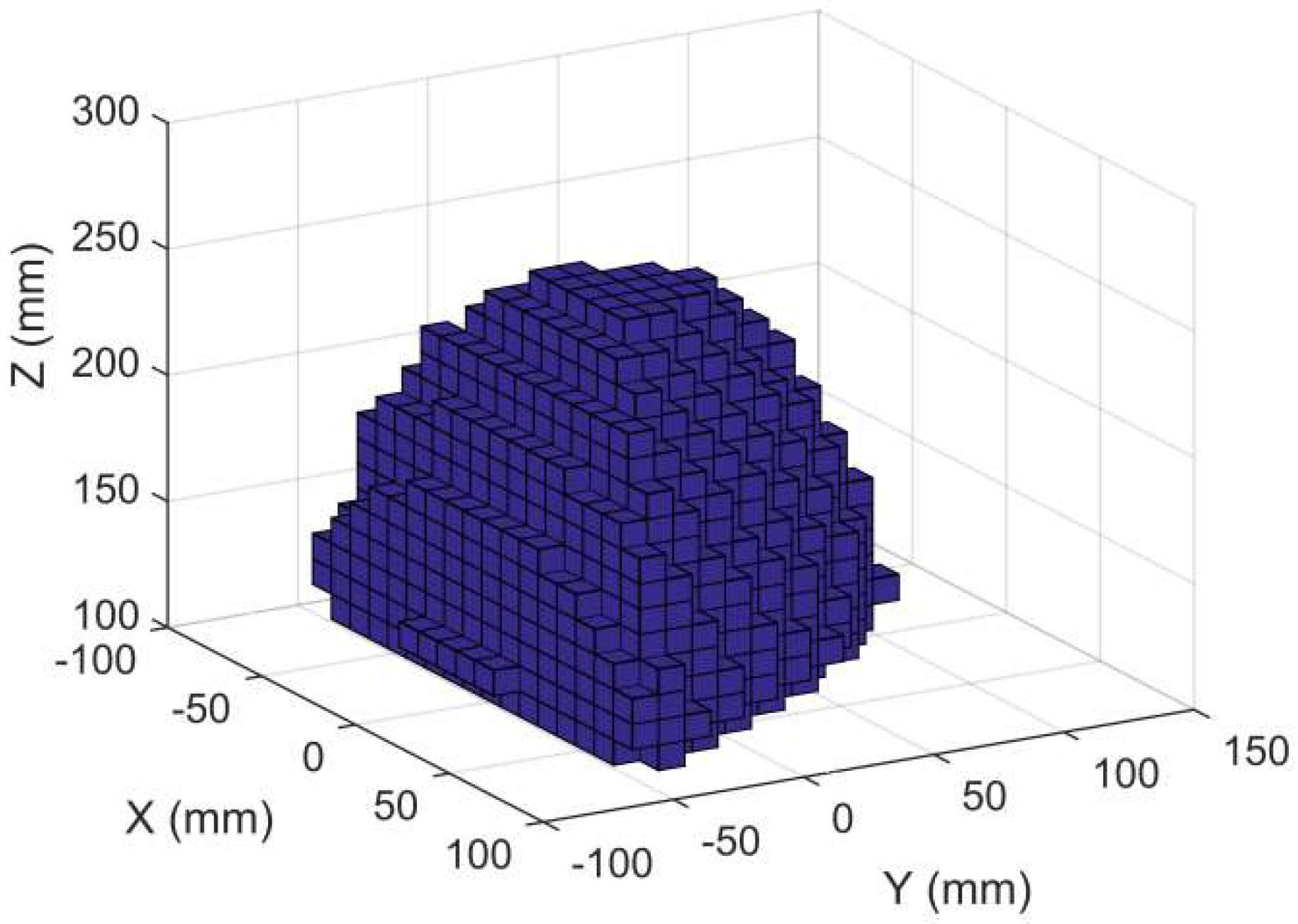
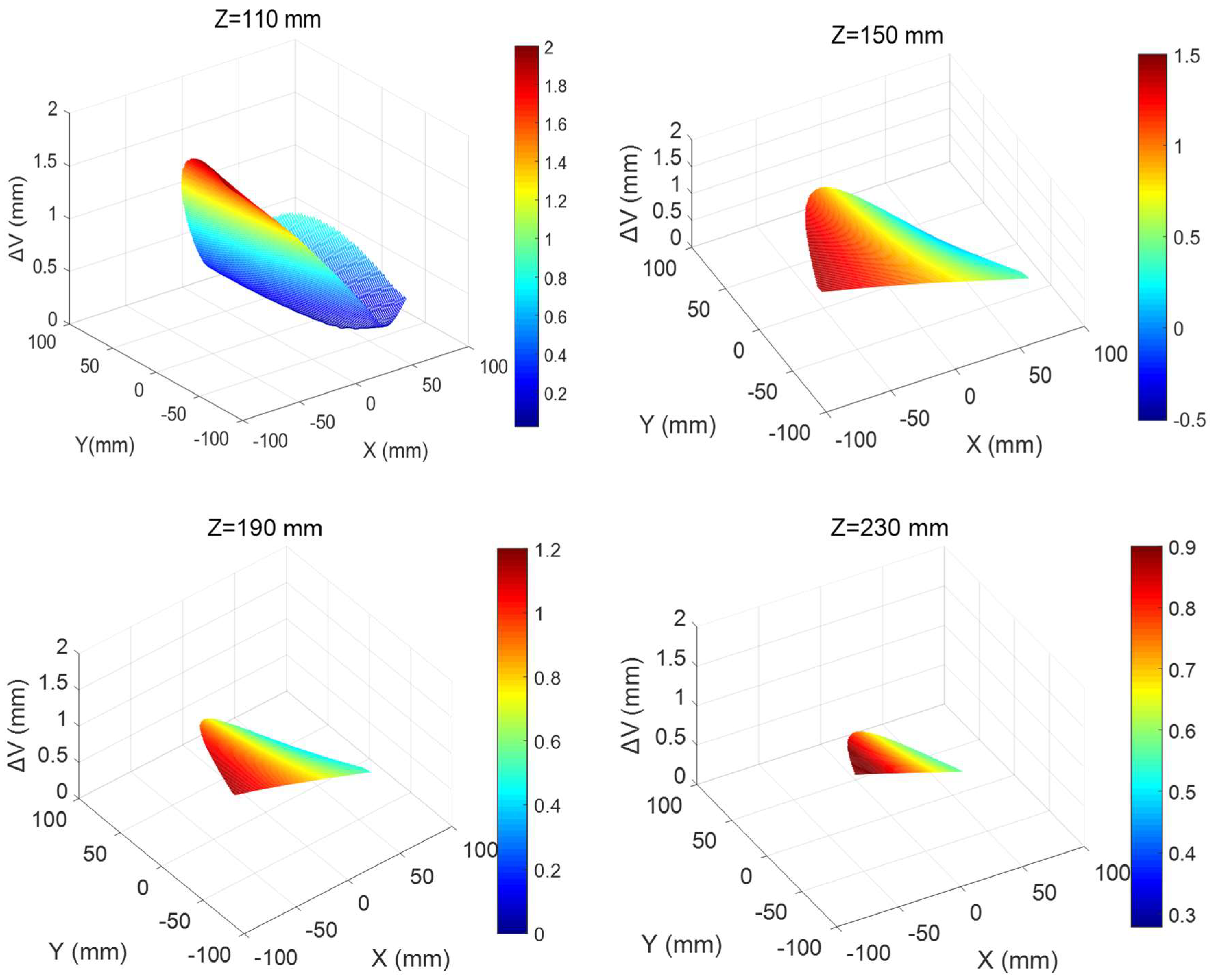
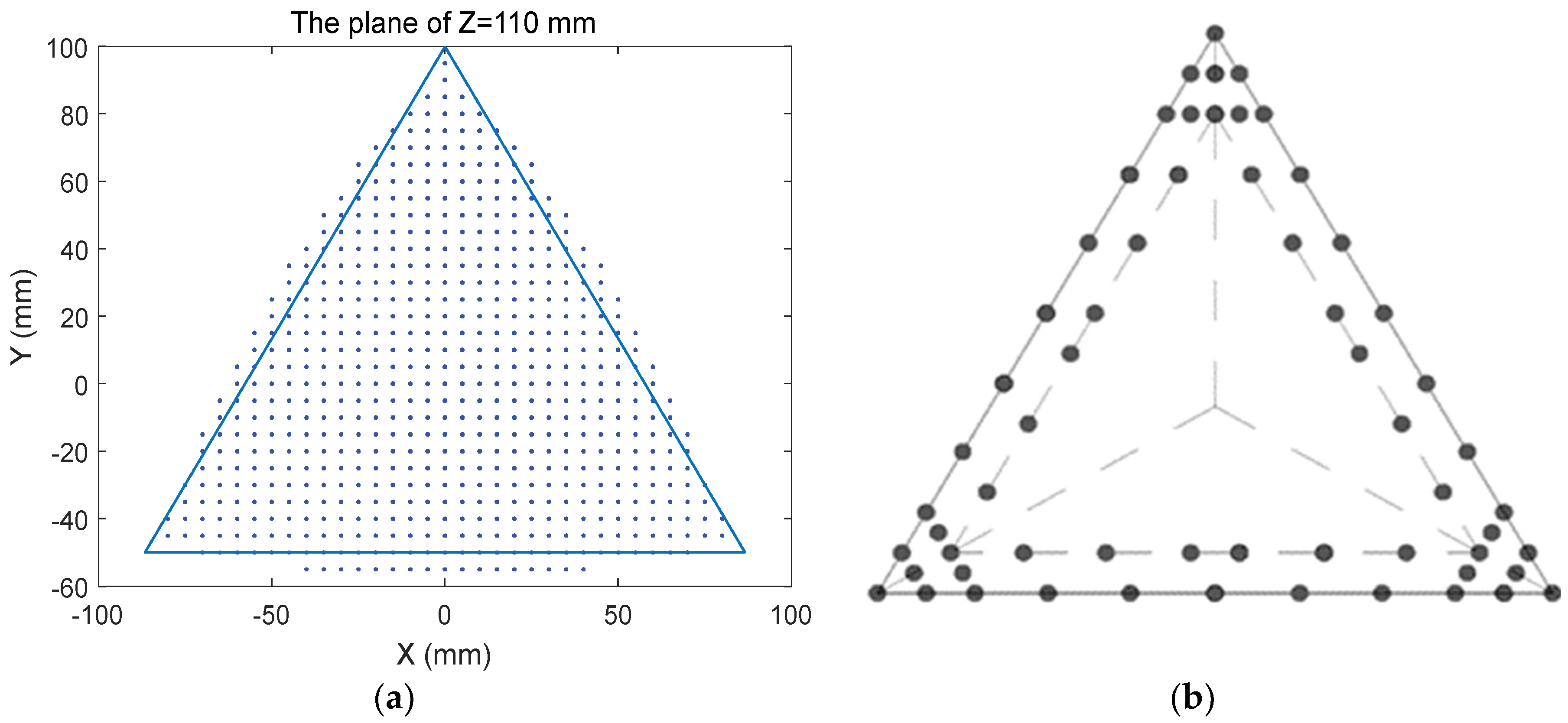
4.1. Analysis of Workspace and Preliminary Selection
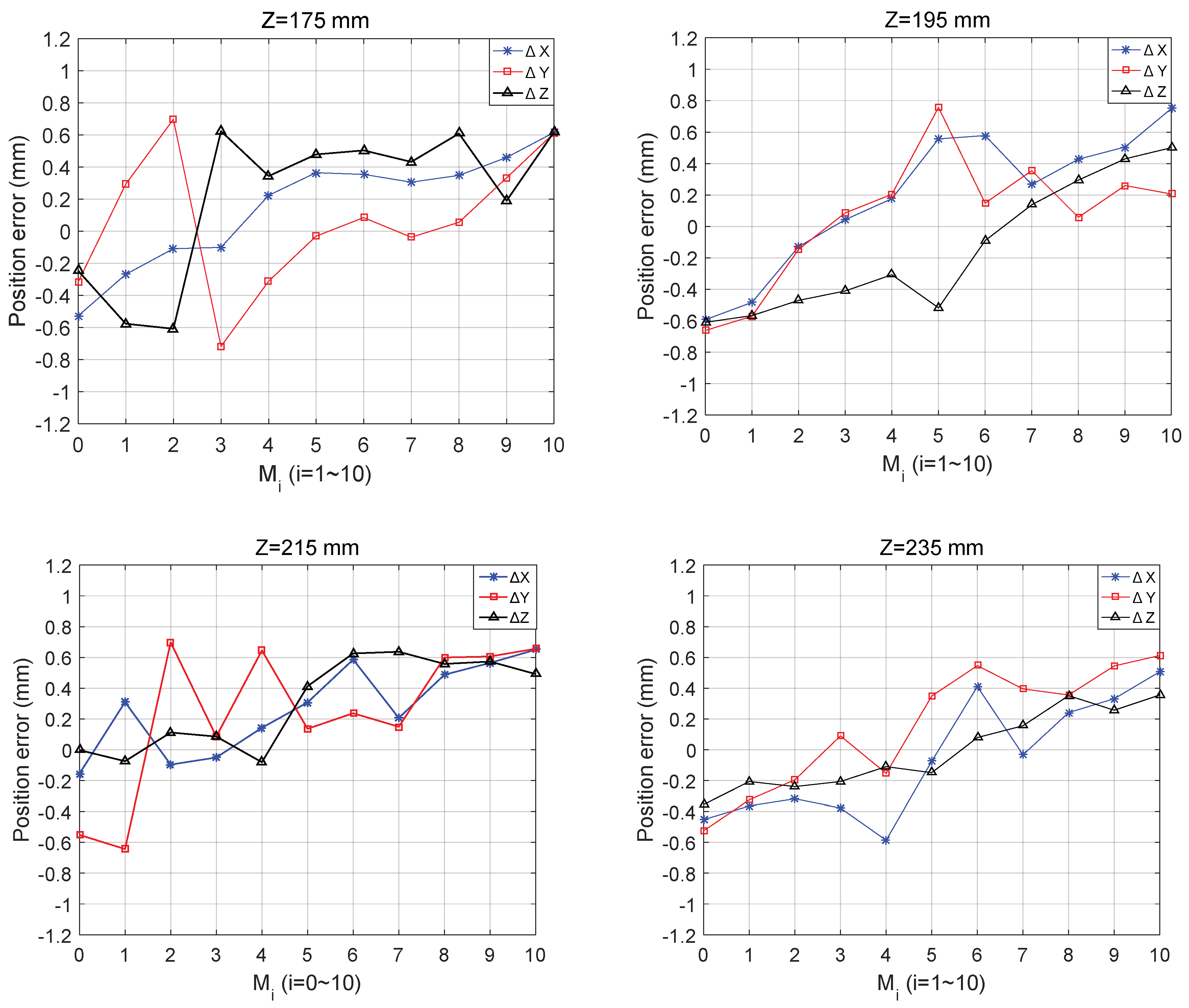
4.2. Optimal Positions Selection
5. Simulation
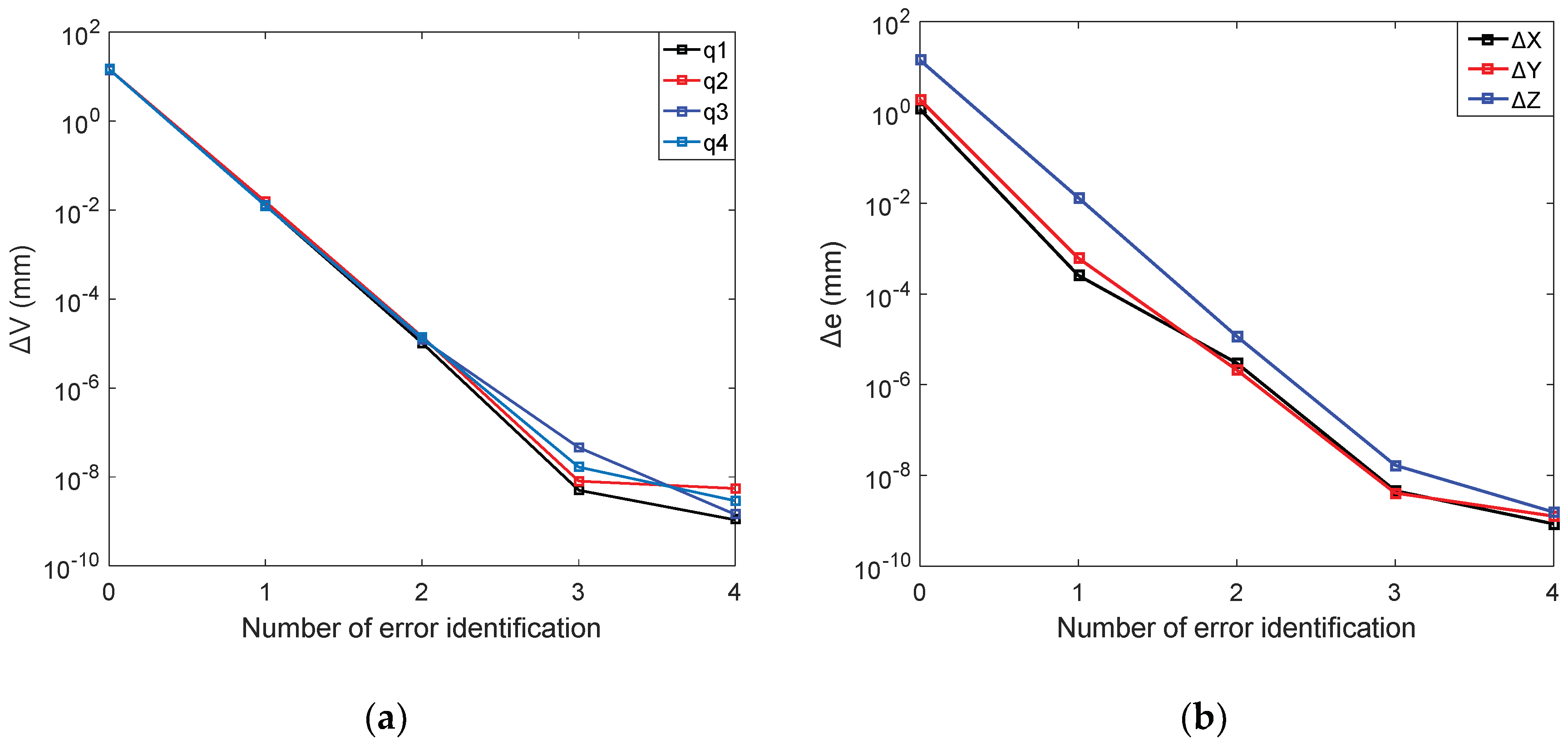
5.1. Error Identification Model
5.2. Simulation Verification
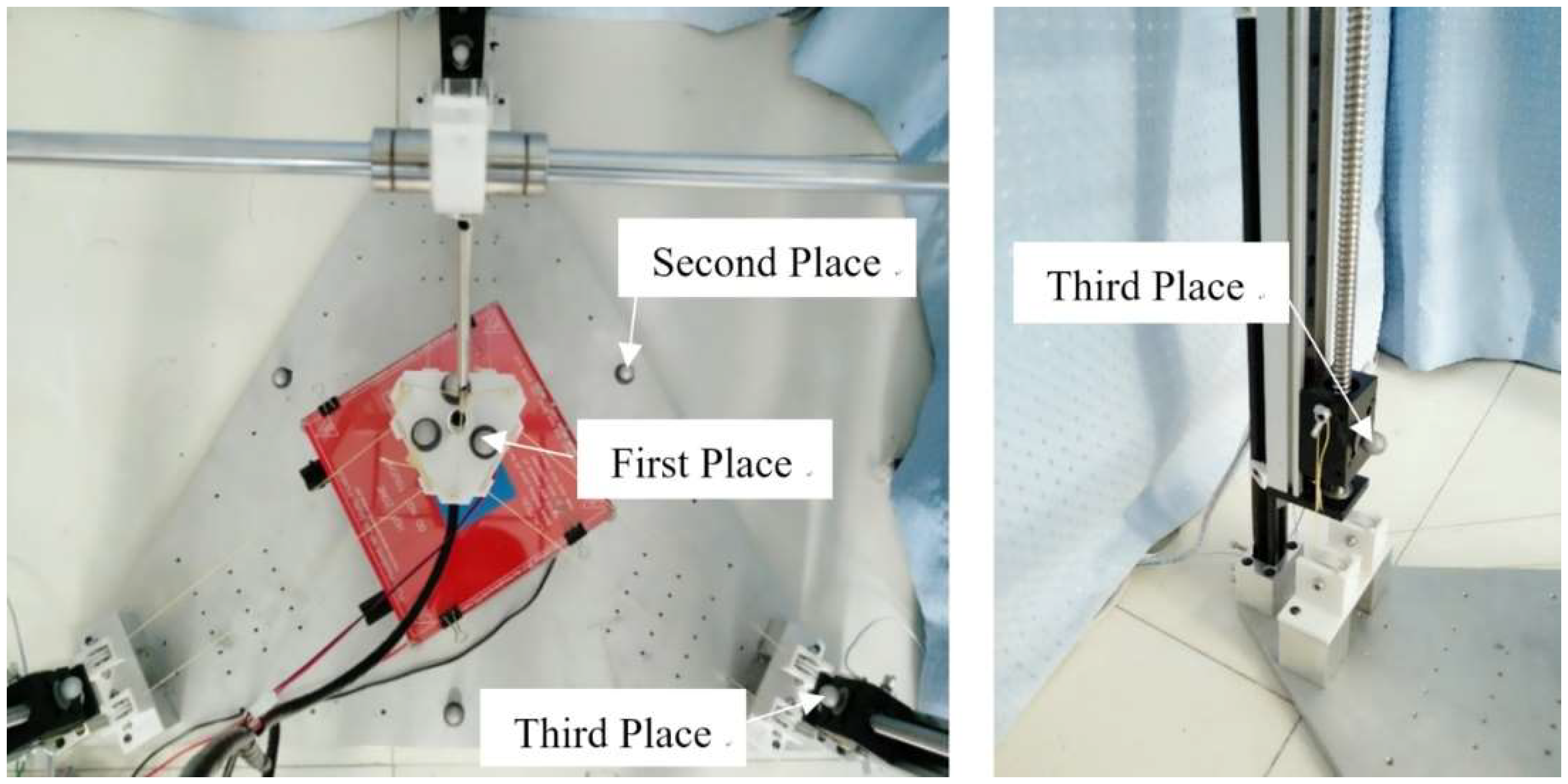
6. Calibration Experiment
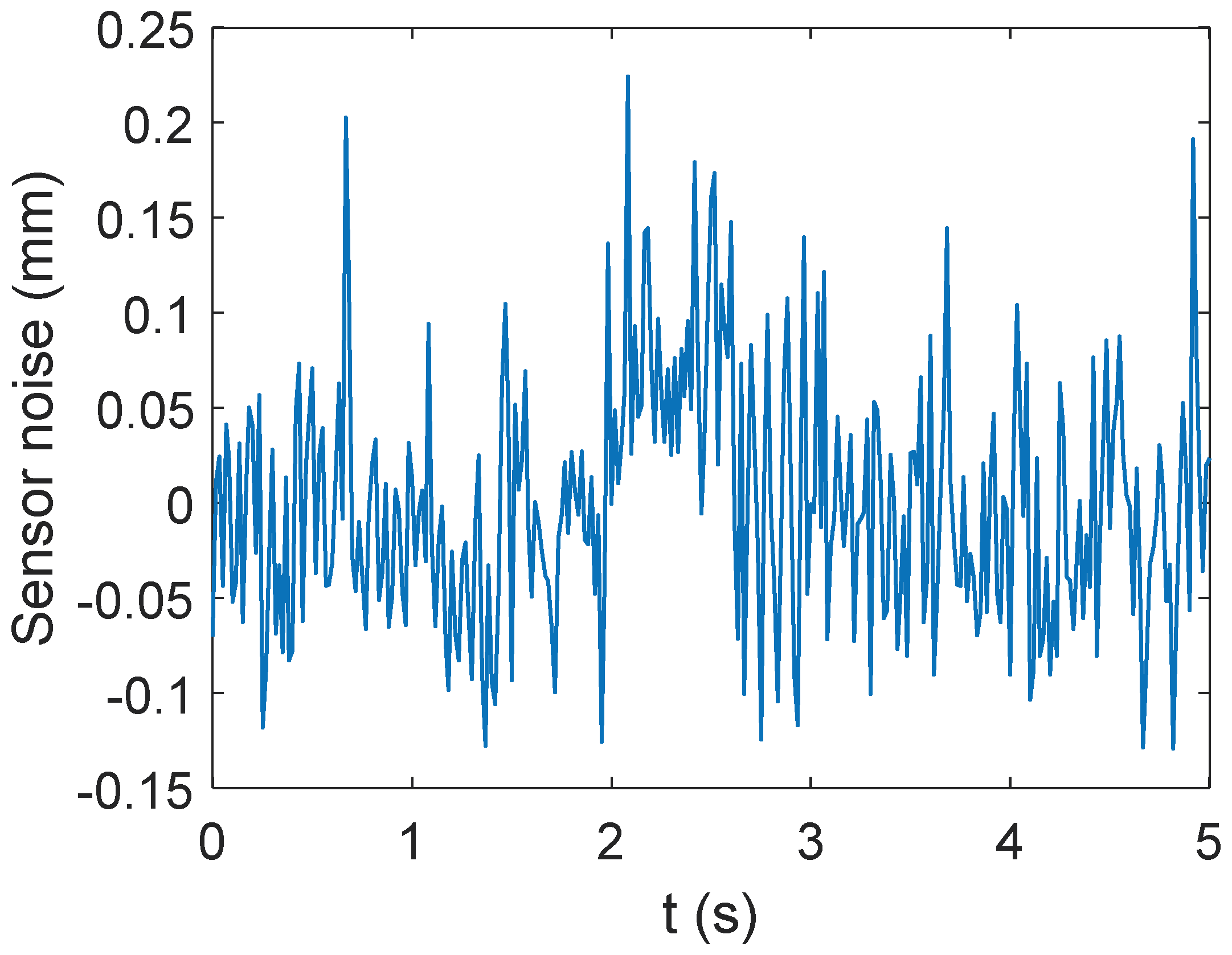
6.1. Measurement
6.2. Data Processing
6.3. Calibration Result Verification
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berti, A.; Merlet, J.P.; Carricato, M. Solving the direct geometrico-static problem of underconstrained cable-driven parallel robots by interval analysis. Int. J. Robot. Res. 2016, 35, 723–739. [Google Scholar] [CrossRef]
- Zi, B.; Qian, S. Design, Analysis and Control of Cable-Suspended Parallel Robots and Its Applications; Springer: Singapore, 2017. [Google Scholar]
- Zi, B.; Li, Y. Conclusions in theory and practice for advancing the applications of cable-driven mechanisms. Chin. J. Mech. Eng. 2017, 30, 763–765. [Google Scholar] [CrossRef]
- Zhou, B.; Zi, B.; Qian, S. Dynamics-based nonsingular interval model and luffing angular response field analysis of the dacs with narrowly bounded uncertainty. Nonlinear Dyn. 2017, 90, 2599–2626. [Google Scholar] [CrossRef]
- Zi, B.; Sun, H.; Zhang, D. Design, analysis and control of a winding hybrid-driven cable parallel manipulator. Robot. Comput. Integr. Manuf. 2017, 48, 196–208. [Google Scholar] [CrossRef]
- Barnett, E.; Gosselin, C. Large-scale 3d printing with a cable-suspended robot. Addit. Manuf. 2015, 7, 27–44. [Google Scholar] [CrossRef]
- Izard, J.B.; Dubor, A.; Hervé, P.E.; Cabay, E.; Culla, D.; Rodriguez, M.; Barrado, M. Large-scale 3d printing with cable-driven parallel robots. Constr. Robot. 2017, 1, 69–76. [Google Scholar] [CrossRef]
- Qian, S.; Zi, B.; Shang, W.; Xu, Q. A review on cable-driven parallel robots. Chin. J. Mech. Eng. 2018, 31, 66. [Google Scholar] [CrossRef]
- Gang, C.; Tong, L.; Ming, C.; Xuan, J.Q.; Xu, S.H. Review on kinematics calibration technology of serial robots. Int. J. Precis. Eng. Manuf. 2014, 15, 1759–1774. [Google Scholar] [CrossRef]
- Zhuang, H.; Yan, J.; Masory, O. Calibration of stewart platforms and other parallel manipulators by minimizing inverse kinematic residuals. J. Robot. Syst. 1998, 15, 395–405. [Google Scholar] [CrossRef]
- Dong, W.; Lin, W.; Qian, C.; Ye, C.; Gao, H. GA-based modified D-H method calibration modelling for 6-DoFs serial robot. In Proceedings of the Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 225–230. [Google Scholar]
- Du, G.; Shao, H.; Chen, Y.; Zhang, P.; Liu, X. An online method for serial robot self-calibration with CMAC and UKF. Robot. Comput. Integr. Manuf. 2016, 42, 39–48. [Google Scholar] [CrossRef]
- Joubair, A.; Long, F.Z.; Bigras, P.; Bonev, I.A. Use of a force-torque sensor for self-calibration of a 6-DOF medical robot. Sensors 2016, 16, 798. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Kaneko, A.M.; Endo, G.; Fukushima, E.F. In-field self-calibration of robotic manipulator using stereo camera: Application to humanitarian demining robot. Adv. Robot. 2015, 29, 1045–1059. [Google Scholar] [CrossRef]
- Yin, S.; Ren, Y.; Zhu, J.; Yang, S.; Ye, S. A vision-based self-calibration method for robotic visual inspection systems. Sensors 2013, 13, 16565–16582. [Google Scholar] [CrossRef] [PubMed]
- Daney, D.; Andreff, N.; Chabert, G.; Papegay, Y. Interval method for calibration of parallel robots: Vision-based experiments. Mech. Mach. Theor. 2006, 41, 929–944. [Google Scholar] [CrossRef]
- Majarena, A.C.; Santolaria, J.; Samper, D.; Aguilar, J.J. An overview of kinematic and calibration models using internal/external sensors or constraints to improve the behavior of spatial parallel mechanisms. Sensors 2010, 10, 10256–10297. [Google Scholar] [CrossRef] [PubMed]
- Joubair, A.; Slamani, M.; Bonev, I.A. Kinematic calibration of a five-bar planar parallel robot using all working modes. Robot. Comput. Integr. Manuf. 2013, 29, 15–25. [Google Scholar] [CrossRef]
- Joubair, A.; Nubiola, A.; Bonev, I. Calibration efficiency analysis based on five observability indices and two calibration models for a six-axis industrial robot. SAE Int. J. Aerosp. 2013, 6, 161–168. [Google Scholar] [CrossRef]
- Joshi, S.A.; Surianarayan, A. Calibration of a 6-DOF cable robot using two inclinometers. Perform. Metr. Intell. Syst. 2003, 3660–3665. [Google Scholar]
- Ren, X.D.; Feng, Z.R.; Su, C.P. A new calibration method for parallel kinematics machine tools using orientation constraint. Int. J. Mach. Tools Manuf. 2009, 49, 708–721. [Google Scholar] [CrossRef]
- Lau, D. Initial length and pose calibration for cable-driven parallel robots with relative length feedback. In Cable-Driven Parallel Robots; Springer: Cham, Switzerland, 2018; pp. 140–151. [Google Scholar]
- Duan, X.; Qiu, Y.; Duan, Q.; Du, J. Calibration and motion control of a cable-driven parallel manipulator based triple-level spatial positioner. Adv. Mech. Eng. 2014, 6, 368018. [Google Scholar] [CrossRef]
- Mustafa, S.K.; Yang, G.; Song, H.Y.; Lin, W.; Chen, I.M. Self-calibration of a biologically inspired 7 DOF cable-driven robotic arm. IEEE/ASME Trans. Mechatron. 2010, 13, 66–75. [Google Scholar] [CrossRef]
- Borm, J.H.; Menq, C.H. Determination of optimal measurement configurations for robot calibration based on observability measure. Int. J. Robot. Res. 1991, 10, 51–63. [Google Scholar] [CrossRef]
- Menq, C.H.; Borm, J.H.; Lai, J.Z. Identification and observability measure of a basis set of error parameters in robot calibration. J. Mech. Transm. Autom. Des. 1989, 111, 513–518. [Google Scholar] [CrossRef]
- Driels, M.R.; Pathre, U.S. Significance of observation strategy on the design of robot calibration experiments. J. Field Robot. 2010, 7, 197–223. [Google Scholar] [CrossRef]
- Nahvi, A.; Hollerbach, J.M.; Hayward, V. Calibration of a parallel robot using multiple kinematic closed loops. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 407–412. [Google Scholar]
- Jia, Q.; Wang, S.; Chen, G.; Wang, L.; Sun, H. A novel optimal design of measurement configurations in robot calibration. Math. Probl. Eng. 2018, 4689710. [Google Scholar] [CrossRef]
- Li, T.; Sun, K.; Jin, Y.; Liu, H. A novel optimal calibration algorithm on a dexterous 6 DOF serial robot-with the optimization of measurement poses number. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 975–981. [Google Scholar]
- Zhou, J.; Nguyen, H.N.; Kang, H.J. Selecting optimal measurement poses for kinematic calibration of industrial robots. Adv. Mech. Eng. 2014, 6, 291389. [Google Scholar] [CrossRef]
- Wang, D.; Wang, J.; Zhu, X.; Shao, Y. Determination of optimal measurement configurations for polishing robot calibration. Int. J. Model. Identif. Control 2014, 21, 211–222. [Google Scholar] [CrossRef]
- Daney, D.; Papegay, Y.; Madeline, B. Choosing measurement poses for robot calibration with the local convergence method and tabu search. Int. J. Robot. Res. 2005, 24, 501–518. [Google Scholar] [CrossRef]
- Sun, Y.; Hollerbach, J.M. Active robot calibration algorithm, IEEE International Conference on Robotics and Automation. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1276–1281. [Google Scholar]
- Nategh, M.J.; Agheli, M.M. A total solution to kinematic calibration of hexapod machine tools with a minimum number of measurement configurations and superior accuracies. Int. J. Mach. Tools Manuf. 2009, 49, 1155–1164. [Google Scholar] [CrossRef]
- Wang, H.; Gao, T.; Kinugawa, J.; Kosuge, K. Finding measurement configurations for accurate robot calibration: Validation with a cable-driven robot. IEEE Trans. Robot. 2017, 33, 1156–1169. [Google Scholar] [CrossRef]
- Bo, O. Efficient computation method of force-closure workspace for 6-dof cable-driven parallel manipulators. J. Mech. Eng. 2013, 49, 34–41. [Google Scholar]


| x/mm | y/mm | z/mm | |
|---|---|---|---|
| −30.2310 | 24.5370 | 110 | |
| −42.5000 | 24.5370 | 110 | |
| −31.8320 | 43.015 | 110 | |
| −36.3660 | 13.9120 | 110 |
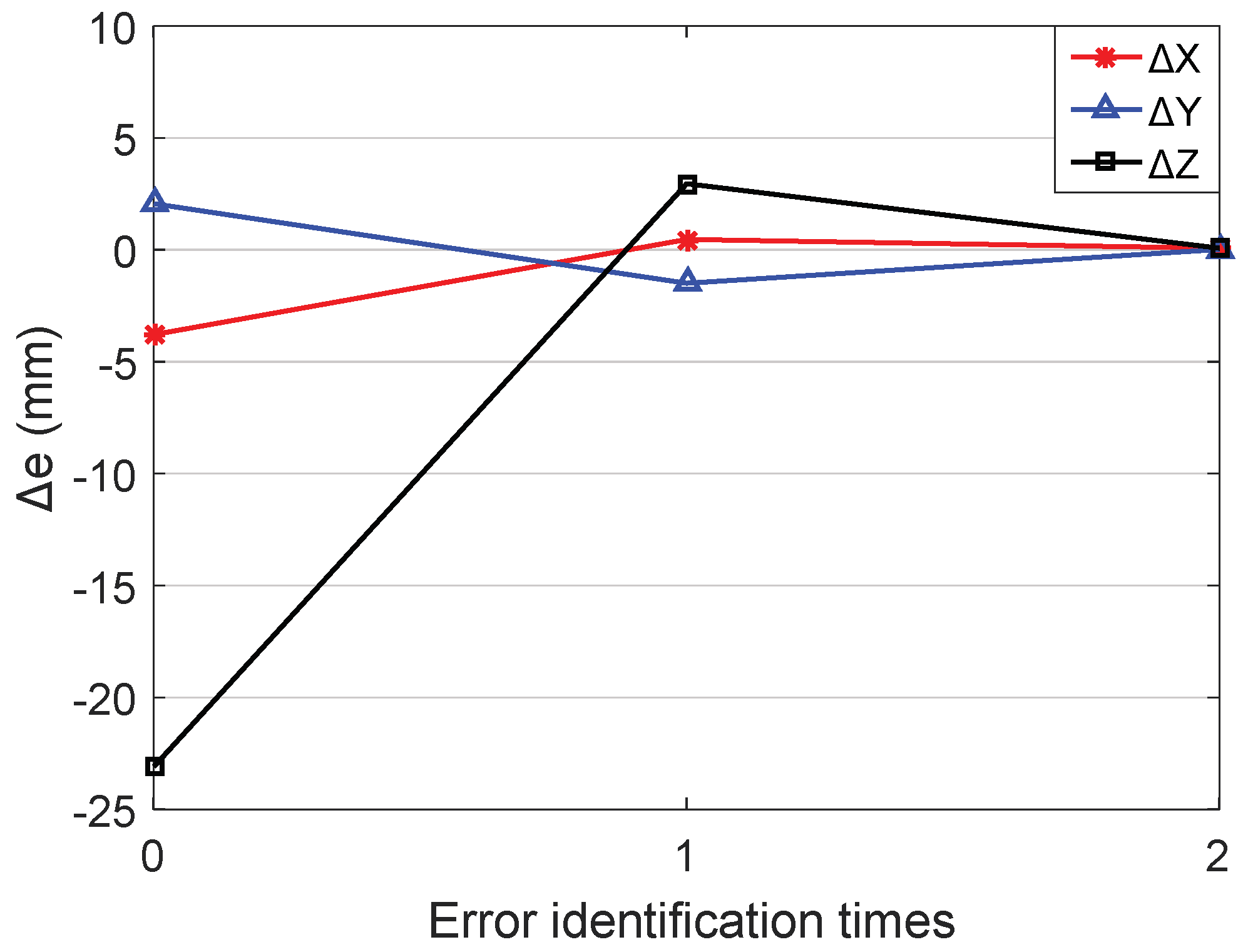
| Geometric Errors | Preliminary Errors (mm) | Error Identification Values (i = 1, 2, 3, 4)/(mm) | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Δx1a | 2.0000 | 2.3485 | −0.3485 | ||
| Δy1a | −1.1110 | −1.3170 | 0.2060 | ||
| Δz1a | −1.0000 | −1.0225 | 0.0225 | ||
| Δx2a | 3.0000 | 3.2568 | −0.2568 | ||
| Δy2a | −2.1110 | −1.9264 | −0.1845 | ||
| Δz2a | 1.0000 | 1.0648 | −0.0648 | ||
| Δx3a | 0.0000 | −0.1376 | 0.1376 | ||
| Δy3a | −0.7780 | −1.9027 | 1.1245 | ||
| Δz3a | −0.5000 | −0.2944 | 0.2055 | ||
| Δl1 | 2.0000 | 2.4042 | 0.4042 | ||
| Δl2 | 1.0000 | 0.1776 | 0.3223 | ||
| Δl3 | 3.0000 | 1.8487 | 1.1509 | ||
| Kinematic Parameters | Parameters without Calibration (mm) |
|---|---|
| A group cable length | 382.0 |
| B group cable length | 387.0 |
| C group cable length | 388.0 |
| The cable outlet A1 | (306.0, −149.5, 77.0) |
| The cable outlet A2 | (282.5, −188.5, 78.0) |
| The cable outlet B1 | (−305.2, −149.1, 81.0) |
| The cable outlet B2 | (−281.6, −189.7, 81.0) |
| The cable outlet C1 | (−23.5, 339.0, 75.0) |
| The cable outlet C2 | (23.5, 338.6, 77.0) |
| Virtual Cable Outlets | Parameters without Calibration (mm) |
|---|---|
| A | (253.90, −146.50, 77.5) |
| B | (−253.30, −146.25, 81) |
| C | (0, 292.50, 76) |
| Markers on the Base | Coordinate Value (mm) |
|---|---|
| F1 | (547.7330, 160.4733, 24.0144) |
| F2 | (362.9547, −147.6336, 22.0150) |
| F3 | (716.6375, −158.7557, 23.4959) |
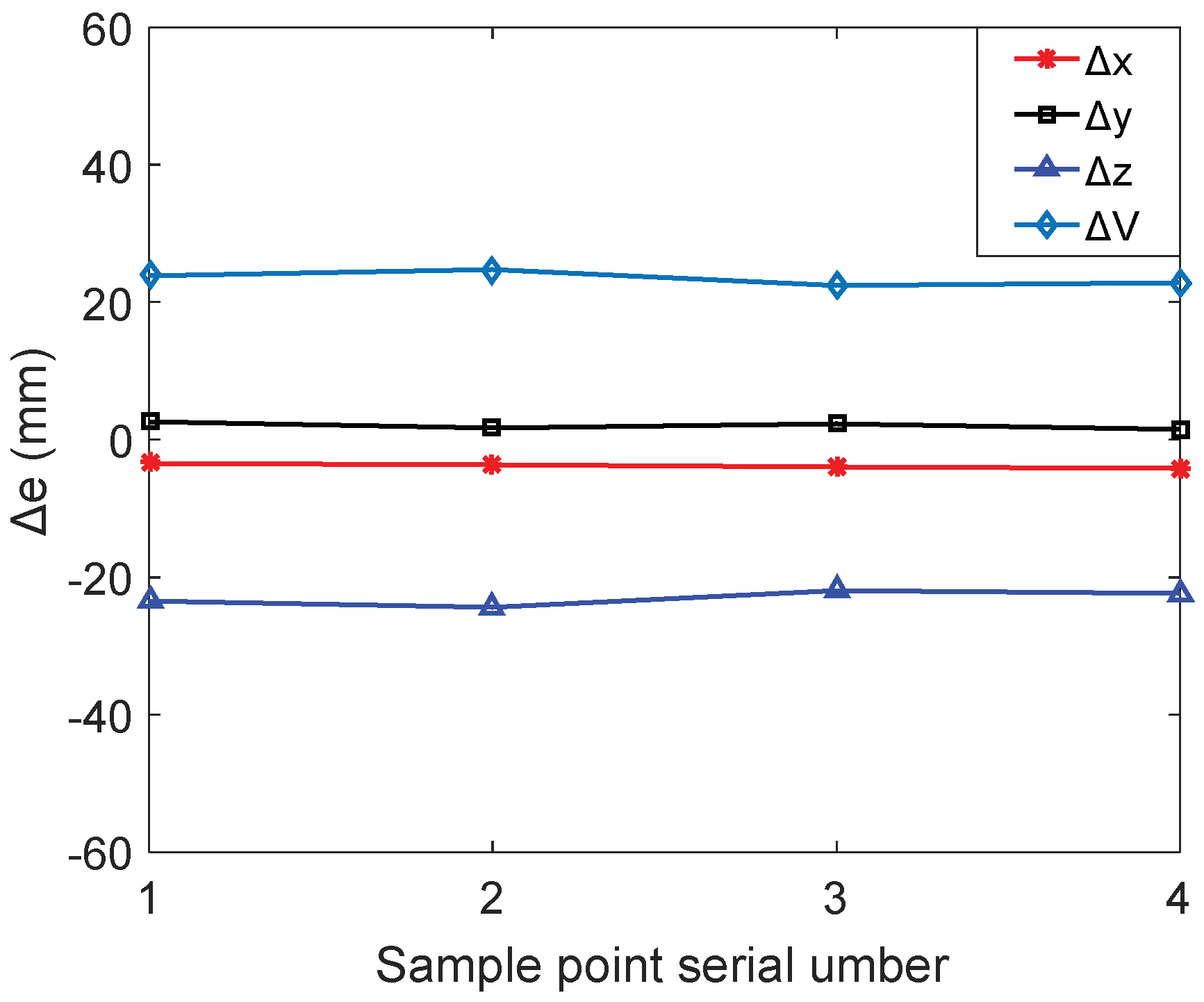
| Maximal value | −3.4567 | 2.5909 | −21.9312 | 22.3526 |
| Minimum value | −4.1500 | 1.5527 | −24.4203 | 24.8190 |
| Average value | −3.8023 | 2.0687 | −23.0636 | 23.4662 |
| Maximal value | 0.4251 | 0.2145 | 0.4146 | 0.6314 |
| Minimum value | −0.1354 | −0.4783 | 0.3427 | 0.6038 |
| Average value | 0.2674 | −0.1547 | 0.3594 | 0.4740 |
| Kinematic Parameters | Before Calibration (mm) | Error Identification Value (l = 1, 2) (mm) | After Calibration (mm) | |
|---|---|---|---|---|
| First Time | Second Time | |||
| 253.9000 | 2.07820 | 1.16230 | 257.1405 | |
| −146.5000 | −1.25331 | −0.68765 | −148.4410 | |
| 77.5000 | 1.85782 | −0.46523 | 78.8926 | |
| −253.3000 | −3.31530 | −0.40253 | −257.0180 | |
| −146.2500 | −1.87986 | −0.32561 | −148.4550 | |
| 81.0000 | −1.72365 | −0.25632 | 79.0201 | |
| 0.0000 | −0.12250 | 0.12585 | 0.0033 | |
| 292.5000 | 5.71754 | 0.53260 | 298.7501 | |
| 76.0000 | 4.66235 | −2.18561 | 78.4767 | |
| 382.0000 | 1.60682 | 1.26320 | 384.8700 | |
| 387.0000 | −2.65896 | 0.54825 | 384.8893 | |
| 388.0000 | −4.85620 | 2.15421 | 385.2980 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, S.; Bao, K.; Zi, B.; Wang, N. Kinematic Calibration of a Cable-Driven Parallel Robot for 3D Printing. Sensors 2018, 18, 2898. https://doi.org/10.3390/s18092898
Qian S, Bao K, Zi B, Wang N. Kinematic Calibration of a Cable-Driven Parallel Robot for 3D Printing. Sensors. 2018; 18(9):2898. https://doi.org/10.3390/s18092898
Chicago/Turabian StyleQian, Sen, Kunlong Bao, Bin Zi, and Ning Wang. 2018. "Kinematic Calibration of a Cable-Driven Parallel Robot for 3D Printing" Sensors 18, no. 9: 2898. https://doi.org/10.3390/s18092898
APA StyleQian, S., Bao, K., Zi, B., & Wang, N. (2018). Kinematic Calibration of a Cable-Driven Parallel Robot for 3D Printing. Sensors, 18(9), 2898. https://doi.org/10.3390/s18092898




