Improving the Performance of Multi-GNSS Time and Frequency Transfer Using Robust Helmert Variance Component Estimation
Abstract
1. Introduction
2. Observation Equation of Multi-GNSS CP Time Transfer
3. Robust Helmert Variance Component Estimation (RVCE)
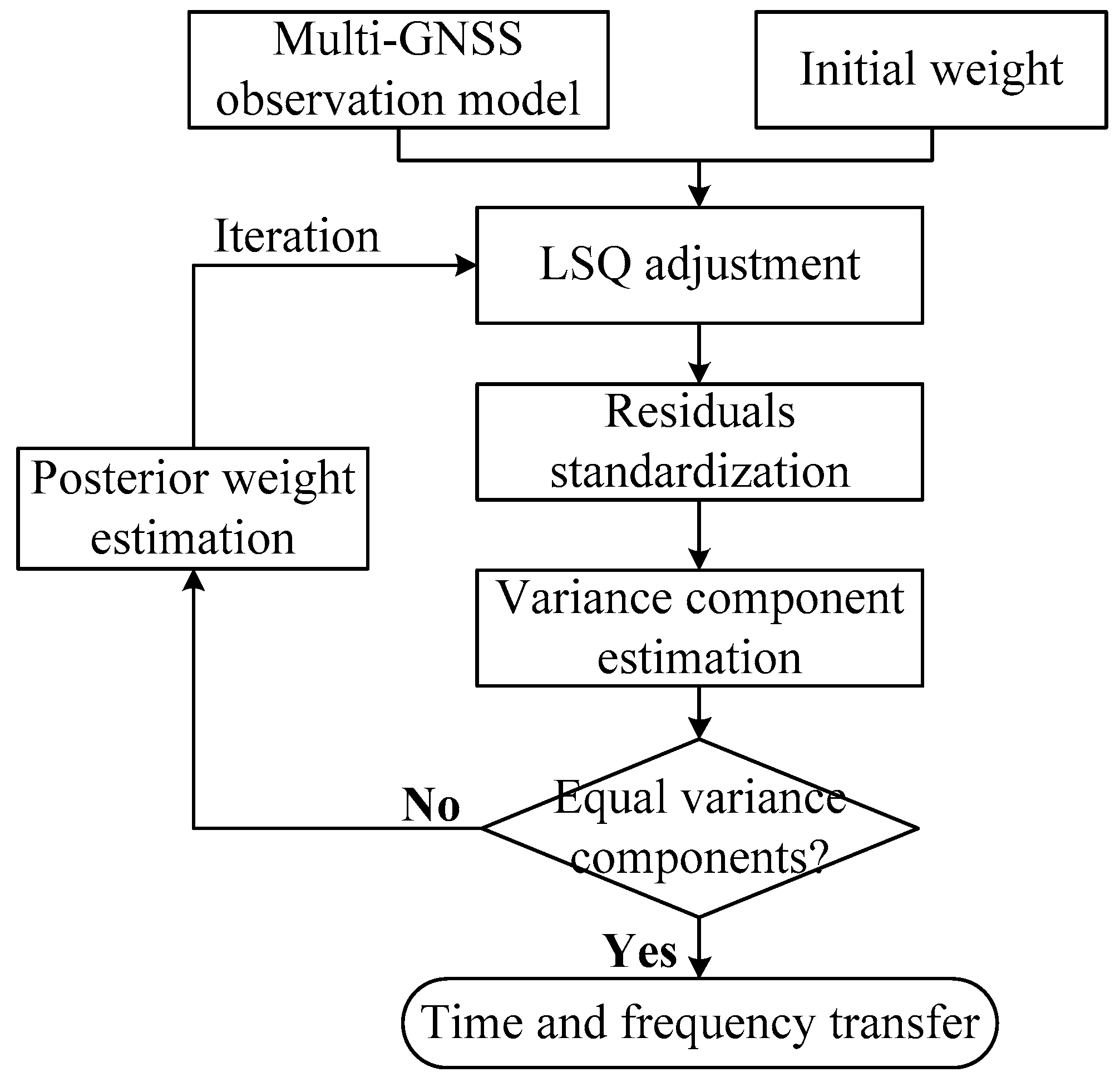
4. Implementation of Multi-GNSS Time and Frequency Transfer using RVCE
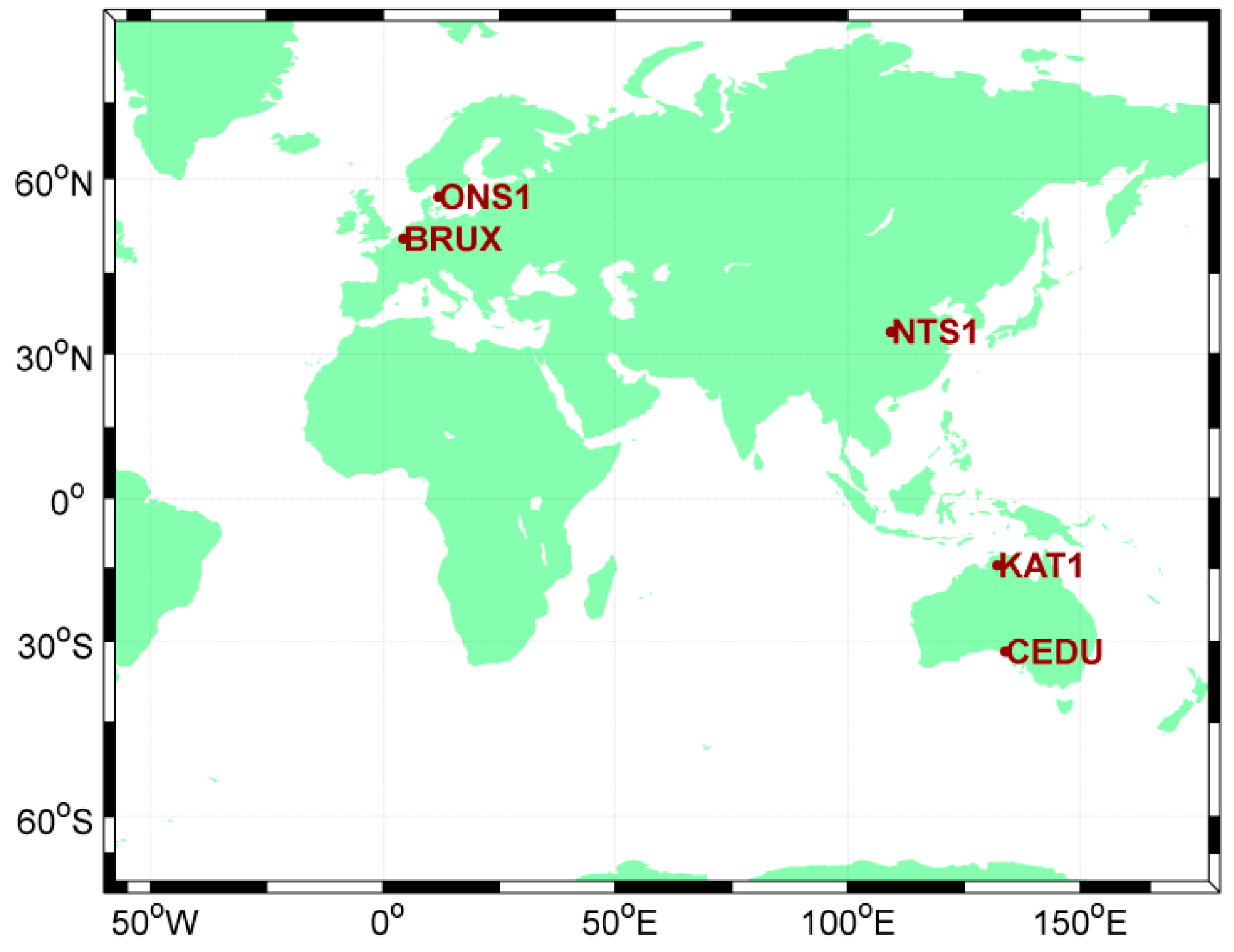
5. Experimental Design
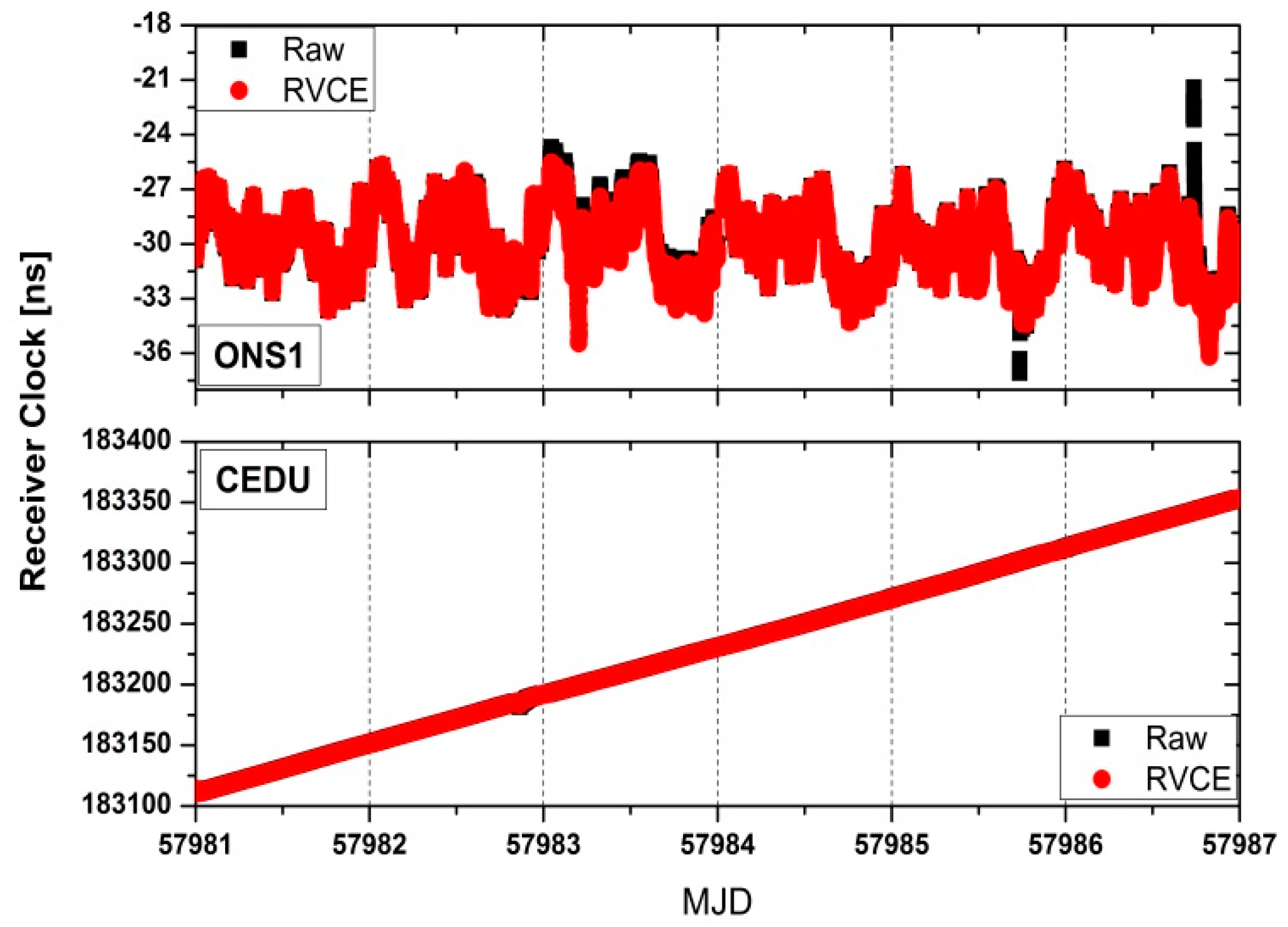
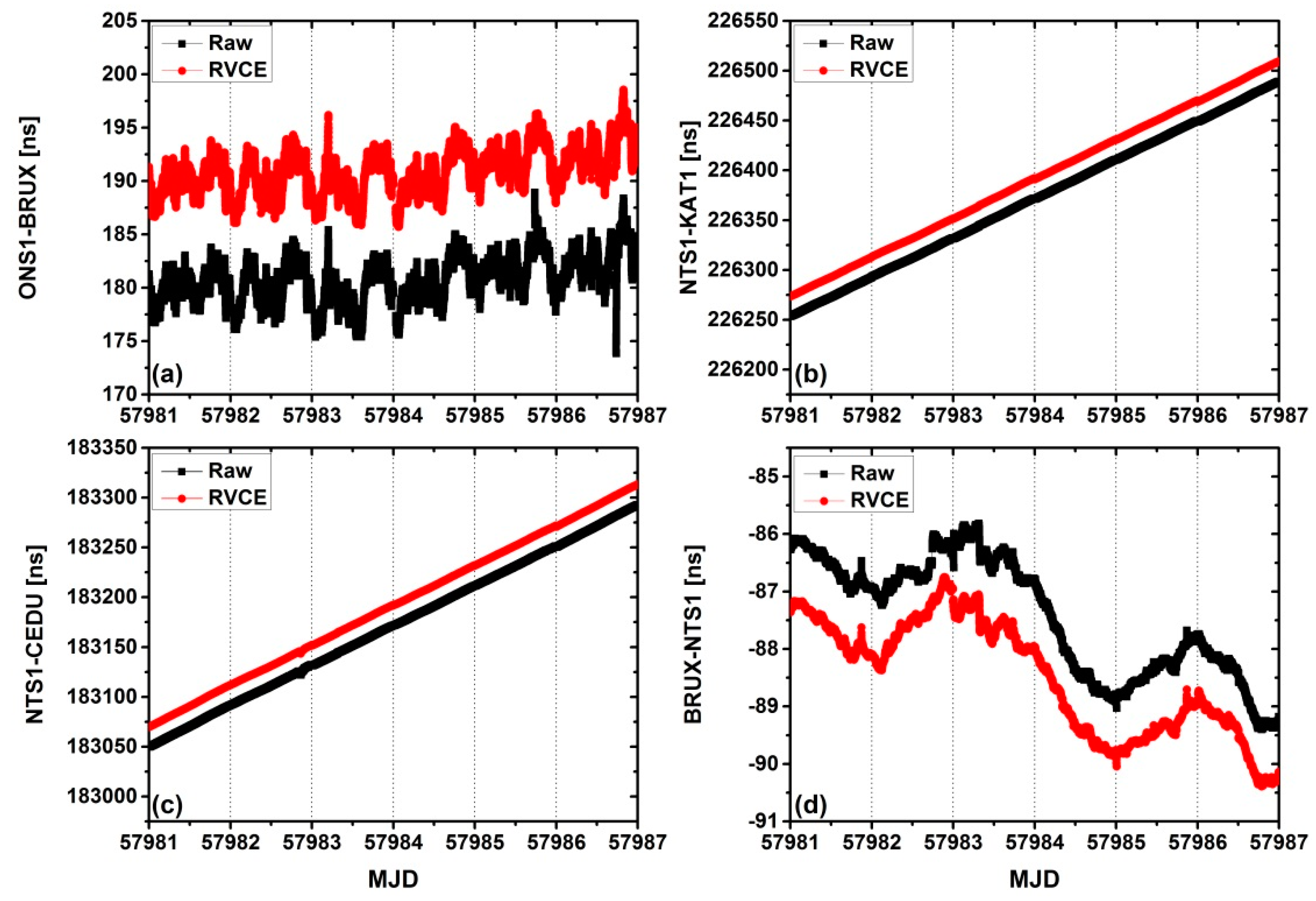
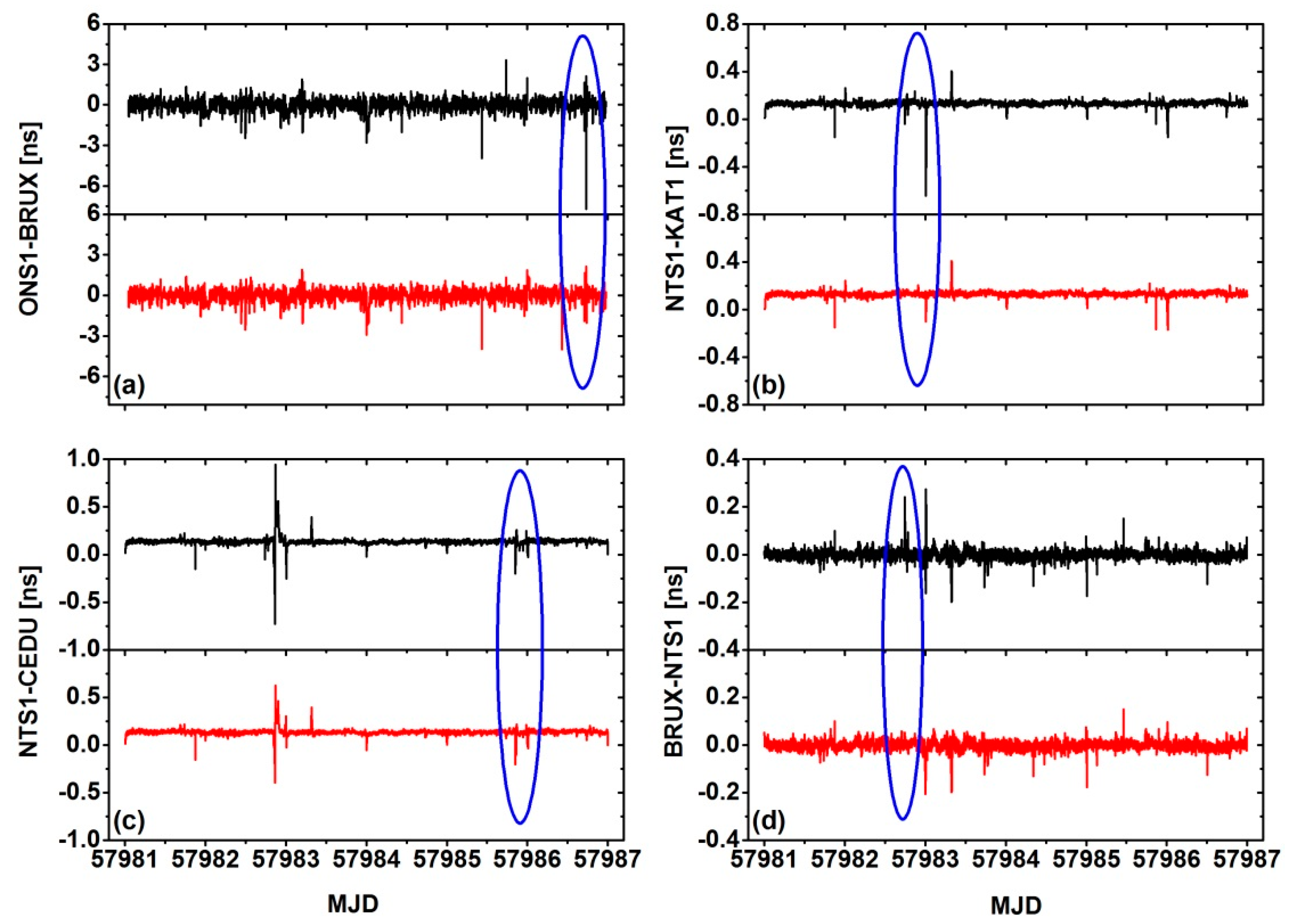
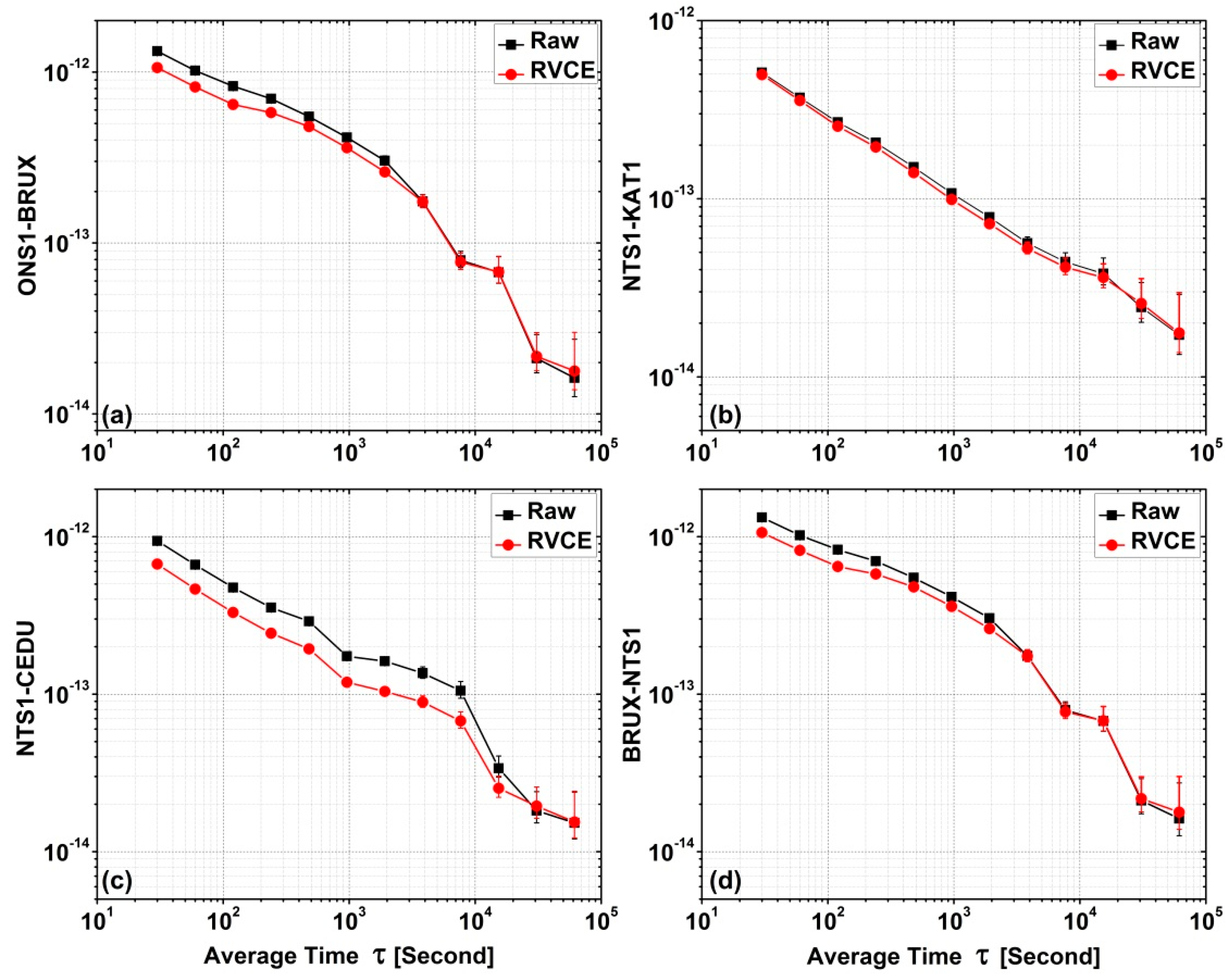
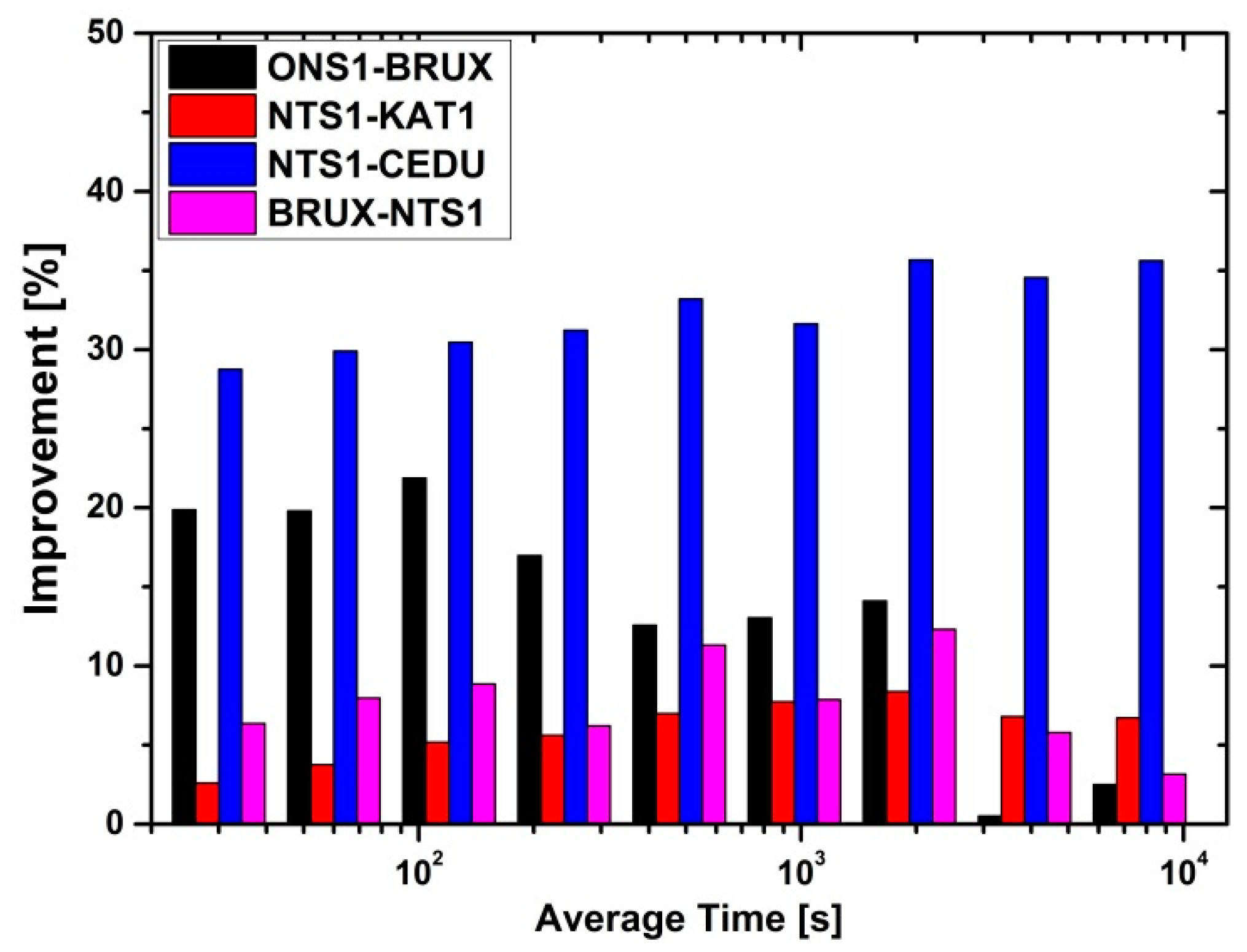
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Allan, D.W.; Weiss, M. Accurate time and frequency transfer during common-view of a GPS satellite. In Proceedings of the 1980 IEEE Frequency Control Symposium, Philadelphia, PA, USA, 28–30 May 1980; pp. 334–356. [Google Scholar]
- Weiss, M.A.; Petit, G.; Jiang, Z. A comparison of GPS common-view time transfer to all-in-view. In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005. [Google Scholar]
- Petit, G.; Jiang, Z. GPS All in View time transfer for TAI computation. Metrologia 2008, 45, 35–45. [Google Scholar] [CrossRef]
- Ray, J.; Senior, K. Geodetic techniques for time and frequency comparisons using GPS phase and code measurements. Metrologia 2005, 42, 215–232. [Google Scholar] [CrossRef]
- Jiang, Z.; Lewandowski, W. Use of GLONASS for UTC time transfer. Metrologia 2012, 49, 57–61. [Google Scholar] [CrossRef]
- Jiang, Z.; Lewandowski, W. Accurate GLONASS Time Transfer for Generation of the Coordinated Universal Time. Int. J. Navig. Obs. 2012, 2012. [Google Scholar] [CrossRef]
- Martínez-Belda, M.C.; Defraigne, P. Single-frequency time and frequency transfer with Galileo E5. In Proceedings of the IEEE Frequency Control and the European Frequency and Time Forum, San Francisco, CA, USA, 2–5 May 2011; pp. 1–6. [Google Scholar]
- Defraigne, P.; Martínez-Belda, M.C.; Baire, Q. Using Galileo E5 for time and frequency transfer. In Proceedings of the 3rd Galileo Scientific Colloquium, Copenhaguen, Denmark, 30 August–2 September 2011. [Google Scholar]
- Huang, W.; Defraigne, P. BeiDou Time Transfer with the Standard CGGTTS. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1005–1012. [Google Scholar] [CrossRef] [PubMed]
- Guang, W.; Dong, S.; Wu, W.; Zhang, J.; Yuan, Y.; Zhang, S. Progress of BeiDou time transfer at NTSC. Metrologia 2018, 55, 175–187. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Hugentobler, U.; Schildknecht, T.; Gäde, A. Combined multi-system GNSS analysis for time and frequency transfer. In Proceedings of the 20th European Frequency and Time Forum, Braunschweig, Germany, 27–30 March 2006; pp. 530–537. [Google Scholar]
- Defraigne, P.; Baire, Q. Combining GPS and GLONASS for time and frequency transfer. Adv. Space Res. 2011, 47, 265–275. [Google Scholar] [CrossRef]
- Harmegnies, A.; Defraigne, P.; Petit, G. Combining GPS and GLONASS in all-in-view for time transfer. Metrologia 2013, 50, 277–287. [Google Scholar] [CrossRef]
- Geng, J.; Zhao, Q.; Shi, C.; Liu, J. A review on the inter-frequency biases of GLONASS carrier-phase data. J. Geod. 2017, 91, 329–340. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Torre, A.D.; Caporali, A. An analysis of inter-system biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—the challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Zhang, R.; Gao, Y.; Cai, H. Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations. Remote Sens. 2018, 10, 324. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2018, 22. [Google Scholar] [CrossRef]
- Defraigne, P.; Bruyninx, C. On the link between GPS pseudorange noise and day-boundary discontinuities in geodetic time transfer solutions. GPS Solut. 2007, 11, 239–249. [Google Scholar] [CrossRef]
- Petit, G.; Defraigne, P. The performance of GPS time and frequency transfer: comment on ‘A detailed comparison of two continuous GPS carrier-phase time transfer techniques’. Metrologia 2016, 53, 1003–1008. [Google Scholar] [CrossRef]
- Knight, N.L.; Wang, J. A comparison of outlier detection procedures and robust estimation methods in GPS positioning. J. Navig. 2009, 62, 699–709. [Google Scholar] [CrossRef]
- Zair, S.; Hégarat-Mascle, S.L.; Seignez, E. Outlier Detection in GNSS Pseudo-Range/Doppler Measurements for Robust Localization. Sensors 2016, 16, 580. [Google Scholar] [CrossRef] [PubMed]
- Kouba, J. A guide to using International GNSS Service (IGS) Products. Available online: https://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf (accessed on 15 August 2018).
- Gao, Z.; Shen, W.; Zhang, H.; Ge, M.; Niu, X. Application of Helmert Variance Component Based Adaptive Kalman Filter in Multi-GNSS PPP/INS Tightly Coupled Integration. Remote Sens. 2016, 8, 553. [Google Scholar] [CrossRef]
- Guo, H.R. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites. Ph.D. Thesis, Information Engineering University, Zhengzhou, China, October 2006. [Google Scholar]
- Guo, H.R.; Yang, Y.X. Analyses of main error sources on time domain frequency stability for atomic clocks of navigation satellites. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 218–221. [Google Scholar]
- Huang, G.; Zhang, Q. Real-time estimation of satellite clock offset using adaptively robust Kalman filter with classified adaptive factors. GPS Solut. 2012, 16, 531–539. [Google Scholar] [CrossRef]
- Ou, J.K. Design of a new scheme of robust estimation by three steps. Acta Geod. Cartogr. Sin. 1996, 25, 173–179. [Google Scholar]
- Zhou, J.W. Classical theory of errors and robust estimation. Acta Geod. Cartogr. Sin. 1989, 18, 115–120. [Google Scholar]
- Kubik, K. An error theory for the Danish method. In Proceedings of the International Symposium on Numerical Methods for Photogrammetric Mapping, Helsinki, Finland, 26–29 September 1982; pp. 299–309. [Google Scholar]
- Yang, Y.X. Robust estimation for dependent observations. Manuscr. Geod. 1994, 19, 10–17. [Google Scholar]
- Yang, Y.X.; Song, L.J.; Xu, T.H. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Yang, Y.X.; Song, L.J.; Xu, T.H. Robust parameter estimation for geodetic correlated observation. Acta Geod. Cartogr. Sin. 2002, 31, 95–99. [Google Scholar]
- Yang, Y.X.; Cheng, M.K.; Shum, C.K.; Tapley, B.D. Robust estimation of systematic errors of satellite laser range. J. Geod. 1999, 73, 345–349. [Google Scholar] [CrossRef]
- Defraigne, P.; Banerjee, P.; Lewandowski, W. Time transfer through GPS. Indian J. Radio Space Phys. 2007, 36, 303–312. [Google Scholar]
- Defraigne, P. GNSS Time Transfer. Available online: https://www.bipm.org/ws/CCTF/TAI_TRAINING/Allowed/Fundamentals/Training-2012-GNSS-Defraigne.pdf (accessed on 19 August 2018).
- Guidelines for Providing Data for PPP links. Available online: ftp://ftp2.bipm.org/pub/tai/timelinks/taippp/ppp_for_tai_guidelines_v2.pdf (accessed on 19 August 2018).
- Hatch, R. The synergism of GPS code and carrier measurements. In Proceedings of the Third International Symposium on Satellite Doppler Positioning, Las Cruces, NM, USA, 8–12 February 1982; pp. 1213–1231. [Google Scholar]
- Prange, L.; Dach, R.; Lutz, S.; Schaer, S.; Jäggi, A. The CODE solution for the IGS MGEX. In Proceedings of the IGS workshop, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Jiang, Z.; Petit, G. Combination of TWSTFT and GNSS for accurate UTC time transfer. Metrologia 2009, 46, 305–314. [Google Scholar] [CrossRef]
| Site Name | GNSS Receiver | Antenna | Frequency Standard |
|---|---|---|---|
| NTS1 | SEPT POLARX4TR | SEPCHOKE_MC | UTC (NTSC) |
| BRUX | SEPT POLARX4TR | JAVRINGANT_DM | UTC (ORB) |
| KAT1 | SEPT POLARX5 | LEIAR25.R3 | EXTERNAL H-MASER |
| CEDU | SEPT POLARX5 | AOAD/M_T | EXTERNAL H-MASER |
| ONS1 | TRIMBLE NETR9 | LEIAR25.R3 | EXTERNAL H-MASER |
| Time Link Name | Geodetic Distance (km) |
|---|---|
| ONS1-BRUX | 883.7 |
| NTS1-KAT1 | 5704.2 |
| NTS1-CEDU | 7294.5 |
| BRUX-NTS1 | 7537.5 |
| Items | Models and Strategies |
|---|---|
| Observations | Undifferenced carrier phase and code observation |
| Signal selection | GPS:L1/L2; BeiDou: B1/B2; Galileo: E1/E5a |
| Satellite orbit and clock | Using the precise satellite products from CODE [40] |
| Satellite antenna phase center | Corrected using MGEX value |
| Initial weight between code and phase | 0.0001:1 |
| Ionosphere | Eliminated by ionosphere-free combination [36,37,38] |
| Tropospheric delay | Initial model + random-walk process |
| Tropospheric mapping function | Neill mapping function (NMF) [41] |
| Elevation cutoff | 7° |
| Sampling rate | 30 s |
| Observation weight | Elevation dependent weight |
| Estimator | LS in sequential mode |
| Receiver clock offset | Estimated with white noise |
| ISB | Estimated with epoch-wise variable method |
| Phase wind-up effect | Model corrected |
| Time Link Name | Raw (ns) | RVCE (ns) | Improvement (%) |
|---|---|---|---|
| ONS1-BRUX | 0.420 | 0.397 | 5.48 |
| NTS1-KAT1 | 0.133 | 0.132 | 0.75 |
| NTS1-CEDU | 0.141 | 0.138 | 2.13 |
| BRUX-NTS1 | 0.019 | 0.018 | 5.26 |
| τ (seconds) | Time Link Name | |||||||
|---|---|---|---|---|---|---|---|---|
| ONS1-BRUX | NTS1-KAT1 | NTS1-CEDU | BRUX-NTS1 | |||||
| Raw | RVCE | Raw | RVCE | Raw | RVCE | Raw | RVCE | |
| 30 | 1.32 × 10−12 | 1.06 × 10−12 | 5.10 × 10−13 | 4.97 × 10−13 | 9.38 × 10−13 | 6.69 × 10−13 | 4.08 × 10−13 | 3.82 × 10−13 |
| 60 | 1.02 × 10−12 | 8.17 × 10−13 | 3.69 × 10−13 | 3.55 × 10−13 | 6.63 × 10−13 | 4.65 × 10−13 | 2.58 × 10−13 | 2.37 × 10−13 |
| 120 | 8.27 × 10−13 | 6.46 × 10−13 | 2.69 × 10−13 | 2.55 × 10−13 | 4.75 × 10−13 | 3.30 × 10−13 | 1.60 × 10−13 | 1.46 × 10−13 |
| 240 | 6.98 × 10−13 | 5.79 × 10−13 | 2.06 × 10−13 | 1.95 × 10−13 | 3.54 × 10−13 | 2.44 × 10−13 | 1.03 × 10−13 | 9.68 × 10−14 |
| 480 | 5.48 × 10−13 | 4.79 × 10−13 | 1.50 × 10−13 | 1.40 × 10−13 | 2.90 × 10−13 | 1.94 × 10−13 | 8.00 × 10−14 | 7.10 × 10−14 |
| 960 | 4.14 × 10−13 | 3.60 × 10−13 | 1.07 × 10−13 | 9.90 × 10−14 | 1.74 × 10−13 | 1.19 × 10−13 | 5.95 × 10−14 | 5.48 × 10−14 |
| 1920 | 3.03 × 10−13 | 2.60 × 10−13 | 7.88 × 10−14 | 7.22 × 10−14 | 1.62 × 10−13 | 1.04 × 10−13 | 4.33 × 10−14 | 3.80 × 10−14 |
| 3840 | 1.75 × 10−13 | 1.74 × 10−13 | 5.63 × 10−14 | 5.25 × 10−14 | 1.36 × 10−13 | 8.91 × 10−14 | 2.83 × 10−14 | 2.67 × 10−14 |
| 7680 | 7.92 × 10−14 | 7.72 × 10−14 | 4.42 × 10−14 | 4.13 × 10−14 | 1.05 × 10−13 | 6.76 × 10−14 | 2.26 × 10−14 | 2.19 × 10−14 |
| 15,360 | 6.74 × 10−14 | 6.77 × 10−14 | 3.80 × 10−14 | 3.61 × 10−14 | 3.39 × 10−14 | 2.53 × 10−14 | 1.90 × 10−14 | 1.57 × 10−14 |
| 30,720 | 2.11 × 10−14 | 2.17 × 10−14 | 2.46 × 10−14 | 2.58 × 10−14 | 1.82 × 10−14 | 1.95 × 10−14 | 1.22 × 10−14 | 1.19 × 10−14 |
| 61,440 | 1.62 × 10−14 | 1.78 × 10−14 | 1.72 × 10−14 | 1.76 × 10−14 | 1.52 × 10−14 | 1.55 × 10−14 | 1.56 × 10−14 | 1.37 × 10−14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Liu, N. Improving the Performance of Multi-GNSS Time and Frequency Transfer Using Robust Helmert Variance Component Estimation. Sensors 2018, 18, 2878. https://doi.org/10.3390/s18092878
Zhang P, Tu R, Gao Y, Zhang R, Liu N. Improving the Performance of Multi-GNSS Time and Frequency Transfer Using Robust Helmert Variance Component Estimation. Sensors. 2018; 18(9):2878. https://doi.org/10.3390/s18092878
Chicago/Turabian StyleZhang, Pengfei, Rui Tu, Yuping Gao, Rui Zhang, and Na Liu. 2018. "Improving the Performance of Multi-GNSS Time and Frequency Transfer Using Robust Helmert Variance Component Estimation" Sensors 18, no. 9: 2878. https://doi.org/10.3390/s18092878
APA StyleZhang, P., Tu, R., Gao, Y., Zhang, R., & Liu, N. (2018). Improving the Performance of Multi-GNSS Time and Frequency Transfer Using Robust Helmert Variance Component Estimation. Sensors, 18(9), 2878. https://doi.org/10.3390/s18092878




