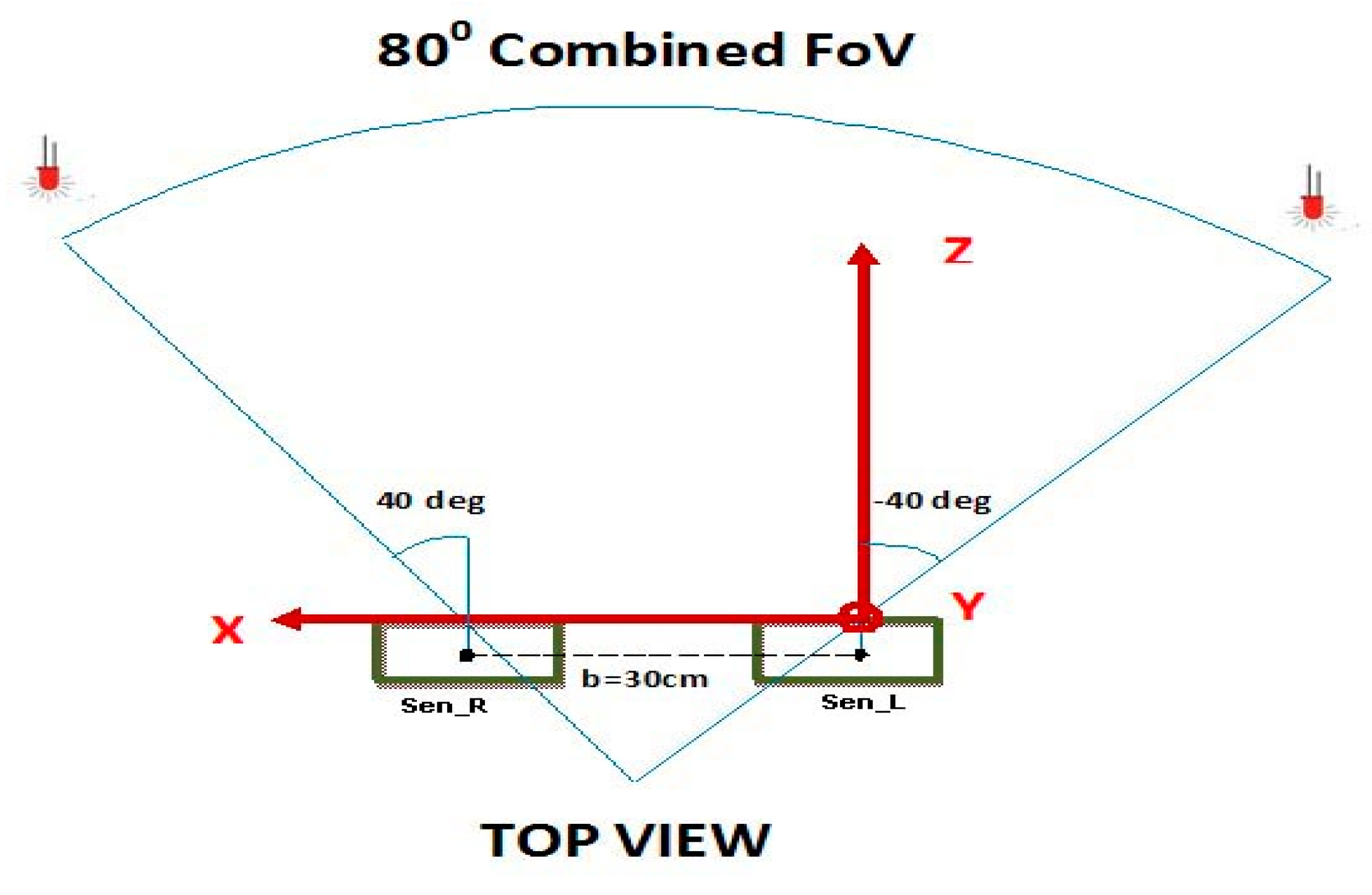
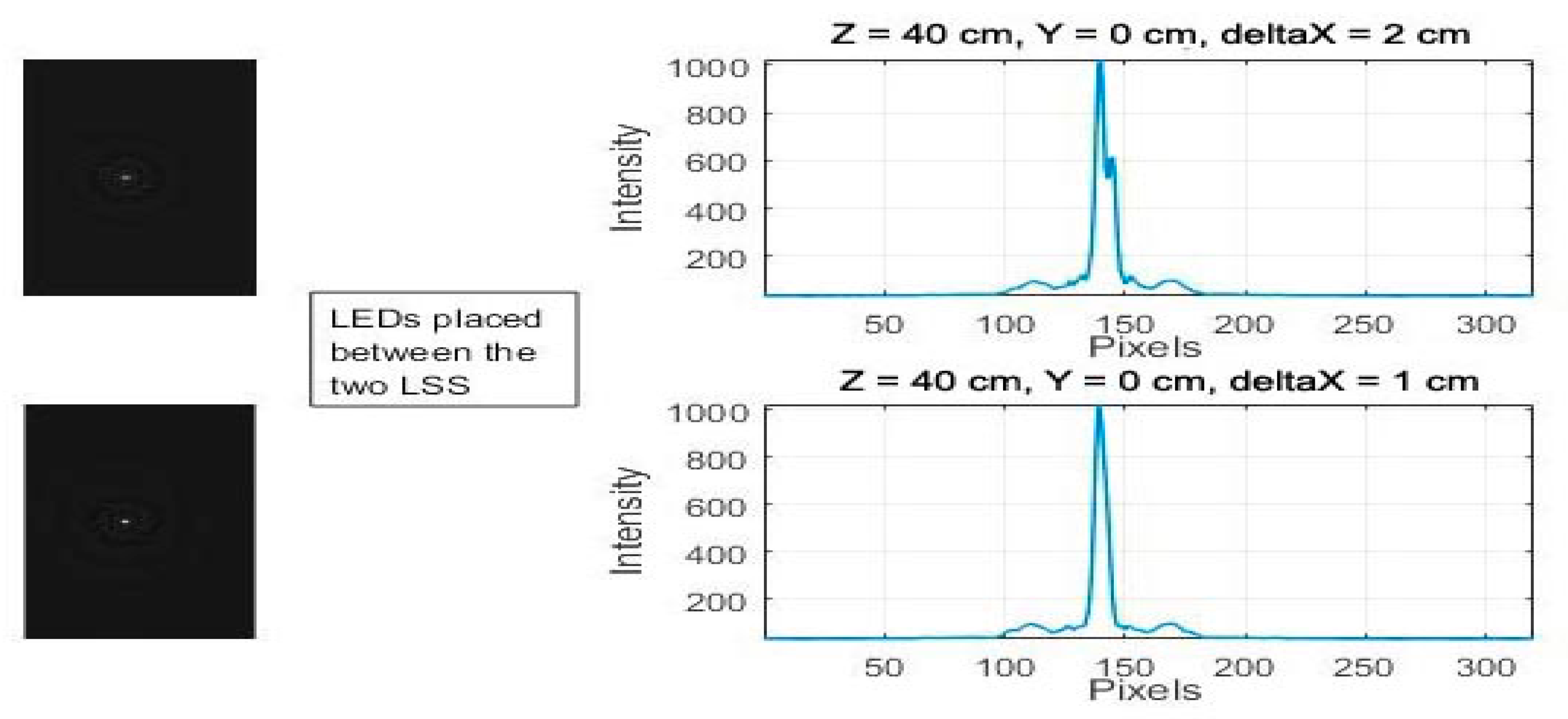
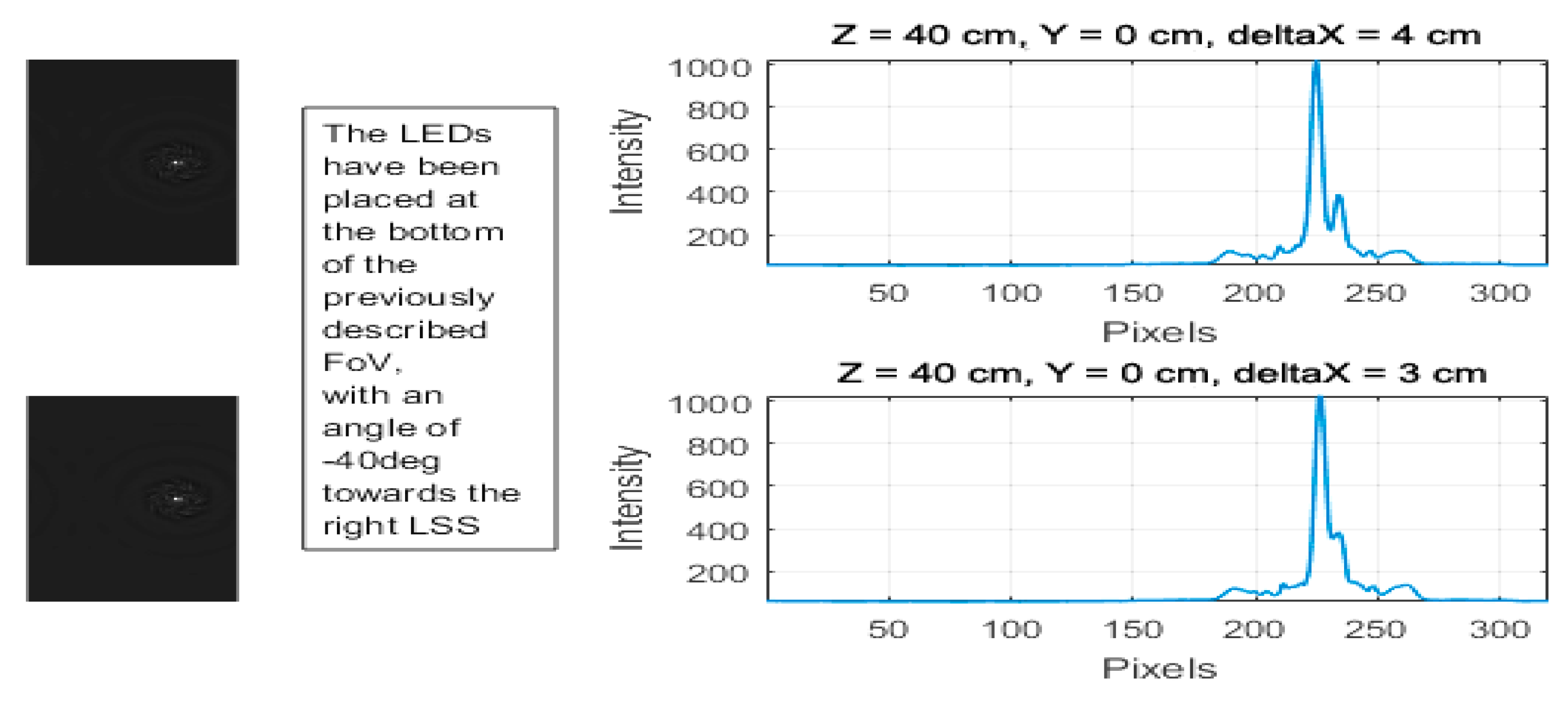
3.5.1. Calibration Phase
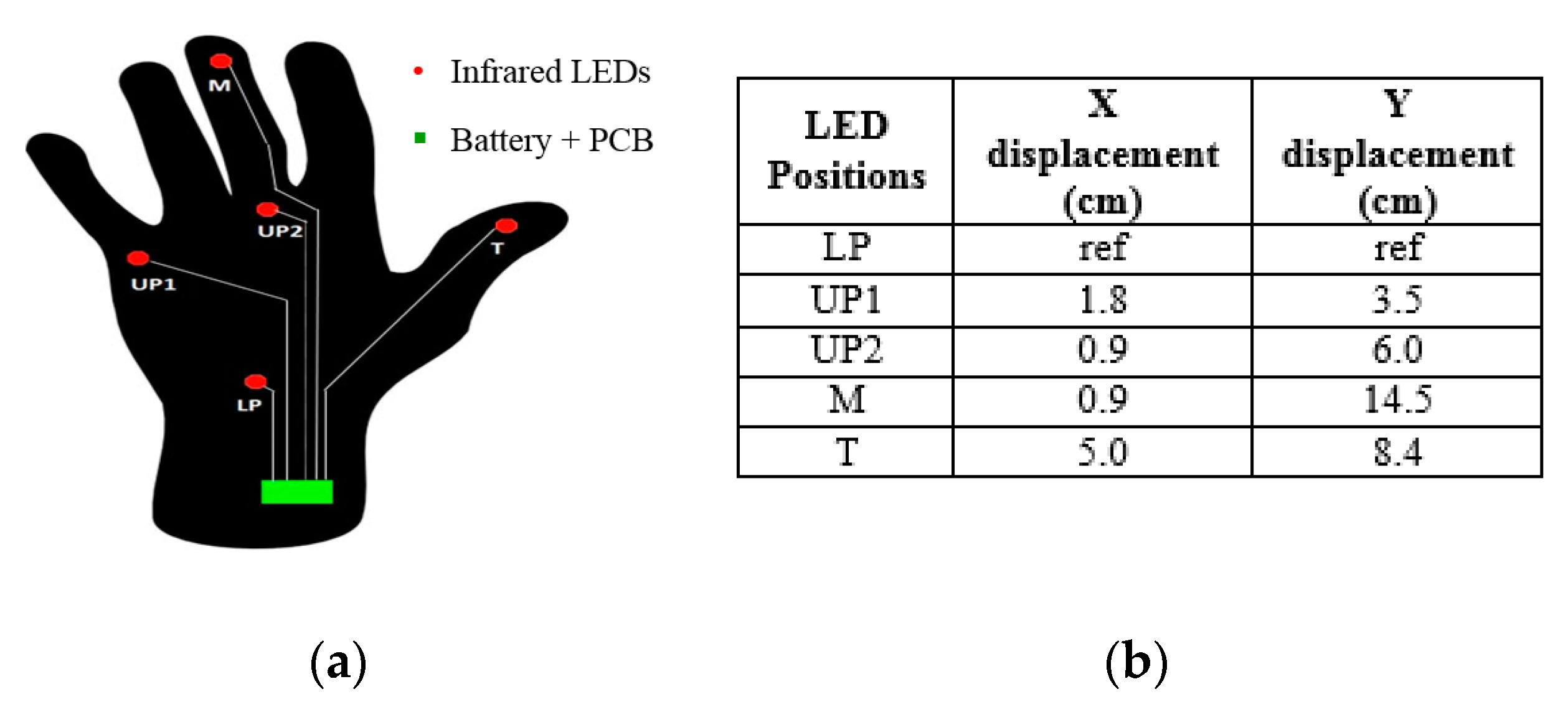
In this phase, the hand must be kept stationary in front of the sensors, with the palm and fingers open, and the middle finger pointing upwards. The calibration is performed only once to save the relative distances of LEDs, and use them as a reference in the next phase of tracking. The raw images are captured and reconstructed according to the method explained in [
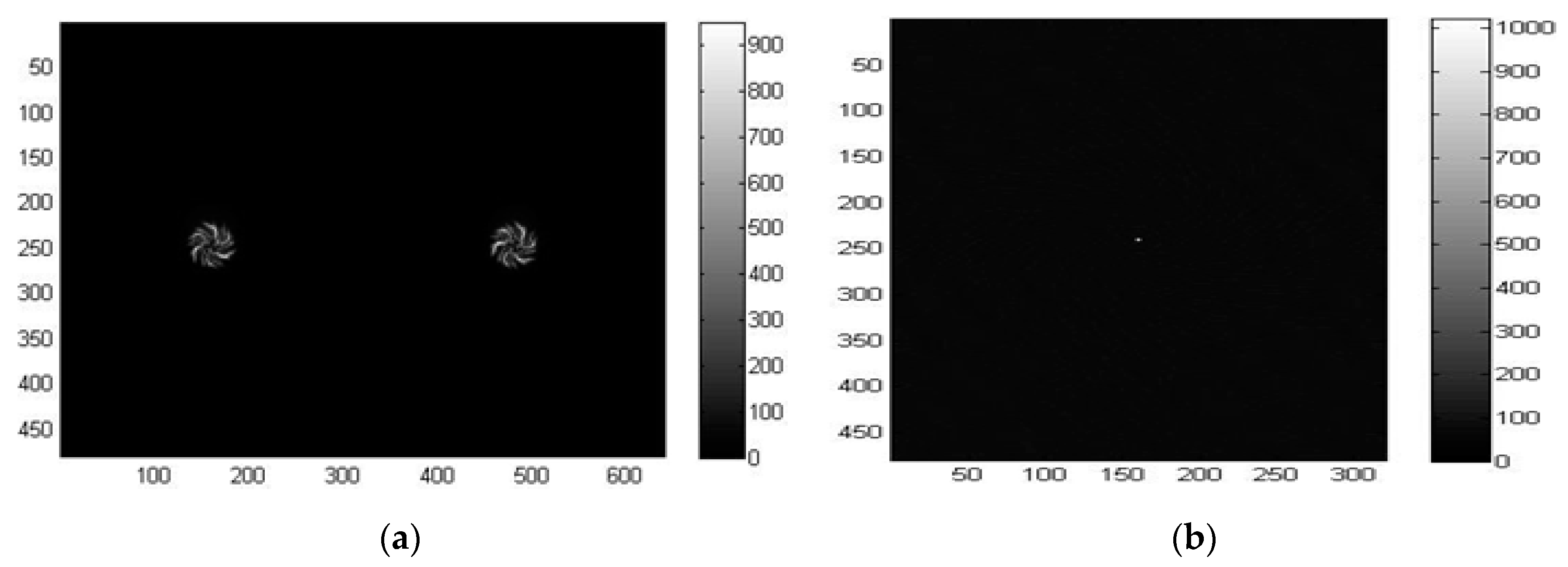
41]. In short, the spiral-shaped diffractive grating of the LSS creates equally spaced dual spirals for a single point source of the light, as shown in
Figure 6a. This is taken as the reference point-spread function (PSF) for the LSS. The regularized inverse of the Fourier transformation of the PSF, which is also called the kernel, is then calculated. The inverse Fourier transform of the product between the kernel and the raw image obtained from the LSS, which is the dual spiral image itself for a point source of light, is the final reconstructed image. It is seen from
Figure 6b that the point source of light is reconstructed with low noise from the dual spiral pattern provided by the LSS. The two spirals on the dual gratings are not identical to each other; indeed, one is rotated 22° with respect to the other so that one spiral could cover the potential deficiencies present in the other sensor, and vice versa. Therefore, the reconstruction result for each spiral is used separately and then added together. This also allows effectively doubling the amount of light captured, thus reducing noise effects.
The algorithm then looks for as many points as specified as the inputs (three for the palm, two for fingers) by searching the local maxima. The maxima detection algorithm starts with the highest threshold (
th = 1) and iteratively decreases the threshold for each image frame until all five LEDs are detected correctly by both sensors. The lowest threshold is saved as the reference (
thref) for the tracking phase. When the five detected points are correctly identified during the process, every point is labeled in order to assign each to the right part of the hand. The reconstructed frames have their origin in the top-left corner, with a resolution of 320 × 480, which is half the size along the
X-direction and the full size along the
Y-direction compared to the original image frames, as shown in
Figure 6b.
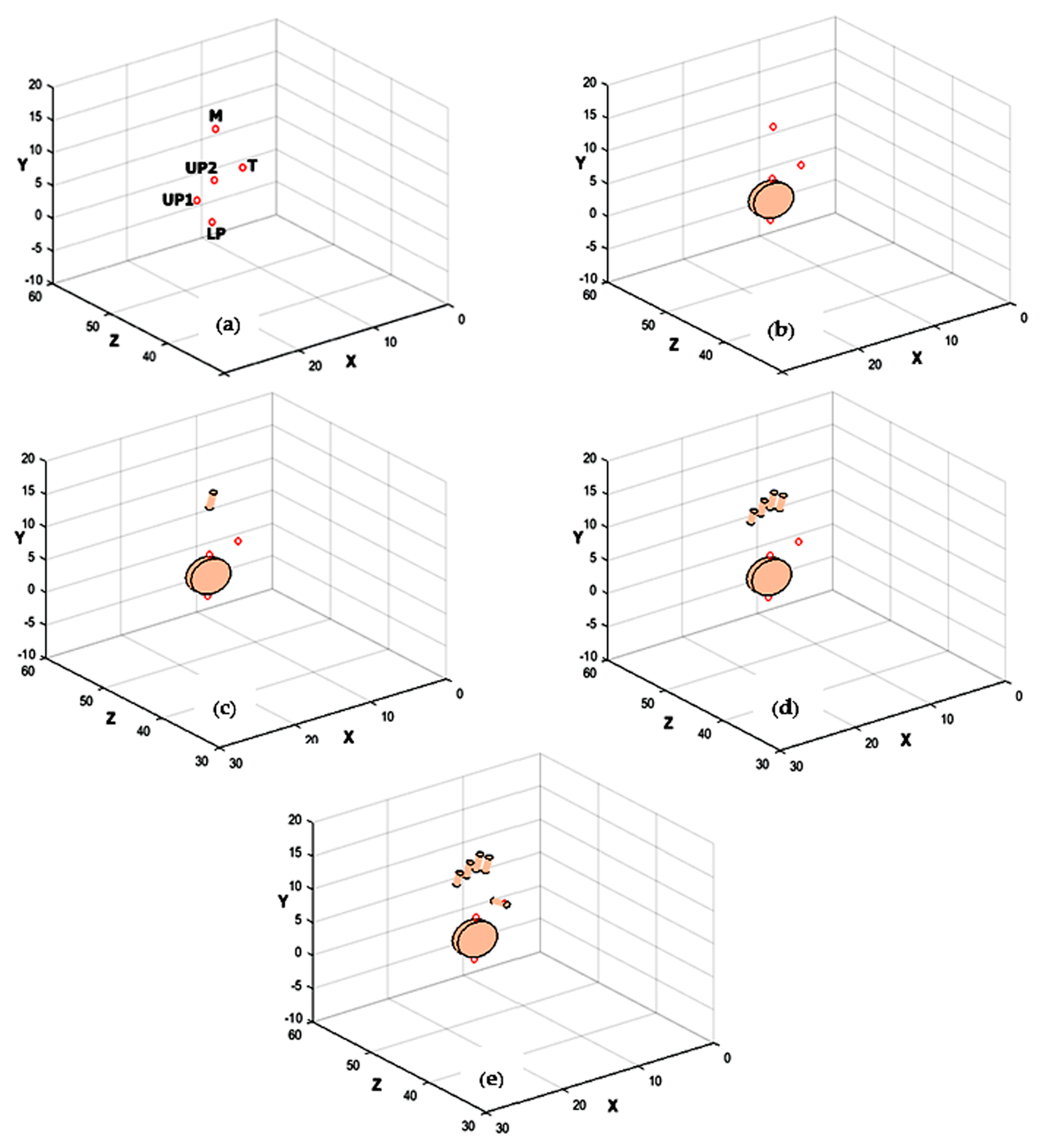
Consequently, the following a priori information is considered for labeling based on the positioning of LEDs in the hand (
Figure 5a):
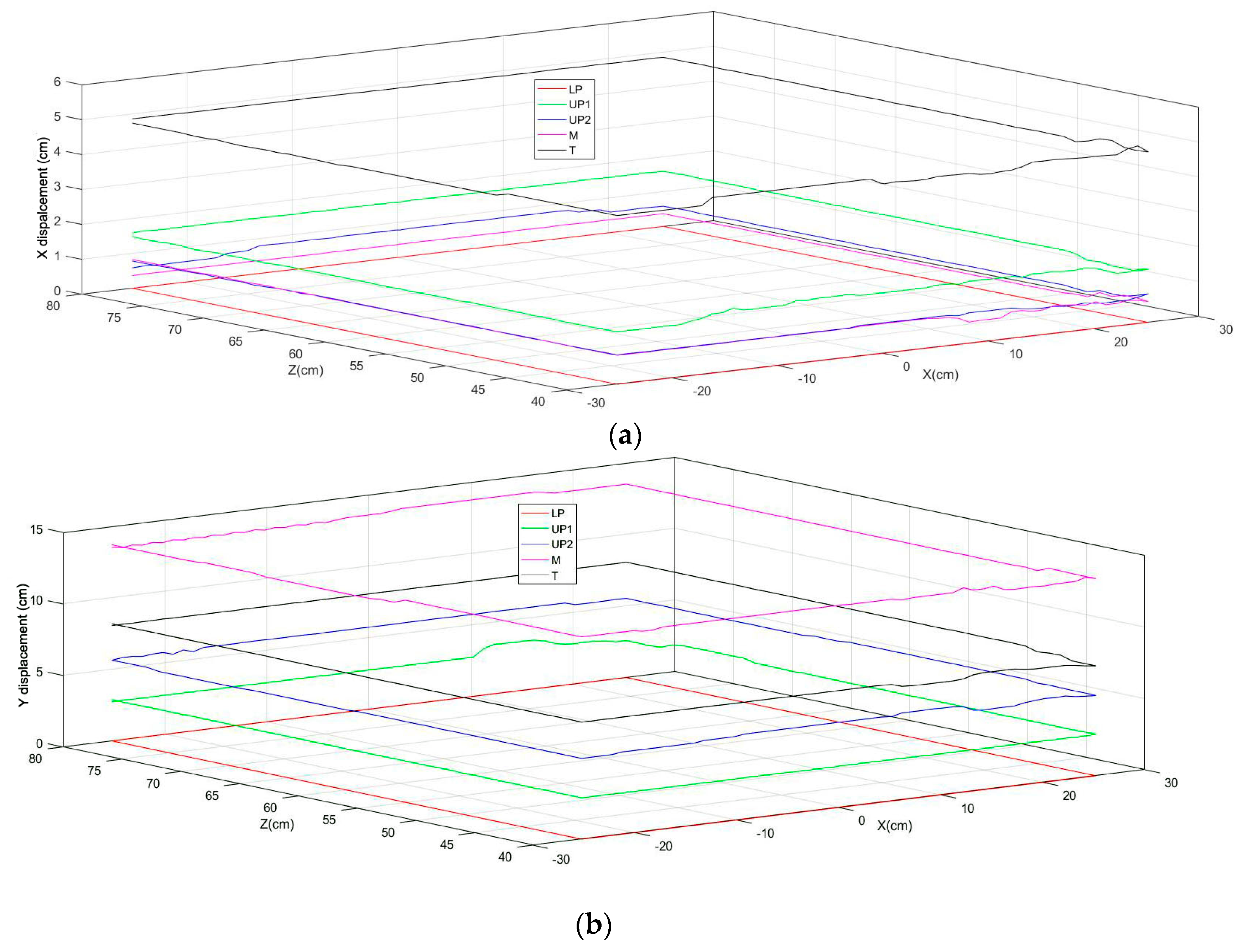
The middle finger point (M) has the lowest row coordinate in both images.
The lower palm point (LP) has the highest row coordinate in both images.
The first upper palm point (UP1) has the lowest column coordinate in both images.
The second upper palm point (UP2) has the second column coordinate in both images.
The thumb point (T) has the highest column coordinate in both images.
The 2D coordinates in the image domain, relative to the two sensors together with the assigned labels, are processed according to the point tracking algorithm [
41,
42], using the reference that the PSF created. Thus, a matrix of relative distances of the palm coordinates is computed, as given in
Table 1 using Equation (1). This unique measure together with the reference threshold will be used in the following phase to understand the configuration of the hand.
3.5.2. Tracking Phase
During the tracking phase also, the raw images from the left and right sensors are captured and reconstructed according to the procedure explained in [
39], which is briefly described in the calibration phase. The algorithm then looks for local maxima that lie above the reference threshold
thref, which was saved during the calibration phase. The tracking phase is developed in such a way that it is impossible to start tracking if at least three LEDs are not visible for the first 10 frames, and the number of points in the left and right frames is not equal, in order to always maintain a consistent accuracy. As such, if
mL and
mR represent the detected maxima for
sen_L and
sen_R respectively, the following different decisions are taken according to the explored image:
|mL| ≠ |mR| and |mL|, |mR| > 3: a matrix of zeros is saved and a flag = 0 is set encoding “Unsuccessful Detection”.
|mL|, |mR| < 3: a matrix of zeros is saved and a flag = 0 is set encoding “Unsuccessful Detection”.
|mL| = |mR| and |mL|, |mR| > 3: the points are correctly identified, flag = 1 is set encoding “Successful Detection”, and the 2D coordinates of LED positions are saved.
(a) Unsuccessful Detection (Flag = 0)
In this case, the useful information to provide an estimate of the current coordinates is determined using a polynomial fit function based on the 10 previous positions of each LED. The current coordinates to be estimated are defined as in Equation (2):
At each iteration, the progressive time stamp of the 10 previous iterations (3) and tracked 3D coordinates of each axis relative to the 10 iterations (4) are saved.
The saved quantities are passed to a polynomial function, as shown in Equation (5):
The polynomial function performs the fitting using the least squares method, as defined in Equation (6):
Thus, the function
fpoly estimates the coordinates of all five LED positions related to the current iteration, based on the last 10 iterations, as shown in Equation (7):
(b) Successful Detection (Flag = 1)
In this case, the coordinates are preprocessed by a sub-pixel level point detection algorithm [
42,
48], which enhances the accuracy of peak detection by overcoming the limitation of the pixel resolution of the imaging sensor. The method will avoid many worst case scenarios, such as the striking of the LEDs on the sensors being too close to one another and the column coordinates of different points perhaps sharing the same value, ending in a wrong 3D ranging. The matrix of coordinates can then be used to perform the labeling according to the proposed method, as described below:
(i) Labeling Palm Coordinates
Given
mi, where
i =
L,
R, as the number of maxima detected by both sensors, the combinations without repetitions of three previously ranged points are computed. Indeed, if five points are detected, there will be 10 combinations: four combinations for four detected points, and one combination for three detected points. Thus, triple combinations of
C points are generated. The matrix of relative distances for each candidate combination of points, as
k ∈ [1, …, |C|], is calculated using Equation (1). The sum of squares of relative distances for each matrix is then determined by Equations (8) and (9) for both the calibration and tracking Phases, as
k ∈ [1, …, |C|]:
The results are summed again to obtain a scalar, which is the measure of the distance between the points in the tracking phase and the calibration phase, as shown in Equations (10) and (11), respectively:
where both
and
are vectors.
The minimum difference between the quantities
Sumk and
Sumref can be associated with the palm coordinates. To avoid inaccurate results caused by environmental noise and possible failures in the local maxima detection, this difference is compared to a threshold to make sure that the estimate is sufficiently accurate. Several trials and experiments were carried out to find a suitable threshold to the value
thdistance = 30 cm. The closest candidate
was then found using Equation (12):
The final step was to compute all of the permutations of the matrix of relative distances
, and the corresponding residuals with respect to the reference matrix
(13):
The permutation, which shows the minimum residual, corresponds to the labeled triple of the 3D palm coordinates. The appropriate labels are assigned to each of the points, as follows: , , .
(ii) Labeling Finger Coordinates
After identifying the palm coordinates, the fingers that are not occluded are identified using their positions with respect to the palm plane by knowing their length and the position of the fingertips. The plane identified by the detected palm coordinates
Xplane is the normal vector to the palm plane. It is calculated using the normalized cross-product of the 3D palm coordinates of the points using the right-hand rule, as in Equation (14):
The projections of the unlabeled LEDs onto the palm plane (if there are any) are computed based on the two possible cases:
Case 1—Two Unlabeled LEDs:
The projected vectors for unlabeled LEDs
UL1 and
UL2 onto the palm plane are calculated by finding the inner product of
Xplane and (
−
). It is then multiplied by
Xplane and subtracted from the unlabeled LED positions, as shown in Equation (15):
Two candidate segments
and
are then calculated as shown in Equations (16) and (17) and compared to the reference palm segment defined by
in Equation (18):
The results are used for the calculation of angles between them, as shown in Equations (19) and (20):
The middle finger is selected as the unlabeled LED
ULi, which exposes the minimum angle, while the thumb is selected as the maximum one, as shown in Equations (21) and (22):
Case 2—One Unlabeled LED:
If only one of them is visible, the single projected vector is used to compute the angle between the segment
XUL and the segment
Xref in the same way, as shown in Equation (19)
. The decision is made according to an empirically designed threshold
thangle = 30°, as shown in Equation (23):
(c) Occlusion Analysis
When the flag is set to 1, but one of the LEDs is occluded, its position is predicted using the method given in
Section 3.5.2(a). The possibility of two different cases are as follows:
Case 1—Occluded Finger:
In this case, if there is no occlusion in the previous frame, the procedure is same as that of
Section 3.5.2(ii)
. If a previous frame has occlusion, the coordinate is chosen according to the coordinate
.
Case 2—Occluded Palm:
If none of the candidate combinations satisfy the
thdistance constraint given in Equation (12), proceed in the same way as that of
Section 3.5.2(a). Thus, the proposed novel multiple points live tracking algorithm labels and tracks all of the LEDs placed on the hand.
3.5.3. Orientation Estimation
Although the proposed tracking technique has no other sensors fitted on the hand to provide the angle information, and the tracking based on light sensors is able to provide only the absolute positions, the hand and finger orientations can be estimated. The orientation of the hand is computed by finding the plane identified by the palm
Xplane in Equation (14) and the direction given by the middle finger. If the palm orientation, the distance between initial and final segments (
S0 and
S3) of middle finger (
d), and the segment lengths (
,
i = 0,1,2,3) are assigned as known variables, the orientation of all of the segments can be estimated using a pentagon approximation model, as shown in
Figure 7.
For this purpose, the angle
between the normal vector exiting the palm plane
Xplane, as previously calculated in Equation (14), and the middle finger segment (
−
XM), is calculated as shown in Equation (24). The angle between
S0 and
d (=
α) is its complementary angle is shown in Equation (25).
For the approximation model, it is assumed that the angle between
S0 and
d is equal to the angle between
S3 and
d. Thus, knowing that the sum of the internal angles of a pentagon is 540°, the value of the other angles (=
β) is also computed assuming that they are equal to each other, as shown in Equation (26).
The vector perpendicular to the middle finger segment and
Xplane is then computed as shown in Equation (27), and the rotation matrix
R is built using angle
α around the derived vector according to Euler’s rotation theorem [
49]. This rotation matrix is used to calculate the orientation of segment S
0 in Equation (28) and its corresponding 2D location in Equation (29).
Thus, the orientation of all of the phalanges (S1, S2, and S3), as well as their 2D locations, is calculated. The same method is applied for finding the orientation of all of the thumb segments using the segment lengths and 2D location of lower palm LED (XLP), but with a trapezoid approximation for estimating the angles.