Characterization of the Fat Channel for Intra-Body Communication at R-Band Frequencies
Abstract
1. Introduction
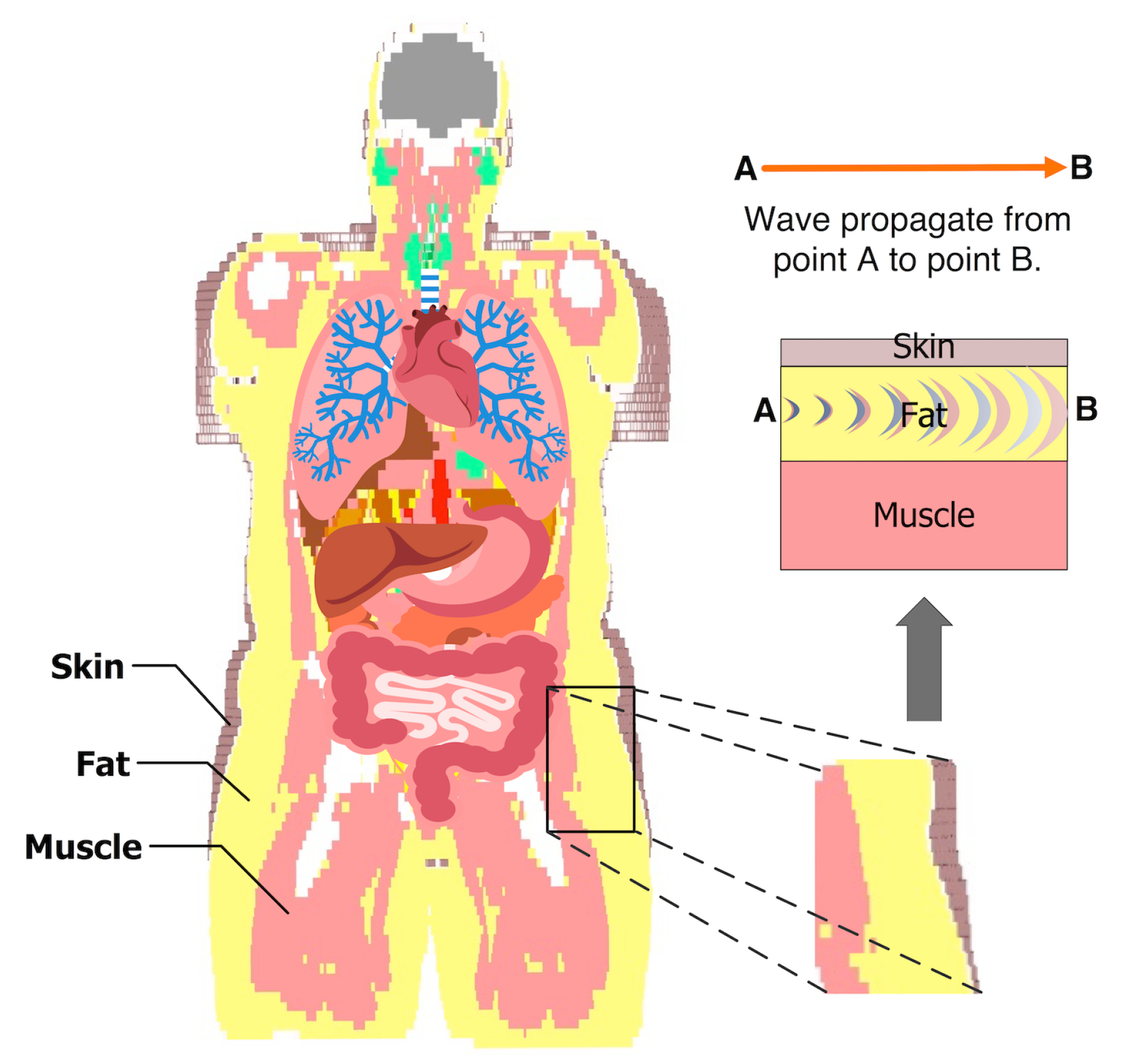
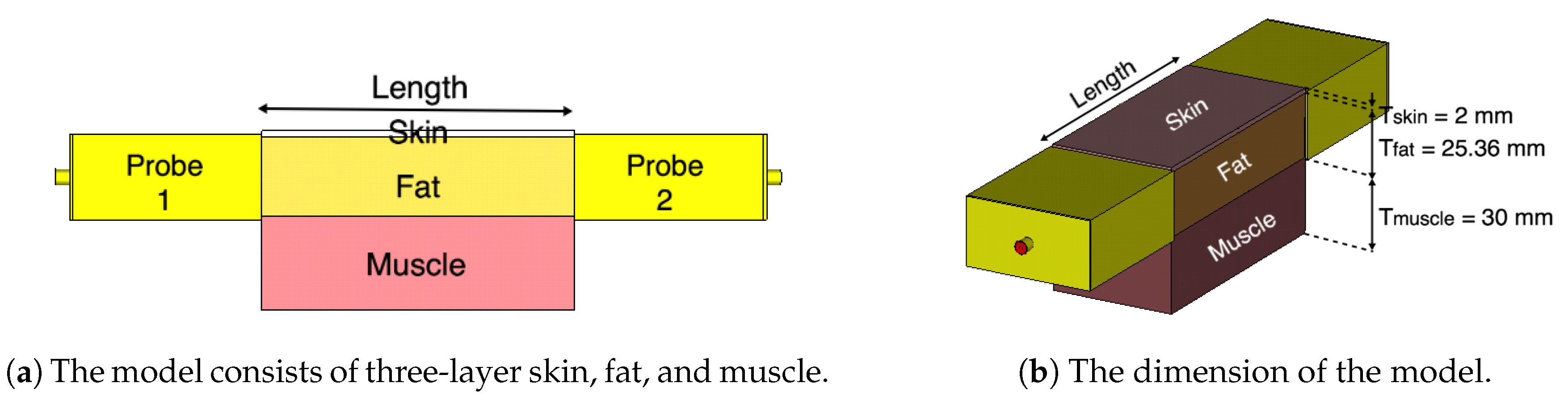
2. Fat Channel Model
3. Probe Design Optimization
3.1. Probe Optimization
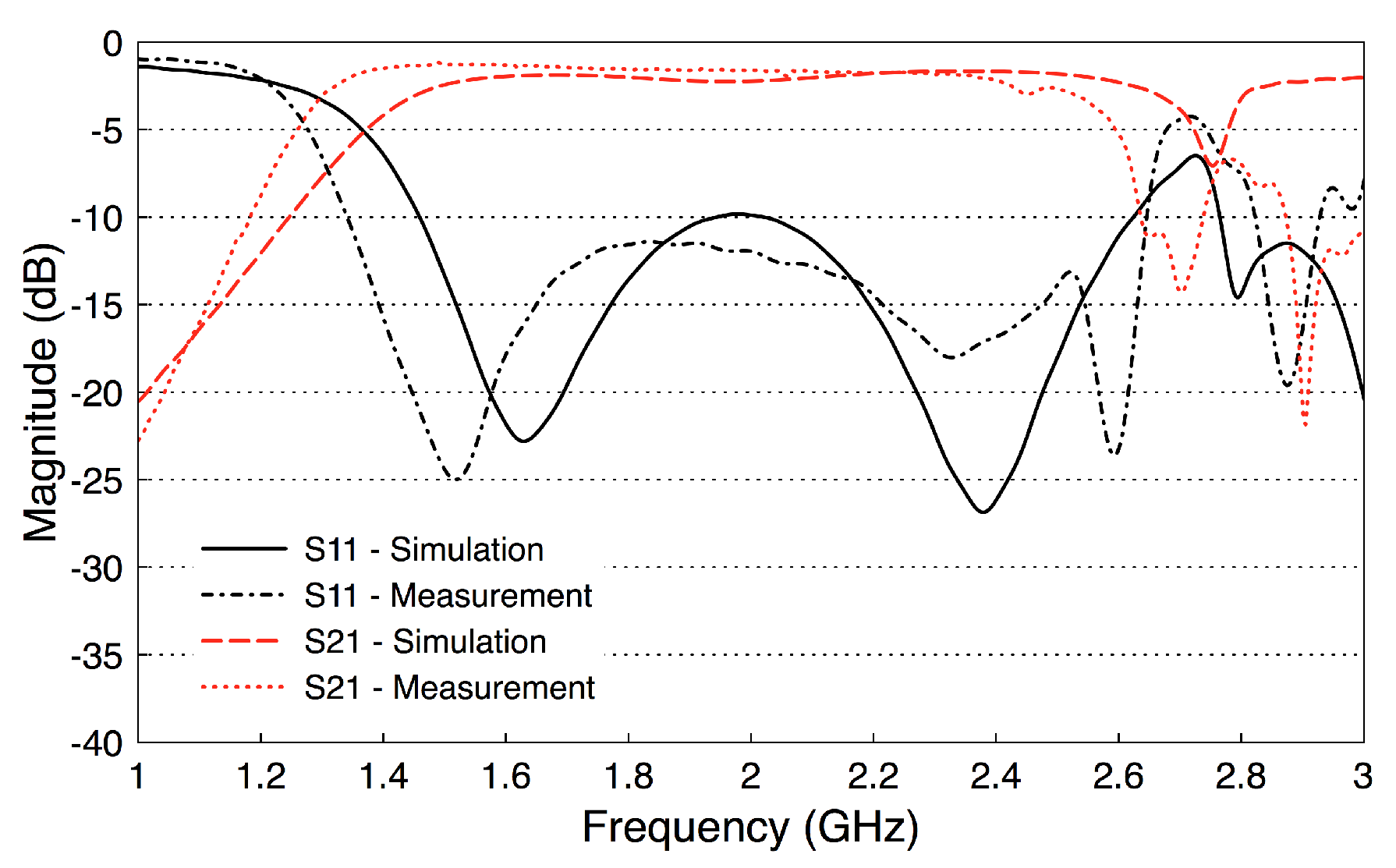
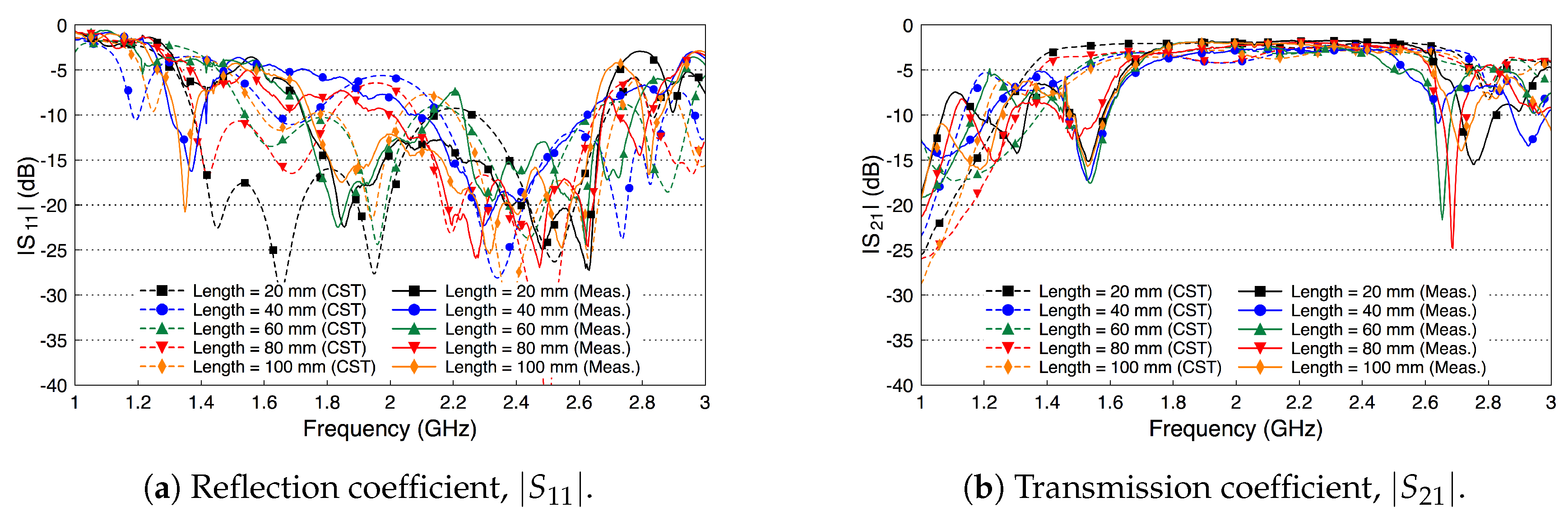
3.2. Probe Fabrication and Validation
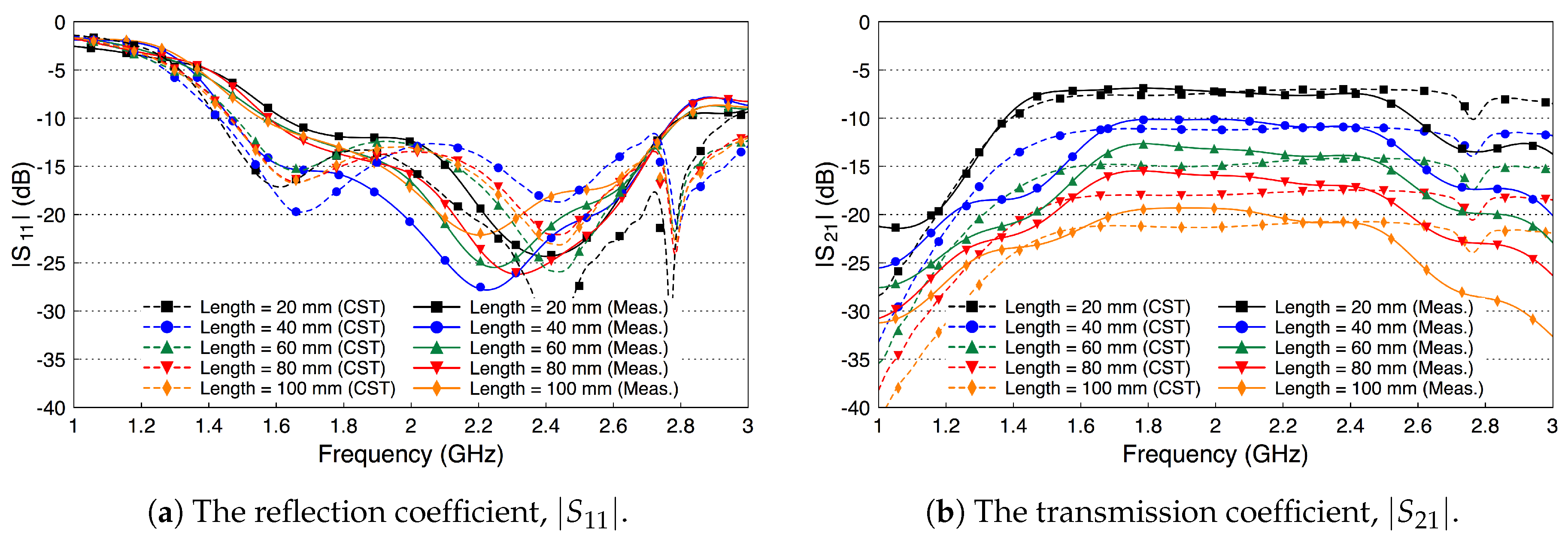
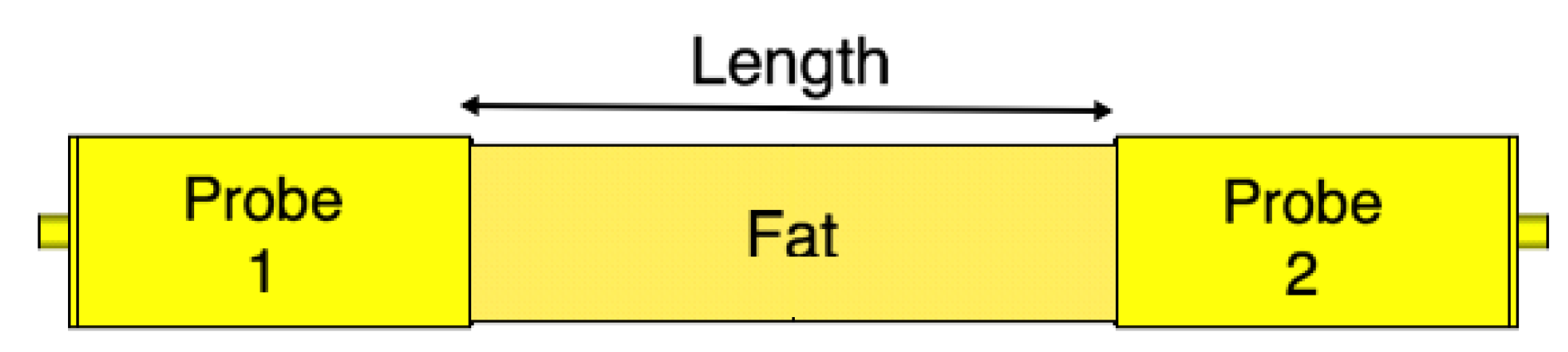
4. Fat Channel Characterization
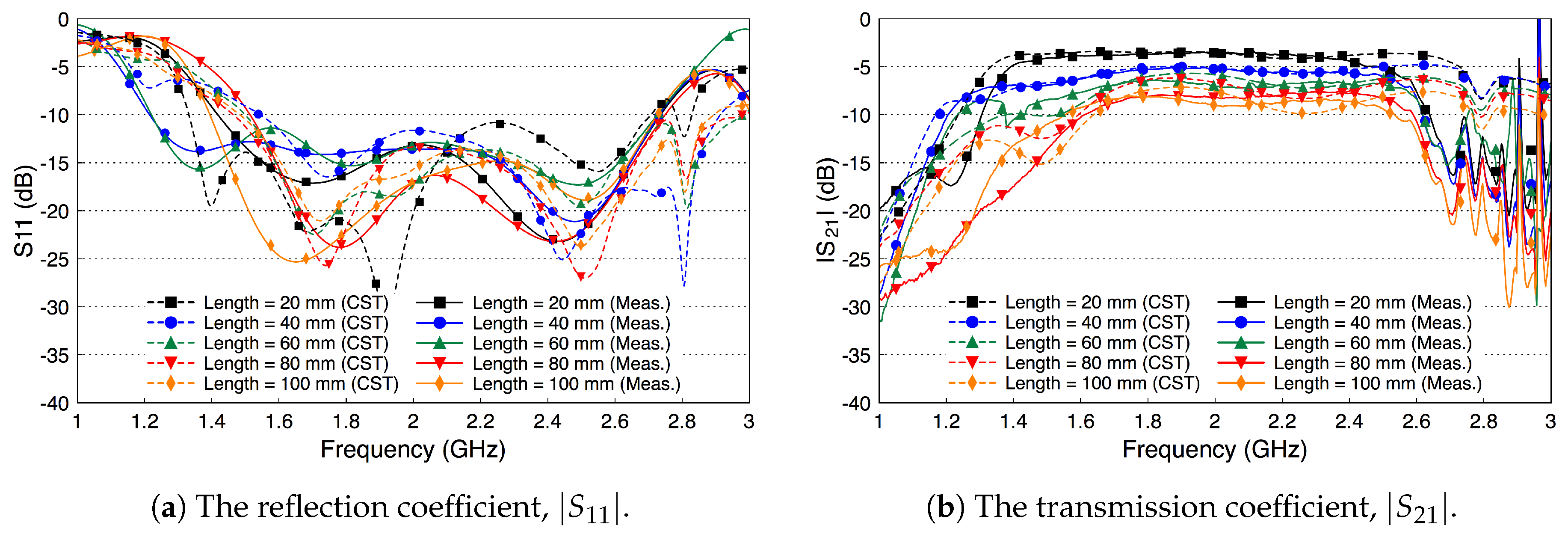
4.1. Path Loss Characterization
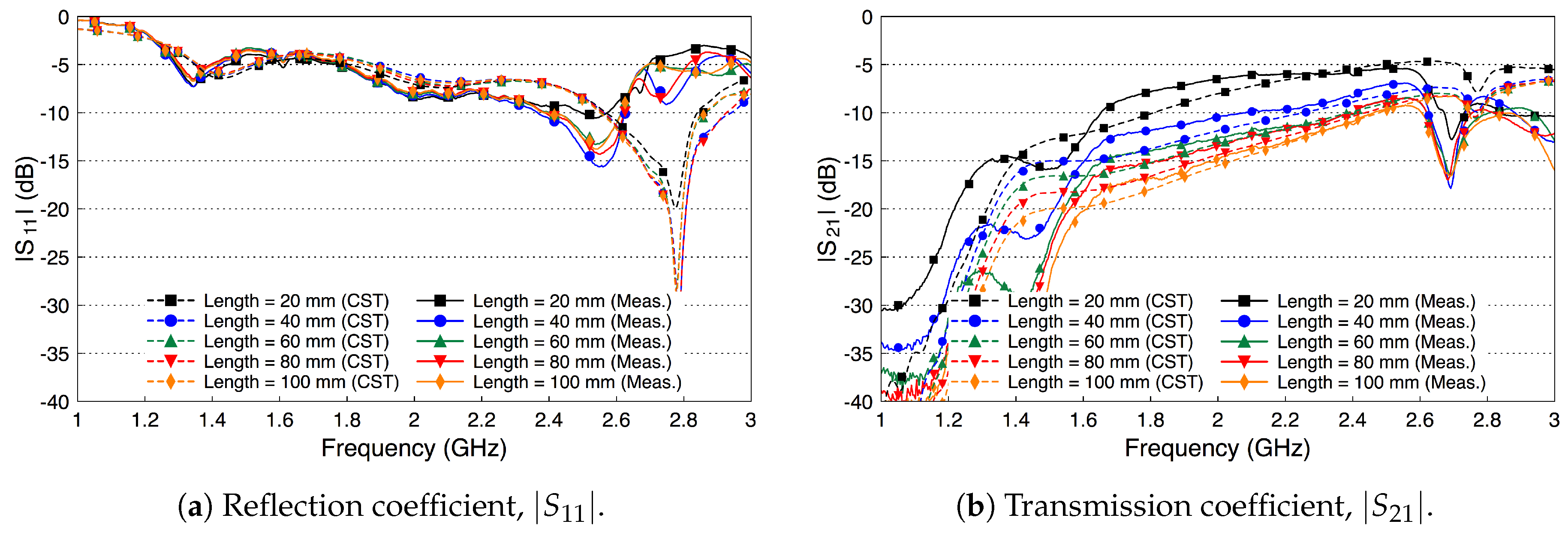
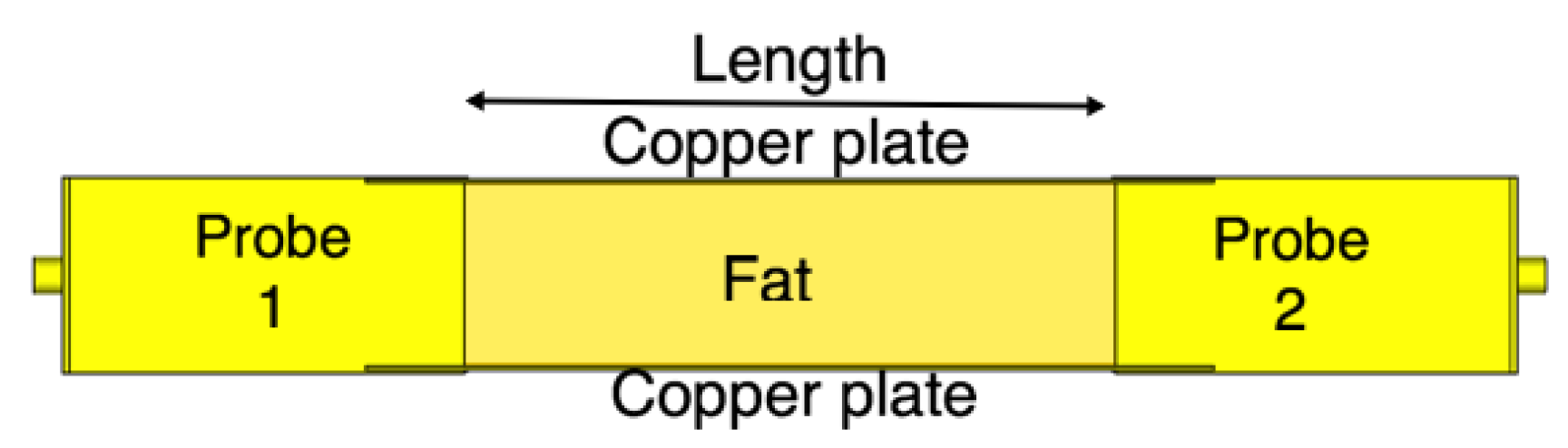
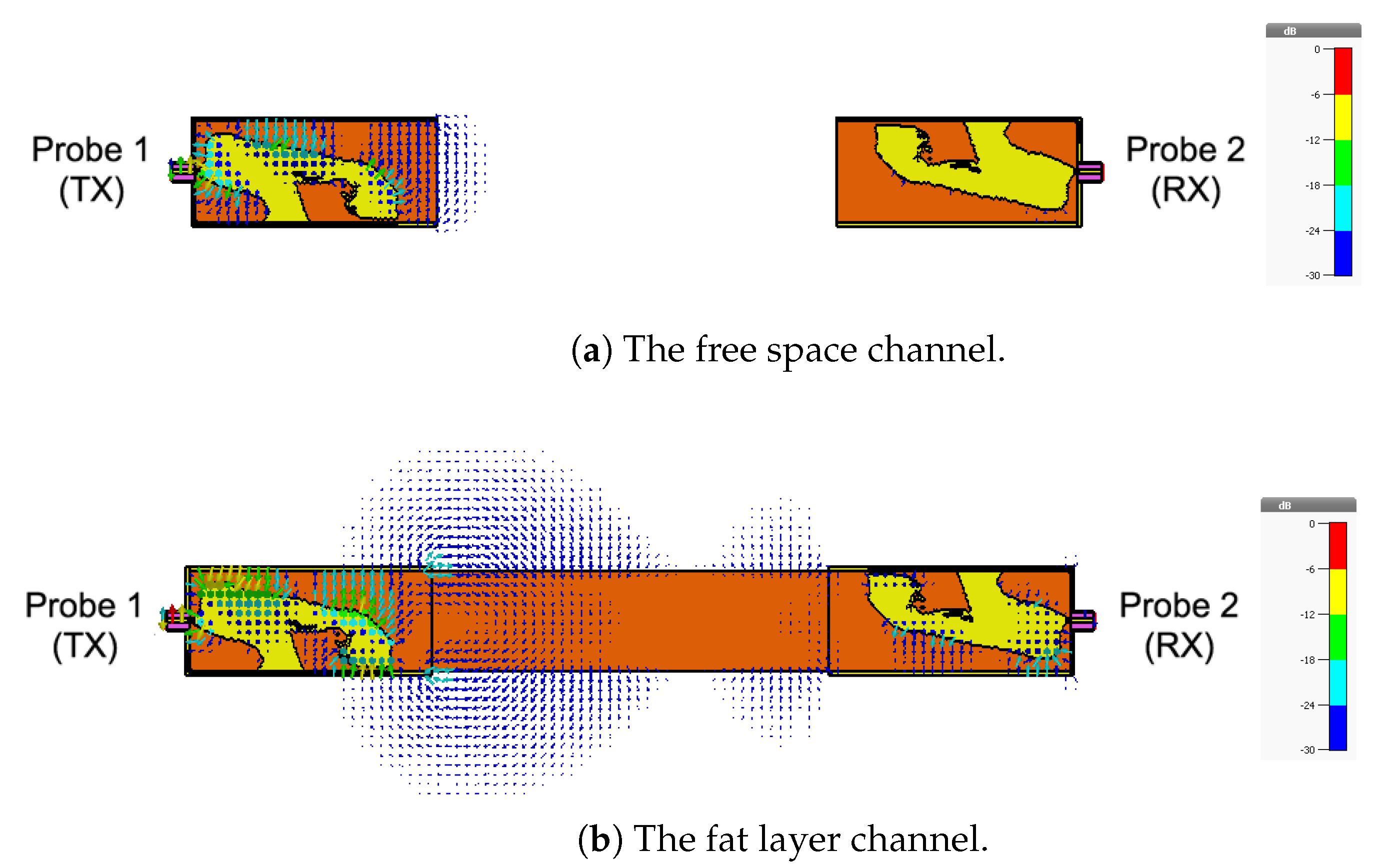
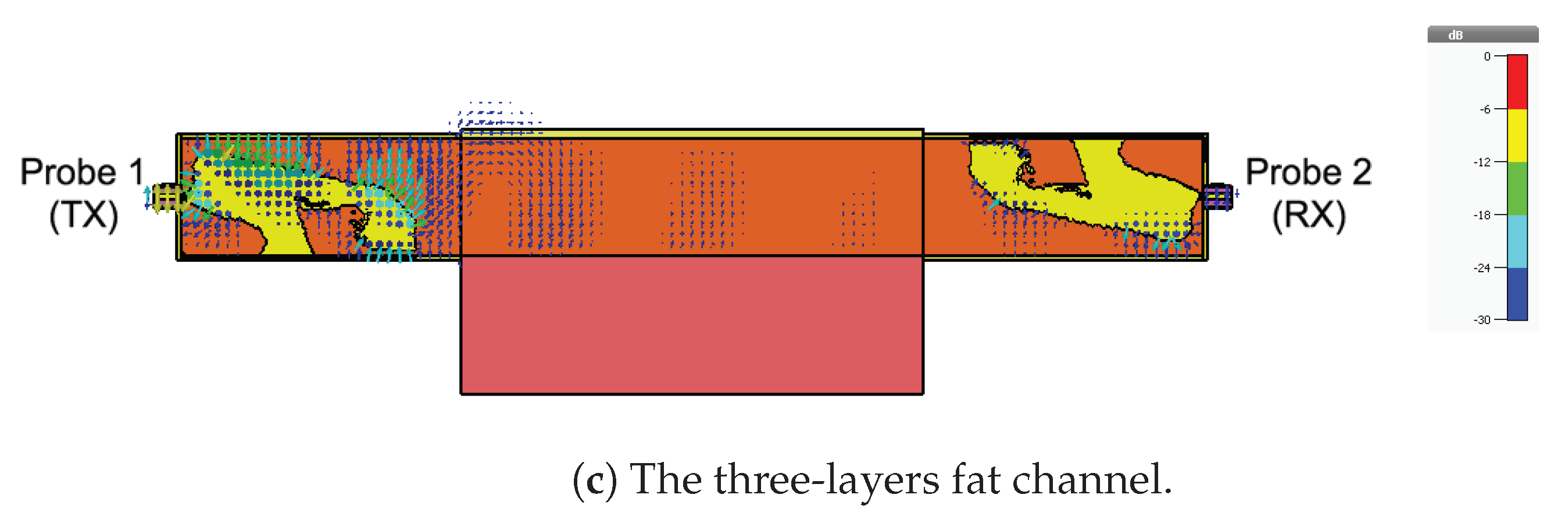
4.2. Fat Channel as a Waveguide
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WHO | World Health Organization |
| NCD | Noncommunicable Diseases |
| IMDs | Implantable Medical Devices |
| i-BAN | Intra-Body Area Network |
| RF | Radio Frequency |
| MICS | Medical Implant Communication Service |
| ISM | Industrial, Scientific, and Medical |
| CST | Computer Simulation Technology |
| FDTD | Finite Difference Time Domain |
| TOPA | Topology Optimized Planar Antenna |
| SMA | Sub-Miniature version A |
| TX | Transmitter |
| RX | Receiver |
| TE | Transverse Electric |
| E-Field | Electric Field |
| SAR | Specific Absorption Rate |
References
- Centers for Disease Control and Prevention. Chronic Diseases: The Leading Causes of Death and Disability in the United States, 2015. Available online: https://www.cdc.gov/nchs/data/hus/hus15.pdf (accessed on 23 June 2017).
- World Health Organization. Global Status Report on Noncommunicable Diseases 2014. Available online: http://apps.who.int/iris/bitstream/10665/148114/1/9789241564854{_}eng.pdf (accessed on 15 July 2017).
- U.S. Food & Drug Administration. Medical Devices, Products and Medical Procedures, Implants and Prosthetics. Available online: https://www.fda.gov/MedicalDevices/default.htm (accessed on 10 January 2018).
- Joung, Y.-H. Development of Implantable Medical Devices: From an Engineering Perspective. Int. Neurourol. J. 2013, 17, 98–106. [Google Scholar] [CrossRef] [PubMed]
- Khan, W.; Muntimadugu, E.; Jaffe, M.; Domb, A.J. Implantable Medical Devices. In Focal Controlled Drug Delivery; Domb, A., Khan, W., Eds.; Advances in Delivery Science and Technology; Springer: Boston, MA, USA, 2014; pp. 33–59. [Google Scholar]
- Hafezi, H.; Robertson, T.L.; Moon, G.D.; Au-Yeung, K.Y.; Zdeblick, M.J.; Savage, G.M. An Ingestible Sensor for Measuring Medication Adherence. IEEE Trans. Biomed. Eng. 2015, 62, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Nie, Z.; Liu, Y.; Wang, L.; Hao, Y. Characterization of In-Body Radio Channels for Wireless Implants. IEEE Sensors J. 2017, 17, 1528–1537. [Google Scholar] [CrossRef]
- Moradi, E.; Koski, K.; Bjorninen, T.; Sydanheimo, L.; Rabaey, J.M.; Carmena, J.M.; Rahmat-Samii, Y.; Ukkonen, L. Miniature implantable and wearable on-body antennas: Towards the new era of wireless body-centric systems [antenna applications corner]. IEEE Antennas Propag. Mag. 2014, 56, 271–291. [Google Scholar]
- Swaminathan, M.; Cabrera, F.S.; Pujol, J.S.; Muncuk, U.; Schirner, G.; Chowdhury, K.R. Multi-Path Model and Sensitivity Analysis for Galvanic Coupled Intra-Body Communication Through Layered Tissue. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 339–351. [Google Scholar] [CrossRef] [PubMed]
- Kibret, B.; Seyedi, M.; Lai, D.T.H.; Faulkner, M. Investigation of Galvanic-Coupled Intrabody Communication Using the Human Body Circuit Model. IEEE J. Biomed. Health Inform. 2014, 18, 1196–1206. [Google Scholar] [CrossRef] [PubMed]
- Callejón, M.A.; Reina-Tosina, J.; Naranjo-Hernández, D.; Roa, L.M. Galvanic Coupling Transmission in Intrabody Communication: A Finite Element Approach. IEEE Trans. Biomed. Eng. 2014, 61, 775–783. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Garudadri, H.; Mercier, P.P. Channel Modeling of Miniaturized Battery-Powered Capacitive Human Body Communication Systems. IEEE Trans. Biomed. Eng. 2017, 64, 452–462. [Google Scholar] [CrossRef] [PubMed]
- Pereira, M.D.; Alvarez-Botero, G.A.; de Sousa, F.R. Characterization and Modeling of the Capacitive HBC Channel. IEEE Trans. Instrum. Meas. 2015, 64, 2626–2635. [Google Scholar] [CrossRef]
- Mao, J.; Yang, H.; Zhao, B. An Investigation on Ground Electrodes of Capacitive Coupling Human Body Communication. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 910–919. [Google Scholar] [CrossRef] [PubMed]
- Khaleghi, A.; Chavez-Santiago, R.; Balasingham, I. Ultra-wideband statistical propagation channel model for implant sensors in the human chest. IET Microw. Antennas Propag. 2011, 5, 1805–1812. [Google Scholar] [CrossRef]
- Werber, D.; Schwentner, A.; Biebl, E.M. Investigation of RF transmission properties of human tissues. Adv. Radio Sci. 2006, 4, 357–360. [Google Scholar] [CrossRef]
- Chávez-Santiago, R.; Garcia-Pardo, C.; Fornes-Leal, A.; Vallés-Lluch, A.; Vermeeren, G.; Joseph, W.; Balasingham, I.; Cardona, N. Experimental path loss models for in-body communications within 2.36–2.5 GHz. IEEE J. Biomed. Health Inform. 2015, 19, 930–937. [Google Scholar]
- Texas Instruments. ISM-Band and Short Range Device Regulatory Compliance Overview; Technical Report, Application Report-SWRA048; Texas Instruments: Dallas, TX, USA, 2005. [Google Scholar]
- Asan, N.B.; Noreland, D.; Hassan, E.; Shah, S.R.M.; Rydberg, A.; Blokhuis, T.J.; Carlsson, P.O.; Voigt, T.; Augustine, R. Intra-body microwave communication through adipose tissue. Healthc. Technol. Lett. 2017, 4, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Asan, N.B.; Penichet, C.P.; Shah, S.R.M.; Noreland, D.; Hassan, E.; Rydberg, A.; Blokhuis, T.J.; Voigt, T.; Augustine, R. Data Packet Transmission Through Fat Tissue for Wireless IntraBody Networks. IEEE J. Electromagn. RF Microw. Med. Biol. 2017, 1, 43–51. [Google Scholar] [CrossRef]
- Asan, N.B.; Velander, J.; Redzwan, S.; Hassan, E.; Noreland, D.; Blokhuis, T.; Voigt, T.; Augustine, R. Reliability of the Fat Tissue Channel for Intra-body Microwave Communication. In Proceedings of the 2017 IEEE Conference on Antenna Measurements & Applications, Tsukuba, Japan, 4–6 December 2017; pp. 310–313. [Google Scholar]
- Hassan, E.; Noreland, D.; Wadbro, E.; Berggren, M. Topology optimisation of wideband coaxial-to-waveguide transitions. Sci. Rep. 2017, 7, 45110. [Google Scholar] [CrossRef] [PubMed]
- CST. CST-Computer Simulation Technology GmbH, Version 2017.05; Available online: https://www.cst.com/ (accessed on 1 June 2018).
- Asan, N.B.; Redzwan, S.; Rydberg, A.; Augustine, R.; Noreland, D.; Hassan, E.; Voigt, T. Human fat tissue: A microwave communication channel. In Proceedings of the 2017 First IEEE MTT-S International Microwave Bio Conference (IMBIOC), Gothenburg, Sweden, 15–17 May 2017; pp. 1–4. [Google Scholar]
- Akkus, O.; Oguz, A.; Uzunlulu, M.; Kizilgul, M. Evaluation of Skin and Subcutaneous Adipose Tissue Thickness for Optimal Insulin Injection. J. Diabetes Metab. 2012, 3, 216. [Google Scholar] [CrossRef]
- Kim, C.W.; See, T.S.P. RF transmission power loss variation with abdominal tissues thicknesses for ingestible source. In Proceedings of the 13th IEEE International Conference on e-Health Networking Applications and Services (Healthcom), Columbia, MO, USA, 13–15 June 2011; pp. 282–287. [Google Scholar]
- Gabriel, C.; Peyman, A. Dielectric measurement: Error analysis and assessment of uncertainty. Phys. Med. Biol. 2006, 51, 6033–6046. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 225–2269. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization. Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Hassan, E.; Wadbro, E.; Hägg, L.; Berggren, M. Topology optimization of compact wideband coaxial-to-waveguide transitions with minimum-size control. Struct. Multidiscip. Optim. 2018, 57, 1765–1777. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.-S.; Ding, X.; Wang, B.-Z. Antenna radiation characteristics optimization by a hybrid topological method. IEEE Trans. Antennas Propag. 2017, 65, 2843–2854. [Google Scholar] [CrossRef]
- Aage, N.; Egede Johansen, V. Topology optimization of microwave waveguide filters. Int. J. Num. Meth. Eng. 2017, 112, 283–300. [Google Scholar] [CrossRef]
- Hassan, E.; Wadbro, E.; Berggren, M. Topology optimization of metallic antennas. IEEE Trans. Antennas Propag. 2014, 63, 2488–2500. [Google Scholar]
- Taflove, A.; Hagness, S. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Svanberg, K. A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef]
- Yeh, C.; Shimabukuro, F.I. The Essence of Dielectric Waveguides; Springer: Los Angeles, CA, USA, 2008; ISBN 978-0-387-30929-3. [Google Scholar]









| Tissue | Parameter | Phantom | Ex-vivo | Human [28] |
|---|---|---|---|---|
| Skin | Conductivity | 1.7 ± 0.2 | 1.4 ± 0.1 | 1.4 ± 0.1 |
| Relative permittivity | 45 ± 4 | 31 ± 3 | 38 ± 4 | |
| Loss tangent | 0.28 ± 0.03 | 0.33 ± 0.03 | 0.28 ± 0.03 | |
| Fat | Conductivity | 0.009 ± 0.001 | 0.12 ± 0.01 | 0.10 ± 0.01 |
| Relative permittivity | 4.6 ± 0.4 | 3.5 ± 0.3 | 5.3 ± 0.5 | |
| Loss tangent | 0.015 ± 0.001 | 0.25 ± 0.02 | 0.15 ± 0.01 | |
| Muscle | Conductivity | 1.8 ± 0.2 | 2.2 ± 0.2 | 1.7 ± 0.2 |
| Relative permittivity | 52 ± 5 | 51 ± 5 | 53 ± 5 | |
| Loss tangent | 0.25 ± 0.02 | 0.32 ± 0.03 | 0.24 ± 0.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asan, N.B.; Hassan, E.; Velander, J.; Mohd Shah, S.R.; Noreland, D.; Blokhuis, T.J.; Wadbro, E.; Berggren, M.; Voigt, T.; Augustine, R. Characterization of the Fat Channel for Intra-Body Communication at R-Band Frequencies. Sensors 2018, 18, 2752. https://doi.org/10.3390/s18092752
Asan NB, Hassan E, Velander J, Mohd Shah SR, Noreland D, Blokhuis TJ, Wadbro E, Berggren M, Voigt T, Augustine R. Characterization of the Fat Channel for Intra-Body Communication at R-Band Frequencies. Sensors. 2018; 18(9):2752. https://doi.org/10.3390/s18092752
Chicago/Turabian StyleAsan, Noor Badariah, Emadeldeen Hassan, Jacob Velander, Syaiful Redzwan Mohd Shah, Daniel Noreland, Taco J. Blokhuis, Eddie Wadbro, Martin Berggren, Thiemo Voigt, and Robin Augustine. 2018. "Characterization of the Fat Channel for Intra-Body Communication at R-Band Frequencies" Sensors 18, no. 9: 2752. https://doi.org/10.3390/s18092752
APA StyleAsan, N. B., Hassan, E., Velander, J., Mohd Shah, S. R., Noreland, D., Blokhuis, T. J., Wadbro, E., Berggren, M., Voigt, T., & Augustine, R. (2018). Characterization of the Fat Channel for Intra-Body Communication at R-Band Frequencies. Sensors, 18(9), 2752. https://doi.org/10.3390/s18092752







