Enhanced Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences †
Abstract
1. Introduction
2. e-IpDFT Synchrophasor Estimator
2.1. Signal Model
2.2. Classical IpDFT
2.3. Adaptive Equivalent Filters of the IpDFT
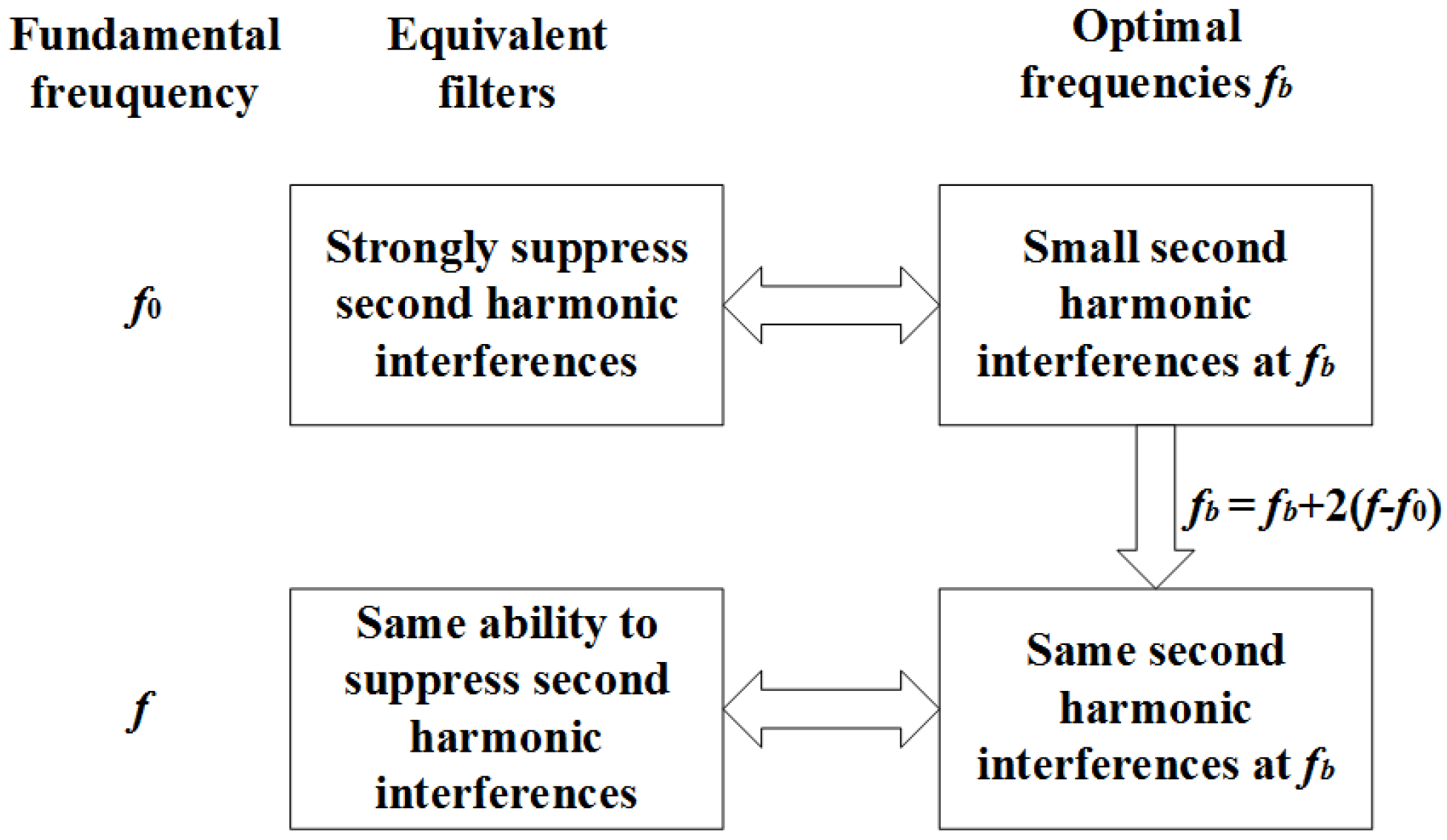
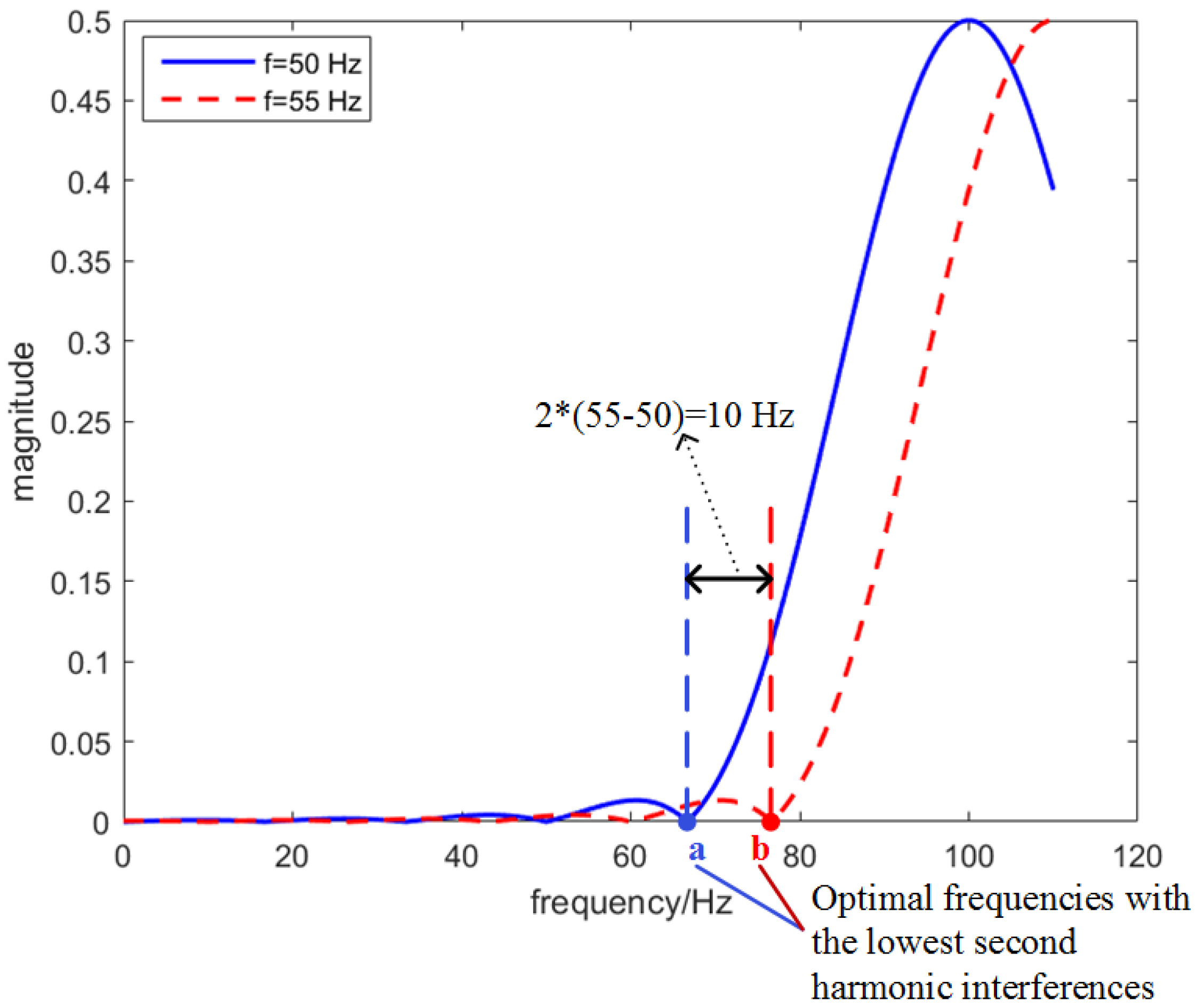
2.4. DTFT Frequency Selection for Accuracy Enhancement of the IpDFT
- Compute and using the optimal frequencies of the no frequency deviation condition, and estimate the actual fundamental frequency f using Equation (9).
- Modify as (with ), and recompute and to estimate the actual fundamental frequency again.
- Repeat the above two steps twice (i.e., another two iterations) for high accuracy.
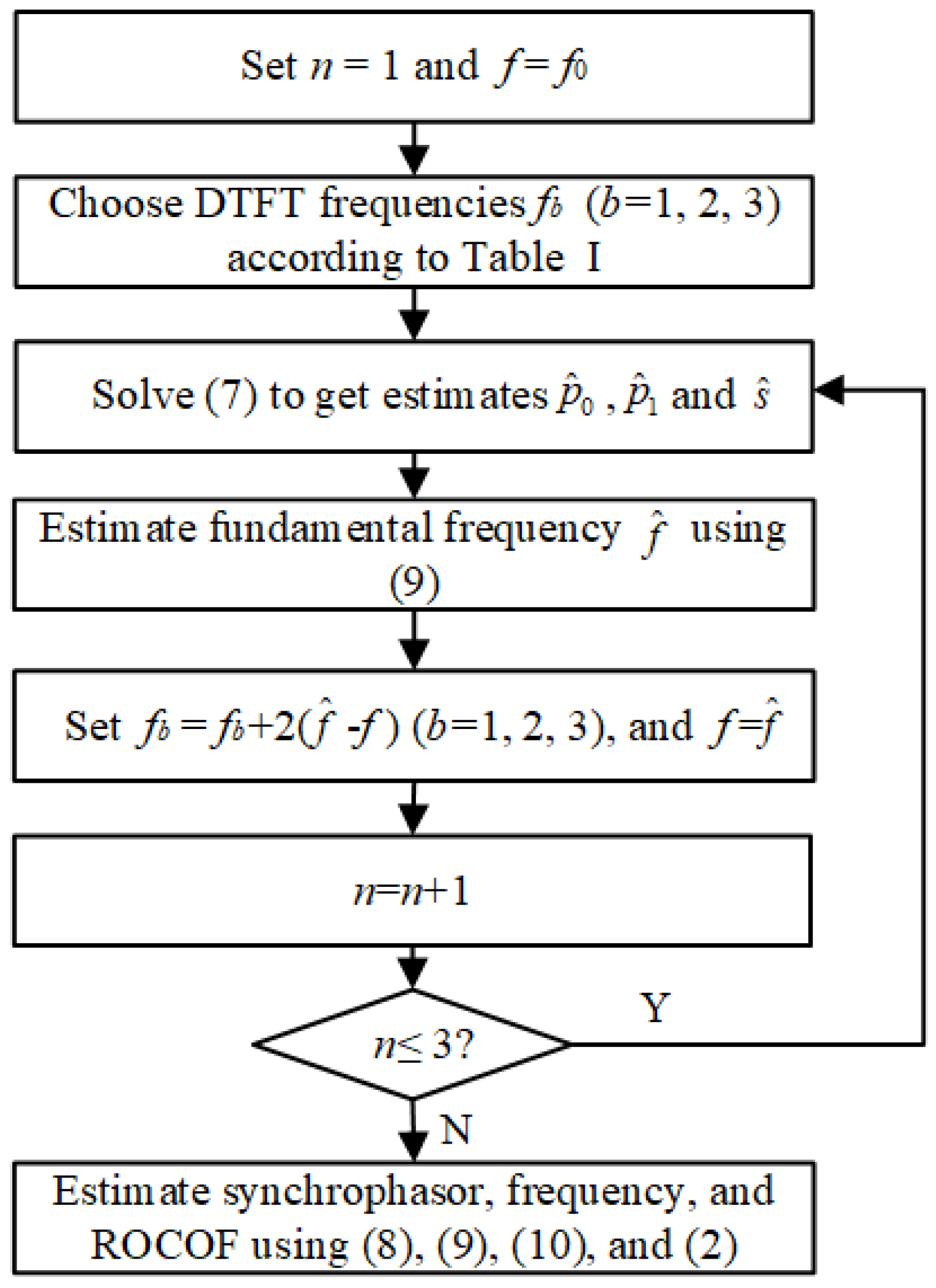
2.5. Implementation Steps of the e-IpDFT
2.6. Computational Complexity
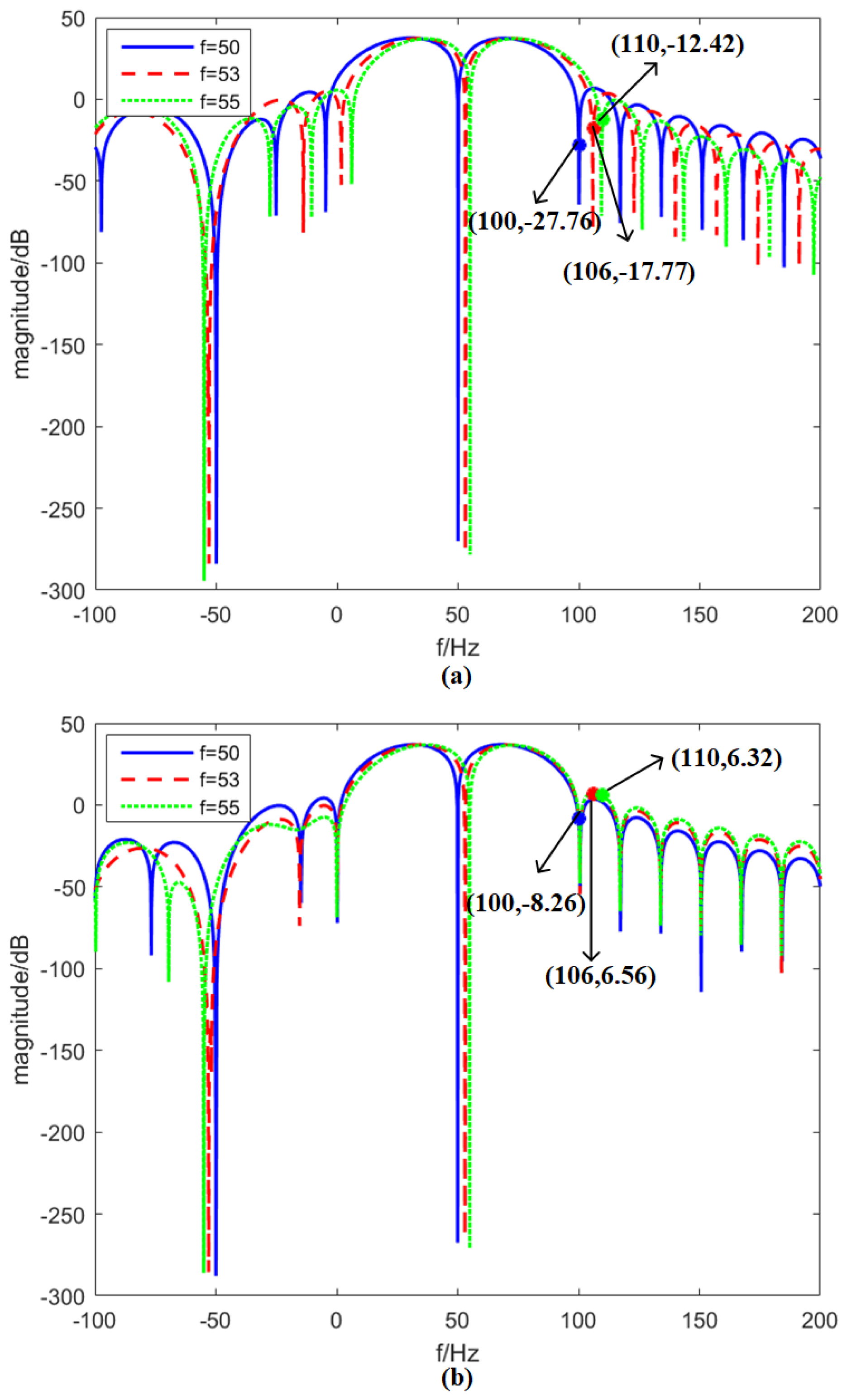
3. Instantaneous Frequency Response
4. Simulation Tests
4.1. Canonical Tests
4.2. Frequency Deviation + Second Harmonic
4.3. Frequency Deviation + Second Harmonic + Modulation
4.4. Other Complex Scenarios
4.5. Sampling Rate
4.6. A Real World Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Equations (16)–(18)
Appendix B. Proof of Equations (19)–(21)
References
- IEEE Standard for Synchrophasor Measurements for Power Systems. In IEEE Std C37.118.1-2011 (Revision of IEEE Std C37.118-2005); IEEE: Piscataway, NJ, USA, 2011; pp. 1–61. [CrossRef]
- IEEE Standard for Synchrophasor Measurements for Power Systems—Amendment 1: Modification of Selected Performance Requirements. In IEEE Std C37.118.1a-2014 (Amendment to IEEE Std C37.118.1-2011); IEEE: Piscataway, NJ, USA, 2014; pp. 1–25. [CrossRef]
- Petri, D.; Fontanelli, D.; Macii, D. A Frequency-Domain Algorithm for Dynamic Synchrophasor and Frequency Estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2330–2340. [Google Scholar] [CrossRef]
- Belega, D.; Fontanelli, D.; Petri, D. Dynamic Phasor and Frequency Measurements by an Improved Taylor Weighted Least Squares Algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 2165–2178. [Google Scholar] [CrossRef]
- Belega, D.; Macii, D.; Petri, D. Fast Synchrophasor Estimation by Means of Frequency-Domain and Time-Domain Algorithms. IEEE Trans. Instrum. Meas. 2014, 63, 388–401. [Google Scholar] [CrossRef]
- Macii, D.; Petri, D.; Zorat, A. Accuracy Analysis and Enhancement of DFT-Based Synchrophasor Estimators in Off-Nominal Conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2653–2664. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy Analysis of the Multicycle Synchrophasor Estimator Provided by the Interpolated DFT Algorithm. IEEE Trans. Instrum. Meas. 2013, 62, 942–953. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced Interpolated-DFT for Synchrophasor Estimation in FPGAs: Theory, Implementation, and Validation of a PMU Prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Serna, J.A.D.L.O. Dynamic Phasor Estimates for Power System Oscillations. IEEE Trans. Instrum. Meas. 2007, 56, 1648–1657. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Platas-Garza, J.; Serna, J.A.D.L.O. Dynamic Phasor and Frequency Estimates through Maximally Flat Differentiators. IEEE Trans. Instrum. Meas. 2010, 59, 1803–1811. [Google Scholar] [CrossRef]
- Mai, R.K.; He, Z.Y.; Fu, L.; Kirby, B.; Bo, Z.Q. A Dynamic Synchrophasor Estimation Algorithm for Online Application. IEEE Trans. Power Deliv. 2010, 25, 570–578. [Google Scholar] [CrossRef]
- Bi, T.; Liu, H.; Feng, Q.; Qian, C.; Liu, Y. Dynamic Phasor Model-Based Synchrophasor Estimation Algorithm for M-Class PMU. IEEE Trans. Power Deliv. 2015, 30, 1162–1171. [Google Scholar] [CrossRef]
- Ling, F.; Zhang, J.; Xiong, S.; He, Z.; Mai, R. A Modified Dynamic Synchrophasor Estimation Algorithm Considering Frequency Deviation. IEEE Trans. Smart Grid 2017, 8, 640–650. [Google Scholar]
- Serna, J.A.D.L.O.; Rodriguez-Maldonado, J. Instantaneous Oscillating Phasor Estimates With TaylorK-Kalman Filters. IEEE Trans. Power Syst. 2011, 26, 2336–2344. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications; Springer: New York, NY, USA, 2008; pp. 121–128. [Google Scholar]
- Castello, P.; Lixia, M.; Muscas, C.; Pegoraro, P.A. Impact of the Model on the Accuracy of Synchrophasor Measurement. IEEE Trans. Instrum. Meas. 2012, 61, 2179–2188. [Google Scholar] [CrossRef]
- Serna, J.A.D.L.O.; Rodríguez-Maldonado, J. Taylor-Kalman-Fourier Filters for Instantaneous Oscillating Phasor and Harmonic Estimates. IEEE Trans. Instrum. Meas. 2012, 61, 941–951. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Serna, J.A.D.L.O. Dynamic Harmonic Analysis Through Taylor–Fourier Transform. IEEE Trans. Instrum. Meas. 2011, 60, 804–813. [Google Scholar] [CrossRef]
- Castello, P.; Liu, J.; Muscas, C.; Pegoraro, P.A.; Ponci, F.; Monti, A. A Fast and Accurate PMU Algorithm for P + M Class Measurement of Synchrophasor and Frequency. IEEE Trans. Instrum. Meas. 2014, 63, 2837–2845. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Serna, J.A.D.L.O. Polynomial Implementation of the Taylor–Fourier Transform for Harmonic Analysis. IEEE Trans. Instrum. Meas. 2014, 63, 2846–2854. [Google Scholar] [CrossRef]
- Serna, J.A.D.L.O. Synchrophasor Measurement With Polynomial Phase-Locked-Loop Taylor-Fourier Filters. IEEE Trans. Instrum. Meas. 2015, 64, 328–337. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Yu, Y.; Wang, Q.; Huang, S. Improved Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference, Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Wang, F.; Zhao, W.; Guo, L.; Wang, C.; Jiang, X.; Wang, Z. Optimal filter design for frequency and synchrophasor measurement. Proc. CSEE 2017, 37, 6691–6699. [Google Scholar]
- Alomar, A.M.A.; Shamseldin, B.E.M. Alternative Approaches for Distinguishing between Faults and Inrush Current in Power Transformers. Energy Power Eng. 2014, 6, 143–160. [Google Scholar] [CrossRef]
| c | Hanning | Hamming |
|---|---|---|
| 2 | {25.0, 26.0, 27.2} | {28.2, 33.8, 46.0} |
| 3 | {29.2, 53.0, 66.2} | {35.2, 45.4, 65.0} |
| Method | Comp. | Comp. Type | ||
|---|---|---|---|---|
| + | × | |||
| e-IpDFT | ||||
| (7) | – | |||
| IpDFT | ||||
| (7) | – | |||
| Parameter | Fre. Dev. | Harm. Dist. | AM + FM | ||||||
| std | e-IpDFT | IpDFT | std | e-IpDFT | IpDFT | std | e-IpDFT | IpDFT | |
| TVE | 1 | 0.00 | 0.00 | 1.00 | 0.09 | 0.05 | 3.00 | 0.03 | 0.01 |
| |FE| | 0.005 | 0.00 | 0.00 | 0.03 | 0.00 | 0.01 | 0.30 | 0.02 | 0.02 |
| |RFE| | 0.1 | 0.00 | 0.00 | – | 0.06 | 1.73 | 14.00 | 0.95 | 0.92 |
| Parameter | Amp. Step Change (±10%) | Ph. Step Change () | Fre. Ramp | ||||||
| std | e-IpDFT | IpDFT | std | e-IpDFT | IpDFT | std | e-IpDFT | IpDFT | |
| TVE | 2.00 | 0.82 | 0.82 | 2.00 | 1.60 | 0.95 | 1.00 | 0.00 | 0.00 |
| |FE| | 4.50 | 2.35 | 2.35 | 4.50 | 2.38 | 2.57 | 0.01 | 0.00 | 0.00 |
| |RFE| | 6.00 | 2.70 | 2.70 | 6.00 | 2.78 | 2.53 | 0.20 | 0.00 | 0.00 |
| Parm. | Std. | c | Hanning | Hamming | ||
|---|---|---|---|---|---|---|
| e-IpDFT | IpDFT | e-IpDFT | IpDFT | |||
| TVE | 1 | 2 | 1.97 | 7.47 | 0.47 | 7.14 |
| 3 | 0.10 | 2.42 | 0.11 | 1.61 | ||
| |FE| | 0.025 | 2 | 0.36 | 1.21 | 0.11 | 1.15 |
| 3 | 0.01 | 0.11 | 0.01 | 0.12 | ||
| |RFE| | – | 2 | 120.66 | 472.07 | 14.97 | 423.75 |
| 3 | 0.56 | 88.66 | 2.97 | 52.26 | ||
| Parm. | Std. | c | Hanning | Hamming | ||
|---|---|---|---|---|---|---|
| e-IpDFT | IpDFT | e-IpDFT | IpDFT | |||
| TVE | 3 | 2 | 2.25 | 8.40 | 0.62 | 7.99 |
| 3 | 0.23 | 2.78 | 0.19 | 1.88 | ||
| |FE| | 0.3 | 2 | 0.40 | 1.35 | 0.14 | 1.29 |
| 3 | 0.04 | 0.15 | 0.04 | 0.16 | ||
| |RFE| | 14 | 2 | 134.41 | 540.20 | 19.30 | 482.36 |
| 3 | 4.12 | 100.35 | 5.69 | 61.10 | ||
| Test Type | Method | TVE | |FE| | |RFE| | |
|---|---|---|---|---|---|
| Fre. Dev. + 2nd Harm + 3rd Harm | e-IpDFT | 0.12 | 0.01 | 1.32 | |
| IpDFT | 2.43 | 0.11 | 89.09 | ||
| Fre. Dev. + 2nd Harm + 60 dB Noise | e-IpDFT | mean | 0.09 | 0.00 | 0.33 |
| std. dev. | 0.00 | 0.00 | 0.06 | ||
| IpDFT | mean | 2.38 | 0.06 | 55.93 | |
| std. dev. | 0.00 | 0.00 | 712.73 | ||
| Parm. | Method | Sampling Rate (Hz) | |||
|---|---|---|---|---|---|
| 2000 | 2400 | 4000 | 4800 | ||
| TVE | e-IpDFT | 0.04 | 0.04 | 0.04 | 0.04 |
| IpDFT | 0.06 | 0.06 | 0.07 | 0.07 | |
| |FE| | e-IpDFT | 0.00 | 0.00 | 0.00 | 0.00 |
| IpDFT | 0.01 | 0.01 | 0.01 | 0.01 | |
| |RFE| | e-IpDFT | 0.06 | 0.06 | 0.06 | 0.06 |
| IpDFT | 2.04 | 2.13 | 2.30 | 2.34 | |
| Harm. Comp. | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|
| Magnitude (% of the fundamental) | 63 | 26.8 | 5.1 | 4.1 | 3.7 | 2.4 |
| Test Type | Method | TVE | |FE| | |RFE| | |
|---|---|---|---|---|---|
| Fre. Dev. + Harmonics + 60 dB Noise | e-IpDFT | mean | 0.55 | 0.01 | 0.98 |
| std. dev. | 0.00 | 0.00 | 0.36 | ||
| IpDFT | mean | 1.86 | 0.12 | 41.94 | |
| std. dev. | 0.00 | 0.00 | 398.88 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhao, W.; Wang, F.; Wang, Q.; Huang, S. Enhanced Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences. Sensors 2018, 18, 2748. https://doi.org/10.3390/s18092748
Chen L, Zhao W, Wang F, Wang Q, Huang S. Enhanced Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences. Sensors. 2018; 18(9):2748. https://doi.org/10.3390/s18092748
Chicago/Turabian StyleChen, Lei, Wei Zhao, Fuping Wang, Qing Wang, and Songling Huang. 2018. "Enhanced Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences" Sensors 18, no. 9: 2748. https://doi.org/10.3390/s18092748
APA StyleChen, L., Zhao, W., Wang, F., Wang, Q., & Huang, S. (2018). Enhanced Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences. Sensors, 18(9), 2748. https://doi.org/10.3390/s18092748






