A New Approach to Unwanted-Object Detection in GNSS/LiDAR-Based Navigation
Abstract
1. Introduction
2. Background: Integrity Risk Bound Accounting for Incorrect Associations
2.1. Integrity Risk Definition and Integrity Risk Bound
| is an index identifying a time step; | |
| designates a range of indices: , from filter initiation to time ; | |
| is the correct association hypothesis for all landmarks, at all times 0, ..., ; | |
| is the tail probability function of the standard normal distribution; | |
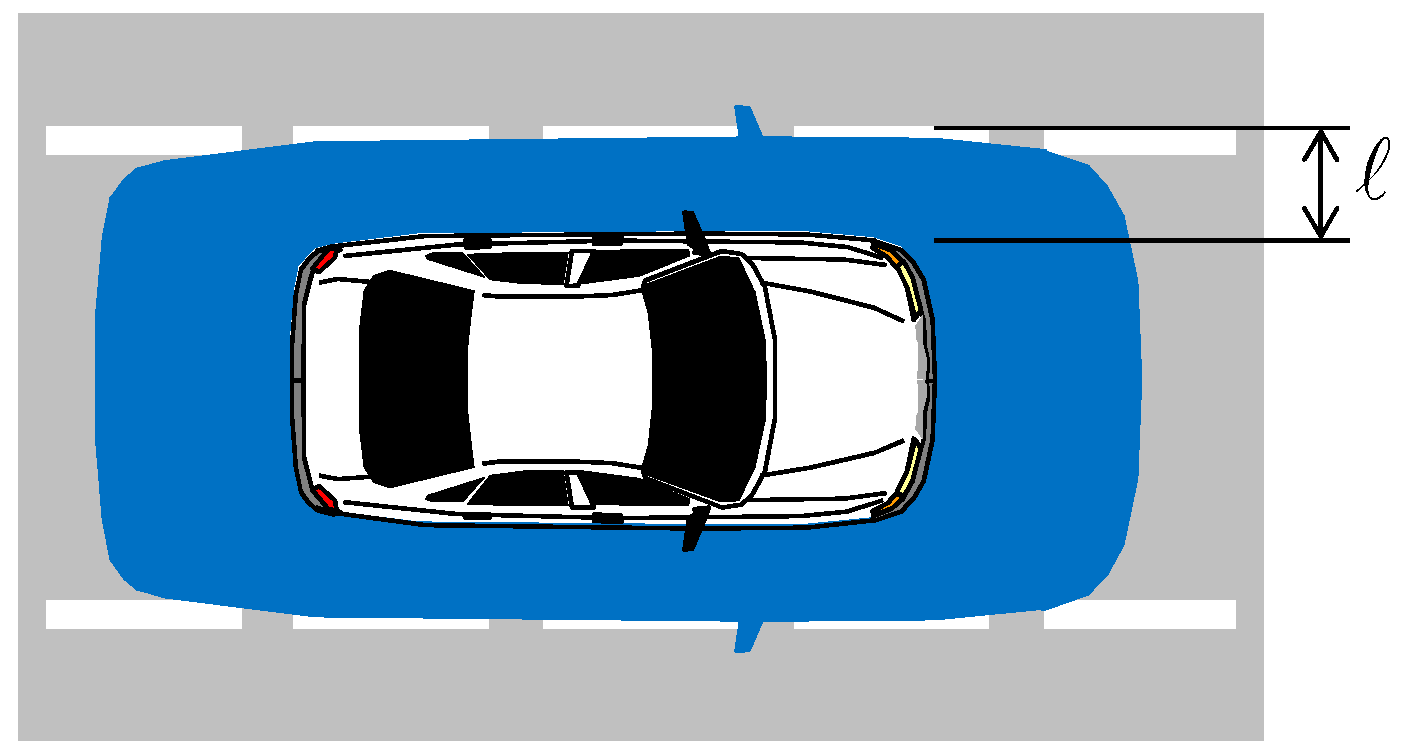
| is the specified alert limit that defines a hazardous situation [4,5,8] (e.g., see Figure 1); | |
| is the standard deviation of the estimation error for the vehicle state of interest (or linear combination of states); | |
| is the probability that a chi-squared-distributed random variable with “dof” degrees of freedom is lower than some value T; | |
| is the number of measurements at time step ; | |
| is the number of estimated state parameters at time step ; | |
| is an integrity risk budget allocation, i.e., a fraction of that we choose to satisfy: ; | |
| is the minimum mean normalized separation between landmark features that can be guaranteed with probability larger than . The normalized feature separation metric is derived in [28]. is derived at FE using a map or database of landmarks or using landmark observations at previous time-steps in SLAM; | |
| is a mapping coefficient from separation space to EKF innovation space. This coefficient is determined by solving an eigenvalue problem in [28]. The minimum eigenvalue is taken to lower bound , which is conservative; | |
| forms a probabilistic lower bound on the mean innovation’s norm, which is further described in the Section 2.2. |
2.2. Innovation-Based Data Association
| includes vehicle pose parameters and may also include landmark feature parameters (for SLAM-type approaches); | |
| is the extracted measurement noise vector: , where is an matrix of zeros. |
3. Risks Involved with Unwanted Object Detection
3.1. Innovation-Based Detector
3.2. Integrity Risk in Presence of UO
| is the event of hazardous information (HI) at time , defined as ; | |
| is the event of no detection (ND) at all previous times 0, ..., , defined as ; | |
| is the event of ND at time , defined as ; | |
| is the CA hypothesis for all landmarks, at all times 0, ..., ; | |
| is the IA hypothesis for any landmarks, at any time 0, ..., . |
4. Analytical Bounds on Risks Caused by Undetected Unwanted Objects
4.1. Risk of HMI Due to Undetected UO
4.2. Risk of Incorrect Association Due to Undetected UO
- (i)
- the events and are correlated because both events depend on the same innovation vectors; and
- (ii)
- unlike on the left-hand side in Equation (17), there is no condition on association (no “given ”), so we do not know which association is used to compute the innovations in the detection test statistic .
4.3. Summary of the New Integrity Risk Bound, Accounting for Presence of UO
| is derived from and where, in addition to the variables defined under Equations (1)–(3), we used: | |
| is a scalar search parameter (fault magnitude) that is varied to maximize the integrity risk at each time ; | |
| is the worst-case failure mode slope (FMS) over all UO hypotheses, determined using the method given in [35]; | |
| is the probability that a non-centrally chi-squared distributed random variable with “dof” degrees of freedom and noncentrality parameter is lower than some value T; | |
| . | is a detection threshold set in accordance to a continuity risk requirement in Equation (11); |
| is an integrity risk budget allocation, i.e., a fraction of , chosen to satisfy |
5. Performance Analysis
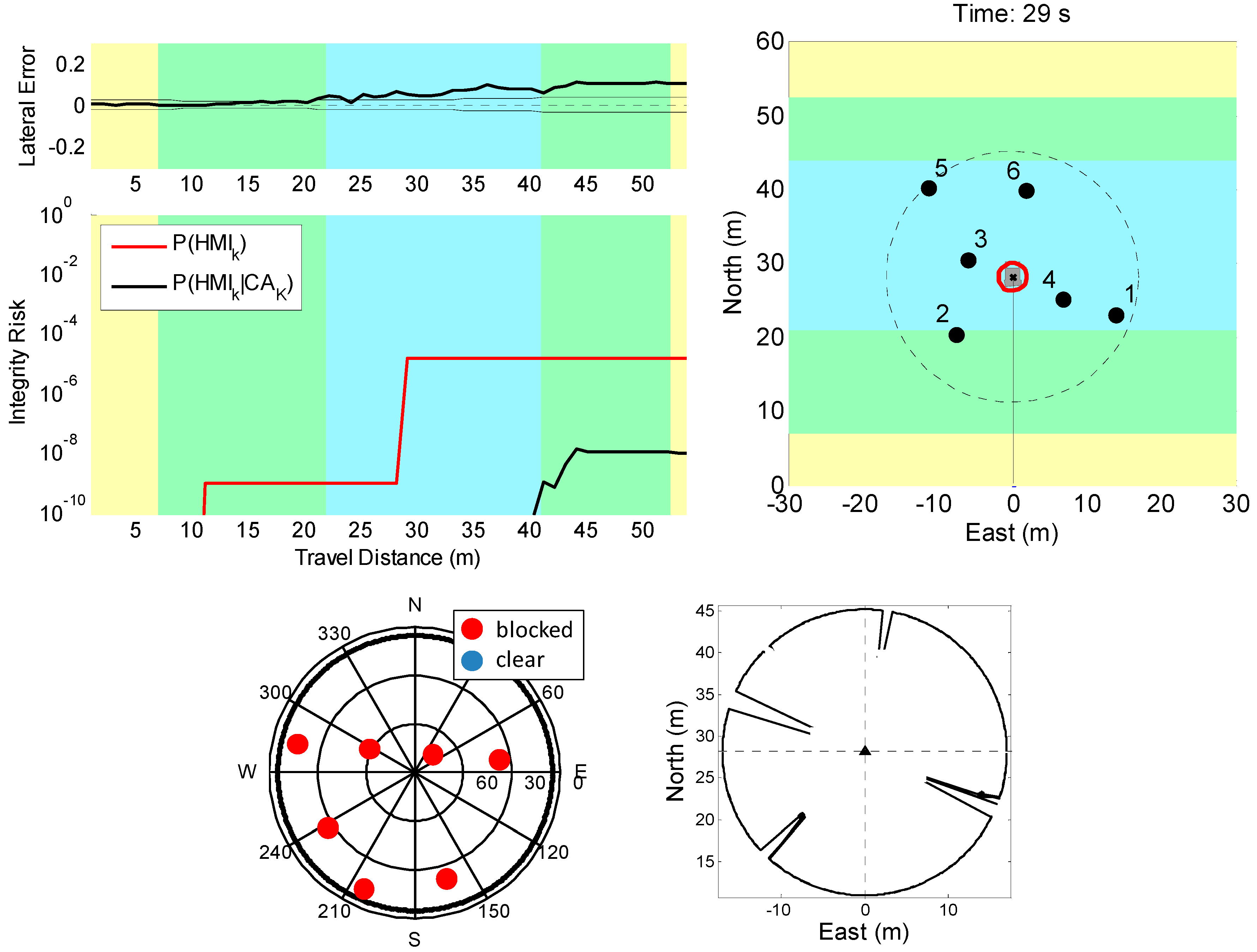
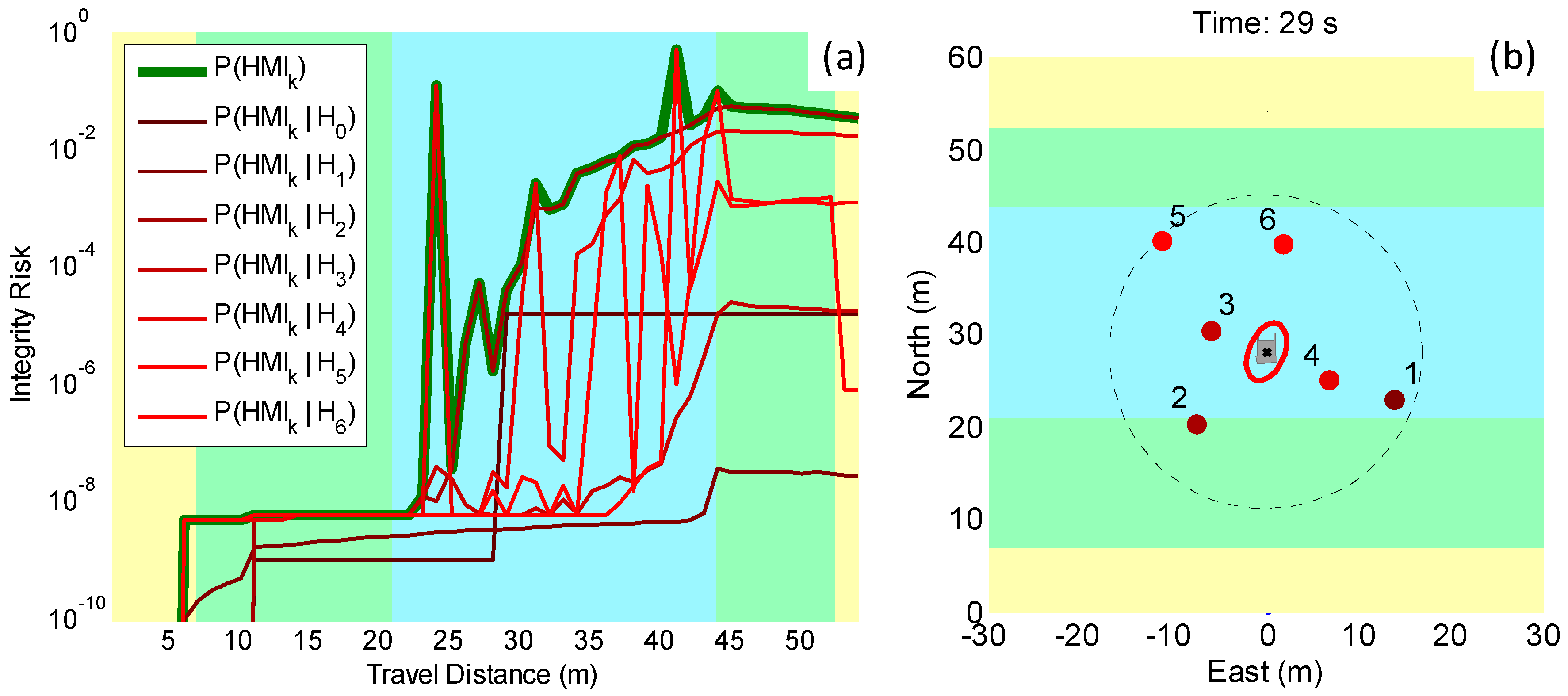
5.1. Direct Simulation: Vehicle Roving through a GNSS-Denied Area
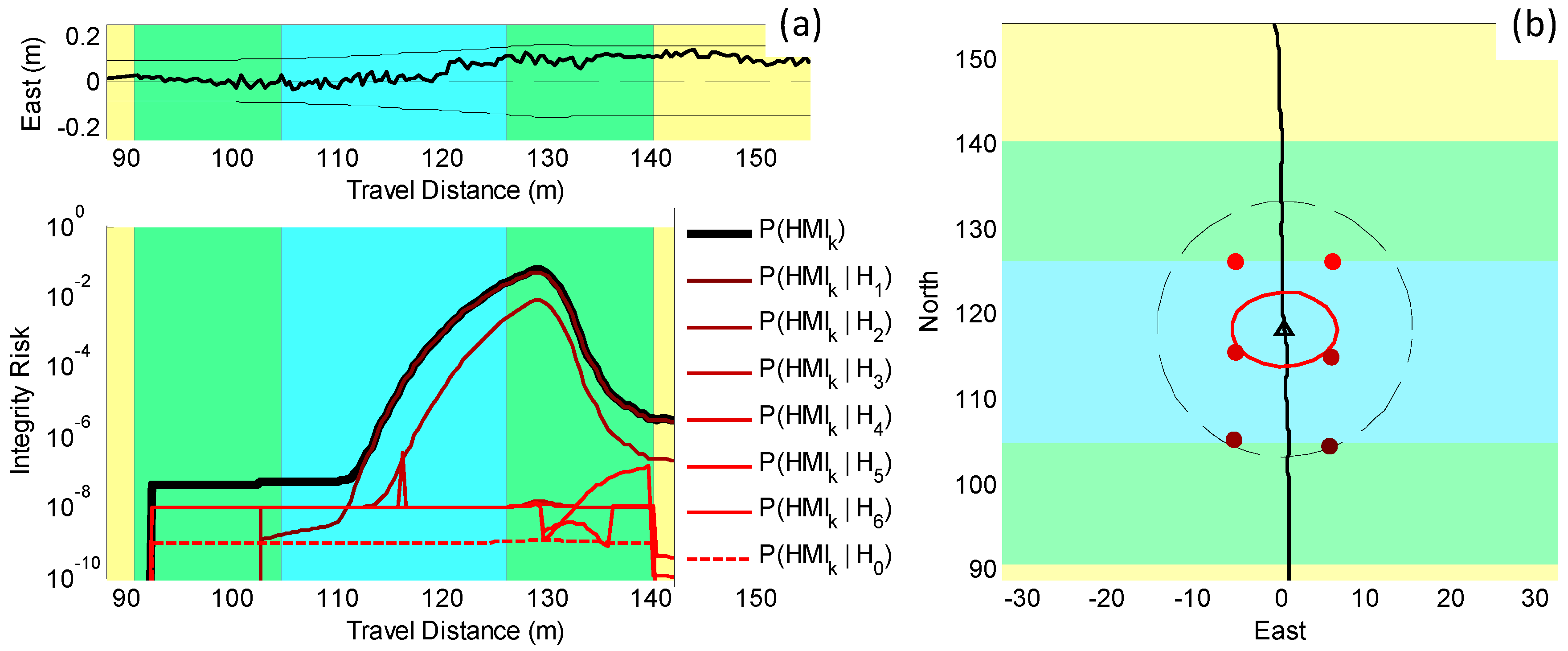
5.2. Preliminary Testing in an Incorrect-Association-Free Environment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Upper Bound on the Probability of Incorrect Association in the Presence of Unwanted Objects
| is defined in Equation (7) and is not zero because of IA (not due to UOs); | |
| is defined in Equation (9); | |
| is an vector such that ; | |
| 4 | the factor four is derived in [28] by solving an eigenvalue problem involving a sum of two idempotent matrices. |
References
- Joerger, M.; Duenas Arana, G.; Spenko, M.; Pervan, B. Landmark Data Selection and Unmapped Obstacle Detection in Lidar-Based Navigation. In Proceedings of the ION GNSS+, Portland, OR, USA, 25–29 September 2017. [Google Scholar]
- U.S. Department of Transportation (DOT) National Highway Traffic Safety Administration (NHTSA). Available online: https://www.nhtsa.gov/manufacturers/automated-driving-systems (accessed on 18 May 2018).
- Federal Automated Vehicles Policy—September 2016. Available online: https://www.transportation.gov/AV/federal-automated-vehicles-policy-september-2016 (accessed on 18 May 2018).
- RTCA Special Committee 159, Minimum Aviation System Performance Standards for the Local Area Augmentation System (LAAS). Available online: https://standards.globalspec.com/std/11988/rtca-do-245 (accessed on 18 May 2018).
- DOT Federal Highway Administration (FHWA), Vehicle Positioning Trade Study for ITS Applications. Available online: https://rosap.ntl.bts.gov/view/dot/3319/Print (accessed on 18 May 2018).
- Lee, Y.C. Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver. In Proceedings of the 42nd Annual Meeting of The Institute of Navigation (1986), Seattle, WA, USA, 24–26 June 1986. [Google Scholar]
- Parkinson, B.W.; Axelrad, P. Autonomous GPS Integrity Monitoring Using the Pseudorange Residual. J. Inst. Navig. 1988, 35, 255–274. [Google Scholar] [CrossRef]
- RTCA Special Committee 159, Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment. Available online: https://standards.globalspec.com/std/1239716/rtca-do-229 (accessed on 18 May 2018).
- Lu, F.; Milios, E. Globally Consistent Range Scan Alignment for Environment Mapping. Ayton. Robots 1997, 4, 333–349. [Google Scholar] [CrossRef]
- Röfer, T. Using Histogram Correlation to Create Consistent Laser Scan Maps. IEEE Intell. Robots Syst. 2002, 1, 625–630. [Google Scholar]
- Diosi, A.; Kleeman, L. Laser scan matching in polar coordinates with application to SLAM. IEEE Robots Syst. 2005, 5, 3317–3322. [Google Scholar]
- Bengtsson, O.; Baerveldt, A.J. Robot localization based on scan-matching-estimating the covariance matrix for the IDC algorithm. Robot. Autom. Syst. 2003, 44, 29–40. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient Variants of the ICP Algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001. [Google Scholar]
- Bar-Shalom, Y.; Fortmann, T.E.; Cable, P.G. Tracking and Data Association. Math. Sci. Eng. 1988, 179, 918–919. [Google Scholar] [CrossRef]
- Leonard, J.; Durrant-Whyte, H. Directed Sonar Sensing for Mobile Robot Navigation; Springer: New York, NY, USA, 1992. [Google Scholar]
- Thrun, S. Robotic Mapping: A Survey. In Exploring Artificial Intelligence in the New Millenium; Lakemeyer, G., Nebel, B., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 2003. [Google Scholar]
- Cooper, A.J. A Comparison of Data Association Techniques for Simultaneous Localization and Mapping. Master’s Thesis, Massachussetts Institute of Technology, Cambrige, MA, USA, 2005. [Google Scholar]
- Ruiz, I.T.; Petillot, Y.; Lane, D.M.; Salson, C. Feature Extraction and Data Association for AUV Concurrent Mapping and Localisation. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Tareen, S.A.K.; Saleem, Z. A comparative analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018. [Google Scholar]
- Dissanayake, G.; Newman, P.; Clark, S.; Durrant-Whyte, H.; Csorba, M. A Solution to the Simultaneous Localization and Map Building (SLAM) Problem. IEEE Trans. Robot. Autom. 2001, 17, 229–241. [Google Scholar] [CrossRef]
- Feng, Y.; Schlichting, A.; Brenner, C. 3D Feature Point Extraction from LiDAR Data Using a Neural Network. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Cezch, 12–19 July 2016. [Google Scholar]
- Li, Y.; Olson, E.B. A General Purpose Feature Extractor for Light Detection and Ranging Data. Sensors 2010, 10, 10356–10375. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kang, H. A New 3D Object Pose Detection Method Using LIDAR Shape Set. Sensors 2018, 18, 882. [Google Scholar] [CrossRef] [PubMed]
- Bar-Shalom, Y.; Daum, F.; Huang, J. The Probabilistic Data Association Filter. IEEE Control Syst. Mag. 2009, 29, 82–100. [Google Scholar]
- Areta, J.; Bar-Shalom, Y.; Rothrock, R. Misassociation Probability in M2TA and T2TA. J. Adv. Inf. Fusion 2007, 2, 113–127. [Google Scholar]
- Joerger, M.; Jamoom, M.; Spenko, M.; Pervan, B. Integrity of Laser-Based Feature Extraction and Data Association. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016. [Google Scholar]
- Joerger, M.; Pervan, B. Continuity Risk of Feature Extraction for Laser-Based Navigation. In Proceedings of the 2017 International Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 30 January–2 February 2017. [Google Scholar]
- Joerger, M.; Pervan, B. Quantifying Safety of Laser-Based Navigation. IEEE Trans. Aerosp. Electron. Syst. 2018. [Google Scholar] [CrossRef]
- Kim, C.; Lee, Y.; Park, J.; Lee, J. Diminishing unwanted objects based on object detection using deep learning and image inpainting. In Proceedings of the 2018 International Workshop on Advanced Image Technology (IWAIT), Chiang Mai, Thailand, 7–9 January 2018. [Google Scholar]
- Asvadi, A.; Premebida, C.; Peixoto, P.; Nunes, U. 3D Lidar-based static and moving obstacle detection in driving environments: An approach based on voxels and multi-region ground planes. Robot. Autom. Syst. 2016, 83, 299–311. [Google Scholar] [CrossRef]
- DeCleene, B. Defining Pseudorange Integrity—Overbounding. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000. [Google Scholar]
- Rife, J.; Pullen, S.; Enge, P.; Pervan, B. Paired Overbounding for Nonideal LAAS and WAAS Error Distributions. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1386–1395. [Google Scholar] [CrossRef]
- Arana, G.D.; Joerger, M.; Spenko, M. Minimizing Integrity Risk via Landmark Selection in Mobile Robot Localization. IEEE Trans. Robot. 2017, in press. [Google Scholar]
- Tanil, C.; Khanafseh, S.; Joerger, M.; Pervan, B. An INS Monitor to Detect GNSS Spoofers Capable of Tracking Vehicle Position. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 131–143. [Google Scholar] [CrossRef]
- Tanil, C.; Joerger, M.; Khanafseh, S.; Pervan, B. A Sequential Integrity Monitoring for Kalman Filter Innovations-Based Detectors. In Proceedings of the ION GNSS+, Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- Joerger, M.; Chan, F.-C.; Pervan, B. Solution Separation Versus Residual-Based RAIM. J. Inst. Navig. 2014, 64, 273–291. [Google Scholar] [CrossRef]
- Joerger, M.; Pervan, B. Kalman Filter-Based Integrity Monitoring Against Sensor Faults. J. Guid. Control Dyn. 2013, 36, 349–361. [Google Scholar] [CrossRef]
- Pullen, S.; Lee, J.; Luo, M.; Pervan, B.; Chan, F.-C.; Gratton, L. Ephemeris Protection Level Equations and Monitor Algorithms for GBAS. In Proceedings of the ION GPS 2001, Salt Lake City, UT, USA, 11–14 September 2001. [Google Scholar]
- Pullen, S. Augmented GNSS: Fundamentals and Keys to Integrity and Continuity. In Proceedings of the ION GNSS 2011, Portland, OR, USA, 19–23 September 2011. [Google Scholar]
- Joerger, M.; Pervan, B. Measurement-Level Integration of Carrier-Phase GPS and Laser-Scanner for Outdoor Ground Vehicle Navigation. J. Dyn. Syst. Meas. Control 2009, 131, 021004. [Google Scholar] [CrossRef]
- Joerger, M. Carrier Phase GPS Augmentation Using Laser Scanners and Using Low Earth Orbiting Satellites. Ph.D. Dissertation, Illinois Institute of Technology, Chicago, IL, USA, 2009. [Google Scholar]
- Ye, C.; Borenstein, J. Characterization of a 2-D Laser Scanner for Mobile Robot Obstacle Negotiation. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002. [Google Scholar]


| System Parameters | Values |
|---|---|
| Standard deviation of raw LiDAR ranging measurement | 0.02 m |
| Standard deviation of raw LiDAR angular measurement | 0.5 deg |
| LiDAR range limit | 20 m |
| GNSS and LiDAR data sampling interval | 0.5 s |
| Standard deviation of raw GNSS code ranging signal | 1 m |
| Standard deviation of raw GNSS carrier ranging signal | 0.015 m |
| GNSS multipath correlation time constant | 90 s |
| Vehicle speed | 1 m/s |
| Alert limit ℓ | 0.5 m |
| Integrity risk allocation for FE, IFE,k | 10−9 |
| Integrity risk allocation for MDE, IMDE,k | 10−10 |
| Continuity risk requirement, CREQ,k | 10−3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joerger, M.; Duenas Arana, G.; Spenko, M.; Pervan, B. A New Approach to Unwanted-Object Detection in GNSS/LiDAR-Based Navigation. Sensors 2018, 18, 2740. https://doi.org/10.3390/s18082740
Joerger M, Duenas Arana G, Spenko M, Pervan B. A New Approach to Unwanted-Object Detection in GNSS/LiDAR-Based Navigation. Sensors. 2018; 18(8):2740. https://doi.org/10.3390/s18082740
Chicago/Turabian StyleJoerger, Mathieu, Guillermo Duenas Arana, Matthew Spenko, and Boris Pervan. 2018. "A New Approach to Unwanted-Object Detection in GNSS/LiDAR-Based Navigation" Sensors 18, no. 8: 2740. https://doi.org/10.3390/s18082740
APA StyleJoerger, M., Duenas Arana, G., Spenko, M., & Pervan, B. (2018). A New Approach to Unwanted-Object Detection in GNSS/LiDAR-Based Navigation. Sensors, 18(8), 2740. https://doi.org/10.3390/s18082740





