A Probabilistic Target Search Algorithm Based on Hierarchical Collaboration for Improving Rapidity of Drones
Abstract
1. Introduction
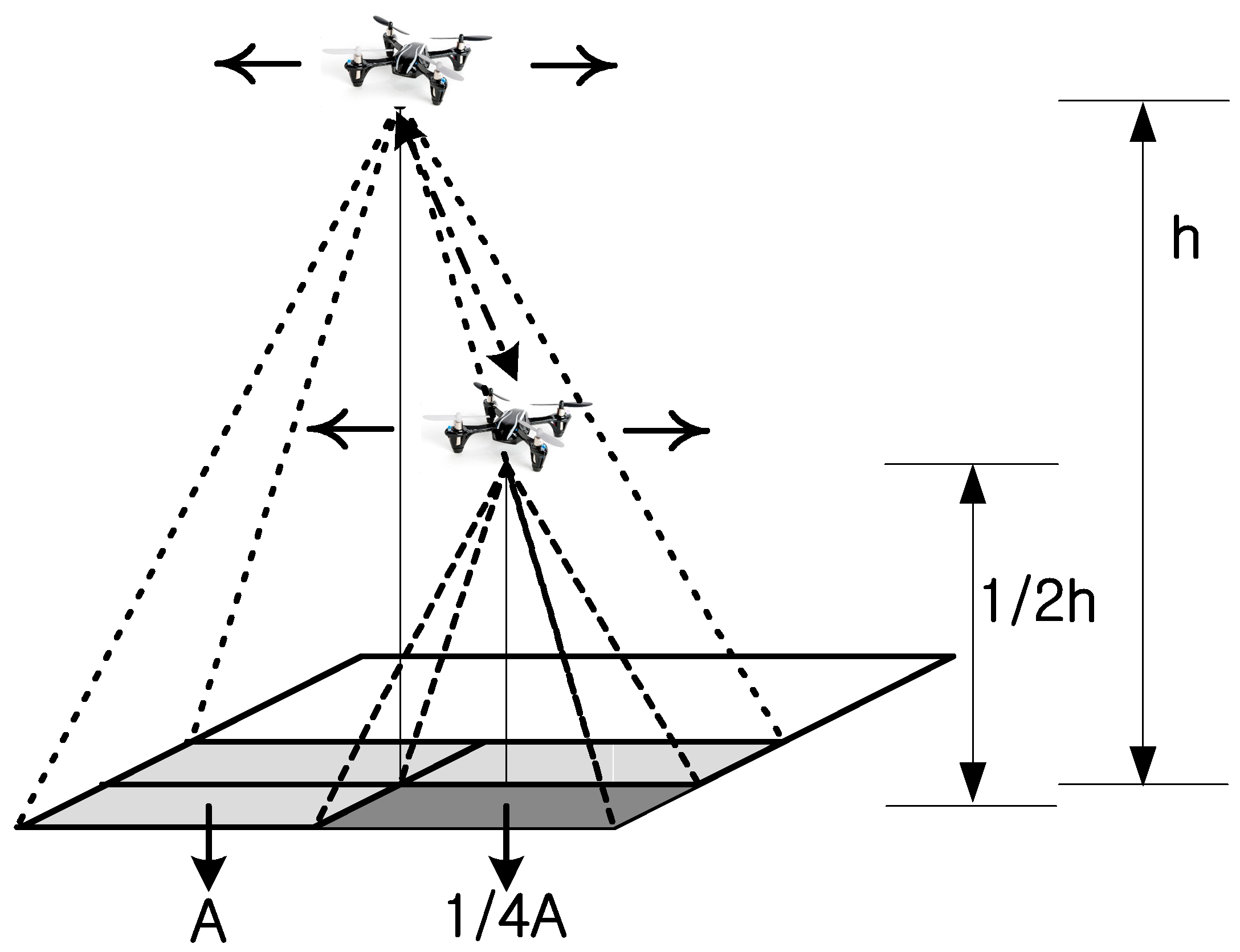
- First, an improved hierarchical probabilistic target search algorithm based on the collaboration of drones at different altitudes is proposed. This is a method for reducing the search time and search distance by improving the information transfer methods between high-altitude and low-altitude drones. Specifically, to improve the speed of target detection, a high-altitude drone performs a preliminary search of a wide area.
- Second, this study suggests a method of using thresholds for information transfer between high altitude and low altitude to improve the efficiency of a search, i.e., to reduce the search time and search travel distance. In this method, when the probability of the existence of a target at a high altitude is higher than a certain threshold, the search information is transmitted to a low-altitude drone.
- Third, several drone collaboration scenarios that can be performed by two drones at different altitudes are introduced and compared to the proposed algorithm. These methods are hierarchical cooperation methods of drones that can be used in an actual search. Through simulations, it is demonstrated that methods utilizing hierarchical searches with drones are comparatively excellent and that the proposed algorithm has better performance compared to other scenarios.
2. Related Works
2.1. Target Detection Method
2.2. Target Detection Based on Probabilistic Search
2.3. Altitude Control Strategies
3. Advanced Hierarchical Probabilistic Search Algorithm
3.1. Improvement of the Probabilistic Search
| Algorithm 1 Basic Outline of Proposed Algorithm | |
| 1: | while Maxb < Thb |
| 2: | //high-altitude search |
| 3: | high-altitude drone searches for the target sequentially in four search areas |
| 4: | and computes a belief value for each cell in the search areas, |
| 5: | it then selects an Areah |
| 6: | if Maxb > Thn then |
| 7: | //low-altitude search |
| 8: | send search information to the low-altitude drone, |
| 9: | low-altitude drone searches for the target sequentially in the Areah |
| 10: | and computes Maxb |
| 11: | end |
| 12: | end |
| 13: | stop searching |
3.2. Altitude Control Strategy
3.3. Advanced Hierarchical Probabilistic Search Algorithm
| Algorithm 2 Downward Delay Search | |
| 1: | //Initialize |
| 2: | found = 0; |
| 3: | roundh = 0; |
| 4: | roundl = 0; |
| 5: | while found ! = 1 |
| 6: | //High-altitude search |
| 7: | if roundh < round_limit then |
| 8: | the drone searches four Areahs at high altitude |
| 9: | select the Areah containing the cell with the highest probability |
| 10: | if HPh ≥ Thsp then |
| 11: | found = 1 |
| 12: | stop searching |
| 13: | break |
| 14: | else |
| 15: | if HPh > Thlp then |
| 16: | //Low-altitude search |
| 17: | if roundl < round_limit then |
| 18: | send information to low-altitude drone |
| 19: | low-altitude drone searches four Areals at low altitude |
| 20: | if HPl ≥ Thsp then |
| 21: | found = 1 |
| 22: | break |
| 23: | end |
| 24: | else |
| 25: | change altitude upward |
| 26: | end |
| 27: | end |
| 28: | end |
| 29: | else |
| 30: | move to the next area for another high-altitude search |
| 31: | end |
| 32: | roundh = roundh + 1 |
| 33: | end |
4. Simulation
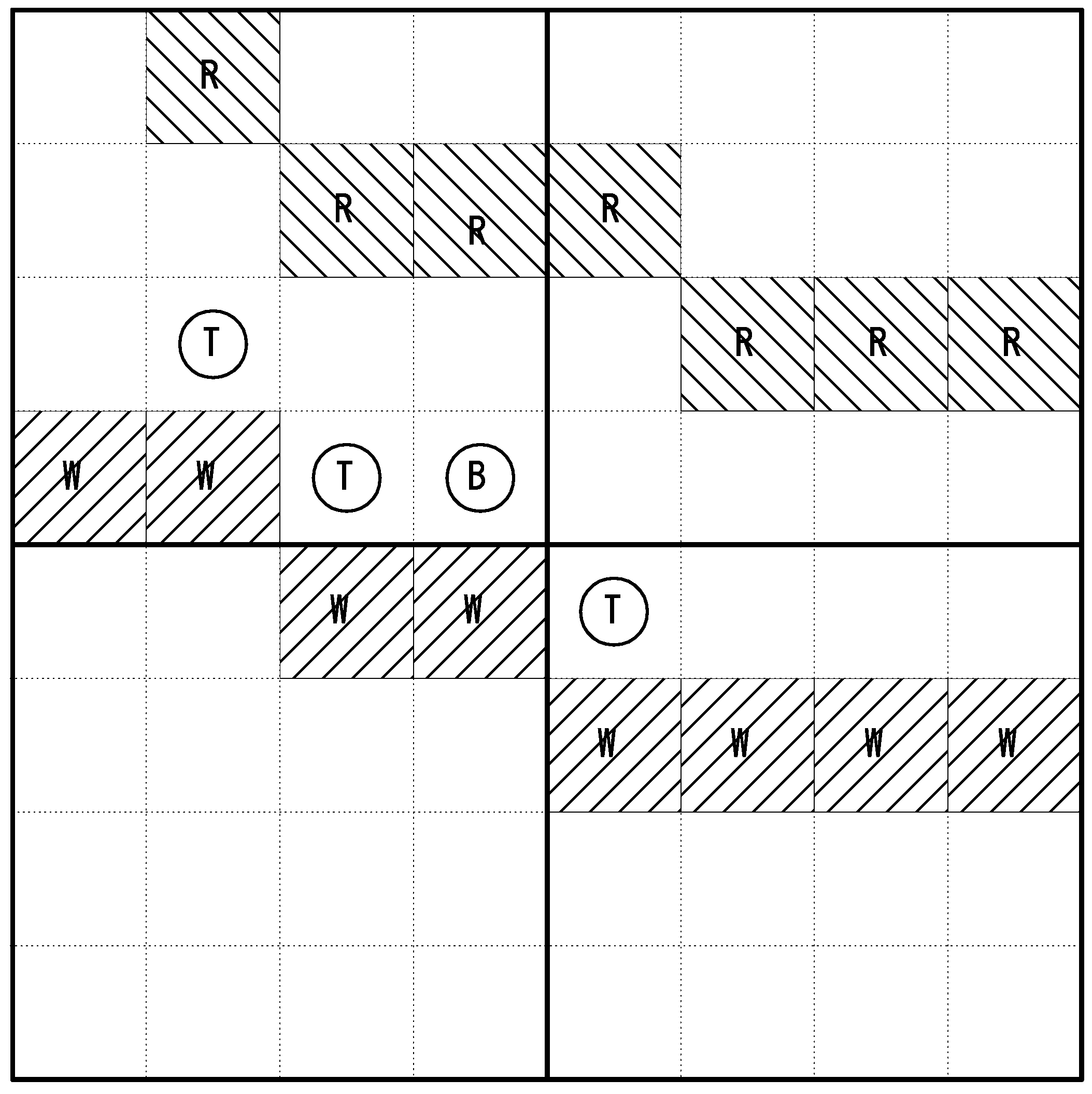
4.1. Simulation Environment
4.2. Search Scenarios
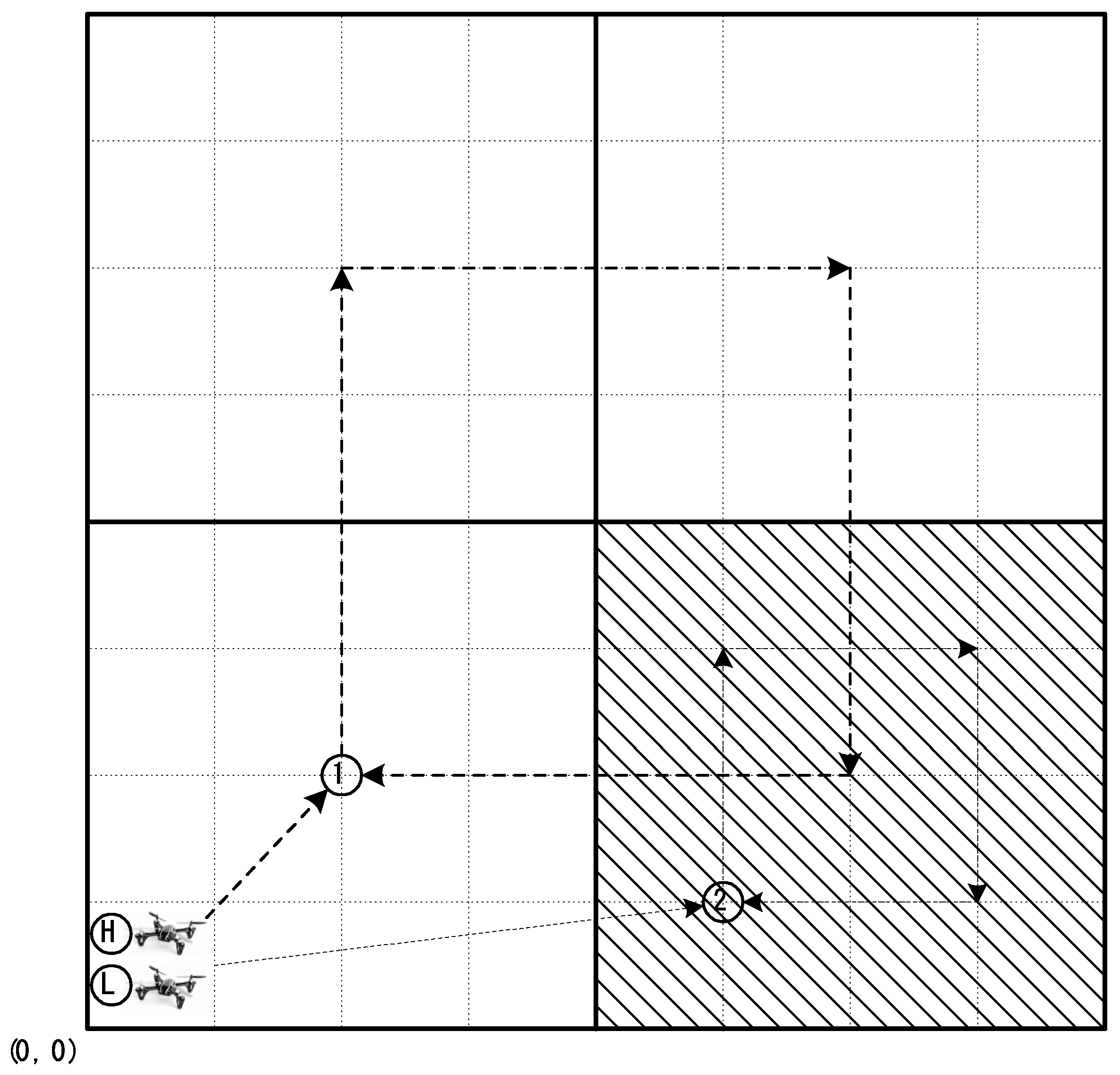
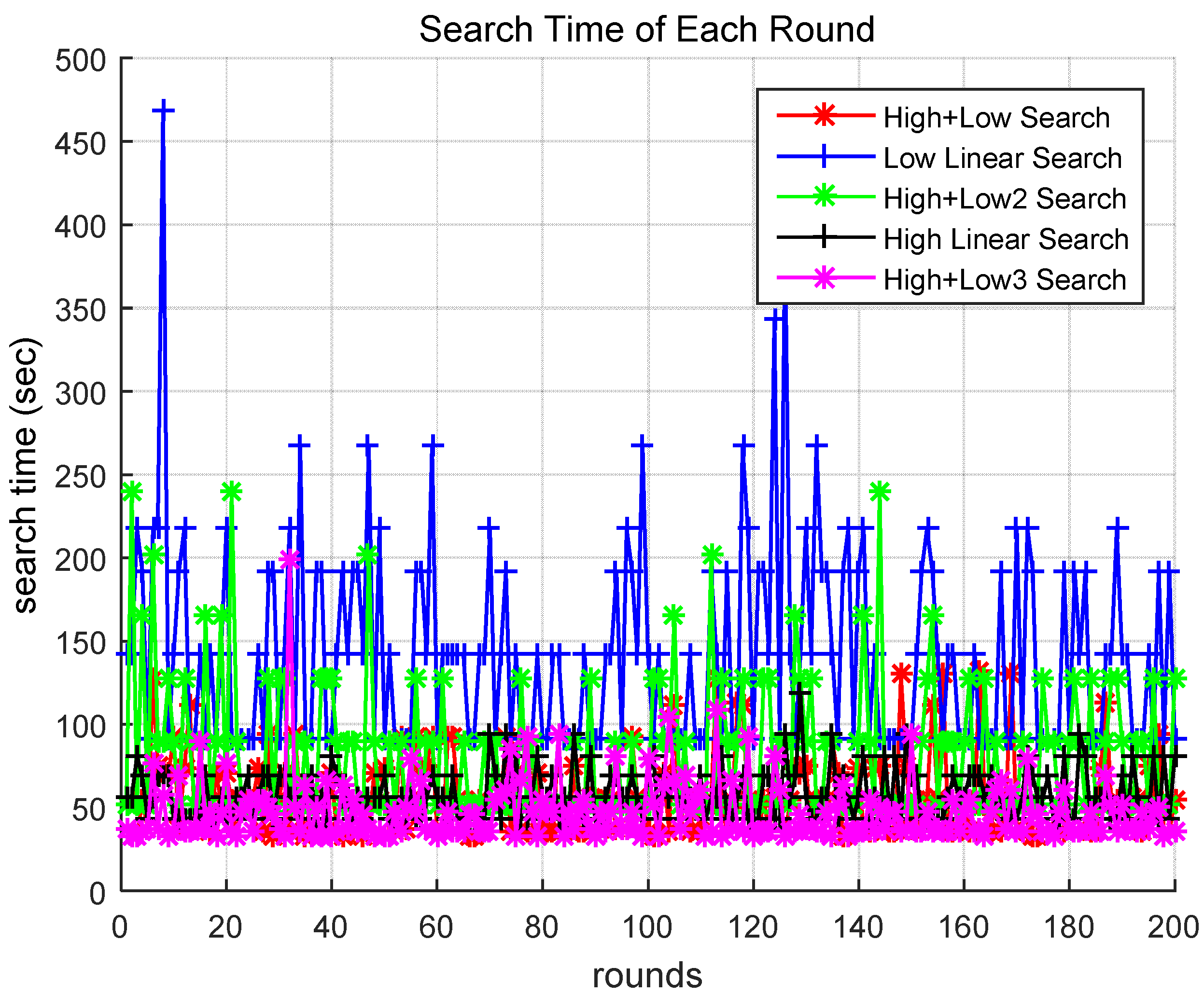
- Scenario 1This scenario is the initial version of the proposed algorithm. In this method, the first drone searches four high-altitude search areas for quick navigation. Then, the area with the highest probability is selected and searched more precisely by a drone at a low altitude. In this method, control is transferred from the high-altitude drone to the low-altitude drone without verifying control transfer. This method operates based on a hierarchical control of drones.
- Scenario 2In the second scenario, a low-altitude drone performs a linear probability search. Specifically, the drone searches each low-altitude search area linearly. The low-altitude drone moves linearly in the direction in which the values of x and y increase and searches for the target. The values of α and β of the low-altitude drone are applied to obtain the target existence probability. The low-altitude drone continues searching based on the α and β values. The probability of the existence of a target in each cell is calculated recursively utilizing Equation (4).
- Scenario 3The third scenario utilizes another altitude-control strategy to detect a target in the search area. The search scenario is as follows. Unlike Scenario 1, the drone searches only one high-altitude search area. The drone selects a low-altitude search area (2 × 2) within the high-altitude search area and sends the search information to the low-altitude drone for more precise searching of the low-altitude search area. This drone then searches the low-altitude search area in detail.
- Scenario 4In this scenario, a high-altitude drone performs a linear probability search. This scenario is very similar to the second scenario. The only difference is that the drone is at a high altitude. In addition, since it has a higher altitude, different α and β values for high altitude are utilized to calculate the probability of each cell.
- Scenario 5This scenario represents the full method proposed in this study. The high-altitude drone sequentially searches an area corresponding to four times its search range from a high altitude. The search range containing the cell with the highest probability of existence of the target is selected. The drone then checks if the highest probability of target existence is greater than or equal to a threshold value to determine if the search control should be transferred to the low-altitude drone. If the value is above the threshold, the search information is transmitted to the low-altitude drone, which then performs a more precise search at a low altitude.
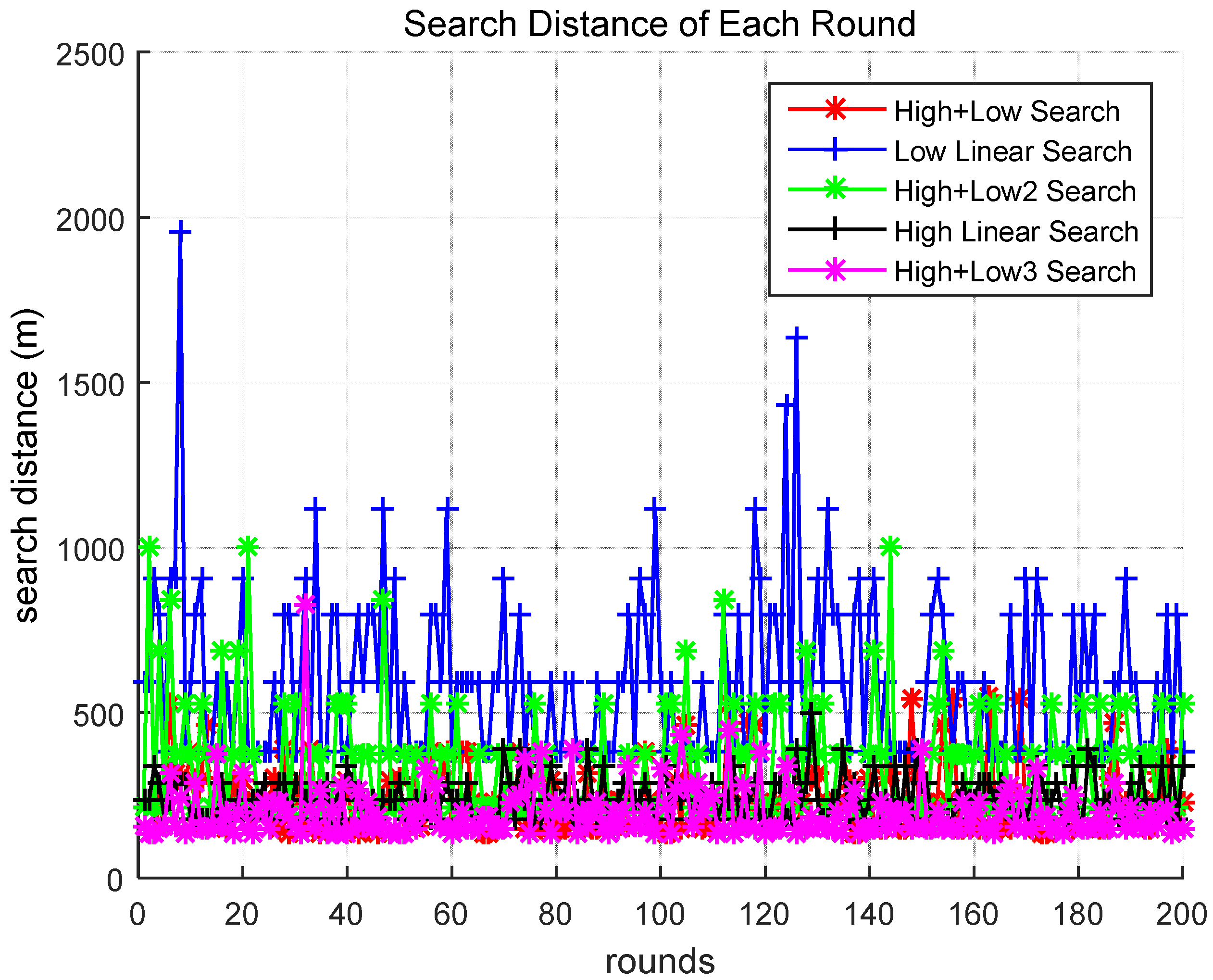
4.3. Simulation Results and Analysis
5. Conclusions
- This study proposed an improved hierarchical probabilistic target search algorithm based on the collaboration of drones at different altitudes. This method reduced the search time and search travel distance by improving the information transfer between high-altitude and low-altitude drones. In addition, the information transfer method increased the efficiency of the proposed algorithm by using thresholds in the information transmission process.
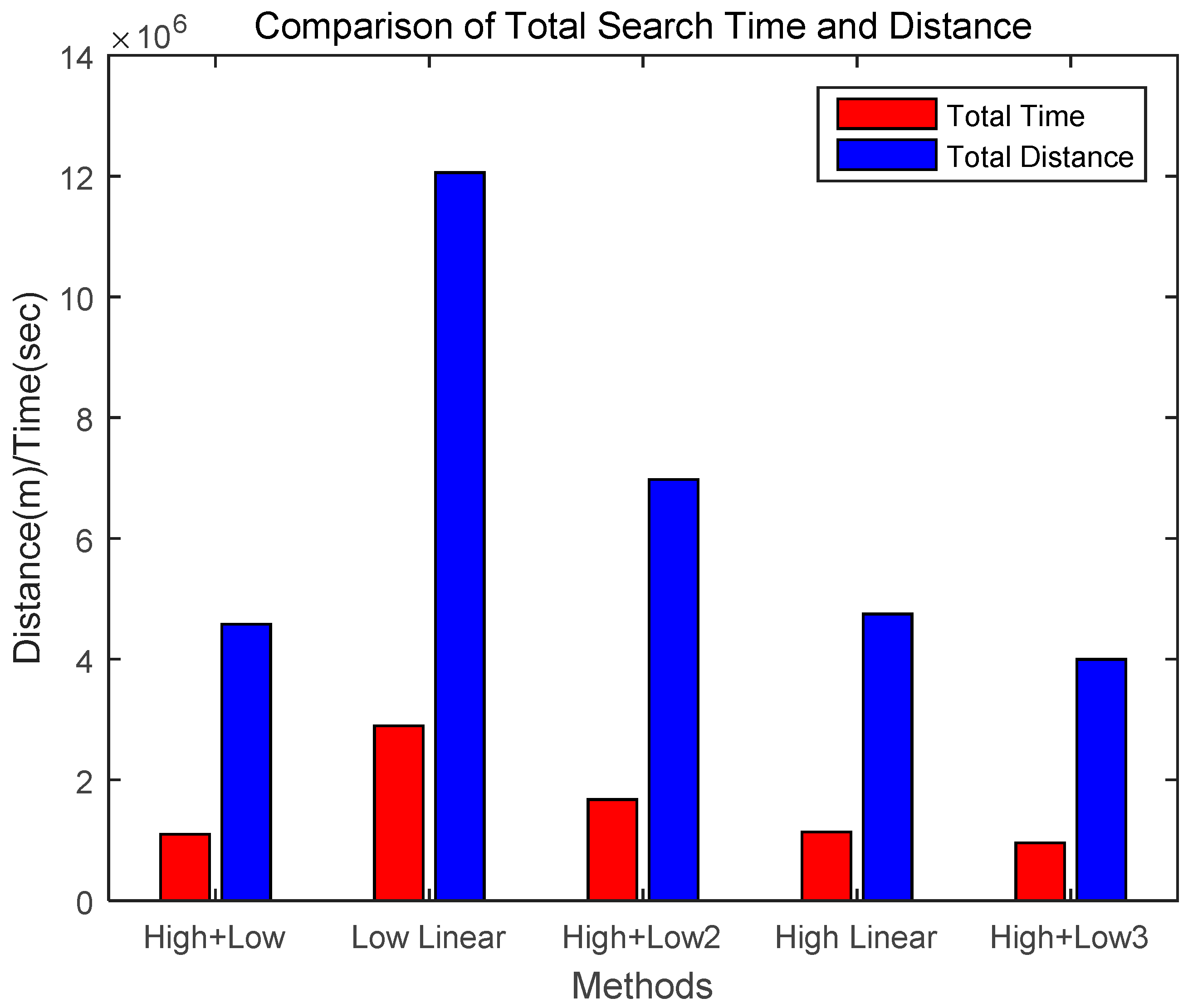
- This study introduced several drone collaboration scenarios performed by two drones at different altitudes and compared the scenarios to the proposed algorithm. Through simulations, the performance of the proposed algorithm and the cooperation scenarios were analyzed. It was demonstrated that methods utilizing hierarchical searches with drones are comparatively excellent and that the proposed algorithm is approximately 13% more effective than a previous method with much better performance compared to other scenarios.
Funding
Acknowledgments
Conflicts of Interest
References
- Bekmezci, I.; Sahingoz, O.K.; Temel, Ş. Flying ad-hoc Networks (FANETs): A survey. Ad Hoc Netw. 2013, 11, 1254–1270. [Google Scholar] [CrossRef]
- Sahingoz, O.K. Networking models in flying ad-hoc networks (FANETs): Concepts and Challenges. J. Intell. Robot. Syst. 2014, 74, 513–527. [Google Scholar] [CrossRef]
- Ha, I.-K. Analysis of importance of search altitude control for rapid target detection of drones. J. Inf. Commun. Converg. Eng. 2018, 16, 78–83. [Google Scholar]
- Chung, T.H.; Burdick, J.W. A decision-making framework for control strategies in probabilistic search. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation (ICRA 2007), Roma, Italy, 10–14 April 2007; pp. 4386–4393. [Google Scholar]
- Liu, Y.; Dai, Q. A survey of computer vision applied in aerial robotic vehicles. In Proceedings of the 2010 International Conference on Optics, Photonics and Energy Engineering (OPEE 2010), Wuhan, China, 10–12 May 2010; pp. 277–280. [Google Scholar]
- Wang, X.; Zhu, H.; Zhang, D.; Zhou, D.; Wang, X. Vision-based detection and tracking of a mobile ground target using a fixed-wing UAV. Int. J. Adv. Robot. Syst. 2014, 11, 1–10. [Google Scholar] [CrossRef]
- Mejias, L.; Mcnamara, S.; Lai, J.; Ford, J. Vision-based detection and tracking of aerial targets for UAV collision avoidance. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2010), Taibei, Taiwan, 18–22 October 2010; pp. 87–92. [Google Scholar]
- Minaeian, S.; Liu, J.; Son, Y. Vision-based target detection and localization via a team of cooperative UAV and UGVs. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1005–1016. [Google Scholar] [CrossRef]
- Arora, A.; Dutta, P.; Bapat, S.; Kulathumani, V.; Zhang, H.; Naik, V.; Mittal, V.; Cao, H.; Demirbas, M.; Gouda, M.; et al. A line in the sand: A wireless sensor network for target detection, classification, and tracking. Comput. Netw. 2004, 46, 605–634. [Google Scholar] [CrossRef]
- Costa, F.G.; Ueyama, J.; Braun, T.; Pessin, G.; Osorio, F.S.; Vargas, P.A. The use of unmanned aerial vehicles and wireless sensor network in agricultural applications. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2012), Munich, Germany, 22–27 July 2012; pp. 5045–5048. [Google Scholar]
- Jawhar, I.; Mohamed, N.; Al-Jaroodi, J.; Zhang, S. Data communication in linear wireless sensor networks using unmanned aerial vehicles. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS 2013), Atlanta, GA, USA, 28–31 May 2013; pp. 492–499. [Google Scholar]
- Chung, T.H.; Burdick, J.W. Analysis of search decision making using probabilistic search strategies. IEEE Trans. Robot. 2012, 28, 132–144. [Google Scholar] [CrossRef]
- Washburn, A.R. Search and Detection (Topics in Operations Research Series), 4th ed.; Institute for Operations Research and the Management Sciences: Linthicum, MD, USA, 2002. [Google Scholar]
- Choset, H. Coverage for robotics—A survey of recent results. Ann. Math. Artif. Intell. 2001, 31, 113–126. [Google Scholar] [CrossRef]
- Robie, A.A. Multimodal Sensory Control of Exploration by Walking Drosophila Melanogaster. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2010. [Google Scholar]
- Itti, L.; Koch, C. A saliency-based search mechanism for overt and covert shifts of visual attention. Vis. Res. 2000, 40, 1489–1506. [Google Scholar] [CrossRef]
- Waharte, S.; Trigoni, N. Supporting search and rescue operations with UAVs. In Proceedings of the 2010 International Conference on Emerging Security Technologies (EST 2010), Canterbury, UK, 6–7 September 2010; pp. 142–147. [Google Scholar]
- Symington, A.; Waharte, S.; Julier, S.; Trigoni, N. Probabilistic target detection by camera-equipped UAVs. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA 2010), Anchorage, AK, USA, 3–8 May 2010; pp. 4076–4082. [Google Scholar]
- Morse, B.S.; Engh, C.H.; Goodrich, M.A. UAV video coverage quality maps and prioritized indexing for wilderness search and rescue. In Proceedings of the 5th ACM/IEEE International Conference on Human-Robot Interaction (HRI 2010), Osaka, Japan, 2–5 March 2010; pp. 227–234. [Google Scholar]
- Waharte, S.; Symington, A.; Trigoni, N. Probabilistic search with agile UAVs. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA 2010), Anchorage, AK, USA, 3–8 May 2010; pp. 2840–2845. [Google Scholar]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileria, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Lin, Y.; Hyyppa, J.; Jaakkola, A. Mini-UAV-borne LIDAR for fine-scale mapping. IEEE Geosci. Remote Sens. Lett. 2011, 8, 426–430. [Google Scholar] [CrossRef]
- Waharte, S.; Trigoni, N.; Julier, S.J. Coordinated search with a swarm of UAVs. In Proceedings of the 6th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks Workshops (SECON 2009), Rome, Italy, 22–26 June 2009; pp. 1–3. [Google Scholar]
- Deisenroth, M.P.; Fox, D.; Rasmussen, C.E. Gaussian processes for data-efficient learning in robotics and control. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 408–423. [Google Scholar] [CrossRef] [PubMed]
- Smaragdis, P.; Fevotte, C.; Mysore, G.J.; Mohammadiha, N.; Hoffman, M. Static and dynamic source separation using nonnegative factorizations: A unified view. IEEE Signal Process. Mag. 2014, 31, 66–75. [Google Scholar] [CrossRef]
- Schneider, N.; Gavrila, D.M. Pedestrian path prediction with recursive Bayesian filters: A comparative study. In Proceedings of the 35th German Conference on Pattern Recognition (GCPR 2013), Saarbrücken, Germany, 3–6 September 2013; pp. 174–183. [Google Scholar]
- Kim, D.H.; Lee, J.S.; Choi, J.D.; Kim, K.E. A POMDP framework for dynamic task allocation and reconnaissance of multiple unmanned aerial vehicles. J. KIISE Softw. Appl. 2012, 39, 453–463. [Google Scholar]



| Variable | Definition |
|---|---|
| Areah | search area of drone at high altitude |
| Areal | search area of drone at low altitude |
| Thsp | threshold probability value for search success |
| Thlp | threshold probability value for low-altitude search |
| HPh | highest probability among cells at high altitude |
| HPl | highest probability among cells at low altitude |
| found | binary variable for found alarm |
| roundh | number of rounds executed at high altitude |
| roundl | number of rounds executed at low altitude |
| Category | Value |
|---|---|
| Size of search area | 8 × 8 units |
| Number of drones | 2 |
| Average drone speed | 15 km/h |
| High-altitude search area of drone | 4 × 4 units (altitude: 20 m) |
| Low-altitude search area of drone | 2 × 2 units (altitude: 10 m) |
| Threshold probability1 (THsp) | 0.95 |
| Threshold probability2 (THlp) | 0.75 |
| Length of a side of one unit | 7.592 m |
| Probability variables for high-altitude drone | α = 0.00130, β = 0.34593 [17] |
| Probability variables for low-altitude drone | α = 0.06286, β = 0.20000 [17] |
| Algorithm | Search Method | Total Time (sec) | Total Distance (m) | Comparison (%) |
|---|---|---|---|---|
| High + Low | After high-altitude search, low-altitude search | 1,099,028 | 4,579,283 | 100 |
| Low Linear | Search linearly at low altitude | 2,893,980 | 12,058,251 | 263 |
| High + Low2 | After high-altitude search, low-altitude search (search by one high-altitude area) | 1,673,795 | 6,974,146 | 152 |
| High Linear | Search linearly at high altitude | 1,139,097 | 4,746,240 | 104 |
| High + Low3 (Proposed) | After high-altitude search with threshold value, low-altitude search | 959,327 | 3,997,199 | 87 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, I.-K.; Cho, Y.-Z. A Probabilistic Target Search Algorithm Based on Hierarchical Collaboration for Improving Rapidity of Drones. Sensors 2018, 18, 2535. https://doi.org/10.3390/s18082535
Ha I-K, Cho Y-Z. A Probabilistic Target Search Algorithm Based on Hierarchical Collaboration for Improving Rapidity of Drones. Sensors. 2018; 18(8):2535. https://doi.org/10.3390/s18082535
Chicago/Turabian StyleHa, Il-Kyu, and You-Ze Cho. 2018. "A Probabilistic Target Search Algorithm Based on Hierarchical Collaboration for Improving Rapidity of Drones" Sensors 18, no. 8: 2535. https://doi.org/10.3390/s18082535
APA StyleHa, I.-K., & Cho, Y.-Z. (2018). A Probabilistic Target Search Algorithm Based on Hierarchical Collaboration for Improving Rapidity of Drones. Sensors, 18(8), 2535. https://doi.org/10.3390/s18082535





